Теоретические основы химической технологии, 2019, T. 53, № 2, стр. 146-151
Разделение изотопов никеля в процессе заполнения каскада газовых центрифуг с различным количеством ступеней
А. А. Орлов 1, А. А. Ушаков 2, *, В. П. Совач 2
1 Национальный исследовательский Томский политехнический университет
Томск, Россия
2 АО “ПО "Электрохимический завод”
Красноярский край, Зеленогорск, Россия
* E-mail: ushakovaa2015@sibmail.com
Поступила в редакцию 18.10.2017
После доработки 10.10.2018
Принята к публикации 28.09.2018
Аннотация
Приведены результаты исследования процесса заполнения каскада газовых центрифуг с различным количеством ступеней для случая разделения изотопов никеля, которые используются в ядерно-физических исследованиях и для получения радиоактивных изотопов. В процессе заполнения каскада происходит разделение природной смеси изотопов никеля и концентрирование изотопов в различных ступенях каскада. Показаны концентрации изотопов никеля в ступенях и потоках легкой и тяжелой фракций после заполнения каскада в зависимости от количества ступеней в каскаде.
ВВЕДЕНИЕ
При эксплуатации каскада газовых центрифуг (ГЦ) для разделения многокомпонентных изотопных смесей (МИС) возникают нестационарные гидравлические процессы, в ходе которых изменяются величины давлений и потоков рабочего вещества в ступенях каскадов и выходящих потоках. Нестационарный гидравлический процесс порождает нестационарный разделительный процесс, в ходе которого происходит изменение изотопного состава рабочего вещества в ступенях и потоках каскадов. Во всех нестационарных процессах необходимо обеспечить безопасную эксплуатацию разделительного оборудования и свести к минимуму потери работы разделения. Каскады ГЦ имеют меньшее газосодержание по сравнению с газодиффузионными каскадами, следовательно, и меньшую инерционность. Малая инерционность приводит к усилению влияния нестационарных процессов на эффективность работы каскадов. Особенно это может отразиться на работе каскадов ГЦ для разделения МИС, которые в отличие от каскадов для разделения изотопов урана имеют существенно меньшее количество ГЦ и отличаются регулирующими устройствами.
В связи с этим приобрело актуальность решение задачи изучения и полномасштабного учета нестационарных процессов при разделении МИС. Использование экспериментального подхода к решению данной задачи является достаточно затратным и требует создания дополнительных исследовательских установок. Поэтому целесообразно изучать нестационарные процессы путем их математического моделирования. Известные математические модели [1–4] описывают нестационарные гидравлические процессы для случая длинного каскада и нестационарные разделительные процессы при постоянных гидравлических параметрах. Для устранения указанных недостатков нами была разработана математическая модель нестационарных гидравлических и разделительных процессов [5–7] и проведена ее верификация на примере разделения изотопов германия, криптона и кремния.
Стационарному режиму разделения МИС в каскаде ГЦ предшествует нестационарный процесс, который условно можно разделить на две стадии: 1 – заполнение каскада рабочим веществом, 2 – установление равновесных концентраций компонентов в каскаде. Основное внимание исследователей было приковано ко второй стадии ввиду ее значительной длительности [1–4]. Изучение процесса заполнения каскада до настоящего времени никем не проводилось, поэтому для расчета второй стадии при задании начальных условий использовалось допущение, что концентрации компонентов в ступенях каскада после его заполнения соответствуют их концентрациям в МИС. Учитывая, что от начальных условий зависит характер изменения концентраций компонентов в ходе нестационарного процесса и его длительность [6, 7], целесообразно провести исследование процесса разделения МИС в ходе заполнения каскада и проверить справедливость этого допущения. Ранее в работе [8] установлено, что концентрации изотопов в потоках легкой и тяжелой фракций каскада после его заполнения зависят от величины потока питания каскада.
В данной статье приведены результаты исследований процесса заполнения каскада с различным количеством ступеней для случая разделения изотопов никеля, которые используются в ядерно-физических исследованиях и для получения радиоактивных изотопов (например, изотоп 62Ni используется для получения радиоактивного изотопа 63Ni).
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
Напомним основные уравнения, входящие в математическую модель нестационарного процесса разделения МИС.
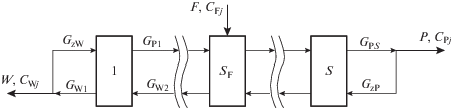
Разделение МИС происходит в каскаде ГЦ. Рабочее вещество содержит n компонентов (изотопов) с индексом j ($j = \overline {1;n} $). Каскад состоит из S ступеней (рис. 1) с индексом i ($i = \overline {1;S} $). Ступени соединены по противоточно-симметричной схеме. В каскад подается поток питания F и отбираются потоки легкой P и тяжелой W фракций. Поток питания подается в ступень с индексом SF, поток тяжелой фракции отбирается из первой ступени, поток легкой фракции – из ступени S.
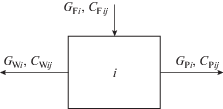
Разделительная ступень состоит из Ni параллельно соединенных ГЦ. В нее подается поток питания GFi. Из ступени отбираются потоки легкой GPi и тяжелой GWi фракций (рис. 2). Концентрация j-го компонента в потоках питания, легкой и тяжелой фракций i-й ступени обозначили CFij, CPij и CWij соответственно. Тяжелая фракция первой ступени может частично возвращаться потоком закрутки тяжелой фракции GzW на питание первой ступени. Легкая фракция ступени S может частично возвращаться потоком закрутки легкой фракции GzP на питание ступени S.
При отсутствии коррозионных потерь рабочего вещества потоки ступеней и концентрации компонентов в них в стационарном гидравлическом режиме связаны уравнениями баланса рабочего вещества и компонента (изотопа):
(2)
${{G}_{{{\text{F}}i}}}{{C}_{{Fij}}} = {{G}_{{{\text{P}}i}}}{{C}_{{{\text{P}}ij}}} + {{G}_{{{\text{W}}i}}}{{C}_{{{\text{W}}ij}}},$Сумма концентраций всех компонентов для любого потока равна единице.
Разделение компонентов в ступени определяется выражениями [9]
где χijl – коэффициент разделения j-го и l-го компонента в i-й ступени; χ0i – коэффициент разделения, приходящийся на единицу разности массовых чисел; Mj, Ml – массовые числа j-го и l-го компонента соответственно, а. е. м.Величина χ0i зависит от гидравлических параметров ступени:
Потоки каскада в стационарном гидравлическом режиме связаны уравнениями баланса:
Методика расчета нестационарных гидравлических и разделительных процессов основана на следующих положениях [5, 6]:
в каждой ступени каскада выделяется конечное число объемов, в которых содержится рабочее вещество;
в любой момент времени температура, давление рабочего вещества и концентрация j-го компонента одинаковы во всем объеме;
основными уравнениями модели являются уравнения баланса рабочего вещества и компонентов в каждом объеме и уравнение разделения МИС в ГЦ.
Выделенный объем V имеет следующие характеристики: давление рабочего вещества p; концентрация j-го компонента Cj; физические свойства рабочего вещества (молярная масса μ, динамическая вязкость η, температура T); масса рабочего вещества (газосодержание объема) H, значение которой определяется величинами V, p, μ и T.
Все газосодержание каскада принято сосредоточенным в 4S объемах: S объемов ГЦ ступени; S объемов коллектора питания; S объемов коллектора легкой фракции; S объемов коллектора тяжелой фракции.
Поступающий в i-ю ступень поток GFi определяется как
(9)
${{G}_{{{\text{F}}i}}} = \left\{ \begin{gathered} {{\delta }_{i}}F + {{G}_{{{\text{zW}}}}} + {{G}_{{{\text{W}}i + 1}}},{\text{ }}i = 1 \hfill \\ {{\delta }_{i}}F + {{G}_{{{\text{P}}i - 1}}} + {{G}_{{{\text{W}}i + 1}}},{\text{ }}i = \overline {2;S - 1} \hfill \\ {{\delta }_{i}}F + {{G}_{{{\text{P}}i - 1}}} + {{G}_{{{\text{zP}}}}},{\text{ }}i = S \hfill \\ \end{gathered} \right.,$(10)
${{\delta }_{i}} = \left\{ \begin{gathered} 1,{\text{ }}i = {{S}_{{\text{F}}}} \hfill \\ 0,{\text{ }}i \ne {{S}_{{\text{F}}}} \hfill \\ \end{gathered} \right.,$Концентрация СFij в потоке GFi определяется выражением
(11)
${{C}_{{{\text{F}}ij}}} = \frac{1}{{{{G}_{{Fi}}}}}\left\{ \begin{gathered} {{\delta }_{i}}F{{C}_{{{\text{F}}j}}} + {{G}_{{{\text{zW}}}}}{{C}_{{{\text{W}}ij}}} + {{G}_{{{\text{W}}i + 1}}}{{C}_{{{\text{W}}i + 1j}}},{\text{ }}i = 1 \hfill \\ {{\delta }_{i}}F{{C}_{{{\text{F}}j}}} + {{G}_{{{\text{P}}i - 1}}}{{C}_{{{\text{P}}i - 1j}}} + {{G}_{{{\text{W}}i + 1}}}{{C}_{{{\text{W}}i + 1j}}},{\text{ }}i = \overline {2;S - 1} \hfill \\ {{\delta }_{i}}F{{C}_{{{\text{F}}j}}} + {{G}_{{{\text{P}}i - 1}}}{{C}_{{{\text{P}}i - 1j}}} + {{G}_{{{\text{zP}}}}}{{C}_{{{\text{P}}ij}}},{\text{ }}i = S \hfill \\ \end{gathered} \right..$Частота вращения роторов ГЦ и температурный режим их работы не изменяются.
Алгоритм решения дифференциальных уравнений, описывающих нестационарные гидравлические и разделительные процессы, приведен в работах [5, 6].
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Рассмотрен каскад постоянной ширины, имеющий одинаковую производительность GF всех ступеней в стационарном режиме. В качестве рабочего вещества для разделения изотопов никеля использовался тетракис (трифторфосфин) никеля (Ni(PF3)4, молярная масса μ ≈ 411 кг/кмоль). Коэффициент разделения ГЦ – χ0 = 1.1. Количество ступеней каскада S принималось равным 20, 60 и 100. Поток питания подавался в ступень средней части каскада (SF = 0.5S). Изотопный состав исходного тетракиса никеля приведен в табл. 1.
Таблица 1.
Изотопный состав исходного тетракиса никеля
| M, а.е.м. | 58 | 60 | 61 | 62 | 64 |
| CF, % | 68.0769 | 26.2231 | 1.1399 | 3.6345 | 0.9256 |
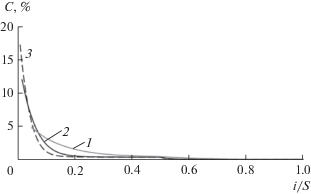
В начальный момент времени каскад пуст (газосодержание равно нулю). В процессе заполнения в каскад подается поток питания постоянной величины, величины потоков легкой и тяжелой фракций каскада равны нулю. В ходе заполнения происходит увеличение давлений, газосодержаний и потоков рабочего вещества в ступенях каскада до стационарных значений. Проведено моделирование процесса заполнения каскада, состоящего из различного числа ступеней. На рис. 3 и 4 приведены концентрации изотопов никеля в потоках легкой и тяжелой фракций каскада после его заполнения в зависимости от количества ступеней в каскаде S.
Рис. 3.
Концентрация изотопа 58Ni в потоке легкой фракции каскада после его заполнения в зависимости от количества ступеней каскада.
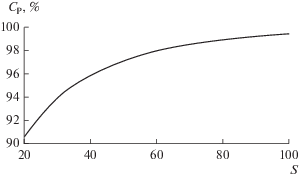
Рис. 4.
Концентрация изотопов никеля в потоке тяжелой фракции каскада после его заполнения в зависимости от количества ступеней каскада: 1 – 58Ni, 2 – 60Ni, 3 – 61Ni, 4 – 62Ni, 5 – 64Ni.
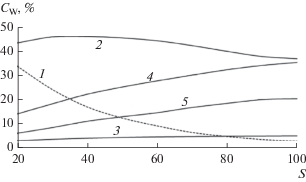
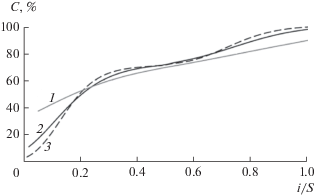
Концентрация изотопов никеля в потоках легкой и тяжелой фракций каскада после его заполнения зависит от количества ступеней каскада. Изотоп 58Ni является самым легким компонентом в природной смеси изотопов никеля. В процессе заполнения каскада и подачи природного никеля в середину каскада изотоп переносится в направлении отбора легкой фракции и накапливается в ступени i = S. При этом происходит увеличение концентрации данного изотопа в потоке легкой фракции и снижение его концентрации в потоке тяжелой фракции каскада. С увеличением длины каскада происходит интенсификация этого процесса и рост градиента концентрации 58Ni по каскаду (рис. 5). Концентрация 58Ni в потоке легкой фракции возрастает с 90.6 до 99.4% при увеличении количества ступеней каскада в 5 раз (с 20 до 100). При этом значительного роста концентрации этого изотопа в ступенях от подачи потока питания (i/S = 0.5) до отбора легкой фракции (i/S = 1) не происходит, что объясняется повышением влияния процесса смешения потока питания каскада и межступенных потоков, подаваемых в ступень i/S = 0.5 и имеющих различный изотопный состав (отличное друг от друга содержание изотопов никеля). В результате концентрация 58Ni в ступени i/S = 0.5 не превышает 72% при концентрации данного изотопа в природном никеле около 68.1%.
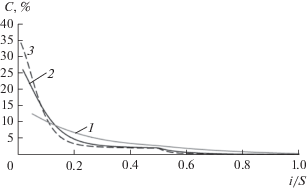
Аналогичные особенности наблюдаются для переноса изотопа 64Ni, который имея наибольшее массовое число из смеси изотопов природного никеля, концентрируется в ступени i = 1 за счет переноса из ступеней каскада в процессе заполнения (рис. 6). Это позволяет сконцентрировать в концевых ступенях каскада (i/S < 0.2) изотоп 64Ni в количестве до 86% относительно суммарного количества данного изотопа в каскаде и повысить его концентрацию не менее чем в 22 раза относительно значения в природном никеле и получить никель, обогащенный по 64Ni до 20.3%.
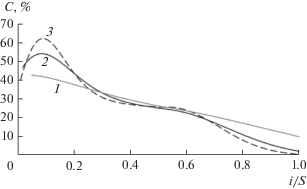
Изотоп 62Ni имеет максимальную концентрацию в ступени отбора тяжелой фракции i = 1 независимо от количества ступеней каскада (рис. 7) и несмотря на то, что в природной смеси присутствует изотоп с большим массовым числом 64Ni. Однако концентрация 64Ni в природной смеси и количество в каскаде существенно меньше по сравнению с изотопом 62Ni, в результате чего в процессе заполнения 62Ni имеет максимальную концентрацию в отборе тяжелой фракции каскада. Увеличение длины каскада приводит к росту максимальной концентрации 62Ni, которое обусловлено переносом этого изотопа в направлении отбора тяжелой фракции в процессе заполнения каскада природным никелем.
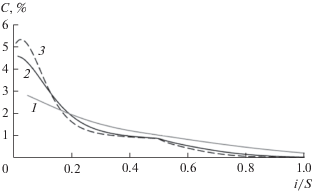
Другие изотопы никеля с промежуточным массовым числом (60Ni и 61Ni) после подачи в каскад концентрируются в средней части каскада (рис. 8 и 9). При этом максимум концентрации этих изотопов в каскаде смещается в направлении отбора легкой фракции каскада при увеличении количества ступеней в каскаде, что объясняется концентрированием в данной ступени изотопов 62Ni и 64Ni при одновременном уменьшении концентрации 58Ni и, как следствие, ростом средневзвешенного массового числа смеси изотопов никеля. Максимальные концентрации 60Ni и 61Ni наблюдаются в ступенях, в которых средневзвешенное массовое число изотопной смеси равно массовым числам данных изотопов. Как видно из рис. 8 и 9, при увеличении количества ступеней в каскаде с 20 до 100 происходит рост максимума концентрации 60Ni и 61Ni с 40.3 и 5.1% до 62.2 и 5.3% соответственно и смещение его положения из ступени i = 1 в ступень i = 9 и i = 3. Эти особенности переноса изотопов 60Ni и 61Ni внутри каскада в ходе его заполнения объясняют характер изменения их концентраций в потоке тяжелой фракции.
Полученные результаты позволяют сделать вывод, что в процессе заполнения каскада ГЦ исходной изотопной смесью происходит разделение изотопов, в результате которого изотопы распределяются по длине каскада в соответствии с их массовыми числами и при увеличении количества ступеней каскада происходит увеличение максимальных концентраций изотопов никеля в ступенях каскада.
При расчете такого нестационарного разделительного процесса, как вывод каскада на режим, используется допущение, что после заполнения каскада концентрации изотопов в ступенях соответствуют концентрациям в исходной смеси. Результаты проведенного исследования показывают, что концентрации изотопов никеля в каскаде после заполнения находятся в широком диапазоне значений, в результате чего можно сделать вывод, что указанное выше допущение является достаточно грубым приближением.
В табл. 2 приведены параметры нестационарного процесса накопления 58Ni до концентрации в потоке легкой фракции 95% и длительность этого процесса τ [6] при различных начальных условиях: вариант № 1 – концентрации изотопов никеля в ступенях каскада определяются из расчета процесса заполнения; вариант № 2 – концентрации изотопов никеля в ступенях каскада соответствуют их значениям в исходной смеси (потоке питания каскада).
Таблица 2.
Параметры процесса накопления 58Ni в каскаде
| S | F/GF | P/F | τ | |
|---|---|---|---|---|
| вариант № 1 | вариант № 2 | |||
| 20 | 0.147 | 0.223 | 38.7 | 45.3 |
| 60 | 0.147 | 0.503 | 0.0 | 171.5 |
| 100 | 0.147 | 0.527 | 0.0 | 237.1 |
Как видно из табл. 2, для варианта № 2 увеличение количества ступеней каскада приводит к увеличению его газосодержания и, как следствие, требуется накопить в каскаде большее количество целевого изотопа 58Ni. При неизменной величине потока питания каскада процесс накопления будет иметь большую длительность для каскада, состоящего из большего числа ступеней.
При проведении моделирования процесса заполнения каскада и использовании начальных условий варианта № 1 длительность процесса накопления целевого изотопа 58Ni уменьшается с 45.3 до 38.7 для каскада, состоящего из 20 ступеней. При большем количестве ступеней в составе каскада длительность нестационарного процесса накопления равна нулю, что обусловлено накоплением в S-й ступени к концу заполнения каскада 58Ni с концентрацией выше 95% (рис. 5). В этом случае после окончания заполнения каскада устанавливается стационарное значение потока легкой фракции, в котором концентрация 58Ni асимптотически снижается с 97–99 до 95.1%.
Таким образом, использование начальных условий, когда концентрации изотопов никеля в ступенях каскада соответствуют их значениям в исходной смеси (потоке питания каскада), приводит к значительной переоценке длительности нестационарного процесса накопления целевого изотопа в каскаде. Моделирование процесса заполнения каскада позволяет уточнить динамику концентрации целевого изотопа в выходящем потоке каскада и длительность нестационарного процесса накопления.
ЗАКЛЮЧЕНИЕ
Проведено исследование процесса заполнения каскада с различным количеством ступеней для разделения изотопов никеля с использованием разработанной ранее математической модели нестационарных процессов. Изотопы никеля распределяются по каскаду в соответствии с их массовыми числами независимо от количества ступеней каскада. Увеличение числа ступеней в каскаде приводит к повышению максимальных значений концентраций изотопов в каскаде. Установлено, что концентрации изотопов никеля в потоках легкой и тяжелой фракций после заполнения каскада зависят от количества ступеней в каскаде. Концентрации изотопов никеля в каскаде после заполнения находятся в широком диапазоне значений, в результате чего можно сделать вывод, что использование допущения о равенстве концентраций изотопов в ступенях их значениям в потоке питания каскада приводит к отклонению расчетной динамики изменения концентраций в ходе дальнейшего нестационарного процесса от экспериментальных данных.
Работа была поддержана Программой повышения конкурентоспособности Томского политехнического университета (проект CEP-PTI-72/2017).
ОБОЗНАЧЕНИЯ
| C | концентрация, % |
| F | поток питания каскада, кг/с |
| G | поток, кг/с |
| H | газосодержание (количество рабочего вещества), кг |
| M | массовое число, а.е.м. |
| n | количество компонентов смеси |
| P | поток легкой фракции каскада, кг/с |
| p | давление, Па |
| S | количество ступеней каскада |
| T | температура, К |
| V | объем, м3 |
| W | поток тяжелой фракции каскада, кг/с |
| δ | коэффициент наличия потока питания каскада в ступень |
| η | динамическая вязкость, кг м–1 с–1 |
| θ | коэффициент деления потока |
| μ | молярная масса, кг/кмоль |
| τ | безразмерная длительность нестационарного процесса |
| χ | коэффициент разделения |
ИНДЕКСЫ
Список литературы
Левин Д.М., Забелин Ю.П. Распространение динамических возмущений в каскаде для разделения изотопов // Сб. тр. XII Межд. науч. конф. “Физико-химические процессы при селекции атомов и молекул и в лазерных, плазменных и нанотехнологиях”. М., 2008. С. 417.
Левин Е.В., Лагунцов Н.И., Сулаберидзе Г.А. Об одном методе численного исследования нестационарных процессов в многосекционных установках для разделения многокомпонентных изотопных смесей // Инж.-физ. журн. 1982. Т. 43. № 3. С. 456.
Вецко В.М., Девдариани О.А., Левин Е.В. и др. Моделирование переходных процессов в каскадных установках для разделения многокомпонентных изотопных смесей стабильных изотопов // Isotopenpraxis. 1982. V. 18. № 8. P. 288.
Smirnov A.Yu., Bonarev A.K., Sulaberidze G.A. et al. Peculiarities of the transient processes in cascades for separation of isotope mixtures with various numbers of components // Journal of Physics: Conference Series. 2016. V. 751. Article 012006.
Orlov A.A., Ushakov A.A., Sovach V.P. Mathematical model of nonstationary hydraulic processes in gas centrifuge cascade for separation of multicomponent isotope mixtures // MATEC Web of Conf. 2017. V. 92. Article 01033.
Orlov A.A., Ushakov A.A., Sovach V.P., Malyugin D.V. Mathematical modeling of nonstationary separation processes in a cascade of gas centrifuges in for separation of tungsten isotopes // J. Eng. Phys. Thermophys. 2018. V. 91. № 3. P. 565. [Орлов А.А., Ушаков А.А., Совач В.П., Малюгин Р.В. Математическое моделирование нестационарных разделительных процессов в каскаде газовых центрифуг для разделения изотопов вольфрама // Инж.-физ. журн. 2018. Т. 91. № 3. С. 605.]
Орлов А.А., Ушаков А.А., Совач В.П. Математическое моделирование нестационарных разделительных процессов в каскаде газовых центрифуг для разделения изотопов криптона // Вопросы атомной науки и техники. Серия Матем. модел. физ. процессов. 2017. № 3. С. 51.
Ushakov A.A., Orlov A.A., Sovach V.P. Mathematical modeling of filling of gas centrifuge cascade for nickel isotope separation by various feed flow rate // AIP Conference Proceedings. 2018. V. 1938. Article 020017.
Shmelev A.N., Smirnov A.Yu., Bonarev A.K., Borisevich V.D., Kulikov G.G., Sulaberidze G.A. Isotopically modified molybdenum for safe nuclear power // Theor. Found. Сhem. Eng. 2016. V. 50. № 6. P. 1049. [Шмелев А.Н., Смирнов А.Ю., Бонарев А.К., Борисевич В.Д., Куликов Г.Г., Сулаберидзе Г.А. Изотопомодифицированный молибден для безопасной ядерной энергетики // Теорет. основы хим. технологии. 2016. Т. 50. № 6. С. 663.]
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии