1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 53, № 3, 2019

Теоретические основы химической технологии, 2019, T. 53, № 3, стр. 324-337

Способ получения высокодисперсных жидкокапельных систем в ультразвуковых полях

В. Н. Хмелев 1, А. В. Шалунов 1, Р. Н. Голых 1, *, Р. С. Доровских 1, В. А. Нестеров 1

1 Бийский технологический институт (филиал), Алтайский государственный технический университет им. И.И. Ползунова
Бийск, Россия

* E-mail: grn@bti.secna.ru

Поступила в редакцию 30.05.2017
После доработки 20.03.2018
Принята к публикации 10.04.2018

Полный текст (PDF)

Аннотация

Статья посвящена теоретическим исследованиям процесса двухстадийного высокодисперсного распыления жидкостей, состоящего из первичного образования крупных капель при ультразвуковом воздействии на тонкую пленку жидкости и вторичного распада полученных капель под действием высокочастотного акустического поля в воздушно-капельной среде. Выявлен физический механизм и предложена физико-математическая модель распада капель, позволившая определить пороговые уровни звукового давления при различных размерах капель, свойствах распыляемой жидкости и типах воздействия. Установлено, что наиболее эффективный способ акустического воздействия состоит в излучении последовательности разночастотных импульсов при высокой концентрации аэрозоля (более 10 об. %), создающей условия для межмодовой дисперсии. Показано, что при воздействии непрерывных моночастотных колебаний мощность излучателя, необходимая для распада капель, может превышать 550 кВт. При импульсном воздействии требуемая мощность снижается до 2 кВт при площади излучающей поверхности 800 см2.

Ключевые слова: ультразвук, распыление, жидкокапельные системы, производительность, уровень звукового давления, оптимальные режимы

ВВЕДЕНИЕ

Применение гетерогенных систем с высокодисперсной жидкой фазой является перспективным направлением обеззараживания помещений, нейтрализации опасных аэрозолей, создания новых и повышения энергетических показателей существующих видов топлив, сушки различных материалов и т.д.

Эффективность применения гетерогенных систем с высокодисперсной жидкой фазой для решения различных задач [1–4] обусловлена, в первую очередь, большой удельно-массовой поверхностью раздела фаз по сравнению с системами, имеющими пленочную или пенообразную структуру.

Известно, что распыление даже 2 мл дезинфицирующего аэрозоля, содержащего 0.16 об. % полигексаметиленгуанидина гидрохлорид и 0.03 об. % дидецилдиметиламмония хлорид (“Аэрон”), обеспечивает обеззараживание 1 м3 воздуха. Другой пример – диспергирование даже 1% воды [3] в углеводородном топливе (бензин, дизель, топочный мазут и т.д.) обеспечивает повышение коэффициента полезного действия (КПД) двигателей внутреннего сгорания и форсуночных горелок более чем на 5% (при размере капель эмульсии 2–3 мкм).

На сегодняшний день основные применяемые способы создания дисперсной фазы в жидкостях или газах основаны либо на введении вспомогательных веществ – поверхностно-активных веществ (ПАВ) или эмульгаторов, либо на гидродинамических явлениях – механические, гидродинамические (форсунки), роторно-импульсные [4] и т.д., разработанные еще в конце 19-го–начале 20-го в. Однако наиболее распространенные на сегодняшний день способы позволяют эффективно создавать лишь достаточно грубодисперсные системы с размерами капель более 100 мкм. Попытки создания высокодисперсных систем (с размерами капель менее 10 мкм) с помощью традиционных способов приводили к непропорциональному возрастанию энергозатрат (КПД процесса диспергирования оказывался меньше 0.1%) или вторичной коагуляции капель.

Один из наиболее перспективных подходов к формированию жидкой дисперсной фазы – низкочастотное ультразвуковое (УЗ) воздействие (на частотах 22–250 кГц), позволяющее осуществлять диспергирование жидкости как в газовой несущей фазе (распыление), так и в другой жидкости (эмульгирование).

УЗ-диспергирование обладает такими преимуществами, как отсутствие необходимости в использовании вспомогательных веществ (эмульгаторов, ПАВ или распыляющих агентов), возможность диспергирования высоковязких жидкостей, малый разброс размеров формируемых капель относительно среднего значения, высокий КПД процесса.

О перспективности указанного способа формирования жидких дисперсных капель свидетельствует значительное число публикаций [5–17], посвященных установлению зависимостей дисперсных характеристик формируемых капель, как в жидкой (эмульсия), так и газовой фазе (аэрозоль) от режимов ультразвукового воздействия.

Однако, несмотря на перечисленные преимущества и большое внимание со стороны исследователей [1–3, 5–17], ультразвуковое диспергирование не получило достаточно широкого распространения в промышленности. Это связано с необходимостью решения двух взаимоисключающих задач – обеспечения высокой производительности и, одновременно, высокой дисперсности формируемой капельной жидкости. При этом производительность, согласно полученным ранее теоретическим и экспериментальным результатам [5–17], является обратно пропорциональной размеру капель и оказывается недостаточной для промышленного применения при формировании высокодисперсных капель.

На сегодняшний день максимально достигнутая производительность получения капель размером 60–100 мкм составляет 1 т/ч за счет использования УЗ-излучателей с увеличенной площадью поверхности (до 800 см2) [18, 19], а капель размером менее 10 мкм – не более 4 л/ч.

Столь малая производительность формирования высокодисперсных капель связана в первую очередь с тем, что УЗ-воздействие осуществлялось в кавитационном режиме, когда под действием кавитации происходит отрыв капель со свободной поверхности жидкости, граничащей с газовой фазой (распыление) или другой жидкостью (эмульгирование).

При возникновении кавитации в диспергируемой жидкой фазе непосредственно на перевод жидкости в дисперсное состояние уходит малая доля энергии колебаний (менее 1%). При этом большая часть энергии затрачивается на нагрев жидкости из-за локальных повышений температуры в микроскопических ядрах кавитационных пузырьков до 5000 К (в момент схлопывания) [2, 3].

Таким образом, актуальной является задача поиска и научного обоснования новых способов формированию высокодисперсной жидкой фазы с увеличенной производительностью в УЗ-полях.

Цель работы – создание высокопроизводительного способа получения высокодисперсных жидкокапельных систем на базе теоретических исследований формирования капель в высокоинтенсивных ультразвуковых полях.

СПОСОБ ФОРМИРОВАНИЯ ВЫСОКОДИСПЕРСНОЙ ЖИДКОЙ ФАЗЫ В УЛЬТРАЗВУКОВЫХ ПОЛЯХ

Недостаточная производительность УЗ-диспергирования при формировании высокодисперсных капель связана, в первую очередь, с тем, что диспергирование состоит из одной стадии, заключающейся в отрыве капли от поверхности раздела слоя диспергируемой жидкой фазы и несущей среды.

При применении известных подходов для формирования высокодисперсных жидких капель требуются частоты колебаний вплоть до 5 МГц [5, 7, 8, 20]. Однако высокочастотные колебания ограничивают площадь излучающей поверхности, быстро затухают в диспергируемой жидкости и интенсивно поглощаются в материале ультразвукового излучателя. Таким образом, обеспечить высокую производительность диспергирования при высокой дисперсности с помощью УЗ-воздействия принципиально невозможно в рамках одной стадии.

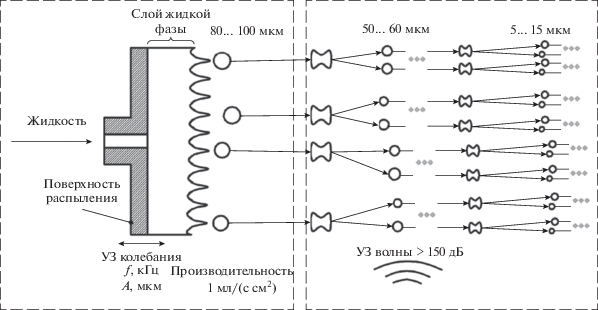
Поэтому предлагается многостадийный способ ультразвукового диспергирования жидкостей. Согласно предлагаемому способу на первой стадии с поверхности раздела слоя диспергируемой жидкости и несущей среды формируются крупные капли под воздействием низкочастотных УЗ-колебаний (20–30 кГц). Диаметр формируемых капель определяется профилем капиллярных волн, формируемых на поверхности слоя жидкости под действием кавитации, создаваемой низкочастотным УЗ-воздействием. Влияние режимов УЗ-воздействия на профиль капиллярных волн и, как следствие, на диаметр капель наиболее полно исследовано в работах Р.Дж. Ланга, Ю.Я. Богуславского, О.К. Экнадиосянца [21, 22]. Указанными авторами получено следующее выражение для диаметра капель, формируемых с поверхности слоя жидкости, и производительности диспергирования по массе жидкости, отделяемой с единицы поверхности в единицу времени:

(1)
${{D}_{1}} = 0.34\lambda = 0.34\sqrt[3]{{\frac{{8\pi \sigma }}{{\rho {{f}^{2}}}}}},$
(2)
${{\Pi }_{1}} = 2\frac{f}{{{{\lambda }^{2}}}}\pi \frac{{D_{1}^{3}}}{6},$
где λ – длина капиллярной волны, м; f – частота УЗ-колебаний, Гц; σ – поверхностное натяжение диспергируемой жидкости на границе раздела с газовой фазой или другой жидкостью, Н/м; ρ – плотность жидкости, кг/м3; D1 – диаметр капель, м; Π1 – удельная производительность диспергирования, м3/(м с).

Дисперсная фаза, сформированная на первой стадии и находящаяся во взвешенном состоянии в несущей среде, подвергается воздействию ультразвукового поля со стороны несущей среды. За счет этого капли деформируются и разрушаются, а дисперсный состав капель претерпевает дальнейшую эволюцию. Описанный процесс повторяется для каждой из вновь образовавшихся капель многократно, как показано на рис. 1.

Рис. 1.

Способ высокопроизводительного формирования высокодисперсных капель в УЗ-полях.

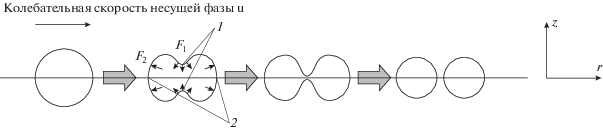
На стадии деформации капли под действием потока несущей среды происходит цилиндрически симметричное изменение формы стенки капли относительно оси, направление которой совпадает с направлением УЗ-колебаний. В свою очередь изменение формы капли связано с образованием капиллярных волн на ее поверхности. Формирование капиллярных волн на поверхности раздела газа и жидкости или двух несмешивающихся жидкостей широко исследовано в работах Дж.У. Стрэтта (лорда Релея), Ю.Я. Богуславского, О.К. Экнадиосянца и др. и вызвано чередованием максимумов и минимумов сил поверхностного натяжения из-за закона сохранения массы жидкости, составляющей объем капли. Разность сил между соседними точками максимума F1 и минимума поверхностного натяжения F2 приводит к перетеканию жидкости из зон наибольшей кривизны поверхности в зоны наименьшей кривизны. В результате этого максимумы и минимумы сил поверхностного натяжения меняются местами. Далее процесс периодически повторяется.

Поскольку капля изначально имеет сферическую форму, возмущение стенок капли имеет характер радиальных капиллярных волн с профилем R(θ), где R – длина радиуса вектора r точки стенки капли, равная $\sqrt {{{r}^{2}} + {{z}^{2}},} $ θ – полярный угол – угол между радиусом-вектором r и осью z.

При углах θ = 0; θ = π ввиду симметричности деформации капли справедливы условия $\frac{{\partial R}}{{\partial \theta }} = 0,$ аналогичные условиям отражения волн. Поэтому радиальные капиллярные волны на поверхности капли являются стоячими. При этом в пределах половины длины окружности капли должно укладываться целое число волн. Согласно ранее проведенным исследованиям [20] наибольшую амплитуду имеет волна, длина которой равна половине длины окружности капли.

Таким образом, капля в результате деформации капля приобретает форму “гантели”. Когда величина деформации капли $\mathop {\max }\limits_{{\theta } \notin \left[ {0;{\pi }} \right]} \left| {R\left( \theta \right) - \frac{D}{2}} \right|$ превышает критическое значение, равное

(3)
$\mathop {\max }\limits_{{\theta } \notin \left[ {0;{\pi }} \right]} \left| {R\left( \theta \right) - \frac{D}{2}} \right| \geqslant \frac{D}{4},$
где D – диаметр исходной капли, м; на центральном участке “гантели” 1 (см. рис. 2) начинается дальнейшее лавинообразное уменьшение его толщины. Наступает следующая стадия разрушения капли.

Рис. 2.

Схематичное изображение процесса деформации и разрушения капли в УЗ-поле.

Так как длина капиллярной волны на поверхности капли совпадает с половиной длины окружности капли, в результате разрушения одной капли диаметром D и массой m образуется две одинаковых капли диаметром $\frac{D}{{\sqrt[3]{2}}}$ и массой $\frac{m}{2}.$

Затем для каждой из двух вновь образованных капель цикл деформации–разрушения повторяется.

Предлагаемый способ диспергирования позволяет в несколько раз увеличить производительность формирования высокодисперсной жидкой фазы по сравнению с одностадийным диспергированием в кавитационном режиме за счет:

1) возможности получения требуемого размера мелких капель (менее 10 мкм) из полученных при первичном диспергировании крупных капель (40–80 мкм). Согласно ранее проведенным исследованиям [5–17], диспергирование крупных капель характеризуется до 200 раз большей производительностью по сравнению с мелкими. При этом дробление крупных капель на мелкие займет не более чем несколько десятков периодов УЗ-колебаний (не более 0.2 с).

2) сохранения производительности диспергирования при дроблении крупных капель на мелкие в рамках 2-й стадии ввиду закона сохранения массы, выполняющегося для каждого элементарного акта дробления капель:

(4)
$\begin{gathered} \sum\limits_{i \in {{D}_{2}}} {{{m}_{{2i}}}} = \sum\limits_{i \in {{D}_{1}}} {{{m}_{{2i}}}} + \sum\limits_{i \in D_{1}^{'}} {{{m}_{{2i}}}} = \sum\limits_{i \in {{D}_{1}}} {\frac{{{{m}_{{1i}}}}}{2}} + \\ + \,\,\sum\limits_{i \in D_{1}^{'}} {\frac{{{{m}_{{1\left( {i - {{N}_{{before}}}} \right)}}}}}{2}} = \sum\limits_{i \in {{D}_{1}}} {\frac{{{{m}_{{1i}}}}}{2}} + \sum\limits_{i \in {{D}_{1}}} {\frac{{{{m}_{{1i}}}}}{2}} = \sum\limits_{i \in {{D}_{1}}} {{{m}_{{1i}}}} , \\ \end{gathered} $
где D1 = N∩[1; Nbefore] – множество номеров капель до момента дробления; ${{D}_{2}} = {{D}_{1}} \cup D_{1}^{'},$ $D_{1}^{'}$ = = $\left\{ {\left. j \right|\exists i \in {{D}_{1}};\,\,j = i + {{N}_{{before}}}} \right\}$– множество номеров капель после момента дробления; m1i – масса капли с номером i перед дроблением, кг; ${{m}_{{2i}}}$ = = $\frac{{{{m}_{{1\left( {\left( {i - 1} \right)\bmod {{N}_{{before}}} + 1} \right)}}}}}{2}$ – масса капли, образованной после дробления, с номером i, кг; Nbefore – количество исходных капель, подвергаемых дроблению.

Кроме того, двухстадийный способ будет требовать меньших энергозатрат на формирование дисперсной фазы по сравнению с одностадийным за счет малой энергии, требуемой для предварительной генерации грубодисперсных капель, и бескавитационного воздействия УЗ-колебаний на второй стадии диспергирования.

Для подтверждения данного факта были проведены сравнительные оценки энергозатрат на формирование капель при помощи одностадийного и двухстадийного способа согласно следующему выражению:

(5)
$\begin{gathered} \varepsilon = \frac{{{{E}_{2}}}}{{{{E}_{1}}}} = \frac{{\frac{{\sigma \frac{{3V}}{{{{d}_{1}}}}}}{{{{K}_{1}}\left( {f_{1}^{'}} \right)}} + \frac{{3\sigma V\left( {\frac{1}{{{{d}_{2}}}} - \frac{1}{{{{d}_{1}}}}} \right)}}{{{{K}_{2}}\left( {f_{2}^{'}} \right)}}}}{{\frac{{\sigma \frac{{3V}}{{{{d}_{2}}}}}}{{{{K}_{1}}\left( {{{f}_{1}}} \right)}}}} = \\ = \frac{{{{d}_{2}}}}{{{{d}_{1}}}}\frac{{{{K}_{1}}\left( {{{f}_{1}}} \right)}}{{{{K}_{1}}\left( {f_{1}^{'}} \right)}} + \frac{{{{K}_{1}}\left( {{{f}_{1}}} \right)}}{{{{K}_{2}}\left( {f_{2}^{'}} \right)}}\left( {1 - \frac{{{{d}_{2}}}}{{{{d}_{1}}}}} \right), \\ \end{gathered} $
где E2 – энергия, требуемая для двухстадийного распыления жидкости заданного объема V (м3) на капли диаметром d2, Дж; E1 – энергия, требуемая для одностадийного распыления (в слое) жидкости заданного объема V на капли диаметром d2, Дж; σ – поверхностное натяжение распыляемой жидкости, Н/м; K1(f) – коэффициент преобразования энергии ультразвуковых колебаний в отрыв капель от слоя жидкости; K2(f) – коэффициент преобразования энергии ультразвуковых колебаний во вторичный распад капель, взвешенных в воздухе; f1 – частота колебаний распылительной поверхности, необходимая для отрыва капель диаметром d2 от слоя жидкости, Гц; $f_{1}^{'}$ – частота колебаний распылительной поверхности, необходимая для отрыва капель диаметром d1 от слоя жидкости, Гц; f2 – частота колебаний в воздушной среде, необходимая для разрушения капель диаметром d1 до капель диаметром d2, Гц.

Входящий в выражение (5) коэффициент преобразования K1 энергии ультразвуковых колебаний в отрыв капель от поверхности диспергируемой жидкости (КПД диспергирования) не превышает 0.003 [23] и снижается с уменьшением диаметра капель, требующим повышения частоты воздействия, т.е. K1(f1) < K1($f_{1}^{'}$).

Коэффициент преобразования K2 энергии ультразвуковых колебаний во вторичное разрушение уже сформированных капель близок к 1, поскольку не требуется энергия на создание кавитации, а потери на вязкое трение пренебрежимо малы, так как вязкость диспергируемых жидкостей, используемых на практике, не превышает 50 мПа с.

Таким образом, относительные энергозатраты, требуемые для формирования капель при двухстадийном способе диспергирования, по сравнению с одностадийным способом составляют

$\varepsilon < \frac{{{{d}_{2}}}}{{{{d}_{1}}}} + \frac{{{{K}_{1}}\left( {{{f}_{1}}} \right)}}{{{{K}_{2}}\left( {f_{2}^{'}} \right)}} = \frac{{10\;{\text{м к м }}}}{{80\;{\text{м к м }}}} + \frac{{0.003}}{1} = 0.128,$

т.е. энергия, требуемая для получения жидкокапельной системы с заданным диаметром капель и производительностью двухстадийным способом диспергирования, более чем в 7 раз меньше энергии, требуемой для одностадийного способа.

Для обеспечения максимальной эффективности предлагаемого двухстадийного способа необходимо выявление оптимальных режимов УЗ-воздействия на основе комплексных теоретических исследований процессов возбуждения колебаний стенок капель и эволюции дисперсной фазы в УЗ-полях.

Далее описана предложенная физико-математическая модель колебаний стенок капель, возбуждаемых под воздействием высокоинтенсивных УЗ-полей.

ФИЗИКО-МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВОЗБУЖДЕНИЯ КОЛЕБАНИЙ СТЕНОК КАПЕЛЬ В УЛЬТРАЗВУКОВЫХ ПОЛЯХ

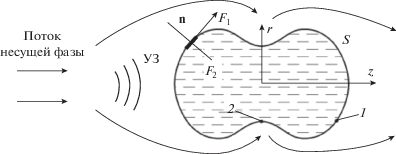
Модель основана на расчете движения жидкости в объеме капли под действием следующих сил (рис. 3) [20]: перепада давления в колеблющемся потоке несущей фазы (Fp), разности сил поверхностного натяжения при волнообразных возмущениях стенки капли (Fs.t), сил вязких напряжений при движении стенок с ненулевой скоростью (Fv).

Рис. 3.

Схематичное изображение деформации капли в УЗ-поле: n – вектор нормали к стенке капли; S – поверхность капли; r, z – оси цилиндрических координат.

Для расчета изменения формы колебаний капли был использован численный метод решеточных уравнений Больцмана [24], основанный на рассмотрении течения жидкости как движения ансамбля псевдочастиц, имеющих некоторую функцию распределения по дискретным скоростям Nk(x, t). Nk(x, t)dx – число псевдочастиц, имеющих скорость ck и находящихся в объеме dx. При этом скорости ck выбираются таким образом, чтобы за шаг по времени Δt частицы переместились в соседние узлы пространственной решетки, вектора которой удовлетворяют условию ek = ckΔt.

При этом концентрации псевдочастиц жидкости на каждом шаге по времени рассчитываются согласно выражению

(6)
$\begin{gathered} {{N}_{k}}\left( {\left( {r + {{c}_{{kr}}}\Delta t} \right){cos\theta },\left( {r + {{c}_{{kr}}}\Delta t} \right){sin\theta },z + } \right. \\ \left. { + \,\,{{c}_{{kz}}}\Delta t,t + \Delta t} \right) = {{N}_{k}}\left( {r{cos\theta },r{sin\theta },z,t} \right) + \\ + \,\,\Omega \left( {{{N}_{k}}} \right) + \Delta {{N}_{k}}, \\ \end{gathered} $
где Ω – оператор столкновений; ΔNk – изменение концентрации частиц за счет действия объемных сил, м–3; r; z, θ – цилиндрические координаты точки поверхности деформированной капли.

Анализ численной модели распада капель позволяет определить величину их максимальной деформации по формуле

(7)
$x = \mathop {{\text{max}}}\limits_{{\theta } \in \left[ {0;{\pi }} \right]} \sqrt {{{{\left( {\frac{d}{2}{sin\theta } - r\left( {\theta } \right)} \right)}}^{2}} + {{{\left( {\frac{d}{2}{cos\theta } - z\left( {\theta } \right)} \right)}}^{2}}} ,$
где d – начальный диаметр капли, м.

Максимальная деформация определяет возможность распада капли. Критерием распада капли служит условие x > d/4, когда число Вебера превышает критическое значение We > Wecr = 6 (силы поверхностного натяжения в центральной области капли 1 превышают силы поверхностного натяжения в периферийной области 2 (см. рис. 3) из-за локального утоньшения капли) [20].

Очевидно, что максимальная деформация капли пропорциональна вводимой энергии колебаний. Поэтому для распада капли энергия колебаний должна превышать некоторое пороговое значение, при котором x = d/4.

На рис. 4, 5 представлены зависимости минимальной энергии УЗ-поля (отношение интенсивности колебаний к скорости звука в несущей фазе Emin = I/c), необходимой для реализации элементарного акта распада капель, при воздействии синусоидальных колебаний одной частоты.

Рис. 4.

Зависимости энергии УЗ-поля от диаметра капель при различных вязкостях жидкости (частота 22 кГц): 1 – 1; 2 – 2; 3 – 3; 4 – 5; 5 – 7; 6 – 10, 7 – 15, 8 – 20, 9 – 30 мПа с; (а) – 20; (б) – 40 мН/м.

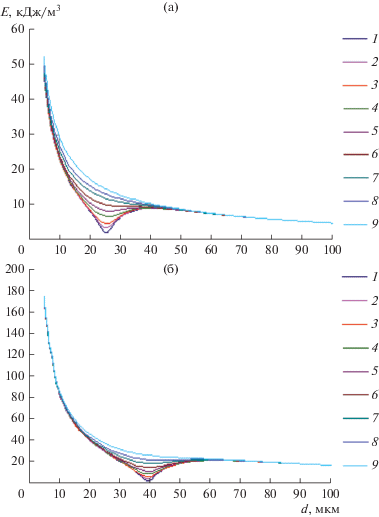
Рис. 5.

Зависимости энергии УЗ-поля от диаметра капель при различных вязкостях жидкости (частота 44 кГц): 1 – 1; 2 – 2; 3 – 3; 4 – 5; 5 – 7; 6 – 10, 7 – 15, 8 – 20, 9 – 30 мПа с; (а) – 20; (б) – 40 мН/м.

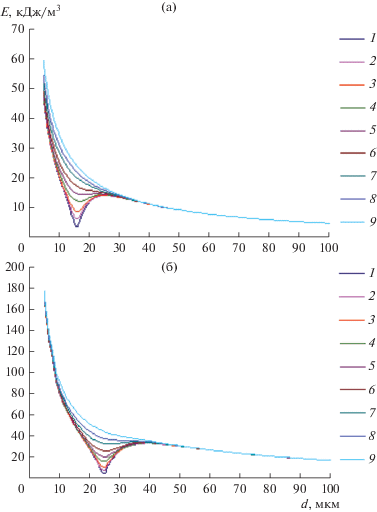
Из полученных зависимостей (рис. 4, 5) следует, что существуют диаметры, при которых энергия колебаний, необходимая для распада капли, достигает локального минимума (менее 10 кДж/м3). Эти диаметры являются резонансными диаметрами при заданных свойствах жидкости. Однако на практике непрерывно воздействовать на частотах, соответствующих резонансным диаметрам капель, невозможно, поскольку диаметр непрерывно изменяется за счет дробления и испарения. При этом УЗ-излучатель способен создавать максимальный уровень звукового давления лишь при конечном наборе частот, обусловленных резонансными свойствами самого излучателя.

Кроме того, рост вязкости приводит к сглаживанию резонансных минимумов порогового уровня энергии УЗ-поля, хотя и слабо влияет на значение резонансного диаметра. Минимумы энергии колебаний полностью исчезают, начиная с вязкости 30 мПа с. Поэтому необходимо рассмотреть характер зависимости энергии колебаний за пределами резонансов. За пределами резонансов энергия колебаний на 20–160 кДж/м3 выше, чем в области резонансов. Из графиков на рис. 5 следует, что пороговая энергия колебаний возрастает с уменьшением диаметра капель. Это связано с возрастанием капиллярных сил, препятствующих деформации капли.

По результатам расчетов установлено, что характеристики УЗ-поля для диспергирования жидкой фазы должны удовлетворять следующим требованиям:

1) удельная энергия формируемого поля должна составлять более 20 кДж/м3 при акустической мощности излучателя не более 2 кВт, определяемой как P = EcS (E – удельная энергия колебаний, Дж/м3; c – скорость звука в несущей фазе, м/с; S – площадь излучающей поверхности), и площади излучающей поверхности от 800 см2;

2) формируемое УЗ-поле должно исключать возникновение кавитации в диспергируемой жидкости, так как это существенно снизит долю энергии колебаний, уходящей на перевод жидкости в дисперсное состояние.

Однако созданию УЗ-полей со столь высокими энергетическими характеристиками препятствуют следующие физические ограничения.

1. При энергии колебаний, требующейся для реализации элементарного акта распада капли, которая составляет свыше 20 кДж/м3 для крупных капель (80–100 мкм) и свыше 80 кДж/м3 для мелких капель (5–15 мкм), в диспергируемой жидкости возникнет кавитация, которая приведет к уходу более 99% энергии на нагрев жидкости за счет локальных повышений температуры в ядрах кавитационных пузырьков до 5000 К [2, 3].

2. При диспергировании в несущей газовой фазе данная удельная мощность недостижима с помощью существующих излучателей, поскольку максимальная энергия колебаний, создаваемых существующими источниками УЗ-воздействия для газовых и газодисперсных сред, не превышает 1 кДж/м3 (при акустической мощности излучателя не более 2 кВт [18, 19, 25–27] и площади излучающей поверхности от 800 см2) даже при создании резонансных условий отражения и распространения УЗ-поля. Таким образом, сформировать поле высокой интенсивности при малой мощности излучателя невозможно путем воздействия синусоидальными колебаниями, состоящими лишь из одной гармоники.

Поэтому был предложен способ воздействия, основанный на формировании последовательности волновых пакетов разной частоты, который описан далее.

СПОСОБ ФОРМИРОВАНИЯ УЛЬТРАЗВУКОВОГО ПОЛЯ ДЛЯ ДИСПЕРГИРОВАНИЯ ЖИДКОЙ ФАЗЫ

Для формирования высокоинтенсивного УЗ-поля с характеристиками, достаточными для диспергирования капель при относительно малой мощности излучателя, необходимо осуществлять концентрирование энергии в пространстве и/или во времени.

Предлагаемый способ концентрирования энергии – излучение последовательности волновых пакетов конечной длительности (не более 10 мс) на кратных частотах (ультразвуковых импульсов). За счет межмодовой дисперсии, обусловленной наличием гетерогенных включений (жидких капель) в многофазной среде, эти пакеты будут иметь разную скорость распространения и на некотором расстоянии от излучателя составят суперпозицию.

Для создания условий формирования высокоинтенсивного УЗ-поля необходимо провести анализ распространения волновых пакетов в газовой среде, учитывая влияние жидких капель. Анализ распространения волновых пакетов проводился на основании волнового уравнения, полученного из общих уравнений динамики газокапельных сред [28]. Полученное волновое уравнение включает ненулевую правую часть, учитывающую влияние жидких капель и представляющую собой двойной интеграл от предыстории изменения звукового давления с экспоненциально убывающими весовыми коэффициентами:

(8)
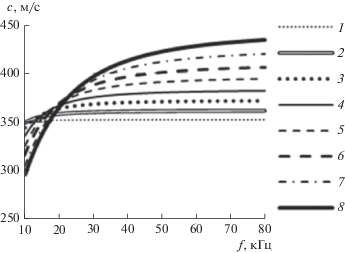
$\begin{gathered} \Delta {{p}_{{11}}} - \frac{{{{{\alpha }}_{{10}}}}}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}{{p}_{{11}}}}}{{\partial {{t}^{2}}}} = - \frac{{9\mu {{{\alpha }}_{{20}}}}}{{2{{a}^{2}}}} \times \\ \times \,\,\frac{1}{{{{{\tau }}_{{21}}}}}\int\limits_0^t {\left[ {\int\limits_0^{{{t}_{{11}}}} {\frac{{{{e}^{{\frac{{{{{\alpha }}_{{20}}}}}{{{{{\alpha }}_{{10}}}{{{\tau }}_{{21}}}}}\left( {{{t}_{{21}}} - t} \right)}}}}}{{{{{\rho }}_{{10}}}{{c}^{2}}}}\frac{{{{\partial }^{2}}{{p}_{{11}}}}}{{\partial {{t}^{2}}}}\partial {{t}_{{21}}}} } \right]\partial {{t}_{{11}}}} , \\ \end{gathered} $
где α10 – равновесное объемное содержание воздуха, %; α20 – равновесное объемное содержание жидкости, %; с – скорость звука в воздухе, м/с; ρ10 – плотность воздуха, кг/м3; μ – вязкость воздуха, Па с; a – радиус капли жидкости, м; p1 – давление воздуха, Па; τ – время релаксации, с.

Проведенные на основании уравнения (8) расчеты скорости звука в среде с дисперсной жидкой фазой позволили установить, что при концентрации аэрозоля в воздухе не менее 10 об. % скорость звука при повышении частоты с 22 до 66 кГц увеличивается до 1.5 раз (рис. 6).

Рис. 6.

Зависимость скорости звука от частоты УЗ-волн при различном объемном содержании водного аэрозоля (диаметр капель 20 мкм): 1 – 5; 2 – 10; 3 – 15; 4 – 20; 5 – 25; 6 – 30, 7 – 35, 8 – 40%.

При такой разнице скоростей звука произойдет наложение волновых пакетов друг на друга на расстоянии не более 400 см от поверхности излучателя (рис. 7).

Рис. 7.

Распределения удельных энергий колебаний волновых пакетов в канале длиной 900 мм (УЗ-излучатель диаметром 20 мм расположен с левого торца канала): (а) – 22; (б) – 44; (в) – 22 + 44 кГц.

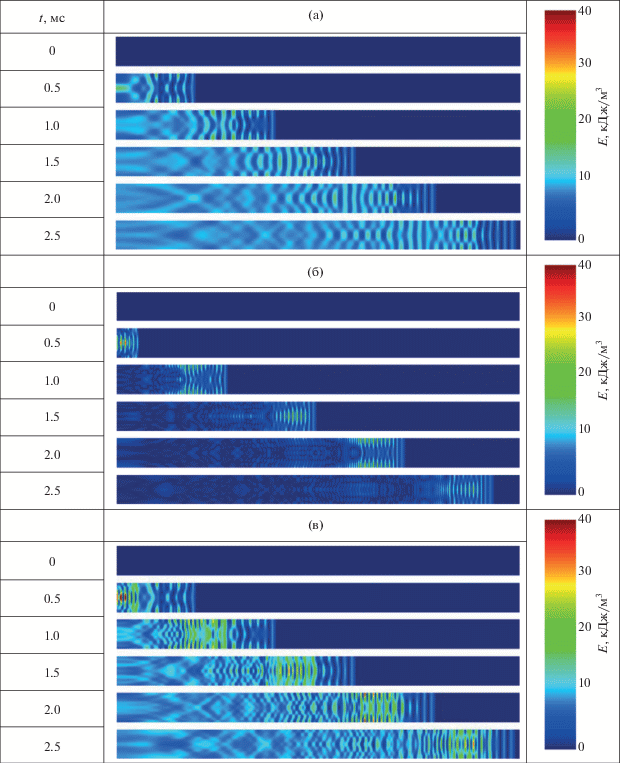
Таким образом, установлена принципиальная возможность концентрирования УЗ-энергии с помощью предлагаемого способа воздействия (последовательностью разночастотных волновых пакетов при обеспечении высокой концентрации дисперсной фазы более 10 об. %) для реализации второй стадии диспергирования (дробление предварительно сформированных грубодисперсных капель).

Для обеспечения максимальной эффективности вторичного диспергирования далее были выявлены оптимальные режимы воздействия волновыми пакетами на основании ранее описанной модели распада капель.

ОПТИМАЛЬНЫЕ ХАРАКТЕРИСТИКИ УЛЬТРАЗВУКОВОГО ПОЛЯ ДЛЯ ДИСПЕРГИРОВАНИЯ ЖИДКОЙ ФАЗЫ

На рис. 8 представлены зависимости минимальной энергии отдельного волнового пакета, необходимой для распада капель, при воздействии 2 чередующимися пакетами с частотами 22 и 44 кГц, создаваемыми одним излучателем.

Рис. 8.

Зависимости энергии отдельного волнового пакета от диаметра капель при различных вязкостях жидкости (частота 22 + 44 кГц): 1 – 1; 2 – 2; 3 – 3; 4 – 5; 5 – 7; 6 – 10, 7 – 15, 8 – 20, 9 – 30 мПа с; (а) – 20; (б) – 40 мН/м.

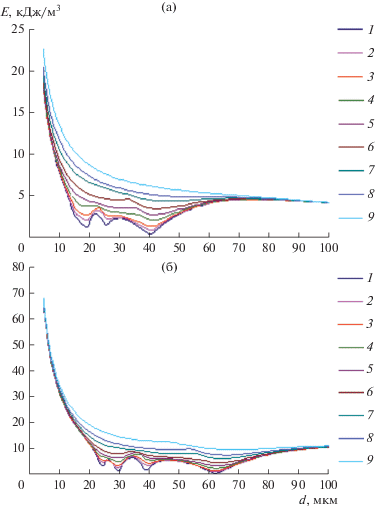
Представленные зависимости свидетельствуют об уменьшении энергии волнового пакета, необходимой для распада капель более чем на 20 кДж/м3 даже при воздействии двумя разночастотными пакетами. Как показывают результаты, энергии 60 кДж/м3 достаточно для разрушения капель до размеров менее 5 мкм.

Кроме того, при воздействии разночастотными волновыми пакетами наблюдается квадратичное увеличение количества резонансных диаметров капель с увеличением числа пакетов в последовательности, так как сила, действующая на каплю со стороны газового потока, пропорциональна квадрату скорости газа. Это означает, что воздействие волновыми пакетами на 2 частотах приведет к возникновению 4 резонансных диаметров, поскольку колебания капли включают в себя 4 временные гармоники с наиболее высокими амплитудами на частотах 22, 44, 66 и 88 кГц. Последнее утверждение связано с тем, что сила со стороны газового потока, действующая на каплю, пропорциональна квадрату скорости потока относительно капли. Таким образом, воздействие на нескольких частотах позволит перекрыть весь диапазон изменения резонансной частоты капли при ее дроблении и испарении, что обеспечивает дополнительное снижение энергии колебаний, которые должен создавать излучатель в дисперсной системе.

Из представленных зависимостей следует, что при предлагаемом способе воздействия для вторичного диспергирования будет достаточно излучателя, способного создать в сплошной воздушной среде энергию колебаний 1–10 кДж/м3 (акустическая мощность не более 2 кВт при площади излучающей поверхности 800 см2). Изготовление такого излучателя (в отличие от излучателя, излучающего колебания с энергией 20–160 кДж/м3) представляет собой технически реализуемую задачу [29].

Для определения эффективности диспергирования при выявленных режимах УЗ-поля был проведен сравнительный анализ времени распада капель и времени, требуемого для возникновения коагуляции, препятствующей диспергированию.

Для этого был проведен расчет эволюции диаметра капель с течением времени. При расчете эволюции жидкой дисперсной фазы в ходе воздействия УЗ-колебаниями анализировался распад одной капли (выбирая каждый раз одну каплю из двух новых, сформированных в результате элементарного акта распада).

Пусть элементарные акты распада реализуются в дискретные моменты времени t1, t2, …, tn, где ti ≤ ti + 1.

Принимая допущение о дроблении капли на две одинаковых при каждом акте распада, для диаметра капли справедливо следующее разностное уравнение, обусловленное тем, что диаметр новых капель, полученных в ходе дробления, в 21/3 меньше диаметра исходной капли:

(9)
$\frac{{d\left( {{{t}_{{n + 1}}}} \right) - d\left( {{{t}_{n}}} \right)}}{{{{t}_{{n + {\text{1}}}}} - {{t}_{n}}}} = - \frac{{d\left( {{{t}_{n}}} \right)}}{{{{t}_{{n + 1}}} - {{t}_{n}}}}\left( {1 - \frac{1}{{\sqrt[3]{2}}}} \right).$

При достаточно большом числе элементарных актов распада и после применения операции усреднения случайных величин, представляющих собой моменты времени актов ti, получается следующее дифференциальное уравнение:

$\frac{{\partial \left\langle d \right\rangle }}{{\partial t}} = - \frac{{\left\langle d \right\rangle }}{{\left\langle {\tau } \right\rangle }}\left( {1 - \frac{1}{{\sqrt[3]{2}}}} \right),$
где $\left\langle {\tau } \right\rangle $ – средний интервал времени между элементарными актами распада капель, определяемый путем сравнения абсолютной величины деформации капли с пороговой деформацией $\frac{{\left\langle d \right\rangle }}{4},$ при которой произойдет распад, с.

Представленное уравнение позволяет рассчитать время, требуемое для распада капли до нужного размера в зависимости от параметров УЗ-поля.

На рис. 9 представлены зависимости времени распада капель от энергии отдельного волнового пакета при различных конечных диаметрах капель и вязкостях диспергируемой жидкости. Зависимости были построены для случая воздействия суперпозиции волновых пакетов двух частот 22 + 44 кГц.

Рис. 9.

Зависимости диаметра капель от времени при различных энергиях отдельных волновых пакетов и вязкостях диспергируемой жидкости (частота 22 + 44 кГц): 1 – 20; 2 – 10; 3 – 5 мкм; (а) – 1; (б) – 10 мПа с.

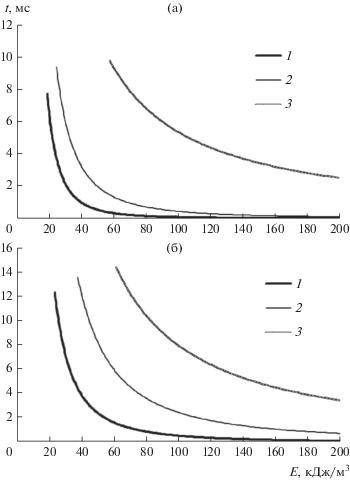
Как следует из представленных зависимостей (рис. 9), при выявленных параметрах формируемого УЗ-поля время распада капель составляет менее 0.015 с, т.е. меньше времени, требуемого для вторичной коагуляции частиц (более 100 с для коагуляции более 50% исходных частиц [30]). При этом воздействие в течение определенного времени распада капель менее 0.015 с позволит до 3 раз увеличить предельно допустимую энергию, при которой будет сохраняться докавитационный режим при диспергировании в несущей жидкой фазе [25, 31].

Это подтверждает эффективность предложенного способа формирования высокодисперсной фазы.

ЗАКЛЮЧЕНИЕ

Предложен способ УЗ-диспергирования, обеспечивающий повышение производительности формирования высокодисперсной жидкой фазы (аэрозоля в несущей газовой фазе или эмульсии в несущей жидкой фазе) с размером капель менее 10 мкм и состоящий из двух стадий: предварительное формирование грубодисперсных капель со свободной поверхности диспергируемой жидкости и дробление предварительно сформированных капель на более мелкие под действием высокоинтенсивного УЗ-поля, возбуждающего колебания стенок капли.

Для обеспечения максимальной производительности диспергирования до требуемого диаметра капель (менее 10 мкм) было проведено комплексное выявление оптимальных режимов формирования высокоинтенсивного УЗ-поля на второй стадии процесса на основании разработанных моделей распространения УЗ-колебаний и эволюции размеров капель в дисперсной среде.

В результате анализа модели было установлено, что при воздействии моночастотными синусоидальными колебаниями минимальная энергия УЗ-поля, требуемая для распада капли, составляет более 20 кДж/м3 для грубодисперсных капель (80–100 мкм) и более 160 кДж/м3 для высокодисперсных капель (1–15 мкм). Такие высокие энергии обеспечить современными излучателями технически невозможно, так как мощность излучателя должна составлять более 550 кВт при площади излучающей поверхности 800 см2 (плоский излучатель круглой формы диаметром 320 мм).

Для снижения требуемой мощности излучателя был предложен способ формирования поля, основанный на излучении последовательности волновых пакетов конечной длительности, имеющих кратные частоты. Предложенный способ воздействия позволил снизить мощностные требования к УЗ-излучателю для реализации диспергирования капель (акустическая мощность менее 2 кВт при площади излучающей поверхности 800 см2).

При воздействии последовательностью волновых пакетов время распада капель до требуемого размера (менее 10 мкм) составляет менее 0.015 с, т.е. мало по сравнению с временем, требуемым для вторичной коагуляции капель (более 100 с для коагуляции 50% капель). При этом воздействие в течение рассчитанного времени распада капель позволит до 3 раз увеличить предельно допустимую энергию, при которой будут отсутствовать нежелательные кавитационные явления при диспергировании в несущей жидкой фазе.

Таким образом, предложенный способ диспергирования капель и формирования УЗ-поля обеспечит увеличение производительности формирования высокодисперсной жидкой фазы по сравнению с одностадийным УЗ-диспергированием.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 16-38-60082 мол_а_дк).

ОБОЗНАЧЕНИЯ

А амплитуда колебаний, м
a радиус, м
c скорость частицы, м/с
c скорость звука, м/с
d диаметр, м
dx элементарный объем, м3
E удельная энергия, Дж/м3
e траектория частицы, м
F сила, Н
f частота колебаний, Гц
I интенсивность колебаний, Вт/м2
N концентрация, об. %
ΔN изменение концентрации, об. %
P акустическая мощность, Вт
p давление, Па
r полярный радиус точки, м
S площадь, м2
t время, с
Δt шаг по времени, с
x величина деформации капли, м
z аппликата точки, м
α равновесное содержание, об. %
θ полярный угол, рад
μ динамическая вязкость, Па с
ρ плотность, кг/м3
τ время релаксации, с
Ω безразмерный оператор столкновения
We число Вебера

ИНДЕКСЫ

10, 20 соответственно для газовой и жидкой фаз при отсутствии ультразвукового поля
11, 21 соответственно для газовой и жидкой фаз при наличии ультразвукового поля
1, 2, n, i номера компонентов
cr критическое значение
k номер направления движения частицы
kr проекция вектора k-го направления на ось r
kz проекция вектора k-го направления на ось z
min минимальное значение
p для сил перепада давления
s.t для сил поверхностного натяжения
v для сил вязких напряжений

Список литературы

  1. Khmelev V.N., Shalunov A.V., Galakhov A.N., Khme-lev M.V., Golykh R.N. The control of ultrasonic coagulation of dispersed nanoscale particles // Proc. 14th Int. Conf. of Young Specialists on Micro/Nanotech. and Electron Devices – EDM. Novosibirsk, 2013. P. 166.

  2. Khmelev V.N., Golykh R.N., Shalunov A.V., Bazhin V.E., Nesterov V.A. Determination of optimum conditions of ultrasonic cavitation treatment of high-viscous and non-Newtonian liquid media // Proc. 16th Int. Conf. of Young Specialists on Micro/Nanotech. and Electron Devices – EDM. Novosibirsk, 2015. P. 208.

  3. Khmelev V.N., Golykh R.N., Shalunov A.V., Khmelev S.S., Karzakova K.A. Determination of ultrasonic effect mode providing formation of cavitation area in high-viscous and non-Newtonian liquids // Proc. 15th Int. Conf. of Young Specialists on Micro/Nanotech. and Electron Devices – EDM. Novosibirsk, 2014. P. 203.

  4. Сакович Г.В., Василишин М.С., Кухленко А.А., Сысолятин С.В., Карпов А.Г. Роторно-пульсационный аппарат для получения преимущественно систем жидкость-жидкость. Пат. 2299091 РФ. 2007.

  5. Yasuda K., Honma H., Asakura Y., Koda S. Effect of frequency on ultrasonic atomization // Proc. of Symposium on Ultrasonic Electronics. 2010. V. 31. P. 363.

  6. Tsai S.C., Song Y.L., Tsai C.S., Yang C.C., Chiu W.Y., Lin H.M. Ultrasonic spray pyrolysis for nanoparticles synthesis // J. Mater. Sci. 2004. V. 39. P. 3647.

  7. Dalmoro A., Angela Barba A., d’Amore M. Analysis of size correlations for microdroplets produced by ultrasonic atomization // The Sci. World J. 2013. P. 7.

  8. Asami T., Yakou R., Ono T., Mlura H. Ultrasonic atomization by difference between vibration displacements of two circular vibrating plates // J. Mech. Eng. Autom. 2016. V. 2. № 6. P. 30.

  9. Khmelev V.N., Golykh R.N., Shalunov A.V. Optimization of these modes and conditions of ultrasonic influence on various technological mediums by mathematical modeling // Proc. 13th Int. Conf. of Young Specialists on Micro/Nanotech. and Electron Devices – EDM. Novosibirsk, 2012. P. 124.

  10. Khmelev V.N., Shalunov A.V., Nesterov V.A., Abramenko D.S., Genne D.V., Dorovskikh R.S. Automated line for ultrasonic spraying of anticoagulant into the blood collection tubes // Proc. 15th Int. Conf. of Young Specialists on Micro/Nanotech. and Electron Devices – EDM. Novosibirsk, 2014. P. 181.

  11. Khmelev V.N., Golykh R.N., Shalunov A.V., Shalunova A.V., Genne D.V. The investigation of modes of ultrasonic influence for atomization of liquids with specified dispersivity and productivity // Proc. 13th Int. Conf. of Young Specialists on Micro/Nanotech. and Electron Devices – EDM. Novosibirsk, 2012. P. 188.

  12. Капелюховская А.А. Интенсификация эмульгирования с применением гидродинамических излучателей // Сб. тр. 6-й Междунар. научно-техн. конф. “Техника и технология нефтехимического и нефтегазового производства”. Омск, 2016. С. 76.

  13. Canselier J.P., Delmas H., Wilhelm A.M., Abismail B. Ultrasound emulsification – An Overview // J. Dispers. Sci. Technol. 2002. V. 23. № 1. P. 333.

  14. Chalothorn K., Warisnoicharoen W. Ultrasonic emulsification of whey protein isolate-stabilized nanoemulsions containing omega-3 oil from plant seed // American J. of Food Technol. 2012. V. 7. № 9. P. 532.

  15. Yoshiyuki T., Takuya H., Takefumi K., Koichi S., Tautomu O., Sotaro I., Kazuyuki I., Kenichi O, Kazutaka H., Yuta Y. The condition of an emulsion generation by using an ultrasonic vibration and a microchannel // Proc. of Symposium on Ultrasonic Electronics. 2010. V. 31. P. 233.

  16. Hielscher T. Ultrasonic production of nano-size dispersions and emulsions // Proc. of Dans European Nano Systems Workshop – ENS. Paris, 2005. P. 6.

  17. Hryniewicka M. Ultrasound-assisted emulsification microextraction in the environmental and food analysis // PhD Interdisciplinary J. 2015. V. 1. P. 185.

  18. Galakhov A.N., Khmelev V.N., Golykh R.N., Shalunov A.V., Nesterov V.A., Shalunova A.V. Study of the process of liquid atomization from the ultrasonic disk radiator // Proc. 14th Int. Conf. of Young Specialists on Micro/Nanotech. and Electron Devices – EDM. Novosibirsk, 2013. P. 119.

  19. Борисов Ю.А., Леонов Г.В., Хмелев В.Н., Абраменко Д.С., Хмелев С.С., Шалунов А.В. Ультразвуковой проточный реактор. Пат. 2403085 РФ. 2010.

  20. Leea M.W., Parka J.J., Faridb M.M., Yoona S.S. Comparison and correction of the drop breakup models for stochastic dilute spray flow // Applied Math. Modelling. 2012. V. 36. № 9. P. 4512.

  21. Lang R.J. Ultrasonic atomization of liquids // The Journal of the Acoustical Society of America. 1962. V. 34. P. 6.

  22. Розенберг Л.Д. Физические основы ультразвуковой технологии. М.: Наука, 1970.

  23. Шалунов А.В. Повышение эффективности химико-технологических процессов в гетерогенных системах методами высокоинтенсивных ультразвуковых воздействий. Дис. … докт. техн. наук. Барнаул: Алтайский государственный технический университет им. И.И. Ползунова, 2013.

  24. Kupershtokh A.L. Lattice Boltzmann methods for modeling of two-phase systems such as liquid-vapor // Modern Science: Collection of Research Papers. 2010. № 2. P. 56. [Куперштох А.Л. Метод решеточных уравнений Больцмана для моделирования двухфазных систем типа жидкость-пар // Современная наука: сб. науч. статей. 2010. № 2. С. 56.]

  25. Khmelev V.N., Golykh R.N., Khmelev M.V., Shakura V.A., Shalunov A.V., Barsukov R.V. Evaluation of optimum modes of ultrasonic pulsed influence for coagulation in liquid-dispersed medium // Proc. 17th Int. Conf. Young Specialists on Micro/Nanotech. and Electron Devices – EDM. Novosibirsk, 2016. P. 225.

  26. Khmelev V.N., Shalunov A.V., Golykh R.N., Shalunova K.V., Galakhov A.N., Nesterov V.A. Revealing of optimum modes of ultrasonic coagulation of submicron particles and determining of the shape of the aggregates by mathematical modeling // Proc. 15th Int. Conf. Young Specialists on Micro/Nanotech. and Electron Devices – EDM. Novosibirsk, 2014. P. 208.

  27. Khmelev V.N., Shalunov A.V., Golykh R.N., Shalunova K.V. Theoretical study of acoustic coagulation of gas-dispersed systems // Proc. 11th Int. Conf. Young Specialists on Micro/Nanotech. and Electron Devices – EDM. Novosibirsk, 2010. P. 328.

  28. Нигматулин Р.И. Динамика многофазных сред. М.: Наука, 1987.

  29. Khmelev V.N., Shalunov A.V., Dorovskikh R.S., Go-lykh R.N., Nesterov V.A. The measurements of acoustic power introduced into gas medium by the ultrasonic apparatuses with the disk-type radiators // Proc. 17th Int. Conf. Young Specialists on Micro/Nanotech. and Electron Devices – EDM. Novosibirsk, 2016. P. 246.

  30. Sheng, C.D., Shen X.L. Modelling acoustic agglomeration processes using direct simulation Monte Carlo method // J. Aerosol Sci. 2006. V. 37. P. 16.

  31. Xie W., Li R., Lu X. Pulsed ultrasound assisted dehydration of waste oil // Ultrason. Sonochem. 2015. P. 136.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал