Теоретические основы химической технологии, 2019, T. 53, № 3, стр. 315-323
Информационно-вероятностный подход к оптимальной организации процесса бинарной ректификации
В. А. Налетов 1, В. А. Колесников 1, М. Б. Глебов 1, А. Ю. Налетов 1, *
1 Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия
* E-mail: energo@muctr.ru
Поступила в редакцию 12.10.2018
После доработки 26.10.2018
Принята к публикации 08.11.2018
Аннотация
Представлен системный подход к оптимальной организации процесса бинарной ректификации с позиции теории информации, позволяющий сформулировать условия по оптимальной дифференциации функций сложного процесса при разделении потока сырья на потоки продуктов. Проведено сравнение результатов вычислительных экспериментов на основе данного подхода и известных термодинамических подходов по минимизации потерь эксергии и производства энтропии на численном примере разделения смеси метанол–вода. Показано, что результаты вычислительных экспериментов на основе информационно-вероятностного подхода к оптимальной организации процесса бинарной ректификации согласуются с результатами на основе термодинамических подходов, что доказывает применимость информационного подхода в контексте его интеграции в общий алгоритм проектирования химико-технологических систем на основе информационной концепции.
ВВЕДЕНИЕ
Задачи оптимизации и синтеза химико-технологических систем (ХТС), предполагающие выбор оптимального технического решения, являются наиболее сложным этапом автоматизированного проектирования. Методология автоматизированного проектирования химических производств представлена в работе [1]. Как правило, этапу синтеза предшествует этап анализа, основной целью которого является связь управляющих параметров с общим критерием посредством математической модели. При этом анализ систем усложняется в случае наличия процессов разделения исходных веществ по потокам продуктов или отборам, в силу чего ХТС становятся “многомаршрутными”, что приводит к усложнению их топологии.
В литературе [2] термин “организация” определен как многосмысловой термин, используемый различными дисциплинами системного анализа. С одной стороны, организация понимается как внутренняя упорядоченность, согласованность, взаимодействие автономных частей целого, ориентированного на определенную предназначенность, т.е. организация как структура, а с другой – это совокупность процессов, ведущих к образованию и развитию взаимосвязей между частями целого (объекта), т.е. организация как процесс. Для оценки организации технологических процессов применяются методы теории информации. Например, в работах В.П. Майкова [3] для моделирования процессов химической технологии было использовано понятие информационной энтропии как меры неопределенности, выражение которой было адекватно термодинамической энтропии, выраженной через мольные расходы и концентрации веществ. При этом классическим математическим моделям В.П. Майков противопоставляет в качестве альтернативы формализм статистической механики Э.Т. Джейнса, описывающий поведение произвольных статистических ансамблей. Совершенно иное использование информационного подхода представлено в работах школы В.В. Кафарова, идеи которой развиты в настоящей статье. Если в работах В.П. Майкова информационная энтропия характеризовала неопределенность или неупорядоченность и являлась функцией состояния, то в работах [4–7] в качестве характеристики организации технологического объекта использовалась энтропия информации как мера организованности или порядка, которая является функцией процесса преобразования информации.
При этом общие постулаты информационно-вероятностного подхода, сформулированные в предшествующих работах и используемые в настоящей статье, сводились к следующим.
1. Каждый технологический поток является носителем информации о его возможных состояниях (возможных результатах технологического процесса) и поэтому может рассматриваться как информационный поток. При этом возможные состояния потока представляются на основе корпускулярной и квантовой теорий о дискретности превращений вещества и энергии.
2. Характеристикой информационного потока является энтропия информации, выраженная через вероятности возможных состояний технологического потока.
3. Ансамбль возможных состояний технологического потока характеризует объем информационного процесса, который опосредованно определяется альтернативными способами его организации, в силу чего данные возможные состояния являются статистически независимыми.
4. Для оценки вероятностей возможных состояний технологического потока используется распределение Больцмана, которое моделирует статистическое распределение идеального газа.
5. Преобразованию информационных потоков в аппарате ставится в соответствие решение некоторой информационной задачи, заключающейся в выборе определенного исхода из возможных альтернатив путем уменьшения исходной неупорядоченности при условии постоянства полной или внутренней энергии преобразования, т.е. при условии изоэнергетичности, что адекватно представлению объекта как замкнутой термодинамической системы.
Целью настоящей работы является вывод с использованием общих постулатов информационно-вероятностного подхода условий оптимальной организации процесса бинарной ректификации и сравнительный анализ полученных результатов с использованием информационного и термодинамических подходов.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
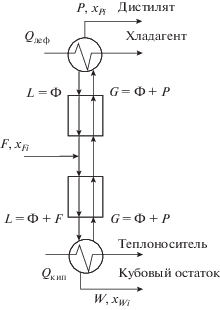
В процессе бинарной ректификации исходный поток питания в колонне разделяется на два продукта: низкокипящий – дистиллят и высококипящий – кубовый остаток. Для простоты проведем анализ различных подходов к оптимальной организации двухсекционной колонны в стационарном режиме при разделении двухкомпонентной смеси, принципиальная схема которой представлена на рис. 1.
С целью сопоставимости полученных результатов, принятые в работе допущения, в основном, повторяют аналогичные предпосылки, представленные в работе [8]:
поток питания – жидкость при температуре кипения;
дефлегматор (конденсатор) – полный;
массообмен – эквимолярный;
эффекты перемешивания между соседними сечениями пренебрежимо малы;
поток питания подается при температуре кипения в то сечение колонны, состав жидкости в котором наиболее близок составу питания.
Уравнения материального баланса для колонны на рис. 1 можно представить следующим образом:
Для вывода условий оптимальной дифференциации функций процесса бинарной ректификации сначала формализуем объект исследования и представим его с позиции теории информации. Поскольку в процессе бинарной ректификации исходный поток разделяется на два, то мы имеем дело с дифференциацией (распределением) функций сложного процесса между потоками продуктов.
В работе [7] была рассмотрена информационная модель при дифференциации функций системы между элементами и подсистемами, и был сделан вывод, что характеристикой, описывающей возможные состояния потоков при дифференциации функций системы, является энтропия информации Шеннона, выраженная через статистические веса элементов или подсистем, которые связаны с вероятностью обратной зависимостью.
Собственно выражение статистического веса можно представить как
(3)
$K = \exp \left( { - \frac{{\Delta {{Z}^{{p,T}}} - \Delta U}}{{{{R}_{\nu }}{{T}_{0}}}}} \right),$Из выражения (3) следует, что величина статистического веса всегда больше единицы, в силу того что выражение под знаком экспоненты положительно и не равно нулю, поскольку равенство нулю означало бы отсутствие процесса как такового.
На рис. 2 представлен процесс бинарной ректификации на основе информационно-вероятностного подхода.
Рис. 2.
Структура информационных потоков в простой колонне ректификации: HF – энтропия информации на входе (питание); HP(W) – энтропия информации на выходе (потоки продуктов: дистиллята и кубового остатка соответственно); {u} – управляющие воздействия; λP,W – безразмерные множители (множители Лагранжа).
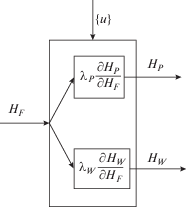
Как следует из рис. 2, информационная система, отображающая процесс бинарной ректификации, распределяет потоки информации между двумя подсистемами.
Задача организации процесса сводится к выбору оптимального варианта согласования двух взаимодействующих друг с другом подсистем, находящихся в рамках замкнутой термодинамической системы в силу условия изоэнергетичности преобразования информации.
Математически задача организации процесса сводится к максимизации энтропии информации системы с учетом ограничений типа равенств, учитывающих связь входной и выходной энтропий информации. Поиск условий оптимальной организации процесса можно осуществить на основании метода неопределенных множителей Лагранжа. Для этого определим функцию Лагранжа, в которую войдут исходный критерий и уравнения с множителями Лагранжа, полученные из ограничений.
Энтропия информации процесса как сложной системы равна
Система ограничений типа равенств для системы, представленной на рис. 2, имеет следующий вид:
Выражение для функции Лагранжа с учетом (4) и (5) по каждому потоку продукта будет равно
(6)
${{L}_{{P,W}}} = {{H}_{{{\text{в х }}}}} + {{\lambda }_{{P,W}}}\left[ {{{H}_{{{\text{в ы х }}P,W}}} - {{h}_{{{\text{в ы х }}P,W}}}\left( {{{H}_{{{\text{в х }}}}}{\text{;}}u} \right)} \right].$Соответственно вычислим производные каждого из выражений (6) по входной энтропии:
(7)
$\frac{{\partial {{L}_{{P,W}}}}}{{\partial {{H}_{{{\text{в х }}}}}}} = 1 - {{\lambda }_{{P,W}}}\frac{{\partial {{h}_{{{\text{в ы х }}P,W}}}}}{{\partial {{H}_{{{\text{в х }}}}}}}.$С учетом представленных в работе [7] выражений, что ${{h}_{{{\text{в ы х }}\,P,W}}} = {{{{H}_{{{\text{в х }}}}}{{\eta }_{T}}} \mathord{\left/ {\vphantom {{{{H}_{{{\text{в х }}}}}{{\eta }_{T}}} {{{K}_{{P,W}}}}}} \right. \kern-0em} {{{K}_{{P,W}}}}},$ имеем
где ηT – термодинамический КПД, КP,W – статистические веса по потокам продуктов (факторы затрат на организацию процесса).По физическому смыслу полученные множители Лагранжа согласно (8) аналогичны таковым в эксергоэкономическом подходе. В частности, множители Лагранжа в задаче оптимизации с позиции эксергоэкономики имели смысл стоимости единицы эксергии потоков продуктов. Постулируя аналогию содержания, можно принять, что множители Лагранжа в задаче оптимальной организации в информационном подходе также имеют смысл “стоимости” (безразмерная величина) единицы информации потоков продуктов. Изменяется только мера стоимости. За единицу стоимости в информационном подходе принимается условная элементарная упорядочивающая операция в зависимости от специфики процесса. По физическому смыслу стоимости единицы эксергии или единицы информации должны быть минимизированы в силу необходимости повышения рентабельности технологий. Принимая во внимание, что $K$ = ${{K}_{P}}{{K}_{W}},$ получим
(9)
${{\lambda }_{P}} = \frac{{{{K}_{P}}}}{{{{\eta }_{T}}}}\,\,{\text{и }}\,\,{{\lambda }_{W}} = \frac{K}{{{{\eta }_{T}}{{K}_{P}}}}.$Поиск оптимального значения критериев (9) по каждому из потоков продуктов возможно осуществить на основании необходимого условия экстремума по фактору затрат (например, для потока продукта Р), а именно
(10)
$\frac{{\partial {{\lambda }_{{P,W}}}}}{{\partial {{K}_{P}}}} = 0\,\,{\text{и }}\,\,\frac{{\partial {{\lambda }_{P}}}}{{\partial {{K}_{P}}}} + \frac{{\partial {{\lambda }_{W}}}}{{\partial {{K}_{P}}}} = 0.$Подставляя выражения (9) в производные, получим
т.е. условие экстремума равносильно равенству факторов затрат или статистических весов по потокам продуктов.Можно показать, что условие (11) является следствием фундаментального закона – нулевого начала термодинамики, основанного на термодинамике взаимодействия подсистем при статистическом их описании. Для этого рассмотрим взаимодействие двух произвольных подсистем 1 и 2, разделенных подвижной перегородкой, способной проводить теплоту, в рамках замкнутой термодинамической системы при условии постоянства ее объема и внутренней энергии.
Обе подсистемы, взаимодействуя друг с другом, могут обмениваться теплотой и работой до момента установления равновесия, которое характеризуется максимумом энтропии системы, аддитивно включающей энтропии подсистем [9]. При этом энтропия системы равна
где К1 и К2 – статистические веса подсистем.Ограничения представляются следующим образом:
(13)
$\left\{ \begin{gathered} {{V}_{{\text{с }}}} = {{V}_{1}} + {{V}_{2}} = {\text{const}} \hfill \\ {{U}_{{\text{с }}}} = {{U}_{1}} + {{U}_{2}} = {\text{const}} \hfill \\ \end{gathered} \right..$Условие равновесия соответствует равенству нулю полного дифференциала энтропии системы:
При выводе условия равновесия подсистем следует учесть, что статистические веса подсистем являются функцией их внутренней энергии и объема, поскольку именно эти два параметра изменяются в ходе взаимодействия подсистем. Запишем выражение для статистического веса, например, для подсистемы 1:
(15)
$d\ln {{K}_{{\text{1}}}} = \left( {\frac{{\partial \ln {{K}_{1}}}}{{\partial {{V}_{1}}}}} \right)d{{V}_{1}} + \left( {\frac{{\partial \ln {{K}_{1}}}}{{\partial {{U}_{1}}}}} \right)d{{U}_{1}}.$Учитывая, что
(16)
$d\ln {{K}_{{\text{1}}}} = \frac{{{{p}_{1}}}}{{R{{T}_{1}}}}d{{V}_{1}} + \frac{1}{{R{{T}_{1}}}}d{{U}_{1}}.$Из ограничений (13) следует, что
Тогда условие равновесия в системе можно записать в виде
(18)
$d{{S}_{{\text{с }}}} = \left( {\frac{{{{p}_{1}}}}{{R{{T}_{1}}}} - \frac{{{{p}_{2}}}}{{R{{T}_{2}}}}} \right)d{{V}_{1}} + \left( {\frac{1}{{R{{T}_{1}}}} - \frac{1}{{R{{T}_{2}}}}} \right)d{{U}_{1}} = 0.$Принимая во внимание, что $d{{V}_{{\text{1}}}} \ne 0$ и $d{{U}_{{\text{1}}}} \ne 0,$ окончательно имеем
что равносильно равенству статистических весов подсистем К1 = К2.
Таким образом, оптимальное согласование или оптимальная дифференциация функций системы между подсистемами с точки зрения термодинамики означает, что при условии постоянства ее полной энергии максимизация энтропии (определяет “связанную” форму энергии в терминологии Гиббса–Гельмгольца) компенсируется уменьшением свободной энергии, т.е. те же технологические операции выполняются при минимуме притоков свободной энергии в систему извне.
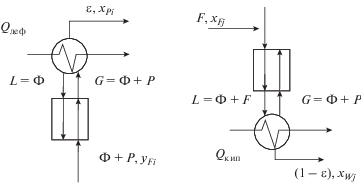
С учетом необходимости масштабирования потенциалов в выражении (3) представим верхнюю и нижнюю части колоны ректификации в удельных мольных расходах как показано на рис. 3.
Сопоставляя рис. 1 и 3, имеем ${P \mathord{\left/ {\vphantom {P F}} \right. \kern-0em} F} = \varepsilon $ – мольная доля потока дистиллята; ${W \mathord{\left/ {\vphantom {W F}} \right. \kern-0em} F} = 1 - \varepsilon $ – мольная доля потока кубового остатка; $R = {{\text{Ф }} \mathord{\left/ {\vphantom {{\text{Ф }} P}} \right. \kern-0em} P}$ – флегмовое число.
Принимая мольный поток питания равным единице, получим
Тогда общие выражения для статистических весов или факторов затрат имеют следующий вид:
(19)
$\begin{gathered} {{K}_{P}} = \exp \left[ {\varepsilon \sum\limits_{i = 1}^m {{{x}_{{Pi}}}\ln } {{x}_{{Pi}}} - \left( {\varepsilon R + \varepsilon } \right)\sum\limits_{i = 1}^m {{{y}_{{Fi}}}\ln } {{y}_{{Fi}}} + } \right. \\ \left. { + \,\,\frac{{\left( {\varepsilon R + \varepsilon } \right)C_{{pF}}^{g}\left( {{{y}_{F}}} \right){{T}_{F}} - \varepsilon C_{{pP}}^{l}\left( {{{x}_{P}}} \right){{T}_{P}}}}{{{{R}_{\nu }}{{T}_{0}}}}} \right] \\ {{K}_{W}} = \exp \left[ {\left( {1 - \varepsilon } \right)\sum\limits_{i = 1}^m {{{x}_{{Wi}}}\ln } {{x}_{{Wi}}} - \left( {\varepsilon R + 1} \right) \times } \right. \\ \times \,\,\sum\limits_{i = 1}^m {{{x}_{{Fi}}}\ln } {{x}_{{Fi}}} + \\ + \,\,\left. {\frac{{\left( {1 - \varepsilon } \right)C_{{pW}}^{l}\left( {{{x}_{W}}} \right){{T}_{W}} - \left( {\varepsilon R + 1} \right)C_{{pF}}^{l}\left( {{{x}_{F}}} \right){{T}_{F}}}}{{{{R}_{\nu }}{{T}_{0}}}}} \right]. \\ \end{gathered} $Принимая во внимание, что нулевое начало термодинамики устанавливает направление поиска оптимального решения и его теоретический (не достижимый в процессе ректификации) предел, можно сформулировать критерий в задаче оптимальной организации как минимизация разности факторов затрат согласно (19) по потокам продуктов $\Delta K$ = ${{K}_{P}} - {{K}_{W}}$ (по абсолютной величине).
В дальнейшем на численном примере будет показано, что имеется корреляция между тепловыми нагрузками на дефлегматор и кипятильник и значением общего фактора затрат на организацию процесса бинарной ректификации. Для сравнения результатов с применением условий (19) представим традиционные термодинамические подходы к оптимальной организации процесса бинарной ректификации.
Один из таких подходов связан с минимизацией потерь эксергии в системе, которые возможно определить непосредственно из эксергетического баланса или из баланса термодинамической энтропии [10].
Запишем, в частности, баланс энтропии для колонны ректификации с кипятильником и дефлегматором:
(20)
$F{{S}_{F}} + \frac{{{{Q}_{{{\text{к и п }}}}}}}{{{{T}_{W}}}} + \Delta {{S}_{{\text{н }}}} = P{{S}_{P}} + W{{S}_{W}} + \frac{{{{Q}_{{{\text{д е ф }}}}}}}{{{{T}_{P}}}},$или в приведенном к удельным мольным расходам виде
(21)
${{S}_{F}} + \frac{{{{{\overline Q }}_{{{\text{к и п }}}}}}}{{{{T}_{W}}}} + \Delta {{S}_{{\text{н }}}} = \varepsilon {{S}_{P}} + \left( {1 - \varepsilon } \right){{S}_{W}} + \frac{{{{{\overline Q }}_{{{\text{д е ф }}}}}}}{{{{T}_{P}}}},$Из выражения (21) можно определить необратимые потери в системе, представленной колонной ректификации, кипятильником и дефлегматором:
(22)
$\Delta {{S}_{{\text{н }}}} = \varepsilon {{S}_{P}} + \left( {1 - \varepsilon } \right){{S}_{W}} + \frac{{{{{\overline Q }}_{{{\text{д е ф }}}}}}}{{{{T}_{P}}}} - {{S}_{F}} - \frac{{{{{\overline Q }}_{{{\text{к и п }}}}}}}{{{{T}_{W}}}}.$Согласно уравнению Гюи–Стодолы потери эксергии выражаются произведением величины необратимых потерь на температуру окружающей среды следующим образом:
Задача оптимальной организации системы с колонной ректификации, кипятильником и дефлегматором в соответствии с данным подходом сводится к минимизации потерь эксергии согласно (23) или необратимых потерь энтропии согласно (22).
Другой подход к оптимальной организации системы с колонной ректификации основан на минимизации производства энтропии. Рассмотрим систему в стационарном состоянии и в неравновесных условиях, вызванных потоками вещества и энергии. Производство энтропии при обмене подсистем веществом и энергией в этом случае равно скалярному произведению вектора потоков на вектор движущих сил [11]. В работе [8] для данного случая приведены выражения для расчета производства термодинамической энтропии для процесса бинарной ректификации.
В частности, производство энтропии определяется следующей зависимостью:
где ${{\sigma }_{T}}$ и ${{\sigma }_{\mu }}$ – производство энтропии в процессах теплообмена и массообмена соответственно.При этом производство энтропии в процессе теплообмена равно [8]
(25)
${{\sigma }_{T}} = {{\overline Q }_{{{\text{к и п }}}}}\left[ {\frac{1}{{{{T}_{W}}}} - \frac{1}{{{{T}_{ + }}}}} \right] + {{\overline Q }_{{{\text{д е ф }}}}}\left[ {\frac{1}{{{{T}_{ - }}}} - \frac{1}{{{{T}_{P}}}}} \right],$Производство энтропии в процессе массообмена вычисляется следующим образом [8]:
(26)
${{\sigma }_{\mu }} = {{R}_{\nu }}\int\limits_{{{x}_{W}}}^{{{x}_{P}}} {G\left( {y{\text{*}},y} \right)\ln \frac{{y{\text{*}}\left( {1 - y} \right)}}{{y\left( {1 - y{\text{*}}} \right)}}dx} .$С учетом ранее введенных обозначений для удельных расходов получим
где G – расход пара, моль/с; y, y* – соответственно текущая и равновесная концентрация вещества в паре. В силу принятых допущений производством энтропии при смешении флегмы с потоком питания можно пренебречь. Проиллюстрируем представленные подходы к оптимальной организации на примере простой колонны ректификации двухкомпонентной смеси.РЕЗУЛЬТАТЫ ВЫЧИСЛИТЕЛЬНЫХ ЭКСПЕРИМЕНТОВ
Рассмотрим численный пример разделения смеси метанол–вода и дадим оценку полученных результатов с позиции представленных подходов.
Расчет производился на основе следующих предпосылок:
расчет ведется от тарелки к тарелке;
тарелки – теоретические (эффективность равна 1);
дефлегматор (конденсатор) – полный;
поток питания – насыщенная жидкость.
Исходные данные для расчета были приняты следующими: расход питания (исходная смесь) 0.01 кмоль/с, состав дистиллята по метанолу xP = = 0.99, давление в процессе 0.1 МПа.
Для проведения сравнительного анализа на основе информационного и термодинамического подходов расчеты проводились в пределах математической реализуемости в широком диапазоне варьирования следующих характеристик:
− состав питания;
− флегмовое число;
− число тарелок;
− положение тарелки питания;
− количества продуктов.
На рис. 4–6 представлены изменения разности факторов затрат ΔK в логарифмических координатах, потерь эксергии и производства энтропии в системе с колонной ректификации, кипятильником и дефлегматором.
Рис. 4.
Изменение разности факторов затрат в логарифмических координатах при различных значениях флегмового числа и содержания метанола в питании.
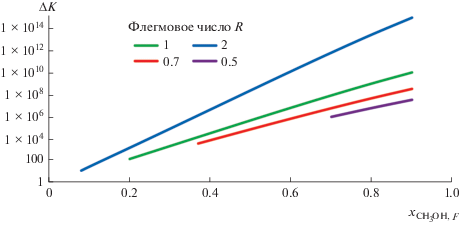
Рис. 5.
Изменение потерь эксергии в системе при различных значениях флегмового числа и содержания метанола в питании.
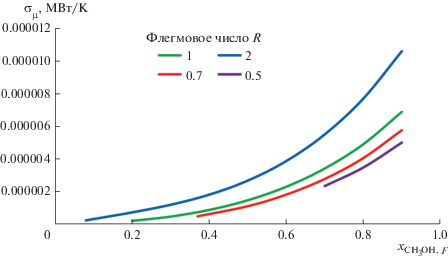
Рис. 6.
Изменение производства энтропии в системе при различных значениях флегмового числа и содержания метанола в питании.
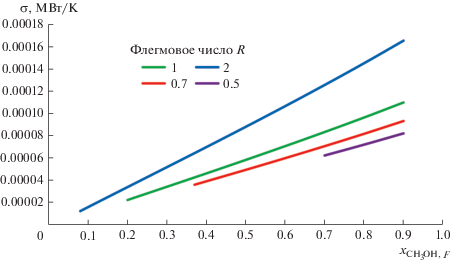
Для оценки вклада составляющих в выражении производства энтропии на рис. 7 представлено производство энтропии только от процесса массообмена согласно (27).
Рис. 7.
Изменение производства энтропии в процессе массообмена при различных значениях флегмового числа и содержания метанола в питании.
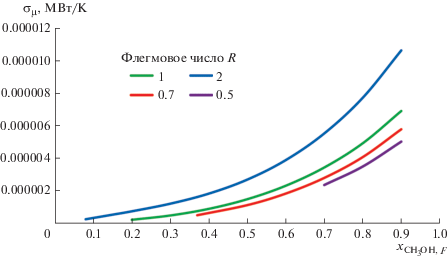
Из сравнения данных, приведенных на рис. 6 и 7, следует, что общее производство энтропии в системе определяется в основном процессами теплообмена.
Характер зависимостей, представленных на рис. 4–7 и реализующих различные подходы к оптимальной организации процесса бинарной ректификации, свидетельствует об их идентичном характере во всем диапазоне варьирования характеристик, что говорит о непротиворечивости выводов на основании информационного и термодинамических подходов к оптимальной организации процесса.
Рассмотрим часто встречающийся на практике случай, когда состав питания смеси, в данном случае, метанол–вода задан и соответствует содержанию метанола в питании, равному 0.4.
В табл. 1 приведены результаты расчета критериев для разделения смеси метанол–вода при варьировании флегмового числа в колонне.
Таблица 1.
Сравнение критериев для заданного состава питания при изменении флегмового числа
| № п/п | Характеристики | |||||||
|---|---|---|---|---|---|---|---|---|
| R | N | ${{Q}_{{{\text{д е ф }}}}}$ | ${{Q}_{{{\text{к и п }}}}}$ | lnKР + lnKW | lnKР–lnKW | $\Delta {{S}_{{\text{н }}}}$ | $\sigma $ | |
| 1 | 0.7 | 25 | 0.2206 | 0.2275 | 9.1663 | 7.0926 | 5.60 × 10–5 | 3.651 × 10–5 |
| 2 | 1 | 13 | 0.2812 | 0.2879 | 11.8306 | 9.7322 | 7.23 × 10–5 | 4.662 × 10–5 |
| 3 | 2 | 10 | 0.4218 | 0.4285 | 18.1257 | 12.2297 | 0.000111 | 7.016 × 10–5 |
Минимальному общему фактору затрат, минимальной разности логарифмов от факторов затрат по потокам целевых продуктов, минимальным потерям эксергии, а также минимальному производству энтропии соответствует минимальное флегмовое число, минимальные тепловые нагрузки на кипятильник и дефлегматор, но максимальное число теоретических тарелок. Данные сравнительного анализа результатов вычислительных экспериментов строго корреспондируются. При этом информационный критерий оптимальной организации процесса в силу экспоненциального его характера является более чувствительным по сравнению с термодинамическими критериями в задачах оптимизации.
ЗАКЛЮЧЕНИЕ
Представленный информационно-вероятностный подход к оптимальной организации процесса бинарной ректификации приводит к условиям сближения факторов затрат или статистических весов по потокам продуктов, что является следствием нулевого начала термодинамики. При этом выводы, полученные на основании вычислительных экспериментов для процесса бинарной ректификации с использованием различных подходов, приводят к непротиворечивым результатам. Общим выводом для рассматриваемых подходов является то, что оптимальная организация процесса бинарной ректификации определяется в основном градиентом температур между кипятильником (источником) и дефлегматором (стоком) и соответствующими тепловыми нагрузками на эти элементы и в меньшей степени капитальными затратами (увеличение количества тарелок). Полученные результаты подтверждают обоснованность идеи об организации сложного процесса путем оптимальной дифференциации его функций между потоками продуктов или отборами в соответствии с постулатами информационного подхода. Целесообразность применения информационного подхода как альтернативы термодинамическим подходам к оптимальной организации процесса мотивирована возможностью выработки единой методологии проектирования неоднородных ХТС в процессе их элементного усложнения, в том числе в части оптимальной дифференциации функций сложного процесса между потоками продуктов или отборами.
ОБОЗНАЧЕНИЯ
| Cp | теплоемкость при постоянном давлении, Дж/(моль К) |
| ΔEп | потери эксергии, Дж/моль |
| F | расход питания, моль/с |
| G | расход пара, моль/с |
| H | энтропия информации |
| h | функция информационного процесса |
| K | статистический вес (фактор затрат) |
| ΔK | разность факторов затрат |
| L | функция Лагранжа; расход жидкости, моль/с |
| m | число компонентов в смеси |
| N | число тарелок |
| P | расход дистиллята, моль/с |
| p | давление, МПа |
| Q | количество теплоты (тепловая нагрузка), МВт |
| $\overline Q $ | удельное количество теплоты, МВт/моль |
| R | флегмовое число |
| Rν | универсальная газовая постоянная, Дж/(моль К) |
| S | термодинамическая энтропия, Дж/(моль К) |
| ΔSн | необратимое увеличение энтропии, Дж/(моль К) |
| T | температура, К |
| ΔU | изменение внутренней энергии в процессе, Дж/моль |
| u | произвольный управляющий параметр |
| W | расход кубового остатка, моль/с |
| x | концентрация вещества в жидкости, мол. д. |
| y | концентрация вещества в паре, мол. д. |
| ΔZ | изменение изобарно-изотермического потенциала в процессе, Дж/моль |
| ε | мольная доля потока дистиллята |
| η | КПД процесса |
| λ | безразмерный множитель Лагранжа, имеет смысл стоимости единицы информации потоков продуктов |
| σ | общее производство энтропии, МВт/К |
| ${{\sigma }_{\mu }}$ | производство энтропии в процессах массообмена, МВт/К |
| ${{\sigma }_{T}}$ | производство энтропии в процессах теплообмена, МВт/К |
| Ф | расход потока флегмы, моль/с |
ИНДЕКСЫ
Список литературы
Кафаров В.В., Мешалкин В.П., Перов В.Л. Математические основы автоматизированного проектирования химических производств. М.: Химия, 1973.
Подлесных В.И. Теория организации. СПб.: Бизнес-пресса, 2003.
Энтропийные методы моделирования в химической технике / Под ред. Майкова В.П. М.: Моск. ин-т хим. машиностр., 1980.
Кафаров В.В. Методы кибернетики в химии и химической технологии. 3-е. изд. М.: Химия, 1976.
Кафаров В.В., Перов В.Л., Бобров Д.А., Налетов А.Ю. Анализ химико-технологических процессов на основе принципов теории информации // Докл. АН СССР. 1977. Т. 232. № 3. С. 663.
Кафаров В.В., Перов В.Л., Боборов Д.А., Налетов А.Ю. Информационный критерий совершенства химико-технологической системы // Докл. АН СССР. 1977. Т. 236. № 2. С. 404.
Naletov V.A., Gordeev L.S., Glebov M.B., Naletov A.Yu. Information-Thermodynamic Principle of the Organization of Chemical Engineering Systems // Theor. Found. Chem. Eng. 2011. V. 45. № 5. P. 631. [Налетов В.А., Гордеев Л.С., Глебов М.Б., Налетов А.Ю. Информационно-термодинамический принцип организации химико-технологических систем // Теорет. основы хим. технологии. 2011. Т. 45. № 5. С. 541.]
Цирлин А.М., Романова Т.С., Григоревский И.Н. Оптимальная организация процесса бинарной ректификации // Теорет. основы хим. технологии. 2008. Т. 42. № 4. С. 435.
Рейф Ф. Статистическая физика. Берклеевский курс физики. М.: Наука, 1977.
Шаргут Я., Петела Р. Эксергия. М.: Энергия, 1968.
Пригожин И., Кондепуди Д. Современная термодинамика. М.: Мир, 2002.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии