Теоретические основы химической технологии, 2019, T. 53, № 3, стр. 309-314
Критерии оценки термодинамической эффективности процесса ректификации
О. И. Сычева 1, *, Ю. А. Писаренко 1
1 МИРЭА – Российский технологический университет, Институт тонких химических технологий
им. М.В. Ломоносова
Москва, Россия
* E-mail: KseniaSy4eva@yandex.ru
Поступила в редакцию 17.01.2018
После доработки 15.05.2018
Принята к публикации 21.08.2018
Аннотация
Проведен термодинамический анализ процесса ректификации на основе критериев, определяющих минимальное количество теплоты и работы, необходимые для проведения процесса. Представленный анализ позволяет сопоставить эффективность различных методов разделения многокомпонентных смесей и в рамках выбранного метода установить оптимальные условия его проведения.
ВВЕДЕНИЕ
Термодинамическая суть процесса ректификации – совершение работы разделения за счет подвода теплоты к кипятильнику колонны при более высокой температуре по сравнению с температурой, при которой отводят тепло из конденсатора. Таким образом, ректификационная колонна напоминает тепловой двигатель, который производит работу, а именно работу разделения, хотя с довольно низкой эффективностью. Последнее объясняется диссипацией энергии или, иначе, потерей полезной работы в связи с необратимостью процесса. Это явление поясняет принцип Гюи–Стодолы – потери эксергии вызваны необратимостью реальной установки, в отличие от обратимого идеального аппарата, где под эксергией понимается максимальная работа, совершенная в обратимом процессе, с окружающей средой в качестве источника тепла и вещества [1]. Из этого следует, что необратимость есть причина увеличения энергозатрат на проведение процесса. Для создания более эффективных, с точки зрения экономии энергозатрат, вариантов организации разделения, позволяющих уменьшить степень необратимости процесса, весьма важную роль играет исследование закономерностей обратимой ректификации [2].
Совместное применение первого и второго законов термодинамики для исследования процессов разделения делает возможным оценить энергопотребление в ректификации. Такой подход называется термодинамическим анализом. Одним из первых термодинамический анализ процессов разделения, в том числе процесса ректификации, выполнил Бенедикт. Именно он, проанализировав минимальный расход энергии, требуемый для проведения процесса, отметил, что большая часть энергии переходит в менее полезную форму [3]. Для того чтобы оценить потери любого процесса разделения или сравнить эффективность нескольких, Бенедикт ввел понятие работы разделения. Так, по мере приближения процесса к обратимому, работа разделения приближается к минимуму, который необходим для осуществления заданного варианта разделения. Объединив все наработанные термодинамические понятия и подходы в единую теорию можно минимизировать степень необратимости процесса разделения [4].
Причины необратимости процесса ректификации впервые описал в 1974 г. Фоньо в серии статей [4, 5], где провел термодинамические исследования, как бинарных смесей, так и многокомпонентных, математически описав колонну и ее характеристики, а также сделал вывод о причинах потери энергии. Последнее Фоньо связывает с движущей силой процесса, самые низкие соответствуют противоточному движению потоков по колонне, наибольшие потери наблюдаются в элементах смешения. Автор рассматривает только внутренние теплопотери, внешние же, возникающие по причине потерь тепла и холода в окружающую среду, гидравлических потерь в теплообменниках и компрессорах и т.д., могут быть уменьшены за счет дополнительных конструкций (тепловые насосы, изоляция теплообменников, компрессоров и других вспомогательных устройств), которые меняют или дополняют уже имеющуюся конструкцию. Внутренние потери обусловлены гидравлическим сопротивлением и конечными движущими силами при массопередаче на тарелках. Первое приводит к увеличению перепада температур в колонне и уменьшению относительной летучести компонентов, что в итоге увеличивает энергозатраты на разделение [5, 6].
В изучении причин необратимости Фоньо пришел к выводам, что для осуществления термодинамически обратимой ректификации концентрации компонентов должны меняться непрерывно вдоль колонны, чего можно добиться использованием теплового насоса в промежуточной зоне колонны, который тепло из укрепляющей части переносит в отгонную часть колонны. В то же время использование дополнительного ввода питания и дополнительных зон отбора продуктов поможет уменьшить необратимости в этих зонах. Автор предлагает использовать колонны со стенкой, схемы с обратимым смешением потоков, где распределение тепла происходит не в некоторых промежуточных точках, а по всей колонне в целом [5].
Воспроизвести схемы обратимой ректификации в промышленности невозможно, но знания об этом процессе исключительны и открывают путь к улучшению термодинамических условий проведения процесса. Как подчеркивает Додж [7], обратимый процесс представляет максимально возможную эффективность, к которой мы должны стремиться приблизиться. Без такого абсолютного стандарта сравнения усилия инженеров в совершенствовании эффективности процесса будут представлять лишь пустой бесцельный поиск. Большинство работ, которые анализируют теплоперенос и процессы разделения с термодинамической точки зрения, пытаются найти компромисс между термодинамическими требованиями и требованиям к оборудованию ректификации. Этот вопрос, по мнению большинства ученых, в будущем будет основным направлением в совершенствовании термодинамической эффективности процесса ректификации.
Поскольку для ректификации характерна поливариантность, возникает задача не только уменьшить потери полезной энергии, но и сопоставить различные схемы и режимы проведения процесса с помощью ряда критериев. В качестве таких критериев нами выбраны количество теплоты, подведенное к кубу ректификационной колонны, работа разделения и производство энтропии в колонне. Проведем термодинамический анализ и последовательно рассмотрим выражения для расчета критериев, условия их использования и соотношения при различных постановках задач [8].
РАБОТА РАЗДЕЛЕНИЯ
Для того чтобы ввести понятие работы разделения, воспользуемся выводами из работ Карно [8] и применим их к процессам разделения. Рассмотрим ректификационную колонну и два совершенных тепловых двигателя, которые позволяют для совершения работы использовать теплоту Q1, подводимую в куб колонны, и Q2, отводимую от конденсатора (рис. 1).
Рис. 1.
Ректификационная колонна: Q1, Q2 – количество теплоты, подводимое и отводимое в колонне соответственно; Q10, Q20 – количество теплоты, отводимое из системы в окружающую среду из куба и конденсатора колонны соответственно; T1–T2 – температура, при которой подводится и отводится теплота в колонну соответственно; T0 – температура окружающей среды.
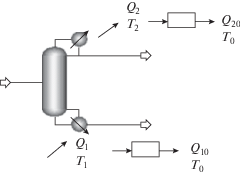
Данные тепловые двигатели совершают работу A1 и A2, при этом в окружающую среду с температурой T0 отводятся тепловые потоки Q10 и Q20 соответственно. Учитывая, что тепловые двигатели являются идеальными, можно для каждого из них записать следующие соотношения:
Количество тепла, которое поглощается и отдается при определенной температуре в обратимом процессе связано соотношением
(3)
$\frac{{{{Q}_{1}}}}{{{{Q}_{2}}}} = \varphi \left( {{{{{T}_{1}}} \mathord{\left/ {\vphantom {{{{T}_{1}}} {{{T}_{2}}}}} \right. \kern-0em} {{{T}_{2}}}}} \right),$Работа равна сумме всех теплот, отдаваемых системой (с отрицательным знаком) и получаемых системой (с положительным знаком). Таким образом, для каждого случая работа разделения может быть представлена в виде выражений
(5)
${{A}_{1}} = {{Q}_{1}} - {{Q}_{{10}}} = {{Q}_{1}} - {{Q}_{1}}\frac{{{{T}_{0}}}}{{{{T}_{1}}}} = {{Q}_{1}}\left( {1 - \frac{{{{T}_{0}}}}{{{{T}_{1}}}}} \right),$аналогично
Работа разделения определяется как разность между полезной работой, которая могла бы быть выполнена в термодинамически совершенном двигателе теплотой, подводимой к системе, и работой, которая могла бы быть выполнена в таком двигателе теплом, удаляемым из процесса [3]. Таким образом, выражение для работы разделения примет вид
(7)
$\begin{gathered} A = {{A}_{1}} - {{A}_{2}} = {{Q}_{1}}\left( {1 - \frac{{{{T}_{0}}}}{{{{T}_{1}}}}} \right) - {{Q}_{2}}\left( {1 - \frac{{{{T}_{0}}}}{{{{T}_{2}}}}} \right) = \\ = {{Q}_{1}} - {{Q}_{2}} + {{T}_{0}}\left( {\frac{{{{Q}_{2}}}}{{{{T}_{2}}}} - \frac{{{{Q}_{1}}}}{{{{T}_{1}}}}} \right). \\ \end{gathered} $Из формулы (7) отметим, что существует такой вариант, при котором теплоты Q1 и Q2 равны: Q1 = = Q2 = Q. В этом случае выражение для работы разделения преобразуется к виду
(8)
$A = Q{{T}_{0}}\left( {\frac{1}{{{{T}_{2}}}} - \frac{1}{{{{T}_{1}}}}} \right) = {{T}_{0}}\Delta S.$Как выражение (7), так и частный случай, выражение (8), есть мера расходуемой энергии – работа разделения, она является критерием термодинамической эффективности процесса ректификации. На основе этого критерия можно сопоставлять различные схемы и варианты проведения процесса.
Рассмотрим условие, при котором теплоты Q1 и Q2 становятся равными. Величины их напрямую зависят от энергетических характеристик исходной смеси, проиллюстрируем это с помощью энтальпийной диаграммы (рис. 2).
Рис. 2.
Энтальпийная диаграмма бинарной смеси бензол–толуол: HF, HD, HW – энтальпия потока питания, потока дистиллята и куба соответственно; Q1, Q2 – количество теплоты, подводимое и отводимое в колонне соответственно; xF, xD, xW – мольная доля легкокипящего компонента в потоке питания, дистилляте и кубе соответственно.
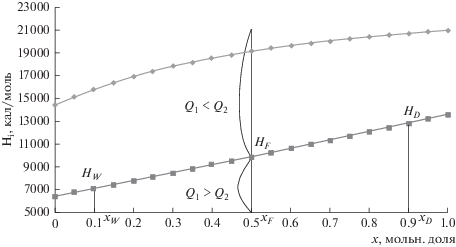
В соответствии с первым законом термодинамики полный энергетический баланс колонны можно представить уравнением
Приведем уравнение (9) к виду
(10)
$(D + W)\left[ {{{H}_{F}} - \frac{{{{Q}_{2}} - {{Q}_{1}}}}{{D + W}}} \right] = D{{H}_{D}} + W{{H}_{W}}.$Введя обозначение
последнее уравнение можно переписать как
или
С другой стороны, в соответствии с материальным балансом
отсюда
Из уравнений (13) и (15) имеем
(16)
$\frac{{{{x}_{W}} - {{x}_{F}}}}{{{{x}_{F}} - {{x}_{D}}}} = \frac{{{{H}_{W}} - H_{F}^{ * }}}{{H_{F}^{ * } - {{H}_{D}}}} = \frac{D}{W}.$Из уравнения (16) следует, что на диаграмме (x, H), представленной на (рис. 2), точки (xW, HW), (xF, $H_{F}^{*}$) и (xD, HD) расположены на одной прямой. Из практически линейного характера линии кипящей жидкости следует, что энтальпии $H_{F}^{*}$ отвечает состояние исходной смеси, близкое к состоянию кипящей жидкости. Из соотношения (11) вытекает, что
Из уравнения (17), в свою очередь, следуют соотношения
(18)
$\begin{gathered} {{H}_{F}} > H_{F}^{*}:{\text{ }}{{Q}_{2}} > {{Q}_{1}}; \hfill \\ {{H}_{F}} = H_{F}^{*}:{\text{ }}{{Q}_{2}} = {{Q}_{1}}; \hfill \\ {{H}_{F}} < H_{F}^{*}:{\text{ }}{{Q}_{2}} < {{Q}_{1}}. \hfill \\ \end{gathered} $Расчетный эксперимент, проведенный нами для пяти бинарных смесей с разным отклонением от идеальности с помощью программного пакета Aspen Plus®, показал, что кривая кипящей жидкости во всех случаях имеет практически линейных характер. Энтальпия жидкости слабо зависит от давления. Таким образом, при подаче исходной смеси в состоянии кипения значения теплот Q1 и Q2 практически совпадают, и работа разделения может быть вычислена по формуле (8) [3].
Отметим, что при варьировании какого-либо внутреннего параметра колонны (положения тарелки питания, флегмового числа, общего числа тарелок в колонне) в условиях закрепленного состава продуктовых потоков и питания, что соответствует проектной постановке задачи расчета колонны, разница между теплотами остается постоянной Q1 – Q2 = const, в то время как сами значения теплот могут изменяться.
СООТНОШЕНИЕ ЭКСТРЕМУМОВ ТЕРМОДИНАМИЧЕСКИХ КРИТЕРИЕВ
Помимо работы разделения и затрат теплоты в кубе критерием термодинамической эффективности процесса может выступать производство энтропии в колонне. Рассмотрим взаимосвязь между различными критериями, на примере процесса ректификации бинарной смеси. Энтропия в системе может изменяться вследствие двух причин, либо в результате переноса ее через границы системы, либо в результате возникновения энтропии в самой системе. Согласно природе возникновения и изменения энтропии, можем выразить ее через два слагаемых:
где ∆eS – приращение энтропии за счет внешнего обмена; ∆iS – производство энтропии внутри колонны.Изменение энтропии системы за счет внешнего переноса тепла и вещества может быть представлено выражением
(20)
${{\Delta }_{e}}S = \frac{{{{Q}_{1}}}}{{{{T}_{1}}}} - \frac{{{{Q}_{2}}}}{{{{T}_{2}}}} + F{{S}^{F}} - D{{S}^{D}} - W{{S}^{W}}.$Если энтропия в ректификационной колонне постоянно производится, то энтропия внутреннего содержимого колонны в условиях стационарности должна оставаться постоянной, и, следовательно, вся произведенная энтропия должна отводиться в окружающую среду:
Таким образом, выражение для производства энтропии в колонне примет вид
(22)
${{\Delta }_{i}}S = \frac{{{{Q}_{2}}}}{{{{T}_{2}}}} - \frac{{{{Q}_{1}}}}{{{{T}_{1}}}} - F{{S}^{F}} + D{{S}^{D}} + W{{S}^{W}}.$Воспользовавшись условием экстремума для производства энтропии
проведем анализ выражения (22). В спецификации ректификационной колонны закрепляем составы продуктовых потоков и варьируем рабочий параметр x, в качестве которого могут выступать положение тарелки питания, общее число тарелок в колонне, флегмовое число и т.д. Из (22) при наличии экстремума имеем
(24)
$\begin{gathered} \frac{{\delta \left( {{{\Delta }_{i}}S} \right)}}{{\delta x}} = \frac{\delta }{{\delta x}}\left( {\frac{{{{Q}_{2}}}}{{{{T}_{2}}}} - \frac{{{{Q}_{1}}}}{{{{T}_{1}}}}} \right) + \\ + \,\,\frac{\delta }{{\delta x}}\left( {D{{S}^{D}} + W{{S}^{W}} - F{{S}^{F}}} \right) = 0. \\ \end{gathered} $Из принятой нами спецификации, при которой состояние материальных потов закреплено (состав, количество, температура), следует равенство нулю выражения δ(DSD + WSW – FSF)/δx. В этом случае (24) можно представить в виде
(25)
$\frac{{\delta \left( {{{\Delta }_{i}}S} \right)}}{{\delta x}} = \frac{\delta }{{\delta x}}\left( {\frac{{{{Q}_{2}}}}{{{{T}_{2}}}} - \frac{{{{Q}_{1}}}}{{{{T}_{1}}}}} \right) = 0.$Рассматривая частный случай, описанный выше, когда значения Q1 и Q2 равны, а также учитывая постоянство температур продуктовых потоков в связи с тем, что состав их закреплен, имеем Q1 = Q2 = Q:
(26)
$\frac{{\delta \left( {{{\Delta }_{i}}S} \right)}}{{\delta x}} = \frac{\delta }{{\delta x}}\left( {\frac{{{{Q}_{2}}}}{{{{T}_{2}}}} - \frac{{{{Q}_{1}}}}{{{{T}_{1}}}}} \right) = \left( {\frac{1}{{{{T}_{2}}}} - \frac{1}{{{{T}_{1}}}}} \right)\frac{{\delta Q}}{{\delta x}}.$Из соотношения (26) следует, что минимальное производство энтропии в колонне при принятой нами спецификации будет соответствовать случаю, когда затраты тепла, подводимого к кубу, будут минимальны, т.е.
(27)
$\frac{{\delta \left( {{{\Delta }_{i}}S} \right)}}{{\delta x}} = 0 \leftrightarrow \frac{{\delta Q}}{{\delta x}} = 0.$Рассмотрим общий случай и проанализируем, будет ли справедлив полученный нами вывод при условии Q1 ≠ Q2. Изменение производства энтропии при варьировании рабочего параметра колонны даст выражение
(28)
$\begin{gathered} \frac{{\delta \left( {{{\Delta }_{i}}S} \right)}}{{\delta x}} = \frac{\delta }{{\delta x}}\left( {\frac{{{{Q}_{2}}}}{{{{T}_{2}}}} - \frac{{{{Q}_{1}}}}{{{{T}_{1}}}}} \right) = \frac{\delta }{{\delta x}}\left( {\frac{{{{T}_{1}}{{Q}_{2}} - {{T}_{2}}{{Q}_{1}}}}{{{{T}_{1}}{{T}_{2}}}}} \right) = \\ = \frac{1}{{{{T}_{1}}{{T}_{2}}}}\left( {{{T}_{1}}\frac{{\delta {{Q}_{2}}}}{{\delta x}} - {{T}_{2}}\frac{{\delta {{Q}_{1}}}}{{\delta x}}} \right). \\ \end{gathered} $Учитывая, что на основании проведенного нами теоретического анализа, подтвержденного расчетным экспериментом, доказано, что при изменении рабочего параметра колонны меняются значения теплот Q1 и Q2, однако разность между ними остается неизменной, поэтому Q1 – Q2 = const, δ(Q1 – Q2) = 0, следовательно, δQ1 = δQ2. Принимая это равенство во внимание, преобразуем формулу (18):
(29)
$\frac{{\delta \left( {{{\Delta }_{i}}S} \right)}}{{\delta x}} = \frac{{({{T}_{1}} - {{T}_{2}})}}{{{{T}_{1}}{{T}_{2}}}}\frac{{\delta Q}}{{\delta x}},$Мы теоретически показали поведение экстремума для критерия – производство энтропии для частного и общего случая. Следующим этапом будет анализ критерия – работы разделения. Формула для расчета последней представлена выражением (8), варьируя рабочий параметр x, получим выражение
(30)
$\frac{{\delta A}}{{\delta x}} = {{T}_{0}}\left( {\frac{1}{{{{T}_{2}}}} - \frac{1}{{{{T}_{1}}}}} \right)\frac{{\delta Q}}{{\delta x}}.$Учитывая уравнение (30), дополним соотношение (27):
(31)
$\frac{{\delta \left( {{{\Delta }_{i}}S} \right)}}{{\delta x}} = 0 \leftrightarrow \frac{{\delta Q}}{{\delta x}} = 0 \leftrightarrow \frac{{\delta A}}{{\delta x}} = 0.$Минимум для производства энтропии в колонне и работы разделения соответствует минимуму затрат теплоты в кубе колонны при условии Q1 = Q2. Рассмотрим общий случай при условии Q1 ≠ Q2.
Варьируя рабочий параметр в формуле (7) $A = {{Q}_{1}} - {{Q}_{2}} + {{T}_{0}}\left( {\frac{{{{Q}_{2}}}}{{{{T}_{2}}}} - \frac{{{{Q}_{1}}}}{{{{T}_{1}}}}} \right),$ получим
(32)
$\frac{{\delta A}}{{\delta x}} = \frac{\delta }{{\delta x}}\left( {{{Q}_{2}} - {{Q}_{1}}} \right) + {{T}_{0}}\frac{\delta }{{\delta x}}\left( {\frac{{{{Q}_{2}}}}{{{{T}_{2}}}} - \frac{{{{Q}_{1}}}}{{{{T}_{1}}}}} \right),$(33)
$\frac{{\delta A}}{{\delta x}} = \frac{\delta }{{\delta x}}\left( {{{Q}_{2}} - {{Q}_{1}}} \right) + {{T}_{0}}\left( {\frac{{({{T}_{1}} - {{T}_{2}})}}{{{{T}_{1}}{{T}_{2}}}}} \right)\frac{{\delta Q}}{{\delta x}}.$Как выяснили ранее, выражение $\delta ({{Q}_{1}} - {{Q}_{2}}) = 0,$ тогда
(34)
$\frac{{\delta A}}{{\delta x}} = {{T}_{0}}\left( {\frac{{({{T}_{1}} - {{T}_{2}})}}{{{{T}_{1}}{{T}_{2}}}}} \right)\frac{{\delta Q}}{{\delta x}}.$Аналогично рассуждениям о минимальном значении производства энтропии имеем
Таким образом, как и в частном случае, где Q1 = = Q2, так и в общем случае Q1 ≠ Q2, выражение прироста энтропии системы и выражение работы разделения процесса принимают минимальное значение, когда затраты тепла, подводимого к кубу колонны, также будут минимальны, при соблюдении введенной спецификации.
Выводы, полученные теоретически, были подтверждены расчетным экспериментом, рассчитан процесс разделения бинарной смеси бензол–толуол в программном комплексе Aspen Plus®, и построены зависимости затрат теплоты в кубе колонны, производства энтропии и работы разделения от положения тарелки питания (рис. 3).
Рис. 3.
К поиску экстремумов термодинамических критериев: A – работа разделения, ккал/ч; N – номер тарелки в ректификационной колонне; Q – количество теплоты, подводимое к кубу колонны, ккал/ч; S – энтропия, ккал/ч.
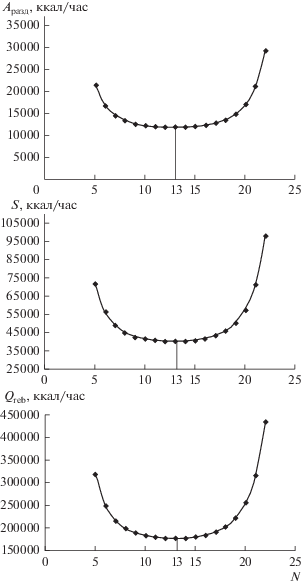
Зависимости показали, что при варьировании внутреннего параметра колонны (положение тарелки питания) минимальное значение каждого из критериев совпадает.
В работе [9] проведен расчетный эксперимент, который показал, что оптимальное расположение тарелки питания соответствует минимальному значению энергозатрат и одновременно минимальному значению производства энтропии. Однако авторы работы теоретического обоснования данного факта не предоставили.
ЗАКЛЮЧЕНИЕ
В результате проведенного термодинамического анализа были получены выражения для расчета производства энтропии внутри колонны, работы разделения в идеальном и реальном процессах.
На основе анализа энтальпийных диаграмм определены условия равенства теплот, подводимой к кубу колонны и отводимой от конденсатора, и показано, что в случае, когда исходная смесь имеет температуру, близкую к температуре кипения, величины двух теплот совпадают.
Для расчета термодинамических критериев в программном пакете Aspen Plus созданы модули, на основе которых могут быть сопоставлены различные варианты организации процесса. Также исследована взаимосвязь термодинамических критериев (теплоты, подведенной к кубу колонны, работы разделения и производства энтропии). В результате установлено, что оптимумы каждого из критериев совпадают при проектном варианте расчета ректификации, что подтвердил вычислительный эксперимент.
Работа выполнена в рамках проекта РНФ № 16-19-10632.
ОБОЗНАЧЕНИЯ
| A | работа разделения, ккал/ч |
| D | поток отбираемого дистиллята, кмоль/ч |
| F | поток питания в колонну, кмоль/ч |
| H | энтальпия, кал/моль |
| N | номер тарелки в ректификационной колонне |
| Q | количество теплоты, ккал/ч |
| S | энтропия, ккал/ч |
| T | температура, °С |
| W | поток кубового продукта, кмоль/ч |
| x | мольная доля |
ИНДЕКСЫ
Список литературы
Шаргут Я., Петела Р. Эксергия. М.: Энергия, 1968.
Петлюк Ф.Б., Серафимов Л.А. Многокомпонентная ректификация. Теория и расчет. М.: Химия, 1983.
Бенедикт М. Многоступенчатые процессы разделения. Дистилляция и ректификация. М.: ИЛ, 1949.
Fonyo Z. Thermodynamic analysis of rectification. I. Reversible model of rectification // Int. Chem. Eng. 1974. V. 14. № 1. P. 18.
Fonyo Z. Thermodynamic analysis of rectification. II. Finite cascade models // Int. Chem. Eng. 1974. V. 14. № 2. P. 203.
Платонов В.М., Берго Б.Г. Разделение многокомпонентных смесей. М.: Химия, 1965.
Додж Б.Ф. Химическая термодинамика. М.: ИЛ, 1950.
Пригожин И., Дэфей Р. Химическая термодинамика. Новосибирск: Наука, 1966.
Zakharov M.K., Pisarenko Yu.A. Theoretical rationale for the selection of the optimal scheme of separation of the three-component mixture // Fine Chem. Tech. 2017. V.12.№4. P.43. [Захаров М. К., Писаренко Ю. А. Теоретическое обоснование выбора оптимальной схемы разделения трехкомпонентной смеси // Тонкие хим. технологии. 2017. Т.12. №4. С.43].
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


