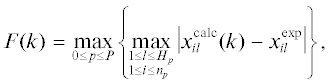1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 53, № 3, 2019

Теоретические основы химической технологии, 2019, T. 53, № 3, стр. 302-308

Интервальный алгоритм глобального поиска областей неопределенности при моделировании кинетики сложных химических реакций

М. В. Сахибгареева *

Уфимский государственный нефтяной технический университет
Уфа, Россия

* E-mail: margarita.vl2011@gmail.com

Поступила в редакцию 29.12.2017
После доработки 28.03.2018
Принята к публикации 10.04.2018

Полный текст (PDF)

Аннотация

Работа посвящена проблеме математического описания кинетического эксперимента в условиях множественности решений обратных задач химической кинетики. Предложен новый алгоритм глобального поиска областей неопределенности, представляющий собой симбиоз методов глобальной оптимизации с интервальным эволюционным подходом. Модели реакций, построенные с использованием кинетических параметров из таких областей, описывают экспериментальный материал в пределах задаваемой исследователем допустимой погрешности измерений. Применение данного алгоритма позволяет построить комплексную многомерную область в глобальном пространстве кинетических параметров, в то время как в работах многих авторов осуществляется поиск наборов локальных решений, описывающих экспериментальный материал практически с одинаковой точностью, либо строятся одно-, двух- или трехмерные проекции областей неопределенности по отдельности. Предложенный алгоритм был опробован на примере моделирования реакции ингибированного окисления н-декана. Благодаря формальному параллелизму его структуры были применены технологии параллельных вычислений для ускорения расчетов.

Ключевые слова: математическая химия, химическая кинетика, анализ неопределенности, глобальная оптимизация, погрешность эксперимента, обратные задачи

ВВЕДЕНИЕ

В наше время существует множество примеров успешного применения результатов исследования кинетики химических превращений для решения академических и производственных проблем. Кинетический анализ механизмов может дать информацию об основных путях протекания реакции. Компьютерное моделирование, основанное на детальных механизмах реакции, позволяет получить более полную информацию о ходе химического процесса, чем при проведении натурного эксперимента, как по целевым продуктам, так и по промежуточным веществам, и оперировать с малыми численными значениями концентраций лабильных компонентов реакций, которые нельзя измерить экспериментальным путем напрямую из-за технических ограничений. Моделирование кинетики сложных химических процессов все шире используется в задачах охраны окружающей среды. С использованием математических моделей детальных механизмов реакции можно максимизировать выход конечного продукта с одновременным подавлением образования вредных побочных продуктов. Используя модели атмосферной химии, исследователи рассчитывают влияние и последствия выбросов различных загрязнителей, в том числе и в зависимости от их объемов.

Чтобы улучшить применимость математических моделей на практике, необходимо определять надежность их прогнозов.

В работах М.Г. Слинько, В.Г. Горского, С.И. Спивака [1–5] поставлена и развита проблема неединственности решения обратной задачи химической кинетики, которая возникает из-за малой информативности кинетических измерений [3] вследствие: а) малого числа веществ, технически доступных экспериментальному измерению; б) погрешности измерений.

Ввиду существования множества решений обратных кинетических задач стало активно развиваться направление численного анализа неопределенности кинетических моделей – построения областей неопределенности параметров и допустимых решений – которое применяется вместо устаревшего подхода к поиску глобального минимума соответствия расчета и химического эксперимента при построении математических моделей реакций. Анализ неопределенности используется при принятии управленческих решений на основе прогнозов, выдаваемых построенной математической моделью.

Вопросам моделирования в условиях неопределенности посвящен ряд работ [6–11]. Методы количественной оценки влияния неопределенности в кинетических параметрах реакций на неопределенность итоговой модели, основанные на вероятностном подходе, рассмотрены в работах [9–12].

Однако построение областей неопределенности кинетических параметров реакций само по себе является отдельной задачей. Поэтому осуществлять анализ неопределенности необходимо как на этапе принятия решений, так и на этапе идентификации математической модели реакции.

Несмотря на многолетнюю историю математического моделирования механизмов химических превращений, проблема разработки эффективных математических методов для анализа неопределенности остается актуальной.

АКТУАЛЬНОСТЬ СОЗДАНИЯ НОВОГО МЕТОДА

Постановка задачи определения интервалов параметров математического описания при условии удовлетворения системы ограничениям на предельно допустимую погрешность экспериментальных измерений была сделана еще в СССР в работе [13]. Интервал неопределенности по параметру ${{k}_{q}}$ определяется как отрезок ${{d}_{q}}$ = = $\left[ {\min {{k}_{q}},\max {{k}_{q}}} \right].$ Вариация значения параметра внутри отрезка dq сохраняет необходимую точность (погрешность) описания измерений, которая, как правило, известна экспериментатору:

(1)
$\sum\limits_{i = 1}^{{{n}_{p}}} {\left| {x_{{il}}^{{{\text{calc}}}}(k) - x_{{il}}^{{\exp }}} \right| \leqslant {{\varepsilon }_{l}},} \,\,\,\,l = \overline {1...{{H}_{p}}} ,$
где Hp – число наблюдаемых веществ эксперимента p; np – число замеров каждой из компонент, число экспериментальных точек; $x_{{il}}^{{{\text{calc}}}}$ и $x_{{il}}^{{{\text{exp}}}}$ – расчетные и экспериментальные значения концентраций l-го наблюдаемого вещества в i-й момент времени, моль/л; k – вектор констант скоростей химической реакции; εl – предельно допустимая погрешность измерений l-го компонента (например, температура измеряется термометром с точностью ±0.5°C, что означает, что ε = 0.5).

Временное распределение состава реагирующей смеси по заданному механизму химического процесса рассчитывается путем решения прямой задачи химической кинетики [14–16], которая в общем виде представляет собой задачу Коши для системы обыкновенных дифференциальных уравнений:

(2)
$\frac{{dx}}{{dt}} = f(k;x),\,\,\,\,x(0) = {{x}^{0}}.$

В работах [17, 18] анализ неопределенности реализуется локальным образом вокруг некоторой точки, удовлетворяющей (1). Ищется такая точка, как правило, путем решения задачи минимизации. Затем находится та или иная проекция многомерной области на двумерную плоскость по паре кинетических констант путем отклонения сначала влево от локальной точки по каждой координате проекции при фиксации остальных констант до достижения предельно допустимой погрешности описания. Затем аналогичным способом вправо от локальной точки. Таким образом, данный алгоритм представляет собой постобработку решения классической обратной задачи химической кинетики, в которой ищется минимум расхождения расчета и эксперимента. В работе [19] этим же подходом предлагается строить области по трем координатам, т.е. трехмерные проекции. Однако при увеличении размерности такой подход становится слишком вычислительно затратным даже при использовании технологий параллельных вычислений.

В [16, 20] показано, как учет дополнительных ограничений позволяет сузить области неопределенности, тем самым уменьшая неоднозначность решений обратной задачи химической кинетики.

В работе [21] построение областей неопределенности осуществляется покоординатно локальным поиском на основе интервальных вычислений с помощью модифицированного метода Хука–Дживса. В данном алгоритме в качестве варьируемых параметров обратной задачи вместо вектора констант скоростей выступает вектор их интервалов dq. Результатом метода является гиперпараллелепипед, вписанный в искомую область.

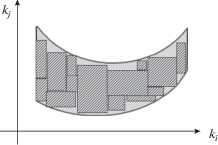
Однако, учитывая неединственность решений обратных задач химической кинетики, методы локального поиска неопределенных интервалов не дают целостной картины истинных многомерных областей неопределенности кинетических параметров, описывающих экспериментальный материал в пределах допустимой погрешности. При попытке использовать получаемые локальными методами области неопределенности для проведения последующих численных экспериментов по исследованию реакции при различных условиях остаются нераскрытыми вопросы: а) принадлежат ли несколько различных локальных решений обратной задачи одной связной области неопределенности или нескольким несвязным? б) как будут выглядеть области неопределенности при учете дополнительных ограничений [16, 20] и будут ли они связанными? в) как из отдельных одно-, двух- или трехмерных проекций сформировать итоговую многомерную область неопределенности (рис. 1) без потери решений? Например, гиперпараллелепипед D со сторонами, равными соответствующим одномерным интервалам, может выходить за пределы искомой области (точка A на рис. 1а находится вне искомой области). Одной двумерной проекцией E искомую область не описать (точка B на рис. 1б выходит за границы области E). А вписанный гиперпараллелепипед P может не покрывать некоторые ее участки (точка С на рис. 1в находится за пределами параллелепипеда P). На примере работ [16–19] видно, что области неопределенности могут иметь произвольную форму.

Рис. 1.

Иллюстрация к проблеме формирования многомерной области неопределенности: (a) – как гиперпараллелепипеда D, описанного вокруг искомой области S; (б) – как проекции E на двумерную плоскость; (в) – как гиперпараллелепипеда P, вписанного в искомую область.

Целью данной работы является разработка нового алгоритма глобального поиска многомерных областей неопределенности. Для достижения поставленной цели необходимо решение следующих задач: формализация и программная реализация алгоритма; разработка визуального программного инструмента для отображения результатов работы алгоритма; апробация алгоритма на примере конкретного химического процесса.

ОПИСАНИЕ АЛГОРИТМА

В основу разработанного алгоритма глобального анализа неопределенности кинетических параметров легла идея, используемая в интервальном эволюционном алгоритме поиска глобального экстремума [22]. Области неопределенности предлагается искать с помощью множества гиперпараллелепипедов, в работе [22] именуемых брусами, которые с задаваемой точностью заполнят искомую область (или области) неопределенности.

Пусть исходная область поиска описывается как некоторый гиперпараллелепипед из N-мерного евклидового пространства:

$D = \{ k \in {{R}^{N}}{\text{:}}\,\,{{a}_{i}} \leqslant {{k}_{i}} \leqslant {{b}_{i}},\,\,{\text{1}} \leqslant i \leqslant N\} ,$
где a и b – границы области поиска констант скоростей стадий; N – число стадий механизма некоторого химического процесса.

В качестве функционала невязки F, являющегося количественной оценкой расхождения экспериментальных данных и расчетов, примем

(3)
где P – число экспериментов, p – индекс эксперимента.

В текущей постановке задачи в отличие от (1) вместо сумм предлагается рассматривать максимумы отклонений, чтобы гарантировать допустимое соответствие расчета и эксперимента компонентов в каждый момент времени. Тогда за общую предельно допустимую погрешность эксперимента для всех наблюдаемых веществ примем

(4)
${{\varepsilon }_{{error}}} = {{\max }_{{1 \leqslant l \leqslant {{H}_{p}}}}}\left\{ {{{\varepsilon }_{l}}} \right\}.$

Данный параметр εerror подается в качестве одного из входных параметров алгоритма.

При запуске работы алгоритма исходная область произвольным образом разбивается на непересекающиеся брусы, из которых формируется начальный рабочий массив. Например, можно разбить исходную область на M равных частей по самой длинной стороне гиперпараллелепипеда. Либо принять брус исходной области в качестве начального разбиения.

Основный цикл алгоритма состоит из следующих шагов.

1. Из рабочего массива выбирается произвольным образом брус с индексом m.

2. В произвольной точке (некоторый вектор y) выбранного m-го бруса вычисляется значение функционала невязки расчета и эксперимента F(k) (3).

3. Сравнивается значение функционала F со значением заданной предельно допустимой погрешности эксперимента εerror (4).

а. В случае если значение F > εerror, то с помощью произвольного метода глобальной оптимизации ищется на брусе m глобальный минимум $F_{m}^{{{\text{min}}}}$ (в программной реализации автора в качестве такого метода использовался генетический алгоритм [23]).

i. Если минимум на брусе больше значения заданной предельно допустимой погрешности эксперимента ($F_{m}^{{{\text{min}}}}$ > εerror), то m-й брус считается не принадлежащим к области неопределенности и исключается из массива брусов.

ii. В противном случае брус делится на части, которые записываются в массив. Сам m-й брус удаляется из массива брусов. Происходит возврат к шагу 1.

б. В случае если значение F ≤ εerror, то с помощью алгоритма глобальной оптимизации ищется глобальный максимум $F_{m}^{{{\text{max}}}}$ на m-м брусе.

i. Если $F_{m}^{{{\text{max}}}}$ > εerror, то m-й брус считается принадлежащим к области неопределенности, записывается в файл результата и исключается из дальнейшего рассмотрения (удаляется из рабочего массива брусов).

ii. В противном случае i-й брус делится на части, которые записываются в рабочий массив. Сам m-й брус удаляется из рабочего массива брусов. Происходит возврат к шагу 1.

Таким образом, алгоритм “прощупывает” во всем пространстве решений границу, при которой результат модели не превышает допустимую погрешность эксперимента εerror.

Во избежание бесконечного деления бруса на шагах а(II) и б(II) вводится специальное ограничение – минимально допустимый размер бруса – задаваемое в качестве входного параметра алгоритма.

Таким образом, решение будет представлять собой некоторый конечный набор брусов, принадлежащих искомой области неопределенности (рис. 2), а также некоторый конечный набор брусов, содержащих в себе границу области.

Рис. 2.

Общий вид решения задачи глобального анализа неопределенности кинетических параметров.

ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ

Вычислительный эксперимент проводился на примере реакции ингибированного окисления н-декана в присутствии параоксидифениламина. При этом рассмотрена классическая схема механизма ингибированного окисления, состоящая из ключевых элементарных стадий [16]:

i1) I → 2r˙

i2) r˙ + RH → R˙ + rH

1) R˙ + O2 → ${\text{RO}}_{{\text{2}}}^{\centerdot }$

2) ${\text{RO}}_{{\text{2}}}^{\centerdot }\quad\, + \,\,{\text{RH}} \to {{{\text{R}}}^{\centerdot }} + {\text{ROOH}}$

6) ${\text{RO}}_{{\text{2}}}^{\centerdot } + {\text{RO}}_{{\text{2}}}^{\centerdot }\quad \to {\text{ROOR}} + {{{\text{O}}}_{{\text{2}}}}$

7) ${\text{RO}}_{{\text{2}}}^{\centerdot } + {\text{InH}} \to {\text{I}}{{{\text{n}}}^{\centerdot }} + {\text{ROOH}}$

←7) ${\text{I}}{{{\text{n}}}^{\centerdot }} + {\text{ROOH}} \to {\text{RO}}_{{\text{2}}}^{\centerdot } + {\text{InH}}{\text{.}}$

В качестве инициатора I использовался пероксид дикумила [C6H5C(CH3)2O]2. Символом RH обозначен субстрат окисления (н-декан), InH – ингибитор параоксидифениламин.

В качестве математической формулировки (2) данной реакции использовалось описание прямой задачи изотермической нестационарной модели без изменения объема в закрытой системе на основе закона действующих масс, которое состоит из системы обыкновенных нелинейных дифференциальных уравнений:

$\begin{gathered} \frac{{d{{x}_{i}}}}{{dt}} = f(k,x),\,\,\,\,i = 1...M;\,\,\,\,{{f}_{i}} = \sum\limits_{j = 1}^N {{{S}_{{ij}}}{{W}_{j}}} ; \\ {{W}_{j}} = k_{j}^{ + }\prod\limits_{i = 1}^M {x_{i}^{{\left| {{{{\alpha }}_{{ij}}}} \right|}}} - k_{j}^{ - }\prod\limits_{i = 1}^M {x_{i}^{{\left| {{{{\beta }}_{{ij}}}} \right|}}} ,\,\,\,\,{{x}_{i}}(0) = x_{i}^{0}, \\ \end{gathered} $
где xi – концентрации веществ, участвующих в реакции, мол. д.; М – количество веществ; N – количество стадий; αij и βij – положительные и отрицательные элементы стехиометрической матрицы соответственно; Wj – скорость j-й стадии, 1/c; $k_{j}^{ + }$ и $k_{j}^{ - }$ – приведенные константы скорости прямой и обратной стадии соответственно, 1/c.

Далеко не все элементарные стадии этого механизма охарактеризованы кинетическими константами скорости, что связано с методическими сложностями регистрации малых концентраций и крайне малого время жизни промежуточных частиц (атомов и радикалов). И даже для тех стадий, которые считаются хорошо изученными, значения их констант варьируются в пределе порядка в различных источниках литературы, даже при использовании одинаковых методов измерения. К примеру, значение константы скорости стадии (2) при температуре 30°С, измеренной методом прерывистого освещения в случае, когда в качестве субстрата окисления RH выступает (C6H5)2CH2k2, варьируется от 0.30 [24] до 0.68 [25]. А когда в качестве RH выступает C6H5CH2CH3, значение константы k2 варьируется от 0.04 [25] до 0.115 [24].

Вычислительная программа реализована на языке С++ с применением стандарта MPI для распараллеливания вычислений. В качестве метода глобальной оптимизации, используемого в шагах 3a и 3б, выбран генетический алгоритм. Его подробное описание применительно к задачам химической кинетики приведено в работе [23]. Расчет проводился на кластере Центра высокопроизводительной обработки данных Карельского научного центра РАН.

В результате моделирования данной реакции была получена глобальная область неопределенности кинетических параметров. Пример проекции на двумерную плоскость по паре констант скорости k(i1)– k(2) представлен на рис. 3.

Рис. 3.

Проекция многомерной области неопределенности реакции ингибированного окисления н-декана на двумерную плоскость k(i1)– k(2): А (розовый цвет) – область поиска; В (голубой цвет) – проекция области; С (зеленый цвет) – область, содержащая границу проекции искомой области неопределенности.

ЗАКЛЮЧЕНИЕ

Апробация предложенного алгоритма на примере реакции ингибированного окисления н-декана демонстрирует принципиальную возможность построения многомерной области неопределенности разом, а не отдельных ее проекций, как это делается в работах многих других авторов. Такой способ позволяет повысить надежность получаемых математических моделей за счет целостности картины и упрощает их использование на практике или при планировании дальнейших численных экспериментов по исследованию реакции при различных условиях или поиску оптимальных режимов проведения.

Данный алгоритм интегрирован в облачный сервис математического моделирования химической кинетики Galo GO [26], в котором автоматизируется удаленный запуск расчета с поддержкой параллельных вычислений на суперкомпьютере Карельского научного центра РАН, а также представлены инструменты для графического отображения проекций по выбираемым пользователем константам скоростей.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 17-47-020068).

ОБОЗНАЧЕНИЯ

k приведенная к одноразмерному виду константа скорости элементарной стадии механизма реакции, 1/с
t время, с
x концентрация вещества, моль/л
εl предельно допустимая погрешность измерений, моль/л

ИНДЕКСЫ

0 начальное значение
calc расчетное значение наблюдаемого вещества, получаемое в результате решения прямой кинетической задачи (2)
exp экспериментальное значение наблюдаемого вещества
i индекс момента времени
j индекс константы скорости стадии механизма реакции
l индекс наблюдаемого вещества
m индекс бруса в приведенном алгоритме

Список литературы

  1. Клибанов М.В., Спивак С.И., Тимошенко В.И., Слинько М.Г. О числе независимых параметров стационарной кинетической модели // ДАН СССР. 1973. Т. 208. № 6. С. 1387.

  2. Спивак С.И., Горский В.Г. О полноте доступных кинетических измерений при определении констант скорости сложной химической реакции // Хим. физика. 1982. Т. 1. № 2. С. 237.

  3. Спивак С.И. Информативность эксперимента и проблема неединственности решения обратных задач химической кинетики. Автореф. Дис. … докт. физ.-мат. наук. Черноголовка, 1984.

  4. Spivak S.I., Ismagilova A.S., Akhmerov A.A. Analysis of the informativity of kinetic measurements in solving inverse problems of chemical kinetics for multi-route reactions // Kinetics and Catalysis. 2014. V. 55. № 5. P. 538. [Спивак С.И., Исмагилова А.С., Ахмеров А.А. Анализ информативности кинетических измерений при решении обратных задач химической кинетики для многомаршрутных реакций // Кинетика и катализ. 2014. Т. 55. № 5. С. 566.]

  5. Бадртдинова Ф.Т., Спивак С.И., Бигаева Л.А. Множественность решения обратной задачи процесса поликонденсации аспарагиновой кислоты // Матем. и прогр. обесп. систем в пром. и соц. сферах. 2011. № 1. С. 133.

  6. Gomez-Acata R.V., Neria-Gonzalez M.I., Aguilar-Lopez R. Robust software sensor design for the state estimation in a sulfate-reducing bioreactor // Theor. Found. Chem. Eng. 2016. V. 50. № 1. P. 67.

  7. Orazbayev B.B., Orazbayeva K.N., Utenova B.E. Development of mathematical models and modeling of chemical engineering systems under uncertainty // Theor. Found. Chem. Eng. 2014. V. 48. № 2. P. 138. [Оразбаев Б.Б., Оразбаева К.Н., Утенова Б.Е. Разработка математических моделей и моделирование химико-технологической системы в условиях неопределенности // Теорет. основы хим. технологии. 2014. Т. 48. № 2. С. 152.]

  8. Ostrovsky G.M., Lapteva T.V., Ziyatdinov N.N. Optimal design of chemical processes under uncertainty // Theor. Found. Chem. Eng. 2014. V. 48. № 5. P. 583. [Островский Г.М., Лаптева Т.В., Зиятдинов Н.Н. Проектирование оптимальных химико-технологических систем в условиях неопределенности // Теорет. основы хим. технологии. 2014. Т. 48. № 5. С. 527.]

  9. Zsély I.Gy., Zádor J., Turány T. Uncertainty analysis of NO production during methane combustion // Int. J. Chem. Kinet. 2008. V. 40. P. 754.

  10. Nagy T., Turányi T. Uncertainty of Arrhenius parameters // Int. J. Chem. Kinet. 2011. V. 43. P. 359.

  11. Muñoz-Carpena R., Zajac Z., Kuo Y.M. Global sensitivity and uncertainty analysis of the water quality model VFSMOD-W // Trans. Am. Soc. Agricul. Biol. Eng. 2007. V. 50. № 5. P. 1719.

  12. Urzay J., Kseib N., Davidson D.F., Iaccarino G., Hanson R.K. Uncertainty-quantification analysis of the effects of residual impurities on hydrogen-oxygen ignition in shock tubes // Combustion and Flame. 2014. V. 161. P. 1.

  13. Канторович Л.В. О некоторых новых подходах к вычислительным методам и обработке наблюдений // Сиб. матем. журн. 1962. Т. 3. № 5. С. 701.

  14. Gerchikov A.Y., Sharipova G.M., Safarova I.V., Sakhibgareeva M.V., Spivak S.I. Reactivity and Mechanism of the Action of С60 Fullerene Used as an Inhibitor for the Radical Chain Oxidation of 1,4-Dioxine // Russ. J. Phys. Chem. A. 2017. V. 91. № 6. P. 1010. [Герчиков А.Я., Шарипова Г.М., Сафаровa И.В., Сахибгареева М.В., Спивак С.И. Реакционная способность и механизм действия фуллерена с60 в качестве ингибитора радикально-цепного окисления 1,4-диоксана // Журн. физ. химии. 2017. Т. 91. № 6. С. 957.]

  15. Gerchikov A.Y., Sharipova G.M., Akhatova G.R., Mustafin A.G., Spivak S.I., Sakhibgareeva M.V. Kinetics, mechanism, and mathematical model of the reaction between uracil and hydrogen peroxide in aqueous solution // Kinetics and Catalysis. 2015. V. 56. № 5. P. 563. [Герчиков А.Я., Шарипова Г.М., Ахатова Г.Р., Мустафин А.Г., Сахибгареева М.В., Спивак С.И. Кинетика и механизм реакции урацила с пероксидом водорода в водных растворах. Математическая модель реакции // Кинетика и катализ. 2015. Т. 56. № 5. С. 571.]

  16. Tikhonova M.V., Garifullina G.G., Gerchikov A.Ya., Spivak S.I. The kinetic model of n-decane oxidation in the presence of inhibitory composition // International Journal of Chemical Kinetics. 2014. V. 46. № 4. P. 220.

  17. Аристархов А.В., Спивак С.И., Губайдуллин И.М. Определение областей пространства кинетических параметров и интервалов неопределенностей для частных реакций гидроалюминирования олефинов // Вестн. Баш. ун-та, серия “Химия”. 2009. Т. 14. № 4. С. 1331.

  18. Райманова Г.К., Спивак С.И. Область неопределенности по кинетическим константам для одной кинетической модели // Обоз. прикл. и пром. мат. 2007. Т. 4. № 5. С. 923.

  19. Бобренёва Ю.О., Новичкова А.В. Интервальный поиск параметров кинетической модели частных реакций гидроалюминирования олефинов // Тез. докл. Всерос. мол. науч.-практ. конф. “Актуальные вопросы науки и образования”. 2013. С. 98.

  20. Асанова Н.В. Методы и алгоритмы восстановления аналитических зависимостей по экспериментальным данным в условиях неопределенности. Дис. … канд. техн. наук. Волгоград, 2011.

  21. Вайтиев В.А., Мустафина С.А. Поиск областей неопределенности кинетических параметров математических моделей химической кинетики на основе интервальных вычислений // Вест. Юж.-Урал. гос. ун-та. 2014. Т. 7. № 2. С. 99.

  22. Панов Н.В., Шарый С.П. Интервальный эволюционный алгоритм для поиска глобального оптимума // Изв. Алт. гос. ун-та. 2011. Т. 2. № 1(69). С. 108.

  23. Тихонова М.В., Губайдуллин И.М. Компьютерная обработка химических экспериментов при решении обратных кинетических задач на основе параллельных вычислений // Вестн. Омск. ун-та. 2012. № 2(64). С. 194.

  24. Howard J.A., Ingold K.U., Symonds M. Absolute rate constants for hydrocarbon oxidation: VIII. The reactions of cumylperoxy radicals // Can. J. Chem. 1968. V. 46. № 6. P. 1017.

  25. Howard J.A., Ingold K.U. Absolute rate constants for hydrocarbon autoxidation: IV. Tetralin, cyclohexene, diphenylmethane, ethylbenzene, and allylbenzene // Can. J. Chem. 1966. V. 44. № 10. P. 1119.

  26. Сахибгареева М.В., Глущенко Е.И., Еникеева Л.В., Шарипова Г.М. Облачный сервис решения задач химической кинетики с использованием параллельных вычислений // Сис. и сред. информ. 2017. № 1. С. 155.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал