Теоретические основы химической технологии, 2019, T. 53, № 3, стр. 243-255
Изучение фазового равновесия в трехкомпонентных системах, образованных 2,2,2-трифторэтанолом, водой и органическими спиртами
Е. В. Лупачев 1, *, А. В. Полковниченко 1, 2, С. Я. Квашнин 1, В. А. Лотхов 1, Н. Н. Кулов 1
1 Институт общей и неорганической химии им. Н.С. Курнакова РАН
119071 Москва, Россия
2 МИРЭА – Российский технологический университет (Институт тонких химических технологий)
119571 Москва, Россия
* E-mail: egorlu91@gmail.com
Поступила в редакцию 21.12.2018
После доработки 14.01.2019
Принята к публикации 17.01.2019
Аннотация
Экспериментально изучено фазовое равновесие бинарных составляющих трехкомпонентных систем, образованных 2,2,2-трифторэтанолом, водой и органическим спиртом (метанолом, этанолом или изопропанолом). Показано, что системы метанол–2,2,2-трифторэтанол, 2,2,2-трифторэтанол– этанол и 2,2,2-трифторэтанол–изопропанол при атмосферном давлении характеризуются наличием бинарных азеотропов с максимумом температуры кипения. С помощью программного комплекса Aspen Plus® V. 9.0 рассчитано фазовое равновесие следующих трехкомпонентных систем: 2,2,2-трифторэтанол–метанол–вода, 2,2,2-трифторэтанол–этанол–вода, 2,2,2-трифторэтанол– изопропанол–вода.
ВВЕДЕНИЕ
Одним из способов, используемых в настоящее время для получения фторорганических спиртов, является восстановление эфира соответствующей фторорганической кислоты гидроборатом натрия или алюмогидридами [1]. В результате синтеза образуется смесь, состоящая из фторированного и органического спиртов и побочные неорганические соединения. Для выделения неорганических продуктов реакции смесь разбавляют водой, в результате чего образуется две фазы. После отделения водной фазы, оставшаяся органическая фаза содержит фторорганический спирт, воду и органический спирт. Следующая стадия очистки, предполагает выделение из образованной смеси фторорганического спирта требуемой чистоты. Однако, технологические аспекты этого этапа выделения фторорганических спиртов, освещены в литературе недостаточно полно. Для разработки технологии выделения и очистки фторорганического спирта, требуется наличие исчерпывающей информации о фазовом равновесии жидкость-пар в изучаемых системах.
В зависимости от способа используемого при получении 2,2,2-трифторэтанола сырья, на финальную стадию очистки поступает смесь 2,2,2-трифторэтанола, воды и одного из перечисленных далее спиртов: метанола, этанола или изопропанола. Данных по фазовому равновесию исследуемых трехкомпонентных систем в литературе нет, а данные по парожидкостному равновесию (ПЖР) их бинарных составляющих, включающих 2,2,2-трифторэтанол, весьма ограничены.
В работах [2–5] приведены данные ПЖР для бинарной системы 2,2,2-трифторэтанол–вода. К сожалению, в работе [5] отсутствует информация о составе паровой фазы, а изотермические данные работ [3, 4] не соответствуют рабочему диапазону давлений. Изобарические данные по ПЖР, приведенные в работе [2] для системы 2,2,2-трифторэтанол–вода при давлении 101 кПа, ограничены диапазонами от 0.15 до 0.9 мол. д. по составу жидкой фазы и от 0.55 до 0.93 мол. д. по составу паровой фазы и не охватывают весь диапазон концентраций.
В работе [6] приведены данные по фазовому равновесию системы 2,2,2-трифторэтанол–этанол. Материалы этой работы представляют собой локализованную точку азеотропа, а приведенные в статье [6] зависимости равновесной температуры от состава паровой и жидкой фаз не позволяют использовать полученные данные из-за возникающей погрешности при интерпретации графических данных.
Цель настоящей работы – экспериментальное и вычислительное исследование фазового равновесия жидкость-пар в трехкомпонентных системах 2,2,2-трифторэтанол–метанол–вода, 2,2,2-трифторэтанол–этанол–вода, 2,2,2-трифторэтанол–изопропанол–вода в широком диапазоне концентраций.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Реактивы. В качестве реактивов использовали 2,2,2-трифторэтанол (CF3CH2OH), дополнительно очищенный в лаборатории путем ректификации. Содержание основного вещества составило 99.4 мас. %, содержание воды было не более 0.05 мас. %; метанол и этанол имели чистоту 99.5 мас. %, а изопропанол (CH3CHOHCH3) категории ОСЧ 99.9 мас. %. Содержание воды не более 0.09 мас. %. Чистоту используемых веществ определяли на газовом хроматографе GC2010 Plus Shimadzu с пламенноионизационным детектором, газ-носитель – азот. Содержание воды определяли по методу Фишера.
Исследуемые системы. В настоящей работе проведено исследование фазового равновесия жидкость-пар трех трехкомпонентных систем: CF3CH2OH–CH3OH–H2O, CF3CH2OH–CH3CH2OH–H2O и CF3CH2OH– CH3CHOHCH3–H2O.
Оборудование. Эксперименты проводили на модифицированном эбулиометре Свентославского с объемом загрузки 50 мл, снабженном насосом Коттреля. Схема установки представлена на рис. 1. Давление измеряли аналоговым барометром с точностью 0.5 мм рт. ст., равновесную температуру измеряли ртутным термометром с точностью 0.1°С.
Рис. 1.
Эбулиометр Свентославского, снабжeнный трубкой Коттреля: 1 – куб, 2 – насос Коттреля, 3 – карман для термометра, 4 – стеклянная спираль, 5 – сепарационное пространство, 6 – холодильник, 7 – счетчик капель, 8 – переточная трубка.
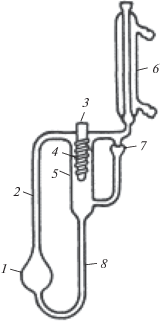
Масса навесок измерялась на аналитических весах с точностью 0.0001 г. Пробы кубовой жидкости и парового конденсата анализировали на рефрактометре ИРФ-454 Б2М; диапазон показателей преломления nD от 1.2 до 1.7 с точностью измерения 1 × 10–4.
Методика проведения эксперимента. Все эксперименты проводили при атмосферном давлении. Чтобы убедиться, что фазовое равновесие достигнуто, после установления температуры систему выдерживали в течение 30 мин и более, после чего проводили отбор кубовой жидкости и парового конденсата.
ОБРАБОТКА РЕЗУЛЬТАТОВ
Использованные в расчетах физико-химические свойства чистых веществ взяты из базы программного комплекса Aspen Plus® V.9.0 (табл. 1).
Таблица 1.
Данные по чистым веществам, представленные в программном комплексе Aspen Plus® V.9.0
| i | М, г/моль | Ткип, °С при 760 мм рт.ст. | ρ, г/см3 при 20°С |
|---|---|---|---|
| CF3CH2OH | 100.04 | 73.81 | 1.3912 |
| CH3OH | 32.04 | 64.53 | 0.7943 |
| CH3CH2OH | 46.069 | 78.31 | 0.7903 |
| CH3CHOHCH3 | 60.095 | 82.05 | 0.7867 |
| Вода | 18.015 | 100.02 | 0.9965 |
При моделирование ПЖР изучаемых систем давления чистых компонентов метанола, этанола, изопропанола и воды рассчитывались по уравнению Антуана:
(1)
$\ln {{p}_{i}} = {{C}_{{1i}}} + \frac{{{{C}_{{2i}}}}}{{T + {{C}_{{3i}}}}} + {{C}_{{4i}}}T + {{C}_{{5i}}}\ln T + {{C}_{{6i}}}{{T}^{{{{C}_{{7i}}}}}}.$Параметры уравнения Антуана, взятые из программного комплекса Aspen Plus® V.9.0 для диапазона температур ${{С }_{{8i}}} \leqslant T \leqslant {{C}_{{9i}}},$ приведены в табл. 2.
Таблица 2.
Коэффициенты уравнения Антуана
| i | Метанол | Этанол | Изопропанол | Вода |
|---|---|---|---|---|
| С1i | 77.8252 | 68.4112 | 105.8272 | 68.7562 |
| C2i | –6904.5 | –7122.3 | –9040 | –7258.2 |
| C3i | 0 | 0 | 0 | 0 |
| С4i | 0 | 0 | 0 | 0 |
| С5i | –8.8622 | –7.1424 | –12.6760 | –7.3037 |
| С6i | 7.47 × 10–6 | 2.89 × 10–6 | 5.54 × 10–6 | 4.17 × 10–6 |
| С7i | 2 | 2 | 2 | 2 |
| С8i | –97.68 | –114.10 | –87.89 | 0.01 |
| С9i | 239.35 | 240.85 | 235.15 | 373.95 |
Парциальное давление 2,2,2-трифторэтанола рассчитывалось по уравнению Вагнера:
(2)
$\ln {{p}_{i}} = \ln {{p}_{{ci}}} + \frac{{{{C}_{{1i}}}\left( {1 - {{T}_{{ri}}}} \right) + {{C}_{{2i}}}{{{\left( {1 - {{T}_{{ri}}}} \right)}}^{{1,5}}} + {{C}_{{3i}}}{{{\left( {1 - {{T}_{{ri}}}} \right)}}^{{2,5}}} + {{C}_{{4i}}}{{{\left( {1 - {{T}_{{ri}}}} \right)}}^{5}}}}{{{{T}_{{ri}}}}},\quad$Параметры уравнения Вагнера, взятые из программного комплекса Aspen Plus® V.9.0 для диапазона температур ${{T}_{{{\text{low}}}}} \leqslant T \leqslant {{T}_{{{\text{up}}}}},$ приведены в табл. 3.
Таблица 3.
Коэффициенты уравнения Вагнера
| i | 2,2,2-трифторэтанол |
|---|---|
| C1i | –8.85513 |
| C2i | 2.02666 |
| C3i | –6.3807 |
| С4i | –2.93655 |
| lnpci | 10.4929 |
| Tci | 225.42 |
| Tlow | –44.05 |
| Tup | 225.42 |
Проверка полученных экспериментальных данных на термодинамическую сходимость была выполнена по методу, предложенному в работе [7], с помощью уравнения Дюгема–Маргулеса и в программном комплексе Aspen Plus® V.9.0 по методу Херингтона и Редлиха–Кистера [7–9].
Анализа взаимного расположения графических зависимостей коэффициентов активности от состава смеси γ1 = f(x1) и γ2 = f(x2) показал, что экспериментальные данные не противоречат условию, выраженному уравнением Дюгема–Маргулеса и, следовательно, все четыре изученные системы качественно удовлетворяют термодинамическим требованиям.
Количественная проверка адекватности экспериментальных данных путем вычисления интеграла Херингтона и Редлиха–Кистера дала следующие результаты: 2,2,2-трифторэтанол–вода 8.51%, метанол–2,2,2-трифторэтанол 3.77%, 2,2,2-трифторэтанол–этанол 3.60% и 2,2,2-трифторэтанол–изопропанол – 0.35%. Для системы 2,2,2-трифторэтанол–вода величина интеграла Херингтона и Редлиха–Кистера принимает кратно большее значение, которое, однако, близко к значению полученному для данных работы [2] – 10.29%, для остальных систем, полученные результаты позволяют утверждать, что погрешность в определении состава паровой фазы не превышает 1% [7].
При выборе модели к ним предъявлялись следующие требования: применимость для условий эксперимента, возможность моделирования многокомпонентных систем, наличие необходимых для расчета данных о физико-химических свойствах чистых компонентов, наличие параметров выбранных моделей для систем метанол–вода, этанол–вода, изопропанол–вода. Из предложенных программным комплексом Aspen Plus® V.9.0 были выбраны модели локальных составов Non-Random Two-Liquid (NRTL) (3) и Wilson (4) для описания отклонения от идеального поведения жидкой фазы. В процессе расчета ПЖР паровую фазу считали идеальной:
(3)
$\begin{gathered} \ln {{\gamma }_{i}} = \frac{{\sum\nolimits_j {{{x}_{j}}{{\tau }_{{ji}}}{{G}_{{ji}}}} }}{{\sum\nolimits_k {{{x}_{k}}{{G}_{{ki}}}} }} + \\ + \,\,\sum\limits_j {\frac{{{{x}_{j}}{{G}_{{ij}}}}}{{\sum\limits_k {{{x}_{k}}{{G}_{{kj}}}} }}} \left( {{{\tau }_{{ij}}} - \frac{{\sum\limits_m {{{x}_{m}}{{\tau }_{{mj}}}{{G}_{{mj}}}} }}{{\sum\limits_k {{{x}_{k}}{{G}_{{kj}}}} }}} \right), \\ \end{gathered} $(4)
$\ln {{\gamma }_{i}} = 1 - \ln \left( {\sum\limits_j {{{A}_{{ij}}}{{x}_{j}}} } \right) - \sum\limits_j {\frac{{{{A}_{{ji}}}{{x}_{j}}}}{{\sum\limits_k {{{A}_{{jk}}}{{x}_{k}}} }}} ,$Параметры бинарного взаимодействия уравнений NRTL и Wilson для систем органический спирт – вода были взяты для случая идеальной паровой фазы из программного комплекса Aspen Plus® V.9.0 – набор коэффициентов APV90 VLE-IG. Для систем 2,2,2-трифторэтанол–вода, метанол–2,2,2-трифторэтанол, 2,2,2-трифторэтанол–этанол, 2,2,2-трифторэтанол–изопропанол параметры бинарного взаимодействия в программном комплексе Aspen Plus® V.9.0 отсутствуют. В случае описания системы метанол–вода модели NRTL и Wilson коррелируют как между собой, так и с экспериментальными данными [10, 11]. В случае описания системы этанол–вода модели NRTL и Wilson дают различные характеристики азеотропа. Данные по составу азеотропа работы [12] и полученные по моделям NRTL и Wilson представлены в табл. 4.
Таблица 4.
Характеристики азеотропа в системе этанол(1)–2,2,2-трифторэтанол(2) при 101.3 кПа
| Характеристики азеотропа | [12] | NRTL | Wilson |
|---|---|---|---|
| x1, мол. д. | 0.891 | 0.8952 | 0.8722 |
| Т, °C | 78.17 | 78.15 | 77.98 |
Анализ экспериментальных данных работ [13, 14] показал различие равновесных данных по температуре и составу паровой фазы в системе изопропанол–вода при давлении 101.32 кПа. В случае моделирования ПЖР в системе изопропанол–вода также наблюдается существенное различие в описании фазового равновесия доступными в программном комплексе Aspen Plus® V.9.0 параметрами бинарного взаимодействия моделей NRTL и Wilson. При этом, уравнение NRTL дает меньшую погрешность по температуре, а уравнение Wilson дает меньшую погрешность по составу фаз. Так как целью настоящей работы является качественное изучение и анализ концентрационного симплекса рассматриваемых трехкомпонентных систем, описание фазового равновесия бинарных составляющих спирт вода можно считать удовлетворительным.
Для оценки адекватности модели был проведен расчет состава паровой фазы и равновесной температуры для каждой отдельно взятой точки при ее экспериментальном значении давления и составе жидкой фазы. Коэффициенты бинарного взаимодействия уравнений NRTL и Wilson для систем 2,2,2-трифторэтанол–вода, метанол– 2,2,2-трифторэтанол, 2,2,2-трифторэтанол–этанол, 2,2,2-трифторэтанол–изопропанол приведены в табл. 5 и 6 соответственно. Приведенные в табл. 5 и 6 параметры бинарного взаимодействия рекомендуется использовать в исследуемом диапазоне давлений.
Таблица 5.
Коэффициенты бинарного взаимодействия уравнения NRTL
| i | 2,2,2-трифторэтанол | Метанол | 2,2,2-трифторэтанол | 2,2,2-трифторэтанол |
|---|---|---|---|---|
| j | Вода | 2,2,2-трифторэтанол | Этанол | Изопропанол |
| Aij | 1.84590 | 0 | 7.93865 | 0 |
| Aji | 22.4979 | 0 | –3.35524 | 0 |
| Bij | –804.298 | –17.5675 | –2974.84 | –219.124 |
| Bji | –7059.07 | –263.043 | 1051.80 | –140.609 |
| Cij | 0.3 | 0.3 | 0.3 | 0.3 |
Таблица 6.
Коэффициенты бинарного взаимодействия уравнения Wilson
| i | 2,2,2-трифторэтанол | Метанол | 2,2,2-трифторэтанол | 2,2,2-трифторэтанол |
|---|---|---|---|---|
| j | Вода | 2,2,2-трифторэтанол | Этанол | Изопропанол |
| Aij | –2.10336 | 0 | 1.60211 | 0 |
| Aji | –13.0978 | 0 | 45.2462 | 0 |
| Bij | –103.616 | 204.951 | –2976.38 | 151.138 |
| Bji | 4632.42 | 71.5644 | 2480.64 | 194.851 |
| Сij | 0 | 0 | 1.23366 | 0 |
| Cji | 0 | 0 | –8.83805 | 0 |
Экспериментальные и расчетные данные по фазовому равновесию жидкость-пар в системе 2,2,2-трифторэтанол–вода приведены в табл. 7. При оценке параметров бинарного взаимодействия уравнений Wilson и NRTL использовались два набора экспериментальных данных: приведенные в табл. 7 и данные работы [2]. На рис. 2 представлены зависимости x = f(y) и T = f(x, y) в системе 2,2,2-трифторэтанол–вода по данным табл. 7 и работы [2], а также модели NRTL и Wilson при давлении 755 мм рт. ст. Из приведенных зависимостей следует, что полученные в настоящей работе экспериментальные результаты и данные работы [2] согласуются.
Таблица 7.
Экспериментальные и расчетные данные по фазовому равновесию жидкость пар в системе 2,2,2-трифторэтанол(1)–вода(2)
| Р, мм рт. ст. | Т, °С | x1, мол. д. | y1, мол. д. | ||||
|---|---|---|---|---|---|---|---|
| Эксп. | модель | Эксп. | модель | ||||
| NRTL | Wilson | NRTL | Wilson | ||||
| 746 | 89.9 | 89.5 | 89.6 | 0.0157 | 0.3502 | 0.3190 | 0.3147 |
| 746 | 87.4 | 87.0 | 86.9 | 0.0269 | 0.4330 | 0.3855 | 0.3865 |
| 737.1 | 87.5 | 85.9 | 85.7 | 0.0333 | 0.4352 | 0.4084 | 0.4106 |
| 745 | 86.3 | 85.6 | 85.5 | 0.0369 | 0.4632 | 0.4221 | 0.4235 |
| 750 | 83.8 | 84.2 | 84.1 | 0.0527 | 0.5517 | 0.4616 | 0.4606 |
| 748.5 | 82.2 | 82.4 | 82.5 | 0.0853 | 0.5665 | 0.5062 | 0.5005 |
| 753 | 82.6 | 82.5 | 82.6 | 0.0860 | 0.5447 | 0.5077 | 0.5018 |
| 745 | 81.18 | 81.0 | 81.2 | 0.1351 | 0.5880 | 0.5408 | 0.5320 |
| 753 | 80.8 | 80.5 | 80.7 | 0.1837 | 0.5855 | 0.5618 | 0.5546 |
| 752 | 79.4 | 79.6 | 79.5 | 0.2807 | 0.6287 | 0.5924 | 0.5912 |
| 752 | 78.8 | 78.7 | 78.5 | 0.3834 | 0.6426 | 0.6284 | 0.6323 |
| 753.3 | 77.81 | 77.9 | 77.7 | 0.4799 | 0.6919 | 0.6705 | 0.6762 |
| 753 | 76.9 | 77.0 | 76.9 | 0.5781 | 0.7358 | 0.7218 | 0.7270 |
| 747.1 | 75.6 | 75.8 | 75.7 | 0.7004 | 0.8052 | 0.7960 | 0.7993 |
| 747.5 | 74.82 | 74.9 | 74.9 | 0.8070 | 0.8641 | 0.8664 | 0.8680 |
| 736.5 | 74 | 74.2 | 74.2 | 0.8521 | 0.9003 | 0.8979 | 0.8993 |
| 750 | 74.2 | 74.3 | 74.3 | 0.8971 | 0.9315 | 0.9283 | 0.9289 |
| 749 | 74.2 | 74.2 | 74.2 | 0.9056 | 0.9348 | 0.9343 | 0.9349 |
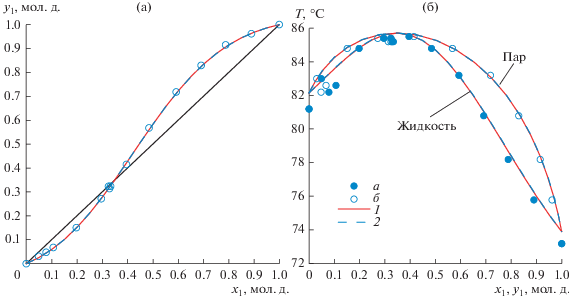
Рис. 2.
Система 2,2,2-трифторэтанол(1)–вода(2): (а) – зависимость состава паровой фазы от состава жидкой фазы; (б) – зависимость температуры кипения смеси от составов жидкой и паровой фаз. а, б – экспериментальные данные; в, г – литературные данные [2]; 1 – модель NRTL 755 мм рт. ст.; 2 – модель Wilson 755 мм рт. ст.
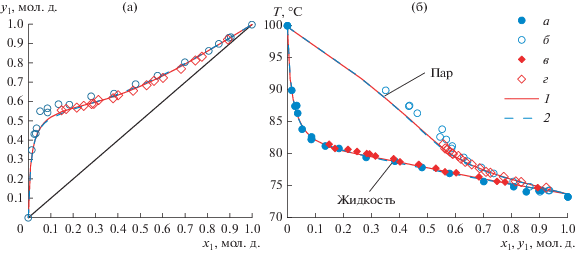
Для полученных в настоящей работе экспериментальных данных (табл. 7) абсолютная ошибка по температуре составляет: для модели NRTL – 0.3°С, для модели Wilson – 0.3°С; абсолютная ошибка по составу паровой фазы составляет: для модели NRTL – 0.0282 мол. д., для модели Wilson – 0.0288 мол. д.; относительная ошибка по составу паровой фазы составляет: для модели NRTL – 5.32%, для модели Wilson – 5.47%. В системе 2,2,2-трифторэтанол–вода следует отметить низкие значения коэффициента относительной летучести компонентов при высоких концентрациях 2,2,2-трифторэтанола, а S образный ход кривой равновесного пара на графике зависимости T = f(x, y) может быть вызван проявлением поверхностно активных свойств 2,2,2-трифторэтанола в водном растворе и, как следствие, наличием градиента концентраций в растворе.
Экспериментальные и расчетные данные по фазовому равновесию жидкость-пар в системе метанол–2,2,2-трифторэтанол приведены в табл. 8. Для системы метанол–2,2,2-трифторэтанол данные ПЖР были получены в настоящей работе впервые. Оценка параметров бинарного взаимодействия уравнений Wilson и NRTL проводилась по полному набору экспериментальных данных табл. 8. На рис. 3 представлены зависимости x = f(y) и T = f(x, y) в системе метанол–2,2,2-трифторэтанол для данных табл. 8, а также модели NRTL и Wilson при давлении 754 мм рт. ст.
Таблица 8.
Экспериментальные и расчетные данные по фазовому равновесию жидкость пар в системе метанол(1)–2,2,2-трифторэтанол(2)
| Р, мм рт. ст. | Т, °С | x1, мол. д. | y1, мол. д. | ||||
|---|---|---|---|---|---|---|---|
| Эксп. | модель | Эксп. | модель | ||||
| NRTL | Wilson | NRTL | Wilson | ||||
| 754 | 74.6 | 74.6 | 74.6 | 0.1146 | 0.0906 | 0.0874 | 0.0873 |
| 754 | 75.2 | 75.3 | 75.3 | 0.2210 | 0.1816 | 0.1965 | 0.1969 |
| 757 | 75.7 | 75.6 | 75.6 | 0.3108 | 0.3099 | 0.3082 | 0.3090 |
| 754 | 75.7 | 75.5 | 75.5 | 0.3578 | 0.3724 | 0.3723 | 0.3733 |
| 757 | 75.6 | 75.4 | 75.4 | 0.3932 | 0.4300 | 0.4222 | 0.4232 |
| 757 | 74.8 | 74.6 | 74.6 | 0.5041 | 0.5734 | 0.5813 | 0.5817 |
| 750 | 73.2 | 73.1 | 73.1 | 0.5927 | 0.7064 | 0.7011 | 0.7010 |
| 750 | 71.2 | 71.2 | 71.2 | 0.6912 | 0.8106 | 0.8149 | 0.8145 |
| 751 | 69 | 69.0 | 69.0 | 0.7898 | 0.8956 | 0.9018 | 0.9014 |
| 734 | 66 | 66.0 | 66.0 | 0.8918 | 0.9619 | 0.9627 | 0.9627 |
| 733.5 | 64.8 | 64.6 | 64.6 | 0.9505 | 0.9858 | 0.9859 | 0.9860 |
Рис. 3.
Система метанол(1)–2,2,2-трифторэтанол(2): (а) – зависимость состава паровой фазы от состава жидкой фазы; (б) – зависимость температуры кипения смеси от составов жидкой и паровой фаз. а, б – экспериментальные данные; 1 – модель NRTL 754 мм рт. ст.; 2 – модель Wilson 754 мм рт. ст.
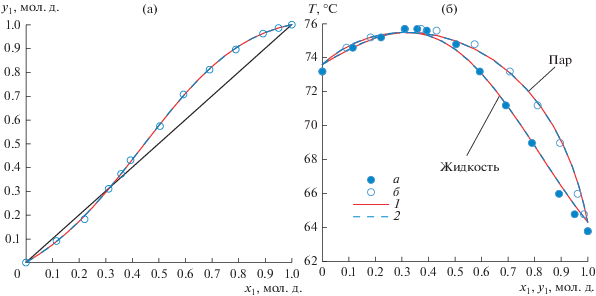
Для полученных в настоящей работе экспериментальных данных (табл. 8) абсолютная ошибка по температуре составляет: для модели NRTL – 0.1°С, для модели Wilson – 0.1°С; абсолютная ошибка по составу паровой фазы составляет: для модели NRTL – 0.0047 мол. д., для модели Wilson – 0.0047 мол. д.; относительная ошибка по составу паровой фазы составляет: для модели NRTL – 1.59%, для модели Wilson – 1.60%. Результаты эксперимента показали наличие в системе метанол(1)–2,2,2-трифторэтанол(2) азеотропа с максимумом температуры кипения. Характеристики азеотропа, полученные по моделям NRTL и Wilson при давлении 755 мм рт. ст.: x1 = 0.3185 мол. д., T = 75.53°С и x1 = 0.3160 мол. д., T = 75.54°С соответственно.
Экспериментальные и расчетные данные по фазовому равновесию жидкость-пар в системе 2,2,2-трифторэтанол–этанол приведены в табл. 9. При оценке параметров бинарного взаимодействия уравнений Wilson и NRTL использовали данные приведенные в табл. 9 с учетом данных по составу азеотропа работы [6]. На рис. 4 представлены зависимости x = f(y) и T = f(x, y) в системе 2,2,2-трифторэтанол–этанол для данных табл. 9, а также модели NRTL и Wilson при давлении 750 мм рт. ст.
Таблица 9.
Экспериментальные и расчетные данные по фазовому равновесию жидкость пар в системе 2,2,2-трифторэтанол(1)–этанол(2)
| Р, мм рт. ст. | Т, °С | x1, мол. д. | y1, мол. д. | ||||
|---|---|---|---|---|---|---|---|
| Эксп. | модель | Эксп. | модель | ||||
| NRTL | Wilson | NRTL | Wilson | ||||
| 747.9 | 78.7 | 78.4 | 78.7 | 0.0524 | 0.0278 | 0.0270 | 0.0268 |
| 747 | 78.7 | 78.6 | 78.6 | 0.0528 | 0.0285 | 0.0273 | 0.0270 |
| 740 | 79.2 | 79.2 | 79.2 | 0.1091 | 0.0660 | 0.0652 | 0.0651 |
| 740 | 79.9 | 79.8 | 79.8 | 0.1606 | 0.1118 | 0.1084 | 0.1088 |
| 753 | 80.9 | 80.8 | 80.7 | 0.2081 | 0.1590 | 0.1558 | 0.1564 |
| 754 | 81.3 | 81.2 | 81.2 | 0.2596 | 0.2143 | 0.2137 | 0.2138 |
| 754 | 81.3 | 81.5 | 81.4 | 0.3030 | 0.2660 | 0.2675 | 0.2667 |
| 744.5 | 81.6 | 81.4 | 81.3 | 0.3500 | 0.3269 | 0.3298 | 0.3282 |
| 747 | 81.6 | 81.6 | 81.5 | 0.4013 | 0.4000 | 0.4018 | 0.3991 |
| 747 | 81.6 | 81.5 | 81.5 | 0.4501 | 0.4709 | 0.4723 | 0.4688 |
| 752 | 81.5 | 81.4 | 81.4 | 0.5055 | 0.5556 | 0.5523 | 0.5485 |
| 753 | 81.2 | 81.1 | 81.1 | 0.5512 | 0.6215 | 0.6169 | 0.6134 |
| 742 | 80.2 | 80.1 | 80.2 | 0.6055 | 0.6912 | 0.6905 | 0.6884 |
| 743 | 79.6 | 79.7 | 79.7 | 0.6447 | 0.7482 | 0.7397 | 0.7384 |
| 748 | 79.0 | 79.0 | 79.0 | 0.7011 | 0.8161 | 0.8037 | 0.8033 |
| 751 | 78.4 | 78.5 | 78.5 | 0.7356 | 0.8491 | 0.8386 | 0.8387 |
| 748.2 | 76.5 | 76.6 | 76.6 | 0.8287 | 0.9228 | 0.9163 | 0.9166 |
| 751 | 75.4 | 75.5 | 75.5 | 0.8908 | 0.9579 | 0.9546 | 0.9546 |
| 753 | 74.6 | 74.6 | 74.5 | 0.9457 | 0.9790 | 0.9805 | 0.9804 |
Рис. 4.
Система 2,2,2-трифторэтанол(1)–этанол(2): (а) – зависимость состава паровой фазы от состава жидкой фазы; (б) – зависимость температуры кипения смеси от составов жидкой и паровой фаз. а, б – экспериментальные данные; 1 – модель NRTL 750 мм рт. ст.; 2 – модель Wilson 750 мм рт. ст.
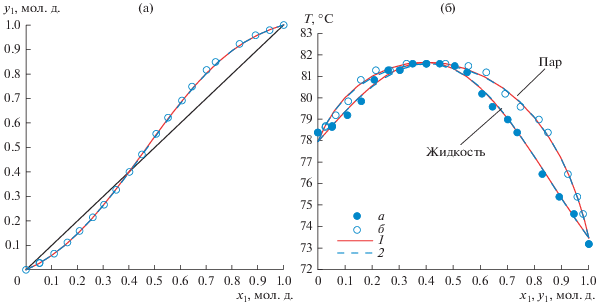
Для полученных в настоящей работе экспериментальных данных (табл. 9) абсолютная ошибка по температуре составляет: для модели NRTL – 0.1°С, для модели Wilson – 0.1°С; абсолютная ошибка по составу паровой фазы составляет: для модели NRTL – 0.0036 мол. д., для модели Wilson – 0.0040 мол. д.; относительная ошибка по составу паровой фазы составляет: для модели NRTL – 1.17%, для модели Wilson – 1.28%. Результаты эксперимента показали наличие в системе 2,2,2-трифторэтанол(1)–этанол(2) азеотропа с максимумом температуры кипения. Характеристики азеотропа, полученные по моделям NRTL и Wilson при давлении 750 мм рт. ст.: x1 = 0.4001 мол. д., T = 81.68°С и x1 = 0.4070 мол. д., T = 81.60°С соответственно.
Экспериментальные и расчетные данные по фазовому равновесию жидкость-пар в системе 2,2,2-трифторэтанол–изопропанол приведены в табл. 10. Для системы 2,2,2-трифторэтанол–изопропанол данные ПЖР были получены впервые. Оценка параметров бинарного взаимодействия уравнений Wilson и NRTL проводили по полному набору экспериментальных данных табл. 10. На рис. 5 представлены зависимости x = f(y) и T = f(x, y) в системе 2,2,2-трифторэтанол–изопропанол для данных табл. 10, а также модели NRTL и Wilson при давлении 763 мм рт. ст.
Таблица 10.
Экспериментальные и расчетные данные по фазовому равновесию жидкость пар в системе 2,2,2-трифторэтанол(1)–изопропанол(2)
| Р, мм рт. ст. | Т, °С | x1, мол. д. | y1, мол. д. | ||||
|---|---|---|---|---|---|---|---|
| Эксп. | модель | Эксп. | модель | ||||
| NRTL | Wilson | NRTL | Wilson | ||||
| 763 | 83 | 82.8 | 82.9 | 0.0489 | 0.0306 | 0.0249 | 0.0247 |
| 728.5 | 82.2 | 82.1 | 82.1 | 0.0787 | 0.0479 | 0.0437 | 0.0434 |
| 729 | 82.6 | 82.5 | 82.5 | 0.1068 | 0.0676 | 0.0640 | 0.0639 |
| 763 | 84.8 | 84.8 | 84.8 | 0.1980 | 0.1510 | 0.1491 | 0.1495 |
| 763 | 85.4 | 85.6 | 85.6 | 0.2965 | 0.2721 | 0.2724 | 0.2733 |
| 759 | 85.4 | 85.5 | 85.6 | 0.3251 | 0.3234 | 0.3133 | 0.3142 |
| 752.5 | 85.2 | 85.3 | 85.3 | 0.3289 | 0.3137 | 0.3189 | 0.3198 |
| 755 | 85.2 | 85.4 | 85.4 | 0.3337 | 0.3243 | 0.3260 | 0.3269 |
| 763 | 85.5 | 85.6 | 85.6 | 0.3958 | 0.4152 | 0.4205 | 0.4212 |
| 763 | 84.8 | 84.9 | 84.9 | 0.4852 | 0.5678 | 0.5595 | 0.5595 |
| 763 | 83.2 | 83.2 | 83.2 | 0.5930 | 0.7183 | 0.7131 | 0.7125 |
| 755 | 80.8 | 80.8 | 80.8 | 0.6911 | 0.8297 | 0.8257 | 0.8250 |
| 753.5 | 78.2 | 78.4 | 78.4 | 0.7882 | 0.9152 | 0.9070 | 0.9068 |
| 753 | 75.8 | 75.9 | 75.9 | 0.8898 | 0.9620 | 0.9636 | 0.9637 |
Рис. 5.
Система 2,2,2-трифторэтанол(1)–изопропанол(2): (а) – зависимость состава паровой фазы от состава жидкой фазы; (б) – зависимость температуры кипения смеси от составов жидкой и паровой фаз. а, б – экспериментальные данные; 1 – модель NRTL 763 мм рт. ст.; 2 – модель Wilson 763 мм рт. ст.
Для полученных в настоящей работе экспериментальных данных (табл. 10) абсолютная ошибка по температуре составляет: для модели NRTL – 0.1°С, для модели Wilson – 0.1°С; абсолютная ошибка по составу паровой фазы составляет: для модели NRTL – 0.0047 мол. д., для модели Wilson – 0.0050 мол. д.; относительная ошибка по составу паровой фазы составляет: для модели NRTL – 3.16%, для модели Wilson – 3.32%. Результаты эксперимента показали наличие в системе 2,2,2-трифторэтанол(1)–изопропанол(2) азеотропа с максимумом температуры кипения. Характеристики азеотропа, полученные по моделям NRTL и Wilson при давлении 763 мм рт. ст.: x1 = 0.3496 мол. д., T = 85.71°С и x1 = 0.3479 мол. д., T = 85.71°С соответственно.
Согласно данным работ [6, 15] неидеальность фазового равновесия жидкость-пар в рассмотренных выше системах можно объяснить образованием межмолекулярных комплексов.
Моделирование фазового равновесия жидкость пар при давлении 760 мм рт. ст. указывает на отсутствие трехкомпонентного азеотропа в системе метанол-2,2,2-трифторэтанол–вода. На рис. 6 приведен ход сепаратрисы и дистилляционных линий и положение бинарного азеотропа метанол–2,2,2-трифторэтанол построенные по модели Wilson. Для сравнения на графике представлен состав азеотропа по модели NRTL.
Рис. 6.
Фазовое равновесие в системе метанол–2,2,2-трифторэтанол–вода по модели Wilson при давлении 760 мм рт. ст.; о – точка азеотропа по модели NRTL.
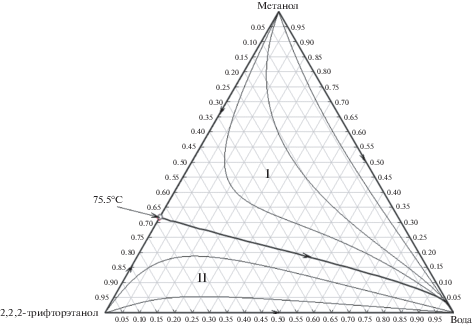
В случае описания фазового равновесия в системе метанол–2,2,2-трифторэтанол–вода моделями NRTL и Wilson различий практически нет. Из анализа рисунка следует, что система разделена на две подобласти дистилляции, границей между ними выступает криволинейное разделяющее многообразие азеотроп–вода. Для каждой из подобластей дистилляции I и II имеется свой набор продуктовых потоков. Неустойчивым узлом N– (фракция с минимальной температурой кипения) подобласти I (метанол–азеотроп–вода) является метанол, а подобласти II – 2,2,2-трифторэтанол. Устойчивым узлом N+, т. е. фракцией с максимальной температурой кипения, для обеих подобластей дистилляции I и II, является вода.
Моделирование фазового равновесия жидкость пар при давлении 760 мм рт. ст. указывает на наличие трехкомпонентного азеотропа в системе 2,2,2-трифторэтанол–этанол–вода. На рис. 7 приведен ход сепаратрис и дистилляционных линий и положение бинарных и трехкомпонентного азеотропов построенные по модели Wilson. Для сравнения на графике представлены составы азеотропов по модели NRTL.
Рис. 7.
Фазовое равновесие в системе 2,2,2-трифторэтанол–этанол–вода по модели Wilson при давлении 760 мм рт. ст.; о – точки азеотропов по модели NRTL.

Согласно табл. 4 описание характеристик азеотропа этанол–вода моделью NRTL лучше согласуется с экспериментальными данными. Из анализа рисунка следует, что система разделена на четыре подобласти дистилляции. Для каждой из подобластей дистилляции I, II, III, и IV имеется свой набор продуктовых потоков. Неустойчивым узлом N– (фракция с минимальной температурой кипения) подобластей I, II является 2,2,2-трифторэтанол, подобластей III и IV – бинарный азеотроп этанол– вода. Устойчивым узлом N+, т. е. фракцией с максимальной температурой кипения, подобластей дистилляции I и IV, является бинарный азеотроп 2,2,2-трифторэтанол–этанол, а подобластей II и III – вода.
Моделирование фазового равновесия жидкость пар при давлении 760 мм рт. ст. указывает на наличие трехкомпонентного азеотропа в системе 2,2,2-трифторэтанол–изопропанол–вода. На рис. 8 приведен ход сепаратрис и дистилляционных линий и положение бинарных и трехкомпонентного азеотропов построенные по модели Wilson. Для сравнения на графике представлены составы азеотропов по модели NRTL.
Рис. 8.
Фазовое равновесие в системе 2,2,2-трифторэтанол–изопропанол–вода по модели Wilson при давлении 760 мм рт. ст.; о – точки азеотропов по модели NRTL.

Из рис. 8 следует, что обе модели имеют сходимость в описании бинарного азеотропа 2,2,2-трифторэтанол–изопропанол, но дают существенное различие в описании трехкомпонентного азеотропа. Данный факт вызван противоречиями в описании ПЖР системы изопропанол–вода используемыми в настоящей работе моделями. В связи с упомянутым ранее отличием приведенных в работах [13, 14] данных о фазовом равновесии жидкость-пар системы изопропанол–вода, дать качественную оценку параметрам бинарного взаимодействия уравнений NRTL и Wilson, приведенным в программном комплексе Aspen Plus® V.9.0, не представляется возможным.
Отметим, что концентрационный симплекс системы 2,2,2-трифторэтанол–изопропанол– вода разделен на четыре подобласти дистилляции. По аналогии с системой 2,2,2-трифторэтанол–этанол–вода, для каждой из подобластей дистилляции I, II, III, и IV имеется свой набор продуктовых потоков. Неустойчивым узлом N– (фракция с минимальной температурой кипения) подобластей I, II является 2,2,2-трифторэтанол, подобластей III и IV – бинарный азеотроп изопропанол-вода. Устойчивым узлом N+, т.е. фракцией с максимальной температурой кипения, подобластей дистилляции I и IV, является бинарный азеотроп 2,2,2-трифторэтанол–изопропанол, а подобластей II и III – вода.
ЗАКЛЮЧЕНИЕ
В настоящей работе получены экспериментальные данные по фазовому равновесию жидкость–пар в системах 2,2,2-трифторэтанол–вода, метанол–2,2,2-трифторэтанол, 2,2,2-трифторэтанол–этанол и 2,2,2-трифторэтанол–изопропанол. Проведена оценка параметров бинарного взаимодействия уравнений NRTL и Wilson. Результаты математического моделирования показали удовлетворительное соответствие между расчетными и опытными данными. Рассчитано ПЖР в трехкомпонентных системах, приведены области дистилляции и соответствующие им составы возможных продуктов.
Таким образом, проведенный анализ указывает на сложную топологию фазового равновесия рассматриваемых систем с множеством областей дистилляции. Система метанол–2,2,2-трифторэтанол–вода в рабочем диапазоне давлений осложнена наличием бинарного азеотропа, что приводит к разбиению концентрационного симплекса на две подобласти дистилляции. Системы 2,2,2-трифторэтанол–этанол–вода и 2,2,2-трифторэтанол–изопропанол–вода осложнены в рабочем диапазоне давлений наличием двух бинарных и одного трехкомпонентного азеотропов, что приводит к формированию четырех подобластей дистилляции. Подобная структура фазовой диаграммы характерна и для других трехкомпонентных систем, типа фторорганический спирт–органический спирт–вода [16, 17].
Качественный анализ фазового равновесия исследуемых трехкомпонентных систем позволяет выделить следующие наиболее перспективные методы очистки 2,2,2-трифторэтанола, такие как: экстрактивная или реэкстрактивная ректификация, реализация принципа перераспределения полей концентрации, для разработки которых необходимы исследования в области фазового равновесию.
Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований в рамках научного проекта № 18-33-00984 мол_а.
ОБОЗНАЧЕНИЯ
| C1i–С9i | коэффициенты уравнения Антуана (Вагнера) |
| aij, bij, cij | коэффициенты бинарного взаимодействия уравнения NRTL (Wilson) |
| M | молекулярная масса, г/моль |
| nD | показатель преломления |
| P | давление, мм рт. ст. |
| pi | давление пара чистого компонента, мм рт. ст. |
| T | температура, °С |
| xi | концентрация компонента в жидкой фазе, мол. д. |
| yi | концентрация компонента в паровой фазе, мол. д. |
| γi | коэффициент активности |
| ρ | плотность, г/см3 |
ИНДЕКСЫ
Список литературы
Игумнов С.М., Игумнова Э.В. Синтезы фторорганических соединений. М.: ЗАО НПО “ПиМ-Инвест”, 2005.
Jadot R., Fraiha M.J. Isobaric Vapor-liquid equilibrium of 2,2,2-trifluoroethanol with water and 1-propanol binary systems // Chem. Eng. Data. 1988. V. 33. P. 237.
Rochester C.H., Symonds J.R. Thermodynamic studies of fluoroalcohols: III the thermodynamics of transfer of five fluoroalcohols from the gas-phase to aqueous solution // J. Chem. Soc., Faraday Trans. 1. 1973. V. 69. P. 1577.
Cooney A., Morcom K.W. Thermodynamic behaviour of mixtures containing fluoroalcohols 1. (water + 2,2,2-trifluoroethanol) // J. Chem. Thermodyn. 1988. V. 20. P. 735.
Kabata Y., Takada M., Sonobe R., Sugiura I., Uematsu M. Properties of {x(2,2,2-trifluoroethanol) + (1 – x)water} at temperatures from 310 K to 420 K. I. Bubble pressures and saturated-liquid densities // J. Chem. Thermodyn. 1993. V. 25. P. 649.
Mukherjee L.M., Grunwald E. Physical properties and hydrogen bonding in the system ethanol – 2,2,2-trifluoroethanol // J. Phys. Chem. 1958. V. 62. P. 1311.
Коган В.Б., Фридман В.М., Кафаров В.В. Равновесие между жидкостью и паром // Справочное пособие. Книга первая. М.: Наука, 1966.
Gmehling J., Onken U. Vapor-liquid equilibrium data collection (DECHEMA Chemistry Data Series. V. I. Part 1) / Eds. Behrens D., Eckermann R. Frankfurt/Main: DECHEMA, Deutsche Gesellschaft fur Chemisches Apparatewesen, 1977.
Voutsas E., Vasiliki L., Boukouvalas C., Magoulas K., Tassios D. Thermodynamic property calculations with the universal mixing rule for EoS/GE models: Results with the Peng-Robinson EoS and a UNIFAC model // Fluid Phase Equilib. 2006. V. 241. P. 216.
Alvarez V.H., Mattedi S., Iglesias M., Gonzalez-Olmos R., Resa J.M. Phase equilibria of binary mixtures containing methyl acetate, water, methanol or ethanol at 101.3 kPa // Phys. Chem. Liq. 2011. V. 49. P. 52.
Yang C., Ma S., Yin X.J. Organic salt effect of tetramethylammonium bicarbonate on the vapor liquid equilibrium of the methanol water system // Chem. Eng. Data. 2011. V. 56. № 10. P. 3747.
Lai H.-S., Lin Y.-F., Tu C.-H. Isobaric (vapor + liquid) equilibria for the ternary system of (ethanol + water + + 1,3-propanediol) and three constituent binary systems at P = 101.3 kPa // J. Chem. Thermodyn. 2014. V. 68. P. 13.
Arce A., Arce A., Martinez-Ageitos J., Rodil E., Soto A. (Vapour + liquid) equilibrium of (DIPE + IPA + water) at 101.32 kPa // J. Chem. Thermodyn. 2003. V. 35. № 6. P. 871.
Yorizane M., Yoshimura S., Yamamoto T. Measurement of the ternary vapor-liquid equilibrium (isopropyl alcohol–water–isopropyl ether system) // Kagaku Kogaku. 1967. V. 31. P. 451.
Chitra R., Smith P.E. Properties of 2,2,2-trifluoroethanol and water mixtures // Journal of Chemical Physics. 2001. V. 114. № 1. P. 426.
Лупачев Е.В., Полковниченко А.В., Квашнин С.Я., Кулов Н.Н. Исследование очистки фторорганических спиртов // Тез. докл. Химическая технология и биотехнология новых материалов и продуктов. IX Международная конференция Российского химического общества имени Д. И. Менделеева, посвященная 150-летию Российского химического общества имени Д.И. Менделеева М.: РХО им. Д.И. Менделеева: РХТУ им. Д.И. Менделеева, 2018. С. 34.
Полковниченко А.В., Лупачев Е.В., Квашнин С.Я., Кулов Н.Н. Основы технологии выделения фторорганических спиртов из промышленных смесей // Наука молодых – будущее России: сборник научных статей 3-й Международной научной конференции перспективных разработок молодых ученых (11–12 декабря 2018 года), в 6-х томах, Т. 5. Юго-Зап. гос. ун-т., Курск: ЗАО Университетская книга, 2018. С. 244.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


