1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 53, № 4, 2019

Теоретические основы химической технологии, 2019, T. 53, № 4, стр. 387-401

Расчет растворимости ароматических углеводородов в сверхкритических средах на основе энтропийного метода теории подобия

Т. Р. Билалов 1, *, Ф. М. Гумеров 2

1 Казанский национальный исследовательский технологический университет
Казань, Россия

2 Государственный научно-исследовательский институт химических продуктов
Казань, Россия

* E-mail: t.bilalov@yandex.ru

Поступила в редакцию 27.09.2018
После доработки 21.01.2019
Принята к публикации 07.02.2019

Полный текст (PDF)

Аннотация

Представлены результаты обобщения растворимости ароматических углеводородов в сверхкритическом диоксиде углерода с применением энтропийного метода теории подобия. Предметом обобщения явились экспериментальные данные различных авторов по растворимости 11 веществ, исследованных в диапазоне температур от 300 до 350 К (всего 728 экспериментальных точек и 50 изотерм). Показано, что полученная в результате обобщения зависимость позволяет с приемлемой точностью рассчитывать растворимость ароматических углеводородов, для которых было проведено обобщение, в сверхкритическом диоксиде углерода.

Ключевые слова: растворимость, ароматические углеводороды, сверхкритический диоксид углерода, давление насыщенных паров, описание, обобщение, прогнозирование, кроссоверное поведение изотерм растворимости

ВВЕДЕНИЕ

Критические явления привлекают неизменный интерес [1–3], оставаясь не в полной мере исследованными, а новые сверхкритические флюидные (СКФ) технологии одна за другой [4–6] движутся в направлении коммерциализации.

Именно величина и характер изменения растворимости веществ в средах, находящихся в СКФ-состоянии, в частности аномальный характер изменения дифференциальной растворимости, во многом определяют целесообразность, достоинства и жизнеспособность ключевых процессов СКФ-технологий.

Основным источником информации по растворимости веществ в СКФ-средах, по-прежнему, остается затратный по средствам и времени эксперимент в рамках различных методов, методик и подходов [7]. В то же время различные исследователи разрабатывают математические модели [8–21], призванные не только обобщить имеющиеся на сегодняшний день многочисленные экспериментальные данные, но и дать возможность прогнозировать растворимость тех или иных веществ с минимальным привлечением экспериментальных данных. Эти модели, в свою очередь, можно условно разделить на два типа. Первый тип моделей основан на различных уравнениях состояния реального газа, таких как уравнение Пенга–Робинсона, Соавва–Редлиха–Квонга, Ван-дер-Ваальса и ряд других [8–16]. Модели этого типа в качестве входных параметров используют критические свойства (температура и давление), фактор ацентричности и давление насыщенных паров или сублимации растворяемого вещества. Экспериментальное определение этих параметров зачастую затруднено или невозможно в силу ряда причин, вследствие чего приходится использовать различные расчетные методы определения этих величин, что часто является причиной некорректностей на этапах описания, обобщения и, тем более, прогнозирования в рамках применяемых моделей. Кроме того, в моделях этого типа для корректного описания растворимости используются так называемые параметры бинарного взаимодействия, вид и количество которых определяет принятый в модели закон смешивания. Имеющийся у авторов настоящей работы опыт подобных расчетов [22–26] показывает, что для получения корректного описания необходим достаточно значимый и не всегда имеющийся в наличии объем экспериментальных данных по растворимости.

Ко второму типу относятся эмпирические модели [17–21], увязывающие растворимость вещества в сверхкритическом флюидном растворителе с его плотностью. Они представляют собой уравнения, константы которых устанавливаются на основе экспериментальных данных по растворимости и являются сугубо индивидуальными. Хотя эти модели и просты, нельзя не обратить внимания на такую некорректность, как оперирование в качестве ключевого фактором термодинамического поведения лишь растворителя, а не раствора в целом. Как следствие, подобные модели способны лишь описывать результаты исследования растворимости. Они не дают качественной информации о взаимодействии растворитель–растворяемое вещество и практически не позволяют корректно предсказывать поведение растворимости.

Таким образом, задача разработки моделей описания и прогнозирования растворимости в сверхкритических флюидных растворителях, позволяющая использовать минимально возможный объем экспериментальных данных и использующая в своей основе альтернативные подходы, является актуальной. К одному из таких подходов можно отнести и энтропийный метод теории подобия, разработанный А.Г. Усмановым [27], позволяющий описывать и обобщать поведение теплофизических свойств веществ и их смесей с достаточно высокой точностью.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ

Исходными предпосылками для разработки энтропийного метода теории подобия явилась необходимость обобщения опытных данных по теплопроводности, вязкости и диффузии различных веществ [27].

Анализ условий подобия любого процесса заключается в выяснении предпосылок инвариантности уравнений, описывающих этот процесс, по отношению к подобному преобразованию переменных. Если при этом иметь в виду процессы переноса, то здесь уравнения Фурье, Ньютона и Фика оказываются непригодными для решения такой задачи, так как вид их зависимости от температуры и давления в общем случае не известен. Это обстоятельство заставляет искать другие пути анализа условий подобия процессов переноса, которые будут рассмотрены далее.

Процессы переноса относятся к категории неравновесных, поэтому для того чтобы описать состояние системы, в которой протекают эти процессы, в работе [27] предложено разбить ее на ряд макроскопических подсистем. Когда градиенты параметров не слишком велики, состояние каждой такой подсистемы в любой момент времени можно характеризовать определенным значением параметров состояния Р, Т, S и т.д.

В то же время, если рассматриваемая подсистема изменяется, то ее фазовая точка перемещается, описывая какую-то траекторию. Если подсистема составляет часть системы, находящейся в термодинамическом равновесии, траектория фазовой точки лежит в тонком слое вблизи поверхности постоянной энергии. В том случае, когда подсистема составляет часть неравновесной системы, фазовая траектория не остается в пределах этого слоя. В настоящее время записать уравнение движения фазовой точки в явном виде невозможно. Однако, поскольку ее движение происходит в некотором изменяющемся поле плотностей распределения вероятностей, естественно предположить, что относительная скорость перемещения фазовой точки $\overline {{{U}_{{{\text{о т н }}}}}} $ определяется зависимостью вида

(1)
$\overline {{{U}_{{{\text{о т н }}}}}} = \varphi \left( {{\text{grad}}\quad\bar {\rho }} \right),$
где $\bar {\rho }{\;}$ – распределение плотности вероятности.

Очевидно, что зависимость (1) в равной мере относится ко всем молекулярным процессам, так как в этом отношении авторы работы [27] не вводили никаких ограничений.

Средняя относительная скорость движения фазовой точки, или, что равнозначно, средняя относительная скорость молекулярного процесса, будет

(2)
$\overline {{{U}_{{{\text{о т н }}}}}} = \varphi \left( {\frac{{{{S}_{1}} - {{S}_{2}}}}{R}} \right),$
где S1, S2 – мольные энтропии, Дж/(моль К), R – универсальная газовая постоянная, Дж/(моль К).

Последнее и принимается за основу при обобщении опытных данных по молекулярному переносу. В этом уравнении скорость $\overline {{{U}_{{{\text{о т н }}}}}} $ сохраняет свой прежний смысл и применительно к различным частным проявлениям эффекта переноса должна пониматься как отношения потоков тепла, количества движения и диффузионных потоков. Обобщения этих величин, полученные на основе формулы (2), представлены в работе [27].

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

В случае с растворимостью в работе [28] предложено уравнение для обобщения полученных автором работы экспериментальных данных по растворимости моно-, ди- и триэтиленгликоля в сверхкритическом диоксиде углерода вида

(3)
$\frac{{y\Delta \mu }}{{{{y}_{{\Delta S}}}\Delta {{\mu }_{{\Delta S}}}}} = \varphi \left( {\frac{{{{S}_{1}} - {{S}_{i}}}}{R}} \right),$
где y – растворимость исследуемого вещества во флюиде, мол. д.; Δµ – химический потенциал сверхкритического флюида при параметрах процесса, Дж/моль; уΔSΔµΔS – масштабный коэффициент.

Одной из сложностей при разработке модели явилось то, что для определения масштабного коэффициента уΔSΔµΔS необходимо для каждой системы располагать экспериментальными точками, в которых энтропии S1 и S2 имели бы одну и ту же величину. В отсутствие таких данных авторы метода в работе [30] предложили для определения масштабного коэффициента уравнение, которое для разрабатываемой модели примет следующий вид:

(4)
${{y}_{{\Delta S}}}\Delta {{\mu }_{{\Delta S}}} = \frac{{{{y}_{k}}\Delta {{\mu }_{k}}}}{{{{S}_{1}} - {{S}_{k}}}},$
где yk – растворимость исследуемого вещества в последней точке обобщаемой системы, мол. д.; Δµk – химический потенциал сверхкритического флюида при параметрах последней точки обобщаемой системы, Дж/моль; Sk – энтропия сверхкритического флюида при параметрах последней точки обобщаемой системы, Дж/(моль К).

Как и в работе [28], химический потенциал и энтропия диоксида углерода при параметрах обобщаемых систем определялись из уравнения состояния Алтунина [31]. Так как большая часть обобщаемых изотерм находится в диапазоне 308–338 К, то в качестве начального значения энтропии S1 было принято значение S1 = 3.5 кДж/(кг К), которое входит в диапазон энтропий этих систем. Масштабный поток определялся в соответствии с уравнением (4).

При выборе экспериментальных систем, на основании которых планировалось проводить обобщение, мы ориентировались на работу [18], также посвященную описанию и обобщению растворимости ароматических соединений. Данные по растворимости выбранных нами веществ были взяты из книги [29]. Таким образом, на начальном этапе работ в расчеты было включено 11 веществ, по которым были найдены данные по растворимости на 59 изотермах, исследованных различными авторами, что составило в общей сложности 840 экспериментальных точек, представленных в табл. 1. В графическом виде эти изотермы представлены на рис. 1. Из графика видно, что разброс обобщаемых данных составляет 4 порядка – минимальные значения имеют порядок 10–6, а максимальные – 10–2 мол. д.

Таблица 1.  

Исходные системы при разработке модели

№ п/п Название вещества Т, К Источник № п/п Название вещества Т, К Источник
1 Флуорантен 308 [32] 31 Аценафтен 308 [32]
2 318 32 318
3 328 33 328
4 338 34 338
5 348 35 348
6 Фенантрен 313 [33] 36 Перилен 323 [33]
7 323 37 333
8 333 38 Антрацен 308 [34]
9 308 [34] 39 313 [33]
10 318 [35] 40 323
11 328 41 333
12 308 [36] 42 308 [41]
13 328 43 318
14 Пирен 323 [35] 44 328
15 333 45 313 [42]
16 308 46 Бифенил 308 [43]
17 Трифенилен 318 [32] 47 328
18 328 48 308 [44]
19 338 49 314
20 308 50 323
21 328 51 328
22 Трифенилметан 308 [37] 52 Флуорен 308 [45]
23 318 53 318
24 318 54 323
25 Нафталин 348 [38] 55 328
26 333 56 303 [46]
27 338 [39] 57 308
28 313 [40] 58 323
29 323 59 343
30 333 [37]   
Рис. 1.

Примеры растворимости (логарифмическая шкала) веществ из табл. 1 в сверхкритическом диоксиде углерода при различных температурах и давлениях (по одной изотерме для каждого вещества): 1 – флуорантен, Т = 328 К, 2 – фенантрен, Т = 323 К, 3 – пирен, Т = 313 К, 4 – трифенилен, Т = 328 К, 5 – трифенилметан, T = 308 К, 6 – нафталин, T = 318 К, 7 – аценафтен, T = 348 К, 8 – перилен, Т = 323 К, 9 – антрацен, Т = 323 К, 10 – бифенил, Т = 328 К, 11 – флуорен, Т = 328 К.

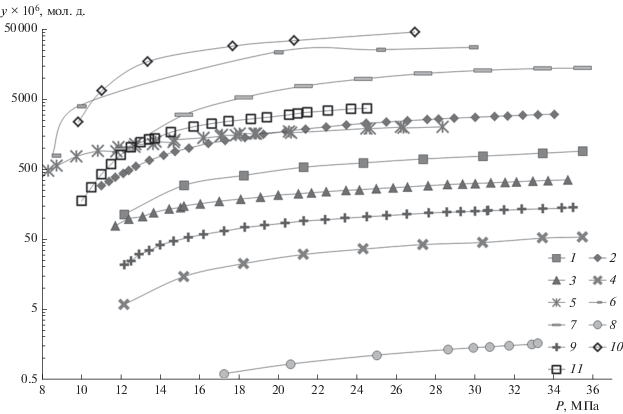
Анализ предварительных результатов, полученных в соответствии с уравнением (3) и представленных на рис. 2, выявил следующее.

Рис. 2.

Результаты обобщения растворимости исследуемых в работе систем: 1 – экспериментальные данные по растворимости из табл. 1, 2 – обобщение растворимости на основе уравнения (3).

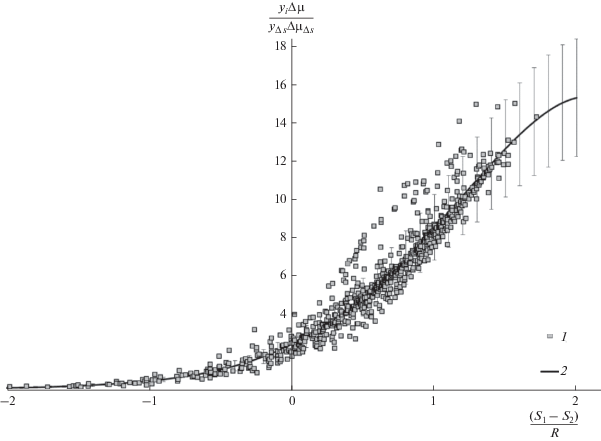
1. Полученный в результате обобщения массив данных описывается полиномом 8-й степени с достаточно большой точностью, однако разброс экспериментальных точек относительно описывающей их кривой превышает 30%.

2. С ростом температуры системы погрешность обратного пересчета растворимости в соответствии с полученным полиномом экспоненциально увеличивается и при температурах более 343 К превышает 40%, а при температуре выше 390 К обратный пересчет дает отрицательные значения растворимости. Это связано с тем, что выбранное нами начальное значение энтропии S1 меньше минимальной энтропии диоксида углерода при температурах и давлениях соответствующих систем.

3. Для большинства веществ растворимость на одних и тех же изотермах была измерена в разное время разными авторами. В большинстве случаев результаты разных измерений коррелировали друг с другом, однако бывали и случаи, когда результаты измерений одного автора значительно отличались от результатов других авторов. В этом случае результаты, которые явно выбивались из общего тренда, исключались из расчетов. В случае, если заметно отличающиеся друг от друга измерения были сделаны только двумя авторами, то оставлялись лишь те результаты, которые вписывались в общую тенденцию изменения растворимости и уравнения обобщающей модели. Анализ исключенных из расчетов работ показал, что основными причинами некорректных с нашей точки зрения данных в них явились, в первую очередь, недостаточная чистота исследуемого авторами вещества, а также неточности в проведении экспериментов. Ранее эти факторы были детально изучены нами на примере растворимости антрацена в сверхкритическом диоксиде углерода. Результаты представлены в работе [23]. Таким образом, из расчетов были исключены системы № 21, 30, 33, 38, 47, 48, 51, 58, 59, а итоговый перечень систем, вошедших в обобщенную модель, представлен в табл. 2.

Таблица 2.  

Системы, использованные при разработке модели

№ п/п Название вещества Т, К Количество эксперимен-тальных точек Источ-ник № п/п Название вещества Т, К Количество эксперимен-тальных точек Источ-ник
1 Флуорантен 308 9 [32] 26 Нафталин 338 15 [39]
2 318 9 27 313 10 [40]
3 328 9 28 323 5
4 338 9 29 Аценафтен 308 9 [32]
5 348 9 30 318 9
6 Фенантрен 313 26 [33] 31 338 9
7 323 30 32 348 9
8 333 30 33 Перилен 323 9 [33]
9 308 5 [34] 34 333 10
10 318 6 [35] 35 Антрацен 313 30 [33]
11 328 6 36 323 29
12 308 5 [36] 37 333 30
13 328 5 38 308 5 [41]
14 Пирен 323 30 [35] 39 318 5
15 333 32 40 328 5
16 308 31 41 313 5 [42]
17 Трифенилен 318 9 [32] 42 Бифенил 308 6 [43]
18 328 9 43 314 6 [44]
19 338 9 44 323 5
20 308 8 45 Флуорен 308 47 [45]
21 Трифенилметан 308 27 [37] 46 318 21
22 318 31 47 323 38
23 318 28 48 328 21
24 Нафталин 348 5 [38] 49 303 5 [46]
25 333 4 50 308 4

Кроме того, для повышения точности расчетов был проведен ряд преобразований уравнения (3).

Поскольку в настоящей работе был исследован более широкий температурный диапазон, чем в работе [28], в уравнение (3) была дополнительно введена приведенная температура ${{T}_{r}} = \frac{T}{{{{T}_{c}}}}$ – отношение температуры системы к критической температуре растворяемого вещества. Это позволило снизить разброс экспериментальных точек относительно обобщающей кривой, однако график принял веерообразную форму. Для нивелирования этого эффекта авторами используемого метода в работе [30] был предложен эмпирический коэффициент, позволяющий выровнять обобщаемые кривые. Применительно к настоящей работе, физический смысл этого коэффициента связан с различием в структуре обобщаемых веществ и их полярности.

В результате всех преобразований уравнение (3) приняло следующий вид:

(5)
${\text{ln}}\left( {\frac{{y{\Delta }\mu }}{{{{y}_{{\Delta S}}}{\Delta }{{\mu }_{{{\Delta }S}}}}}\frac{{{{\rho }_{r}}}}{{{{T}_{r}}}}} \right) = {{\varphi }_{i}}{{\left( {\frac{{{{S}_{1}} - {{S}_{2}}}}{R}} \right)}^{i}},$
где ${{\rho }_{r}} = {{{{\rho }_{i}}} \mathord{\left/ {\vphantom {{{{\rho }_{i}}} {{{\rho }_{c}}}}} \right. \kern-0em} {{{\rho }_{c}}}}$ – отношение плотности углекислого газа к параметрам с экспериментальной точки к плотности СО2 в критической точке.

На рис. 3 представлены результаты итогового обобщения растворимости ароматических соединений в сверхкритическом диоксиде углерода. Расчеты позволили вывести следующую функциональную обобщающую зависимость между $\frac{{y\Delta \mu }}{{{{T}_{r}}{{y}_{{\Delta S}}}\Delta {{\mu }_{{\Delta S}}}}}$ и $\frac{{{{S}_{1}} - {{S}_{i}}}}{R}{\text{:}}$

(6)
$\begin{gathered} f(x) = 0.0{\text{141}}{{x}^{{\text{6}}}}--0.0{\text{1}}{{x}^{{\text{5}}}}--0.0{\text{416}}{{x}^{{\text{4}}}}-- \\ - \,\,0.0{\text{521}}{{x}^{{\text{3}}}}--0.{\text{1777}}{{x}^{{\text{2}}}} + {\text{1}}.{\text{8443}}x + {\text{2}}.{\text{1468}}, \\ \end{gathered} $
где $x = \frac{{{{S}_{1}} - {{S}_{i}}}}{R},$ а f(x) = $\quad{\text{ln}}\left( {\frac{{y\Delta \mu }}{{{{y}_{{\Delta S}}}\Delta {{\mu }_{{\Delta S}}}}}\frac{{{{\rho }_{r}}}}{{{{T}_{r}}}}} \right).$

Рис. 3.

Результаты обобщения растворимости исследуемых в работе систем: 1 – экспериментальные данные по растворимости из табл. 2, 2 – обобщение растворимости на основе уравнения (5).

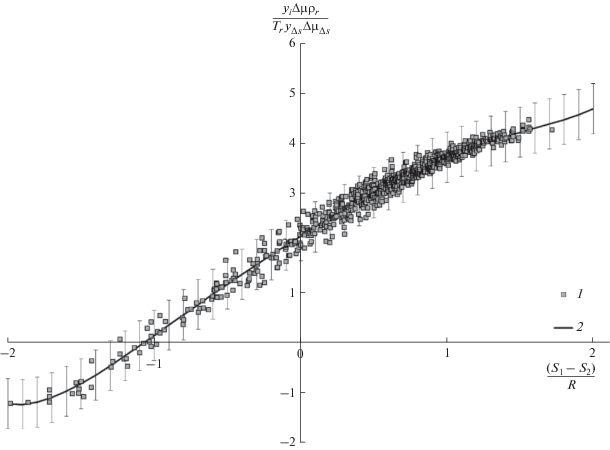
Из рис. 3 видно, что за редким исключением все точки с относительно небольшой погрешностью описываются уравнением (6), что соответствует погрешности экспериментов соответствующих систем [32–43].

В табл. 3 представлены результаты обратного пересчета растворимости некоторых систем из табл. 2 по уравнению

(7)
${{y}_{i}} = \left( {{{e}^{{f\left( x \right)}}}} \right)\frac{{{{T}_{r}}{{y}_{{\Delta S}}}\Delta {{\mu }_{{\Delta S}}}}}{{\Delta \mu {{\rho }_{r}}}},$
Таблица 3.  

Примеры расчета растворимости по уравнениям (6) и (7)

Номер системы из табл. 1 1 Номер системы из табл. 1 7
Т = 308 К yexp, мол. д. ycalc, мол. д. F, % Т = 323 К yexp, мол. д. ycalc, мол. д. F, %
12.16 236 221.6250 6.0911 11.02 299 433.5064 –44.9854
15.2 284 275.2282 3.0887 11.39 340 504.4542 –48.3689
18.24 328 317.4208 3.2254 11.71 390 565.9930 –45.1264
21.28 363 354.0916 2.4541 12.13 446 645.4609 –44.7222
24.32 399 388.2458 2.6953 12.4 487 695.4225 –42.7972
27.36 423 421.8254 0.2777 12.77 560 762.2592 –36.1177
30.4 465 456.2874 1.8737 13.45 680 880.3003 –29.4559
33.44 468 492.8015 –5.2995 14.17 805 999.0776 –24.1090
35.46 497 518.7163 –4.3695 14.76 911 1092.2017 –19.8904
Номер системы из табл. 1 10 15.45 1020 1196.8565 –17.3389
Т = 303 К yexp, мол. д. ycalc, мол. д. F, % 16.45 1188 1341.3214 –12.9058
12 732 612.9204 16.2677 17.29 1302 1456.8398 –11.8925
16 1130 1057.2132 6.4413 18.3 1451 1589.5977 –9.5519
20 1390 1386.7196 0.2360 19.24 1600 1707.7753 –6.7360
24 1680 1657.7274 1.3258 20.38 1770 1844.8333 –4.2279
25.5 1780 1749.3718 1.7207 21.38 1915 1959.9376 –2.3466
27 1840 1836.8732 0.1699 22.43 2048 2076.2002 –1.3770
Номер системы из табл. 1 16 23.47 2189 2187.0880 0.0873
Т = 333 К yexp, мол. д. ycalc, мол. д. F, % 24.46 2300 2289.0001 0.4783
17.41 0.82 0.7292 11.0783 25.49 2400 2391.6488 0.3480
20.9 1.11 1.0495 5.4461 26.57 2514 2495.8613 0.7215
25 1.49 1.4061 5.6311 27.56 2600 2588.5108 0.4419
28.73 1.8 1.7098 5.0120 28.15 2666 2642.5338 0.8802
30.11 1.84 1.8173 1.2361 28.94 2727 2713.5654 0.4927
30.34 1.86 1.8349 1.3486 30 2811 2806.7109 0.1526
31.19 2 1.8996 5.0215 30.99 2893 2891.6298 0.0474
33.12 2.07 2.0429 1.3095 31.65 2940 2947.1799 –0.2442
34.61 2.15 2.1505 –0.0221 32.42 3000 3011.0849 –0.3695
35 2.2 2.1782 0.9907 33.2 3058 3074.7543 –0.5479
– 34.03 3102 3141.5812 –1.2760

а также отклонение расчетных значений растворимости от экспериментальных и среднеквадратичное значение этой величины F, рассчитанное как

(8)
$F = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{{\left( {\frac{{y_{i}^{{{\text{calc}}}} - y_{i}^{{{\text{exp}}}}}}{{y_{i}^{{{\text{exp}}}}}}} \right)}}^{2}}} } .$

Из табл. 3 видно, что модель имеет тенденцию к занижению расчетных значений растворимости при низких давлениях и завышению при высоких. Такое поведение характерно для большинства исследованных в работе систем и связано с методом расчета масштабного коэффициента уΔSΔµΔS для различных систем.

Среднее значение величины F для всех исследованных систем из табл. 2 составляет 11.0707%, что также соответствует точности моделей, основанных на различных уравнениях 1состояния вещества [8–21], однако предлагаемый метод значительно проще в расчетах и требует только одно значение растворимости.

Интересной является возможность сравнить точность расчетов растворимости по предложенному методу с точностью описания растворимости, проводимого с использованием уравнения состояния. Для сравнения была выбрана модель описания растворимости, представленная в работе [47]:

(9)
$y = \frac{{{{P}_{v}}}}{{P\Phi }}{\text{exp}}\left[ {\frac{{PV}}{{RT}}} \right],$

а точнее ее логарифмический вид

(10)
$\ln (y)\,\, = \ln \left( {\frac{{{{P}_{v}}}}{P}} \right) - \ln (\Phi )\quad\, + \,\quad\frac{{PV}}{{RT}},$
где $\ln \left( {\frac{{{{P}_{v}}}}{P}} \right)$ – отношение давления насыщенных паров растворяемого вещества Pv при соответствующей температуре к давлению термодинамической системы P; $\Phi $ – летучесть растворяемого вещества во флюиде при данных P и T; $\frac{{PV}}{{RT}}$ – произведение давления системы на мольный объем вещества, отнесенное к температуре системы и газовой постоянной.

В приведенном уравнении рассчитываемой величиной является летучесть растворяемого вещества во флюиде, тогда как остальные величины, входящие в уравнение (9), определяются экспериментально. Расчет летучести проводится согласно методике, описанной в работе [47].

Сложность проводимых расчетов связана с величиной давления насыщенных паров исследуемого вещества при выбранной температуре. В случае с жидкостями эта величина, как правило, известна с достаточно большой точностью, тогда как в случае с твердыми веществами эта величина часто является неизвестной и трудноопределимой. В связи с этим приходится прибегать к различным расчетным методам и методикам.

Как правило, расчетные методы определения растворимости основаны на использовании принципа соответственных состояний [48].

Если паровая фаза исследуемой жидкости находится в равновесии с ее жидкой фазой, то, исходя из условия равенства химических потенциалов, температуры и давления для обеих фаз, получается уравнение Клаузиуса–Клапейрона (здесь и далее ${{T}_{{{{b}_{r}}}}} = \frac{{{{T}_{b}}}}{{{{T}_{c}}}},$ ${{T}_{r}} = \frac{T}{{{{T}_{c}}}},$ Pv – давление насыщенных паров, Тc и Рc – критические параметры вещества, Т – температура):

(11)
$\frac{{d{{P}_{v}}}}{{dT}} = \frac{{\Delta {{H}_{v}}}}{{T\Delta {{V}_{v}}}} = \frac{{\Delta {{H}_{v}}}}{{({{R{{T}^{2}}} \mathord{\left/ {\vphantom {{R{{T}^{2}}} {{{P}_{v}}}}} \right. \kern-0em} {{{P}_{v}}}})\Delta {{Z}_{v}}}}$

или

(12)
$\frac{{d{\text{ln}}({{P}_{v}})}}{{d\left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0em} T}} \right)}} = - \frac{{\Delta {{H}_{v}}}}{{R\Delta {{Z}_{v}}}}\quad.$

Большинство уравнений для расчета корреляции давлений паров получаются путем интегрирования уравнения (12). После интегрирования должна быть выбрана форма зависимости для ΔHv/ΔZv от температуры, а константа, получаемая при интегрировании, определяется по одной точке давление паров–температура. Различные исследователи предлагали свои интерпретации решения этого уравнения. В табл. 4 представлены только некоторые из многих опубликованных уравнений для давлений паров. Упор сделан на уравнения, которые представляются наиболее точными и общими. Для их использования почти во всех случаях необходимо знать только температуру кипения (обычно это нормальная температура кипения) и значения критических параметров (Тc и Рc). Речь идет об уравнениях Клапейрона, Ли–Кеслера, Риделя, Фроста–Колкуорфа–Тодоса и Риделя–Планка–Миллера, которые могут быть представлены в общем виде как

(13)
${{P}_{{{{v}_{r}}}}} = f\left( {{{T}_{{{{b}_{r}}}}},{{T}_{r}},{{P}_{c}}} \right).$
Таблица 4.  

Методы расчета давления насыщенных паров, разработанные на базе уравнения (12)

№ п/п Авторы методики Расчетное уравнение
1 Уравнение Клайперона ${\text{ln}}({{P}_{{{{v}_{r}}}}}) = h\left( {1 - \frac{1}{{{{T}_{r}}}}} \right),$ где h = ${{T}_{{{{b}_{r}}}}}\frac{{{\text{ln}}{{P}_{c}}}}{{1 - {{T}_{{{{b}_{r}}}}}}}$
2 Метод Ли–Кеслера ${\text{ln}}({{P}_{{{{v}_{r}}}}}) = {{f}^{{\left( 0 \right)}}}\left( {{{T}_{r}}} \right) + w{{f}^{{\left( 1 \right)}}}\left( {{{T}_{r}}} \right),$
где
${{f}^{{\left( 0 \right)}}} = 5.92714 - \frac{{6.09648}}{{{{T}_{r}}}} - 1.28862\ln \left( {{{T}_{r}}} \right) + 0.169347T_{r}^{6}$
${{f}^{{\left( 1 \right)}}} = 15.2518 - \frac{{15.6875}}{{{{T}_{r}}}} - 13.4721\ln \left( {{{T}_{r}}} \right) + \quad0.43577T_{r}^{6}$
3 Метод Риделя ${\text{ln}}({{P}_{v}}) = {{A}^{ + }} + \frac{{{{B}^{ + }}}}{T} + {{C}^{ + }}{\text{ln}}T + {{D}^{ + }}{{T}^{6}},$
где
${{A}^{ + }} = - 35Q;\,\,\,\,\quad{{B}^{ + }} = - 36Q;\,\,\,\,{{C}^{ + }} = 42Q + {{\alpha }_{c}};\,\,\,\,{{D}^{ + }} = - Q;$
$Q = 0.0838\left( {3.758 - {{\alpha }_{c}}} \right)$
${{\alpha }_{c}} = \frac{{0.315{{\psi }_{b}} + {\text{ln}}{{P}_{с }}}}{{0.0838{{\psi }_{b}} - {\text{ln}}{{T}_{{{{b}_{r}}}}}}},$${{\psi }_{b}} = - 35 + \frac{{36}}{{{{T}_{{{{b}_{r}}}}}}} + 42{\text{ln}}{{T}_{{{{b}_{r}}}}} - T_{{{{b}_{r}}}}^{6}$
4 Метод Фроста–Колкуорфа–Тодоса ${\text{ln}}({{P}_{{{{v}_{r}}}}}) = B\left( {\frac{1}{{{{T}_{r}}}} - 1} \right) + \quad\,C{\text{ln}}{{T}_{r}} + \frac{{27}}{{64}}\left( {\frac{{{{P}_{{{{\text{v}}_{r}}}}}}}{{T_{r}^{2}}} - 1} \right),$
где
$B = \frac{{{\text{ln}}{{P}_{c}} + 2.67{\text{ln}}{{T}_{{{{b}_{r}}}}} + \frac{{27}}{{64}}\left[ {\left( {\frac{1}{{{{P}_{c}}T_{{{{b}_{r}}}}^{2}}} - 1} \right)} \right]}}{{{{1 - 1} \mathord{\left/ {\vphantom {{1 - 1} {{{T}_{{{{b}_{R}}}}}}}} \right. \kern-0em} {{{T}_{{{{b}_{R}}}}}}} - 0.7816{\text{ln}}{{T}_{{{{b}_{r}}}}}}},$
$C = 0.7816B + 2.67$
5 Метод Риделя–Планка–Миллера ${\text{ln}}({{P}_{{{{v}_{r}}}}}) = - \frac{G}{{{{T}_{r}}}}\left[ {1 - T_{r}^{2} + k\left( {3 + {{T}_{r}}} \right){{{\left( {1 - {{T}_{r}}} \right)}}^{3}}} \right],$
где
h = ${{T}_{{{{b}_{r}}}}}\frac{{{\text{ln}}{{P}_{{cr}}}}}{{1 - {{T}_{{{{b}_{r}}}}}}},$$G = 0.4835 + 0.4605h,$$k = \frac{{{h \mathord{\left/ {\vphantom {h G}} \right. \kern-0em} G} - \left( {1 + {{T}_{r}}} \right)}}{{\left( {3 + {{T}_{r}}} \right){{{\left( {1 - {{T}_{r}}} \right)}}^{2}}}}$

Результаты сравнения результатов расчетов представлены в табл. 5. Из нее видно, что практически во всех случаях точность расчетов растворимости по предложенному в работе методу существенно выше, чем результаты, получаемые при описании растворимости. Это связано, во-первых, с большим разбросом значений давления насыщенных паров исследуемых веществ, получаемым при применении того или иного метода из табл. 3. Кроме того, на качество описания оказывает влияние точность определения критических параметров исследуемых веществ, и при отсутствии экспериментальных данных по этим величинам приходится также прибегать к различным расчетным методикам. В то же время предложенный в работе метод использует в своей основе только растворимость исследуемого вещества и энтропию диоксида углерода. Эти величины можно определить с достаточно высокой точностью, что позволяет расчетным методом определить значение растворимости того или иного ароматического соединения из табл. 1 в широком интервале давлений и температурах до 350 К, а интерполяция, проведенная таким образом, существенно расширяет возможности применения данных по растворимости ароматических соединений в сверхкритическом диоксиде углерода на области, не охваченные экспериментами.

Таблица 5.  

Среднеквадратичные отклонения расчетных значений растворимости, полученных по уравнениям (6) и (9), от экспериментальных значений растворимости

Название вещества № сис-темы Расчет растворимости по уравнению (6) Расчет растворимости по уравнению (9) с давлением насыщенных паров, рассчитанным по разным методам
Уравнение Клапейрона Метод Ли–Кеслера Метод Риделя Метод Фроста–Колкуорфа-Тодоса Метод Риделя–Планка–Миллера Метод Питерсона
Флуорантен 1 3.2639 17.6294 14.0403 13.2181 13.2181 13.2181 13.2181
2 5.6598 15.4838 13.5396 13.5396 13.5396 13.5396 13.5396
3 7.5745 15.2529 14.5381 14.5381 14.5381 14.5381 14.5381
4 6.1886 14.0207 13.5521 13.5521 13.5521 13.5521 13.5521
5 15.4798 18.9436 18.9137 18.9137 18.9137 18.9137 17.6074
Фенантрен 6 11.1206 50.4697 34.4468 32.5895 32.5895 31.0474 31.0474
7 13.6012 54.7235 34.8431 32.3174 32.3174 30.3243 30.3243
8 18.4210 52.0774 29.1129 26.3710 26.3710 24.6724 24.6724
9 8.4644 26.1827 15.1164 13.9877 13.6257 12.4466 12.4466
10 4.3602 28.8188 13.3348 12.2489 11.7745 11.0112 11.0112
11 6.6986 39.8647 14.0062 11.2084 11.2084 9.4421 9.4421
12 1.9256 31.9764 19.3030 18.2628 18.2628 16.9449 16.9449
13 7.7626 39.6199 14.9255 12.2461 12.2461 10.5886 10.5886
Пирен 14 11.9802 61.8374 45.8948 39.4253 39.3903 35.7202 35.7202
15 10.8415 64.4720 44.1628 35.1439 35.1439 30.5598 30.5598
16 22.9716 69.4595 41.8486 30.0246 30.0246 24.7123 24.7123
Трифинилен 17 3.9990 10100 31.3731 31.3731 31.3731 10100 32.4860
18 8.2526 10100 30.6235 30.6235 30.6235 10100 33.5712
19 12.0935 10100 30.8543 30.8543 30.8543 10100 31.1792
20 10.6443 10100 29.5245 29.5245 29.5245 10100 30.7210
Трифенилметан 21 3.1259 52.9613 32.1053 28.9582 28.7577 20.8547 20.8547
22 10.8002 73.2215 37.8691 31.7085 31.5409 18.2942 18.2942
23 11.0003 52.4175 29.2305 27.3065 26.9933 26.8107 26.8107
Нафталин 24 9.7158 17.9264 13.9729 13.7875 13.7875 13.7875 13.7875
25 14.3768 26.5916 22.2942 22.0689 22.0689 22.0689 22.0689
26 8.2355 21.6640 18.0904 17.8425 17.8425 17.8425 17.8425
27 17.8185 32.9473 25.5328 25.3803 25.3803 25.3803 25.3803
28 17.2042 55.9265 31.9769 31.2571 31.2571 31.2571 31.2571
Аценафтен 29 7.8742 34.8039 19.1916 19.1916 19.1916 19.1916 19.1916
30 12.3026 28.3661 11.7068 11.7068 11.7068 11.7068 11.7068
31 23.7940 26.6511 7.9334 7.9334 7.9334 7.9334 7.9334
32 25.1743 27.7358 9.0347 9.0347 9.0347 9.0347 9.0347
Перилен 33 6.0856 7.3751 7.3751 7.3751 7.3751 7.3751 7.3751
34 3.7096 18.8044 18.8044 18.8044 18.8044 18.8044 16.6033
Антрацен 35 5.5431 56.7908 43.1965 43.1965 43.1965 42.6510 42.6510
36 4.8236 71.7962 56.7932 56.7932 56.7932 56.0623 56.0623
37 14.4963 71.6216 52.1737 52.1737 52.1737 51.3292 51.3292
38 12.2865 51.6219 33.4419 33.4419 33.4419 32.7535 32.7535
39 15.7181 69.9520 39.3998 39.3998 39.3998 38.1046 38.1046
40 21.2621 71.7028 26.5743 26.5743 26.5743 25.4591 25.4591
41 11.8885 50.6662 36.0347 36.0347 36.0347 35.4332 35.4332
Бифенил 42 6.7837 29.5219 22.2019 20.4696 20.4696 19.1145 19.1145
43 5.0012 24.3916 21.5142 20.4865 20.4865 20.0980 20.0980
44 9.7398 30.7306 27.7513 26.8141 26.8141 26.4994 26.4994
Флуорен 45 9.5730 33.0266 10.5801 10.5801 10.5801 9.8399 9.8399
46 15.0578 53.2331 6.4829 6.4829 6.4829 6.0341 6.0341
47 23.7644 48.1140 6.0593 6.0593 6.0593 5.6691 5.6691
48 22.9577 37.4852 4.7474 3.6542 3.4634 3.4634 3.4634
49 2.8385 19.8776 5.8803 5.8803 5.8803 4.9126 4.9126
50 9.2803 45.0687 18.7311 18.7311 18.7311 17.3876 17.3876

ЗАКЛЮЧЕНИЕ

В работе представлена основанная на энтропийном методе теории подобия модель описания и обобщения растворимости ароматических углеводородов в сверхкритическом диоксиде углерода. В отличие от ранее разработанных моделей, представленная модель использует для описания и обобщения растворимости термодинамические параметры сверхкритического диоксида углерода и одно значение растворимости исследуемого вещества в крайней точке на изотерме. Определены граничные условия применимости модели.

Показано, что среднеквадратичное отклонение результатов описания модели в интервале температур от 300 до 350 К в большинстве случаев не превышает 16%, а среднее значение этой величины составляет 11.1%, что сопоставимо с возможностями альтернативных моделей, а также с экспериментальными методами определения растворимости.

Проведено сравнение точности расчета растворимости предложенным методом с методом описания растворимости, использующим в своей основе критические параметры описываемого вещества и его давление насыщенных паров. Показано, что предложенная модель позволяет получить более качественное описание растворимости, а временные затраты на проведение расчетов существенно снижаются за счет прямого расчета искомой величины.

Работа выполнена при финансовой поддержке Российского научного фонда (проект № 18-19-00478).

ОБОЗНАЧЕНИЯ

F среднеквадратичное отклонение расчетных значений растворимости от экспериментальных, %
f(x) обобщающая функция
ΔHv теплота парообразования, Дж/кг
Р давление, Па
R универсальная газовая постоянная, Дж/(моль К)
S энтропия, Дж/(моль К)
Т температура, К
$\overline {{{U}_{{{\text{о т н }}}}}} $ относительная скорость перемещения фазовой точки
V молярный объем исследуемого вещества, м3/моль
ΔVv изменение молярного объема при парообразовании, м3/моль
w фактор ацентричности
x аргумент обобщающей функции
y растворимость, мол. д.
Z коэффициент сжимаемости
Δµ химический потенциал сверхкритического флюида при параметрах процесса, Дж/моль
$\bar {\rho }{\;}$ распределение плотности вероятности
Φ летучесть растворяемого вещества во флюиде

ИНДЕКСЫ

1 начальное значение энтропии
2 конечное значение энтропии
b кипение
CO2 свойства диоксида углерода
c критические параметры вещества
calc расчетное значение
exp экспериментальное значение
i порядковый номер экспериментальной точки на описываемой изотерме
k последняя экспериментальная точка на описываемой изотерме
n количество экспериментальных точек
r приведенная величина
ΔS индекс масштабного коэффициента
$v$ процесс парообразования

Список литературы

  1. Gumerov F.M., Amirchanov D.G., Usmanov A.G., Le Neindre B. The thermal diffusivity of argon in the critical region // Int. J. Thermophys. 1991. V. 12. № 1. P. 67.

  2. Le Neindre B., Garrabos Y., Gumerov F., Sabirzianov A. Measurements of the thermal conductivity of HFC-134a in the supercritical region // J. Chem. Eng. Data. 2009. V. 54. № 9. P. 2678.

  3. Le Neindre B., Lombardi G., Desmarest P.H., Kayser M., Zaripov Z.I., Gumerov F.M., Garrabos Y. Measurements of the thermal conductivity of ethene in the supercritical region // Fluid Phase Equilibria. 2018. V. 459. P. 119.

  4. Hung T.N., Gumerov F., Gabitov F., Usmanov R., Hairutdinov V., Le Neindre B. Improvement of the water brewing of Vietnamese green tea by pretreatment with supercritical carbon dioxide // J. Supercrit. Fluids. 2012. V. 62. P. 73.

  5. Usmanov R.A., Gumerov F.M., Gabitov F.R., Zaripov Z.I., Shamsetdinov F.N., Abdulagatov I.M. High yield biofuel production from vegetable oils with supercritical alcohols // Liquid Fuels: Types, Properties and Production. N.Y.: Nova Science Publisher, Inc., 2012. Ch. 3. P. 99.

  6. Khairutdinov V.F., Akhmetzyanov T.R., Gumerov F.M., Khabriev I.Sh., Farakhov M.I. Supercritical fluid propane–butane extraction treatment of oil-bearing sands // Theor. Found. Chem. Eng. 2017. V. 51. № 3. P. 299. [Хайрутдинов В.Ф., Ахметзянов Т.Р., Гумеров Ф.М., Хабриев И.Ш., Фарахов М.И. Сверхкритическая флюидная пропан-бутановая экстракционная обработка нефтеносных песков // Теорет. основы хим. технологии. 2017. Т. 51. № 3. С. 288.]

  7. Gumerov F.M., Sagdeev A.A., Amirkhanov D.G. Solubility of substances in supercritical fluid media. Saarbrücken: LAP LAMBERT Academic Publishing GmbH & Co. KG, 2016.

  8. Li H., Jia D., Li S., Liu R. Correlating and predicting the solubilities of structurally similar organic solid compounds in supercritical CO2 using the compressed gas model and the reference solubilities // Fluid Phase Equilibria. 2013. V. 350. P. 13. https://doi.org/10.1016/j.fluid.2013.04.010

  9. Nasri L., Bensaad S., Bensetiti Z. Correlation and prediction of the solubility of solid solutes in chemically diverse supercritical fluids based on the expanded liquid theory // Advances in Chemical Engineering and Science. 2013. V. 3. № 4. P. 255. https://doi.org/10.4236/aces.2013.34033

  10. Trabelsi F., Abaroudi K., Recasens F. Predicting the approximate solubilities of solids in dense carbon dioxide // J. Supercritical Fluids. 1999. V. 14. № 2. P. 151.

  11. da Silva M.V., Barbosa D. Prediction of the solubility of aromatic components of wine in carbon dioxide // J. Supercritical Fluids. 2004. V. 31. № 1. P. 9.

  12. Hartono R., Mansoori G.A., Suwono A. Prediction of solubility of biomolecules in supercritical solvents // Chem. Eng. Sci. 2001. V. 56. P. 6949.

  13. Manohar B., Sankar K.U. Prediction of solubility of Psoralea corylifolia L. Seed extract in supercritical carbon dioxide by equation of state models // Theor. Found. Chem. Eng. 2011. V. 45. P. 409.

  14. Ajchariyapagorn A., Douglas P.L., Douglas S., Pongamphai S., Teppaitoon W. Prediction of solubility of solid biomolecules in supercritical solvents using group contribution methods and equations of state // American J. Food Technology. 2008. V. 3. P. 275.

  15. Madras G., Kulkarni C., Modak J. Modeling the solubilities of fatty acids in supercritical carbon dioxide // Fluid Phase Equilib. 2003. V. 209. P. 207.

  16. Coimbra P., Duarte C.M.M., de Sousa H.C. Cubic equation-of-state correlation of the solubility of some anti-inflammatory drugs in supercritical carbon dioxide // Fluid Phase Equilib. 2006. V. 239. P. 188. https://doi.org/10.1016/j.fluid.2005.11.028

  17. Del Valle J.M., Aguilera J.M. An improved equation for predicting the solubility of vegetable oils in supercritical carbon dioxide // Ind. Eng. Chem. Res. 1988. V. 27. P. 1551.

  18. Nasri L., Bensetiti Z., Bensaad S. Correlation of the solubility of some organic aromatic pollutants in supercritical carbon dioxide based on the UNIQUAC equation // Energy Procedia. 2012. V. 18. P. 1261.https://doi.org/10.1016/j.egypro.2012.05.142

  19. Rathnam V.M., Lamba N., Madras G. Evaluation of new density based model to correlate the solubilities of ricinoleic acid, methyl ricinoleate and methyl 10-undecenoate in supercritical carbon dioxide // Journal of Supercritical Fluids. 2017. V. 130. P. 357.

  20. Tomberli B., Goldman S., Gray C. Predicting solubility in supercritical solvents using estimated virial coefficients and fluctuation theory // Fluid Phase Equilibria. 2001. V. 187. P. 111.

  21. Sparks D.L., Hernandez R., Estévez L.A. Evaluation of density-based models for the solubility of solids in supercritical carbon dioxide and formulation of a new model // Chemical Engineering Science. 2008. V. 63. № 17. P. 4292. https://doi.org/10.1016/j.ces.2008.05.031

  22. Zakharov A.A., Bilalov T.R., Gumerov F.M. Solubility of ammonium palmitate in supercritical carbon dioxide // Russ. J. Phys. Chem. В. 2016. V. 10. P. 1092. [Заха-ров А.А., Билалов Т.Р., Гумеров Ф.М. Растворимость пальмитата аммония в сверхкритическом диоксиде углерода // Сверхкритические флюиды: теория и практика. 2015. Т. 10. № 2. С. 60.]https://doi.org/10.1134/S1990793116070204

  23. Jaddoa A.A., Zakharov A.A., Bilalov T.R., Nakipov R.R., Gabitov I.R., Zaripov Z.I., Gumerov F.M. Some thermodynamic processes of anthracite–carbon dioxide mixture in supercritical fluid state // Russ. J. Phys. Chem. В. 2016. V. 10. P. 1180. [Jaddoa A.A., Захаров А.А., Билалов Т.Р., Накипов Р.Р., Габитов И.Р., Зарипов З.И., Гумеров Ф.М. Некоторые термодинамические свойства смеси “антрацен–диоксид углерода” в сверхкритической флюидной области состояния // Сверхкритические флюиды: теория и практика. 2015. Т. 10. № 4. С. 18.]https://doi.org/10.1134/S1990793116080029

  24. Билалов Т.Р., Гумеров Ф.М., Гатина Р.Ф. Растворимости тротила и его экстракционное извлечение из жестких сгорающих картузов с использованием чистого и модифицированного сверхкритического СО2 // Сверхкритические флюиды: теория и практика. 2016. Т. 11. № 4. С. 17.

  25. Gumerov F.M., Le Neindre B., Bilalov T.R. et al. Regeneration of spent catalyst and impregnation of catalyst by supercritical fluid. N.Y.: Nova Science Publisher, Inc., 2016.

  26. Bilalov T.R., Zakharov A.A., Jaddoa A.A., Gumerov F.M., Le Neindre B. Treatment of different types of cotton fabrics by ammonium palmitate in a supercritical CO2 environment // J. Supercritical Fluids. 2017. V. 130. P. 47.

  27. Усманов А.Г. Об одном дополнительном условии подобия молекулярных процессов // Теплофизика и тепловое моделирование. М.: АН СССР, 1959. С. 298.

  28. Sabirzyanov A.N., Gumerov F.M. Generalizing binary solubility data for low-volatile liquids in supercritical fluids // Theor. Found. Chem. Eng. 2001. V. 35. № 2. P. 129. [Сабирзянов А.Н., Гумеров Ф.М. Обобщение бинарной растворимости низколетучих жидкостей в сверхкритических флюидах // Теорет. основы хим. технологии. 2001. Т. 35. № 2. С. 138.]https://doi.org/10.1023/A:1010373321731

  29. Gupta R.B., Shim J.-J. Solubility in Supercritical Carbon Dioxide. Boca Raton, Fla.: CRC, 2006.

  30. Усманов А.Г., Бережной А.Н. Применение метода подобия при исследовании процессов переноса массы // Журн. физ. химии. 1960. Т. 34. № 4. С. 907.

  31. Алтунин В.В. Теплофизические свойства двуокиси углерода. М.: Изд-во стандартов, 1975.

  32. Yamini Y., Bahramifar N. Solubility of polycyclic aromatic hydrocarbons in supercritical carbon dioxide // J. Chem. Eng. Data. 2000. V. 41. № 1. P. 53.

  33. Anitescu G., Tavlarides L.L. Solubilities of solids in supercritical fluids–I. New quasistatic experimental method for polycyclic aromatic hydrocarbons (PAHs) + pure fluids // J. Supercrit. Fluids. 1997. V. 10. P. 175.

  34. Goodarznia I., Esmaeilzadeh F. Solubility of an anthracene, phenanthrene, and carbazole mixture in supercritical carbon dioxide // J. Chem. Eng. Data. 2002. V. 47. № 2. P. 333.

  35. Lee L.-S. Huang J.-F., Zhu O.-X. Solubilities of solid benzoic acid, phenanthrene, and 2,3-dimethylhexane in supercritical carbon dioxide // J. Chem. Eng. Data. 2001. V. 46. № 5. P. 1156.

  36. Sane A., Taylor S., Sun Y.-P., Thies M.C. A semicontinuous flow apparatus for measuring the solubility of opaque solids in supercritical solutions // J. Supercrit. Fluids. 2004. V. 28. № 2–3. P. 277.

  37. Pauchon V., Cisse Z., Chavret M., Jose J. A new apparatus for the dynamic determination of solid compounds solubility in supercritical carbon dioxide: Solubility determination of triphenylmethane // J. Supercrit. Fluids. 2004. V. 32. № 1–3. P. 115.

  38. Diefenbacher A., Turk M. Phase equilibria of organic solid solutes and supercritical fluids with respect to the RESS process // J. Supercrit. Fluids. 2002. V. 22. № 3. P. 175.

  39. Kalaga A., Trebble M. Density changes in supercritical solvent + hydrocarbon solute binary mixtures // J. Chem. Eng. Data. 1999. V. 44. № 5. P. 1063.

  40. Sauceau M., Fages J., Letoumeau J.J., Richon D. A novel apparatus for accurate measurements of solid solubilities in supercritical phases // Ind. Eng. Chem. Res. 2000. V. 39. № 12. P. 4609.

  41. Li Q., Zhang Z., Zhong C., Liu Y., Zhou Q. Solubility of solid solutes in supercritical carbon dioxide with and without cosolvents // Fluid Phase Equilib. 2003. V. 207. № 1–2. P. 183.

  42. Ngo T.T., Bush D., Eckert C.A., Liotta C.L. Spectroscopic measurement of solid solubility in supercritical fluids // AIChE J. 2001. V. 47. № 11. P. 2566.

  43. Chung S.T., Shing K.S. Multiphase behavior of binary and ternary systems of heavy aromatic hydrocarbons with supercritical carbon dioxide: Part I. Experimental results // Fluid Phase Equilib. 1992. V. 81. P. 321.

  44. McHugh M., Paulaitis M.E. Solid solubilities of naphthalene and biphenyl in supercritical carbon dioxide // J. Chem. Eng. Data. 1980. V. 25. № 4. P. 326.

  45. Bartle K.D., Clifford A.A., Jafar S.A. Measurement of solubility in supercritical fluids using chromatographic retention: The solubility of fluorene, phenanthrene, and pyrene in carbon dioxide // J. Chem. Eng. Data. 1990. V. 35. № 3. P. 355.

  46. Johnston K.P., Ziger D.H., Eckert C.A. Solubilities of hydrocarbon solids in supercritical fluids. The augmented van der Waals treatment // Ind. Eng. Chem. Fundam. 1982. V. 21. № 3. P. 191.

  47. Mukhopadhyay M. Natural Extracts Using Supercritical Carbon Dioxide. Boca Raton, Fla.: CRC, 2000.

  48. Рид Р., Праусниц Д., Шервуд Т. Свойства газов и жидкостей. Л.: Химия, 1982.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал