Теоретические основы химической технологии, 2019, T. 53, № 4, стр. 402-409

Математическое моделирование процесса непрерывной ферментации при получении молочной кислоты

Ю. Л. Гордеева^1, *, А. Г. Бородкин², Е. Л. Гордеева², Е. Г. Рудаковская²

¹ Московская государственная академия ветеринарной медицины и биотехнологии им. К.И. Скрябина
Москва, Россия

² Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия

^* E-mail: l.s.gordeev@yandex.ru

Поступила в редакцию 07.11.2018
После доработки 07.12.2018
Принята к публикации 07.02.2019

DOI: 10.1134/S0040357119040031

Полный текст (PDF)

Аннотация

Приведены уравнения обобщенной математической модели непрерывной ферментации молочной кислоты. Система уравнений включает соотношения материального баланса по биомассе, субстрату, молочной кислоте, побочному продукту и компоненту сырья, воспроизводящего субстрат. Удельная скорость роста биомассы учитывает все эффекты ингибирования – биомассой, субстратом и продуктом. Приведены численные решения уравнений модели в дискретной и непрерывной форме для базового варианта значений констант. Дана оценка влияния значений показателей ингибирования на показатели процесса, в том числе и на значения максимальной продуктивности в зависимости от величины протока. Обобщенная математическая модель позволяет учитывать большинство частных вариантов исследования и моделирования синтеза молочной кислоты в непрерывной ферментации, опубликованные в литературных источниках. Уравнения математической модели рекомендуются для изучения процессов в полупериодических условиях, процессов с рециркуляцией, с выделением продукта в мембранной технологии и т.п.

Ключевые слова: математическое моделирование, молочная кислота, непрерывная ферментация, биомасса

ВВЕДЕНИЕ

Анализ исследований процесса ферментативного получения молочной кислоты с использованием математических моделей [1–3] показал следующее.

1. Исследования носят частный характер, т.е. изучались конкретные штаммы микроорганизмов и, как следствие, использовались математические модели применительно к изучаемому процессу.

2. Исследования преимущественно относились к процессам периодической ферментации.

3. Математические модели, используемые для изучения процессов частного характера, в большинстве базировались на упрощенных соотношениях для удельной скорости роста микроорганизмов, не учитывали совместно протекающих процессов образования побочных продуктов и дополнительного образования основного субстрата из компонентов исходного сырья.

4. Уравнения образования молочной кислоты и побочных продуктов как продуктов метаболизма имеют разнообразный вид, не получивший, как правило, какого-либо обоснования.

5. Условия реализации процессов ферментативного получения молочной кислоты отражаются на количественных оценках констант уравнений математических моделей и практически не влияют на их структуры. Так, влияние pH и температуры приведены в публикациях [4–6]. Отметим, что область изменения физических величин невелика. Так, значение pH использовалось обычно в области нейтральности (т.е. вблизи 7.0), температуры в области 30°C. Практическое использование показателей pH и температуры при моделировании весьма ограничено.

Указанные факторы 1–5 явились основанием для формирования уравнений обобщенной математической модели с последующим моделированием непрерывной ферментации.

ОБОБЩЕННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ НЕПРЕРЫВНОЙ ФЕРМЕНТАЦИИ

Уравнение для биомассы молочнокислых бактерий:

(1)

$ - DX + \mu X = 0,$

где D – величина протока, ч^–1 (D = υ/V, υ – объемная скорость через ферментер, м³/ч; V – объем заполнения ферментера, м³); X – концентрация биомассы на выходе из ферментера, г/л; µ – удельная скорость роста микроорганизмов, ч^–1.

Обобщенный вариант удельной скорости роста µ, учитывающий все возможные эффекты торможения (ингибирования) компонентами процесса – биомассой (X), субстратом (S) и продуктом (P), следуя публикациям [1–3], представлен в виде

(2)

$\begin{gathered} \mu = {{\mu }_{{{\text{max}}}}}{{\left( {1 - \frac{X}{{{{X}_{{{\text{max}}}}}}}} \right)}^{{{{n}_{1}}}}}{{\left( {1 - \frac{P}{{{{P}_{{{\text{max}}}}}}}} \right)}^{{{{n}_{2}}}}} \times \\ \times \,\,\frac{S}{{{{K}_{m}} + S + {{{{S}^{2}}} \mathord{\left/ {\vphantom {{{{S}^{2}}} {{{K}_{i}}}}} \right. \kern-0em} {{{K}_{i}}}}}}, \\ \end{gathered} $

где µ_max – максимальная удельная скорость роста, ч^–1; P – концентрация продукта, г/л; P_max – максимальная концентрация продукта, г/л; S – концентрация субстрата, г/л; X_max – максимальная концентрация биомассы, г/л; K_m – константа насыщения субстрата, г/л; K_i – константа ингибирования, г/л.

Возможность учета частных условий организации процесса ферментации определяется численными значениями констант в (2).

Так как молочная кислота и образуемые побочные продукты (если они имеются) являются продуктами метаболизма, целесообразно их образование описать однотипными соотношениями

(3)

$\left( {\alpha \mu + \beta } \right)X - DP = 0;$

(4)

$\left( {{{\alpha }_{B}}\mu + {{\beta }_{B}}} \right)X - DB = 0,$

где P и B – концентрация молочной кислоты и концентрация суммарного количества побочных продуктов соответственно, г/л; α, β, α_B, β_B – константы.

Концентрация субстрата S определяется двумя процессами – потреблением микроорганизмами, учитываемого стехиометрическим коэффициентом Y_X/S, и образованием дополнительного количества субстрата, если используется сырье, в котором имеется компонент, способный воспроизводить субстрат в процессе ферментации. Уравнение для воспроизведения дополнительного количества субстрата имеет вид

(5)

$D\left( {{{M}_{0}} - M} \right) - {{k}_{M}}M = 0,$

где M₀ – концентрация компонента, воспроизводящего дополнительное количество субстрата в поступающем потоке, г/л; M – текущая концентрация сырья, дополнительно воспроизводящего субстрат, г/л; k_M – константа, определяющая количество воспроизведенного субстрата, ч^–1.

Таким образом, уравнение баланса по концентрации субстрата получаем в виде

(6)

$D\left( {{{S}_{0}} - S} \right) - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\mu X + {{k}_{M}}M = 0,$

где S₀ – концентрация субстрата в поступающем потоке, г/л; Y_X/S – стехиометрический коэффициент, г/г.

Окончательно система уравнений с использованием обобщенной математической модели для непрерывной ферментации имеет следующий вид:

(7)

$\left\{ \begin{gathered} - DX + \mu X = 0 \hfill \\ \left( {\alpha \mu + \beta } \right)X - DP = 0 \hfill \\ \left( {{{\alpha }_{B}}\mu + {{\beta }_{B}}} \right)X - DB = 0 \hfill \\ D\left( {{{S}_{0}} - S} \right) - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\mu X + {{k}_{M}}M = 0 \hfill \\ D\left( {{{M}_{0}} - M} \right) - {{k}_{M}}M = 0 \hfill \\ \mu = {{\mu }_{{\max }}}{{\left( {1 - \frac{X}{{{{X}_{{\max }}}}}} \right)}^{{{{n}_{1}}}}}{{\left( {1 - \frac{P}{{{{P}_{{\max }}}}}} \right)}^{{{{n}_{2}}}}}\frac{S}{{{{K}_{m}} + S + {{{{S}^{2}}} \mathord{\left/ {\vphantom {{{{S}^{2}}} {{{K}_{i}}}}} \right. \kern-0em} {{{K}_{i}}}}}} \hfill \\ \end{gathered} \right..$

Отметим, что в большинстве исследований, приведенных в обзорах [1–3], уравнения математических моделей не учитывают условия гибели микроорганизмов и затраты субстрата на поддержание жизнедеятельности микроорганизмов. Последнее связано с тем, что эти составляющие обычно являются достаточно малыми и, как правило, не влияют на результаты моделирования.

МОДЕЛИРОВАНИЕ ПРОЦЕССА

Для моделирования процесса система уравнений (14)–(18) приводится к одному нелинейному уравнению с одной неизвестной величиной, зависящей от значения D.

Из первого уравнения системы (7) получаем

(8)

$\mu = D.$

Используя (8), перепишем систему (7) в виде

(9)

$\left( {\alpha D + \beta } \right)X - DP = 0;$

(10)

$\left( {{{\alpha }_{B}}D + {{\beta }_{B}}} \right)X - DB = 0;$

(11)

$D\left( {{{S}_{0}} - S} \right) - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}DX + {{k}_{M}}M = 0;$

(12)

$D\left( {{{M}_{0}} - M} \right) - {{k}_{M}}M = 0;$

(13)

$\begin{gathered} D = {{\mu }_{{{\text{max}}}}}{{\left( {1 - \frac{X}{{{{X}_{{{\text{max}}}}}}}} \right)}^{{{{n}_{1}}}}}{{\left( {1 - \frac{P}{{{{P}_{{{\text{max}}}}}}}} \right)}^{{{{n}_{2}}}}} \times \\ \times \,\,\frac{S}{{{{K}_{m}} + S + {{{{S}^{2}}} \mathord{\left/ {\vphantom {{{{S}^{2}}} {{{K}_{i}}}}} \right. \kern-0em} {{{K}_{i}}}}}}. \\ \end{gathered} $.

Уравнения (9)–(13) преобразуются к виду

(14)

$P = \left( {\alpha + {\beta \mathord{\left/ {\vphantom {\beta D}} \right. \kern-0em} D}} \right)X;$

(15)

$B = \left( {{{\alpha }_{B}} + {{{{\beta }_{B}}} \mathord{\left/ {\vphantom {{{{\beta }_{B}}} D}} \right. \kern-0em} D}} \right)X;$

(16)

$S = {{S}_{0}} + \frac{{{{k}_{M}}{{M}_{0}}}}{{D + {{k}_{M}}}} - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}X;$

(17)

$M = \frac{{D{{M}_{0}}}}{{D + {{k}_{M}}}};$

(18)

$\begin{gathered} {{\left( {1 - \frac{X}{{{{X}_{{{\text{max}}}}}}}} \right)}^{{{{n}_{1}}}}}{{\left( {1 - \frac{P}{{{{P}_{{{\text{max}}}}}}}} \right)}^{{{{n}_{2}}}}}\frac{S}{{{{K}_{m}} + S + {{{{S}^{2}}} \mathord{\left/ {\vphantom {{{{S}^{2}}} {{{K}_{i}}}}} \right. \kern-0em} {{{K}_{i}}}}}} - \\ - \,\,\frac{D}{{{{\mu }_{{{\text{max}}}}}}} = 0. \\ \end{gathered} $

Задачей математического моделирования является получение значений X, S, P и B в виде решения системы (14)–(18) с исходными данными – концентрацией в поступающем потоке X₀, S₀, P₀ и B₀ и данными по величине протока D. Начальное значение X₀ равно нулю.

Одним из важнейших положений при моделировании является необходимость учета ограничения на величину протока D (смысл ограничения заключается в том, что при некотором D ≥ D_пред субстрат выводится из аппарата, не вступив в процесс синтеза, т.е. вымывается из ферментера).

Обозначим через $S{\text{'}}$ концентрацию субстрата, с которой он вымывается из ферментера, не вступив в процесс синтеза. Отметим, что $S{\text{'}}$ имеет две составляющие – ${{S}_{0}}$ (концентрация субстрата в поступающем потоке) и ${{k}_{M}}M$ (концентрация субстрата, образуемого из компонента сырья при значении $D = {{D}_{{{\text{п р е д }}}}}$). Вычислим $S{\text{':}}$

(19)

$S{\text{'}} = {{S}_{0}} + {{k}_{M}}M = {{S}_{0}} + \frac{{{{k}_{M}}{{M}_{0}}}}{{{{D}_{{{\text{п р е д }}}}} + {{k}_{M}}}}.$

В работе [7] вторая составляющая принята в виде M, т.е. $S{\text{'}} = {{S}_{0}} + M,$ что практически дает некоторый запас при вычислении D_пред.

Таким образом, D_пред вычисляется по формуле

(20)

${{D}_{{{\text{п р е д }}}}} = {{\mu }_{{{\text{max}}}}}\frac{{{{K}_{i}}S{\text{'}}}}{{{{K}_{m}}{{K}_{i}} + {{K}_{i}}S{\text{'}} + {{{\left( {S{\text{'}}} \right)}}^{2}}}}.$

При этом $S{\text{'}} = {{S}_{0}},$ если отсутствует образование дополнительного количества субстрата; S' = S₀ + + M по работе [7] и $S{\text{'}}$ по (19).

Поскольку при D_пред субстрат полностью вымывается из ферментера, не вступив в процесс синтеза, концентрации компонентов в этом случае имеют значения: P = 0; B = 0; X = 0; значение $S{\text{'}}$ соответствует (19). По формуле (20) с учетом (19) получаем

(21)

$\begin{gathered} {{D}_{{{\text{п р е д }}}}}{{K}_{m}}{{K}_{i}}{{\left( {{{D}_{{{\text{п р е д }}}}} + {{k}_{M}}} \right)}^{2}} + \\ + \,\,{{K}_{i}}\left( {{{D}_{{{\text{п р е д }}}}} - {{\mu }_{{\max }}}} \right)\left( {{{D}_{{{\text{п р е д }}}}} + {{k}_{M}}} \right) \times \\ \times \,\,\left[ {{{S}_{0}}\left( {{{D}_{{{\text{п р е д }}}}} + {{k}_{M}}} \right) + {{k}_{M}}{{M}_{0}}} \right] + \\ + \,\,{{D}_{{{\text{п р е д }}}}}{{\left[ {{{S}_{0}}\left( {{{D}_{{{\text{п р е д }}}}} + {{k}_{M}}} \right) + {{k}_{M}}{{M}_{0}}} \right]}^{2}} = 0. \\ \end{gathered} $

Для решения нелинейного уравнения (21) можно использовать начальное приближение $D_{{{\text{п р е д }}}}^{{\text{н }}},$ вычисленное по формуле для максимального значения D_пред:

(22)

$D_{{{\text{п р е д }}}}^{{\text{н }}} < \frac{{{{\mu }_{{{\text{max}}}}}}}{{2{{{\left( {\frac{{{{K}_{m}}}}{{{{K}_{i}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + 1}},$

полученное при условии, что подпитка отсутствует, т.е. когда $S{\text{'}} = {{S}_{0}}.$

Так, для K_m = 1.2 и K_i = 164 $D_{{{\text{п р е д }}}}^{{\text{н }}}$ = 0.41.

Уравнение (21) частично преобразуем, поделив на D_пред. Получим

(23)

$\begin{gathered} {{K}_{m}}{{K}_{i}}{{\left( {{{D}_{{{\text{п р е д }}}}} + {{k}_{M}}} \right)}^{2}} + {{K}_{i}}\left( {{{D}_{{{\text{п р е д }}}}} + {{k}_{M}}} \right) \times \\ \times \,\,\left( {1 - \frac{{{{\mu }_{{{\text{max}}}}}}}{{{{D}_{{{\text{п р е д }}}}}}}} \right)\left[ {{{S}_{0}}\left( {{{D}_{{{\text{п р е д }}}}} + {{k}_{M}}} \right) + {{k}_{M}}{{M}_{0}}} \right] + \\ + \,\,{{\left[ {{{S}_{0}}\left( {{{D}_{{{\text{п р е д }}}}} + {{k}_{M}}} \right) + {{k}_{M}}{{M}_{0}}} \right]}^{2}} = 0. \\ \end{gathered} $

Из показателей ингибирования в D_пред входит только K_i.

Приведем три значения D_пред, полученные по (23); по условию, когда подпитка отсутствует ($S{\text{'}} = {{S}_{0}}$); по условию $S{\text{'}} = {{S}_{0}} + M$ из публикации [7], используя значения констант базового варианта (константы базового варианта приведены ниже):

для соотношения (23) – D_пред = 0.3437 ч^–1;

при отсутствии подпитки – D_пред = 0.3464 ч^–1;

для уравнения из [7] – D_пред = 0.3219 ч^–1.

Таким образом, самое малое значение D_пред получает для условий расчета по формулам работы [7]. Последнее означает, что для решения конкретной технологической задачи это значение D_пред дает некоторый запас по D для случая возможной технологической реализации процесса.

Для вычисления X, S и P система уравнений (14)–(18) приводится к одному нелинейному алгебраическому уравнению. Возможны следующие три варианта.

Вариант 1. Из уравнения (14) имеем

(24)

$X = \frac{P}{{\alpha + {\beta \mathord{\left/ {\vphantom {\beta D}} \right. \kern-0em} D}}}.$

Из уравнения (16) с использованием (24) получаем

(25)

$S = {{S}_{0}} + \frac{{{{k}_{M}}{{M}_{0}}}}{{D + {{k}_{M}}}} - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{P}{{\left( {\alpha + {\beta \mathord{\left/ {\vphantom {\beta D}} \right. \kern-0em} D}} \right)}}.$

Используя (24) и (25) в (18), получаем

(26)

$\frac{{{{K}_{i}}\left[ {{{S}_{0}} + \frac{{{{k}_{M}}{{M}_{0}}}}{{D + {{k}_{M}}}} - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{P}{{\left( {\alpha + {\beta \mathord{\left/ {\vphantom {\beta D}} \right. \kern-0em} D}} \right)}}} \right]{{{\left[ {1 - \frac{P}{{{{X}_{{{\text{max}}}}}\left( {\alpha + {\beta \mathord{\left/ {\vphantom {\beta D}} \right. \kern-0em} D}} \right)}}} \right]}}^{{{{n}_{1}}}}}{{{\left[ {1 - \frac{P}{{{{P}_{{{\text{max}}}}}}}} \right]}}^{{{{n}_{2}}}}}}}{{{{K}_{m}}{{K}_{i}} + {{K}_{i}}\left[ {{{S}_{0}} + \frac{{{{k}_{M}}{{M}_{0}}}}{{D + {{k}_{M}}}} - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{P}{{\left( {\alpha + {\beta \mathord{\left/ {\vphantom {\beta D}} \right. \kern-0em} D}} \right)}}} \right] + {{{\left[ {{{S}_{0}} + \frac{{{{k}_{M}}{{M}_{0}}}}{{D + {{k}_{M}}}} - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{P}{{\left( {\alpha + {\beta \mathord{\left/ {\vphantom {\beta D}} \right. \kern-0em} D}} \right)}}} \right]}}^{2}}}} - \frac{D}{{{{\mu }_{{{\text{max}}}}}}} = 0.$

В результате решения (26) получаем значение P для любого заданного D (естественно в заданных пределах).

Остальные показатели X, S, M, B вычисляются с использованием (14)–(18).

Вариант 2. Из уравнения (16) выражается X:

(27)

$X = {{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}\left[ {\left( {{{S}_{0}} - S} \right) + \frac{{{{k}_{M}}{{M}_{0}}}}{{D + {{k}_{M}}}}} \right].$

Из уравнения (14) выражаем P, используя (27):

(28)

$P = \left( {\alpha + {\beta \mathord{\left/ {\vphantom {\beta D}} \right. \kern-0em} D}} \right){{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}\left[ {\left( {{{S}_{0}} - S} \right) + \frac{{{{k}_{M}}{{M}_{0}}}}{{D + {{k}_{M}}}}} \right].$

Подстановка (27) и (28) в (18) дает

(29)

$\begin{gathered} {{\left\{ {1 - \frac{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}{{{{X}_{{{\text{max}}}}}}}\left[ {\left( {{{S}_{0}} - S} \right) + \frac{{{{k}_{M}}{{M}_{0}}}}{{D + {{k}_{M}}}}} \right]} \right\}}^{{{{n}_{1}}}}} \times \\ \times {{\left\{ {1 - \frac{{\left( {\alpha + {\beta \mathord{\left/ {\vphantom {\beta D}} \right. \kern-0em} D}} \right){{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}{{{{P}_{{{\text{max}}}}}}}\left[ {\left( {{{S}_{0}} - S} \right) + \frac{{{{k}_{M}}{{M}_{0}}}}{{D + {{k}_{M}}}}} \right]} \right\}}^{{{{n}_{2}}}}} \times \\ \times \frac{{{{K}_{i}}S}}{{{{K}_{m}}{{K}_{i}} + {{K}_{i}}S + {{S}^{2}}}} - \frac{D}{{{{\mu }_{{{\text{max}}}}}}} = 0. \\ \end{gathered} $

Уравнение (29) является нелинейным алгебраическим уравнением относительно S для любых значений D (в заданных пределах). По вычисленным значениям S рассчитываются показатели процессов по решению системы (14)–(17).

Вариант 3. В соотношение (18) подставляем P из (14) и S из (16), получаем

(30)

$\begin{gathered} {{\left( {1 - \frac{X}{{{{X}_{{{\text{max}}}}}}}} \right)}^{{{{n}_{1}}}}}{{\left[ {1 - \frac{{\left( {\alpha + {\beta \mathord{\left/ {\vphantom {\beta D}} \right. \kern-0em} D}} \right)X}}{{{{P}_{{{\text{max}}}}}}}} \right]}^{{{{n}_{2}}}}} \times \\ \times \,\,\frac{{{{K}_{i}}\left( {{{S}_{0}} + \frac{{{{k}_{M}}{{M}_{0}}}}{{D + {{k}_{M}}}} - \frac{X}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}} \right)}}{{{{K}_{m}}{{K}_{i}} + {{K}_{i}}\left( {{{S}_{0}} + \frac{{{{k}_{M}}{{M}_{0}}}}{{D + {{k}_{M}}}} - \frac{X}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}} \right) + {{{\left( {{{S}_{0}} + \frac{{{{k}_{M}}{{M}_{0}}}}{{D + {{k}_{M}}}} - \frac{X}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}} \right)}}^{2}}}} - \frac{D}{{{{\mu }_{{{\text{max}}}}}}} = 0. \\ \end{gathered} $

По решению (30) вычисляется X для любого значения D (в заданных пределах) и вычисляются остальные показатели процесса по решению (14)–(17).

Таким образом, для моделирования процесса имеется возможность использовать любое уравнение из трех: (26), (29), (30).

В данной публикации будет использовано уравнение (30).

Величина D изменяется в пределах ограничений

$0 < D < {{D}_{{{\text{п р е д }}}}}.$

Последовательность решения задачи моделирования:

1) По исходным данным S₀ и M₀ и численным значениям констант для уравнений (7) рассчитывается D_пред по решению (23).

2) Принимаются значения D в области 0 < D < < D_пред.

3) Для каждого принятого значения D вычисляется X по решению (30).

4) Для каждого вычисленного значения X рассчитываются P по (14), В по (15), S по (16) и M по (17).

Полученные результаты представляют зависимости показателей процесса в функции D при заданных значениях S₀ и M₀, что дает возможность для пользователя выбирать приемлемое решение технологической организации процесса.

Далее приведем результаты практической реализации алгоритма по пунктам 1–4.

Подготовительная часть. Для моделирования процесса выполняется подготовка данных, включающая следующее.

Формируется перечень численных значений констант уравнений (7). Поскольку исследований по оценке констант для обобщенной модели не имеется, перечень численных значений сформирован в виде базового варианта по исследованиям частных задач [8] в виде табл. 1.

Таблица 1.

Численные значения констант для базового варианта

K_m, г/л	K_i, г/л	µ_max, ч^–1	X_max, г/л	P_max, г/л	n₁	n₂	Y_X/S, г/г	k_M, ч^–1	α, г/г	β, ч^–1	α_B, г/г	β_B, ч^–1
1.2	164	0.48	30	98.0	0.5	0.5	0.4	0.035	2.2	0.02	1.1	0.01

Задаются значения показателей S₀, M₀, P₀, B₀, X₀ в поступающем потоке. Для S₀ и M₀ по работе [10]: S₀ = 60 г/л; M₀ = 20 г/л; значения P₀ = 0; B₀ = 0; X₀ = 0. На этом завершается подготовительная часть. В соответствии с п. 1 вычисляется D_пред по решению уравнения (23).

Предельное значение D для базового варианта при S₀ = 60 г/л и M₀ = 20 г/л: D_пред = 0.3437 ч^–1.

В соответствии с п. 2 расчет выполнен для трех значений D: D₁ = 0.1 ч^–1, D₂ = 0.2 ч^–1, D₃ = 0.3 ч^–1.

В соответствии с п. 3 вычисляем значения X по решению уравнения (30):

X₁ (при D₁ = 0.1 ч^–1) = 24.41 г/л;

X₂ (при D₂ = 0.2 ч^–1) = 17.67 г/л;

X₃ (при D₃ = 0.3 ч^–1) = 6.48 г/л.

В соответствии с п. 4 вычисляются показатели P, B, S и M, а также величина продуктивности по соотношению Q_p = PD, г/(л ч).

Результаты расчета сведены в табл. 2.

Таблица 2.

Результаты моделирования процесса для трех показателей D

Показатели процесса	X, г/л	P, г/л	S, г/л	B, г/л	M, г/л	Q_p, г/(л ч)
D₁= 0.1 ч^–1	24.41	58.58	4.16	29.29	14.81	5.86
D₂= 0.2 ч^–1	17.67	40.64	18.80	20.32	17.02	8.13
D₃= 0.3 ч^–1	6.48	14.69	45.89	7.34	17.91	4.40

Решение задачи моделирования удобно представить также в графической форме.

В этом варианте в п. 2 задание D формируется с шагом ΔD, например, равным 0.005 в области 0.1–0.33 (0 < D < D_пред).

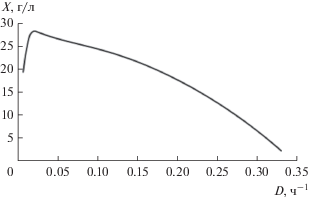
Вычисление X по п. 3 осуществляется во всей области изменения D с аппроксимацией непрерывной кривой.

Результат приведен на рис. 1 для базового варианта.

Рис. 1.

Зависимость X от D.

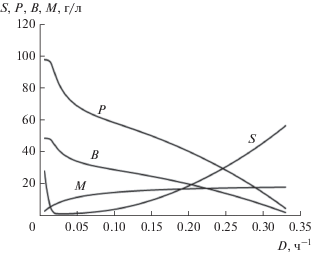
По значениям X вычисляются в соответствии с п. 4 значения P, B, S и M с аппроксимацией непрерывными кривыми. Результат приведен на рис. 2.

Рис. 2.

Зависимости показателей P, B, S, M от D.

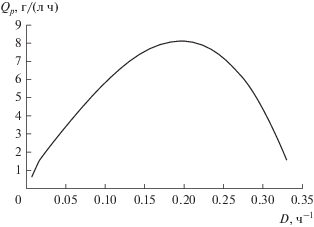
Аналогично рассчитывается величина продуктивности. Результат приведен на рис. 3.

Рис. 3.

Зависимость продуктивности от D (max Q_p = = 8.12 г/(л ч), D = 0.185 ч^–1, D_пред = 0.3437 ч^–1).

Далее с использованием графических зависимостей приведены примеры влияния показателей ингибирования на результаты моделирования.

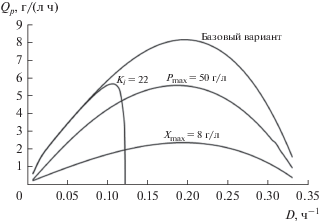
Поскольку ингибирование проявляется при оценке скорости образования биомассы, результаты влияния ингибирования показаны в виде зависимости X от D в сравнении с базовым вариантом (рис. 4).

Рис. 4.

Сравнение зависимостей X от D для базового варианта и при ингибировании.

Ингибирование оценивалось путем изменения констант в уравнениях обобщенной модели. Так, величина K_i на рис. 4 равна 22 г/л (в базовом варианте 164 г/л). Отметим, что ингибирование субстратом (K_i) влияет одновременно и на величину D_пред, т.е. область изменения D для этого варианта:

$0 < D < {{D}_{{{\text{п р е д }}}}} = 0.1215{\text{ }}{{{\text{ч }}}^{{--1}}}.$

Таким образом, область изменения D значительно уже по сравнению с базовым вариантом и с вариантами ингибирования по продукту (P_max = = 50, в базовом 98 г/л) и по биомассе (X_max = 8, в базовом 30 г/л).

На предельное значение D ингибирование продуктом и биомассой влияния не оказывают, т.е. значение D_пред в этих вариантах равно 0.3437 ч^–1 – такое же как и для базового варианта.

Численные значения X и продуктивности Q_p приведены в табл. 3 для D = 0.1, 0.2 и 0.3 ч^–1.

Таблица 3.

Оценка влияния ингибирования на концентрацию биомассы и на величину продуктивности

Вариант	Параметр	D = 0.1 ч^–1	D = 0.2 ч^–1	D = 0.3 ч^–1	D_пред, ч^–1
Базовый вариант	X	24.41	17.67	6.48	0.3437
Базовый вариант	Q_p	5.86	8.13	4.40	0.3437
K_i = 22 г/л	X	23.28	–	–	0.1215
K_i = 22 г/л	Q_p	5.59	–	–	0.1215
P_max = 50 г/л	X	17.7	18.08	4.14	0.3437
P_max = 50 г/л	Q_p	4.26	5.56	2.82	0.3437
X_max = 8 г/л	X	7.27	5.21	1.86	0.3437
X_max = 8 г/л	Q_p	1.75	2.40	1.27	0.3437

Отметим, что влияние ингибирования для всех вариантов табл. 3 уменьшает величину продуктивности Q_p по сравнению с базовым вариантом.

Приведем результаты оценки max Q_p по влиянию показателей ингибирования.

В табл. 4 приведены значения max Q_p и соответствующие им значения D, при которых эти показатели получены. Ингибирование, как и прежде, определялось значениями констант.

Таблица 4.

Значения max Q_p при изменении констант уравнений модели, определяющих уровень ингибирования

Параметр	Базовый вариант	K_i = 22 г/л	P_max = 50 г/л	X_max = 8 г/л
maxQ_p, г/(л ч)	8.13	5.65	5.78	2.40
D, ч^–1	0.195	0.105	0.195	0.195

В соответствии с табл. 4 наиболее сильное влияние ингибирования на max Q_p проявляется при ингибировании биомассой. При ингибировании по K_i и P_max значения max Q_p отличаются незначительно.

В то же время положения max Q_p по D при ингибировании по X_max, P_max и для базового варианта практически совпадают. Для ингибирования по K_i положение экстремума существенно смещается в сторону меньшего значения D. Таким образом, полученные оценки по max Q_p могут служить основой для выбора соответствующих штаммов микроорганизмов при технологическом обеспечении процесса с учетом условий ингибирования.

ЗАКЛЮЧЕНИЕ

Научные исследования в области получения молочной кислоты ферментативным методом показали, что молочная кислота является одним из основных продуктов микробиологического синтеза, используемых для получения широкого спектра многих видов товаров потребления.

Наиболее полная обзорная публикация [9], в которой приведен список микроорганизмов, продуцирующих молочную кислоту, и перечень субстратов для ее получения, содержит 326 ссылок.

Кроме того, уместно привести научные публикации, содержащие анализ и моделирование технологических аспектов получения молочной кислоты, а также оценку оптимальных условий и технологических ограничений, неучет которых затрудняет практическую реализацию технологии. В работе [1] содержится 100 ссылок; в [2] – 106; в [3] – 43; в [10] – 98; в [11] – 191; в [12] – 39.

Понятно, что ряд ссылок повторяются, однако их общее количество впечатляет и выводит молочную кислоту, получаемую ферментативным методом, в один из наиболее востребованных продуктов промышленного производства. Рассмотренная обобщенная математическая модель практически дает возможность моделировать большинство частных случаев, рассмотренных в вышеприведенных публикациях, открывает возможность моделирования полупериодических процессов, процессов с рециркуляцией, с мембранным выделением продукта и др.

ОБОЗНАЧЕНИЯ

B	концентрация суммарного количества побочных продуктов, г/л
D	величина протока, ч^–1
K_i	константа ингибирования, г/л
K_m	константа насыщения субстрата, г/л
k_M	константа, определяющая количество воспроизведенного субстрата, ч^–1
M	концентрация сырья, дополнительно воспроизводящего субстрат, г/л
P	концентрация продукта, г/л
Q_p	продуктивность, г/(л ч)
S	концентрация субстрата, г/л
X	концентрация биомассы, г/л
Y_X/S	стехиометрический коэффициент, г/г
α, α_B, β, β_B	константы
µ	удельная скорость роста микроорганизмов, ч^–1

ИНДЕКСЫ

0	начальное значение
max	максимальное значение
пред	предельное значение

Список литературы

Bouguettoucha A., Balannec B., Amrane A. Unstructured models for lactic acid fermentation – A review // Food Technol. Biotechnol. 2011. V. 49. P. 3.
Gordeev L.S., Koznov A.V., Skichko A.S., Gordeeva Yu.L. Unstructured mathematical models of lactic acid biosynthesis kinetics: A review // Theor. Found. Chem. Eng. 2017. V. 51. № 2. P. 175. [Гордеев Л.С., Кознов А.В., Скичко А.С., Гордеева Ю.Л. Неструктурированные математические модели кинетики биосинтеза молочной кислоты. Обзор // Теорет. основы хим. технологии. 2017. Т. 51. № 2. С. 8.]
Gordeeva Yu.L., Rudakovskaya E.G., Gordeeva E.L., Borodkin A.G. Mathematical modeling of biotechnological process of lactic acid production by batch fermentation: A review // Theor. Found. Chem. Eng. 2017. V. 51. № 3. P. 282. [Гордеева Ю.Л., Рудаковская Е.Г., Гордеева Е.Л., Бородкин А.Г. Математическое моделирование биотехнологического процесса периодической ферментации получения молочной кислоты. Обзор // Теорет. основы хим. технологии. 2017. Т. 51. № 3. С. 270.]
Schepers A.W., Thibault J., Lacroix C. Lactobacillus helveticus growth and lactic acid production during pH-controlled batch cultures in whey permeate/yeast extract medium. Part II: kinetic modeling and model validation // Enzyme Microb. Technol. 2002. V. 30. № 2. P. 187.
Åkerberg C., Hofvendahl K., Zacchi G., Hahn-Hӓgerdal B. Modelling the influence of pH, temperature, glucose and lactic acid concentrations on the kinetics of lactic acid production by Lactococcus lactis ssp. lactis ATCC 19435 in whole-wheat flour // Appl. Microbiol. Biotechnol. 1998. V. 49. № 6. P. 682.
Ohara H., Hiyama K., Yoshida T. Kinetic study on pH dependence of growth and death of Streptococcus faecalis // Appl. Microbiol. Biotechnol. 1992. V. 38. № 3. P. 403.
Gordeeva Yu.L., Borodin A.V., Gordeev L.S. Estimating the limiting rate of dilution in technology for lactic acid production by continuous fermentation // Theor. Found. Chem. Eng. 2018. V. 52. № 1. P. 64. [Гордеева Ю.Л., Бородин А.В., Гордеев Л.С. К оценке предельного значения протока в технологии получения молочной кислоты непрерывной ферментацией // Теорет. основы хим. технологии. 2018. Т. 52. № 1. С. 68.]
Gordeeva Yu.L., Borodkin A.G., Gordeev L.S. Optimal process parameters of the synthesis of lactic acid by continuous fermentation // Theor. Found. Chem. Eng. 2018. V. 52. № 3. P. 386. [Гордеева Ю.Л., Бородкин А.Г., Гордеев Л.С. Оптимальные технологические показатели процесса получения молочной кислоты непрерывной ферментацией // Теорет. основы хим. технологии. 2018. Т. 52. № 3. С. 334.]
Abdel-Rahman M.A., Tashiro Y., Sonomoto K. Recent advances in lactic acid production by microbial fermentation processes // Biotechnology Advances. 2013. V. 31. № 6. P. 877.
Wee Y.-J., Kim J.-N., Ryu H.-W. Biotechnological production of lactic acid and its recent applications // Food Technol. Biotechnol. 2006. V. 44. P. 163.
Hofvendahl K., Hahn-Hägerdel B. Factors affecting the fermentative lactic acid production from renewable resources // Enzyme and Microbial Technol. 2000. V. 26. P. 87.
Datta R., Henry M. Lactic acid: recent advances in products, processes and technologies – a review // J. Chemical Technology and Biotechnology. 2006. V. 81. P. 1119.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал