Теоретические основы химической технологии, 2019, T. 53, № 4, стр. 372-386
Молекулярное моделирование процесса первапорации леннард-джонсовской смеси на мембране кристаллического типа
А. В. Клинов 1, *, И. П. Анашкин 1, А. И. Разинов 1, Л. Р. Минибаева 1
1 Казанский национальный исследовательский технологический университет
Казань, Россия
* E-mail: alklin@kstu.ru
Поступила в редакцию 28.12.2018
После доработки 14.01.2019
Принята к публикации 14.01.2019
Аннотация
На основе метода молекулярной динамики проведено численное моделирование процесса первапорации. Были рассмотрены различные условия разделения идеальной бинарной леннард-джонсовской смеси с помощью мембраны кристаллического типа. Компоненты разделяемой смеси отличались энергией взаимодействия к молекулам мембраны. В результате моделирования были получены поля концентраций и плотностей вдоль ячейки, а также величины потоков компонентов. Кроме того, были рассчитаны коэффициенты диффузии компонентов в мембране. Было показано, что во всех случаях наблюдалось соответствие данных численного моделирования макроскопическим уравнениям массопереноса. В результате можно сделать вывод, что в неравновесной системе масштаба несколько десятков диаметров молекул поведение макросвойств соответствует уравнениям переноса линейной неравновесной термодинамики. Результаты численного моделирования показали селективность мембраны по отношению к компоненту с большей энергией взаимодействия. Было показано, что молекулярное моделирование оказывается способным предсказывать основные характеристики мембранного разделения (потоки, селективность, адсорбцию, коэффициенты диффузии).
ВВЕДЕНИЕ
В настоящее время существенно расширяется область применения процессов мембранного разделения газовых и жидких смесей. Разнообразие мембранных процессов обусловливается типом мембран и аппаратурным оформлением. Так, в процессах первапорации и газоразделения применяются непористые мембраны из различных материалов: полимеры [1, 2], керамика [3], металлические пленки [4, 5] и т.д. Считается, что процесс переноса массы через такие мембраны осуществляется диффузионным механизмом, а эффективность разделения достигается за счет различия у компонентов смеси способности в адсорбции на поверхности мембраны и скорости диффузии внутри нее. Поэтому известные макромодели [6], позволяющие описывать процесс мембранного разделения на непористых мембранах, содержат параметры, характеризующие изотермы адсорбции и коэффициенты диффузии или некоторые интегральные величины – коэффициенты проницаемости. Для определения таких параметров необходимы экспериментальные исследования, что очевидно является сдерживающем фактором для успешного промышленного внедрения процессов мембранного разделения новых смесей или с использованием мембран из новых материалов.
Одним из перспективных методов определения характеристик мембранного процесса являются молекулярно-статистические методы [7–13]. Эти методы основаны на использовании данных только о межмолекулярном взаимодействии компонентов и мембраны, что позволяет производить прогнозирование разделительной способности мембраны к конкретной разделяемой смеси с минимальным количеством экспериментальных данных или вообще в отсутствие последних. Кроме того, молекулярное моделирование позволяет выявить локальные особенности процесса мембранного разделения, что может быть основой для построения надежных макромоделей.
В данной работе объектом исследований являлся процесс первапорационного разделения жидкой смеси с помощью кристаллической мембраны. Межмолекулярное взаимодействие компонентов смеси между собой и с молекулами мембраны описывалось потенциалом Леннард-Джонса:
(1)
$\varphi ({{r}_{{ij}}}) = 4{{\varepsilon }_{{ij}}}\left( {{{{\left( {\frac{{{{\sigma }_{{ij}}}}}{{{{r}_{{ij}}}}}} \right)}}^{{12}}} - {{{\left( {\frac{{{{\sigma }_{{ij}}}}}{{{{r}_{{ij}}}}}} \right)}}^{6}}} \right),$В связи с тем, что изучалась модельная система, параметры состояния и коэффициенты переноса удобнее определять в безразмерном виде по следующим соотношениям: расстояние $r{\text{*}} = \frac{r}{\sigma },$ температура $T{\text{*}} = \frac{{{{k}_{{\text{B}}}}T}}{\varepsilon },$ числовая плотность $n{\text{*}} = n{{\sigma }^{3}},$ коэффициент диффузии $D{\text{*}}$ = $\frac{D}{\sigma }\sqrt {\frac{m}{\varepsilon }} ,$ поток $j{\text{*}} = j{{\sigma }^{3}}\sqrt {\frac{m}{\varepsilon }} ,$ конвективная скорость $w{\text{*}}$ = $w\sqrt {\frac{m}{\varepsilon }} ,$ время $t{\text{*}}$ = $\frac{t}{\sigma }\sqrt {\frac{\varepsilon }{m}} ,$ где m – масса молекулы, kB – константа Больцмана. В качестве масштаба использовались меньшие из значений ε и σ для разделяемых компонентов.
МОДЕЛИРОВАНИЕ ПРОЦЕССА ПЕРВАПОРАЦИИ
Для моделирования процесса первапорации использовался метод двойного контрольного объема (dual control volume grand canonical molecular dynamics – DCV-GCMD) [11, 14–16], который широко применялся для плотных газов [17–24]. Как показали наши исследования, данный метод не позволяет добиться плотностей, соответствующих жидкости, поэтому в этой работе метод был модифицирован. В отличие от оригинального метода, в контрольных объемах поддерживалось постоянство числовой плотности каждого из компонентов вместо химического потенциала. Данный подход ранее был использован нами при исследовании разделения смеси этанол–вода [25].
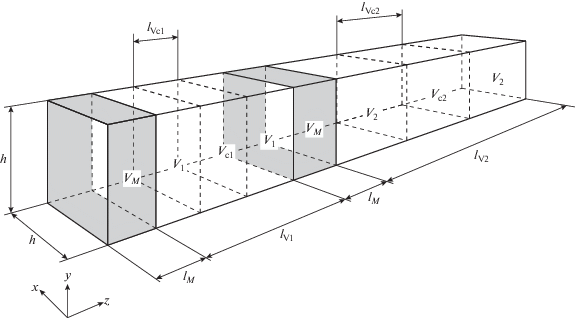
На рис. 1 представлена схема ячейки, в которой проводится моделирование. В ячейке, вытянутой по оси z, в определенном порядке располагаются три типа зон: зона мембраны – VM, сырьевая зона – V1 и зона пермеата – V2. В средней части сырьевой и пермеатной зон выделяются контрольные объемы Vc1 и Vc2. Ширина контрольного объема принималась равной высоте ячейки (lVc1 = h = 16σ). Между контрольным объемом Vc1 и мембраной задавалось расстояние, равное h, для формирования пограничного слоя. Таким образом, lV1 = 48σ. Плотность газовой фазы существенно ниже, поэтому контрольный объем и расстояние до мембраны было в 3 раза больше (lV2 = 3; lV1 = 144σ).
Рис. 1.
Схема разделения моделируемой ячейки на области. Значения индексов: V1 – область исходной смеси, V2 – область пермеата, М – область мембраны, Vс1, Vс2 – контрольные объемы.
Все моделирование разбивалось на циклическое повторение следующего алгоритма:
1) В начале каждого шага добавлялись молекулы в контрольный объем Vc1 до достижения заданной плотности каждого из компонентов.
2) Из контрольного объема Vc2 удалялись все молекулы для поддержания вакуума.
3) После добавления и удаления молекул проводилось моделирование молекулярной динамикой. Шаг интегрирования по времени составлял t* = 0.0003. Постоянная температура поддерживалась термостатом Nosé–Hoover. Радиус обрезания потенциала равен половине размера ячейки rcut = h/2 = 8σ. После 20 тыс. итераций интегрирования уравнений движения алгоритм повторялся.
Для поддержания постоянной плотности каждого из компонентов в контрольном объеме применялся следующий алгоритм добавления молекул:
1) Выбирается случайное расположение молекулы в контрольном объеме.
2) Рассчитывается расстояние до каждой из молекул в контрольном объеме и изменение энергии: $\Delta U$ = $\sum\limits_{i = 1}^N {\varphi ({{r}_{{in - i}}})} ,$ где N – количество молекул в системе, φ – потенциал межмолекулярного взаимодействия, индекс in соответствует добавляемой молекуле.
3) Если изменение энергии меньше заданного максимального значения $\Delta U < {{U}_{{\max }}},$ то молекула добавляется, и взаимодействие с ней будет учитываться на следующих шагах моделирования.
На каждом этапе принималось 100 000 попыток добавления молекул. Величина Umax динамически изменялась таким образом, чтобы обеспечивать заданную плотность. Время моделирования динамики молекул подбиралось таким образом, чтобы на каждом цикле в контрольный объем добавлялось не более 10 молекул. Количество молекул в контрольном объеме для условий моделирования составляет около 3000. Таким образом, флуктуации плотности составляли менее 0.3%, что незначительно влияло на термодинамические условия в контрольном объеме.
В начальном состоянии жидкая фаза содержит случайным образом расставленные молекулы с заданной плотностью каждого из компонентов, а мембрана и газовая фаза пустые. В процессе моделирования молекулы заполняют мембрану и область пермеата. Расчет усредненных по микросостояниям свойств системы начинается только после достижения стационарного состояния, при котором суммарное количество молекул каждого из компонентов в системе остается постоянным.
Значения потоков определялись по количеству молекул, перешедших из жидкой фазы в мембрану и из мембраны в область пермеата:
где ΔNi – изменение количества молекул компонента i в объеме V1 или V2, Δt – временной интервал измерения, S – площадь поперечного сечения мембраны. Значение ΔNi рассчитывалось как разница количества молекул компонентов в объеме V1 или V2 после добавления молекул и по истечении времени каждого из циклов алгоритма.Как показали исследования, после достижения стационарности потоки, определенные по изменению количества молекул в V1 и V2, были равны. Исходя из рассчитанных потоков и концентрации компонентов в исходной смеси, можно рассчитать селективность:
(3)
${{\alpha }_{i}} = \frac{{\frac{{{{x}_{{iP}}}}}{{{{x}_{{jP}}}}}}}{{\frac{{{{x}_{{iF}}}}}{{{{x}_{{jF}}}}}}} = \frac{{{{j}_{i}}{{x}_{{jF}}}}}{{{{j}_{j}}{{x}_{{iF}}}}},$Для определения статистического отклонения (далее в тексте обозначаемое как Δ) рассчитываемых величин использовался метод деления времени моделирования на блоки. Для определения распределения плотности компонентов вдоль мембраны использовался метод гистограмм [26].
Моделирование динамики молекул проводилось с использованием пакета GROMACS 4.7 [27–29]. Для процедуры добавления и удаления молекул, усреднения величин были разработаны собственные программы [30].
В данной работе исследована мембрана, состоящая из леннард-джонсовских центров взаимодействия, расположенных в узлах кубической кристаллической решетки. Во всех проведенных в данной работе численных экспериментах расстояние между молекулами мембраны равнялось 2σ. Молекулы мембраны фиксировались в узлах кристаллической решетки. Расчет температуры системы проводился с учетом скоростей только молекул разделяемой смеси, без учета молекул мембраны.
В данной работе исследовалось разделение смеси двух компонентов (обозначенных A и B), масса и межмолекулярное взаимодействие которых не отличается (mA = mB, σAA = σAB = σBB, εAA = εAB = εBB). Таким образом, данную смесь невозможно разделить ректификацией. Отличие двух компонентов заключалось лишь во взаимодействии с мембраной. Компонент A в два раза сильнее взаимодействовал с молекулами мембраны (εAM = 2εBM).
РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ
На первом этапе был исследован массоперенос чистых веществ и компонентов эквимолярной смеси через мембрану толщиной $l_{M}^{*}$ = 20 при температурах T* = 1.5 и 1.0. Условия и результаты моделирования приведены в табл. 1.
Таблица 1.
Результаты моделирования массопереноса чистых веществ и компонентов эквимолярной смеси через мембрану толщиной $l_{M}^{*}$ = 20 (nF – плотность жидкости в контрольном объеме Vc1)
| Условия моделирования | Численный эксперимент | Математическая модель | ||||
|---|---|---|---|---|---|---|
| $j_{A}^{*}$ | $\Delta j_{A}^{*}$ | $j_{B}^{*}$ | $\Delta j_{B}^{*}$ | α | w* | |
| Компонент A (T* = 1.5, $n_{F}^{*} = 0.73$) | 0.018728 | 0.000022 | – | – | – | 0.0216 |
| Компонент B (T* = 1.5, $n_{F}^{*} = 0.73$) | – | – | 0.023261 | 0.000054 | – | 0.0246 |
| Смесь (xAF = 0.5, T* =1.5, $n_{F}^{*} = 0.73$) | 0.010548 | 0.000043 | 0.010168 | 0.000058 | 1.0373 | 0.0246 |
| Смесь (xAF = 0.5, T* = 1.0, $n_{F}^{*} = 0.8$) | 0.003123 | 0.000159 | 0.002395 | 0.000058 | 1.3040 | 0.0065 |
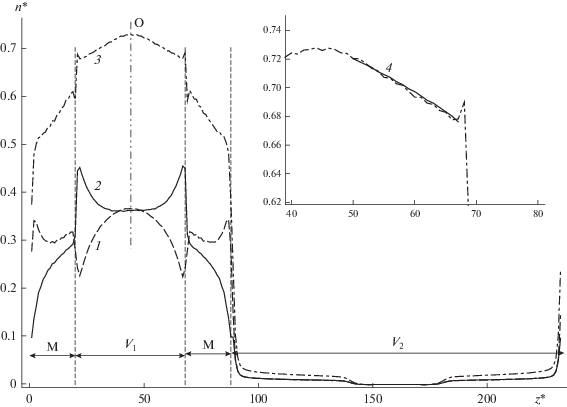
Видно, что чистый компонент B имеет больший поток через мембрану по сравнению с чистым компонентом A, что объясняется большей энергией взаимодействия с мембраной последнего. Как будет показано дальше, коэффициент диффузии чистого компонента B в мембране больше, чем A. Однако для бинарной смеси поток компонента А оказывается выше, чем компонента В. Причем разница в потоках увеличивается с уменьшением температуры. Таким образом, мембрана является селективной по отношению к компоненту А и с уменьшением температуры селективность увеличивается. На рис. 2 представлено распределение плотностей компонентов смеси вдоль моделируемой ячейки. Видно, что плотность компонента А на поверхности мембраны и внутри нее больше, чем компонента В. Очевидно что, селективность мембраны в данном случае определяется разной сорбционной способностью компонентов к мембране.
Рис. 2.
Распределение плотностей компонентов разделяемой эквимолярной смеси и суммарной плотности вдоль моделируемой ячейки при T * = 1.5, $n_{F}^{*}$ = 0.73, $l_{М }^{*}$ = 20, xAF = 0.5 (O – плоскость симметрии ячейки; на дополнительном рисунке представлено распределение суммарной плотности в жидкой фазе): 1 – компонент A, 2 – компонент B, 3 – суммарная плотность, 4 – из решения дифференциального уравнения (14).
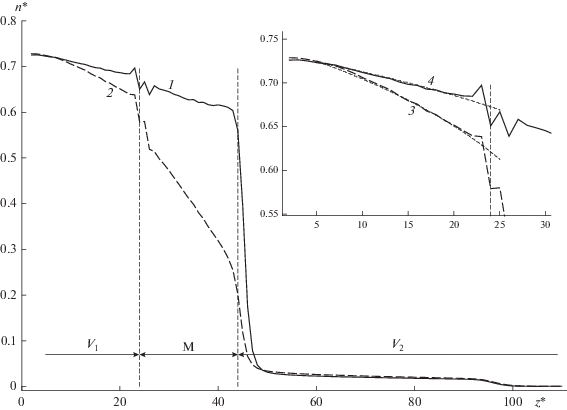
На рис. 3 представлено распределение плотности компонентов А и В при массопереносе чистых веществ. На этом и последующих рисунках распределение плотности и концентрации компонентов вдоль моделируемой ячейки усреднялось относительно плоскости симметрии ячейки.
Рис. 3.
Сравнение распределения плотности чистых компонентов вдоль моделируемой ячейки при массопереносе чистых веществ при T* = 1.5, $n_{F}^{*}$ = 0.73, $l_{М }^{*}$ = 20 (на дополнительном рисунке представлено распределение плотности в объеме V1): 1 – компонент A, 2 – компонент B, 3 – плотность компонента B из решения дифференциального уравнения, 4 – плотность компонента A из решения дифференциального уравнения (13).
Далее в работе исследовалось влияние различных факторов на характеристики процесса первапорационного разделения идеальной леннард-джонсовской смеси с помощью мембраны кристаллического типа.
Влияние толщины мембраны. Были проведены исследования влияния толщины мембраны на характеристики процесса разделения бинарной эквимолярной смеси при T* = 1. Плотность исходной смеси $n_{F}^{*}$ = 0.8. Результаты представлены в табл. 2.
Таблица 2.
Значения потоков компонентов в зависимости от толщины мембраны ($n_{F}^{*}$ = 0.8, T* = 1, xAF= 0.5)
| $l_{M}^{*}$ | $j_{A}^{*}$ | $\Delta j_{A}^{*}$ | $j_{B}^{*}$ | $\Delta j_{B}^{*}$ | αA |
|---|---|---|---|---|---|
| 20 | 0.003123 | 0.000159 | 0.002395 | 0.000058 | 1.303967 |
| 40 | 0.002222 | 0.000126 | 0.001302 | 0.000035 | 1.706605 |
| 60 | 0.001790 | 0.000109 | 0.000860 | 0.000035 | 2.081395 |
| 80 | 0.001520 | 0.000099 | 0.000626 | 0.000018 | 2.428115 |
| 100 | 0.001336 | 0.000097 | 0.000502 | 0.000011 | 2.661355 |
Как видно из таблицы, с увеличением толщины мембраны поток компонентов падает, однако селективность по компоненту A увеличивается. Распределение плотности компонентов вдоль моделируемой ячейки представлено на рис. 4 (полные данные представлены в дополнительных материалах [31]).
Рис. 4.
Распределение плотности компонентов разделяемой эквимолярной смеси вдоль моделируемой ячейки при различной толщине мембраны $l_{М }^{*}$ ($n_{F}^{*}$ = 0.8, T* = 1, xAF = 0.5, на дополнительном рисунке представлено распределение суммарной плотности в объеме V1): 1 – компонент A, 2 – компонент B, 3 – суммарная плотность, 4 – из решения дифференциального уравнения; (а) – $l_{М }^{*}$ = 20; (б) – $l_{М }^{*}$ = 60; (в) – $l_{M}^{*}$ = 100.
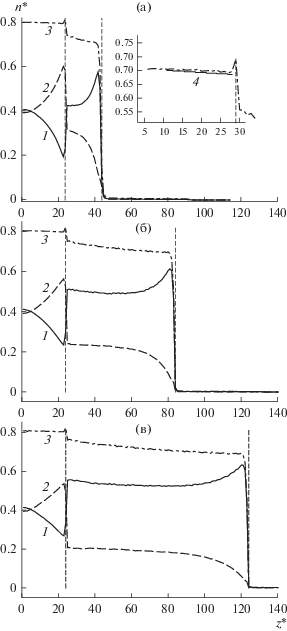
Из рис. 4 видно, что в жидкой фазе суммарная плотность разделяемой смеси практически не меняется, в мембране суммарная плотность изменяется примерно на 7%. В пограничной с мембраной области наблюдается уменьшение плотности компонента A, т.е. наблюдается эффект концентрационной поляризации. Изменение плотности тем больше, чем больше поток компонентов.
Влияние состава разделяемой смеси. В работе исследовалась зависимость характеристик процесса первапорации от концентрации разделяемой смеси при T* = 1 для толщины мембраны $l_{M}^{*}$ = 40. Плотность исходной смеси $n_{F}^{*}$ = 0.8. Результаты представлены в табл. 3.
Таблица 3.
Значения потоков компонентов в зависимости от концентрации компонентов в исходной смеси ($n_{F}^{*}$ = 0.8, T* = 1, $l_{M}^{*}$ = 40)
| xAF | $j_{A}^{*}$ | $\Delta j_{A}^{*}$ | $j_{B}^{*}$ | $\Delta j_{B}^{*}$ | αA |
|---|---|---|---|---|---|
| 0.125 | 0.00074 | 0.000214 | 0.003886 | 0.000151 | 1.3330 |
| 0.250 | 0.001322 | 0.000080 | 0.002729 | 0.000071 | 1.4533 |
| 0.375 | 0.001767 | 0.000108 | 0.001900 | 0.000050 | 1.5500 |
| 0.500 | 0.002251 | 0.000126 | 0.001302 | 0.000035 | 1.7289 |
| 0.625 | 0.002594 | 0.000152 | 0.000823 | 0.000023 | 1.8911 |
| 0.750 | 0.002906 | 0.000168 | 0.000446 | 0.000015 | 2.1719 |
| 0.875 | 0.003132 | 0.000168 | 0.000185 | 0.000005 | 2.4185 |
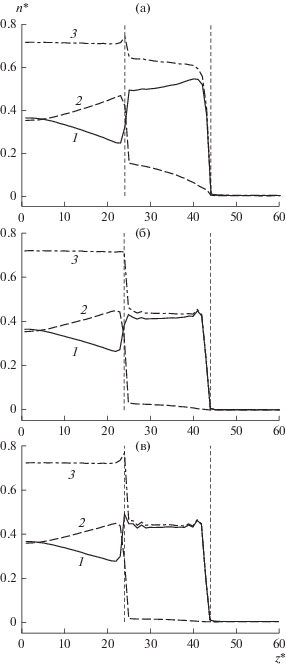
Как показали результаты моделирования, с увеличением доли компонента A его поток и селективность разделения увеличиваются. Распределения плотности для некоторых из проведенных экспериментов представлены на рис. 5. Полные данные по распределению плотности компонентов вдоль моделируемой ячейки приведены в дополнительных материалах [31].
Рис. 5.
Распределение плотности компонентов вдоль моделируемой ячейки при различном составе исходной смеси ($n_{F}^{*}$ = 0.8, T * = 1, $l_{М }^{*}$ = 40): 1 – компонент A, 2 – компонент B, 3 – суммарная плотность; (а) – ${{x}_{{AF}}}$ = 0.125; (б) – ${{x}_{{AF}}}$ = 0.5; (в) – ${{x}_{{AF}}}$ = 0.875.
Влияние доли свободного объема в мембране. Внутренняя структура мембраны оказывает значительное влияние на характеристики процесса мембранного разделения. В работе исследовалось влияние доли свободного объема мембраны на величины потоков компонентов и селективность процесса. Доля свободного объема изменялась за счет увеличения диаметра молекул мембраны при их фиксированных положениях в решетке. Увеличение размера молекул мембраны задавалось путем изменения параметра взаимодействия молекул мембраны и компонентов s = σAM/σAB = σBM/σAB. Доля свободного объема в мембране зависит от s как ${{V}_{0}}$ = ${{\left( {1 - n_{M}^{*}s} \right)}^{3}},$ где $n_{M}^{*}$ − плотность мембраны при s = 1. Моделирование проводилось при $n_{F}^{*}$ = 0.8, T* = 1.0, xAF = 0.5, $l_{M}^{*}$ = 20. Результаты представлены в табл. 4.
Таблица 4.
Поток и селективность при различном значении доли свободного объема мембраны (параметр s)
| s | Численный эксперимент | Математическая модель, коэффициент взаимной диффузии | ||||
|---|---|---|---|---|---|---|
| $j_{A}^{*}$ | $\Delta j_{A}^{*}$ | $j_{B}^{*}$ | $\Delta j_{B}^{*}$ | αA | $D_{{AB}}^{*}$ | |
| 1.03 | 0.001751 | 0.000082 | 0.000689 | 0.000015 | 2.54 | 0.0425 |
| 1.07 | 0.001586 | 0.000067 | 0.000482 | 0.000017 | 3.29 | 0.042 |
| 1.1 | 0.001429 | 0.000074 | 0.000293 | 0.000011 | 4.88 | 0.039 |
| 1.17 | 0.001231 | 0.000107 | 0.000105 | 0.000006 | 11.72 | 0.031 |
| 1.2 | 0.00105 | 0.000116 | 0.000079 | 0.000017 | 13.29 | 0.025 |
| 1.23 | 0.00093 | 0.000139 | 0.000046 | 0.000004 | 20.22 | 0.019 |
| 1.27 | 0.0008 | 0.000138 | 0.000030 | 0.000003 | 26.67 | 0.014 |
| 1.3 | 0.00061 | 0.000123 | 0.000018 | 0.000001 | 33.89 | 0.009 |
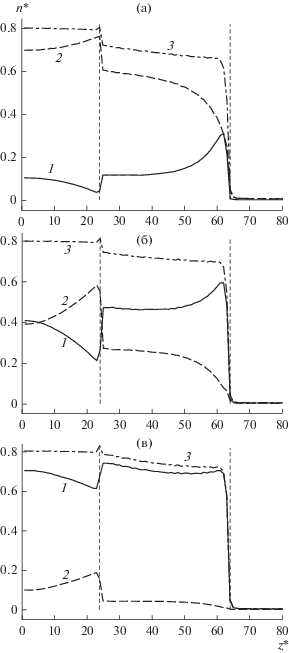
Из таблицы видно, что при увеличении размеров молекул мембраны снижается суммарный поток и значительно возрастает селективность разделения по компоненту А. На рис. 6 представлено распределение плотностей компонентов вдоль моделируемой ячейки. Видно, что с увеличением размера молекул мембраны существенно снижается плотность компонента B в мембране. Суммарная плотность компонентов при увеличении размеров молекул мембраны снижается. Однако после достижения значения s, равного 1.17, суммарная плотность достигает значения n* = 0.45 и изменяется несущественно. Это можно объяснить тем, что в этом случае в свободное сечение между узлами решетки помещается только одна молекула. Молекулы при этом двигаются друг за другом.
Рис. 6.
Распределение плотностей компонентов в моделируемой ячейке при различном значении s ($n_{F}^{*}$ = = 0.73, T* = 1.0, xAF = 0.5 $l_{М }^{*}$ = 20): 1 – компонент A, 2 – компонент B, 3 – суммарная плотность; (а) – $s$ = = 1.03; (б) – $s$ = 1.17; (в) – $s$ = 1.27.
Коэффициенты диффузии компонентов в мембране в равновесных условиях. Расчет массопереноса через мембрану можно провести как неравновесными методами, так и на основании математических моделей, используя данные об адсорбции компонентов и коэффициентах диффузии. Различные подходы для описания транспорта через мембрану влекут за собой различные определения коэффициентов транспортной диффузии, между которыми есть явная связь [32].
Полученные результаты моделирования анализировались на их соответствие макромоделям массопереноса. Для этого были рассчитаны неизвестные коэффициенты диффузии компонентов разделяемой смеси в мембране. Коэффициенты диффузии определялись в зависимости от плотности и состава смеси в мембране.
Моделирование проводилось в кубической ячейке, длина стороны в которой подбиралась из условия, чтобы суммарное количество молекул внутри ячейки было примерно 4000. Молекулы мембраны располагались равномерно по всей ячейке и были зафиксированы в узлах кубической кристаллической решетки.
Моделирование разбивалось на несколько этапов: на первом этапе проводилось моделирование при T* = 10 для достижения равномерного распределения компонентов; далее в течение 500 тыс. итераций проводилось установление термодинамического равновесия при заданной температуре; на последнем этапе проводилось 2 млн итераций пересчета положения молекул.
Коэффициент диффузии компонента i определялся по траекториям молекул, рассчитанным на последнем этапе по уравнению Эйнштейна:
(4)
${{D}_{i}} = \frac{1}{{6t}}\mathop {\lim }\limits_{t \to \infty } \left\langle {\Delta {{r}_{i}}{{{(t)}}^{2}}} \right\rangle ,$Таблица 5.
Зависимость коэффициента диффузии чистых компонентов в мембране от плотности при T* = 1 и 1.5
| n* | T* = 1 | T* = 1.5 | ||||||
|---|---|---|---|---|---|---|---|---|
| $D_{A}^{*}$ | $\Delta D_{A}^{*}$ | $D_{В }^{*}$ | $\Delta D_{В }^{*}$ | $D_{A}^{*}$ | $\Delta D_{A}^{*}$ | $D_{В }^{*}$ | $\Delta D_{В }^{*}$ | |
| 0.1 | 0.2652 | 0.0006 | 0.3400 | 0.0006 | 0.4197 | 0.0100 | 0.5122 | 0.1081 |
| 0.2 | 0.1823 | 0.0025 | 0.2269 | 0.0069 | 0.2958 | 0.0005 | 0.3585 | 0.0097 |
| 0.3 | 0.1358 | 0.0034 | 0.1683 | 0.0033 | 0.2169 | 0.0085 | 0.2561 | 0.0097 |
| 0.4 | 0.1033 | 0.0021 | 0.1301 | 0.0050 | 0.1666 | 0.0065 | 0.1944 | 0.0090 |
| 0.5 | 0.0739 | 0.0016 | 0.0982 | 0.0032 | 0.1196 | 0.0007 | 0.1483 | 0.0057 |
| 0.6 | 0.0511 | 0.0009 | 0.0683 | 0.0047 | 0.0888 | 0.0009 | 0.1074 | 0.0011 |
| 0.7 | 0.0313 | 0.0003 | 0.0416 | 0.0001 | 0.0584 | 0.0005 | 0.0720 | 0.0008 |
| 0.8 | 0.0094 | 0.0002 | 0.0181 | 0.0005 | 0.0291 | 0.0005 | 0.0407 | 0.0005 |
Для дальнейшего использования полученных данных при математическом описании массопереноса через мембрану значения коэффициентов диффузии были аппроксимированы. Зависимость коэффициента диффузии чистого компонента от плотности выражалась соотношением
Концентрационная зависимость для смеси определялась по выражениям
Значения найденных параметров в (5)–(7) представлены в табл. 6. Максимальное относительное отклонение рассчитанных по (5)–(7) данных с численным экспериментом составило 18%, среднее отклонение – менее 4%.
Таблица 6.
Значения параметров в выражениях (5)–(7) для определения коэффициентов диффузии в мембране
| Температура | T* = 1 | T* = 1.5 | ||
|---|---|---|---|---|
| Вещество | A | B | A | B |
| a | –2.0610 | –0.2151 | –0.0726 | –0.0564 |
| b | 0.2433 | 0.3875 | 8.8723 | 8.9412 |
| c | 0.1231 | 0.0711 | 0.0021 | 0.0011 |
| d | 2.2410 | 0.5073 | 0.5756 | 0.6803 |
| e | 10.1300 | 1.0290 | 0.4638 | 0.4136 |
| k | 0.0080 | 0.0080 | 0.0125 | 0.0125 |
Из табл. 5 видно, что компонент A, сильнее взаимодействующий с мембраной, имеет меньший коэффициент диффузии. Таким образом, селективность мембраны по отношению к компоненту A в проведенных численных экспериментах определяется адсорбционной способностью этого компонента к мембране.
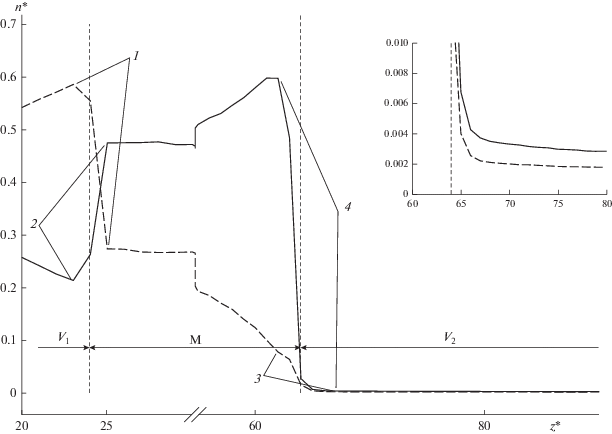
Изотерма адсорбции. Полученные в результате молекулярного моделирования распределения плотностей компонентов позволяют проанализировать явление адсорбции–десорбции на границах жидкость–мембрана и мембрана–пар. В данном случае под адсорбцией будем понимать явление скачкообразного изменения плотности компонента на границе раздела фаз. На рис. 7 видно, что такое изменение плотности происходит в некотором переходном слое, внутри которого находится поверхность мембраны. Границы этого слоя можно определить по характерным экстремумам на профиле плотности компонентов. Единственная неопределенность границы переходного слоя существует в паровой фазе, так как там не наблюдается характерного экстремума в профиле плотности. Однако можно заметить, что в большей части объема V2 плотность меняется слабо. Поэтому предлагается границу переходного слоя в паре определять как расстояние до мембраны, на котором плотность отличается менее чем на 10% от средней плотности в объеме V2. Определенная таким образом толщина переходного слоя, выделенная на рис. 7 пунктирными линиями, составляет несколько молекулярных диаметров, что намного меньше линейного размера объемов V1 и V2. Будем считать, что связь между концентрациями на границах переходного слоя (показана стрелками на рис. 7) определяет изотерму адсорбции. Как показал анализ, поведение этой связи хорошо аппроксимируется изотермой Ленгмюра:
(8)
${{n}_{{AM}}} = \frac{{\theta {{p}_{A}}{{n}_{A}}}}{{1 + {{p}_{A}}{{n}_{A}} + {{p}_{B}}{{n}_{B}}}},$Рис. 7.
Распределение плотностей на границах мембраны ($n_{F}^{*}$ = 0.8, xAF = 0.5, T* = 1.0, $l_{M}^{*}$ = 40; стрелками показаны плотности на границах адсорбционного слоя, соответствующие изотерме Ленгмюра; на дополнительном рисунке представлено изменение плотности компонентов со стороны пермеата): 1 – плотности компонента B со стороны исходной смеси, 2 – плотности компонента A со стороны исходной смеси, 3 – плотности компонента B со стороны пермеата, 4 – плотности компонента A со стороны пермеата.
Минимизацией квадрата отклонения рассчитываемых и экспериментальных данных были определены следующие значения параметров в выражении (8): θ = 0.741546, pA = 1748.13, pB = 376.587. В табл. 7 представлены значения плотностей для проведенных экспериментов и рассчитанные по изотерме адсорбции значения. Видно хорошее согласование используемой аппроксимации с результатами численного эксперимента.
Таблица 7.
Сравнение плотностей компонентов на границах переходной области. Данные численного эксперимента при Т * = 1 и расчет по изотерме адсорбции (8); l/m и m/v – граница жидкость/мембрана и мембрана/вакуум соответственно, Δ – отклонение от результатов численного эксперимента
| Вид эксперимента | Численный эксперимент | Изотерма Ленгмюра | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Условия эксперимента | Граница | $n_{A}^{*}$ | $n_{В }^{*}$ | $n_{{AМ }}^{*}$ | $n_{{В М }}^{*}$ | $n_{{AМ }}^{*}$ | Δ, % | $n_{{В М }}^{*}$ | Δ, % | |
| Переменная толщина мембраны | $l_{М }^{*} = 20$ | l/m | 0.1955 | 0.6030 | 0.4260 | 0.3159 | 0.4447 | 4.4 | 0.2955 | –6.4 |
| m/v | 0.0049 | 0.0040 | 0.5785 | 0.1188 | 0.5746 | –0.7 | 0.1002 | –15.7 | ||
| $l_{М }^{*} = 60$ | l/m | 0.2354 | 0.5643 | 0.5133 | 0.2416 | 0.4882 | –4.9 | 0.2522 | 4.4 | |
| m/v | 0.0027 | 0.0014 | 0.6047 | 0.0584 | 0.5603 | –7.4 | 0.0617 | 5.6 | ||
| $l_{М }^{*} = 100$ | l/m | 0.2675 | 0.5350 | 0.5554 | 0.2075 | 0.5175 | –6.8 | 0.2229 | 7.4 | |
| m/v | 0.0020 | 0.0008 | 0.6038 | 0.0390 | 0.5399 | –10.6 | 0.0449 | 15 | ||
| Переменная концентрация в области исходной смеси | xAF = 0.125 | l/m | 0.0357 | 0.7595 | 0.1161 | 0.6042 | 0.1325 | 14.1 | 0.6069 | 0.4 |
| m/v | 0.0011 | 0.0064 | 0.3086 | 0.3070 | 0.2742 | –11.2 | 0.3298 | 7.4 | ||
| xAF = 0.5 | l/m | 0.2135 | 0.5856 | 0.4750 | 0.2727 | 0.4654 | –2 | 0.2749 | 0.8 | |
| m/v | 0.0034 | 0.0020 | 0.5972 | 0.0777 | 0.5711 | –4.4 | 0.0740 | –4.7 | ||
| xAF = 0.875 | l/m | 0.6144 | 0.1875 | 0.7429 | 0.0433 | 0.6952 | –6.4 | 0.0457 | 5.5 | |
| m/v | 0.0046 | 0.0003 | 0.6904 | 0.0103 | 0.6513 | –5.7 | 0.0093 | –9.6 | ||
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МАКРОСКОПИЧЕСКОГО ОПИСАНИЯ ПЕРЕНОСА МАССЫ
Процессы массопереноса как в объеме разделяемой смеси, так и в мембране могут быть описаны на основе уравнений для потоков компонентов [33]:
(9)
${{j}_{i}} = \frac{{{{D}_{i}}}}{{{{k}_{{\text{B}}}}T}}\frac{{d{{\mu }_{i}}}}{{dz}}{{n}_{i}} + w{{n}_{i}},$здесь Di – коэффициент диффузии, определяемый соотношением (4), µi – химический потенциал, w – конвективная скорость, которая характеризует движение системы как целого. Значение конвективной скорости определяется как среднее значение скоростей всех молекул системы $w$ = = $\left\langle {\frac{1}{N}\sum\limits_{k = 1}^N {{{v}_{k}}} } \right\rangle ,$ где ${{v}_{k}}$ – скорость k-й молекулы. Скорости молекул обычно задаются относительно лабораторной системы отсчета (системы отчета относительно мембраны). Таким образом, в уравнении (9) диффузионный перенос массы определяется тепловым движением молекул относительно лабораторной системы отсчета. Очевидно, что если рассматриваемая система находится в равновесии и неподвижна относительно выбранной системы отсчета, то w = 0.
Как видно из приведенных результатов моделирования, вдоль ячейки могут изменяться как концентрации компонентов, так и общая плотность смеси. Тогда при условии, что T* = const, вдоль всей ячейки выражение (9) можно записать в виде
(10)
${{j}_{i}} = - \frac{{{{D}_{i}}}}{{{{k}_{{\text{B}}}}T}}\left( {\frac{{d{{x}_{i}}}}{{dz}}\frac{{\partial {{\mu }_{i}}}}{{\partial {{x}_{i}}}} + \frac{{dn}}{{d{{z}_{i}}}}\frac{{\partial {{\mu }_{i}}}}{{\partial n}}} \right){{n}_{i}} + w{{n}_{i}}.$Учитывая определение химического потенциала ${{\mu }_{i}} = \mu _{i}^{0}(T)$ + ${{k}_{{\text{B}}}}T\ln (n{{x}_{i}}{{\gamma }_{i}}),$ где γi – коэффициент активности, можно определить термодинамические факторы как
В результате выражение для потока компонента будет иметь вид
(11)
${{j}_{i}} = - {{D}_{i}}\Gamma _{i}^{X}\frac{{d{{x}_{i}}}}{{dz}}n - {{D}_{i}}\Gamma _{i}^{n}\frac{{dn}}{{dz}}{{x}_{i}} + w{{n}_{i}}.$В случае бинарной смеси, используя соотношения Гиббса–Дюгема, можно получить выражение для общего потока, аналогичное выражению (11):
(12)
$\begin{gathered} j = {{j}_{A}} + {{j}_{B}} = - ({{D}_{A}} - {{D}_{B}})\Gamma _{A}^{X}\frac{{d{{x}_{A}}}}{{dz}}n - \\ - \,\,({{D}_{A}}\Gamma _{A}^{n}{{x}_{A}} + {{D}_{B}}\Gamma _{B}^{n}{{x}_{B}})\frac{{dn}}{{dz}} + wn. \\ \end{gathered} $Соотношение (11), записанное, например, для компонента A, и соотношение (12) при известных значениях потоков, коэффициентов диффузии, термодинамических факторов и конвективной скорости позволяют определить профили плотности и концентрации вдоль ячейки. Для области жидкой фазы значения этих параметров, кроме конвективной скорости, известны, что позволяет проверить адекватность макроскопических моделей массопереноса на масштабах ячейки, в которой проводилось молекулярное моделирование. Для области внутри мембраны неизвестными являются еще и термодинамические факторы, что приводит к необходимости использовать какие-либо допущения по их поведению. Данная модель была применена для описания проведенных численных экспериментов.
Массоперенос чистого компонента. В однокомпонентном случае система уравнений (11), (12) сводится к одному:
Используя данные для леннард-джонсовских флюидов о коэффициентах диффузии [34] и уравнение состояния Бенедикта–Вебба–Рубина [35] для определения термодинамического фактора ${{\Gamma }^{n}} = 1 + \frac{{\partial {{Z}_{V}}(T,n)}}{{\partial n}}$ + $\frac{{{{Z}_{V}}(T,n) - 1}}{n},$ где ZV – фактор сжимаемости, были рассчитаны профили плотности в области жидкой фазы при массопереносе чистых флюидов A и B при Т* = 1.5. Значение конвективной скорости (табл. 1) подбиралось из условия наилучшего согласования рассчитанных и экспериментальных данных. Решение (13) искалось для граничных условий, заданных на границе контрольного объема Vc1. На рис. 3 видно хорошее согласование решения уравнения (13) и данных численного эксперимента. Необходимо отметить, что удовлетворительный результат удается получить только при правильном учете термодинамического фактора. В противном случае, например для допущения ${{\Gamma }^{n}}$ = 1, решение уравнения (13) даже качественно не согласуется с данными численного эксперимента. Поэтому в отсутствие данных о термодинамическом факторе компонента внутри мембраны адекватное решение удается получить только в предположении определенного поведения термодинамического фактора от плотности, например линейного. Однако при этом оказываются неизвестными несколько параметров (конвективная скорость и параметры в аппроксимации термодинамического фактора), что приводит к определению разных наборов параметров, позволяющих адекватно описывать профиль плотности внутри мембраны.
Двухкомпонентный случай. В проведенных численных экспериментах для двухкомпонентной смеси в объеме V1, где находится разделяемая смесь, компоненты не отличаются друг от друга по межмолекулярным взаимодействиям. Тогда $\Gamma _{A}^{X} = \Gamma _{B}^{X} = 1,$ $\Gamma _{A}^{n} = \Gamma _{B}^{n},$ DA = DB и система уравнений (11), (12) сводится к выражениям
Второе уравнение не зависит от первого, что позволяет определить профиль плотности, а затем из первого уравнения можно рассчитать профиль концентрации. Результаты таких расчетов для разделения эквимолярной смеси при двух температурах приведены на рис. 2 и 4. Видно, что при температуре Т* = 1.5 плотность меняется вдоль ячейки, а при Т* = 1.0 − изменения почти не происходит. Как показали расчеты, в обоих случаях хорошего согласования профиля концентраций можно добиться и при подстановке в первое уравнение средних значений плотности в ячейке. Таким образом, можно утверждать, что макроуравнения массопереноса хорошо согласуются с данными численного эксперимента, что означает их применимость на масштабах несколько десятков молекулярных диаметров.
Для описания массопереноса в мембране ввиду отсутствия данных о конвективной скорости выразим w из уравнения (12) и подставим в (11). В результате получим следующее соотношение для потока компонента:
(14)
$\begin{gathered} {{j}_{A}} = - {{D}_{{AB}}}\Gamma _{A}^{x}\frac{{d{{x}_{A}}}}{{dz}}n - \\ - \,\,({{D}_{A}}\Gamma _{A}^{n} - {{D}_{B}}\Gamma _{B}^{n})\frac{{dn}}{{dz}}{{x}_{A}}{{x}_{B}} + j{{x}_{A}}, \\ \end{gathered} $здесь ${{D}_{{AB}}}$ = $({{D}_{A}}{{x}_{B}} + {{D}_{B}}{{x}_{A}})$ – коэффициент взаимной диффузии.
Так как в мембране не были известны значения термодинамических факторов, то везде расчеты по соотношению (14) проводились при допущении $\Gamma _{A}^{X} = \Gamma _{B}^{X} = 1,$ $\Gamma _{A}^{n} = \Gamma _{B}^{n} = 1.$ Кроме того, анализ членов, входящих в уравнение (14), показал, что даже для Т* = 1.5, где наблюдается самое значительное изменение плотности вдоль мембраны (рис. 2), вторым членом можно пренебречь, так как его величина оказывается на три порядка меньше остальных. Таким образом, массоперенос внутри мембраны анализировался на основе соотношения
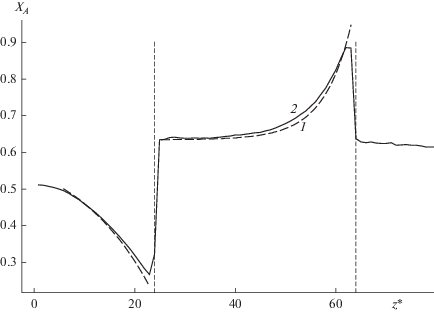
На рис. 8 показано сравнение данных численного эксперимента по профилю концентраций компонентов внутри мембраны с результатами расчета по уравнению (15). Видно хорошее согласование, это подтверждает, что внутри мембраны молекулярного масштаба формируется профиль концентраций, соответствующий макроуравнению массопереноса. Аналогичная точность была получена для других проведенных численных экспериментов.
Рис. 8.
Распределение концентрации компонента А вдоль моделируемой ячейки (T* = 1.0, $n_{F}^{*}$ = 0.8, xAF = 0.5, $l_{М }^{*}$ = 40): 1 – численный эксперимент, 2 – результат решения уравнения (15).
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
В результате численного моделирования были рассмотрены различные условия мембранного разделения идеальной бинарной леннард-джонсовской смеси с помощью мембраны кристаллического типа. Компоненты разделяемой смеси по межмолекулярному взаимодействию различались только энергией взаимодействия с молекулами мембраны. В результате моделирования были получены поля концентраций и плотностей вдоль ячейки, а также величины потоков компонентов. Кроме того, по среднеквадратичному отклонению молекул были рассчитаны коэффициенты диффузии компонентов в мембране (табл. 5). Как было показано на некоторых примерах выше, во всех случаях наблюдалось соответствие полученных в результате численного моделирования данных уравнениям массопереноса в виде (11), (12) и их следствиям (13) и (15). В результате можно сделать следующие выводы: в неравновесной системе масштаба несколько десятков диаметров молекул поведение макросвойств соответствует уравнениям переноса линейной неравновесной термодинамики; метод контрольных объемов оказывается способным адекватно предсказывать основные характеристики мембранного разделения (потоки, селективность, адсорбцию, коэффициенты диффузии). Было показано, что изотерма сорбции в системах с межмолекулярным потенциалом Леннард-Джонса адекватно описывается уравнением Ленгмюра.
Во всех рассмотренных случаях численного моделирования прослеживается селективность по отношению к компоненту с большей энергией притяжения к мембране. При этом в чистом виде поток этого компонента через мембрану был меньше потока второго компонента. Таким образом, селективность мембранного разделения достигалась только за счет разницы сорбционной способности компонентов по отношению к мембране. Как видно, в этом случае приближение идеального проницания [36], предполагающее пропорциональность проницаемости компонентов смеси проницаемости чистых компонентов, не применимо даже качественно. Сравнивая значения конвективной скорости и общего потока (табл. 1), можно заметить, что вклад диффузионного и конвективного механизма в процесс массопереноса через рассматриваемый тип мембраны является соизмеримым.
На рис. 4 и в табл. 2 представлено поведение характеристик мембранного разделения в зависимости от толщины мембраны. С увеличением последней происходит снижение величины потока и увеличение селективности процесса. Такое поведение объясняется известным в теории массопереноса через мембраны явлением концентрационной поляризации, которое определяет уменьшение концентрации легкопроникающего компонента на поверхности мембраны по сравнению с концентрацией в ядре потока. С увеличением толщины мембраны сопротивление переносу массы через нее возрастает, что приводит к снижению величины концентрационной поляризации и сорбцией большего количества легкопроникающего компонента. Увеличение селективности при увеличении толщины мембраны также наблюдалось в экспериментах при газоразделении и первапорации [37, 38].
На рис. 5 и в табл. 4 представлены результаты численного моделирования разделения бинарной смеси с разным составом. При увеличении концентрации легкопроникающего компонента происходит монотонное уменьшение суммарного потока и увеличение селективности. Причем последняя увеличивается более чем в два раза.
Для анализа результатов моделирования массопереноса при изменении размера молекул мембраны, которые представлены на рис. 6, решалась обратная задача. По значениям потоков и профилю концентраций в мембране были определены коэффициенты взаимной диффузии в уравнении (15) (табл. 4). С увеличением размера молекул мембраны происходит уменьшение доли свободного объема. Как следствие, падает поток вещества, также уменьшается значение коэффициента взаимной диффузии. Однако при этом происходит сильное увеличение селективности процесса. Например, при уменьшении потока в два раза селективность возрастает на порядок. Таким образом, для мембран, для которых эффект разделения в основном связан с различной сорбционной способностью компонентов, значительное увеличение селективности возможно за счет уменьшения свободного объема.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 17-03-01133).
ОБОЗНАЧЕНИЯ
| a, b, c, d, e, k | параметры |
| D | эйнштейновский коэффициент диффузии, м2/с |
| h | высота ячейки, м |
| j | поток компонента, моль/(м2 с) |
| kB | константа Больцмана, Дж/К |
| l | толщина, м |
| m | масса молекулы, кг |
| N | количество молекул |
| n | числовая плотность, нм–3 |
| pA, pB | параметры уравнения Ленгмюра |
| r | расстояние, м |
| S | площадь, м2 |
| s | отношение диаметров молекул |
| T | температура, К |
| t | время, с |
| U | энергия, Дж |
| V0 | свободный объем, м3 |
| w | конвективная скорость, м/с |
| x | мольная доля |
| z | координата вдоль толщины мембраны, м |
| α | коэффициент разделения |
| Γ | термодинамический фактор |
| γ | коэффициент активности |
| Δ | статистическая погрешность численного эксперимента |
| ε | глубина потенциальной ямы, Дж |
| θ | параметр уравнения Ленгмюра |
| μ | химический потенциал, Дж/моль |
| σ | расстояние, на котором потенциал равен нулю, нм |
| $v$ | скорость молекулы |
| φ | потенциал межмолекулярного взаимодействия, Дж |
ИНДЕКСЫ
Список литературы
Bell C.M., Gerner F.J., Strathmann H. Selection of polymers for pervaporation membranes // J. Membr. Sci. 1988. V. 36. P. 315.
Kagramanov G.G., Farnosova E.N. Scientific and engineering principles of membrane gas separation systems development // Theor. Found. Chem. Eng. 2017. V. 51. № 1. P. 38.
Akberov R.R., Fazlyev A.R., Klinov A.V., Malygin A.V., Farakhov M.I., Maryakhina V.A., Kirichenko S.M. Dehydration of diethylene glycol by pervaporation using HybSi ceramic membranes // Theor. Found. Chem. Eng. 2014. V. 48. № 5. P. 650.
Babak V.N., Didenko L.P., Kvurt Y.P., Sementsova L.A. The recovery of hydrogen from binary gas mixtures using a membrane module based on a palladium foil taking into account the deactivation of the membrane // Theor. Found. Chem. Eng. 2018. V. 52. № 3. P. 371.
Babak V.N., Didenko L.P., Kvurt Y.P., Sementsova L.A. Studying the operation of a membrane module based on palladium foil at high temperatures // Theor. Found. Chem. Eng. 2018. V. 52. № 2. P. 181.
Wijmans J.G., Baker R.W. The solution-diffusion model: A review // J. Membr. Sci. 1995. V. 107. № 1–2. P. 1.
Krishna R. Diffusion in porous crystalline materials // Chem. Soc. Rev. 2012. V. 41. № 8. P. 3099.
Oulebsir F., Vermorel R., Galliero G. Diffusion of supercritical fluids through single-layer nanoporous solids: Theory and molecular simulations // Langmuir. 2018. V. 34. № 2. P. 561.
Hinkle K., Wang X., Gu X., Jameson C., Murad S. Computational molecular modeling of transport processes in nanoporous membranes // Processes. 2018. V. 6. № 8. P. 124.
Wang L., Dumont R.S., Dickson J.M. Nonequilibrium molecular dynamics simulation for studying the effect of pressure difference and periodic boundary conditions on water transport through a CNT membrane // Mol. Phys. 2017. V. 115. № 8. P. 981.
MacElroy J.M.D. Computer simulation of diffusion within and through membranes using nonequilibrium molecular dynamics // Korean J. Chem. Eng. 2000. V. 17. № 2. P. 129.
Cao W., Tow G.M., Lu L., Huang L., Lu X. Diffusion of CO2/CH4 confined in narrow carbon nanotube bundles // Mol. Phys. 2016. V. 114. № 16–17. P. 2530.
Richard R., Anthony S., Aziz G. Pressure-driven molecular dynamics simulations of water transport through a hydrophilic nanochannel // Mol. Phys. 2016. V. 114. № 18. P. 2655.
Heffelfinger G.S., van Swol F. Diffusion in Lennard-Jones fluids using dual control volume grand canonical molecular dynamics simulation (DCV-GCMD) // J. Chem. Phys. 1994. V. 100. № 10. P. 7548.
Firouzi M., Sahimi M. Molecular dynamics simulation of transport and separation of carbon dioxide–alkane mixtures in a nanoporous membrane under sub- and supercritical conditions // Transp. Porous Media. 2016. V. 115. № 3. P. 495.
Arya G., Chang H.-C., Maginn E.J. A critical comparison of equilibrium, non-equilibrium and boundary-driven molecular dynamics techniques for studying transport in microporous materials // J. Chem. Phys. 2001. V. 115. № 17. P. 8112.
Cracknell R.F., Nicholson D., Quirke N. Direct molecular dynamics simulation of flow down a chemical potential gradient in a slit-shaped micropore // Phys. Rev. Lett. 1995. V. 74. № 13. P. 2463.
Thompson A.P., Ford D.M., Heffelfinger G.S. Direct molecular simulation of gradient-driven diffusion // J. Chem. Phys. 1998. V. 109. № 15. P. 6406.
Kazemi M., Takbiri-Borujeni A. Flow of gases in organic nanoscale channels: A boundary-driven molecular simulation study // Energy Fuels. 2016. V. 30. № 10. P. 8156.
Jin Z., Firoozabadi A. Flow of methane in shale nanopores at low and high pressure by molecular dynamics simulations // J. Chem. Phys. 2015. V. 143. № 10. P. 104315.
Kazemi M., Takbiri-Borujeni A. Modeling and simulation of gas transport in carbon-based organic nano-capillaries // Fuel. 2017. V. 206. P. 724.
Kirchofer A., Firouzi M., Psarras P., Wilcox J. Modeling CO2 Transport and sorption in carbon slit pores // J. Phys. Chem. C. 2017. V. 121. № 38. P. 21018.
Wang S., Yu Y., Gao G. Non-equilibrium molecular dynamics simulation on pure gas permeability through carbon membranes // Chin. J. Chem. Eng. 2006. V. 14. № 2. P. 164.
Firouzi M., Wilcox J. Slippage and viscosity predictions in carbon micropores and their influence on CO2 and CH4 transport // J. Chem. Phys. 2013. V. 138. № 6. P. 064705.
Klinov A.V., Anashkin I.P., Akberov R.R. Molecular dynamics simulation of pervaporation of an ethanol–water mixture on a hybrid silicon oxide membrane // High Temp. 2018. V. 56. № 1. P. 70.
Allen M.P., Tildesley D.J. Computer Simulation of Liquids. Oxford: Clarendon Press, 1989.
Pronk S., Pall S., Schulz R., Larsson P., Bjelkmar P., Apostolov R., Lindahl E. GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit // Bioinformatics. 2013. V. 29. № 7. P. 845.
Abraham M.J., Murtola T., Schulz R., Páll S., Smith J.C., Hess B., Lindahl E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers // SoftwareX. 2015. V. 1–2. P. 19.
Berendsen H.J.C., van der Spoel D., van Drunen R. GROMACS: A message-passing parallel molecular dynamics implementation // Comput. Phys. Commun. 1995. V. 91. № 1–3. P. 43.
GitHub. The world’s leading software development platform. https://github.com/KSTU/gromem (дата обращения: 28.11.2018).
GitHub. The world’s leading software development platform. https://github.com/KSTU/articles/tree/master/ membrane-simple-lj (дата обращения: 28.11.2018).
Medvedev O.O. Diffusion Coefficients in Multicomponent Mixtures. Copenhagen: Technical University of Denmark, 2004.
Shewmon P.G. Diffusion in Solids. Warrendale, Pa: Minerals, Metals & Materials Society, 1989.
Meier K., Laesecke A., Kabelac S. Transport coefficients of the Lennard-Jones model fluid. II Self-diffusion // J. Chem. Phys. 2004. V. 121. № 19. P. 9526.
Johnson J.K., Zollweg J.A., Gubbins K.E. The Lennard-Jones equation of state revisited // Mol. Phys. 1993. V. 78. № 3. P. 591.
Hwang S.T., Kammermeyer K. Membranes in Separations. N.Y.: Wiley, 1975.
Shen Y., Lua A.C. Effects of membrane thickness and heat treatment on the gas transport properties of membranes based on P84 polyimide // J. Appl. Polym. Sci. 2010. V. 116. № 5. P. 2906.
Koops G.H., Nolten J.A.M., Mulder M.H.V., Smolders C.A. Selectivity as a function of membrane thickness: Gas separation and pervaporation // J. Appl. Polym. Sci. 1994. V. 53. № 12. P. 1639.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


