Теоретические основы химической технологии, 2019, T. 53, № 4, стр. 431-439

Особенности течения высококонцентрированной суспензии в гидроциклоне

И. Дик^1, 2, Л. Л. Миньков^3, *

¹ Университет Эрланген-Нюрнберг
Эрланген, Германия

² Казахстанско-Немецкий университет
Алматы, Казахстан

³ Томский государственный университет
Томск, Россия

^* E-mail: lminkov@ftf.tsu.ru

Поступила в редакцию 24.05.2017
После доработки 24.01.2018
Принята к публикации 12.04.2018

DOI: 10.1134/S004035711904002X

Полный текст (PDF)

Аннотация

Приведены экспериментальные данные о границах протекания суспензии барита в зависимости от ее концентрации и объемного расхода для 10 мм высоконапорного гидроциклона. Проведено компьютерное моделирование разделения фаз концентрированной суспензии в гидроциклоне высокого давления. Получено полуколичественное соответствие между результатами численного моделирования и результатами эксперимента по условиям запирания нижнего слива гидроциклона.

Ключевые слова: запирание гидроциклона, концентрированная суспензия, эксперимент, численное моделирование

ВВЕДЕНИЕ

Большой класс индустриальных аппаратов перерабатывает (переносит, разделяет по фазам, классифицирует и т.д.) дисперсные материалы. Одной из особенностей процессов в таких аппаратах является возможность (желательной или нежелательной) сегрегации материала. Например, и это здесь будет объектом нашего внимания, может иметь место локальное накопление твердой фазы. Такая локализация может затруднять движение материала и воздействовать на технологические процессы.

Классификация в гидроциклонах базируется на действии силы, направленной поперек к потоку протекающей через аппарат суспензии [1–4]. Принципиальная схема гидроциклона показана на рис. 1.

Рис. 1.

Принципиальная схема гидроциклона с отложением седимента на стенках: 1 – верхний слив; 2 – входной поток; 3 – основной вихрь; 4 – вторичный вихрь; 5 – седимент; 6 – нижний слив.

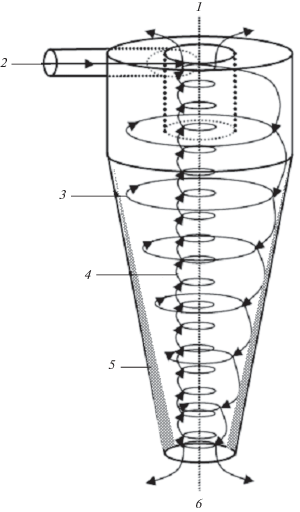
Рассмотрим явление осаждения твердых частиц на поверхности стенок в аппарате типа гидроциклон. Смещение частиц к стенке здесь вызывается центробежной силой. Скорость смещения (седиментации) тем больше, чем крупнее частица. И этим, в сущности, обусловливается классификационный эффект. В отсутствие сопровождающих обстоятельств (неравенство условий на входе и сложности течения, включая турбулентность) острота сепарации была бы полной, т.е. все частицы размером меньше некоторого критического диаметра разделения d_c покидали бы аппарат через верхний слив, в то время как более крупные захватывались бы стенкой и выносились бы через нижний слив.

Размер зерна разделения d_c при эксплуатации гидроциклонов при давлениях в пределах от 1 до 3 бар обычно можно снизить до нескольких микрон. Запросы современной биотехнологии или техника разделения жидких фаз (нефть–вода) простираются до субмикронной области. Малость размеров зерен разделения связана с величиной центробежного ускорения, возникающего в гидроциклоне ${{{{V}_{t}}^{2}} \mathord{\left/ {\vphantom {{{{V}_{t}}^{2}} {\left( {{{{{D}_{c}}} \mathord{\left/ {\vphantom {{{{D}_{c}}} 2}} \right. \kern-0em} 2}} \right)}}} \right. \kern-0em} {\left( {{{{{D}_{c}}} \mathord{\left/ {\vphantom {{{{D}_{c}}} 2}} \right. \kern-0em} 2}} \right)}},$ где D_c – диаметр гидроциклона и V_t – величина тангенциальной скорости, развиваемой в аппарате, которая растет с давлением p на входе.

Уменьшение зерна разделения достигается путем уменьшения размеров гидроциклона и увеличения давления на входе. Минигидроциклоны обычно питаются центробежными насосами, создающими давления не выше 5–7 бар. Зерно разделения слабо зависит от давления ${{d}_{c}}\quad{{\sim }_{\quad}}{\kern 1pt} {{p}^{{--0.25}}},$ так что только давления, превышающие 10 бар, могут существенно повлиять на размер зерна разделения.

В стремлении понизить размер зерна разделения в субмикронную область, в [5] и в настоящей работе использовался 10 мм гидроциклон в области давлений до 60 бар. Для обеспечения непульсирующей подачи суспензии в указанном интервале давлений в работе использовался мембранный поршневой насос.

Приближенно-аналитический метод анализа классификационных процессов в гидроциклоне впервые был предложен в [6] и в дальнейшем обобщен в [1], а численные расчеты осуществлены в работах [7–11] и многих других.

В то же время целый ряд важных аспектов процессов сепарации и классификации до сих пор не был включен в рассмотрение. Одним из таких аспектов является возможность осаждения частиц на стенке и, особенно, вблизи относительно узкого нижнего слива.

Проблема отложения седимента связывается с иногда возникающей проблемой запирания гидроциклона, т.е. непроходимостью пульпы через нижнее отверстие, предназначенное для потока сгущенной суспензии. Отложение седимента на стенках аппарата становится актуальным при работе с концентрированными суспензиями, особенно когда целью является не столько классификация, сколько отделение твердой фазы [12–14]. В современных практических приложениях, прежде всего, расширяется круг перерабатываемых трудно отделяемых материалов, к которым относятся, например, частицы биологической природы (отделение крахмала, составных компонентов крови и т.д.), что связано с низкой плотностью частиц (несколько процентов тяжелее несущей жидкости). В настоящее время актуальными стали разработки в области разделения субмикронных частиц (на один-два порядка мельче обычно используемых).

Здесь гидроциклоны, не имеющие подвижных деталей, обладают определенными преимуществами, но и в гидроциклонировании безусловно существуют границы применимости. Использование малоразмерных гидроциклонов имеет следствием низкую производительность. Увеличить массу перерабатываемой суспензии и, соответственно, количества выделенной твердой фазы можно было бы, повышая концентрацию суспензии, но это может приводить к закупорке аппарата. Особенно важной эта проблема может оказаться как раз для малоразмерных высоконапорных гидроциклонов [5], предлагаемых для разделения материала в области субмикронных размеров частиц.

Целью данной работы является определение условий запирания нижнего слива 10 мм гидроциклона на основе экспериментального исследования и разъяснения картины явления с использованием компьютерного моделирования.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Описание схемы эксперимента. Эксперименты с использованием 10 мм гидроциклона были проведены на испытательном стенде [5], схема которого показана на рис. 2. Оба потока из гидроциклона 1, и верхний 2 и нижний 3, собирались в 10-литровый бак 4 и затем подавались насосом 5 обратно в циклон (таким образом, обеспечивался замкнутый цикл). Давление, генерируемое насосом, изменялось от 1 до 60 бар. Порошок сульфата бария (барит), который аккуратно смешивался с водным раствором полиакрилата, служил в качестве твердой фазы суспензии, вводимой в гидроциклон. Гранулометрический анализ проводился с использованием лазерно-дифракционного прибора MasterSizerX фирмы Malvern. Входное давление потока измерялось манометром, а потоки продуктов определялись через объем вытекающей за единицу времени суспензии. Размеры гидроциклона и параметры эксперимента приведены в табл. 1.

Рис. 2.

Схема испытательного стенда с 10 мм гидроциклоном: 1 – гидроциклон; 2 – верхний слив; 3 – нижний слив; 4 – сборный бак; 5 – насос.

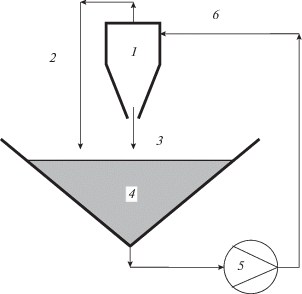
Таблица 1.

Параметры эксперимента

Диаметр гидроциклона	10 мм
Входной патрубок	2.2 × 2.3 мм
Диаметр верхнего слива	2.5 мм
Диаметр нижнего слива	1.6 мм
Длина гидроциклона	83 мм
Диапазон давления	2–60 бар
Твердая фаза	Барит <7 мкм
Плотность барита	4500 кг/м³
Содержание твердой фазы в исходной суспензии	150–2300 г/л
Диспергатор полиакрилат	1% твердой фазы

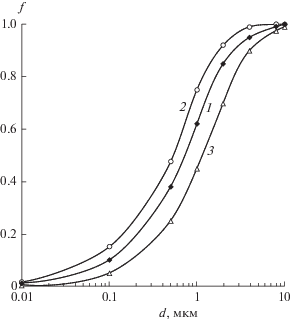
На рис. 3 показан пример распределения частиц по размерам во всех трех потоках гидроциклона.

Рис. 3.

Распределения частиц по размерам в потоках в гидроциклоне при давлении на входе, равном 2 бар: 1 – вход; 2 – верхний слив; 3 – нижний слив.

Оценку уровня центробежного ускорения, действующего на частицы в гидроциклоне, можно дать, используя известные полуэмпирические формулы, например, приведенные в [3]:

(1)

$\frac{{2V_{t}^{{\text{2}}}}}{{{{D}_{c}}}} = {\text{7}}{\text{.68 }}\frac{{D_{{of}}^{{\text{2}}}}}{{D_{c}^{{\text{3}}}}}\frac{p}{\rho }{\text{.}}$

Для испытуемого аппарата при давлении в 1 бар имеем величину 1.23 × 10⁶ м/с², что в 1.25 × × 10⁵ больше ускорения свободного падения g. При давлении в 40 бар центробежное ускорение уже в 5 × 10⁶ раз превышает g.

Обсуждение результатов эксперимента. Кроме величины зерна разделения для решения технологических задач имеет значение производительность циклона, т.е. объем перерабатываемой суспензии в единицу времени. Расходные характеристики испытуемого гидроциклона показаны на рис. 4 (тут же, предваряя описание компьютерного моделирования, приведены и расчетные данные, демонстрирующие неплохую согласованность с экспериментами).

Рис. 4.

Зависимость величины потока суспензии через гидроциклон от давления на входе при различных концентрациях подаваемой суспензии: 1–3 – эксперимент; 4–6 – расчет; 1, 4 – С = 150 г/л; 2, 5 – С = 1200 г/л; 3, 6 – С = 2000 г/л.

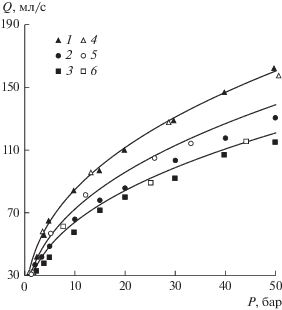
Видно, что расход суспензии снижается при повышении концентрации подаваемой суспензии. Полученные в ходе экспериментов данные хорошо аппроксимируются зависимостью

(2)

$Q = 32.78{\kern 1pt} \,{{p}^{{0.43}}}{\text{exp}}\left( { - 2\, \times {{{10}}^{{ - 4}}}C} \right),$

в которой концентрация твердой фазы связана с объемной долей частиц и плотностью вещества частицы соотношением $С $ = $\alpha {{\rho }_{p}}.$ Известно, что при α = α_max ≈ 0.62 частицы примыкают друг к другу, образуя плотную упаковку – седимент [1, 3].

В случае высококонцентрированных суспензий возникают ситуации, когда вывод подаваемой суспензии осуществляется лишь через верхний слив, а нижний слив фактически запирается. Причем такая ситуация имеет место тогда, когда давление на входе становится достаточно высоким. Очевидно, что развиваемые центробежные силы становятся настолько большими, что отбрасываемые на стенку частицы образуют в области нижнего, относительно узкого выходного отверстия слой седимента, не позволяющего суспензии вытекать из гидроциклона.

Сепарационные характеристики испытываемого аппарата для суспензии не очень высокой концентрации (до 600 г/л) приводятся в [5]. В настоящей работе мы сосредоточимся на исследовании гидравлических характеристик гидроциклона для высококонцентрированной суспензии (до 2300 г/л) и границ блокировки аппарата.

Рис. 5 содержит информацию о потоках суспензии (при концентрации твердой фазы на входе, равной 150 г/л) через выходные сопла исследуемого гидроциклона при вариации давления на входе. Как и ожидалось, оба потока растут с ростом давления (с разной скоростью). Суспензия в нижнем выводе сгущается, а в верхнем ожижается. Но и в нижнем потоке объемная доля твердой фазы не превышает α = 0.12α_max, что очень далеко от границ образования седимента.

Рис. 5.

Зависимость характеристик суспензии в выводных сечениях от давления питающего насоса: (а) – объемный расход; (б) – относительные объемные доли твердого; 1 – нижний слив; 2 – верхний слив; C = 150 г/л.

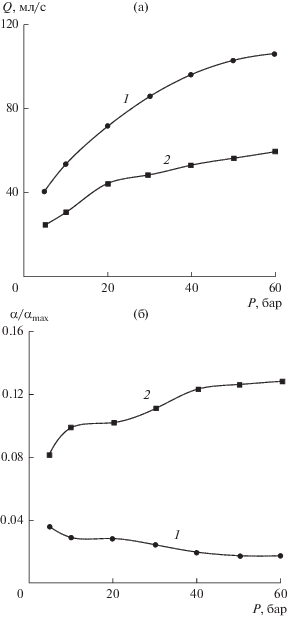
Иначе дело обстоит при работе с высококонцентрированной суспензией. На рис. 6 показаны данные, аналогичные рис. 5, но для суспензии с содержанием 1200 г/л порошка баррита. Особенность проявляется уже при рассмотрении поведения потоков суспензии в выводных каналах при разных давлениях, а именно, при достижении достаточно высокого давления поток через нижний вывод резко падает, что можно характеризировать как блокировку аппарата.

Рис. 6.

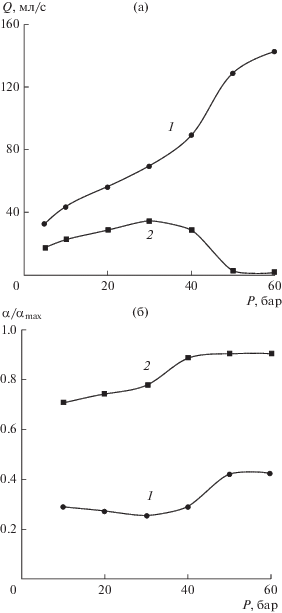
Это иллюстрирует рис. 7, на котором показано отношение потоков через верхний и нижний выходные каналы (так называемый сплит-параметр ${{{{Q}_{{{\text{ov}}}}}} \mathord{\left/ {\vphantom {{{{Q}_{{{\text{ov}}}}}} {{{Q}_{{{\text{un}}}}}}}} \right. \kern-0em} {{{Q}_{{{\text{un}}}}}}}$) для случаев разбавленной и сгущенной суспензий. Характерно, что для сгущенной суспензии сплит-параметр резко взмывает вверх, если давление становится больше определенного значения. Соответствующая пара значений концентрации суспензии и давления на входе в аппарат может служить параметром, характеризующим явление блокировки гидроциклона.

Рис. 7.

Зависимость отношения выходных потоков от величины давления на входе в гидроциклон: 1, 2 –расчет; 3, 4 – эксперимент; 1, 3 – С = 150 г/л; 2, 4 – С = 1200 г/л.

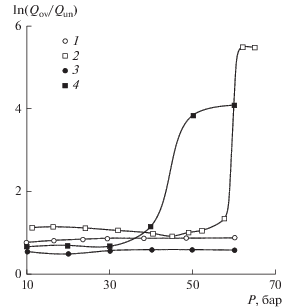
Ясно, что при этом происходит: стенки нижнего выводного сопла покрываются седиментом, перекрывающем поток. Суспензия, поступающая в гидроциклон, разворачивается и почти полностью выводится через верхний слив (“короткое замыкание”).

Это явление демонстрируют графики относительной объемной доли суспензии в выводимых потоках (рис. 6б). По мере роста давления концентрация твердого в нижнем потоке растет, почти достигая граничного значения, соответствующего седименту, т.е. объемной доле твердой фазы, равной 0.62. При этом концентрация твердого в верхнем выводном потоке становится близкой к таковой входного потока. Здесь также приведены и расчетные данные, качественно совпадающие с экспериментами, количественные отличия которых будут обсуждаться ниже.

На рис. 8 показаны результаты численного моделирования и экспериментов, которые состояли в том, что при фиксированном давлении на входе (расход суспензии при этом нетрудно измерить) последовательно повышалась концентрация твердой фазы в смесительном баке. При достаточно высокой концентрации истечение суспензии через нижний слив нарушалось и даже прекращалось, т.е. происходило запирание. Осветленные символы указывают на ситуации, в которых суспензия вытекает из обоих сопел гидроциклона, затемненные – ситуациям, в которых истечение из нижнего сопла исчезало. Другими словами, для режима истечения через нижнее сопло при достаточно высоком давлении концентрация суспензии должна быть достаточно низкой.

Рис. 8.

Карта проходимости и блокировки гидроциклона в эксперименте: 1 – проходимость нижнего слива; 2 – блокировка нижнего слива; 3 – численное моделирование границы блокировки.

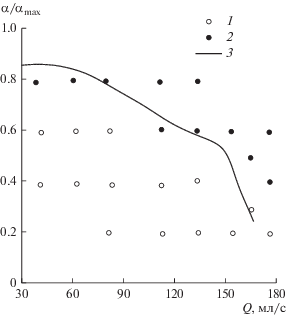
Как уже отмечалось, с увеличением входного давления (и, соответственно, общего расхода суспензии) при фиксированном достаточно высоком значении концентрации подаваемой в аппарат суспензии могут достигаться условия блокировки нижнего потока.

Отметим еще изменение формы струи, вытекающей из нижнего сопла [15, 16]. По мере повышения концентрации подаваемой суспензии угол раскрытия струи падает, характер истечения при приближении к границе блокировки аппарата становится нестабильным.

КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ

Описание модели. Для понимания гидродинамики течения суспензии внутри гидроциклона было проведено численное моделирование с помощью пакета Ansys-Fluent [17]. За основу была выбрана модель “смеси”, подробно описанная в [18, 19] и хорошо зарекомендовавшая себя при расчете параметров течения суспензии в гидроциклоне [10, 11]. Моделирование выполнялось в двумерном осесимметричном приближении для нестационарных закрученных несжимаемых вязких двухфазных турбулентных течений, которые описываются уравнениями Рейнольдса для смеси с использованием гипотезы Буссинеска и уравнением изменения объемной доли частиц. Для определения параметров турбулентности смеси привлекалась модель турбулентности k–ε–RNG [20, 21].

Система уравнений, описывающая турбулентное течение суспензии в гидроциклоне, состоит из следующих уравнений:

уравнение изменения массы смеси

$\frac{{\partial {{\rho }_{m}}}}{{\partial t}} + \nabla \cdot \left( {{{\rho }_{m}}{{{\mathbf{V}}}_{m}}} \right) = 0,$

уравнение изменения объемной доли

$\frac{{\partial {{\alpha }_{k}}}}{{\partial t}} + \nabla \cdot \left( {{{\alpha }_{k}}{{{\mathbf{V}}}_{k}}} \right) = 0,\,\,\,\,k = 2,\,\,3$

${{\alpha }_{1}} = 1 - {{\alpha }_{2}} - {{\alpha }_{3}},$

уравнение изменения количества движения смеси

$\begin{gathered} \frac{{\partial {{\rho }_{m}}{{{\mathbf{V}}}_{m}}}}{{\partial t}} + \nabla \cdot \left( {{{\rho }_{m}}{{{\mathbf{V}}}_{m}}{{{\mathbf{V}}}_{m}}} \right) = - \nabla p + \nabla \cdot {{T}_{{eff}}} + \\ + \,\,{{\rho }_{m}}{\mathbf{g}} - \nabla \cdot \left( {\sum\limits_{k = 1}^3 {{{\alpha }_{k}}{{\rho }_{k}}{{{\mathbf{V}}}_{{d,k}}}{{{\mathbf{V}}}_{{d,k}}}} } \right), \\ \end{gathered} $

уравнение изменения кинетической энергии турбулентных пульсаций

$\begin{gathered} \frac{{\partial {{\rho }_{m}}k}}{{\partial t}} + \nabla \cdot \left( {{{\rho }_{m}}k{{{\mathbf{V}}}_{m}}} \right) = \\ = \nabla \cdot \left[ {{{\alpha }_{{{\text{RNG}}}}}{{\mu }_{{eff}}}\nabla k} \right] + {{G}_{k}} - {{\rho }_{m}}\varepsilon , \\ \end{gathered} $

уравнение изменения скорости диссипации турбулентной энергии

$\begin{gathered} \frac{{\partial {{\rho }_{m}}\varepsilon }}{{\partial t}} + \nabla \cdot \left( {{{\rho }_{m}}\varepsilon {{{\mathbf{V}}}_{m}}} \right) = \nabla \cdot \left[ {{{\alpha }_{{{\text{RNG}}}}}{{\mu }_{{eff}}}\nabla \varepsilon } \right] + \\ + \,\,{{C}_{1}}\frac{\varepsilon }{k}{{G}_{k}} - {{C}_{2}}{{\rho }_{m}}\frac{{{{\varepsilon }^{2}}}}{k} - {{R}_{\varepsilon }}, \\ \end{gathered} $

где

${{R}_{\varepsilon }} = \frac{{{{C}_{\mu }}{{\eta }^{3}}\left( {1 - {\eta \mathord{\left/ {\vphantom {\eta {{{\eta }_{0}}}}} \right. \kern-0em} {{{\eta }_{0}}}}} \right)}}{{1 + \beta {{\eta }^{3}}}}{{\rho }_{m}}\frac{{{{\varepsilon }^{2}}}}{k},\,\,{{\mu }_{{turb}}} = {{\rho }_{m}}{{C}_{\mu }}\frac{{k{}^{2}}}{\varepsilon },$${{\mu }_{{turb}}} = {{\rho }_{m}}{{C}_{\mu }}\frac{{k{}^{2}}}{\varepsilon },$

${{T}_{{eff}}} = {{\mu }_{{eff}}}\left( {\nabla {{{\mathbf{V}}}_{m}} + \nabla {\mathbf{V}}_{m}^{T}} \right) - \frac{2}{3}{{\rho }_{m}}kU,$

$\begin{gathered} \eta = s\frac{k}{\varepsilon },\,\,{{G}_{k}} = {{\mu }_{{turb}}}{{s}^{2}},\,\,s = \sqrt {2SS} , \\ S = \frac{1}{2}\left( {\nabla {{{\mathbf{V}}}_{m}} + \nabla {\mathbf{V}}_{m}^{T}} \right), \\ \end{gathered} $

$\begin{gathered} {{\eta }_{0}} = 4.38,\,\,\beta = 0.012,\,\,{{C}_{1}} = 1.42,\,\,{{C}_{2}} = 1.68, \\ {{\alpha }_{{{\text{RNG}}}}} = 1.393,\,\,{{C}_{\mu }} = 0.0845. \\ \end{gathered} $

Согласно идеологии модели “смеси” [19] скорость частиц ${{{\mathbf{V}}}_{k}}$ определяется через осредненную скорость смеси ${{{\mathbf{V}}}_{m}}$ и скорость “скольжения” частицы относительно жидкости ${{{\mathbf{V}}}_{{k,1}}}{\text{:}}$

${{{\mathbf{V}}}_{k}} = {{{\mathbf{V}}}_{m}} + {{{\mathbf{V}}}_{{k,1}}} - \sum\limits_{j = 2}^3 {\frac{{{{\alpha }_{j}}{{\rho }_{j}}}}{{{{\rho }_{m}}}}{{{\mathbf{V}}}_{{j,1}}}} .$

Индекс k = 2 соответствует бариту, k = 3 – воздуху.

Скорость “скольжения” частицы относительно жидкости определялась с учетом влияния турбулентной диффузии со стороны жидкости на процесс движения частицы:

${{{\mathbf{V}}}_{{k,1}}} = \frac{{\left( {{{\rho }_{k}} - {{\rho }_{m}}} \right)d_{k}^{2}}}{{18{{\mu }_{1}}{{f}_{{drag}}}}}{\mathbf{a}} - {{D}_{{t,k}}}\left( {\frac{{\nabla {{\alpha }_{k}}}}{{{{\alpha }_{k}}}} - \frac{{\nabla {{\alpha }_{1}}}}{{{{\alpha }_{1}}}}} \right).$

Коэффициент турбулентной диффузии частиц определялся по зависимости [22, 23]

${{D}_{{t,k}}} = K{{C}_{\mu }}\frac{{{{k}^{2}}}}{\varepsilon }\left( {\frac{{{{\gamma }_{k}}}}{{1 + {{\gamma }_{k}}}}} \right)\frac{1}{{\sqrt {1 + {{C}_{{\beta ,k}}}\varsigma _{k}^{2}} }},$

где

$\begin{gathered} {{\varsigma }_{k}} = \frac{{\left| {{{{\mathbf{V}}}_{{k,1}}}} \right|}}{{\sqrt {{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}k} }},\,\,{{C}_{{\beta ,k}}} = 1.8 - 1.35{\text{co}}{{{\text{s}}}^{2}}\left( {{{\theta }_{k}}} \right), \\ {\text{cos}}\left( {{{\theta }_{k}}} \right) = \frac{{{{{\mathbf{V}}}_{{k,1}}}}}{{\left| {{{{\mathbf{V}}}_{{k,1}}}} \right|}} \cdot \frac{{{{{\mathbf{V}}}_{1}}}}{{\left| {{{{\mathbf{V}}}_{1}}} \right|}}, \\ \end{gathered} $

$\begin{gathered} K = 0.05,\,\,{{f}_{{drag}}} = 1 + 0.15{\text{R}}{{{\text{e}}}^{{0.687}}}, \\ {\text{Re}}\,{\text{ = }}\,\frac{{{{\rho }_{1}}{{d}_{2}}\left| {{{{\mathbf{V}}}_{{2.1}}}} \right|}}{{{{\mu }_{1}}}},\,\,{\mathbf{a}} = {\mathbf{g}} - \left( {{{{\mathbf{V}}}_{m}} \cdot \nabla } \right){{{\mathbf{V}}}_{m}} - \frac{{\partial {{{\mathbf{V}}}_{m}}}}{{\partial t}}, \\ \end{gathered} $

γ_k – отношение характерного времени турбулентных пульсаций ${k \mathord{\left/ {\vphantom {k {\varepsilon }}} \right. \kern-0em} {\varepsilon }}$ к характерному времени динамической релаксации частиц $\frac{{{{\rho }_{k}}d_{k}^{{\text{2}}}}}{{{\text{18}}{{\mu }_{{\text{1}}}}}}.$

Зависимость вязкости смеси от объемной доли частиц можно описать дробно-рациональной функцией [24]. Вид этой зависимости можно предложить, опираясь на известную линейную формулу Эйнштейна для малой концентрации частиц в жидкости, и переформулируя ее так, что вязкость суспензии становилась бы бесконечной при образовании плотной случайной упаковки твердой фазы (примерно при α = 0.62).

Из экспериментов, цитируемых, например, в [24], известно, что в окрестности предельного значения объемной доли частиц, когда движение смеси практически прекращается, имеет место большой разброс в значениях вязкости суспензии, и не существует единой зависимости, описывающей поведение вязкости от объемной доли частиц. Нужно иметь в виду, что и для предельных значений концентрации твердого (α ≈ 0.6) суспензия обычно приобретает консистенцию пасты, но сохраняет текучесть, свойства которой зависят от многих факторов (формы частиц, размеров частиц и т.д.).

Зависимость вязкости суспензии от объемной доли частиц в настоящей работе описывалась следующей функцией:

(3)

${{\mu }_{m}} = \left\{ {\begin{array}{*{20}{c}} {\frac{{{{\mu }_{1}}}}{{{{{\left( {1 - {\alpha \mathord{\left/ {\vphantom {\alpha {{{\alpha }_{{\max }}}}}} \right. \kern-0em} {{{\alpha }_{{\max }}}}}} \right)}}^{\beta }}}},\,\,\,\,\alpha < \alpha {\text{*}}} \\ {\mu {\text{*}},\,\,\,\,\alpha \geqslant \alpha {\text{*}}} \end{array}} \right.,$

где ${{\alpha }_{{\max }}}$ = 0.62, $\beta $ = 1.55, $\mu {\text{*}}$ = 100 Па с, ${{\mu }_{1}}$ = = 0.001 Па с. Значение $\alpha {\text{*}}$ находится из выражения

$\alpha {\text{*}} = {{\alpha }_{{\max }}}\left[ {1 - {{{\left( {{{{{\mu }_{1}}} \mathord{\left/ {\vphantom {{{{\mu }_{1}}} {\mu {\text{*}}}}} \right. \kern-0em} {\mu {\text{*}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0em} \beta }}}}} \right].$

Задание вязкости смеси в таком виде (с обрезкой) позволяет избежать “сингулярности” в численном решении при значениях объемной доли частиц, близких к предельному ${{\alpha }_{{\max }}}.$

На входе в гидроциклон задавались объемная доля частиц α₂, радиальная и тангенциальная скорости суспензии. Скорости жидкости и частиц полагались равными друг другу: v₁ = v₂, ${{w}_{1}} = {{w}_{2}}.$ Осевая скорость задавалась равной нулю: ${{u}_{1}} = {{u}_{2}} = 0\,.$ Предполагалось, что воздух не попадает во входной патрубок: α₃ = 0. На выходе (в нижнем и верхнем соплах) задавалось давление на оси, равное атмосферному, и условие равновесия сил в радиальном направлении $\frac{{\partial p}}{{\partial r}}$ = $\frac{{{{\rho }_{m}}w_{m}^{2}}}{r}.$ В случае возникновения обратного течения в выходных соплах, задавалась объемная доля воздуха, равная единице: α₃ = 1.

Размер частиц задавался равным 5 мкм. В начальный момент времени давление в гидроциклоне полагалось равным атмосферному, объемная доля частиц – равной объемной доле частиц на входе в гидроциклон, жидкость принималась покоящейся, кинетическая энергия турбулентных пульсаций – 10^–3 м²/c², скорость диссипации турбулентной энергии – 10^–2 м²/c³.

Для численного решения определяющей системы уравнений расчетная область была разбита на 41 252 четырехугольные ячейки. Размер и количество ячеек задавались так, чтобы разница в расчетных и измеренных значениях расхода от входного давления не превышала 5%.

Решение системы уравнений Рейнольдса и уравнения изменения объемной доли выполнялось с помощью противопоточной схемы второго порядка точности с привлечением алгоритма PRESTO для расчета давления на гранях ячеек. Согласование между полем давления и полем скорости было реализовано на основе алгоритма SIMPLE [25].

Тангенциальная скорость на входе в гидроциклон подбиралась таким образом, чтобы при заданном расходе давление, полученное при моделировании, и давление, полученное в эксперименте, совпадали. Такой подбор проводился для расхода воды, равного 138 мл/с. При этом отношение тангенциальной скорости к радиальной скорости на входе в гидроциклон оказалось равным 70/3. Во всех остальных случаях это отношение не менялось.

Обсуждение результатов моделирования. Сравнение рассчитанной зависимости расхода воды от давления с экспериментальной зависимостью при других расходах приведено на рис. 4 и показывает хорошее соответствие между численными и экспериментальными значениями.

Для определения условий запирания нижнего слива проводились расчеты с постепенно изменяющейся объемной долей частиц на входе в гидроциклон. Абсолютная погрешность объемной доли частиц, с которой определялись условия запирания, составляла 0.01. На рис. 8 сплошной кривой обозначена граница запирания нижнего слива гидроциклона, полученная в результате численного моделирования. В области малых расходов суспензии значения предельных концентраций, полученных в на основе численного моделирования, являются завышенными по сравнению с экспериментальными данными, в то время как в области высоких расходов численный расчет дает заниженные значения предельной концентрации частиц. В целом, предложенная модель позволяет качественно и полуколичественно правильно предсказать зависимость предельной концентрации частиц суспензии от расхода.

Расхождение между результатами численного моделирования и эксперимента можно объяснить тем, что реальная суспензия является полидисперсной, в то время как в расчетах суспензия полагалась монодисперсной. Другой причиной расхождения может служить тот факт, что зависимость вязкости суспензии от объемной доли частиц намного сложнее, чем описываемая формулой (3). Несмотря на это, области проходимости и запирания нижнего слива и в экспериментах, и в расчетах в значительной степени близки друг к другу.

ЗАКЛЮЧЕНИЕ

Работа с суспензиями высокой концентрации с применением гидроциклонов таит в себе возможность блокировки аппарата. Причина блокировки нижнего выходного (как правило, относительно узкого) канала связана с образованием малоподвижного седимента на стенках под действием центробежной силы, которая тем сильнее, чем выше рабочее давление в питательном блоке гидроциклона.

Таким образом, при заданном уровне концентрации подаваемой суспензии повышение давления приводит к нарастанию концентрации твердой фазы у стенок и, при достаточных условиях, к образованию седимента и, в конечной ситуации, к блокировке истечения суспензии через нижний слив.

Очевидно, что, проводя работы по классификации частиц, следует избегать суспензий повышенной концентрации, тем более что классификационные характеристики гидроциклов ухудшаются по мере повышения густоты суспензии. Но и при решении задачи сепарации твердой и жидких фаз нужно учитывать возможность блокирования нижнего слива, что приводит, естественно, к “короткому замыканию” подаваемого потока сразу к верхнему сливу, чем полностью обесценивается применение аппарата.

В работе отражено исследование проблемы на примере малоразмерного гидроциклона высокого давления, предназначенного для работы с очень мелким материалом (в микронном диапазоне размера частиц), но явление запирания потока наблюдается нередко и в более крупных аппаратах, при стремлении повысить производительность гидроциклонов (повысить концентрацию суспензии и/или повысить давление).

ОБОЗНАЧЕНИЯ

a	вектор ускорения, м/с²
С	концентрация частиц, г/л
C_μ, K	константы модели
D_c	диаметр гидроциклона, м
D_of	диаметр верхнего сливного патрубка, м
D_t,k	коэффициент турбулентной диффузии частиц, м²/с
d_c	зерно разделения, м
f	кумулятивная функция распределения частиц по размерам
f_drag	коэффициент трения
g	вектор ускорения свободного падения, м/с²
k	кинетическая энергия турбулентных пульсаций, м²/с²
p	давление на входе в гидроциклон, бар
Q	объемный расход суспензии, мл/с
r	радиальная координата, м
S	тензор скоростей деформации, 1/с
s	модуль тензора скоростей деформаций, 1/с
T	тензор напряжения, Па
u, v, w	компоненты вектора скорости, м/с
${\mathbf{V}}$	вектор скорости, м/с
V_t	тангенциальная скорость суспензии в гидроциклоне, м/с
$\alpha $	объемная доля частиц
γ	отношение характерных времен
ε	скорость диссипации турбулентной энергии, м²/с³
θ	угол между векторами скорости жидкости и частицы, рад
μ	динамическая вязкость, Па с
ρ	плотность, кг/м³
Re	критерий Рейнольдса

ИНДЕКСЫ

1	жидкость
2	барит
3	воздух
eff	эффективный
L	предельное значение
m	смесь
max	максимальное значение
ov	верхний слив
un	нижний слив

Список литературы

Heiskanen K. Particle Classification. London: Chapman and Hall, 1993.
Bradley D. The Hydrocyclone. London: Pergamon Press, 1965.
Schubert H., Heidenreich E., Liepe F., Neeße Th. Mechanische Verfahrenstechnik, 3. Aufl. Leipzig: Deutscher Verlag fuer Grundstoffindustrie, 1990.
Терновский И.Г., Кутепов Ф.М. Гидроциклонирование. M.: Наука, 1994.
Neesse Th., Dueck J., Schwemmer H., Faghaly M. Using a high pressure hydrocyclone for solids classification in the submicron range // Miner. Eng. 2015. V. 71. P. 85.
Schubert H., Neesse T. A hydrocyclone separation model in consideration of the multi-phase flow // Proc. Int. Conf. on Hydrocyclones. Cambridge: BHRA Fluid Engineering, 1980. P. 23.
Dyakovski T., Williams R.A. Prediction of high solids concentration regions within a hydrocyclone // Powder Technology. 1996. V. 87. P. 43.
Dueck J.G., Matvienko O.V., Neesse T. Modeling of hydrodynamics and separation in a hydrocyclone // Theor. Found. Chem. Eng. 2000. V. 34. № 5. P. 428. [Дик И.Г., Матвиенко О.В., Неессе Т. Моделирование гидродинамики и сепарации в гидроциклоне // Теорет. основы хим. технологии. 2000. Т. 34. № 5. С. 478.]
Ko J., Zahrai S., Macchion O., Vomhoff H. Numerical modeling of highly swirling flows in a through-flow cylindrical hydrocyclone // AIChE J. 2006. V. 52. № 10. P. 3334.
Neesse T., Dueck J. Dynamic modelling of the hydrocyclone // Miner. Eng. 2007. V. 20. № 4. P. 380.
Min’kov L.L., Dueck J.H. Numerical modeling of a nonmonotonic separation hydrocyclone curve // J. Eng. Phys. Thermophys. 2012. V. 85. № 6. P. 1317. [Миньков Л.Л., Дик И.Г. Численное моделирование немонотонной сепарационной кривой гидроциклона // Инж. физ. журн. 2012. Т. 85. № 6. С. 1214.]
Schubert H., Bohme S., Neesse Th., Espig D. Classification in turbulent two-phase flows // Aufbereitungstechnik. 1986. V. 27. № 6. P. 295.
Neesse Th., Schubert H., Graichen K. Practical and theoretical aspects of dense-flow classification // Aufbereitungstechnik. 1991. V. 32. № 9. P. 459.
Dueck J. Modeling for solid–liquid separation. Saabrücken: LAP Lambert Academic Publishing, 2015.
Dueck J., Schneider M., Neesse Th. Numerical Calculation of the Umbrella and Rope Discharge of a Hydrocyclone // Aufbereitungstechnik. 2003. V. 44. № 8. P. 13.
Neesse Th., Schneider M., Dueck J., Golyk V., Buntenbach S., Tiefel H. Hydrocyclone operation at the transition point rope/spray discharge // Miner. Eng. 2004. V. 17. № 5. P. 733.
Ansys Fluent. User Guide. Release 14.0. ANSYS Inc, 2011.
Нигматулин Р.И. Динамика многофазных сред. Ч. 1. М.: Наука, 1987.
Manninen M., Taivassalo V., Kallio S. On the mixture model for multiphase flow (VTT Publications. V. 288). Espoo: Technical Research Centre of Finland, 1996.
Launder B.E., Spalding D.B. Lectures in Mathematical Models of Turbulence. London: Academic Press, 1972.
Yakhot V., Orszag S.A. Renormalization Group Analysis of Turbulence: I. Basic Theory // J. Sci. Comput. 1986. V. 1. № 1. P. 1.
Csanady G.T. Turbulent Diffusion of Heavy Particles in the Atmosphere // J. Atmos. Sci. 1963. V. 20. P. 201.
Simonin C., Viollet P.L. Predictions of an Oxygen Droplet Pulverization in a Compressible Subsonic Coflowing Hydrogen Flow // Numerical Methods for Multiphase Flows. Spring Meeting of the Fluids Engineering Division. Toronto, 1990. P. 65.
Brouwers H.J.H. Viscosity of a concentrated suspension of rigid monosized particles // Physical Review E. 2010. V. 81. P. 051402.
Патанкар С.В. Численные методы решения задач теплообмена и динамики жидкости. М.: Энергоатомиздат, 1984. [Patankar S.V. Numerical Heat Transfer and Fluid Flow. Washington: Hemisphere Publishing Corporation, 1980.]

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал