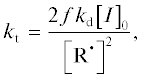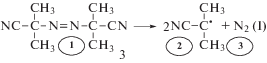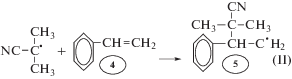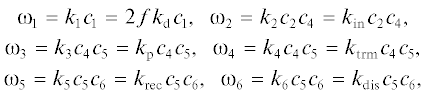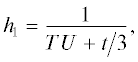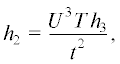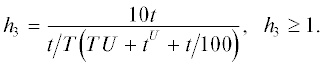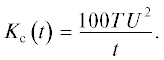Теоретические основы химической технологии, 2019, T. 53, № 4, стр. 410-415

Моделирование процесса радикальной полимеризации с использованием поправочных коэффициентов

М. Н. Патрушева^1, *, Э. Р. Мухамедзянова¹, Р. М. Хузаханов¹

¹ Институт полимеров, Казанский национальный исследовательский технологический университет
Казань, Россия

Поступила в редакцию 04.05.2018
После доработки 07.12.2018
Принята к публикации 06.02.2019

DOI: 10.1134/S0040357119040110

Аннотация

На примере радикальной полимеризации стирола, проводимой при 343, 348 и 353 К, рассмотрен расчет среднечисловой степени полимеризации. Для расчета применена система дифференциальных уравнений на графе с введением поправок, заданных в виде формул. При использовании минимального набора исходных данных погрешность вычисленного и экспериментального значения составила 40% при 343 К, 33.3% при 348 К и 37.5% при 353 К. Решена обратная кинетическая задача.

Ключевые слова: дифференциальное уравнение на графе, математическая модель, радикальная полимеризация, степень полимеризации, стирол

ВВЕДЕНИЕ

Несмотря на то, что непосредственные кинетические данные обычно представляют собой значения концентраций химических компонентов в различные моменты времени, математическое описание оперирует с другим понятием, а именно с производными концентраций (скоростью реакций). Совсем не случайно и не произвольно эмпирическое, а также теоретическое описание реагирующих систем имеют дело с параметрами, входящими в дифференциальное, а не в интегральное уравнение; эти параметры наиболее удобны. Текущие скорости изменения концентраций n-х веществ, т.е. $\frac{{{\text{d}}{{c}_{n}}}}{{{\text{d}}t}},$ имеют вполне определенный физический смысл. Эта производная по времени представляет физически многозначную величину, которая может описывать множество различных процессов, протекающих во времени, а именно: скорость реакции, скорость перемещения, скорость движения молекул [1, с. 19].

Основная идея описания схемы реакций с помощью двудольных ориентированных графов состоит в том, чтобы связать свойства решений системы с геометрическими свойствами графа. Многие важные свойства решений определяются только геометрией графа и не зависят от частного вида функций, выражающих зависимость скоростей стадий радикального процесса от концентраций реагентов. Это позволяет охватить широкий круг задач, не только задачи химической кинетики [2, с. 352].

Математическому моделированию процессов полимеризации посвящено много работ, среди которых можно отметить работу [3] по моделированию полимеризации бутилакрилата и работу [4] по расчету вязкости бутилкаучука. Нередко системой дифференциальных уравнений на графе описывают процессы с участием неорганических веществ. В основном, поправочные коэффициенты при моделировании задаются в численном виде либо в виде формул путем учета большого количества параметров процесса (как в работе [5]), в настоящей статье для описания процессов радикальной полимеризации органических веществ рассмотрено применение системы дифференциальных уравнений на графе, оптимизированной путем применения поправочных коэффициентов, которые являются зависимостями от температуры, конверсии и времени, прошедшего с начала полимеризационного процесса.

ТЕОРЕТИЧЕСКИЙ АНАЛИЗ

Исходные данные. В качестве примера возьмем процесс радикальной полимеризации стирола, проводимый при температурах 343, 348 и 353 К. Инициируется данный процесс азобисизобутиронитрилом, эффективность инициирования которого $f = {\text{89}}{\text{.91}}\quad{\text{exp}}\left( {\frac{{ - {\text{14240}}}}{{{\text{8}}{.314\;}T}}} \right),$ а константа скорости распада – ${{k}_{{\text{d}}}} = {\text{1}}{{{\text{0}}}^{{{\text{15}}{\text{.2}}}}}\quad{\text{exp}}\left( {\frac{{ - {\text{128960}}}}{{{\text{8}}{.314\;}T}}} \right).$ Концентрация мономера в начальный момент времени составляет [M]₀ = 5.2 моль/л, а исходная концентрация инициатора – [I]₀ = 0.015 моль/л (0.45 мас. % от стирола). При вычислении также использованы данные графиков конверсий мономера в зависимости от времени t [6].

Вычисление параметров процесса. Вычислим скорость полимеризации ${{\vartheta }_{{{\text{pm}}}}},$ концентрации мономера $\left[ M \right]$ и радикалов @$\left[ {{{{\text{R}}}^{\centerdot }}} \right],$ вступающих в реакцию роста, константу скорости обрыва ${{k}_{{\text{t}}}}$ и ее отношение к справочному значению ${\text{g}}$ по формулам (1) [7], (2), (3) [8, с. 13], (4) [6], (5) соответственно:

(1)

${{\vartheta }_{{{\text{pm}}}}} = \frac{{U\quad{{{\left[ M \right]}}_{0}}}}{t}{\text{,}}$

где $U$ – конверсия мономера;

(2)

$\left[ M \right] = {{\left[ M \right]}_{0}} - U\quad{{\left[ M \right]}_{0}}{\text{,}}$

(3)

$\left[ {{{{\text{R}}}^{\centerdot }}} \right] = \frac{{{{\vartheta }_{{{\text{pm}}}}}}}{{{{k}_{{\text{р }}}}\quad\left[ M \right]}}{\text{,}}$

где ${{k}_{{\text{р }}}} = {\text{1}}{{{\text{0}}}^{{{\text{8}}{\text{.21}}}}}\quad{\text{exp}}\left( {\frac{{ - {\text{36100}}}}{{{\text{8}}{.314\;}T}}} \right)$ – константа скорости роста цепи, $\frac{{\text{л }}}{{{м о л ь \;с }}}$ [6];

(4)

(5)

${\text{g}} = {{{{k}_{{\text{t}}}}} \mathord{\left/ {\vphantom {{{{k}_{{\text{t}}}}} {{{k}_{{{{{\text{t}}}_{0}}}}}}}} \right. \kern-0em} {{{k}_{{{{{\text{t}}}_{0}}}}}}}{\text{,}}$

где ${{k}_{{\text{t}}}}_{{_{0}}} = {\text{1}}{{{\text{0}}}^{{{\text{11}}{\text{.01}}}}}\quad{\text{exp}}\left( {\frac{{ - {\text{18660}}}}{{{\text{8}}{.314\;}T}}} \right)$ – константа скорости обрыва цепи, $\frac{{\text{л }}}{{{м о л ь \;с }}}$ [6].

Рассмотрим вычисление вышеперечисленных параметров на примере процесса, проводимого при температуре 343 К, результаты вычислений занесем в табл. 1.

Таблица 1.

Параметры процесса, вычисленные по графику временной зависимости конверсии стирола

t	U	${{\vartheta }_{{{\text{pm}}}}}$ × 10⁴	$\left[ M \right]$	$\left[ {{{{\text{R}}}^{\centerdot }}} \right]{\;} \times {\text{1}}{{{\text{0}}}^{{\text{7}}}}$	${{k}_{{\text{t}}}}{\;} \times {\text{1}}{{{\text{0}}}^{{\text{7}}}}$	g
0	0	0	5.2	0	15	1
1800	0.08	2.31	4.78	0.937	7.6	0.514
5400	0.208	2	4.12	0.943	7.5	0.507
7200	0.256	1.85	3.87	0.927	7.7	0.525
16 200	0.488	1.57	2.66	1.14	5.1	0.346
18 000	0.512	1.48	2.54	1.13	5.2	0.353
19 800	0.576	1.51	2.2	1.33	3.8	0.255
21 600	0.608	1.46	2.04	1.39	3.4	0.233
23 400	0.656	1.46	1.79	1.58	2.7	0.181
27 000	0.784	1.51	1.12	2.61	1	0.066
28 800	0.9	1.63	0.52	6.06	0.18	0.012
30 600	0.923	1.57	0.4	7.6	0.11	0.008

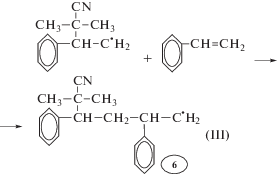
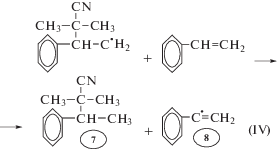
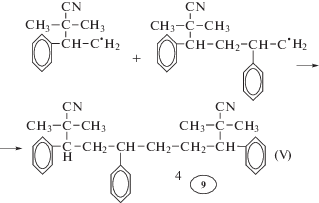
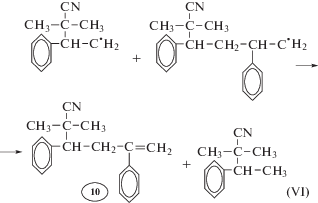
Составление матриц процесса радикальной полимеризации. Рассмотрим процесс радикальной термической полимеризации стирола, инициируемой азобисизобутиронитрилом, по стадиям [9, с. 85]:

1. Распад инициатора (k_d)

2. Инициирование (k_in)*

3. Рост активных цепей (k_p)

4. Передача активных цепей на молекулы мономера (k_trm)

5. Обрыв цепи рекомбинацией (k_rec = k_t)

6. Обрыв цепи диспропорционированием (принимаем упрощение, что k_dis = 0)

* – процесс инициирования рассмотрим отдельно от диссоциации инициатора на радикалы, примем приближение, что константа скорости инициирования ${{k}_{{{\text{in}}}}}$ равна 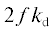[8, с. 34].

Пронумеруем вещества, входящие в схему выше, в порядке их написания в стадиях без учета повторений и составим атомную матрицу ${\text{D}}$ аналогично [10, с. 50], где строки – это вещества с первого по десятое, первый столбец – атомы углерода, второй столбец – атомы водорода, третий столбец – атомы азота:

${\text{D}} = \left( {\begin{array}{*{20}{c}} 8&{12}&4 \\ 4&6&1 \\ 0&0&2 \\ 8&8&0 \\ {12}&{14}&1 \\ {20}&{22}&1 \\ {12}&{15}&1 \\ 8&7&0 \\ {32}&{36}&2 \\ {20}&{21}&1 \end{array}} \right).$

Также составим стехиометрическую матрицу G аналогично [10, с. 15], в которой строки – это рассматриваемые стадии реакции (с первой по шестую), а столбцы – вещества с первого по десятое, атомный состав которых отображен в матрице D:

${\text{G}} = \left( {\begin{array}{*{20}{c}} { - 1}&2&1&0&0&0&0&0&0&0 \\ 0&{ - 1}&0&{ - 1}&1&0&0&0&0&0 \\ 0&0&0&{ - 1}&{ - 1}&1&0&0&0&0 \\ 0&0&0&{ - 1}&{ - 1}&0&1&1&0&0 \\ 0&0&0&0&{ - 1}&{ - 1}&0&0&1&0 \\ 0&0&0&0&{ - 1}&{ - 1}&1&0&0&1 \end{array}} \right).$

Отрицательные значения в матрице ${\text{G}}$ обусловлены стехиометрическими коэффициентами, которые стоят перед реагентами, положительные значения – это коэффициенты перед продуктами реакции, присутствующими в данной стадии (строке матрицы).

Согласно [10, с. 44–45] необходимо выполнение условия: произведение матриц ${\text{G}}$ и ${\text{D}}$ должно равняться нулю. Действительно, при умножении представленных выше матриц ${\text{G}}$ (6 × 10) и ${\text{D}}$ (10 × 3) получаем нулевую матрицу (6 × 3).

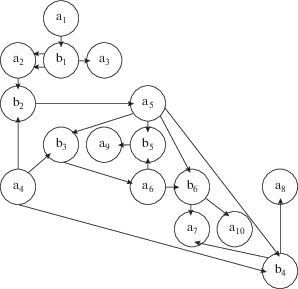
Составление кинетической модели процесса радикальной полимеризации. На рис. 1 представлен граф радикального процесса, соответствующий постадийной схеме:

Рис. 1.

Граф радикальной полимеризации.

Конечный ориентированный двудольный граф включает в себя множества ${\text{A}} = \left\{ {{{{\text{а }}}_{{\text{1}}}}{,\; \ldots ,\;}{{{\text{а }}}_{{\text{n}}}}} \right\}$ – вершины графа, соответствующие веществам, участвующим в реакциях, и ${\text{B}} = \left\{ {{{{\text{b}}}_{{\text{1}}}}{,\; \ldots ,\;}{{{\text{b}}}_{{\text{m}}}}} \right\}$ – вершины графа, соответствующие самим реакциям, т.е. стадиям процесса [2, с. 351].

Составим кинетическую модель процесса радикальной полимеризации в виде системы дифференциальных уравнений скоростей изменения концентраций веществ ${{c}_{n}}$ за единицу времени $t,$ где коэффициенты соответствуют столбцам матрицы ${\text{G:}}$

(6)

$\begin{gathered} \frac{{{\text{d}}{{c}_{{\text{1}}}}}}{{{\text{d}}t}} = - {{{\omega }}_{{\text{1}}}}{\text{,}}\,\,\,\,\frac{{{\text{d}}{{c}_{{\text{2}}}}}}{{{\text{d}}t}} = {\text{2}}\quad{{{\omega }}_{{\text{1}}}} - {{{\omega }}_{{\text{2}}}}{\text{,}}\,\,\,\,\frac{{{\text{d}}{{c}_{{\text{3}}}}}}{{{\text{d}}t}} = {{{\omega }}_{{\text{1}}}}{\text{,}} \\ \frac{{{\text{d}}{{c}_{{\text{4}}}}}}{{{\text{d}}t}} = - {{{\omega }}_{{\text{2}}}} - {{{\omega }}_{{\text{3}}}} - {{{\omega }}_{{\text{4}}}}{\text{,}}\,\,\,\,\frac{{{\text{d}}{{c}_{{\text{5}}}}}}{{{\text{d}}t}} = {{{\omega }}_{{\text{2}}}} - {{{\omega }}_{{\text{3}}}} - {{{\omega }}_{{\text{4}}}} - \\ - \,\,{{{\omega }}_{{\text{5}}}} - {{{\omega }}_{{\text{6}}}}{\text{,}}\,\,\,\,\frac{{{\text{d}}{{c}_{{\text{6}}}}}}{{{\text{d}}t}} = {{{\omega }}_{{\text{3}}}} - {{{\omega }}_{{\text{5}}}} - {{{\omega }}_{{\text{6}}}}{\text{,}} \\ \frac{{{\text{d}}{{c}_{{\text{7}}}}}}{{{\text{d}}t}} = {{{\omega }}_{{\text{4}}}} + {{{\omega }}_{{\text{6}}}}{\text{,}}\,\,\,\,\frac{{{\text{d}}{{c}_{{\text{8}}}}}}{{{\text{d}}t}} = {{{\omega }}_{{\text{4}}}}{\text{,}}\,\,\,\,\frac{{{\text{d}}{{c}_{{\text{9}}}}}}{{{\text{d}}t}} = {{{\omega }}_{{\text{5}}}}{\text{,}}\,\,\,\,\frac{{{\text{d}}{{c}_{{{\text{10}}}}}}}{{{\text{d}}t}} = {{{\omega }}_{{\text{6}}}}{\text{,}} \\ \end{gathered} $

где, согласно закону действующих масс [11, с. 101], скорость реакции ${{{\omega }}_{m}}$ прямо пропорциональна произведению концентраций реагентов в степенях, равных стехиометрическим коэффициентам в уравнении реакции (отрицательные значения в строках матрицы ${\text{G}}$), т.е.

(7)

где ${{k}_{{{\text{trm}}}}} = {\text{0}}{\text{.473}}\quad{\text{exp}}\left( {\frac{{ - {\text{24300}}}}{{{\text{8}}{.314\;}T}}} \right)\quad{{k}_{{\text{р }}}}$ [6].

Введем в систему ${\text{(6)}}$ поправку ${{h}_{{\text{1}}}}$ при расчете константы инициирования ${{k}_{{{\text{in}}}}}$ = 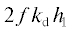в формуле ${{{\omega }}_{{\text{2}}}}{\text{:}}$

(8)

${{{\omega }}_{{\text{2}}}} = {{k}_{{\text{2}}}}\quad{{c}_{{\text{2}}}}\quad{{c}_{{\text{4}}}} = {{k}_{{{\text{in}}}}}\quad{{h}_{{\text{1}}}}\quad{{c}_{{\text{2}}}}\quad{{c}_{{\text{4}}}}{\text{,}}$

поправку ${{h}_{{\text{2}}}}$ в производную $\frac{{{\text{d}}{{c}_{{\text{2}}}}}}{{{\text{d}}t}}{\text{:}}$

(9)

$\frac{{{\text{d}}{{c}_{{\text{2}}}}}}{{{\text{d}}t}} = {\text{2}}\quad{{{\omega }}_{{\text{1}}}} - {{{\omega }}_{{\text{2}}}} + {{h}_{{\text{2}}}}$

и поправку ${{h}_{{\text{3}}}}$ в производную $\frac{{{\text{d}}{{c}_{{\text{4}}}}}}{{{\text{d}}t}}{\text{:}}$

(10)

$\frac{{{\text{d}}{{c}_{{\text{4}}}}}}{{{\text{d}}t}} = - {{{\omega }}_{{\text{2}}}} - {{{\omega }}_{{\text{3}}}} - {{{\omega }}_{{\text{4}}}} - {{h}_{{\text{3}}}}{\text{,}}$

которые позволят регулировать равенство данной производной с концентрацией мономера, вычисленной по формуле (2) в соответствующий момент времени. Данные поправки позволяют решить обратную кинетическую задачу с помощью системы (6) и найти среднечисловую степень полимеризации.

Были аппроксимированы введенные поправки в виде формул с целью рассмотрения возможности применения их для других радикальных процессов:

(11)

(12)

(13)

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

В программе MathCAD получена математическая модель, позволяющая вычислить концентрации участвующих в процессе радикальной полимеризации веществ. При решении обратной кинетической задачи и поиске поправок использовалась формула для вычисления среднечисловой степени полимеризации ${{P}_{n}}$ в момент времени $t{\text{:}}$

(14)

${{P}_{n}}\left( t \right) = \frac{{{{{\rho }}_{{\text{9}}}}}}{{m\quad{{c}_{{\text{9}}}}\left( t \right)}}{\text{,}}$

где ${{{\rho }}_{{\text{9}}}}$ = ${\text{1084}} - {\text{0}}{\text{.605}}\quad{{T}^{{\left( {\text{C}} \right)}}}$ – плотность полимера при температуре процесса, взятой в градусах Цельсия, г/л [6]; $m$ = 104.15 – молекулярная масса мономера, г/моль; ${{c}_{{\text{9}}}}\left( t \right)$ – вычисленная системой ${\text{(6)}}$ концентрация полимера в момент времени $t,$ моль/л.

После аппроксимирования поправок ${{h}_{{\text{1}}}},$ ${{h}_{{\text{2}}}},$ ${{h}_{{\text{3}}}}$ в формулу $\left( {{\text{14}}} \right)$ был введен коэффициент корреляции ${{K}_{{\text{с }}}}$ в виде функции

(15)

Результаты вычислений в сравнении с экспериментальными данными приведены на рис. 2–4 для процесса, проводимого при температурах 343, 348 и 353 К соответственно.

Рис. 2.

Зависимость среднечисловой степени полимеризации от времени при температуре 343 К: 1 – кривая, построенная по экспериментальным данным; 2 – кривая, построенная по вычисленным данным.

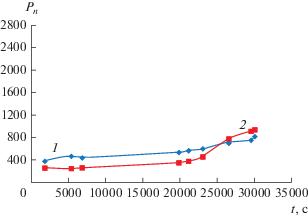
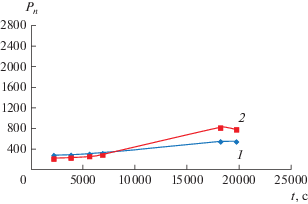
Рис. 3.

Зависимость среднечисловой степени полимеризации от времени при температуре 348 К: 1 – кривая, построенная по экспериментальным данным; 2 – кривая, построенная по вычисленным данным.

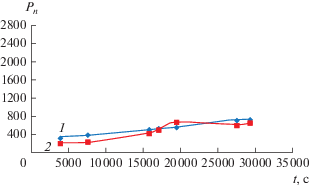
Рис. 4.

Зависимость среднечисловой степени полимеризации от времени при температуре 353 К: 1 – кривая, построенная по экспериментальным данным; 2 – кривая, построенная по вычисленным данным.

Максимальная погрешность вычисленного и экспериментального значения среднечисловой степени полимеризации составляет 40% при 343 К, 33.3% при 348 К и 37.5% при 353 К.

ЗАКЛЮЧЕНИЕ

Представлена математическая модель радикального процесса полимеризации на примере термической радикальной полимеризации стирола. Полученная кинетическая модель соответствует виду системы дифференциальных уравнений на графе:

(16)

$\frac{{{\text{d}}{{c}_{n}}}}{{{\text{d}}t}} = \sum\limits_{i = 1}^m {{{{\gamma }}_{{{\text{in}}}}}\quad{{{\omega }}_{i}}\left( {t{\text{,}}c} \right) + {{e}_{n}}\left( t \right)} {\text{,}}$

где ${{\gamma }_{{{\text{in}}}}}$ – элементы стехиометрической матрицы -й стадии ($i$-й строки матрицы ${\text{G}}$), ${{e}_{n}}\left( t \right) = {\text{0}}$ [12].

В статье представлен подробный алгоритм нахождения недостающих для расчета данных из графиков конверсии и составления кинетической модели радикального процесса полимеризации с использованием минимального набора исходных данных. Разница вычисленного и экспериментального значения среднечисловой степени полимеризации составляет порядка 40%, что обусловлено идеей задать поправочные коэффициенты в виде формул, в которых учитываются только такие параметры процесса, как температура, конверсия и время, прошедшее с начала полимеризации. Применимость аналогичных поправок и коэффициента корреляции необходимо проверить на других радикальных процессах.

ОБОЗНАЧЕНИЯ

$\left[ I \right]$	концентрация инициатора, моль/л
$\left[ M \right]$	концентрация мономера, моль/л
$[{{{\text{R}}}^{\centerdot }}]$	концентрация радикалов, моль/л
c	молярная концентрация вещества, моль/л
e	безразмерная поправка в общем виде системы дифференциальных уравнений на графе
f	безразмерная эффективность инициатора
g	коэффициент константы скорости реакции обрыва, учитывающий гель-эффект
h	безразмерная поправка в системе дифференциальных уравнений
K	безразмерный коэффициент корреляции
k	константа скорости реакции, $\frac{{\text{л }}}{{{м о л ь \;с }}}$
m	молекулярная масса мономера, г/моль
P	безразмерная среднечисловая степень полимеризации
T	температура, К
t	время, с
U	безразмерная конверсия мономера
γ	безразмерная сумма элементов стехиометрической матрицы
ρ	плотность, г/л
ϑ	скорость реакции, $\frac{{{\text{м о л ь }}}}{{{л \;с }}}$
ω	скорость реакции в системе дифференциальных уравнений, $\frac{{\text{1}}}{{\text{с }}}$ или $\frac{{{\text{м о л ь }}}}{{{л \;с }}}$

ИНДЕКСЫ

0	начальное значение
c	корреляция
d	распад инициатора
dis	обрыв цепи диспропорционированием
i, m	номера стадии
in	инициирование
n	номера компонентов
p	рост цепи
pm	полимеризация
rec	обрыв цепи рекомбинацией
t	обрыв цепи
trm	передача цепи на мономер

Список литературы

Бенсон С. Основы химической кинетики. М.: Мир, 1964.
Вольперт А.И., Худяев С.И. Анализ в классах разрывных функций и уравнения математической физики. М.: Наука, 1975.
Галеев Э.Р., Лежнева Н.В., Елизаров В.В., Елизаров В.И. Математическое моделирование процесса полимеризации бутилкаучука // Вестник технологического университета. 2016. Т. 19. № 23. С. 92.
Улитин Н.В., Терещенко К.А., Дебердеев Т.Р., Насыров И.И., Самарин Е.В., Калинина Д.Ш. Псевдоживая радикальная полимеризация бутилакрилата в присутствии тритиокарбонатов: моделирование кинетики и регулирование молекулярно-массовых характеристик полимера // Теорет. основы хим. технологии. 2015. Т. 49. № 1. С. 79.
Аминова Г.А., Антонова И.О., Бронская В.В., Мануйко Г.В., Игнашина Т.В., Исмагилова А.И. Математическое моделирование процесса синтеза бутилкаучука // Вестник технологического университета. 2012. Т. 15. № 4. С. 103.
Tefera N., Weickert G., Bloodworth R., Schweer J. Free radical suspension polymerization kinetics of styrene up to high conversion // Macromol. Chem. Phys. 1994. V. 195. P. 3067.
Ханукаева И.А., Колесников Г.С. Изучение кинетики полимеризации стирола в вязких средах // Высокомол. соединения. Сер. А. 1968. Т. 10. № 5. С. 1127.
Багдасарьян Х.С. Теория радикальной полимеризации. М.: Наука, 1966.
Савада Х. Термодинамика полимеризации. М.: Химия, 1979.
Исмагилова А.С., Спивак С.И. Математическое моделирование химических процессов. Уфа: РИЦ БашГУ, 2014.
Краснов К.С., Воробьев Н.К., Годнев И.Н., Васильева В.Н., Васильев В.П., Киселева В.Л., Белоногое К.Н., Гостикин В.П. Физическая химия. В 2 кн. Кн. 2. Электрохимия. Химическая кинетика и катализ. М.: Высшая школа, 1995.
Вольперт А.И. Дифференциальные уравнения на графах // Мат. сб. 1972. Т. 88(130). № 4(8). С. 578.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал