Теоретические основы химической технологии, 2019, T. 53, № 5, стр. 559-571
Моделирование и оптимизация циклических адсорбционных процессов обогащения газовых смесей водородом
А. А. Ишин 1, С. А. Скворцов 1, В. Г. Матвейкин 2, Д. С. Дворецкий 1, С. И. Дворецкий 1, *
1 Тамбовский государственный технический университет
Тамбов, Россия
2 ОАО “Корпорация “Росхимзащита”
Тамбов, Россия
* E-mail: sdvoretsky@mail.tstu.ru
Поступила в редакцию 16.10.2017
После доработки 12.10.2018
Принята к публикации 04.12.2018
Аннотация
Разработана математическая модель динамики процесса короткоцикловой безнагревной адсорбции, осуществляемого в четырехадсорберной установке с цеолитовым адсорбентом CaA при разделении многокомпонентных газовых смесей с целью концентрирования водорода. Предложено оригинальное описание процесса массопереноса адсорбтива (H2, CO2, СO) из газовой фазы в твердую фазу адсорбента для смешанно-диффузионной области в зависимости от скорости газовой фазы в слое адсорбента. Проведено численное исследование влияния нагрузки по сырью и управляющих переменных на динамику циклического адсорбционного процесса обогащения газовой смеси водородом. Сформулирована и методом имитационного моделирования исследована задача адаптивной оптимизации режимных переменных этого процесса.
ВВЕДЕНИЕ
В последние десятилетия все более распространенным становится использование циклических адсорбционных процессов для разделения газовых смесей и концентрирования целевых продуктов (в русскоязычной литературе КБА – короткоцикловая безнагревная адсорбция, в англоязычной PSA – pressure swing adsorption), которые не предполагают наличия внешнего источника тепла.
Короткоцикловые процессы адсорбционного разделения смесей газов широко применяют в промышленности для выделения водорода, обогащения воздуха кислородом, безнагревной осушки газов, разделения углеводородов, концентрирования диоксида углерода, извлечения метана и т.п. Одной из актуальных задач в области адсорбционного разделения является извлечение водорода из водородсодержащих технологических потоков (газы конверсии и окисления углеводородов, нефтезаводские газы, синтез-газ и др.). Типичными веществами, сопутствующими водороду, являются азот, оксид и диоксид углерода, метан. Особенностью адсорбционного концентрирования водорода является тот факт, что в смесях водородсодержащих газов сопутствующие водороду компоненты имеют более высокие значения адсорбционной селективности [1].
Анализ многочисленных работ зарубежных и российских ученых в области адсорбционного разделения многокомпонентных газовых смесей и концентрирования целевого продукта (водорода, кислорода, углекислого газа и др.) позволил определить место данной статьи среди других работ, ее актуальность и перспективность [2–11].
Так, в работах [2–8] представлены результаты численных исследований влияния режимных переменных (давления, температуры, расхода исходной смеси) на динамику и эффективность адсорбционного разделения двух- (H2–CO2), трех- (H2–CO2–CO), четырех- (H2–CO2–CO–CH4), пяти- (H2–CO2–CO–CH4–N2) и шестикомпонентных (H2–CO2–CO–H2O–Ar–N2) смесей и концентрирования водорода с использованием активного угля и металлоорганических соединений в качестве адсорбентов. В работах [2, 3] при расчете условий равновесия многокомпонентной смеси используются изотермы сорбции индивидуальных веществ, методом вычислительного эксперимента изучены особенности функционирования десятиадсорберной установки с вакуумной регенерацией (в английской литературе – VPSA) и четырехадсорберной установки PSA с металлоорганическим адсорбентом нового типа, установлена возможность извлечения водорода с чистотой 99.981 об. % при степени извлечения 81.6% [2] и 99.9 об. % при степени извлечения 48.05% [4]. В работах [6, 7] представлены результаты численных исследований влияния количества стадий выравнивания давлений, их последовательности и использования комбинаций различных слоев адсорбентов на чистоту и степень извлечения водорода из двухкомпонентной смеси (H2–CH4) в установке PSA с использованием изотермы равновесия Ленгмюра–Фрейндлиха. Установлено, что использование шестиадсорберной установки с двумя операциями выравнивания давлений обеспечивает наилучшее сочетание чистоты продукционного водорода (~99 об. %) при достижении степени извлечения ~83%.
В работе [9] методом вычислительного эксперимента исследованы зависимости чистоты извлекаемого углекислого газа из девятикомпонентной газовой смеси с использованием активного угля и установлено, что использование 7 адсорберов установки КБА (вместо 3 или 4 адсорберов) позволяет повысить чистоту продукционного углекислого газа с 95.1 до 98.9 об. % при снижении степени извлечения от 90.2 до 86.1%. В работах [10, 11] исследуются математические модели динамики циклического адсорбционного процесса извлечения CO2 из двухкомпонентной газовой смеси (CO2–N2) на цеолите 13X с использованием изотермы Ленгмюра, сформулирована и исследована задача оптимального проектирования PSA-установок (вакуум-напорного типа – VPSA и фракционного вакуум-напорного типа – FVPSA) по комплексному критерию – отношение энергозатрат установки PSA к чистоте продукционного диоксида углерода. Установлено, что установки, реализованные по схемам FVPSA и VPSA, обеспечивают извлечение диоксида углерода с чистотой ~90 и ~72 об. % соответственно, причем удельная мощность установки по схеме FVPSA в среднем в 2.5 раза выше.
Целью данной работы является разработка математической модели динамики циклического процесса адсорбционного разделения многокомпонентной газовой смеси и применение метода математического моделирования для исследования системных связей и закономерностей этого процесса и повышения эффективности функционирования установок КБА при концентрировании водорода.
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИНАМИКИ ПРОЦЕССА ОБОГАЩЕНИЯ ГАЗОВОЙ СМЕСИ ВОДОРОДОМ
Технологический процесс концентрирования водорода методом адсорбционного разделения газовой смеси с циклически изменяющимся давлением осуществляется в четырехадсорберной установке КБА (рис. 1) [12].
Рис. 1.
Технологическая схема четырехадсорберной установки КБА для концентрирования водорода: А1–А4 – адсорберы, К – управляемые клапаны, Р – ресивер.
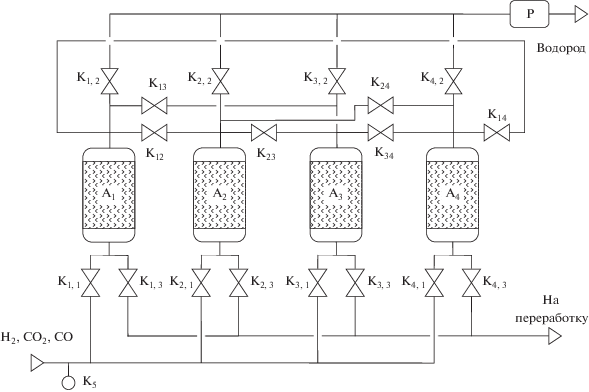
Установка предназначена для концентрирования водорода до 99.99 об. % из газовой смеси, содержащей водород в количестве 65 ± 2 об. %, диоксид углерода – 34 ± 2 об. % и оксид углерода – 1 ± 0.5 об. %. Исходная газовая смесь подается в установку после предварительной осушки (стадия осушки в данной работе не рассматривается) с избыточным давлением 2.1 МПа и температурой 30°С. Подъем давления в адсорберах А1–А4 производится открытием управляемых клапанов К1.1, К2.1, К3.1 и К4.1 соответственно, через которые газовая смесь подводится к слою адсорбента. Продукционный водород выводится из адсорберов через управляемые клапаны К1.2, К2.2, К3.2 и К4.2 и направляется к потребителям через ресивер Р. Противоточная регенерация слоя адсорбента в колоннах осуществляется путем пропускания продувочной (обогащенной водородом) газовой смеси через клапаны К12, К13, К14, К23, К24 и К34, а через клапаны К1.3, К2.3, К3.3 и К4.3 осуществляется отвод продувочного газа на этапе регенерации адсорбента.
Согласованная работа клапанов установки КБА обеспечивает последовательное осуществление в каждом адсорбере всех стадий циклического адсорбционного процесса, представленных в табл. 1.
Таблица 1.
Стадии адсорбционного процесса концентрирования водорода в четырехадсорберной установке КБА (А1–А4 – адсорберы, АД – адсорбция, ВД – выравнивание давления, СБ – сброс (уменьшение) давления, РГ – регенерация, ПД – подъем давления)
| А1 | АД | ВД1 | ВД2 | СБ | РГ | ВД3 | ВД4 | ПД | ||||
| А2 | ВД4 | ПД | АД | ВД1 | ВД2 | СБ | РГ | ВД3 | ||||
| А3 | СБ | РГ | ВД3 | ВД4 | ПД | АД | ВД1 | ВД2 | ||||
| А4 | ВД1 | ВД2 | СБ | РГ | ВД3 | ВД4 | ПД | АД | ||||
В качестве адсорбентов в циклических адсорбционных процессах широко используются гранулированные активные угли и цеолит СаА, обладающие наибольшей емкостью и селективностью по CO2 и CO [1, 13]. При адсорбции (десорбции) H2, CO2 и CO цеолитовым адсорбентом в адсорберах А1–А4 установки КБА протекают следующие массо- и теплообменные процессы: а) диффузия H2, CO2 и CO в потоке газовой смеси; б) массообмен H2, CO2, CO и теплообмен между газовой фазой и адсорбентом; в) адсорбция H2, CO2, CO на поверхности и в микропорах гранул цеолитового адсорбента с выделением тепла и десорбция H2, CO2, CO из микропор и с поверхности гранул с поглощением тепла. Анализ результатов физического моделирования показал, что диффузия H2, CO2, CO и распространение тепла в газовом потоке и гранулированном адсорбенте осуществляются в основном в продольном направлении относительно движения потока газовой смеси в адсорбере (по высоте слоя адсорбента). При этом процесс обогащения газовой смеси водородом при адсорбции преимущественно CO2 и CO гранулированным цеолитовым адсорбентом осуществляется в смешанно-диффузионной области и определяется коэффициентами внешней массоотдачи и внутренней диффузии, скоростью газовой смеси в слое адсорбента, а также равновесными соотношениями концентраций H2, CO2 и CO в фазах.
При математическом описании процесса обогащения газовой смеси водородом в установке КБА принимали следующие допущения: 1) исходная газовая смесь является трехкомпонентной (содержит 1 – H2 с концентрацией 65 ± 2 об. %, 2 – СО2 с концентрацией 34 ± 2 об. % и 3 – CO с концентрацией 1 ± 0.5 об. %) и рассматривается как идеальный газ, что вполне допустимо при давлении в адсорбере до 200 × 105 Па [14]; 2) диаметр и высота насыпного слоя цеолитового адсорбента СаА составляли 0.26 и 1.9 м соответственно; диаметр гранул – 3.2 мм, коэффициент пористости гранул ~0.394 и диаметр транспортных пор ~0.5 × 10–3 м; 3) геометрические размеры адсорбционного слоя считали постоянными в течение заданного срока эксплуатации ~105 ч [15]; 4) слой адсорбента представляет собой сплошную среду с коэффициентом порозности $\varepsilon ,$ учитывающим пористость гранул; 5) десорбционная ветвь изотерм сорбции H2, CO2 и CO на гранулированном цеолите СаА совпадает с адсорбционной и носит нелинейный характер [16].
В соответствии с принятыми допущениями математическое описание циклического процесса адсорбционного разделения многокомпонентной газовой смеси и концентрирования водорода в установке КБА включает следующие уравнения [17].
1. Уравнение покомпонентного (k = 1 – H2, 2 – CO2, 3 – CO) материального баланса в потоке газовой смеси по высоте слоя адсорбента:
(1)
$\begin{gathered} \frac{{\partial {{c}_{k}}(x,t)}}{{\partial t}} + \frac{{(1 - \varepsilon )}}{\varepsilon }\frac{{\partial {{a}_{k}}}}{{\partial t}} + \frac{{\partial ({{v}_{{\text{g}}}}{{с}_{k}}(x,t))}}{{\partial x}} = \\ = \frac{\partial }{{\partial x}}\left( {D_{{\text{g}}}^{k}(x)\frac{\partial }{{\partial x}}{{c}_{k}}(x,t)} \right), \\ \end{gathered} $В уравнении (1) первое слагаемое описывает скорость накопления k-го компонента смеси в газовой фазе; второе слагаемое – скорость накопления k-го компонента в адсорбенте; третье слагаемое – конвективный перенос вещества в слое адсорбента; четвертое слагаемое – продольное перемешивание k-го компонента в слое адсорбента.
2. Уравнение массопереноса адсорбтива (H2, CO2, CO) из газовой фазы в твердую фазу адсорбента (через границу раздела фаз):
(2)
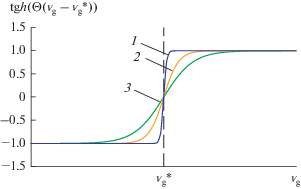
$\begin{gathered} \frac{{\partial {{a}_{k}}}}{{\partial t}} = \frac{{F_{k}^{2} - F_{k}^{1}}}{2}{\text{(tgh}}(\theta ({{v}_{{\text{g}}}} - v_{{\text{g}}}^{*})) + 1) + F_{k}^{1}, \\ k = {\text{1,2,3}}, \\ \end{gathered} $Уравнение (2) представляет собой описание кинетики адсорбции для смешанно-диффузионной области переноса адсорбтива (H2, CO2, CO) через границу раздела фаз (рис. 2): при скорости газовой смеси ниже переходной скорости $v_{{\text{g}}}^{*}$ процесс адсорбции лимитируется процессом внешней массоотдачи с коэффициентом $\beta _{k}^{1},$ в противном случае – процессом внутренней диффузии в гранулах адсорбента с кинетическим коэффициентом $\beta _{k}^{2}.$ Гиперболический тангенс и формальный коэффициент $\theta $ наряду с $v_{{\text{g}}}^{*}$ описывают непрерывный переход из области внешнего массообмена в область внутридиффузионного процесса адсорбции H2, CO2 и CO цеолитовым адсорбентом CaA.
Рис. 2.
Описание непрерывного перехода из области внешнего массообмена к области внутридиффузионного процесса адсорбции H2, CO2 и CO цеолитовым адсорбентом CaA в зависимости от переходной скорости $v_{{\text{g}}}^{*}$ газовой фазы: 1 – при $\theta = {{\theta }_{1}},$ 2 – при $\theta = {{\theta }_{2}},$ 3 – при $\theta = {{\theta }_{3}},$ ${{\theta }_{1}} < {{\theta }_{2}} < {{\theta }_{3}}.$
Кинетические коэффициенты массоотдачи $\beta _{k}^{1},$ $\beta _{k}^{2},$ граничная скорость $v_{{\text{g}}}^{*}$ и формальный параметр $\theta $ определялись путем решения регуляризованной экстремальной задачи идентификации кинетических параметров математической модели адсорбционного процесса концентрирования водорода с использованием экспериментальных данных, полученных методом физического моделирования установки КБА в лабораторных и опытно-промышленных условиях: $v_{{\text{g}}}^{*}$ = 0.022 м/с; $\beta _{{{{{\text{H}}}_{{\text{2}}}}}}^{1}$ = 0.816 1/с; $\beta _{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}^{1}$ = 0.021 1/с; $\beta _{{{\text{CO}}}}^{1}$ = 0.084 1/с; $\beta _{{{{{\text{H}}}_{{\text{2}}}}}}^{2}$ = 0.73 1/с; $\beta _{{{\text{C}}{{{\text{O}}}_{{\text{2}}}}}}^{2}$ = 0.012 1/с; $\beta _{{{\text{CO}}}}^{2}$ = 0.059 1/с, $\theta $ = 18.2.
Величина адсорбции $a_{k}^{ * },$ равновесная текущей концентрации адсорбтива ${{с}_{k}}$ в потоке на внешней поверхности гранул, рассчитывается по уравнению изотермы Ленгмюра–Фрейндлиха [18].
3. Уравнение, описывающее распространение тепла в потоке газовой смеси по высоте адсорбента:
(3)
$\begin{gathered} c_{p}^{{\text{g}}}{{\rho }_{{\text{g}}}}\frac{{\partial {{T}_{{\text{g}}}}(x,t)}}{{\partial t}} + с_{p}^{{\text{g}}}{{\rho }_{{\text{g}}}}{{v}_{{\text{g}}}}\frac{{\partial {{T}_{{\text{g}}}}(x,t)}}{{\partial x}} - \frac{\alpha }{\varepsilon }{{S}_{{{\text{ud}}}}} \times \\ \times \,\,[{{T}_{{\text{a}}}}(x,t) - {{T}_{{\text{g}}}}(x,t)] - \frac{{4{{K}_{{{\text{env}}}}}}}{{\varepsilon {{d}_{{\text{А}}}}}}\left[ {{{T}_{{{\text{env}}}}} - {{T}_{{\text{g}}}}(x,t)} \right] = \\ = {{\lambda }_{{\text{g}}}}\frac{{{{\partial }^{2}}{{T}_{{\text{g}}}}}}{{\partial {{x}^{2}}}},\,\,\,0 < x < L, \\ \end{gathered} $В уравнении (3) первое слагаемое описывает накопление тепла в газовой фазе; второе слагаемое – конвективную составляющую переноса тепла; третье слагаемое – теплоотдачу от газовой фазы к твердой фазе (адсорбенту); четвертое слагаемое – теплопередачу от газовой фазы к окружающей среде через стенку адсорбера; пятое слагаемое – продольную теплопроводность газовой фазы по высоте слоя адсорбента.
4. Уравнение, описывающее изменение температуры в адсорбенте:
(4)
$\begin{gathered} с_{p}^{{\text{а}}}{{\rho }_{{\text{a}}}}\frac{{\partial {{T}_{{\text{a}}}}(x,t)}}{{\partial t}} + \alpha {{S}_{{u{\text{d}}}}}\left[ {{{T}_{{\text{а}}}}(x,t) - {{T}_{{\text{g}}}}(x,t)} \right] - \\ - \,\,\sum\limits_k {h_{k}^{{{\text{ads}}}}\frac{{\partial {{a}_{k}}(x,t)}}{{\partial t}}} = {{\lambda }_{{\text{a}}}}\frac{{{{\partial }^{2}}{{T}_{{\text{a}}}}(x,t)}}{{\partial {{x}^{2}}}}, \\ \end{gathered} $В уравнении (4) первое слагаемое описывает энтальпию твердой фазы (адсорбента); второе слагаемое – теплоотдачу от твердой фазы (адсорбента) к газовой фазе; третье слагаемое – выделение теплоты сорбции компонентов газовой смеси; четвертое слагаемое – теплопроводность в адсорбенте вдоль вертикальной оси адсорбера.
5. Уравнение Эргуна, связывающее изменение давления и скорости газовой смеси по высоте адсорбента [19]:
(5)
$\begin{gathered} \frac{{\partial P}}{{\partial x}} = - \left( {\frac{{150{{{\left( {1 - {{\varepsilon }_{0}}} \right)}}^{2}}}}{{{{{\left( {2{{r}_{{{\text{gr}}}}}\psi } \right)}}^{2}}\varepsilon _{0}^{2}}}{{\mu }_{{\text{g}}}}{{v}_{{\text{g}}}} + } \right. \\ \left. { + \,\,1.75{{M}_{{\text{g}}}}{{\rho }_{{\text{g}}}}\frac{{\left( {1 - {{\varepsilon }_{0}}} \right)}}{{2{{r}_{{{\text{gr}}}}}\psi {{\varepsilon }_{0}}}}{{v}_{{\text{g}}}}^{2}} \right), \\ \end{gathered} $Начальные и граничные условия для уравнений (1)–(5) приведены в табл. 2.
Таблица 2.
Начальные и граничные условия для уравнений (1)–(5)
| Адсорбция | Десорбция |
|---|---|
| Начальные условия ($\,0 \leqslant x \leqslant L$) | |
| $t = 0{\text{:}}$${{c}_{k}}\left( {x,0} \right) = c_{k}^{0}(x),$${{a}_{k}}(0) = 0,$${{T}_{{\text{g}}}}(x,0) = T_{{\text{g}}}^{0}(x),$${{T}_{{\text{a}}}}(x,\;0) = T_{{\text{a}}}^{0}(x),$ (6) $k = \left( {1 - {{{\text{H}}}_{2}},\,\,2 - {\text{C}}{{{\text{O}}}_{2}},\,\,3 - {\text{CO}}} \right).$ | $t = {{t}_{{{\text{ads}}}}}{\text{:}}$$c_{k}^{{{\text{des}}}}(x,t) = c_{k}^{{{\text{ads}}}}(x,{{t}_{{{\text{ads}}}}}),\,$$a_{k}^{{{\text{des}}}}\left( t \right) = a_{k}^{{{\text{ads}}}}({{t}_{{{\text{ads}}}}}),$ (6') $T_{{\text{g}}}^{{{\text{des}}}}(x,t) = T_{{\text{g}}}^{{{\text{ads}}}}(x,{{t}_{{{\text{ads}}}}}),$$T_{{\text{a}}}^{{{\text{des}}}}(x,t) = T_{{\text{a}}}^{{{\text{ads}}}}(x,{{t}_{{{\text{ads}}}}}).$ |
| $t = (n - 1)4{{t}_{{{\text{ads}}}}},$n = 1, 2…, $c_{k}^{{{\text{ads}}}}(x,t) = c_{k}^{{{\text{des}}}}(x,{{t}_{{{\text{des}}}}}),$ $a_{k}^{{{\text{ads}}}}\left( t \right) = a_{k}^{{{\text{des}}}}({{t}_{{{\text{des}}}}}),$$\,T_{{\text{g}}}^{{{\text{ads}}}}(t) = T_{{\text{g}}}^{{{\text{des}}}}(x,{{t}_{{{\text{des}}}}}),\,$$\,T_{{\text{а}}}^{{{\text{аds}}}}(t) = T_{{\text{a}}}^{{{\text{des}}}}(x,{{t}_{{{\text{des}}}}}).$ |
|
| Граничные условия: $x = 0,$$x = L$ | |
| $\begin{gathered} {{с}_{k}}(0,t) = c_{k}^{{{\text{in}}}}(t),\,\,\,\,{{T}_{{\text{g}}}}(0,t) = T_{{\text{g}}}^{{{\text{in}}}}(t), \hfill \\ \frac{{\partial {{T}_{{\text{a}}}}(0,t)}}{{\partial x}} = \alpha {{S}_{{{\text{ud}}}}}({{T}_{{\text{a}}}}(0,t) - T_{{\text{g}}}^{{{\text{in}}}}(t)) \hfill \\ \end{gathered} $ (7) | $\frac{{\partial \,{{c}_{k}}(0,t)}}{{\partial \,x}} = 0,$$\frac{{\partial \,{{T}_{{\text{g}}}}(0,t)}}{{\partial \,x}} = 0,$$\frac{{\partial {{T}_{{\text{a}}}}(0,t)}}{{\partial x}} = \alpha {{S}_{{{\text{ud}}}}}({{T}_{{\text{a}}}}(0,t) - {{T}_{{\text{g}}}}(0,t)),$ (7') $\frac{{\partial {{v}_{{\text{g}}}}(0,t)}}{{\partial x}} = 0$ |
| $\frac{{\partial {{c}_{k}}(L,t)}}{{\partial x}} = 0,\,\,\frac{{\partial {{T}_{{\text{g}}}}(L,t)}}{{\partial x}} = 0,$$\frac{{\partial {{T}_{{\text{a}}}}(L,t)}}{{\partial x}} = \alpha {{S}_{{{\text{ud}}}}}({{T}_{{\text{a}}}}(L,t) - {{T}_{{\text{g}}}}(L,t)),$ (8) $\frac{{\partial {{v}_{{\text{g}}}}(L,t)}}{{\partial x}} = 0$ |
${{с}_{k}}(L,\,\,t) = с_{k}^{{{\text{ads}}}}(L,t),$ ${{T}_{{\text{g}}}}(L,t) = T_{{\text{g}}}^{{{\text{ads}}}}(L,t),$ (8') $\frac{{\partial {{T}_{{\text{a}}}}(L,t)}}{{\partial x}} = \alpha {{S}_{{{\text{ud}}}}}({{T}_{{\text{a}}}}(L,t) - T_{{\text{g}}}^{{{\text{ads}}}}(L,t))$ |
Формулы для расчета коэффициентов математической модели представлены в работе [17] и здесь не приводятся.
Объемный расход потока, направляемого в ресивер Р (рис. 1), определялся как ${{G}^{{{\text{out}}}}}$ = $G_{{{\text{ads}}}}^{{{\text{out}}}} - G_{{{\text{des}}}}^{{{\text{in}}}},$ где $G_{{{\text{des}}}}^{{{\text{in}}}}$ = $\chi \;G_{{{\text{ads}}}}^{{{\text{out}}}}\frac{{{{P}_{{{\text{des}}}}}}}{{{{P}_{{{\text{ads}}}}}}}$ – объемный расход потока, обогащенного водородом, направляемого на десорбцию преимущественно CO2, CO и отвод в атмосферу, $\chi $ – коэффициент обратного потока.
Таким образом, уравнения (1)–(5) с начальными и граничными условиями (6)–(8) представляют собой математическое описание циклических процессов адсорбции–десорбции, осуществляемых в адсорберах А1–А4 установки КБА (рис. 1).
Для численного решения системы нелинейных дифференциальных уравнений с частными производными (1)–(5) применяли метод прямых, в соответствии с которым производилась аппроксимация производных по пространственной переменной x конечно-разностными формулами. При этом производная по времени остается в непрерывной форме. В результате получается система обыкновенных дифференциальных уравнений вдоль заданного семейства прямых с начальными и граничными условиями, которая решалась методом Рунге–Кутты 4-го порядка с автоматическим выбором шага. Метод прямых обладает приемлемыми для практики точностью и скоростью сходимости, что делает его наиболее предпочтительным при решении уравнений математической модели (1)–(5) с начальными (6) и граничными (7), (8) условиями.
Далее концентрации водорода, диоксида и оксида углерода будем обозначать через ${\mathbf{y}}$ = = $({{y}_{1}},\;{{y}_{2}},\;{{y}_{3}})$ об. %.
Проверка адекватности математической модели производилась по результатам независимых экспериментов, т.е. отличных от экспериментальных данных, использованных для идентификации модели. Рассогласование расчетных по модели (1)–(8) и экспериментальных данных оценивали по формуле
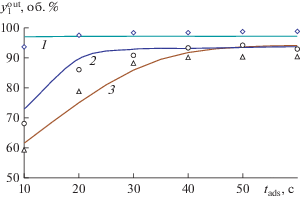
Максимальная относительная погрешность ${{\delta }_{{\max }}}$ рассогласования расчетных $y_{1}^{{{\text{out}}}}$ и экспериментальных данных $y_{1}^{{{\text{out}},{\text{e}}}}$ на стадии адсорбции не превышает 11.4% (рис. 3), что позволяет с приемлемой для практики точностью использовать модель для целей технологического расчета, оптимизации и управления процессом концентрирования водорода методом адсорбционного разделения газовой смеси.
Рис. 3.
Динамика концентрации продукционного водорода $y_{1}^{{{\text{out}}}}$ в зависимости от концентрации CO2 в исходной смеси: 1 – 10; 2 – 40; 3 – 50 об. %; точки – эксперимент, сплошная линия – расчет по модели.
ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ПРОЦЕССА ОБОГАЩЕНИЯ ГАЗОВОЙ СМЕСИ ВОДОРОДОМ
Анализ КБА-процесса обогащения газовой смеси водородом как объекта управления позволил определить: входные переменные (состав ${{{\mathbf{y}}}^{{{\text{in}}}}}$ = $\left( {y_{1}^{{{\text{in}}}},\,\,y_{2}^{{{\text{in}}}},\,\,y_{3}^{{{\text{in}}}}} \right),$ температуру $T_{{\text{g}}}^{{{\text{in}}}}$ и давление $P_{{}}^{{{\text{in}}}}$ исходной газовой смеси); режимные (управляющие) переменные (давление ${{P}_{{{\text{ads}}}}}$ на стадии адсорбции и ее длительность ${{t}_{{{\text{ads}}}}},$ аналогично и для стадии десорбции); выходные переменные – состав ${{{\mathbf{y}}}^{{{\text{out}}}}}$ = $\left( {y_{1}^{{{\text{out}}}},\,\,y_{2}^{{{\text{out}}}},\,\,y_{3}^{{{\text{out}}}}} \right),$ расход ${{G}^{{{\text{out}}}}}$ и температуру $T_{{\text{g}}}^{{{\text{out}}}}$ продукционной газовой смеси на выходе из установки КБА, степень извлечения $\eta $ водорода и производительность $Q$ установки.
С целью исследования системных связей, закономерностей и повышения эффективности функционирования установки КБА проводился численный анализ влияния входных переменных и управляющих воздействий на выходные переменные процесса адсорбционного разделения газовой смеси и концентрирования водорода. Варьируемые переменные и диапазоны их изменения представлены в табл. 3.
Таблица 3.
Исходные данные для вычислительного эксперимента
| Наименование параметра | Диапазон изменения |
|---|---|
| Длительность стадии адсорбции ${{t}_{{{\text{ads}}}}},$ с | 25–200 |
| Отношение длительности стадии десорбции к длительности стадии адсорбции $\gamma = {{{{t}_{{{\text{des}}}}}} \mathord{\left/ {\vphantom {{{{t}_{{{\text{des}}}}}} {{{t}_{{{\text{ads}}}}}}}} \right. \kern-0em} {{{t}_{{{\text{ads}}}}}}}$ | 0.2–0.8 |
| Состав исходной газовой смеси: | |
| концентрация диоксида углерода $y_{2}^{{{\text{in}}}},$ об. % | 25–45 |
| концентрация оксида углерода $y_{3}^{{{\text{in}}}},$ об. % | 1 |
| Температура исходной смеси $T_{{\text{g}}}^{{{\text{in}}}},$ °C | 10–50 |
| Давление исходной газовой смеси ${{P}^{{{\text{in}}}}},$ МПа | 0.5–3 |
Проведена серия вычислительных экспериментов по исследованию влияния длительности стадии адсорбции ${{t}_{{{\text{ads}}}}}$ (от 50 до 175 c), производительности установки (от 70 до 850 нл/мин), давления исходной газовой смеси (от 0.5 до 3 МПа), концентрации $y_{2}^{{{\text{in}}}}$ диоксида углерода (от 25 до 45 об. %) в исходной газовой смеси, температуры $T_{{\text{g}}}^{{{\text{in}}}}$ (от 10 до 50°C) и отношения $\gamma = {{{{t}_{{{\text{des}}}}}} \mathord{\left/ {\vphantom {{{{t}_{{{\text{des}}}}}} {{{t}_{{{\text{ads}}}}}}}} \right. \kern-0em} {{{t}_{{{\text{ads}}}}}}}$ (от 0.2 до 0.8) на концентрацию $y_{1}^{{{\text{out}}}}$ и степень извлечения $\eta $ продукционного водорода.
На рис. 4 и 5 представлены графики зависимостей концентрации $y_{1}^{{{\text{out}}}}$ и степени извлечения $\eta $ водорода от продолжительности ${{t}_{{{\text{ads}}}}}$ стадии адсорбции и производительности $Q$ установки КБА при $\gamma = {{{{t}_{{{\text{des}}}}}} \mathord{\left/ {\vphantom {{{{t}_{{{\text{des}}}}}} {{{t}_{{{\text{ads}}}}}}}} \right. \kern-0em} {{{t}_{{{\text{ads}}}}}}}$ = 0.5, $T_{{\text{g}}}^{{{\text{in}}}}$ = 30°С и $y_{{\text{2}}}^{{{\text{in}}}}$ = 25 об. % (кривые 1, 4), 34 об. % (кривые 2, 5), 45 об. % (кривые 3, 6).
Рис. 4.
Зависимости концентрации $y_{1}^{{{\text{out}}}}$ и степени извлечения $\eta $ водорода от продолжительности ${{t}_{{{\text{ads}}}}}$ стадии адсорбции при $y_{2}^{{{\text{in}}}}{\text{:}}$ 1, 4 – 25; 2, 5 – 34; 3, 6 – 45 об. %.
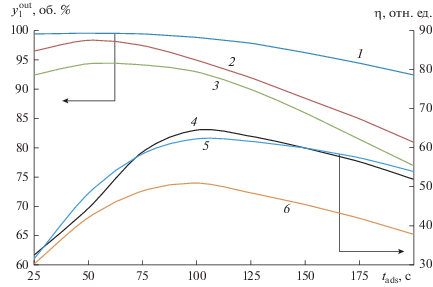
Рис. 5.
Зависимости концентрации $y_{1}^{{{\text{out}}}}$ и степени извлечения $\eta $ водорода от производительности $Q$ установки КБА при $y_{2}^{{{\text{in}}}}{\text{:}}$ 1, 4 – 25; 2, 5 – 34; 3, 6 – 45 об. %.
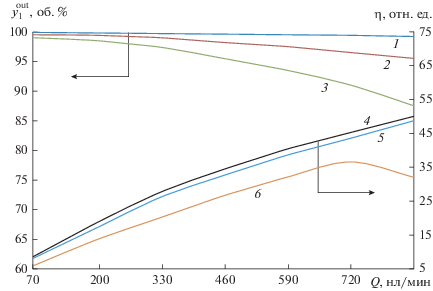
Анализ графиков на рис. 4 показывает, что максимальные значения $y_{2}^{{{\text{out}}}}$ ≈ 99.7 об. % и $\eta $ = 65% достигаются при$y_{2}^{{{\text{in}}}}$ = 25 об. %, $\gamma $ = 0.5, ${{t}_{{{\text{ads}}}}}$ = 50 и 100 с соответственно. При этом температура $T_{{\text{g}}}^{{{\text{out}}}}$ газовой смеси, обогащенной водородом, повышается в среднем на 10°С. При $y_{2}^{{{\text{in}}}}$ = 34 об. % на отрезке времени адсорбции $50 \leqslant {{t}_{{{\text{ads}}}}} \leqslant 125\,\,{\text{с}}$ концентрация продукционного водорода $y_{1}^{{{\text{out}}}}$ уменьшается с 98 до 80 об. %.
Зависимости концентрации продукционного водорода $y_{1}^{{{\text{out}}}}$ от давления исходной смеси носят экстремальный характер при всех рассматриваемых значениях температуры и содержания диоксида углерода в исходной газовой смеси (на рисунке не показаны). Максимальное значение $y_{1}^{{{\text{out}}}}$ продукционного водорода наблюдается в интервале давлений ${{P}^{{{\text{in}}}}}$ = 0.5–1 МПа, а при $y_{2}^{{{\text{in}}}}$ = 45 об. % – при ${{P}^{{{\text{in}}}}}$ ≈ 0.75 МПа. С уменьшением доли СО2 в исходной смеси максимум смещается вправо; при $y_{2}^{{{\text{in}}}}$ = 25 об. % график практически приобретает вид кривой насыщения. При этом температура $T_{{\text{g}}}^{{{\text{out}}}}$ газовой смеси, обогащенной водородом, повышается от 295 до 330 К.
Из анализа графиков на рис. 5 следует, что концентрация $y_{1}^{{{\text{out}}}}$ продукционного водорода обратно пропорциональна производительности при всех рассматриваемых температурах и концентрациях CO2 в исходной газовой смеси. Повышение производительности $Q$ установки КБА приводит к тому, что на стадии регенерации десорбция адсорбата производится недостаточно полно и наблюдается некоторое снижение поглотительной способности адсорбента и чистоты получаемого продукта. При малых значениях производительности $Q$ чистота продукта $y_{1}^{{{\text{out}}}}$ практически постоянна и равна ее предельному значению для данных условий, кривые стремятся к насыщению, а для значений производительности $Q$ выше некоторого порога $y_{1}^{{{\text{out}}}}$ начинает заметно уменьшаться практически линейно, причем величина этого порога зависит от температуры $T_{{\text{g}}}^{{{\text{in}}}}$ исходной газовой смеси: при $T_{{\text{g}}}^{{{\text{in}}}}$ = 50°С пороговое значение расхода продукционного водорода равно ${{G}^{{{\text{out}}}}}$ = 550 × 10–5 м3/c, а при $T_{{\text{g}}}^{{{\text{in}}}}$ = 10, 30°С – ${{G}^{{{\text{out}}}}}$ = = 250 × 10–5 м3/с.
Наибольшая чувствительность $y_{1}^{{{\text{out}}}}$ к изменению производительности $Q$ установки КБА наблюдается при $y_{2}^{{{\text{in}}}}$ = 45 об. %, а при $y_{2}^{{{\text{in}}}}$ = 25 об. % уменьшение $y_{1}^{{{\text{out}}}}$ незначительно. Это означает, что повышение $T_{{\text{g}}}^{{{\text{in}}}}$ в некоторых пределах или уменьшение $y_{2}^{{{\text{in}}}}$ до 25 об. % позволяет существенно повысить производительность установки $Q$ практически без снижения чистоты продукционного водорода.
Температура $T_{{\text{g}}}^{{{\text{out}}}}$ продукционного водорода пропорциональна производительности $Q$ установки при всех рассматриваемых значениях $y_{2}^{{{\text{in}}}}.$ Наибольшее значение температуры $T_{{\text{g}}}^{{{\text{out}}}}$ = 323 K продукционного потока газовой смеси наблюдается при $y_{2}^{{{\text{in}}}}$ = 45 об. %, что объясняется высокими значениями концентрации СО2 в адсорбенте и, как следствие, большим тепловым эффектом процесса адсорбции. С уменьшением доли примеси в исходном газе $T_{{\text{g}}}^{{{\text{out}}}}$ падает, а при $y_{2}^{{{\text{in}}}}$ = 25 об. % наблюдается наименьшая чувствительность $T_{{\text{g}}}^{{{\text{out}}}}$ к производительности $Q$ установки КБА.
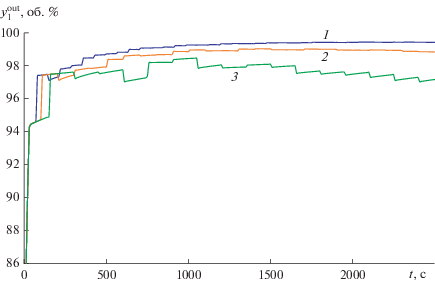
На рис. 6 представлены графики изменения концентрации водорода $y_{1}^{{{\text{out}}}}$в зависимости от времени функционирования установки КБА при отношении $\gamma = {{{{t}_{{{\text{des}}}}}} \mathord{\left/ {\vphantom {{{{t}_{{{\text{des}}}}}} {{{t}_{{{\text{ads}}}}}}}} \right. \kern-0em} {{{t}_{{{\text{ads}}}}}}}$ = 0.5, температуре $T_{{\text{g}}}^{{{\text{in}}}}$ = 30°С для различных значений времени стадии адсорбции ${{t}_{{{\text{ads}}}}}$ = 70, 100 и 150 с. Из анализа графиков следует, что с увеличением времени функционирования установки происходит некоторое снижение концентрации $y_{1}^{{{\text{out}}}}$ продукционного водорода, что объясняется соответствующим ростом температуры адсорбента.
Рис. 6.
Динамика концентрации продукционного водорода $y_{1}^{{{\text{out}}}}$ в зависимости от времения функционирования установки КБА при различных значениях ${{t}_{{{\text{ads}}}}}{\text{:}}$ 1 – 70 с, 2 – 100 с, 3 – 150 с.
Методом вычислительного эксперимента также исследованы профили температуры по длине слоя адсорбента для ряда значений времени адсорбции 20, 40, 60, 80 и 100 с (на рисунке не показаны). Анализ результатов дает основание утверждать, что в результате теплового эффекта сорбции СО2 и СО происходит рост температуры слоя адсорбента и возникает тепловой фронт, движущийся в аксиальном направлении вместе с сорбционным. Следует отметить также существенный рост температуры в “лобовом” слое адсорбента, что связано со значительным содержанием адсорбтива (главным образом СО2 и СО) в газовой смеси и теплотой сорбции на цеолите CaA. Тепловые потери для данного режима минимальны, что способствует проведению десорбции сорбата (преимущественно СО2 и СО) на стадии регенерации адсорбента без затрат энергии для дополнительного нагрева адсорбента.
ОПТИМИЗАЦИЯ ПРОЦЕССА ОБОГАЩЕНИЯ ГАЗОВОЙ СМЕСИ ВОДОРОДОМ
Численные исследования процесса концентрирования водорода методом короткоцикловой безнагревной адсорбции при разделении многокомпонентной газовой смеси позволили определить наиболее опасные возмущения (состав ${{{\mathbf{y}}}^{{{\text{in}}}}}$ = = $\left( {y_{{\text{1}}}^{{{\text{in}}}}{\text{,}}\,\,y_{{\text{2}}}^{{{\text{in}}}}{\text{,}}\,\,y_{{\text{3}}}^{{{\text{in}}}}} \right){\text{,}}$ температуру $T_{{\text{g}}}^{{{\text{in}}}}$ и давления $P_{{}}^{{{\text{in}}}}$ газовой смеси на входе в адсорберы установки КБА, на продукционном $P_{{}}^{{{\text{out}}}}$ и сбросном $P_{{\text{1}}}^{{{\text{out}}}}$ выходах установки) и эффективные управляющие воздействия (давление ${{P}_{{{\text{ads}}}}}$ газовой смеси на стадии адсорбции и длительность ${{t}_{{{\text{ads}}}}}$ стадии адсорбции). Задача оптимизации технологического процесса концентрирования водорода по технологии КБА может быть сформулирована следующим образом: при заданных диапазонах изменения возмущающих воздействий ${\mathbf{x}}$ = $\left\{ {{{y}^{{{\text{in}}}}}{\text{,}}\,\,T_{{\text{g}}}^{{{\text{in}}}}{\text{,}}\,\,{{G}^{{{\text{in}}}}}{\text{,}}\,\,{{P}^{{{\text{in}}}}}{\text{,}}\,\,{{P}^{{{\text{out}}}}}{\text{,}}\,\,P_{{\text{1}}}^{{{\text{out}}}}} \right\}$ требуется найти вектор допустимых управлений ${\mathbf{u}}$ = = $({{P}_{{{\text{ads}}}}}{\text{,}}\,\,{{t}_{{{\text{ads}}}}}),$ при котором целевая функция – среднее значение концентрации $y_{{\text{1}}}^{{{\text{out}}}}$ продукционного водорода на отрезке времени [0, tpr], соответствующем выходу установки КБА на стационарный периодический режим работы, – достигает максимального значения, т.е.
(9)
$\begin{gathered} I({\mathbf{u}}{\text{*}}) = \left( {\frac{{\text{1}}}{{{{t}_{{{\text{pr}}}}}}}\int\limits_0^{{{t}_{{{\text{pr}}}}}} {y_{{\text{1}}}^{{{\text{out}}}}({\mathbf{u}}{\text{*}})dt} } \right) = \\ = \mathop {\max }\limits_{{\mathbf{u}} = \{ {{P}_{{{\text{ads}}}}}{\text{,}}{{t}_{{{\text{ads}}}}}\} } \left( {\frac{{\text{1}}}{{{{t}_{{{\text{pr}}}}}}}\int\limits_0^{{{t}_{{{\text{pr}}}}}} {y_{{\text{1}}}^{{{\text{out}}}}({\mathbf{u}})dt} } \right), \\ \end{gathered} $выполняются связи в форме уравнений математической модели (1)–(8) и ограничения на:
− чистоту продукционного водорода $y_{1}^{{{\text{out}}}}$
(10)
$y_{{\text{1}}}^{{{\text{out}}}}({\mathbf{u}}) \geqslant \underline y _{{\text{1}}}^{{{\text{out}}}},$− производительность $Q$ установки КБА
− скорость газовой смеси в “лобовом” слое адсорбента
(12)
$\mathop {\max }\limits_{t \in {{t}_{{\text{ц}}}}} \left| {{{v}_{{\text{g}}}}({\mathbf{u}})} \right| \leqslant v_{{\text{g}}}^{ + },$− перепад давления в слое адсорбента на стадиях адсорбции и десорбции
(13)
$\begin{gathered} \Delta {{P}_{{{\text{ads}}}}} = \mathop {\max }\limits_{t \in [0,{{{{t}_{{\text{ц}}}}} \mathord{\left/ {\vphantom {{{{t}_{{\text{ц}}}}} 2}} \right. \kern-0em} 2}]} P_{{{\text{ads}}}}^{{{\text{out}}}}({\mathbf{u}},L) - P_{{{\text{ads}}}}^{{{\text{in}}}}({\mathbf{u}},0) \leqslant \Delta P_{{{\text{ads}}}}^{ + }, \\ \Delta {{P}_{{{\text{des}}}}} = \mathop {\max }\limits_{t \in [{{{{t}_{{\text{ц}}}}} \mathord{\left/ {\vphantom {{{{t}_{{\text{ц}}}}} 2}} \right. \kern-0em} 2},\,\,{{t}_{{\text{ц}}}}]} P_{{{\text{des}}}}^{{{\text{out}}}}(u,0) - P_{{{\text{des}}}}^{{{\text{in}}}}(u,L) \leqslant \Delta P_{{{\text{des}}}}^{ + }, \\ \end{gathered} $Сформулированная аргументная задача оптимизации (9)–(13) относится к классу задач нелинейного программирования, для решения которой задачу условной оптимизации (9)–(13) преобразовывали в задачу безусловной оптимизации методом штрафной функции, а для поиска экстремума целевой функции $I({\mathbf{u}}{\text{*}})$ использовали высокоэффективный метод последовательного квадратичного программирования [20].
Для оперативного решения задачи оптимизации (9)−(13) и управления процессом концентрирования водорода разработана двухуровневая система управления, в которой осуществляется непрерывный контроль за текущими значениями возмущающих воздействий, и при их отклонении от номинальных значений на верхнем уровне системы управления оперативно решается задача (9)−(13) и определяются текущие оптимальные значения режимных переменных ${\mathbf{u}}{\text{*}}$ = $\left( {P_{{{\text{ads}}}}^{{\text{*}}}{\text{,}}\,\,t_{{{\text{ads}}}}^{{\text{*}}}} \right),$ поступающие в качестве заданий ПИД-регулятору давления и программному задатчику циклограммы переключения отсечных клапанов.
Результаты сравнительного анализа работы установки КБА при наличии адаптивной оптимизации (+) и без адаптивной оптимизации (–) в системе управления представлены в табл. 4.
Таблица 4.
К анализу эффективности работы установки КБА ($I*,$ $I$ – значения целевой функции при наличии и без адаптивной оптимизации в системе управления соответственно)
| Возмущающее воздействие – ступенчатое увеличение | $I*,$ об. % (+) | $I,$ об. % (–) | $\Delta I,$ об. % |
|---|---|---|---|
| $y_{{^{{\text{2}}}}}^{{{\text{in}}}}$ от 34 до 45 об. % | 95.76 | 89.46 | 6.3 |
| $T_{{\text{g}}}^{{{\text{in}}}}$ от 30 до 50°С | 98.92 | 94.13 | 4.79 |
| $P_{{}}^{{{\text{out}}}}$ от 0.2 до 0.3 МПа | 98.92 | 95.09 | 3.83 |
| $P_{{\text{1}}}^{{{\text{out}}}}$ от 0 до 0.1 МПа | 96.51 | 90.22 | 6.29 |
ЗАКЛЮЧЕНИЕ
Разработанная математическая модель циклического процесса адсорбционного разделения газовой смеси и концентрирования водорода может быть использована: 1) для исследования динамики циклических адсорбционных процессов разделения многокомпонентных газовых смесей; 2) для оптимизации и повышения эффективности функционирования установок КБА с циклически изменяющимся давлением; 3) для разработки алгоритма и системы адаптивного управления циклическими процессами адсорбционного разделения многокомпонентных газовых смесей.
Новые научные результаты, математическое, информационное и алгоритмическое обеспечение системы адаптивной оптимизации и управления четырехадсорберной установкой КБА, представленные в данной работе, могут быть использованы при проектировании новых автоматизированных процессов и адсорбционных технологических установок с циклически изменяющимся давлением для разделения и очистки многокомпонентных газовых смесей.
Работа выполнена в рамках проектной части государственного задания № 10.3533.2017/ПЧ.
ОБОЗНАЧЕНИЯ
| ${{a}_{k}}$ | величина сорбции k-го компонента в адсорбенте, моль/м3 |
| $a_{k}^{ * }$ | величина адсорбции, равновесная текущей концентрации адсорбтива в потоке газовой смеси на внешней поверхности гранул, моль/м3 |
| ${{с}_{k}}$ | мольная концентрация k-го компонента газовой смеси, моль/м3 |
| $c_{k}^{ * }$ | концентрация адсорбтива на поверхности раздела фаз или равновесная текущей величине адсорбции, моль/м3 |
| $с_{p}^{{\text{g}}}$, $с_{p}^{{\text{a}}}$ | удельные теплоемкости газовой смеси и адсорбента соответственно, Дж/(моль К) |
| $D_{{\text{g}}}^{k}$ | эффективный коэффициент продольного перемешивания k-го компонента в газовой смеси, м2/с |
| ${{G}^{{{\text{in}}}}}$ | объемный расход газовой смеси на входе в установку КБА, м3/с |
| ${{G}^{{{\text{out}}}}}$ | объемный расход потребляемой продукционной газовой смеси, м3/с |
| $G_{{{\text{ads}}}}^{{{\text{out}}}}$ | объемный расход газовой смеси, обогащенной водородом, на выходе из адсорбера, м3/с |
| $G_{{{\text{des}}}}^{{{\text{in}}}}$ | объемный расход потока, обогащенного водородом, направляемого на десорбцию, м3/с |
| $h_{k}^{{\text{a}}}$ | теплота адсорбции k-го компонента газовой смеси, Дж/моль |
| ${{K}_{{{\text{env}}}}}$ | коэффициент теплопередачи от потока газовой смеси к окружающей среде, Вт/(К м2) |
| $L$ | высота насыпного слоя адсорбента, м |
| ${{M}_{{\text{g}}}}$ | молярная масса газовой смеси, кг/моль |
| ${{P}^{{{\text{in}}}}}$ | давление газовой смеси на входе в установку КБА, Па |
| ${{P}_{{{\text{ads}}}}},\,\,{{P}_{{{\text{des}}}}}$ | давления на стадиях адсорбции и десорбции соответственно, Па |
| ${{P}^{{{\text{out}}}}},\,\,P_{1}^{{{\text{out}}}}$ | давления на продукционном и отводном выходах установки КБА, Па |
| $\Delta P_{{{\text{ads}}}}^{ + },\,\,\Delta P_{{{\text{des}}}}^{ + }$ | максимально допустимые значения перепада давления в адсорбционном слое адсорбера на стадиях адсорбции и десорбции |
| $Q,\,\,\underline Q $ | текущее и заданное значение производительности (расхода продукционного потока воздуха при заданной концентрации $\underline y _{1}^{{{\text{out}}}}\;$ кислорода) установки КБА, нл/мин |
| ${{r}_{{{\text{gr}}}}}$ | радиус гранулы адсорбента, м |
| $S$ | площадь поперечного сечения адсорбера, м2 |
| ${{S}_{{{\text{ud}}}}}$ | коэффициент удельной поверхности гранул адсорбента, м2/м3 |
| ${{T}_{{\text{a}}}}$ | температура адсорбента, K |
| ${{T}_{{\text{g}}}}$ | температура газовой смеси, К |
| ${{T}_{{{\text{env}}}}}$ | температура окружающей среды, K |
| $t$ | время, с |
| ${{t}_{{{\text{ads}}}}},\,\,{{t}_{{{\text{des}}}}}$ | длительности стадий адсорбции и десорбции, с |
| ${{t}_{{{\text{pr}}}}}$ | период времени, соответствующий установившемуся режиму работы установки КБА, с |
| ${{v}_{{\text{g}}}},$$v_{{\text{g}}}^{*},$$v_{{\text{g}}}^{ + }$ | линейная, переходная и максимально допустимая скорости газовой смеси в слое адсорбента соответственно, м/с |
| x | пространственная координата по вертикальной оси адсорбера (высоте слоя адсорбента), м |
| ${{y}_{k}}$ | объемная концентрации k-го компонента газовой смеси, об. % |
| $\underline y _{1}^{{{\text{out}}}}\;$ | заданное значение концентрации кислорода в продукционном потоке воздуха |
| $\alpha $ | коэффициент теплоотдачи от поверхности гранул адсорбента к потоку газовой смеси, Вт/(К м2) |
| $\beta _{k}^{1}$ | коэффициент массоотдачи, 1/с |
| $\beta _{k}^{2}$ | кинетический коэффициент внутренней диффузии, 1/с |
| ${\gamma }$ | отношение длительности стадии десорбции $\;{{t}_{{{\text{des}}}}}$ к длительности стадии адсорбции ${{t}_{{{\text{ads}}}}}$ |
| $\delta $ | относительная погрешность рассогласования расчетных по модели и экспериментальных данных, % |
| $\varepsilon $, ${{\varepsilon }_{0}}$ | коэффициенты порозности слоя адсорбента с учетом и без учета пористости гранул соответственно, м3/м3 |
| $\eta $ | степень извлечения (концентрирования) водорода, % |
| $\theta $ | формальный коэффициент, устанавливающий размеры смешанно-диффузионной области |
| ${{\lambda }_{{\text{g}}}},\,\,{{\lambda }_{{\text{a}}}}$ | коэффициенты теплопроводности газовой смеси и адсорбента соответственно, Вт/(м К) |
| ${{\mu }_{{\text{g}}}}$ | динамическая вязкость газовой смеси, Па с |
| ${{\rho }_{{\text{g}}}}$ | мольная плотность газовой смеси, моль/м3 |
| ${{\rho }_{{\text{a}}}}$ | плотность адсорбента, кг/м3 |
| $\chi $ | коэффициент обратного потока, отн. ед. |
| $\psi $ | коэффициент сферичности гранул адсорбента, отн. ед. |
ИНДЕКСЫ
| 1, 2, 3, 4 | номер адсорбционной колонны в технологической схеме установки КБА; |
| a | адсорбент |
| ads | относящийся к стадии адсорбции |
| des | относящийся к стадии десорбции |
| e | эксперимент |
| env | относящийся к окружающей среде |
| g | газовая смесь |
| gr | гранула |
| in | вход |
| k | номер компонента газовой смеси |
| out | выход |
| p | относящийся к удельной теплоемкости |
| pr | относящийся к стационарному периодическому режиму |
Список литературы
Ruthven D.M., Farooq S., Knaebel K.S. Pressure Swing Adsorption. N.Y.: VCH, 1993.
Lopes F.V.S., Grande C.A., Rodrigues A.E. Activated carbon for hydrogen purification by pressure swing adsorption: Multicomponent breakthrough curves and PSA performance // Chemical Engineering Science. 2011. V. 66. P. 303.
Xiao J., Li R., Benard P., Chahine R. Heat and mass transfer model of multicomponent adsorption system for hydrogen purification // International Journal of Hydrogen Energy. 2015. V. 30. P. 1.
Silva B., Solomon I., Ribeiro A.M., Lee U.-H., Hwang Y.K., Chang J.-S., Loureiro J.M., Rodrigues A.E. H2 purification by pressure swing adsorption using CuBTC // Separation and Purification Technology. 2013. V. 118. P. 744.
Yavary M., Ebrahim H.A., Falamaki C. The effect of number of pressure equalization steps on the performance of pressure swing adsorption process // Chemical Engineering and Processing. 2015. V. 87. P. 35.
Papadias D.D., Lee S.H.D., Ahmed S. Facilitating analysis of trace impurities in hydrogen: Enrichment based on the principles of pressure swing adsorption // Int. J. Hydrogen Energy. 2012. V. 37. P. 14413.
Kim Y.J., Nam Y.S., Kang Y.T. Study on a numerical model and PSA (pressure swing adsorption) process experiment for CH4/CO2 separation from biogas // Energy. 2015. V. 91. P. 732.
Boon J., Cobden P.D., van Dijk H.A.J., van Sint Annaland M. High-temperature pressure swing adsorption cycle design for sorption-enhanced water–gas shift // Chemical Engineering Science. 2015. V. 122. P. 219.
Riboldi L., Bolland O. Evaluating pressure swing adsorption as a CO2 separation technique in coal-fired power plants // International J. Greenhouse Gas Control. 2015. V. 39. P. 1.
Ko D., Siriwardane R., Biegler L.T. Optimization of a pressure-swing adsorption process using zeolite 13X for CO2 sequestration // Ind. Eng. Chem. Res. 2003. V. 42. № 2. P. 339.
Ko D., Siriwardane R., Biegler L.T. Optimization of pressure swing adsorption and fractionated vacuum pressure swing adsorption processes for CO2 capture // Ind. Eng. Chem. Res. 2005. V. 44. № 21. P. 8084.
Baksh M.S.A., Ackley M.W. Pressure swing adsorption process for the production of hydrogen. Pat. 6340382 USA. 2002.
Шумяцкий Ю.И. Промышленные адсорбционные процессы. М.: КолосС, 2009.
Кириллин В.А. Техническая термодинамика. М.: Изд. дом МЭИ, 2008.
Акулов А.К. Моделирование разделения бинарных газовых смесей методом адсорбции с колеблющимся давлением. Дис. … докт. техн. наук. СПб.: СПбГТИ, 1996.
Кельцев Н.В. Основы адсорбционной техники. М.: Химия, 1976.
Akulinin Y.I., Ishin A.A., Skvortsov S.A., Dvoretskiy D.S. Mathematical modeling of hydrogen production process by pressure swing adsorption method // Advanced Materials and Technologies. 2017. V. 2. P. 38.
Jee J.G., Kim M.B., Lee C.H. Adsorption characteristics of hydrogen mixtures in a layered bed: Binary, ternary, and five-component mixtures // Ind. Eng. Chem. Res. 2001. V. 40. № 3. P. 868.
Белоглазов И.Н., Голубев В.О. Основы расчета фильтрационных процессов. М.: Издательский дом “Руда и Металлы”, 2002.
Реклейтис Г., Рейвиндран А., Рэгсдел К. Оптимизация в технике: в 2-х кн. Кн. 2. М.: Мир, 1986.
Dvoretsky D.S., Dvoretsky S.I. Integrated design of flexible chemical processes, devices, and control systems // Theor. Found. Chem. Eng. 2014. V. 48. № 5. P. 614. [Дворецкий Д.С., Дворецкий С.И. Интегрированное проектирование гибких химико-технологических процессов, аппаратов и систем управления // Теорет. основы хим. технологии. 2014. Т. 48. № 5. С. 557.]
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


