Теоретические основы химической технологии, 2019, T. 53, № 5, стр. 572-594
Придонный слой в топке с циркулирующим кипящим слоем
В. И. Ковенский *
ООО “Петрокотел-ВЦКС”
Санкт-Петербург, Россия
* E-mail: kvico@tut.by
Поступила в редакцию 07.06.2018
После доработки 25.01.2019
Принята к публикации 07.02.2019
Аннотация
Рассмотрен подобный неоднородному кипящему слою придонный слой в топке с циркулирующим кипящим слоем. Показано, что в формировании придонного слоя, наряду с силой тяжести и силой гидродинамического сопротивления, участвует дополнительная сила, обусловленная циркуляцией образующих слой частиц. Предложена методика расчета параметров придонного слоя, учитывающая эту силу. Сформулированы условия образования и существования подобного слоя. Определены транспортная скорость, средняя порозность, время пребывания и другие характеристики придонного слоя для типичных условий работы топок. Выполнены расчеты для известных из литературы экспериментов. Проведено сравнение результатов с имеющимися в литературе опытными данными.
ВВЕДЕНИЕ
Технология циркулирующего кипящего слоя (ЦКС) используется в химической промышленности и энергетике [1, 2]. В аппаратах с ЦКС скорость газа превышает скорость витания частиц дисперсного материала. Поэтому для их устойчивой работы необходимо возвращать уносимую твердую фазу [3]. Уловленный зернистый материал подается в нижнюю часть стояка реактора либо топки. Здесь, в зоне ускорения [4–7], при определенных условиях формируется высококонцентрированная дисперсная среда – придонный слой (ПС). Его структура и размеры, а также условия существования зависят от ряда аппаратных, режимных и физических параметров.
Для топок ЦКС характерно небольшое отношение высоты стояка к эквивалентному диаметру (<10) [1]. В них используется газораспределитель с малым сопротивлением [8]. В качестве рабочего применяется дисперсный материал групп B (топливо) и D (инерт) по классификации Гелдарта (Geldart) при незначительных циркуляционных потоках [1, 8]. Совокупность перечисленных характеристик обусловливает такую же структуру и поведение придонного слоя, как у обычного неоднородного кипящего слоя (КС) [4, 8–11]. Образование КС-подобного придонного слоя, как правило, связывают с неоднородностью псевдоожижения, в том числе из-за низкого сопротивления газораспределителя [8, 12, 13].
Гидродинамические и обменные параметры ПС рассчитываются как для обычного неоднородного кипящего слоя в предположении, что весь избыточный газ (кроме необходимого для взвешивания зернистого материала) проходит в струях и пузырях [8, 14, 15]. При этом не учитывается проточность системы и связанная с ней процедура разгона частиц возвращаемого уноса, хотя влияние эффектов ускорения на плотность придонного слоя выявлено экспериментально [16].
В связи с этим целью настоящей работы является обоснование вклада возникающих во время ускорения частиц сил инерции в образование придонного слоя, разработка учитывающей эти силы методики расчета параметров ПС и условий его существования. Объект исследования – КС-подобный придонный слой, формирующийся в стояке топки с циркулирующим кипящим слоем.
ДОПОЛНИТЕЛЬНАЯ СИЛА, ДЕЙСТВУЮЩАЯ НА ПС
Придонный слой вместе с уносимыми и возвращаемыми частицами представляет собой проточную систему и может рассматриваться как частный случай системы переменного состава [17] (по определению [17] механическая система является системой переменного состава, если либо масса системы, либо материальные точки, из которых она состоит, либо и то и другое меняются со временем).
Рассмотрим придонный слой, содержащий в начальный момент N одинаковых частиц с постоянной массой m. Его масса с течением времени изменяется по закону
где M = mN – начальная масса, ${{M}_{2}}(t)$ = $m\int\limits_0^t {{{N}_{2}}(t)dt} $ и ${{M}_{0}}(t)$ = $m\int\limits_0^t {{{N}_{0}}(t)dt} $ – массы вышедших из системы и вошедших в нее частиц соответственно [17].Слой будет стационарным, а его масса останется неизменной при условии равенства M2(t) и M0(t):
Из соотношения (2), после подстановки определений M0(t) и M2(t), следует
В (3) учтено, что расходы N0 и N2 отличны от 0, а равенство в любой момент времени t возможно только при их постоянном значении вследствие независимого формирования потоков уноса и его возврата.
Из теоремы об изменении количества движения системы переменного состава [17] следует, что дополнительно к внешним силам на такую систему действует реактивная сила
(4)
$F = - \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta {{Q}_{2}}}}{{\Delta t}} + \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta {{Q}_{0}}}}{{\Delta t}},$Преобразуем выражение (4) применительно к придонному слою. Для определенности будем считать, что все частицы, выносимые из слоя в течение времени Δt, покидают его в момент t + Δt, а возвращаемые – присоединяются к системе в момент времени t. Тогда количества движения отделяющихся и присоединяющихся к слою частиц можно представить как
(5)
$\Delta {{Q}_{2}} = m\sum\limits_{i = 1}^{{{N}_{{0 - 2}}}\Delta t} {{{v}_{i}}\left( {t + \Delta t} \right)} ,$(6)
$\Delta {{Q}_{0}} = m\sum\limits_{k = 1}^{{{N}_{{0 - 2}}}\Delta t} {{{v}_{k}}\left( t \right)} ,$(7)
$F = - m\mathop {\lim }\limits_{\Delta t \to 0} \frac{{\sum\limits_{i = 1}^{{{N}_{{0 - 2}}}\Delta t} {{{v}_{i}}\left( {t + \Delta t} \right)} - \sum\limits_{k = 1}^{{{N}_{{0 - 2}}}\Delta t} {{{v}_{k}}\left( t \right)} }}{{\Delta t}}.$Последнее выражение преобразуем следующим образом:
(8)
$\begin{gathered} F = - m\mathop {\lim }\limits_{\Delta t \to 0} \,\, \times \\ \times \,\,\frac{{\sum\limits_{i = 1}^{{{N}_{{0 - 2}}}\Delta t} {{{v}_{i}}\left( {t + \Delta t} \right)} - \sum\limits_{k = 1}^{{{N}_{{0 - 2}}}\Delta t} {{{{v}}_{k}}\left( t \right)} + N\bar {v} - N\bar {v}}}{{\Delta t}}, \\ \end{gathered} $(9)
$\sum\limits_{j = 1}^N {{{v}_{j}}\left( t \right)} = \sum\limits_{j = 1}^{N - {{N}_{{0 - 2}}}\Delta t} {{{v}_{j}}\left( t \right)} + \sum\limits_{i = 1}^{{{N}_{{0 - 2}}}\Delta t} {{{v}_{i}}\left( t \right)} ,$(10)
$\begin{gathered} \sum\limits_{j = 1}^N {{{v}_{j}}\left( {t + \Delta t} \right)} = \sum\limits_{j = 1}^{N - {{N}_{{0 - 2}}}\Delta t} {{{v}_{j}}\left( {t + \Delta t} \right)} + \\ + \,\,\sum\limits_{k = 1}^{{{N}_{{0 - 2}}}\Delta t} {{{v}_{k}}\left( {t + \Delta t} \right)} . \\ \end{gathered} $После подстановки (9) и (10) в формулу (8), группировки слагаемых и предельного перехода получается
(11)
$\begin{gathered} F = - m\mathop {\lim }\limits_{\Delta t \to 0} \sum\limits_{j = 1}^{N + {{N}_{{0 - 2}}}\Delta t} {\frac{{{{v}_{j}}\left( {t + \Delta t} \right) - {{v}_{j}}\left( t \right)}}{{\Delta t}}} = \\ = - m\sum\limits_{j = 1}^N {{{w}_{j}}\left( t \right)} . \\ \end{gathered} $Таким образом, величина реактивной силы, действующей на придонный слой, равна сумме сил инерции, развивающихся в процессе разгона твердой фазы. Она противоположна направленному вверх ускорению частиц и действует совместно с силой тяжести.
УЧЕТ НЕОДНОРОДНОСТИ СЛОЯ
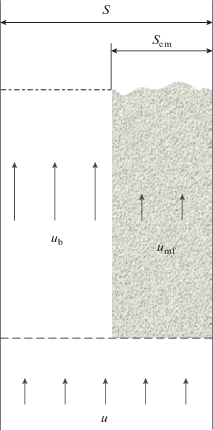
Расчет параметров придонного слоя в топке ЦКС выполняется как для обычного кипящего слоя и основывается на двухфазной теории псевдоожижения. Соответственно, ПС представляют совокупностью эмульсионной фазы, содержащей дисперсный материал в состоянии минимального ожижения и продуваемой со скоростью umf, и практически свободной от частиц дискретной фазы, сквозь которую прорывается весь остальной газ со скоростью ub (рис. 1). Очевидно, что разгон зернистого материала возможен только в дискретной фазе, где достаточно свободного пространства и расход газа максимален. Достигаемые скорость и ускорение частицы определяются величиной ub, зависящей от средней скорости ожижающего агента u и параметра Ub. Безразмерная скорость Ub = ub/u характеризует неоднородность газового потока в аппарате. Выражение для Ub выводится из условия баланса потоков (рис. 1)
(12)
$uS = {{u}_{{\text{b}}}}\left( {S - {{S}_{{{\text{em}}}}}} \right) + {{u}_{{{\text{mf}}}}}{{S}_{{{\text{em}}}}}.$Преобразуя его с использованием формулы $\frac{{{{S}_{{{\text{em}}}}}}}{S}$ = = $\frac{{1 - \bar {\varepsilon }}}{{1 - {{\varepsilon }_{0}}}},$ можно получить
(13)
${{U}_{{\text{b}}}} = \frac{{1 - {{\varepsilon }_{0}}}}{{\bar {\varepsilon } - {{\varepsilon }_{0}}}} - \frac{{1 - \bar {\varepsilon }}}{{\bar {\varepsilon } - {{\varepsilon }_{0}}}}\frac{{{{u}_{{{\text{mf}}}}}}}{u}.$Так как umf$ \ll $ u, соотношение (13) приближенно записывается как
(14)
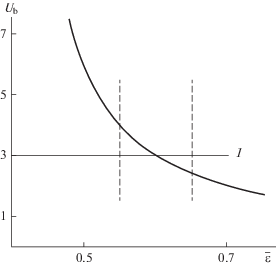
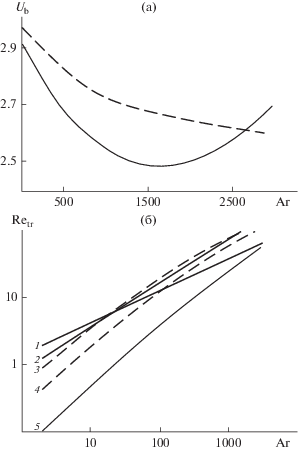
${{U}_{{\text{b}}}} \approx \frac{{1 - {{\varepsilon }_{0}}}}{{\bar {\varepsilon } - {{\varepsilon }_{0}}}}.$Формула (14) позволяет, основываясь на данных [8], оценить диапазон возможных значений Ub. Из рис. 2 следует, что Ub может принимать значения от 2.5 до 4 при среднем ~3.
Рис. 2.
Диапазон вероятных значений относительной скорости газа в дискретной фазе слоя: 1 – ориентировочное среднее значение Ub. Сплошная линия – зависимость (14), штриховые – наибольшее и наименьшее значения $\bar {\varepsilon }$ по данным [8].
Величина δb (рис. 1) определяет долю объема, занятую дискретной фазой
(15)
${{\delta }_{{\text{b}}}} = \frac{{\bar {\varepsilon } - {{\varepsilon }_{0}}}}{{1 - {{\varepsilon }_{0}}}}$и характеризует структурную неоднородность придонного слоя.
СКОРОСТЬ И УСКОРЕНИЕ РАЗГОНЯЕМОЙ ЧАСТИЦЫ
Поскольку предполагается, что дисперсный материал в дискретной фазе слоя отсутствует, движение попавшей сюда частицы можно рассматривать как свободное. Соответствующее уравнение в системе координат, связанной с потоком газа, движущимся со скоростью ub, имеет вид
(16)
$m\frac{{d{{v}_{{\text{b}}}}}}{{dt}} = - mg + \rho {{v}_{{\text{p}}}}g + {{f}_{{{\text{res}}}}},$с коэффициентом сопротивления λ = $\frac{{24}}{{{{{\operatorname{Re} }}_{{{{v}_{{\text{b}}}}}}}}}\left( {1 + \frac{{{{{\operatorname{Re} }}_{{{{v}_{{\text{b}}}}}}}}}{{50}}} \right)$ (здесь ${{\operatorname{Re} }_{{{{v}_{{\text{b}}}}}}}$ = $\frac{{{{v}_{{\text{b}}}}d}}{\nu }$), принятым в соответствии с [18].
Относительная скорость vb меняется от –ub в начальный момент времени (предполагается, что в дискретную фазу частицы попадают с нулевой вертикальной скоростью) до скорости установившегося движения –ut при t → ∞ (ub – ut в системе координат, связанной с аппаратом), оставаясь всегда отрицательной.
После подстановки в (16) и преобразований с учетом знака vb получается
– уравнение Риккати с постоянными коэффициентами $A = \frac{{18}}{{50}}\frac{\rho }{{{{\rho }_{{\text{p}}}}}}\frac{1}{d},$ $B = 18\frac{\rho }{{{{\rho }_{{\text{p}}}}}}\frac{\nu }{{{{d}^{2}}}},$ $C = g\frac{{{{\rho }_{{\text{p}}}} - \rho }}{{{{\rho }_{{\text{p}}}}}}$ [19].
Начальное условие vb(0) = –ub.
Решение (18) имеет вид
(19)
${{v}_{{\text{b}}}}\left( t \right) = \frac{{\left( {B{{u}_{{\text{b}}}} - 2C} \right)\tanh \left( {\frac{t}{{{{t}_{{{\text{ac}}}}}}}} \right) - \frac{2}{{{{t}_{{{\text{ac}}}}}}}{{u}_{{\text{b}}}}}}{{\left( {2A{{u}_{{\text{b}}}} + B} \right)\tanh \left( {\frac{t}{{{{t}_{{{\text{ac}}}}}}}} \right) + \frac{2}{{{{t}_{{{\text{ac}}}}}}}}},$При t = 0 vb(0) = –ub, при t → ∞
(20)
$\mathop {{{v}_{{\text{b}}}}\left( t \right)}\limits_{t \to \infty } \to \frac{{\left( {B - A} \right){{u}_{{\text{b}}}} - 2C}}{{\left( {B + A} \right) + 2A{{u}_{{\text{b}}}}}}.$Используя соотношения $\frac{{4AC}}{{{{B}^{2}}}} = \frac{{\operatorname{Ar} }}{{225}},$ Ar = $\frac{{g{{d}^{3}}}}{{{{\nu }^{2}}}}\frac{{{{\rho }_{{\text{p}}}} - \rho }}{\rho },$ $\frac{2}{{{{t}_{{{\text{ac}}}}}}} = B\sqrt {1 + \frac{{\operatorname{Ar} }}{{225}}} ,$ $B = 18\frac{d}{\nu }\frac{C}{{\operatorname{Ar} }},$ C = $\frac{{{{\nu }^{2}}}}{{{{d}^{3}}}}\frac{\rho }{{{{\rho }_{{\text{p}}}}}}\operatorname{Ar} ,$ $2\frac{A}{B}{{u}_{{\text{b}}}} = \frac{{{{{\operatorname{Re} }}_{{\text{b}}}}}}{{25}},$ ${{\operatorname{Re} }_{{\text{b}}}} = \frac{{d{{u}_{{\text{b}}}}}}{\nu },$ $\operatorname{Re} = \frac{{du}}{\nu },$ Reb = UbRe, можно преобразовать (19) и привести к виду
(21)
${{v}_{{\text{b}}}}\left( t \right) = - {{u}_{{\text{b}}}}\frac{{1 - \frac{{\left( {1 - \frac{{\operatorname{Ar} }}{{9{{{\operatorname{Re} }}_{{\text{b}}}}}}} \right)}}{{\sqrt {1 + {{\operatorname{Ar} } \mathord{\left/ {\vphantom {{\operatorname{Ar} } {225}}} \right. \kern-0em} {225}}} }}\tanh \left( {\frac{t}{{{{t}_{{{\text{ac}}}}}}}} \right)}}{{1 + \frac{{1 + {{{{{\operatorname{Re} }}_{{\text{b}}}}} \mathord{\left/ {\vphantom {{{{{\operatorname{Re} }}_{{\text{b}}}}} {25}}} \right. \kern-0em} {25}}}}{{\sqrt {1 + {{\operatorname{Ar} } \mathord{\left/ {\vphantom {{\operatorname{Ar} } {225}}} \right. \kern-0em} {225}}} }}\tanh \left( {\frac{t}{{{{t}_{{{\text{ac}}}}}}}} \right)}}.$При t = 0 vb(0) = –ub, при t → ∞ должно выполняться
(22)
$\mathop {{{v}_{{\text{b}}}}\left( t \right)}\limits_{t \to \infty } = - {{u}_{{\text{b}}}}\frac{{1 - \frac{{\left( {1 - \frac{{\operatorname{Ar} }}{{9{{{\operatorname{Re} }}_{{\text{b}}}}}}} \right)}}{{\sqrt {1 + {{\operatorname{Ar} } \mathord{\left/ {\vphantom {{\operatorname{Ar} } {225}}} \right. \kern-0em} {225}}} }}}}{{1 + \frac{{1 + {{{{{\operatorname{Re} }}_{{\text{b}}}}} \mathord{\left/ {\vphantom {{{{{\operatorname{Re} }}_{{\text{b}}}}} {25}}} \right. \kern-0em} {25}}}}{{\sqrt {1 + {{\operatorname{Ar} } \mathord{\left/ {\vphantom {{\operatorname{Ar} } {225}}} \right. \kern-0em} {225}}} }}}} = - {{u}_{{\text{t}}}}.$Пусть ub = ut. Тогда Reb = Ret, ${{\operatorname{Re} }_{{\text{t}}}} = \frac{{d{{u}_{{\text{t}}}}}}{\nu }$ и (22) превращается в уравнение для определения Ret. Его решение
(23)
${{\operatorname{Re} }_{{\text{t}}}} = 25\left( {\sqrt {1 + \frac{{\operatorname{Ar} }}{{225}}} - 1} \right).$Пределы (23) $\mathop {{{{\operatorname{Re} }}_{{\text{t}}}}}\limits_{\operatorname{Ar} \to 0} \to \frac{{\operatorname{Ar} }}{{18}}$ и $\mathop {{{{\operatorname{Re} }}_{{\text{t}}}}}\limits_{\operatorname{Ar} \to \infty } \to \frac{5}{3}\sqrt {\operatorname{Ar} } $ = = $1.66\sqrt {\operatorname{Ar} } ,$ равно как и промежуточные значения, согласуются с другими известными формулами для скорости витания (например, [20]). Преимуществом этого соотношения в данной работе является его общее с другими выражениями происхождение. Это упрощает выкладки и позволяет получить более простые и компактные конечные формулы. Подставляя в (21) следующие из (22) и (23) соотношения $\frac{{{{{\operatorname{Re} }}_{{\text{t}}}}}}{{25}} + 1$ = $\sqrt {1 + \frac{{\operatorname{Ar} }}{{225}}} $ и $\frac{{\operatorname{Ar} }}{{9{{{\operatorname{Re} }}_{{\text{t}}}}}}$ = $2 + \frac{{{{{\operatorname{Re} }}_{{\text{t}}}}}}{{25}}$ или $\frac{{25\operatorname{Ar} }}{9}$ = ${{\operatorname{Re} }_{{\text{t}}}}\left( {50 + {{{\operatorname{Re} }}_{{\text{t}}}}} \right),$ окончательно получим
(24)
$\begin{gathered} {{v}_{{\text{b}}}}\left( t \right) = - {{u}_{{\text{b}}}} \times \\ \times \,\,\frac{{\left( {\frac{{{{u}_{{\text{t}}}}}}{{{{u}_{{\text{b}}}}}}\frac{{50 + {{{\operatorname{Re} }}_{{\text{t}}}}}}{{25 + {{{\operatorname{Re} }}_{{\text{t}}}}}} - \frac{{25}}{{25 + {{{\operatorname{Re} }}_{{\text{t}}}}}}} \right)\tanh \left( {\frac{t}{{{{t}_{{{\text{ac}}}}}}}} \right) + 1}}{{\frac{{{{{\operatorname{Re} }}_{{\text{b}}}} + 25}}{{{{{\operatorname{Re} }}_{{\text{t}}}} + 25}}\tanh \left( {\frac{t}{{{{t}_{{{\text{ac}}}}}}}} \right) + 1}}, \\ \end{gathered} $(25)
${{t}_{{{\text{ac}}}}} = \frac{{{{u}_{{\text{t}}}}}}{g}\frac{{{{\rho }_{{\text{p}}}}}}{{{{\rho }_{{\text{p}}}} - \rho }}\frac{{{{{\operatorname{Re} }}_{{\text{t}}}} + 50}}{{{{{\operatorname{Re} }}_{{\text{t}}}} + 25}}$– характерное время разгона, зависящее только от свойств частиц и газа. Пределы (24) по-прежнему удовлетворяют начальному условию и условию установившегося движения.
Продифференцировав (24), можно получить, после преобразований, формулу для ускорения частицы
(26)
$w\left( t \right) = \frac{{{{w}_{0}}}}{{{{{\left[ {\left( {\frac{{{{{\operatorname{Re} }}_{{\text{b}}}} + 25}}{{{{{\operatorname{Re} }}_{{\text{t}}}} + 25}}\tanh \frac{t}{{{{t}_{{{\text{ac}}}}}}} + 1} \right)\cosh \frac{t}{{{{t}_{{{\text{ac}}}}}}}} \right]}}^{2}}}},$где
(27)
${{w}_{0}} = \frac{9}{{25}}g\frac{{{{\rho }_{{\text{p}}}} - \rho }}{{{{\rho }_{{\text{p}}}}}}\frac{{50 + {{{\operatorname{Re} }}_{{\text{b}}}} + {{{\operatorname{Re} }}_{{\text{t}}}}}}{{\operatorname{Ar} }}\left( {{{{\operatorname{Re} }}_{{\text{b}}}} - {{{\operatorname{Re} }}_{{\text{t}}}}} \right)$– начальное ускорение.
В момент времени t = 0 ускорение максимально (w(0) = w0), при t → ∞ w(t) → 0.
Среднее за время T ускорение определяется выражением
(28)
$\bar {w} = \frac{1}{T}\int\limits_0^T {w\left( t \right)dt} = {{w}_{0}}\frac{{{{t}_{{{\text{ac}}}}}}}{T}\frac{{\tanh \frac{T}{{{{t}_{{{\text{ac}}}}}}}}}{{\frac{{{{{\operatorname{Re} }}_{{\text{b}}}} + 25}}{{{{{\operatorname{Re} }}_{{\text{t}}}} + 25}}\tanh \frac{T}{{{{t}_{{{\text{ac}}}}}}} + 1}}.$Его пределы $\bar {w}\mathop \to \limits_{T \to 0} {{w}_{0}}$ и $\bar {w}\mathop \to \limits_{T \to \infty } 0$ совпадают с пределами мгновенного ускорения.
На рис. 3 и 4 представлены зависимости скорости и ускорения разгоняемой частицы от времени.
Рис. 3.
Зависимость отношения скорости разгоняемой в воздухе частицы к скорости витания от безразмерного времени: 1 – ub/ut = 1.1; 2 – 10; 3 – 100. Сплошные линии – 20°C, штриховые – 1000°C.
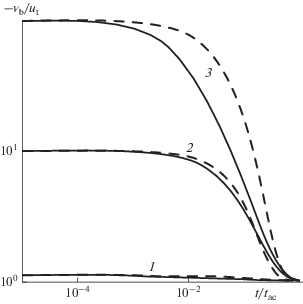
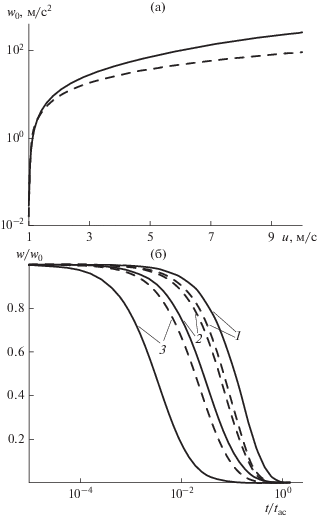
Рис. 4.
Зависимость начального ускорения частицы от скорости газа (а) и отношения w(t)/w0 от безразмерного времени (б). Обозначения те же, что и на рис. 3.
В расчетах используются типичные для топок ЦКС исходные данные: средний размер частиц 0.2 мм при минимальном 0.1 мм и максимальном 0.3 мм [1], их плотность от 1800 до 2600 кг/м3 [1], ожижающий агент – холодный (20°С) либо горячий (1000°С) воздух. Число Архимеда при этом изменяется от 2 до 3000.
Поскольку и скорость, и ускорение зависят от величин ub и ut [формулы (24), (26) и (27)], для уменьшения числа варьируемых переменных в качестве параметра используется их отношение ub/ut. Время разгона во всех вариантах расчета примерно одинаково и равно tac. Существенно различается процесс на промежуточных стадиях – в холодном газе частица движется медленнее, чем в горячем (рис. 3). На рис. 4а представлена зависимость w0 от скорости газа. В горячих условиях при одинаковых значениях отношения ub/ut начальное ускорение ниже (по-видимому, благодаря тому, что с ростом температуры уменьшается скорость витания). Зависимость w(t)/w0 от времени представлена на рис. 4б. Как видно, разгон частиц происходит в пределах характерного времени tac. При малом отношении скоростей ub/ut величина w(t)/w0 в один и тот же момент времени в холодных условиях больше, чем в горячих. С ростом параметра ub/ut уже при высокой температуре при одинаковом t w(t)/w0 становится больше, чем в нормальных условиях, и это различие растет вместе с ub/ut.
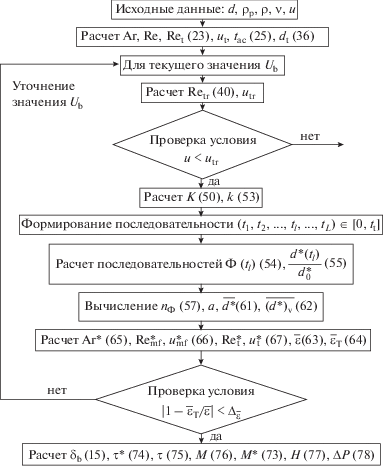
ВЫБОР МЕТОДА РАСЧЕТА ПАРАМЕТРОВ ПРИДОННОГО СЛОЯ
При известной функции w(t) уравнение движения (16) можно рассматривать как условие баланса действующих на частицу сил в момент времени t. Рассмотрим это условие в лабораторной системе координат. Здесь увлекающая частицу сила сопротивления (17) может быть представлена в виде
(29)
$\begin{gathered} {{f}_{{{\text{res}}}}}\left( t \right) = 3\pi \nu \rho d\left( {{{u}_{{\text{b}}}} - v\left( t \right)} \right) + \\ + \,\,\frac{3}{{50}}\rho {{d}^{2}}{{\left( {{{u}_{{\text{b}}}} - v\left( t \right)} \right)}^{2}}. \\ \end{gathered} $С учетом этого соотношения уравнение (16) после преобразований записывается как
(30)
$\begin{gathered} w\left( t \right) = - g + g\frac{\rho }{{{{\rho }_{{\text{p}}}}}} + 18\frac{\rho }{{{{\rho }_{{\text{p}}}}}}\frac{{{{\nu }^{2}}}}{{{{d}^{3}}}} \times \\ \times \,\,\left( {{{{\operatorname{Re} }}_{{\text{v}}}}\left( t \right) + \frac{{{{{\left( {{{{\operatorname{Re} }}_{{\text{v}}}}\left( t \right)} \right)}}^{2}}}}{{50}}} \right), \\ \end{gathered} $После приведения (30) к безразмерной форме получается
(31)
$\begin{gathered} \frac{{g{{d}^{3}}}}{{{{\nu }^{2}}}}\frac{{{{\rho }_{{\text{p}}}} - \rho }}{\rho }\left( {1 + \frac{{w\left( t \right)}}{g}\frac{{{{\rho }_{{\text{p}}}}}}{{{{\rho }_{{\text{p}}}} - \rho }}} \right) = \\ = 18\left( {{{{\operatorname{Re} }}_{{\text{v}}}}\left( t \right) + \frac{{{{{\left( {{{{\operatorname{Re} }}_{{\text{v}}}}\left( t \right)} \right)}}^{2}}}}{{50}}} \right). \\ \end{gathered} $Справа – критериальная запись силы сопротивления. Левую часть равенства (31) можно представить как модифицированный критерий Архимеда двояким образом.
Первый вариант:
(32)
$\operatorname{Ar} _{g}^{*}\left( t \right) = \frac{{g{\text{*}}\left( t \right){{d}^{3}}}}{{{{\nu }^{2}}}}\frac{{{{\rho }_{{\text{p}}}} - \rho }}{\rho },$Такая форма записи непосредственно отражает точку зрения об обеспечивающем формирование придонного слоя совместном противодействии сил тяжести и инерции силе гидродинамического сопротивления. Частица в этом случае движется в переменном внешнем поле, зависящем от ее ускорения. Построить методику расчета параметров ПС, оставаясь в рамках подобного представления, не удалось.
Второй вариант:
(33)
$\operatorname{Ar} *\left( t \right) = \frac{{g{{{\left( {d{\text{*}}\left( t \right)} \right)}}^{3}}}}{{{{\nu }^{2}}}}\frac{{{{\rho }_{{\text{p}}}} - \rho }}{\rho },$(34)
$\begin{gathered} d_{0}^{*} = d{{\left( {1 + \frac{{{{w}_{0}}}}{g}\frac{{{{\rho }_{{\text{p}}}}}}{{{{\rho }_{{\text{p}}}} - \rho }}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} = d \times \\ \times \,\,{{\left( {1 + \frac{9}{{25}}\frac{{50 + {{U}_{{\text{b}}}}\operatorname{Re} \,\, + \,\,{{{\operatorname{Re} }}_{{\text{t}}}}}}{{\operatorname{Ar} }}\left( {{{U}_{{\text{b}}}}\operatorname{Re} \, - {{{\operatorname{Re} }}_{{\text{t}}}}} \right)} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} \\ \end{gathered} $в начальный момент времени до величины
соответствующей установившемуся движению. Придонный слой, при таком косвенном учете влияния сил инерции, представляет собой идеально перемешанную систему сжимающихся частиц. Для расчета параметров ПС и условий его существования можно в этом случае использовать методику, разработанную в [21, 22].
УСЛОВИЯ СУЩЕСТВОВАНИЯ ПРИДОННОГО СЛОЯ
Следуя [21], определим для заданной средней скорости газа u диаметр витания
(36)
${{d}_{{\text{t}}}} = 0.18d\frac{{{{{\operatorname{Re} }}^{2}}}}{{\operatorname{Ar} }}\left( {1 + \sqrt {1 + \frac{{5000}}{9}\frac{{\operatorname{Ar} }}{{{{{\operatorname{Re} }}^{3}}}}} } \right).$Формула (36) представляет собой решение (22) относительно dt при заданном u и определяет наименьшее значение диаметра ожижаемых при такой скорости газа частиц. Рассмотрим, как изменяются начальный эффективный диаметр (34) и диаметр витания (36) с ростом средней скорости газа.
На рис. 5 представлены зависимости $d_{0}^{*}$ и dt от u. Так как dt определяет наименьший допустимый размер частиц, для существования слоя необходимо выполнение неравенства $d_{0}^{*} > {{d}_{{\text{t}}}}.$ Из рис. 5 видно, что, поскольку $d_{0}^{*}$ зависит от Ub (34), это неравенство будет выполняться, если разгон частиц начнется до того, как средняя скорость газа в топке достигнет величины ut. Следовательно, первым необходимым, но недостаточным, условием образования и существования придонного слоя является его неоднородность, как и неоднородность кипящего слоя, из которого формируется ПС. Вторым необходимым условием является возникновение циркуляционного потока (что возможно при условии u > ut) и связанной с ним реактивной силы.
Рис. 5.
Зависимость максимального, минимального начального диаметра и диаметра витания от средней скорости газа в топке: Ub = 3, $\bar {\varepsilon } = 0.6$, ρp = 2600 кг/м3, dmin = 0.1 мм; 1 – $d_{{0\min }}^{*};$ 2 – $d_{{0\max }}^{*};$ 3 – dt; dmax = 1.2dmin (а, в); dmax = 3dmin (б, г); ожижающий агент – воздух при 20°С (а, б) и 1000°С (в, г).
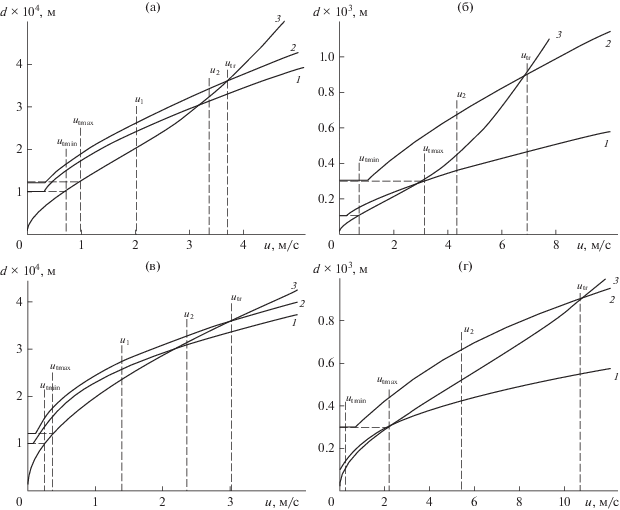
Пусть ut min < u < ut max. Для мелких частиц оба необходимых условия существования придонного слоя уже выполнены, а для более крупных – нет. В этом случае дисперсная среда в зоне ускорения представляет собой смесь кипящего слоя из крупных фракций и придонного слоя мелочи. Внешне это никак качественно не проявляется из-за структурного подобия КС и ПС. Можно лишь констатировать, что полное замещение кипящего слоя придонным произойдет при условии u > ut max. При этом $d_{0}^{*} > {{d}_{{\text{t}}}} > d,$ из чего следует:
в придонном слое возможна только начальная фаза разгона частицы, длительность которой сокращается по мере роста скорости газа;
в формировании придонного слоя участвуют только те фракции, для которых выполнено условие $d_{0}^{*} > {{d}_{{\text{t}}}},$ и их доля с ростом скорости газа уменьшается.
Действие обоих указанных факторов (первого за счет сокращения времени пребывания частиц в слое, второго – за счет уменьшения числа частиц в нем) приводит к уменьшению массы придонного слоя по мере роста скорости газа. Этот механизм работает по-разному в зависимости от дисперсности зернистого материала. В слое узкого фракционного состава при незначительном превышении скорости u над ut в образовании ПС участвуют все частицы.
При u1 > ut max:
(37)
${{d}_{{\min }}} < {{d}_{{\max }}} < {{d}_{{\text{t}}}} < d_{{0{\text{ min}}}}^{*} < d_{{0{\text{ max}}}}^{*}.$Дальнейший рост скорости газа приводит к сокращению доли частиц, участвующих в образовании придонного слоя (рис. 5а, 5в).
При u2 > u1 > ut max:
(38)
${{d}_{{\min }}} < {{d}_{{\max }}} < d_{{0{\text{ min}}}}^{*} < {{d}_{{\text{t}}}} < d_{{0{\text{ max}}}}^{*}.$В полифракционной дисперсной среде всегда выполняется последнее неравенство – действуют оба фактора, определяющие массу и размер ПС (рис. 5б, 5г).
С увеличением скорости фильтрации придонный слой постепенно уменьшается по размеру и массе и, наконец, исчезает при таком значении u, когда
(39)
${{\left. {d_{{0{\text{ max}}}}^{*}} \right|}_{{u = {{u}_{{{\text{tr}}}}}}}} = {{\left. {{{d}_{{\text{t}}}}} \right|}_{{u = {{u}_{{{\text{tr}}}}}}}}.$Соотношение (39) представляет собой определение транспортной скорости. После подстановки выражений (34) и (36) для $d_{0}^{*}$ и dt и преобразований из (39) получается уравнение относительно ${{\operatorname{Re} }_{{{\text{tr}}}}} = \frac{{d{{u}_{{{\text{tr}}}}}}}{\nu }$:
(40)
$\begin{gathered} {{\left( {1 + \frac{9}{{25}}\frac{{50 + {{U}_{{\text{b}}}}{{{\operatorname{Re} }}_{{{\text{tr}}}}} + {{{\operatorname{Re} }}_{{\text{t}}}}}}{{\operatorname{Ar} }}\left( {{{U}_{{\text{b}}}}{{{\operatorname{Re} }}_{{{\text{tr}}}}} - {{{\operatorname{Re} }}_{{\text{t}}}}} \right)} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} - \\ - \,\,0.18\frac{{\operatorname{Re} _{{{\text{tr}}}}^{2}}}{{\operatorname{Ar} }}\left( {1 + \sqrt {1 + \frac{{5000}}{9}\frac{{\operatorname{Ar} }}{{\operatorname{Re} _{{{\text{tr}}}}^{3}}}} } \right) = 0. \\ \end{gathered} $Здесь выполнена подстановка u = utr и опущен индекс max для сокращения записи и с учетом того, что в дальнейшем рассматривается монодисперсная система. Как видно, Retr зависит только от степени неоднородности газового потока Ub и числа Архимеда Ar. При постоянном Ub решение уравнения (40) может быть получено в широком диапазоне значений Ar. Оно аппроксимируется выражениями
(41)
${{\operatorname{Re} }_{{{\text{tr}}}}} = \left\{ \begin{gathered} \frac{{{{{\operatorname{Ar} }}^{{1.025}}}}}{{1.71 + 0.32{{{\operatorname{Ar} }}^{{0.53}}}}},\,\,\,\,{{U}_{{\text{b}}}} = 3 \hfill \\ \frac{{{{{\operatorname{Ar} }}^{{1.02}}}}}{{4 + 0.383{{{\operatorname{Ar} }}^{{0.526}}}}},\,\,\,\,{{U}_{{\text{b}}}} = 2 \hfill \\ \end{gathered} \right.$со средней погрешностью 2.8 и 2.7% соответственно. Зависимости (41) представлены на рис. 6 вместе с формулой Тодеса [20] для скорости витания
(42)
${{\operatorname{Re} }_{{\text{t}}}} = \frac{{\operatorname{Ar} }}{{18 + 0.61{{{\operatorname{Ar} }}^{{0.5}}}}}$Рис. 6.
Зависимость безразмерной транспортной скорости и безразмерной скорости витания от критерия Архимеда: 1 – Ret(Ar); 2, 3 – Retr(Ar, Ub); 2 – Ub = 2; 3 – 3; 4 – зависимость (43) [3].
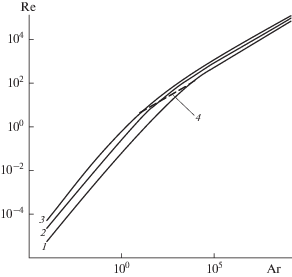
и обработкой опытных данных для транспортной скорости [3]
Из формул (41) и рис. 6 видно, что по мере уменьшения степени неоднородности газового потока Ub транспортная скорость стремится к скорости витания (42). Можно показать, что Ret является решением уравнения (40) при Ub = 1. Для этого преобразуем (40), используя те же соотношения, что и при выводе (24), следующим образом:
(44)
$\begin{gathered} {{\left( {1 + \frac{{50 + {{U}_{{\text{b}}}}{{{\operatorname{Re} }}_{{{\text{tr}}}}} + {{{\operatorname{Re} }}_{{\text{t}}}}}}{{50 + {{{\operatorname{Re} }}_{{\text{t}}}}}}\frac{{{{U}_{{\text{b}}}}{{{\operatorname{Re} }}_{{{\text{tr}}}}} - {{{\operatorname{Re} }}_{{\text{t}}}}}}{{{{{\operatorname{Re} }}_{{\text{t}}}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} - \\ - \,\,0.5\frac{{\operatorname{Re} _{{{\text{tr}}}}^{2}}}{{R{{e}_{{\text{t}}}}\left( {50 + {{{\operatorname{Re} }}_{{\text{t}}}}} \right)}} \times \\ \times \,\,\left( {1 + \sqrt {1 + 200\frac{{R{{e}_{{\text{t}}}}\left( {50 + {{{\operatorname{Re} }}_{{\text{t}}}}} \right)}}{{\operatorname{Re} _{{{\text{tr}}}}^{3}}}} } \right) = 0. \\ \end{gathered} $Подстановка Ub = 1 и Retr = Ret в (44) обращает его в тождество 0 = 0. Таким образом, для однородного слоя транспортная скорость и скорость витания совпадают.
Кривая, отображающая эмпирическую формулу (43), располагается в значительно более узком диапазоне чисел Архимеда, последовательно пересекает семейство линий, представляющих зависимости (41), и заканчивается на кривой Ret(Ar). Столь сильное отличие обусловлено тем, что с ростом скорости фильтрации величина Ub изменяется, а не остается постоянной, как это принято при решении уравнения (40). Зависимость Retr(Ar) при переменном Ub будет рассмотрена далее.
РАСЧЕТ ПАРАМЕТРОВ ПРИДОННОГО СЛОЯ
Дальнейшие оценки проводятся в предположении монодисперсного состава двухфазной среды. Это позволяет уменьшить объем необходимых исходных данных и упростить выкладки. Фиксированному значению истинного диаметра d соответствует точно определенная величина эффективного начального диаметра $d_{0}^{*},$ а распределение попадающих в слой частиц по эффективному диаметру d* имеет вид
В этом случае для полного описания ансамбля сжимающихся частиц, согласно [21, 22], необходимы следующие параметры:
определяющий диапазон допустимых размеров частиц в слое по отношению к $d_{0}^{*},$ легко вычисляется с использованием формул (34) и (36);
(47)
${{v}_{{\text{c}}}}\left( {d{\text{*}}} \right) = \left( {\frac{{d\left( {d{\text{*}}\left( t \right)} \right)}}{{dt}}} \right)\left( {d{\text{*}}} \right)$– скорость сжатия, представленная как функция текущего эффективного диаметра d* (параметры стационарной системы не могут явно зависеть от времени). Вычисление зависимых величин становится особенно простым, если (47) удается представить в виде степенной функции
(48)
${{v}_{{\text{c}}}}\left( {d{\text{*}}} \right) = - k{{\left( {\frac{{d{\text{*}}}}{{d_{0}^{*}}}} \right)}^{a}}.$Оказалось возможным с удовлетворительной точностью аппроксимировать точное выражение скорости сжатия зависимостью вида (48). Чтобы выполнить это, сначала запишем, используя соотношения (26) и (34), выражение для текущего эффективного диаметра как функции времени:
(49)
$\begin{gathered} d{\text{*}}\left( t \right) = \\ = d{{\left( {1 + \frac{K}{{{{{\left( {\frac{{{{U}_{{\text{b}}}}\operatorname{Re} + 25}}{{{{{\operatorname{Re} }}_{{\text{t}}}} + 25}}\tanh \frac{t}{{{{t}_{{{\text{ac}}}}}}} + 1} \right)}}^{2}}{{{\cosh }}^{2}}\frac{t}{{{{t}_{{{\text{ac}}}}}}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}, \\ \end{gathered} $(50)
$K = \frac{9}{{25}}\frac{{50 + {{U}_{{\text{b}}}}\operatorname{Re} + {{{\operatorname{Re} }}_{{\text{t}}}}}}{{\operatorname{Ar} }}\left( {{{U}_{{\text{b}}}}\operatorname{Re} - {{{\operatorname{Re} }}_{{\text{t}}}}} \right).$С учетом последнего соотношения формула для начального эффективного диаметра принимает вид
(51)
$d_{0}^{*} = d{{\left( {1 + K} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}.$Продифференцировав (49) по времени, выполнив группировку и ряд преобразований, можно получить следующую формулу для скорости сжатия как функции времени:
(52)
${{v}_{{\text{c}}}}\left( t \right) = - k\frac{{\Phi \left( t \right)}}{{{{{\left( {\frac{{d{\text{*}}\left( t \right)}}{{d_{0}^{*}}}} \right)}}^{2}}}},$(53)
$k = \frac{2}{3}\frac{K}{{{{{\left( {1 + K} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}\frac{{{{U}_{{\text{b}}}}\operatorname{Re} + 25}}{{{{{\operatorname{Re} }}_{{\text{t}}}} + 25}}\frac{d}{{{{t}_{{{\text{ac}}}}}}}$– модуль максимальной (начальной) скорости сжатия, а функция Φ(t) имеет вид
(54)
$\begin{gathered} \Phi \left( t \right) = \\ = \frac{{1 + \left( {\tanh \frac{t}{{{{t}_{{{\text{ac}}}}}}} + \frac{{{{{\operatorname{Re} }}_{{\text{t}}}} + 25}}{{{{U}_{{\text{b}}}}\operatorname{Re} + 25}}} \right)\sinh \frac{t}{{{{t}_{{{\text{ac}}}}}}}\cosh \frac{t}{{{{t}_{{{\text{ac}}}}}}}}}{{{{{\left( {\frac{{{{U}_{{\text{b}}}}\operatorname{Re} + 25}}{{{{{\operatorname{Re} }}_{{\text{t}}}} + 25}}\tanh \frac{t}{{{{t}_{{{\text{ac}}}}}}} + 1} \right)}}^{3}}{{{\cosh }}^{4}}\frac{t}{{{{t}_{{{\text{ac}}}}}}}}}. \\ \end{gathered} $Сравним эту функцию с отношением текущего и начального эффективных диаметров
(55)
$\frac{{d{\text{*}}\left( t \right)}}{{d_{0}^{*}}} = {{\left( {{{\left( {1 + \frac{K}{{{{{\left( {\frac{{{{U}_{{\text{b}}}}\operatorname{Re} \, + 25}}{{{{{\operatorname{Re} }}_{{\text{t}}}} + 25}}\tanh \frac{t}{{{{t}_{{{\text{ac}}}}}}} + 1} \right)}}^{2}}{{{\cosh }}^{2}}\frac{t}{{{{t}_{{{\text{ac}}}}}}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {1 + \frac{K}{{{{{\left( {\frac{{{{U}_{{\text{b}}}}\operatorname{Re} \, + 25}}{{{{{\operatorname{Re} }}_{{\text{t}}}} + 25}}\tanh \frac{t}{{{{t}_{{{\text{ac}}}}}}} + 1} \right)}}^{2}}{{{\cosh }}^{2}}\frac{t}{{{{t}_{{{\text{ac}}}}}}}}}} \right)} {\left( {1 + K} \right)}}} \right. \kern-0em} {\left( {1 + K} \right)}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}.$В начальный момент времени их значения одинаковы: Φ(0) = 1 и $\frac{{d{\text{*}}\left( 0 \right)}}{{d_{0}^{*}}} = 1.$ В пределе при t → → ∞ $\Phi \left( t \right)\mathop \to \limits_{t \to \infty } 0$ и $\frac{{d{\text{*}}\left( t \right)}}{{d_{0}^{*}}}\mathop \to \limits_{t \to \infty } \frac{d}{{d_{0}^{*}}}.$ Обе функции – монотонно убывающие и, после сжатия частицы за время tt до размера dt, принимают значения 0 < < Φ(tt) < 1 и $\frac{{d{\text{*}}\left( {{{t}_{{\text{t}}}}} \right)}}{{d_{0}^{*}}} = \frac{{{{d}_{{\text{t}}}}}}{{d_{0}^{*}}}.$ Сходный характер изменения Φ(t) и $\frac{{d{\text{*}}\left( t \right)}}{{d_{0}^{*}}}$ со временем дает основание для поиска аппроксимации вида
(56)
$\Phi \left( t \right) = {{\left( {\frac{{d{\text{*}}\left( t \right)}}{{d_{0}^{*}}}} \right)}^{{{{n}_{\Phi }}}}}.$Для этого рассмотрим последовательность моментов времени t1, t2,…,tl,…,tL, равномерно распределенных на отрезке [0, tt], причем t1 < t2 < …< < tl < … < tL ≤ tt. Далее, варьируя показатель степени nΦ, можно определить
(57)
$\mathop {\min }\limits_{{{n}_{\Phi }}} {{\sum\limits_{l = 1}^L {\left( {\Phi \left( {{{t}_{l}}} \right) - {{{\left( {\frac{{d{\text{*}}\left( {{{t}_{l}}} \right)}}{{d_{0}^{*}}}} \right)}}^{{{{n}_{\Phi }}}}}} \right)} }^{2}}.$Погрешность аппроксимации
(58)
${{\Delta }_{\Phi }} = \frac{1}{L}\sum\limits_{l = 1}^L {\left| {1 - {{{{{\left( {\frac{{d{\text{*}}\left( {{{t}_{l}}} \right)}}{{d_{0}^{*}}}} \right)}}^{{{{n}_{\Phi }}}}}} \mathord{\left/ {\vphantom {{{{{\left( {\frac{{d{\text{*}}\left( {{{t}_{l}}} \right)}}{{d_{0}^{*}}}} \right)}}^{{{{n}_{\Phi }}}}}} {\Phi \left( {{{t}_{l}}} \right)}}} \right. \kern-0em} {\Phi \left( {{{t}_{l}}} \right)}}} \right|} .$Дальнейшие расчеты показали, что наибольшая погрешность аппроксимации составляет ~7% при скорости фильтрации, близкой к скорости витания, и быстро уменьшается по мере ее роста. Построение аппроксимирующей функции (56) позволяет исключить из рассмотрения время в качестве аргумента и, после подстановки (56) в (52), записать следующее выражение для скорости сжатия:
(59)
${{v}_{{\text{c}}}}\left( {\frac{{d{\text{*}}}}{{d_{0}^{*}}}} \right) = - k{{\left( {\frac{{d{\text{*}}}}{{d_{0}^{*}}}} \right)}^{a}},$Теперь можно записать следующие функции, характеризующие придонный слой:
распределение частиц по эффективному диаметру
(60)
$p\left( {d{\text{*}}} \right) = \left\{ \begin{gathered} \frac{{4 - a}}{{d_{0}^{*}\left( {1 - {{\alpha }^{{4 - a}}}} \right)}}{{\left( {\frac{{d{\text{*}}}}{{d_{0}^{*}}}} \right)}^{{3 - a}}},\,\,\,\,a \ne 4 \hfill \\ \frac{1}{{d{\text{*}}\ln \left( {{1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0em} \alpha }} \right)}},\,\,\,\,a = 4 \hfill \\ \end{gathered} \right.;$средний эффективный диаметр частиц
(61)
$\overline {d{\text{*}}} = d_{0}^{*}\left\{ \begin{gathered} \frac{{4 - a}}{{5 - a}}\frac{{1 - {{\alpha }^{{5 - a}}}}}{{1 - {{\alpha }^{{4 - a}}}}},\,\,\,\,a \ne 4,\,\,\,\,a \ne 5 \hfill \\ \frac{{1 - \alpha }}{{\ln \left( {{1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0em} \alpha }} \right)}},\,\,\,\,a = 4 \hfill \\ \frac{\alpha }{{1 - \alpha }}\ln \left( {\frac{1}{\alpha }} \right),\,\,\,\,a = 5 \hfill \\ \end{gathered} \right.;$среднеобъемный эффективный диаметр частиц
(62)
$\begin{gathered} {{\left( {\overline {{{{\left( {d{\text{*}}} \right)}}_{{\text{v}}}}} } \right)}^{3}} = {{\left( {d_{0}^{*}} \right)}^{3}} \times \\ \times \,\,\left\{ \begin{gathered} \frac{{4 - a}}{{7 - a}}\frac{{1 - {{\alpha }^{{7 - a}}}}}{{1 - {{\alpha }^{{4 - a}}}}},\,\,\,\,a \ne 4,\,\,\,\,a < 7 \hfill \\ \frac{{1 - {{\alpha }^{3}}}}{{3\ln \left( {{1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0em} \alpha }} \right)}},\,\,\,\,a = 4 \hfill \\ \end{gathered} \right.. \\ \end{gathered} $Функции (60)–(62) определяются коэффициентами a, k и α, которые, в свою очередь, зависят только от одного, специфичного для придонного слоя, параметра – степени неоднородности газового потока Ub. Оказалось возможным однозначно определить эту величину, сравнивая два выражения для средней порозности ПС (значение $\bar {\varepsilon }$ не должно зависеть от способа его определения):
полученное преобразованием формулы (13)
(63)
$\bar {\varepsilon } = \left( {1 - {{\varepsilon }_{0}}} \right)\frac{{1 - {{u_{{{\text{mf}}}}^{*}} \mathord{\left/ {\vphantom {{u_{{{\text{mf}}}}^{*}} u}} \right. \kern-0em} u}}}{{{{U}_{{\text{b}}}} - {{u_{{{\text{mf}}}}^{*}} \mathord{\left/ {\vphantom {{u_{{{\text{mf}}}}^{*}} u}} \right. \kern-0em} u}}} + {{\varepsilon }_{0}}$и формулы Тодеса [20]
(64)
${{\bar {\varepsilon }}_{{\text{T}}}} = {{\varepsilon }_{0}}{{\left( {\frac{{\operatorname{Re} {\text{*}} + 0.02{{{\left( {\operatorname{Re} *} \right)}}^{2}}}}{{\operatorname{Re} _{{{\text{mf}}}}^{*}\, + 0.02{{{\left( {\operatorname{Re} _{{{\text{mf}}}}^{*}} \right)}}^{2}}}}} \right)}^{{0.1}}},$(65)
$\operatorname{Ar} {\text{*}} = \frac{{g{{{\left( {\overline {d{\text{*}}} } \right)}}^{3}}}}{{{{\nu }^{2}}}}\frac{{{{\rho }_{{\text{p}}}} - \rho }}{\rho },$(66)
$\operatorname{Re} _{{{\text{mf}}}}^{*} = \frac{{\operatorname{Ar} *}}{{1400 + 5.22\sqrt {\operatorname{Ar} *} }},\,\,\,\,u_{{{\text{mf}}}}^{*} = \frac{{\operatorname{Re} _{{{\text{mf}}}}^{*}\nu }}{{\overline {d{\text{*}}} }},$(67)
$\operatorname{Re} _{{\text{t}}}^{*} = \frac{{\operatorname{Ar} *}}{{18 + 0.61\sqrt {\operatorname{Ar} *} }},\,\,\,\,u_{{\text{t}}}^{*} = \frac{{\operatorname{Re} _{{\text{t}}}^{*}\nu }}{{\overline {d{\text{*}}} }}.$Значение Ub уточняется вплоть до достижения заданной величины погрешности
(68)
${{\Delta }_{{\bar {\varepsilon }}}} = \left| {1 - \frac{{{{{\bar {\varepsilon }}}_{{\text{T}}}}}}{{\bar {\varepsilon }}}} \right|.$Рассмотрим подробно участвующие в формировании придонного слоя потоки уноса F2 и его возврата F0. Из (3) следует, что в стационарном ПС из N частиц постоянной массы m эти потоки равны:
При скорости фильтрации, превышающей скорость витания, dt больше d и слой покидают отчасти разогнанные частицы с эффективным диаметром d* = dt > d, кажущиеся объем и масса которых увеличена в (dt/d)3 раз. Из них формируется эффективный поток уноса
(70)
$F_{2}^{*} = m{\text{*}}{{N}_{{0 - 2}}} = {{\left( {\frac{{{{d}_{{\text{t}}}}}}{d}} \right)}^{3}}m{{N}_{{0 - 2}}} = {{\left( {\frac{{{{d}_{{\text{t}}}}}}{d}} \right)}^{3}}{{F}_{2}}.$По ходу ускорения кажущийся размер частиц уменьшается и эффективному потоку уноса $F_{2}^{*}$ должен соответствовать эффективный поток подачи $F_{0}^{*} > F_{2}^{*}.$ Его величину можно определить, используя соотношение [21]
из которого, с учетом (70), следует
(72)
$F_{0}^{*} = {{\left( {\frac{{d_{0}^{*}}}{d}} \right)}^{3}}{{F}_{0}} = {{\left( {\frac{{d_{0}^{*}}}{d}} \right)}^{3}}m{{N}_{{0 - 2}}}.$Как видно, эффективный поток подачи представляет собой поток N0–2 частиц, кажущиеся объем и масса которых увеличена в ${{\left( {{{d_{0}^{*}} \mathord{\left/ {\vphantom {{d_{0}^{*}} d}} \right. \kern-0em} d}} \right)}^{3}}$ раз. Аналогично можно определить кажущуюся массу слоя, как совокупности N частиц, масса которых увеличена в ${{\left( {{{\overline {{{{\left( {d{\text{*}}} \right)}}_{{\text{v}}}}} } \mathord{\left/ {\vphantom {{\overline {{{{\left( {d{\text{*}}} \right)}}_{{\text{v}}}}} } d}} \right. \kern-0em} d}} \right)}^{3}}$ раз
(73)
$M{\text{*}} = {{\left( {\frac{{\overline {{{{\left( {d{\text{*}}} \right)}}_{{\text{v}}}}} }}{d}} \right)}^{3}}M,$а также эффективное время пребывания частиц в слое [21]
(74)
$\begin{gathered} \tau {\text{*}} = \frac{{M{\text{*}}}}{{F_{0}^{*}}} = \frac{M}{{{{F}_{0}}}}\frac{{{{{\left( {{{\overline {{{{\left( {d{\text{*}}} \right)}}_{{\text{v}}}}} } \mathord{\left/ {\vphantom {{\overline {{{{\left( {d{\text{*}}} \right)}}_{{\text{v}}}}} } d}} \right. \kern-0em} d}} \right)}}^{3}}}}{{{{{\left( {{{d_{0}^{*}} \mathord{\left/ {\vphantom {{d_{0}^{*}} d}} \right. \kern-0em} d}} \right)}}^{3}}}} = \tau \frac{{{{{\left( {{{\overline {{{{\left( {d{\text{*}}} \right)}}_{{\text{v}}}}} } \mathord{\left/ {\vphantom {{\overline {{{{\left( {d{\text{*}}} \right)}}_{{\text{v}}}}} } d}} \right. \kern-0em} d}} \right)}}^{3}}}}{{{{{\left( {{{d_{0}^{*}} \mathord{\left/ {\vphantom {{d_{0}^{*}} d}} \right. \kern-0em} d}} \right)}}^{3}}}} = \\ = \frac{3}{2}{{t}_{{{\text{ac}}}}}\frac{{d_{0}^{*}}}{d}\frac{{{{{\left( {1 + K} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{K}\frac{{\left( {{{{\operatorname{Re} }}_{{\text{t}}}}\, + 25} \right)}}{{\left( {{{U}_{{\text{b}}}}\operatorname{Re} \, + 25} \right)}} \times \\ \times \,\,\left\{ \begin{gathered} \left( {\frac{{1 - {{\alpha }^{{4 - a}}}}}{{4 - a}}} \right),\,\,\,\,a \ne 4 \hfill \\ \ln \left( {\frac{1}{\alpha }} \right),\,\,\,\,a = 4 \hfill \\ \end{gathered} \right. \\ \end{gathered} $и истинное время пребывания
(75)
$\begin{gathered} \tau = \frac{{{{{\left( {{{d_{0}^{*}} \mathord{\left/ {\vphantom {{d_{0}^{*}} d}} \right. \kern-0em} d}} \right)}}^{3}}}}{{{{{\left( {{{\overline {{{{\left( {d{\text{*}}} \right)}}_{{\text{v}}}}} } \mathord{\left/ {\vphantom {{\overline {{{{\left( {d{\text{*}}} \right)}}_{{\text{v}}}}} } d}} \right. \kern-0em} d}} \right)}}^{3}}}}\tau {\text{*}} = \,\,\frac{3}{2}{{t}_{{{\text{ac}}}}}\frac{{\left( {1 + K} \right)}}{K}\frac{{\left( {{{{\operatorname{Re} }}_{{\text{t}}}}\, + 25} \right)}}{{\left( {{{U}_{{\text{b}}}}\operatorname{Re} \,\, + \,\,25} \right)}} \times \\ \times \,\,\left\{ \begin{gathered} {{\left( {\frac{{1 - {{\alpha }^{{4 - a}}}}}{{4 - a}}} \right)}^{2}}\frac{{7 - a}}{{1 - {{\alpha }^{{7 - a}}}}},\,\,\,\,a \ne 4,\,\,\,\,a < 7 \hfill \\ {{\ln }^{2}}\left( {\frac{1}{\alpha }} \right),\,\,\,\,a = 4 \hfill \\ \end{gathered} \right.. \\ \end{gathered} $.И эффективное и истинное время пребывания определяются только характеристиками частиц, газа и особенностями их взаимодействия. Зная поток подачи F0, можно рассчитать массу придонного слоя
его высоту
и перепад давления на слое
При оценке высоты слоя (как геометрического параметра) используется истинная масса слоя. Перепад давления на слое определяется всеми действующими на него силами, включая силы инерции. Поэтому при вычислении ΔP используется кажущаяся масса слоя, учитывающая все эти силы.
Последовательность вычислений приведена на рис. 7. Значение параметра Ub уточняется вплоть до выполнения условия $\left| {1 - {{{{{\bar {\varepsilon }}}_{{\text{T}}}}} \mathord{\left/ {\vphantom {{{{{\bar {\varepsilon }}}_{{\text{T}}}}} {\bar {\varepsilon }}}} \right. \kern-0em} {\bar {\varepsilon }}}} \right| < {{\Delta }_{{\bar {\varepsilon }}}},$ ${{\Delta }_{{\bar {\varepsilon }}}} = 5 \times {{10}^{{ - 4}}}.$
Расчеты выполнены для типичных условий и скорости газа $u \geqslant 1.05{{u}_{{\text{t}}}}.$ Их результаты представлены на рис. 8–21.
Рис. 8.
Зависимость степени неоднородности газового потока от скорости газа: d = 0.2 мм; 1 – ρp = 1800 кг/м3; 2 – 2600. Сплошные линии – 20°C, штриховые – 1000°C.
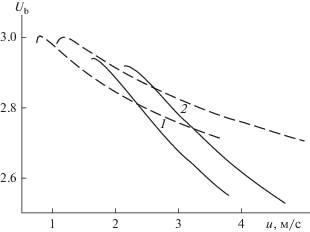
Рис. 11.
Зависимость погрешности аппроксимации функции Φ(t) от скорости газа. Обозначения те же, что и на рис. 8.
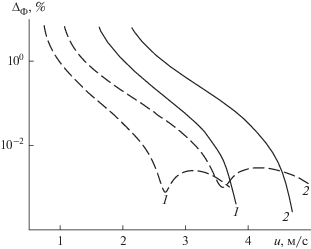
Рис. 12.
Зависимость модуля начальной скорости сжатия от скорости газа. Обозначения те же, что и на рис. 8.
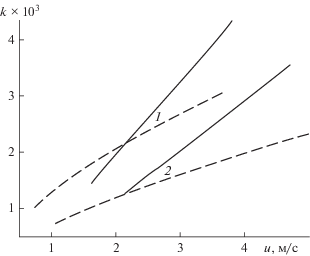
Рис. 13.
Зависимость начального эффективного диаметра, среднего эффективного, среднеобъемного эффективного диаметра и диаметра витания от скорости газа для частиц разной плотности в холодном газе (20°C) (а) и частиц плотностью 2600 кг/м3 в холодных и горячих условиях (б). (а): 1 – ρp = 1800 кг/м3; 2 – 2600; (б): 1 – 1000°C; 2 – 20°C; (а, б): 3 – ${{d_{0}^{*}} \mathord{\left/ {\vphantom {{d_{0}^{*}} d}} \right. \kern-0em} d};$ 4 –${{\overline {d{\text{*}}} } \mathord{\left/ {\vphantom {{\overline {d{\text{*}}} } d}} \right. \kern-0em} d};$ 5 – ${{\overline {d_{{\text{v}}}^{*}} } \mathord{\left/ {\vphantom {{\overline {d_{{\text{v}}}^{*}} } d}} \right. \kern-0em} d};$ 6 – dt.
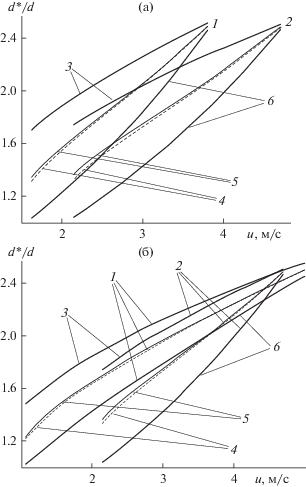
Рис. 14.
Зависимость эффективной скорости начала псевдоожижения (а) и отношения ${{u_{{{\text{mf}}}}^{*}} \mathord{\left/ {\vphantom {{u_{{{\text{mf}}}}^{*}} {{{u}_{{{\text{mf}}}}}}}} \right. \kern-0em} {{{u}_{{{\text{mf}}}}}}}$ от скорости газа (б). Обозначения те же, что и на рис. 8.
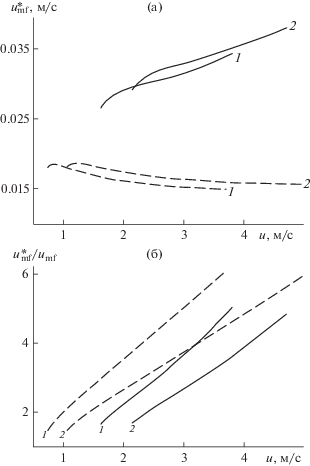
Рис. 15.
Зависимость эффективной скорости витания (а), отношения ${{u_{{\text{t}}}^{*}} \mathord{\left/ {\vphantom {{u_{{\text{t}}}^{*}} {{{u}_{{\text{t}}}}}}} \right. \kern-0em} {{{u}_{{\text{t}}}}}}$ (б) для эффективного среднего диаметра и отношения ${{u_{{\text{t}}}^{*}} \mathord{\left/ {\vphantom {{u_{{\text{t}}}^{*}} u}} \right. \kern-0em} u}$ для эффективного начального (3) и эффективного среднего диаметров от скорости газа. (в): 4 – ${{u_{{\text{t}}}^{*}} \mathord{\left/ {\vphantom {{u_{{\text{t}}}^{*}} u}} \right. \kern-0em} u} = 1.$ Остальные обозначения те же, что и на рис. 8.
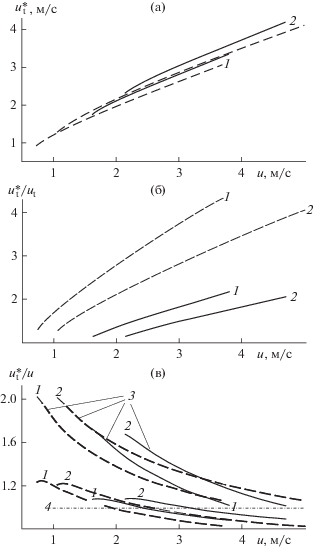
Рис. 16.
Сравнение зависимостей отношений ${{u_{{{\text{mf}}}}^{*}} \mathord{\left/ {\vphantom {{u_{{{\text{mf}}}}^{*}} {{{u}_{{{\text{mf}}}}}}}} \right. \kern-0em} {{{u}_{{{\text{mf}}}}}}}$ и ${{u_{{\text{t}}}^{*}} \mathord{\left/ {\vphantom {{u_{{\text{t}}}^{*}} {{{u}_{{\text{t}}}}}}} \right. \kern-0em} {{{u}_{{\text{t}}}}}}$ от скорости газа: 3 – ${{u_{{{\text{mf}}}}^{*}} \mathord{\left/ {\vphantom {{u_{{{\text{mf}}}}^{*}} {{{u}_{{{\text{mf}}}}}}}} \right. \kern-0em} {{{u}_{{{\text{mf}}}}}}};$ 4 –${{u_{{\text{t}}}^{*}} \mathord{\left/ {\vphantom {{u_{{\text{t}}}^{*}} {{{u}_{{\text{t}}}}}}} \right. \kern-0em} {{{u}_{{\text{t}}}}}}.$ Остальные обозначения те же, что и на рис. 8.
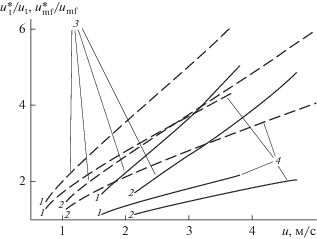
Рис. 17.
Зависимость средней порозности придонного слоя от скорости газа. Обозначения те же, что и на рис. 8.
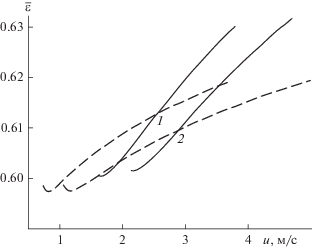
Рис. 18.
Зависимость степени структурной неоднородности придонного слоя от скорости газа. Обозначения те же, что и на рис. 8.
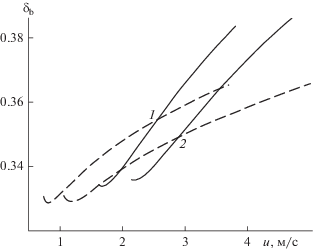
Рис. 19.
Зависимость относительных времен разгона и пребывания в слое (а) и среднего числа попыток разгона (б) от скорости газа. (а): 3 – ${{{{t}_{{\text{t}}}}} \mathord{\left/ {\vphantom {{{{t}_{{\text{t}}}}} {{{t}_{{{\text{ac}}}}}}}} \right. \kern-0em} {{{t}_{{{\text{ac}}}}}}};$ 4 – ${\tau \mathord{\left/ {\vphantom {\tau {{{t}_{{{\text{ac}}}}}}}} \right. \kern-0em} {{{t}_{{{\text{ac}}}}}}}.$ Остальные обозначения те же, что и на рис. 8.
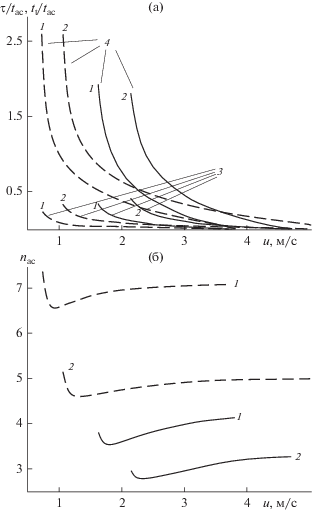
Рис. 20.
Зависимость времени пребывания в слое от скорости газа. Обозначения те же, что и на рис. 8.
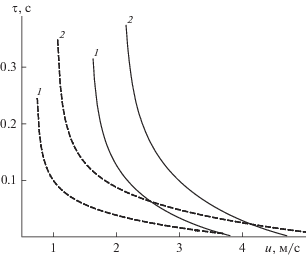
Рис. 21.
Зависимость степени неоднородности газового потока (а) и безразмерной транспортной скорости (б) от числа Архимеда. (а): сплошная линия – 20°C, штриховая – 1000°C; (б): 1–4 – Retr(Ar); 1 – (43); 2 – (80); 3 – (41), Ub = 3; 4 – (41), Ub = 2; 5 – Ret(Ar) (42).
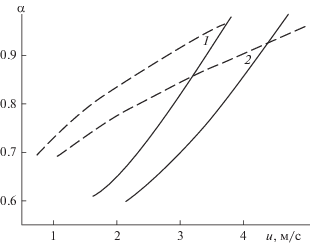
Зависимость степени неоднородности газового потока от скорости фильтрации представлена на рис. 8. По мере увеличения скорости газа степень неоднородности потока монотонно уменьшается в диапазоне от 3 до 2.5. Небольшие максимумы при скорости u, близкой к скорости витания, по-видимому, связаны с неточностью степенной аппроксимации скорости сжатия. При комнатной температуре неоднородность потока снижается быстрее и в большем интервале, чем при 1000°С. В слое из более тяжелых частиц скорости газа выше.
На рис. 9 представлена зависимость параметра α от скорости фильтрации. С ростом скорости эта величина монотонно возрастает, отображая сужение диапазона допустимых размеров частиц. Различается характер кривых. Горячим условиям соответствуют выпуклые кривые, холодным – вогнутые. Для более тяжелых частиц графики смещены в сторону больших скоростей.
Показатель степени в аппроксимации (59) скорости сжатия (рис. 10) монотонно уменьшается с ростом скорости холодного газа. В горячих условиях наблюдается незначительный минимум, более явно выраженный в случае легких частиц. При переходе к более легким частицам и повышенным температурам кривые смещаются в сторону меньших скоростей.
Погрешность степенной аппроксимации скорости сжатия наибольшая (∼7%) при скорости газа, приближающейся к скорости витания (рис. 11). В дальнейшем она быстро уменьшается. Эта погрешность сказывается во всех формулах, использующих аппроксимационные коэффициенты, и возрастает не более чем на 20% от своей величины при расчете времени пребывания (75) (рис. 7) в холодных условиях.
Начальная скорость сжатия (рис. 12) почти линейно возрастает с увеличением скорости газа. В холодных условиях темп роста выше, как и само значение к. Легкие частицы начинают разгоняться быстрее как в нормальных условиях, так и при повышенных температурах.
На рис. 13а представлены зависимости различных эффективных диаметров от скорости фильтрации холодного газа для легких и тяжелых частиц. Для одного и того же значения скорости и начальные и средние диаметры, как и диаметр витания, у легких частиц выше. По мере приближения к транспортной скорости все зависимости для каждого сорта частиц сходятся к одной точке. На рис. 13б такие же зависимости представлены для тяжелых частиц в холодных и горячих условиях. Эффективные диаметры при высокой температуре больше, чем при нормальной при одной и той же скорости газа. Как видно из рисунков, средний и среднеобъемный диаметры различаются мало. Оценки показали, что при а = 2–4 и α = = 0.6–0.95 их расхождение не превышает 4%. Наибольшее различие (∼30%) достигается при а = 5 и α = 0.1.
На рис. 14а представлены зависимости эффективной скорости начала псевдоожижения от скорости фильтрации. При нормальных условиях $u_{{{\text{mf}}}}^{*}$ возрастает с ростом скорости, при повышенной температуре – незначительно снижается как для тяжелых, так и для легких частиц. В то же время отношение ${{u_{{{\text{mf}}}}^{*}} \mathord{\left/ {\vphantom {{u_{{{\text{mf}}}}^{*}} {{{u}_{{{\text{mf}}}}}}}} \right. \kern-0em} {{{u}_{{{\text{mf}}}}}}}$ в обоих случаях с ростом скорости увеличивается (рис. 14б).
Эффективная скорость витания $u_{{\text{t}}}^{*}$ (рис. 15а) с ростом скорости фильтрации монотонно возрастает, равно как и отношение ${{u_{{\text{t}}}^{*}} \mathord{\left/ {\vphantom {{u_{{\text{t}}}^{*}} {{{u}_{{\text{t}}}}}}} \right. \kern-0em} {{{u}_{{\text{t}}}}}}$ (рис. 15б), тогда как отношение ${{u_{{\text{t}}}^{*}} \mathord{\left/ {\vphantom {{u_{{\text{t}}}^{*}} u}} \right. \kern-0em} u}$ падает, становясь меньше 1 для среднего эффективного диаметра (рис. 15в). Для начального эффективного диаметра это отношение всегда остается больше 1 (рис. 15в).
Как видно из рис. 16, во всех случаях отношение ${{u_{{{\text{mf}}}}^{*}} \mathord{\left/ {\vphantom {{u_{{{\text{mf}}}}^{*}} {{{u}_{{{\text{mf}}}}}}}} \right. \kern-0em} {{{u}_{{{\text{mf}}}}}}}$ возрастает с ростом u быстрее, чем ${{u_{{\text{t}}}^{*}} \mathord{\left/ {\vphantom {{u_{{\text{t}}}^{*}} {{{u}_{{\text{t}}}}}}} \right. \kern-0em} {{{u}_{{\text{t}}}}}}.$ Это согласуется со сближением диаметра витания с начальным эффективным диаметром (рис. 13) и ростом параметра α (рис. 9) по мере увеличения скорости фильтрации.
На рис. 17 представлена зависимость средней порозности придонного слоя от скорости фильтрации. При нормальных условиях ее значение увеличивается гораздо быстрее, чем в горячем слое. Одновременно со средней порозностью увеличивается и доля объема слоя, занятая дискретной фазой (рис. 18). И $\bar {\varepsilon },$ и ${{\delta }_{{\text{b}}}}$ больше в случае легких частиц.
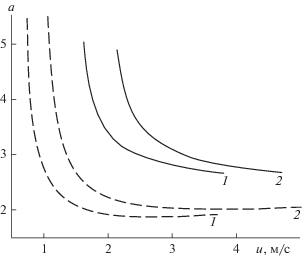
Время ускорения частиц в слое всегда меньше характерного времени разгона и сокращается с ростом скорости газа (рис. 19а). Время пребывания в слое может быть как больше, так и меньше tac, сокращаясь по мере увеличения скорости u. В то же время τ всегда больше tt. Отношение nac = = τ/tt (рис. 19б) характеризует среднее число попыток разгона, необходимых для выхода частицы из слоя (неудачные попытки заканчиваются столкновением, удачная – последняя – выходом в транспортную зону). Как видно из рисунка, эта величина слабо зависит от скорости газа (отклонение от среднего по скорости фильтрации значения ${{\bar {n}}_{{{\text{ac}}}}}$ не превышает 8%) и определяется главным образом свойствами твердой фазы и ожижающего газа. Аппроксимация ${{\bar {n}}_{{{\text{ac}}}}}{\text{:}}$
(79)
${{\bar {n}}_{{{\text{ac}}}}} = 31{{\left( {\frac{{{{\rho }_{{\text{p}}}}}}{\rho }} \right)}^{{ - 0.66}}}\operatorname{Re} _{{\text{t}}}^{{ - 2.14}}{{\operatorname{Ar} }^{{1.45}}}.$Средняя погрешность аппроксимации (79) составляет 7.5%.
На рис. 20 представлена зависимость времени пребывания частиц в придонном слое от скорости газа. Как видно, это время составляет не более 0.5 с, быстро уменьшаясь по мере роста u. Наибольшие времена характерны для тяжелых частиц в холодном слое. Уменьшение плотности ρp, равно как и повышение температуры, приводит к сокращению τ. При высокой температуре и скорости газа, значительно превышающей ut, время пребывания сокращается медленнее, чем в нормальных условиях. В результате при одной и той же скорости фильтрации u $ \gg $ ut величина τ в горячем слое оказывается больше, чем в холодном.
ТРАНСПОРТНАЯ СКОРОСТЬ ПРИ ПЕРЕМЕННОМ Ub
Диапазон чисел Ar, соответствующий типичным для топок параметрам, представляет переходную зону зависимости Re(Ar). Очевидно поэтому зависимость ${{\left. {{{U}_{{\text{b}}}}} \right|}_{{u = {{u}_{{{\text{tr}}}}}}}}$ от числа Архимеда (рис. 21а) оказывается сложнее, чем от скорости фильтрации (рис. 8), и в холодном слое даже имеет явно выраженный экстремальный характер. Расчетные точки Retr(Ar) хорошо укладываются на одну линию, которая аппроксимируется следующей степенной зависимостью, аналогичной (43) [3]
со средней погрешностью ~14%. Средняя погрешность зависимости (43) оказывается ~40%. Однако наилучшим образом результаты расчета аппроксимируются не степенной зависимостью, а функцией вида (41). Погрешность такой аппроксимации составляет ~5% для Ub = 3.
СРАВНЕНИЕ С ЭКСПЕРИМЕНТОМ
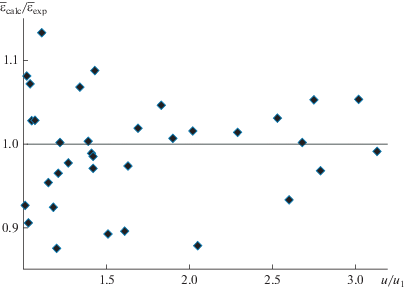
Для сравнения использовались опытные данные из работ [23–27]. Проще всего оказалось оценить соответствие экспериментальных и расчетных значений средней порозности слоя (рис. 22). Наибольшее отклонение опытных данных не превышает 15% вблизи скорости витания и уменьшается с ростом скорости газа. Для оценки данных по перепаду давления на придонном слое и его высоте потребовалась дополнительная информация по величине полного циркуляционного потока, формируемого благодаря уносу частиц. Этот поток распределен между внутренним и внешним циркуляционными контурами. Расход дисперсного материала во внешнем контуре может быть измерен. Определение расхода во внутреннем контуре затруднительно, тем более что благодаря большой площади топки этот контур случайным образом распределен по сечению. Можно предположить, что из придонного слоя уносится вся твердая фаза, которую может удержать поток газа. Поэтому расход уноса, а, следовательно, и циркуляционный поток, определялся исходя из предельной несущей способности газового потока [28]
Рис. 22.
Сравнение опытных и расчетных данных по средней порозности придонного слоя. Сплошная линия – ${{{{{\bar {\varepsilon }}}_{{{\text{calc}}}}}} \mathord{\left/ {\vphantom {{{{{\bar {\varepsilon }}}_{{{\text{calc}}}}}} {{{{\bar {\varepsilon }}}_{{{\text{exp}}}}}}}} \right. \kern-0em} {{{{\bar {\varepsilon }}}_{{{\text{exp}}}}}}} = 1.$
Были проверены следующие пять формул:
(82)
$G_{{\text{s}}}^{*} = \frac{1}{8}\frac{{\nu \rho }}{d}{{\operatorname{Fr} }^{{1.85}}}{{\operatorname{Ar} }^{{0.63}}}{{\left( {\frac{{{{\rho }_{{\text{p}}}}}}{\rho } - 1} \right)}^{{ - 0.44}}}\,\,\,\,\,[28],$(83)
$G_{{\text{s}}}^{*} = 0.82{{\rho }_{{\text{p}}}}\operatorname{Fr} _{{\text{t}}}^{{1.23}}\sqrt {g{{H}_{{\text{r}}}}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,[29],$(84)
$G_{{\text{s}}}^{*} = {{\rho }_{{\text{p}}}}{{u}_{{\text{t}}}}K{{\left( {\frac{u}{{{{u}_{{\text{t}}}}}} - 1} \right)}^{a}}{{\left( {\frac{{{{D}_{{\text{r}}}}}}{d}} \right)}^{b}}\,\,\,\,\,\,\,\,\left[ {30} \right],$где $a$ = $\left\{ \begin{gathered} 2.355 - 0.00191\operatorname{Ar} ,\,\,\,\,\operatorname{Ar} \leqslant 530 \hfill \\ 1.34,\,\,\,\,\operatorname{Ar} > 530 \hfill \\ \end{gathered} \right.,$ $b$ = $\left\{ \begin{gathered} 0,\,\,\,\,{{{{D}_{{\text{r}}}}} \mathord{\left/ {\vphantom {{{{D}_{{\text{r}}}}} d}} \right. \kern-0em} d} > 3200 \hfill \\ 0.115,\,\,\,\,{{{{D}_{{\text{r}}}}} \mathord{\left/ {\vphantom {{{{D}_{{\text{r}}}}} d}} \right. \kern-0em} d} \leqslant 3200\,\,\,\,{\text{and}}\,\,\,\,\operatorname{Ar} \leqslant 100 \hfill \\ - 1.259,\,\,\,\,{{{{D}_{{\text{r}}}}} \mathord{\left/ {\vphantom {{{{D}_{{\text{r}}}}} d}} \right. \kern-0em} d} \leqslant 3200\,\,\,\,{\text{and}}\,\,\,\,\operatorname{Ar} > 100 \hfill \\ \end{gathered} \right.,$ $K$ = $\left\{ \begin{gathered} 3.44 \times {{10}^{{ - 5}}}{{\operatorname{Ar} }^{{0.493}}},{\text{ }}\operatorname{Ar} \leqslant 100 \hfill \\ 7.60,{\text{ }}\operatorname{Ar} > 100 \hfill \\ \end{gathered} \right.;$
(85)
$G_{{\text{s}}}^{*} = {{\rho }_{{\text{p}}}}{{u}_{{\text{t}}}}K{{\left( {\frac{u}{{{{u}_{{\text{t}}}}}} - 1} \right)}^{a}}{{\left( {\frac{{{{D}_{{\text{r}}}}}}{d}} \right)}^{b}}\,\,\,\,[31],$(86)
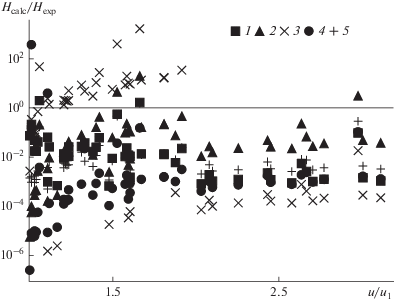
$G_{{\text{s}}}^{*} = u{{\rho }_{{\text{p}}}}\frac{{1 - {{\varepsilon }_{{\text{D}}}}}}{{{{\varepsilon }_{{\text{D}}}}}}\frac{{1 - \sqrt {{\rho \mathord{\left/ {\vphantom {\rho {{{\rho }_{{\text{p}}}}}}} \right. \kern-0em} {{{\rho }_{{\text{p}}}}}}} }}{{\sqrt {{{{{\rho }_{{\text{p}}}}} \mathord{\left/ {\vphantom {{{{\rho }_{{\text{p}}}}} \rho }} \right. \kern-0em} \rho }} - 1}}\,\,\,\,\,\,\,[32],$Результаты сравнения представлены на рис. 23 и 24. Как видно, ни одна из использованных зависимостей не обеспечивает достаточной близости расчетных и опытных данных. Наименьшая средняя погрешность (84% для ΔP и 96% для H) достигается при использовании формулы, предложенной в [28]. Можно лишь отметить, что отклонение от опытных данных уменьшается с ростом скорости газа для всех формул.
Рис. 23.
Сравнение опытных и расчетных данных по перепаду давления на придонном слое: 1 – расчет $G_{s}^{*}$ по (82); 2 – (83); 3 – (84); 4 – (85); 5 – (86). Сплошная линия – ${{\Delta {{P}_{{{\text{calc}}}}}} \mathord{\left/ {\vphantom {{\Delta {{P}_{{{\text{calc}}}}}} {\Delta {{P}_{{{\text{exp}}}}}}}} \right. \kern-0em} {\Delta {{P}_{{{\text{exp}}}}}}}$ = 1.
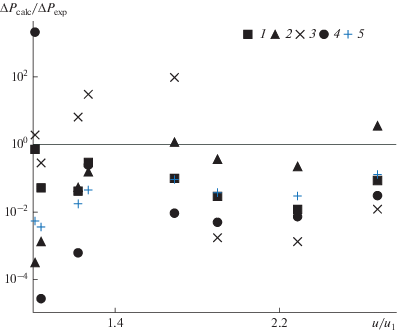
Рис. 24.
Сравнение опытных и расчетных данных по высоте придонного слоя. Сплошная линия – ${{{{H}_{{{\text{calc}}}}}} \mathord{\left/ {\vphantom {{{{H}_{{{\text{calc}}}}}} {{{H}_{{{\text{exp}}}}}}}} \right. \kern-0em} {{{H}_{{{\text{exp}}}}}}}$ = 1. Остальные обозначения те же, что и на рис. 23.
ЗАКЛЮЧЕНИЕ
Представление КС-подобного придонного слоя как идеально перемешанной дисперсной системы сжимающихся частиц позволило учесть дополнительную силу, возникающую при циркуляции твердой фазы и участвующую в формировании ПС наравне с силами тяжести и сопротивления; определить условия существования придонного слоя; сформулировать механизм изменения массы ПС по мере роста скорости газа; рассчитать параметры придонного слоя.
Определение транспортной скорости (40), (41) представляет собой строгую верхнюю границу значений скорости фильтрации газа, при которых может существовать придонный слой. Даже если u < utr, при недостаточном циркуляционном потоке зависящие от него масса, объем и высота ПС могут оказаться слишком малыми и слой не будет восприниматься как таковой.
Примененная методика расчета позволяет использовать любые зависимости для скорости сжатия и любые функции распределения по размерам частиц. Однако при этом существенно возрастает объем вычислений и их трудоемкость.
Сравнение с опытными данными по высоте придонного слоя и перепаду давления на нем показало, что расчетное определение этих параметров невозможно без надежных данных по величине циркуляционного потока.
ОБОЗНАЧЕНИЯ
| a | показатель степени в формуле (48) |
| Dr | эквивалентный диаметр топки, м |
| d | диаметр частиц, м |
| d* | эффективный диаметр частиц, м |
| $d_{0}^{*}$ | максимальный (начальный) эффективный диаметр частиц, м |
| $d_{{0\max }}^{*}$ | наибольший максимальный эффективный диаметр частиц, м |
| $d_{{0\min }}^{*}$ | наименьший максимальный эффективный диаметр частиц, м |
| $\bar {d}{\text{*}}$ | средний эффективный диаметр частиц, м |
| $\bar {d}_{{\text{v}}}^{*}$ | среднеобъемный эффективный диаметр частиц, м |
| dt | диаметр витания, м |
| F | реактивная сила, Н |
| F0 | поток подачи (возврат уноса) в придонный слой, кг/с |
| $F_{0}^{*}$ | эффективный поток подачи (возврат уноса) в придонный слой, кг/с |
| F2 | поток уноса из придонного слоя, кг/с |
| $F_{2}^{*}$ | эффективный поток уноса из придонного слоя, кг/с |
| fres | сила сопротивления, Н |
| $G_{s}^{*}$ | предельная несущая способность потока газа, кг/(м2 с) |
| g | ускорение свободного падения, м/с2 |
| g* | эффективное ускорение свободного падения, м/с2 |
| H | высота придонного слоя, м |
| Hr | высота топки, м |
| k | модуль начальной скорости сжатия, м/с |
| L | число точек на отрезке [0, tt], используемых для аппроксимации Φ(t) |
| M | масса системы переменного состава либо придонного слоя, кг |
| M(t) | масса системы переменного состава в момент времени t, кг |
| M* | эффективная масса слоя, кг |
| M0(t) | масса частиц, вошедших за время t в систему переменного состава, кг |
| M2(t) | масса частиц, вышедших за время t из системы переменного состава, кг |
| m | масса частицы, кг |
| m* | эффективная масса частицы, кг |
| N | число частиц в придонном слое |
| N0(t) | счетный расход частиц, входящих в систему переменного состава, 1/с |
| N2(t) | счетный расход частиц, выходящих из системы переменного состава, 1/с |
| N0–2 | постоянный счетный расход частиц, входящих в стационарный придонный слой и выходящих из него, 1/с |
| ${{\bar {n}}_{{{\text{ac}}}}}$ | среднее число попыток разгона частицы в придонном слое |
| nΦ | показатель степени в аппроксимации Φ(t) (56) |
| ΔP | перепад давления на придонном слое, Па |
| p(d*) | распределение частиц по эффективному диаметру, 1/м |
| p0(d*) | распределение частиц по начальному эффективному диаметру, 1/м |
| ΔQ0 | сумма импульсов частиц, присоединившихся к системе за время Δt, кг м/с |
| ΔQ2 | сумма импульсов частиц, отделившихся от системы за время Δt, кг м/с |
| S | площадь сечения слоя, м2 |
| Sem | площадь сечения слоя, занятая эмульсией, м2 |
| T | заданный интервал времени, с |
| t | время, с |
| tac | характерное время разгона частицы, с |
| tt | время сжатия частицы до размера dt, с |
| Δt | бесконечно малый промежуток времени, с |
| Ub | безразмерная скорость газа в дискретной фазе слоя |
| u | средняя скорость газа в топке, м/с |
| ub | скорость газа в дискретной фазе слоя, м/с |
| umf | скорость минимального псевдоожижения, м/с |
| $u_{{{\text{mf}}}}^{*}$ | эффективная скорость минимального псевдоожижения, м/с |
| ut | скорость витания, м/с |
| $u_{{\text{t}}}^{*}$ | эффективная скорость витания, м/с |
| ut max | скорость витания частиц наибольшего диаметра, м/с |
| ut min | скорость витания частиц наименьшего диаметра, м/с |
| utr | транспортная скорость, м/с |
| $v$ | скорость частицы в лабораторной системе координат, м/с |
| ${{v}_{{\text{b}}}}$ | скорость частицы относительно газового потока в дискретной фазе слоя, м/с |
| ${{v}_{{\text{c}}}}$(d*) | скорость сжатия частицы с эффективным диаметром d*, м/с |
| ${{v}_{{\text{p}}}}$ | объем частицы, м3 |
| w | ускорение частицы, м/с2 |
| w0 | начальное ускорение разгоняемой частицы, м/с2 |
| $\bar {w}$ | среднее за время T ускорение разгоняемой частицы, м/с2 |
| α | безразмерный диаметр витания, определенный по отношению к начальному эффективному диаметру |
| Δε | относительная разность значений средней порозности, рассчитанной по (63) и (64) |
| ΔΦ | погрешность аппроксимации функции Φ(t) (58) |
| $\begin{gathered} \delta \left( x \right) = \hfill \\ = \,\,\left\{ \begin{gathered} 0,\,\,\,\,x \ne 0 \hfill \\ \to \infty ,\,\,\,\,x = 0 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $ | δ-функция Дирака |
| δb | доля объема слоя, занятая дискретной фазой |
| $\bar {\varepsilon }$ | средняя порозность придонного слоя |
| ${{\varepsilon }_{{\text{0}}}}$ | порозность засыпки |
| ${{\bar {\varepsilon }}_{{\text{T}}}}$ | средняя порозность придонного слоя, рассчитанная по формуле Тодеса |
| Φ(t) | безразмерная функция, определенная в (54) |
| λ | коэффициент сопротивления частицы |
| ν | кинематическая вязкость газа, м2/с |
| ρ | плотность газа, кг/м3 |
| ρp | плотность частиц, кг/м3 |
| τ | время пребывания частиц в слое, с |
| τ* | эффективное время пребывания частиц в слое, с |
| $\begin{gathered} \operatorname{Ar} = \frac{{g{{d}^{3}}}}{{{{\nu }^{2}}}} \times \hfill \\ \times \,\,\frac{{{{\rho }_{{\text{p}}}} - \rho }}{\rho }, \hfill \\ \end{gathered} $$\begin{gathered} \operatorname{Ar} * = \frac{{g{{{\left( {d{\text{*}}\left( t \right)} \right)}}^{3}}}}{{{{\nu }^{2}}}} \times \hfill \\ \times \,\,\frac{{{{\rho }_{{\text{p}}}} - \rho }}{\rho }, \hfill \\ \end{gathered} $$\begin{gathered} \operatorname{Ar} _{g}^{*} = \hfill \\ = \,\,\frac{{g{\text{*}}\left( t \right){{d}^{3}}}}{{{{\nu }^{2}}}}\frac{{{{\rho }_{{\text{p}}}} - \rho }}{\rho } \hfill \\ \end{gathered} $ | критерии Архимеда |
| $\operatorname{Fr} = \frac{u}{{\sqrt {gd} }},$${{\operatorname{Fr} }_{{\text{t}}}} = \frac{{{{{\left( {u - {{u}_{{\text{t}}}}} \right)}}^{2}}}}{{g{{H}_{{\text{r}}}}}}$ | критерии Фруда |
| $\operatorname{Re} = \frac{{du}}{\nu },$$\operatorname{Re} * = \frac{{\overline {d{\text{*}}} u}}{\nu },$${{\operatorname{Re} }_{{\text{b}}}} = \frac{{d{{u}_{{\text{b}}}}}}{\nu },$${{\operatorname{Re} }_{{{\text{mf}}}}} = \frac{{d{{u}_{{{\text{mf}}}}}}}{\nu },$$\operatorname{Re} _{{{\text{mf}}}}^{*} = \frac{{\overline {d{\text{*}}} u_{{{\text{mf}}}}^{*}}}{\nu },$${{\operatorname{Re} }_{{\text{t}}}} = \frac{{d{{u}_{{\text{t}}}}}}{\nu },$$\operatorname{Re} _{{\text{t}}}^{*} = \frac{{\overline {d{\text{*}}} u_{{\text{t}}}^{*}}}{\nu },$${{\operatorname{Re} }_{{{\text{tr}}}}} = \frac{{d{{u}_{{{\text{tr}}}}}}}{\nu },$$\begin{gathered} {{\operatorname{Re} }_{{\text{v}}}} = \hfill \\ = \,\,\frac{{d\left( {{{u}_{{\text{b}}}} - v\left( t \right)} \right)}}{\nu }, \hfill \\ \end{gathered} $${{\operatorname{Re} }_{{{\text{vb}}}}} = \frac{{d{{{v}}_{{\text{b}}}}}}{\nu }$ | критерии Рейнольдса |
ИНДЕКСЫ
| – | среднее значение |
| 0 | частицы, присоединившиеся к системе; начальное значение;засыпка |
| 2 | частицы, отделившиеся от системы |
| ac | ускорение |
| b | дискретная фаза слоя |
| c | сжатие |
| calc | расчетное значение |
| em | эмульсионная фаза слоя |
| exp | опытное значение |
| i, j, k, l | индексы в суммах (5)–(11) и (56)–(57) |
| max | максимальное значение |
| mf | состояние минимального ожижения |
| min | минимальное значение |
| p | частица |
| r | топка |
| res | сопротивление |
| s | предельное насыщение |
| T | формула Тодеса |
| t | условия витания |
| tr | транспортный |
| v | объем |
Список литературы
Wang C., Zhu J. Developments in the understanding of gas–solid contact efficiency in the circulating fluidized bed riser reactor: A review // Chin. J. Chem. Eng. 2016. V. 24. P. 53.
Arjunwadkar A., Basu P., Acharya B. A review of some operation and maintenance issues of CFBC boilers // Appl. Therm. Eng. 2016. V. 102. P. 672.
Tuponogov V.G., Baskakov A.P. The influence of the gas distributing grid diameter on the transition velocity and hydrodynamics of the bottom layer in circulating fluidized bed installations // Therm. Eng. 2013. V. 60. № 11. P. 808. [Тупоногов В.Г., Баскаков А.П. Влияние диаметра газораспределительной решетки на переходную скорость и гидродинамику придонного слоя в установках с циркулирующим кипящим слоем // Теплоэнергетика. 2013. № 11. С. 38.]
Schouten J.C., Zijerveld R.C., van den Bleek C.M. Scale-up of bottom-bed dynamics and axial solids-distribution in circulating fluidized beds of Geldart-B particles // Chem. Eng. Sci. 1999. V. 54. № 13–14. P. 2103.
Mo X., Wang P., Yang H., Junfu L., Zhang M., Liu Q. A hydrodynamic model for circulating fluidized beds with low riser and tall riser // Powder Technol. 2015. V. 274. P. 146.
Cho D., Choi J.-H., Khurram M.S., Jo S.-H., Ryu H.-J., Park Y.C., Yi C.-K. Solids circulation rate and static bed height in a riser of a circulating fluidized bed // Korean J. Chem. Eng. 2015. V. 32. № 2. P. 284.
Mahmoudi S., Baeyens J., Seville J. The solids flow in the CFB-riser quantified by single radioactive particle tracking // Powder Technol. 2011. V. 211. P. 135.
Pallares D., Johnsson F. Macroscopic modelling of fluid dynamics in large-scale circulating fluidized beds // Progress Energy Comb. Sci. 2006. V. 32. P. 539.
Schlichthaerle P., Werther J. Solids mixing in the bottom zone of a circulating fluidized bed // Powder Technol. 2001. V. 120. № 1–2. P. 21.
Svensson A., Johnsson F., Leckner B. Fluidization regimes in a circulating fluidized bed boiler // Proc. 7th Eng. Found. Conf. on Fluidization. Brisbane, Australia, 1992. P. 471–478.
Johnsson F., Zijerveld R.C., Schouten J.C., van den Bleek C.M., Leckner B. Characterization of fluidization regimes by time-series analysis of pressure fluctuations // Int. J. Multiphase Flow. 2000. V. 26. P. 663.
Svensson A., Johnsson F., Leckner B. Bottom bed regimes in a circulating fluidized bed boiler // Int. J. Multiphase Flow. 1996. V. 22. P. 1187.
Svensson A., Johnsson F., Leckner B. Fluidization regimes in fluidized bed // Powder Technol. 1996. V. 68. P. 299.
Gungor A. One dimensional numerical simulation of small scale CFB combustors // Energy Convers. Management. 2009. V. 50. № 3. P. 711.
Gungor A., Eskin N. Hydrodynamic modeling of a circulating fluidized bed // Powder Technol. 2007. V. 172. P. 1.
Schlichthaerle P., Werther J. Axial pressure profile and solids concentration distributions in the CFB bottom zone // Proc. 6th Int. Conf. Circulating Fluidized Beds. Würzburg, Germany, 1999. P. 185.
Маркеев А.П. Теоретическая механика. М.: ЧеРо, 1999.
Аэров М.Э., Тодес О.М. Гидравлические и тепловые основы работы аппаратов со стационарным и кипящим зернистым слоем. Л.: Химия, 1968.
Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969.
Тодес О.М., Цитович О.Б. Аппараты с кипящим зернистым слоем. Гидравлические и тепловые основы работы. Л.: Химия, 1981.
Kovenskii V.I. Calculation of the parameters of an ensemble of particles in a well stirred fluidized bed reactor // Theor. Found. Chem. Eng. 2006. V. 40. № 2. P. 190. [Ковенский В.И. К расчету параметров ансамбля частиц в реакторе идеального смешения с кипящим слоем // Теорет. основы хим. технологии. 2006. Т. 40. № 2. С. 206.]
Kovenskii V.I. Calculation of the parameters of an ensemble of particles in a well stirred fluidized bed reactor // Theor. Found. Chem. Eng. 2014. V. 48. № 1. P. 13. [Ковенский В.И. Численный расчет параметров ансамбля частиц в реакторе идеального смешения с кипящим слоем // Теорет. основы хим. технологии. 2014. Т. 48. № 1. С. 15.]
Johnsson F., Svensson A. Vertical bulk density distribution in a CFB-furnace // Proc. of IEA Meeting on Mathematical Modelling. San Diego, 1993. P. 1.
Svensson A., Johnsson F., Leckner B. Fluid-dynamics of the bottom bed of circulating fluidized bed boilers // Proc. of Fluidized Bed Combustion-93. 1993. V. 2. P. 887.
Johnsson F., Leckner B. Vertical distribution of solids in a CFB-furnace // Proc. of 13th Int. Conf. on Fluidized Bed Combustion. Orlando, 1995. P. 1.
van der Schaaf J., Schouten J.C., Johnsson F., van den Bleek C.M. Bypassing of gas through bubble chains and jets in circulating fluidized beds // Proc. of 6th Int. Conf. Circulating Fluidized Beds. Würzburg, Germany, 1999. P. 47.
Johnsson F., Sternens J., Leckner B., Wiesendorf V., Hartge E.-U., Werther J., Montat D., Briand P. Fluid dynamics of the bottom zone of CFB combustors // Proc. of 6th Int. Conf. Circulating Fluidized Beds. Würzburg, Germany, 1999. P. 113.
Bai D., Kato K. Saturation carrying capacity of gas and flow regimes in CFB // J. Chem. Eng. Jpn. 1995. V. 28. P. 179.
Teplitskii Yu.S., Kovenskii V.I. On the circulating boiling bed energy // J. Eng. Physics Thermophysics. 2009. V. 82. № 4. P. 605. [Теплицкий Ю.С., Ковенский В.И. Об энергетике циркулирующего кипящего слоя // Инж.-физ. журн. 2009. Т. 82. № 4. С. 632.]
Xua G., Hartgea E.-U., Werther J., Gao S. Saturation carrying capacity at high Archimedes number of vertical concurrent gas–particle flow // Chem. Eng. Sci. 2006. V. 61. P. 7115.
Xu G., Nomura K., Gao S., Kato K. More fundamentals of dilute suspension collapse and choking for vertical conveying systems // AIChE J. 2001. V. 47. P. 2177.
Day J.Y., Littman H., Morgan III M.H. A new choking correlation for vertical pneumatic conveying // Chem. Eng. Sci. 1990. V. 45. P. 355.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии