Теоретические основы химической технологии, 2019, T. 53, № 5, стр. 500-509
Моделирование процесса гидроизомеризации н-пентана на палладийсодержащем цеолитном катализаторе типа ЦВМ
Е. В. Писаренко 1, *, В. Н. Писаренко 2
1 Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия
2 ООО “Синтон”
Москва, Россия
* E-mail: evpisarenko@mail.ru
Поступила в редакцию 07.03.2019
После доработки 29.03.2019
Принята к публикации 01.04.2019
Аннотация
Изучены два способа формирования активной поверхности палладийсодержащих цеолитных катализаторов типа ЦВМ. Активным центром этих катализаторов являлся палладий, вводимый в цеолит ЦВМ методом пропитки либо методом ионного обмена. Образцы катализаторов испытаны в реакции гидроизомеризации н-пентана. Предложен стадийный механизм реакции гидроизомеризации н-пентана на палладийсодержащем цеолите и построена соответствующая ему кинетическая модель. Кинетические эксперименты проводились в проточном реакторе с объемом реакционной зоны 200 см3. Варьировали давление в реакторе от 10 до 30 атм, температуру от 553 до 633 K, мольное соотношение водород/(н-пентан+изопентан) от 2 до 6, время контакта от 0.05 до 2.0 ч. По результатам последовательно планируемого эксперимента методом максимального правдоподобия оценены константы кинетической модели, дисперсии оценок констант, дисперсии откликов, дисперсии наблюдений, дисперсии ошибок воспроизводимости. Построена прецизионная кинетическая модель реакции гидроизомеризации н-пентана на палладийсодержащем цеолитном катализаторе типа ЦВМ.
ВВЕДЕНИЕ
В настоящее время совершенствование технологий гидроизомеризации н-алканов является исключительно актуальной проблемой, ибо позволяет снизить в моторных топливах содержание алкилароматических углеводородов и разветвленных алканов, получаемых методом алкилирования парафинов олефинами. Последние позволяют получать более дешевые и высокоэкологичные моторные топлива. Для решения этой задачи требуется разработать катализаторы с низкой крекирующей способностью и высокой селективностью по целевым продуктам, а также построить при этом высокоточные модели, прогнозирующие протекание исследуемого процесса с наперед заданной точностью.
Построение высокоточных моделей позволяет сократить объем необходимых расчетов по установлению геометрических размеров и режимов эксплуатации промышленных реакторов, а также технических систем управления ими [1–7]. Одновременно повышается и надежность принимаемых проектных решений по пусковым и пуск-остановочным процессам. Высокоточные кинетические модели способствуют также и дальнейшему развитию теорий катализа. Они при строго определенном преобразовании уравнений кинетических моделей могут позволить рассчитать во многих случаях кинетические константы медленных стадий механизма химической реакции и их энергий активации, а также проверить научные гипотезы о структуре элементарных реакций и их соответствии эксперименту.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Кинетические опыты по изучению реакции гидроизомеризации н-пентана проводились в проточном каталитическом реакторе с объемом реакционной зоны 200 см3 и с объемом Pd-содержащего цеолитного катализатора типа ЦВМ 5 и 10 см3. Использованы два типа катализатора с формированием активной поверхности методом пропитки (катализатор № 1) и методом ионного обмена (катализатор № 2). Восстановление катализаторов осуществлялось водородом при температуре 673 K в течение 3 ч. При проведении кинетических опытов время контакта, т.е. отношение массы катализатора к массовой скорости сырьевого потока, изменяли от 0.05 до 2 ч. При этом варьировали температуру в реакционной зоне от 553 до 633 К, давление от 10 до 30 атм, мольное соотношение реагентов в сырье водород/(н-пентан + + изопентан) от 2 до 6. В продуктовом потоке анализировали газохроматографически массовое содержание н-пентана, 2-метилбутана, водорода. Общее давление в реакторе практически не изменялось. Всего было поставлено 60 опытов.
Так как при исследовании кинетики реакции гидроизомеризации н-пентана используются Pd-содержащие цеолитные катализаторы, полученные методом пропитки (катализатор № 1) и ионного обмена (катализатор № 2), то для них предложен единый стадийный механизм реакции гидроизомеризации для более полного сравнения характеристик их активности и энергетических свойств активных центров (рис. 1).
ПОСТРОЕНИЕ КИНЕТИЧЕСКОЙ МОДЕЛИ РЕАКЦИИ ГИДРОИЗОМЕРИЗАЦИИ н-ПЕНТАНА
Стехиометрическая матрица В стадийного механизма реакции гидроизомеризации н-пентана может быть представлена в виде клеточной матрицы:
где ${{B}_{1}}$ − подматрица стехиометрических коэффициентов небоденштейновских веществ, ${{B}_{2}}$ − подматрица стехиометрических коэффициентов боденштейновских веществ стадийного механизма сложной химической реакции.В системе боденштейновских веществ присутствуют два инварианта. Иначе две линейные независимые комбинации концентраций боденштейновских веществ будут иметь постоянные значения в выбранной области протекания каталитической реакции. Два инварианта существуют и в совокупности небоденштейновских веществ, ибо ранг матрицы стехиометрических коэффициентов итоговых реакций по маршрутам ${{B}_{f}}$ равен единице, а в реакционной системе имеются три небоденштейновских вещества. В качестве ключевого вещества был выбран н-пентан. Концентрации остальных небоденштейновских веществ являются линейными функциями от концентрации н-пентана.
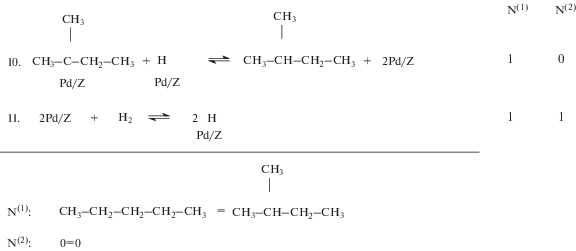
Ранг подматрицы стехиометрических коэффициентов боденштейновских веществ ${{B}_{2}}$ равен 9. В рассматриваемой реакционной системе 11 элементарных химических реакций, следовательно, по правилу Хориути существуют два маршрута, один из которых стехиометрический N1, а другой пустой N2.
Таким образом, проведен предварительный анализ кинетической модели, который позволяет уменьшить как размерность системы дифференциальных уравнений модели, так и установить конкретный вид алгебраических уравнений химических инвариантов. Теперь необходимо приступить к решению задачи об идентифицируемости констант кинетической модели. Иначе сколько и какие константы из общего числа констант допускают оценку в выбранной области экспериментирования. Решение этой задачи в данном конкретном случае определяется рангом информационной матрицы $M(\varepsilon ){\text{:}}$
где $V\left\{ {{{v}_{{ii}}} = \sigma _{i}^{2}} \right\}$ − i − номер вещества, i = 1,…, 3, $\sigma _{i}^{2}$ – его дисперсия, определяемая при измерении, $X\left\{ {{{x}_{{uj}}}} \right\}$ − матрица размерности N × q, ${{x}_{{uj}}} = \frac{{\partial {{P}_{i}}}}{{\partial {{k}_{j}}}}(u),$ N − число опытов, q − число параметров кинетической модели, u − номер, выполняемого опыта.Рассчитывается ранг матрицы $M(\varepsilon ),$ который определяет число кинетических констант, допускающих оценку. Номера независимых вектор-столбцов в $M(\varepsilon )$ характеризуют конкретную совокупность констант, допускающих оценку. При этом, так как элементы матрицы $M(\varepsilon )$ случайные числа, то ранг $M(\varepsilon )$ также случайное число. Необходимо проверить, что вычисленное случайное число значимо отличается от нуля.
Затем с использованием метода максимального правдоподобия проводим оценку параметров кинетических моделей, допускающих оценку. Планируется эксперимент с использованием критерия D-оптимальности, численное значение которого определяет объем доверительной области оценок констант. Если точность полученных значений констант достаточна для решения данной научно-технической задачи, то решение задачи планирования эксперимента на этом этапе завершается.
Однако часто требуется построить высокоточную модель, которая позволит предсказывать значения результатов экспериментов с точностью, превышающей точность первоначальных стартовых опытов. В подобной ситуации целесообразно проводить непрерывное планирование эксперимента с реализацией в точках области экспериментирования G повторных опытов. При этом следует использовать теоремы де Ла Гарза и Каратеодори, которые утверждают, что для любого плана эксперимента $\varepsilon $(x), спектр которого состоит из N-различных условий опытов (N > q − число кинетических констант модели), всегда можно вычислить план эксперимента ${{\varepsilon }_{1}}$(x) со спектром из n условий повторных опытов, причем N > n ≥ q, детерминант информационной матрицы которого $M({{\varepsilon }_{1}})$ будет равен детерминанту матрицы исходного плана $M(\varepsilon )$ со спектром из N различных условий опытов. Причем общее число опытов N в сравниваемых случаях будет одинаковым.
Использование методов последовательно планируемого повторного эксперимента позволяет вычислить кинетические константы модели с существенно большей точностью, чем по результатам неповторного эксперимента. Можно сконструировать и лабораторные реакторы, состоящие из подсистем параллельно работающих лабораторных каталитических реакторов, которые обеспечат проведение единовременного повторного эксперимента. Тем самым резко увеличивается скорость накопления экспериментальной информации в единицу времени. Кинетическая модель реакции гидроизомеризации н-пентана на высококремнистом цеолитном катализаторе ЦВМ в соответствии с механизмом реакции, представленном на рис. 1, имеет вид
(1)
$\frac{{dP{}_{1}}}{{d\tau }} = - \frac{{{{k}_{1}}\left( {A{{P}_{1}}(\tau ) - B} \right)}}{{{{P}_{3}}(\tau ) + \left( {{{k}_{2}} - {{k}_{3}}} \right){{P}_{1}}(\tau ) + {{k}_{3}}{{P}_{2}}(\tau )}},$(3)
$A = 1 + \frac{1}{{{{K}_{{eq}}}}},\,\,\,\,B = \frac{{{{P}_{1}}^{0} + P_{2}^{0}}}{{{{K}_{{eq}}}}},$(4)
${{k}_{1}} = {{k}_{{ + 6}}}\prod\limits_{i = 1}^5 {{{K}_{i}}} ,\,\,\,\,{{k}_{2}} = \prod\limits_{i = 1}^5 {{{K}_{i}}} ,\,\,\,\,{{k}_{3}} = \prod\limits_{i = 7}^{11} {K_{i}^{{ - 1}}} ,$начальные условия:
(5)
$\tau = 0,\,\,\,\,{{P}_{1}}(0) = P_{1}^{0},\,\,\,\,{{P}_{2}}(0) = P_{2}^{0},\,\,\,\,{{P}_{3}}(0) = P_{3}^{0},$Кинетические константы модели оценивались по результатам экспериментов, проведенных в проточном каталитическом реакторе в следующем диапазоне температур и давлений:
(6)
$\begin{gathered} 0 \leqslant {{P}_{1}} \leqslant 15\,\,{\text{атм}}\,\,\,\,0 \leqslant {{P}_{2}} \leqslant 10\,\,{\text{атм}}\,\,\,\, \\ 10 \leqslant {{P}_{3}} \leqslant 25\,\,{\text{атм}}\,\,\,\,10 \leqslant P \leqslant 30\,\,{\text{атм}} \\ 553 \leqslant Т \leqslant 633\,\,{\text{К}}\,\,\,\,0.5 \leqslant \tau \leqslant 2.0\,\,{\text{ч,}} \\ \end{gathered} $Для оценки кинетических констант модели использовался метод максимального правдоподобия, позволяющий не только оценить кинетические константы модели, но и параметры плотности распределения ошибок наблюдений.
Представим дифференциальное уравнение (1) в виде дифференциальных уравнений в вариациях:
(8)
$\frac{{d{{\varphi }_{i}}}}{{d\tau }} = \frac{{\partial f}}{{\partial {{k}_{j}}}} + \frac{{\partial f}}{{\partial{ \hat {\eta }}}}\frac{{\partial{ \hat {\eta }}}}{{\partial {{k}_{j}}}}\,\,\,\,i = 1,...3,$(9)
${{\varphi }_{i}}({{x}_{u}},\hat {k}) = \frac{{\partial{ \hat {\eta }}({{x}_{u}},\hat {k})}}{{\partial {{k}_{j}}}}\,\,\,\,i = 1,...,3\,\,\,\,j = 1,...,3,$начальные условия:
(10)
$\tau = 0,\,\,\,\,\hat {\eta }(0) = {{\hat {\eta }}^{0}},\,\,\,\,{{\varphi }_{i}}(0) = 0,\,\,\,\,i = 1,...,3,$При постановке стартовых опытов задается план эксперимента ε1(х), состоящий из спектра плана:
Также задается частота повторений опытов в каждой точке спектра плана:
(12)
${{\tilde {p}}_{1}},\,\,\,\,{{\tilde {p}}_{2}},...,{{\tilde {p}}_{u}},...,{{\tilde {p}}_{{n - 1}}},\,\,\,\,{{\tilde {p}}_{n}}.$Тогда информационная матрица плана эксперимента может быть представлена в виде
(13)
$М(\varepsilon ) = \sum\limits_{u = 1}^n {{{{\tilde {p}}}_{u}}\omega ({{x}_{u}})} \varphi ({{x}_{u}},k){{\left[ {\varphi ({{x}_{u}},k)} \right]}^{T}},$При общем объеме эксперимента N, причем n < N, имеем
(14)
$\begin{gathered} {{\varphi }_{1}}({{{\mathbf{x}}}_{u}},{\mathbf{k}}) = \frac{{\partial \eta ({{{\mathbf{x}}}_{u}},{\mathbf{k}})}}{{\partial {{k}_{1}}}},..., \\ {{\varphi }_{3}}({{{\mathbf{x}}}_{u}},{\mathbf{k}}) = \frac{{\partial \eta ({{{\mathbf{x}}}_{u}},{\mathbf{k}})}}{{\partial {{k}_{3}}}},\,\,\,\,u = 1,...,N. \\ \end{gathered} $По $М({{\varepsilon }_{1}})$ вычисляется дисперсия отклика $\sigma _{{\eta ({{x}_{u}})}}^{2}$ в точке ${{x}_{u}}$ области экспериментирования G по уравнению
(15)
$\sigma _{{\eta ({{x}_{u}})}}^{2} = {{\left[ {\varphi ({{x}_{u}},k)} \right]}^{T}}{{\left[ {М({{\varepsilon }_{1}})} \right]}^{{ - 1}}}\varphi ({{x}_{u}},k).$По дисперсионно-ковариационной матрице оценок констант кинетической модели ${{\Sigma }_{{\hat {k}}}} = {{\left[ {М({{\varepsilon }_{1}})} \right]}^{{ - 1}}}$ вычисляется дисперсия каждой кинетической константы как в любой точке плана ε1(х), так и в любой, произвольно выбранной точке области экспериментирования. Аналогичное справедливо и для дисперсий откликов. Причем желательно, чтобы в любой области экспериментирования выполнялось условие
(16)
$\sigma _{\eta }^{2}\left( {\varepsilon _{1}^{*}(x)} \right) = \mathop {\min }\limits_{{{\varepsilon }_{1}}(x)} \mathop {\max }\limits_x \sigma _{\eta }^{2}\left( {{{\varepsilon }_{1}}(x)} \right).$Иначе будем считать план $\varepsilon _{1}^{*}(x)$ оптимальным, если и только если он минимизирует максимальную дисперсию отклика модели в точках плана ${{\varepsilon }_{1}}(x).$
Выбор наилучшей стратегии экспериментирования требует проведения большой вычислительной работы, поэтому на каждом этапе работы желательно проверять правильность ее выполнения. Это можно осуществить, проверяя на каждом этапе вычислений справедливость выполнения соотношения
(17)
$\sum\limits_{u = 1}^n {{{{\tilde {p}}}_{u}}\omega ({{x}_{u}})} \left\{ {{{{\left[ {\varphi ({{x}_{u}},k)} \right]}}^{T}}{{{\left[ {М({{\varepsilon }_{1}})} \right]}}^{{ - 1}}}\varphi ({{x}_{u}},k)} \right\} = q,$Для однооткликовых моделей (одно ключевое вещество) имеем
где ${{Y}_{u}}$ − результат u-го эксперимента, ${{\varepsilon }_{u}}$ − ошибка эксперимента.На основании равенства (18) получаем
(19)
$\sigma _{{{{Y}_{u}}}}^{2} = \sigma _{{\hat {\eta }\left( {{{x}_{u}},k} \right)}}^{2} + \sigma _{{{{\varepsilon }_{u}}}}^{2}\,\,\,\,u = 1,...,N,$Так как дисперсии являются положительными вещественными числами, то обычно
(20)
$\sigma _{{{{Y}_{u}}}}^{2} < \sigma _{{\hat {\eta }\left( {{{x}_{u}},k} \right)}}^{2} + \sigma _{{{{\varepsilon }_{u}}}}^{2}.$Следовательно, результат измерений концентраций реагентов на некоторой лабораторной, стендовой или промышленной установке будет осуществлен с меньшей дисперсией, чем сумма дисперсий отклика и ошибки воспроизводимости. Однако для построения высокоточной модели требуется, чтобы сумма дисперсий прогноза результата эксперимента по модели и дисперсия ошибки воспроизводимости была бы меньше дисперсии наблюдений наблюдаемой в эксперименте случайной величины ${{Y}_{u}},$ т.е.
(21)
$\sigma _{{{{Y}_{u}}}}^{2} > \sigma _{{\hat {\eta }\left( {{{x}_{u}},k} \right)}}^{2} + \sigma _{{{{\varepsilon }_{u}}}}^{2} = \sigma _{{{{Y}_{u}},{\text{расч}}}}^{2}.$Очевидно, что дисперсия прогноза по модели может быть понижена на порядок и более при планировании повторных опытов.
Условия проведения первой серии стартовых опытов для оценки кинетических констант и их результаты представлены в табл. 1 для цеолитного катализатора № 1 и в табл. 2 для цеолитного катализатора № 2.
Таблица 1.
Результаты кинетических исследований реакции гидроизомеризации н-пентана на цеолитсодержащем катализаторе типа ЦВМ (катализатор № 1)
| № | Условия проведения эксперимента | Парциальное давление н-пентана на выходе из реактора, атм | |||||
|---|---|---|---|---|---|---|---|
| Время контакта τ, ч | Температура, К |
Парциальные давления реагентов в сырье, атм | |||||
| н-пентан, атм |
изопентан, атм | водород, атм |
Результаты экспериментов, атм | Расчет по модели, атм | |||
| 1 | 0 | 553 | 7.5 | 0.01 | 22.49 | 7.5 | 7.5 |
| 2 | 0.15 | 553 | 7.5 | 0.01 | 22.49 | 7.34 | 7.36 |
| 3 | 0.4 | 553 | 7.5 | 0.01 | 22.49 | 7.12 | 7.15 |
| 4 | 0.8 | 553 | 7.5 | 0.01 | 22.49 | 6.80 | 6.83 |
| 5 | 1.0 | 553 | 7.5 | 0.01 | 22.49 | 6.66 | 6.69 |
| 6 | 1.5 | 553 | 7.5 | 0.01 | 22.49 | 6.40 | 6.36 |
| 7 | 2.0 | 553 | 7.5 | 0.01 | 22.49 | 6.02 | 6.06 |
| 8 | 0 | 553 | 0.01 | 7.5 | 22.49 | 0.01 | 0.011 |
| 9 | 0.15 | 553 | 0.01 | 7.5 | 22.49 | 0.035 | 0.03 |
| 10 | 0.4 | 553 | 0.01 | 7.5 | 22.49 | 0.068 | 0.071 |
| 11 | 1.0 | 553 | 0.01 | 7.5 | 22.49 | 0.165 | 0.163 |
| 12 | 1.5 | 553 | 0.01 | 7.5 | 22.49 | 0.243 | 0.24 |
| 13 | 2.0 | 553 | 0.01 | 7.5 | 22.49 | 0.340 | 0.32 |
| 14 | 0.15 | 598 | 7.5 | 0.01 | 22.49 | 6.50 | 6.53 |
| 15 | 0.8 | 598 | 7.5 | 0.01 | 22.49 | 5.80 | 5.93 |
| 16 | 1.0 | 598 | 7.5 | 0.01 | 22.49 | 5.58 | 5.64 |
| 17 | 1.32 | 598 | 7.5 | 0.01 | 22.49 | 5.28 | 5.24 |
| 18 | 0.4 | 598 | 0.01 | 7.5 | 22.49 | 0.15 | 0.173 |
| 19 | 1.0 | 598 | 0.01 | 7.5 | 22.49 | 0.41 | 0.395 |
| 20 | 2.0 | 598 | 0.01 | 7.5 | 22.49 | 0.69 | 0.709 |
| 21 | 0.4 | 633 | 7.5 | 0.01 | 22.49 | 6.20 | 6.31 |
| 22 | 0.8 | 633 | 7.5 | 0.01 | 22.49 | 3.92 | 3.86 |
| 23 | 1.0 | 633 | 7.5 | 0.01 | 22.49 | 3.40 | 3.48 |
| 24 | 1.5 | 633 | 7.5 | 0.01 | 22.49 | 2.70 | 2.87 |
| 25 | 2.0 | 633 | 7.5 | 0.01 | 22.49 | 2.40 | 2.53 |
Таблица 2.
Результаты кинетических исследований реакции гидроизомеризации н-пентана на цеолитсодержащем катализаторе типа ЦВМ (катализатор № 2)
| № | Условия проведения эксперимента | Парциальное давление н-пентана на выходе из реактора, атм | |||||
|---|---|---|---|---|---|---|---|
| Время контакта τ, ч | Температура, К |
Парциальные давления реагентов в сырье | |||||
| н-пентан, атм |
изопентан, атм |
водород, атм |
Результаты экспериментов, атм | Расчет по модели, атм | |||
| 1 | 0 | 553 | 7.5 | 0.01 | 22.49 | – | – |
| 2 | 0.1 | 553 | 7.5 | 0.01 | 22.49 | 7.42 | 7.39 |
| 3 | 0.4 | 553 | 7.5 | 0.01 | 22.49 | 7.13 | 7.08 |
| 4 | 0.8 | 553 | 7.5 | 0.01 | 22.49 | 6.74 | 6.70 |
| 5 | 1.0 | 553 | 7.5 | 0.01 | 22.49 | 6.40 | 6.53 |
| 6 | 2.0 | 553 | 7.5 | 0.01 | 22.49 | 5.70 | 5.78 |
| 7 | 0.1 | 593 | 7.5 | 0.01 | 22.49 | 6.92 | 7.03 |
| 8 | 0.4 | 593 | 7.5 | 0.01 | 22.49 | 5.50 | 5.34 |
| 9 | 0.8 | 593 | 7.5 | 0.01 | 22.49 | 5.00 | 4.94 |
| 10 | 1.0 | 593 | 7.5 | 0.01 | 22.49 | 4.50 | 4.56 |
| 11 | 1.5 | 593 | 7.5 | 0.01 | 22.49 | 4.0 | 3.84 |
| 12 | 2.0 | 593 | 7.5 | 0.01 | 22.49 | 3.30 | 3.34 |
| 13 | 0 | 633 | 0.01 | 7.5 | 22.49 | – | – |
| 14 | 0.15 | 633 | 0.01 | 7.5 | 22.49 | 0.30 | 0.264 |
| 15 | 0.4 | 633 | 0.01 | 7.5 | 22.49 | 0.605 | 0.627 |
| 16 | 1.0 | 633 | 0.01 | 7.5 | 22.49 | 1.16 | 1.24 |
| 17 | 1.32 | 633 | 0.01 | 7.5 | 22.49 | 1.51 | 1.45 |
| 18 | 0 | 633 | 7.5 | 0.01 | 22.49 | – | – |
| 19 | 0.2 | 633 | 7.5 | 0.01 | 22.49 | 6.01 | 5.93 |
| 20 | 0.4 | 633 | 7.5 | 0.01 | 22.49 | 5.00 | 4.95 |
| 21 | 0.55 | 633 | 7.5 | 0.01 | 22.49 | 4.61 | 4.42 |
| 22 | 1.0 | 633 | 7.5 | 0.01 | 22.49 | 3.62 | 3.42 |
| 23 | 2.0 | 633 | 7.5 | 0.01 | 22.49 | 2.40 | 2.49 |
По результатам экспериментов, представленных в табл. 1 и 2, для температур 553, 593 и 633 К оценены кинетические константы моделей для катализаторов № 1 и 2. Их численные значения представлены в табл. 3.
Таблица 3.
Зависимость величин кинетических констант моделей для катализаторов № 1 и 2 от температуры
| № серии опытов |
Температура в изотермическом реакторе, К | Константы кинетической модели | |||||
|---|---|---|---|---|---|---|---|
| № 1 | № 2 | ||||||
| $k_{1}^{{(1)}}$ | $k_{2}^{{(1)}}$ | $k_{3}^{{(1)}}$ | $k_{1}^{{(2)}}$ | $k_{2}^{{(2)}}$ | $k_{3}^{{(2)}}$ | ||
| I | 553 | 7.39 | 4.24 | 13.2 | 9.98 | 6.03 | 12.0 |
| II | 593 | 28.98 | 6.30 | 16.2 | 34.5 | 6.75 | 16.2 |
| III | 633 | 100.9 | 7.40 | 18.1 | 111.5 | 7.59 | 20.2 |
Как показал анализ кинетических исследований на модифицированных палладийсодержащих катализаторах типа ЦВМ, результаты расчета концентраций ключевого вещества (н-пентана) находятся в согласии с экспериментом в интервале температур 553–633 К для катализаторов № 1 и 2. Однако в исследуемом диапазоне температур концентрации н-пентана на выходе из реактора для катализатора № 2 существенно меньше, чем для катализатора № 1. Причем разность концентраций н-пентана для исследуемых катализаторов существенно больше, чем сумма их концентрационных доверительных интервалов при любой температуре из интервала 553–633 К и одинаковых временах контакта 0.1–2.0 ч. Этот результат указывает на то, что концентрации н-пентана в опытах с испытываемыми катализаторами при одинаковых начальных условиях, температурах, временах контакта статистически значимо различаются между собой. Поэтому дальнейшие кинетические исследования для катализатора № 2 проводились при температурах 598 и 633 К при временах контакта 0.5 и 1.0 ч. При выбранных условиях конверсия ключевого вещества уже близка к равновесной. Испытываемые образцы катализатора № 2 устойчивы к закоксовыванию для времени пробега 150 ч.
Отметим, что активная поверхность катализатора № 1 формировалась методом пропитки, а катализатора № 2 методом ионного обмена. Анализ продуктового потока и поверхностей катализаторов показал, что при эксплуатации катализатора № 1 процессы крекинга н-пентана протекают активно уже при температурах выше 553 К. При 633 К закоксовывание катализатора достигает 3.5 мас. %. Для катализатора № 2 содержание кокса при этих же условиях проведения реакции не превышает 0.02 мас. %. Потери активности катализатора № 2 в испытываемом временном диапазоне замечено не было. Поэтому он был выбран для дальнейших исследований с целью построения прецизионной кинетической модели.
Для оценки точности полученных оценок констант и точности прогноза процесса по модели для катализатора № 2 построен план эксперимента из 9 повторных опытов. Для достижения высоких значений детерминанта информационной матрицы М(ε1) оказалось достаточным провести две серии экспериментов с начальными условиями
Первый компонент вектора $y$ соответствует парциальному давлению н-пентана, второй компонент – парциальному давлению изопентана, третий компонент – парциальному давлению водорода.
Варьируемыми переменными в функционале detМ(ε1) являлись точка спектра плана и весовая функция $\omega (x).$
Результаты 9 последовательно планируемых опытов, ориентированных на построение высокоточной кинетической модели для катализатора № 2, представлены в табл. 4.
Таблица 4.
Характеристики кинетической модели (катализатор № 2), кинетических констант и результатов опытов при Т = 633 К
| № | Время контакта, ч | Дисперсия единичного опыта $\sigma _{{\varepsilon (1)}}^{2}$ |
Дисперсия планированного повторного опыта $\sigma _{{{\text{повт}}}}^{2}$ | Дисперсия отклика ключевого вещества $\sigma _{{\eta \left( {{{x}_{u}},k} \right)}}^{2}$ | Дисперсия прогнозируемого значения наблюдений $\sigma _{{{{Y}_{u}}}}^{2}$ | Отклик по модели η(xu, k) |
|---|---|---|---|---|---|---|
| Начальные условия: $P_{1}^{0}$ =7.5 атм, $P_{2}^{0}$ = 0.01 атм, $P_{3}^{0}$ = 22.49 атм |
||||||
| 1 | 0.05 | 0.05471 | 0.02735 | 1.2240 × 10–4 | 0.02747 | 7.0170 |
| 2 | 0.08 | 0.05080 | 0.02540 | 2.3708 × 10–4 | 0.02563 | 6.7622 |
| 3 | 0.10 | 0.04846 | 0.02423 | 3.1095 × 10–4 | 0.02454 | 6.6041 |
| 4 | 0.20 | 0.03903 | 0.01951 | 5.7386 × 10–4 | 0.02008 | 5.9269 |
| 5 | 0.55 | 0.02176 | 0.01088 | 6.2986 × 10–4 | 0.01150 | 4.4259 |
| 6 | 1.50 | 0.00887 | 0.004435 | 2.3985 × 10–4 | 0.004674 | 2.8255 |
| 7 | 2.0 | 0.00693 | 0.003465 | 8.3333 × 10–4 | 0.004398 | 2.4991 |
| Начальные условия: $P_{1}^{0}$ = 0.01 атм, $P_{2}^{0}$ = 7.4018 атм, $P_{3}^{0}$ = 22.49 атм |
||||||
| 8 | 0.40 | 4.368 × 10–4 | 2.184 × 10–4 | 9.5227 × 10–5 | 0.0003136 | 6.2743 |
| 9 | 1.0 | 1.713 × 10–3 | 0.8575 × 10–7 | 1.9334 × 10–4 | 0.0010508 | 1.2424 |
В табл. 4 приведены условия проведения кинетических опытов, их результаты, оценки точности получаемых кинетических констант и отклика модели (парциальные давления н-пентана на выходе из реактора). Показано, что в области экспериментирования G дисперсия отклика н-пентана удовлетворяет соотношению (21).
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
При построении высокоточной кинетической модели для катализатора № 2 необходимо убедиться в том, что на основании проведенных стартовых опытов все три кинетические константы модели допускают оценку.
По общей совокупности опытов, представленных в табл. 2 и 4, для температуры 633 К оценены кинетические константы модели № 2. Их численные значения следующие:
При этом численное значение детерминанта информационной матрицы $\det \left[ {М({{\varepsilon }_{1}})} \right] = 11.7073.$
Стандартные отклонения кинетических констант ${{\sigma }_{{{{{\hat {k}}}_{1}}}}} = 4.2233,$ ${{\sigma }_{{{{{\hat {k}}}_{2}}}}} = 5.5633 \times {{10}^{{ - 1}}},$ ${{\sigma }_{{{{{\hat {k}}}_{3}}}}} = 5.8407 \times {{10}^{{ - 1}}}$ и элементы корреляционной матрицы вектора оценок констант
показывают, что detM(ε) значимо отличается от нуля и все три кинетические константы допускают оценку в выбранной области экспериментирования G.
Иначе справедливо утверждение, что построена высокоточная кинетическая модель реакции гидроизомеризации н-пентана на Pd-содержащем цеолитном катализаторе типа ЦВМ, которая прогнозирует поведение процесса по результатам прецизионного планируемого эксперимента с точностью, превышающей точность прогноза протекания процесса на основе первоначального стартового непланированного эксперимента, в соответствии с данными, представленными в табл. 4.
ЗАКЛЮЧЕНИЕ
Изучение кинетики реакции гидроизомеризации н-пентана проводилось на двух типах катализатора ЦВМ. Активная поверхность катализатора № 1 формировалась при использовании метода соосаждения, катализатора № 2 – при использовании метода ионного обмена. Проведено экспериментальное исследование кинетики реакции гидроизомеризации н-пентана на этих катализаторах, причем поставлено 60 кинетических опытов, из них 25 опытов на катализаторе № 1 и 35 на катализаторе № 2. Методом максимального правдоподобия оценены кинетические константы конкурирующих моделей. Показано, что они отражают результаты эксперимента в интервале температур 553–633 К, давлений 10–30 атм, времени контакта от 0.05 до 2.0 ч.
Показано также, что катализатор № 2 предпочтительнее катализатора № 1, ибо он превосходит его по активности, селективности и длительности эксплуатации (устойчивости к закоксовыванию). Для катализатора № 2 построена в диапазоне экспериментирования высокоточная кинетическая модель.
ОБОЗНАЧЕНИЯ
| B | матрица стехиометрических коэффициентов стадийного механизма сложной химической реакции |
| ${{B}_{1}}$ | подматрица матрицы В стехиометрических коэффициентов небоденштейновских веществ |
| ${{B}_{2}}$ | подматрица матрицы В стехиометрических коэффициентов боденштейновских веществ |
| ${{B}_{f}}$ | матрица стехиометрических коэффициентов небоденштейновских веществ в итоговых реакциях по маршрутам |
| ${{K}_{{3 \times 3}}}$ | корреляционная матрица вектора оценок констант модели |
| $K_{i}^{{}}$ | константа равновесия i-й стадии механизма химической реакции |
| $K_{{eq}}^{{}}$ | константа равновесия химической реакции гидроизомеризации н-пентана |
| ${{k}_{{ + i}}}$ | константа скорости прямой реакции i-й стадии механизма химической реакции |
| ${{\hat {k}}_{j}}$ | оценка j-й кинетической константы модели ($j = 1,...,3$) |
| $M(\varepsilon (x))$ | информационная матрица плана эксперимента |
| $N$ | общее число поставленных кинетических опытов |
| ${{N}^{{_{{(i)}}}}}$ | номер i-го маршрута химической реакции |
| $n$ | число повторных кинетических опытов спектра плана ε1(х); |
| Р | давление в реакторе, атм |
| ${{P}_{i}}$ | парциальное давление i-го реагента в реакторе, атм |
| ${{p}_{{}}}$ | номер маршрута химической реакции, р = = 1,…,2 |
| ${{\tilde {p}}_{u}}$ | частота повторения опытов в заданном u‑м эксперименте; |
| Q | число элементарных стадий механизма химической реакции |
| $q$ | число кинетических констант модели |
| ${{r}^{{(p)}}}$ | скорость химической реакции по p-му маршруту, атм/ч |
| Т | температура в реакторе, К |
| Т0 | температура на входе в каталитический слой, К |
| ${{x}_{u}}$ | условия проведения u-го опыта |
| ${{Y}_{u}}$ | результат u-го эксперимента |
| $\varepsilon (x)$ | план эксперимента с числом точек спектра плана N |
| ε1(х) | план эксперимента c числом точек спектра плана n |
| ${{\varepsilon }_{u}}$ | ошибка опыта |
| $\hat {\eta }({{x}_{u}},\hat {k})$ | отклик, оцененный по модели (парциальное давление н-пентана) |
| ${{\nu }^{{(p)}}}$ | вектор стехиометрических чисел р-го маршрута химической реакции |
| $\nu {{_{i}^{{(p)}}}^{{}}}$ | стехиометрическое число i-й стадии p-го маршрута химической реакции |
| ${{\Sigma }_{{\hat {k}}}}$ | дисперсионно-ковариационная матрица оценок кинетических констант модели $\hat {k}$, вычисленная в точках ${{x}_{u}}$ спектра плана эксперимента ε1(х) |
| $\sigma _{{{\text{оп}}}}^{2}$ | дисперсия наблюдений в единичных опытах (непланируемых) |
| $\sigma _{{{\text{повт}}}}^{2}$ | дисперсия наблюдений в повторных опытах (планируемых) |
| $\sigma _{{{{Y}_{u}}}}^{2}$ | дисперсия прогнозируемого значения наблюдений в точке ${{x}_{u}}$ спектра плана эксперимента ε1(х), оцененная методом максимального правдоподобия |
| $\sigma _{{{{\varepsilon }_{u}}}}^{2}$ | дисперсия ошибки воспроизводимости ${{\varepsilon }_{u}}$ |
| $\sigma _{{\eta \left( {{{x}_{u}},k} \right)}}^{2}$ | дисперсия прогноза протекания процесса по модели |
| τ | время пребывания реакционной смеси в каталитическом реакторе, ч |
| $\begin{gathered} {{\varphi }_{i}}({{x}_{u}},k) = \hfill \\ = \,\,\frac{{\partial \eta ({{x}_{u}},k)}}{{\partial {{k}_{j}}}} \hfill \\ \end{gathered} $ | частная производная отклика модели по j-й кинетической константе (j = 1,…,3) |
| $\omega ({{x}_{u}})$ | вес ${{x}_{u}}$ наблюдения |
ИНДЕКСЫ
Список литературы
Li S., Song H., Hu Y., Li F., Chen Y. A novel method for the synthesis of highly stable nickel-modified sulfated zirconia catalysts for n-pentane isomerization // Catal. Commun. 2018. V. 104. P. 57.
Li W., Chi K., Liu H., Ma H., Qu W., Wang C., Lu G., Tian Z. Skeletal isomerization of n-pentane: A comparative study on catalytic properties of Pt/WOx–ZrO2 and Pt/ZSM-22 // Appl. Catal., A. 2017. V. 537. P. 59.
Aboul-Gheit A.K., Gad F.K., Abdel-Aleem G.M., El-Desouki D.S., Abdel-Hamid S.M., Ghoneim S.A., Ibrahim A.H. Pt, Re and Pt–Re incorporation in sulfated zirconia as catalysts for n-pentane isomerization // Egypt. J. Pet. 2014. V. 23. № 3. P. 303.
Aliyev A.M., Safarov A.R., Gusynova A.M. Full calculation of a chemical–technological complex for processing of cracking and pyrolysis gases based on the kinetic models of the processes // Theor. Found. Chem. Eng. 2017. V. 51. № 5. P. 716. [Алиев А.М., Сафаров А.Р., Гусейнова А.М. Расчет химико-технологического комплекса по переработке газов крекинга и пиролиза на основе кинетических моделей процессов // Теор. осн. хим. технол. 2017. Т. 51. № 5. С. 569.]
Pisarenko E.V., Ponomarev A.B., Pisarenko V.N. Simulation of hydroisomerization of n-pentane into 2-methylbutane on a palladium-containing mordenite catalyst // Theor. Found. Chem. Eng. 2018 V. 52. № 4. P. 545. [Писаренко Е.В., Пономарев А.Б., Писаренко В.Н. Моделирование процесса гидроизомеризации н-пентана в 2-метилбутан на палладийсодержащем морденитном катализаторе // Теор. осн. хим. технол. 2018. Т. 52. № 4. С. 442.]
Pisarenko E.V., Ponomarev A.B., Pisarenko V.N. Analysis and modeling of n-hexane hydroisomerization process // Theor. Found. Chem. Eng. 2018. V. 52. № 1. P. 24. [Писаренко Е.В., Пономарев А.Б., Писаренко В.Н. Анализ и моделирование процесса гидроизомеризации н-гексана // Теор. осн. хим. технол. 2018. Т. 52. № 1. С. 26.]
Pisarenko E.V., Pisarenko V.N. Analysis and simulation of the nonlinear kinetics of reacting chemical systems // Theor. Found. Chem. Eng. 2013. V. 47. № 2. P. 128. [Писаренко Е.В., Писаренко В.Н. Анализ и моделирование нелинейной кинетики химических реагирующих систем // Теор. осн. хим. технол. 2013. Т. 47. № 2. С. 173.]
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии