Теоретические основы химической технологии, 2019, T. 53, № 6, стр. 634-646
Массообмен в орошаемых плоскопараллельных каналах при прямоточном ламинарном движении жидкости и газа
В. Н. Бабак *
Институт проблем химической физики РАН
Московская область, Черноголовка, Россия
* E-mail: tabor47@mail.ru
Поступила в редакцию 24.07.2018
После доработки 20.02.2019
Принята к публикации 02.04.2019
Аннотация
Исследованы гидродинамика и массообмен в регулярных пленочных устройствах, основными элементами которых являются плоские орошаемые каналы с ламинарным течением газа и жидкости. Решение задачи получено приближенным методом, позволяющим резко сократить объем необходимых вычислений. Доказано, что безразмерный поток как функцию безразмерной длины достаточно найти в ограниченной области параметров. За пределами этой области имеют место упрощения: в одних случаях изменениями концентраций в фазах в поперечном направлении можно пренебречь; в других – на всем участке активного массообмена, т.е. до достижения концентрационного равновесия в системе, в той или иной фазе существуют диффузионные слои; в третьих – сопротивление массопередаче сосредоточено в жидкости или газе и, наконец, существуют области параметров, где изменением концентрации в одной из фаз в поперечном направлении можно пренебречь, а в другой существуют диффузионные пограничные слои.
ВВЕДЕНИЕ
Двухфазные процессы переноса массы в системах жидкость–газ, когда жидкость течет в виде тонкой пленки, представляют интерес для практики. Основное достоинство пленок – это большие коэффициенты массопередачи [1, 2].
В последнее время широкое распространение получили массообменные аппараты с регулярными насадками [3]. Основными элементами таких устройств являются вертикальные плоские каналы, трубки, стандартные блоки, по внутренним или внешним стенкам которых стекают тонкие пленки жидкости в контакте с движущимся вниз (прямоток) или вверх (противоток) газовым потоком, содержащим обычно небольшое количество компонента, который необходимо удалить. Преимуществами таких массообменных устройств по сравнению с традиционными насадочными колоннами являются, во-первых, возможность избежать проблему масштабного перехода [4, 5], а во-вторых, – рассчитать процессы переноса теоретически без использования эмпирических коэффициентов, по крайней мере, при ламинарных режимах движения фаз.
При малых концентрациях растворимого компонента уравнения гидродинамики в фазах решаются независимо от уравнений конвективной диффузии. При слабом влиянии газа на жидкость, что обычно имеет место при ламинарном движении, распределение скорости в пленке, ее толщину можно рассчитать независимо от газа, считая, что трение на границе фаз равно нулю [6].
Толщины стекающих пленок и распределение скоростей в них изучались многими исследователями [7–13]. На входном участке течение пленки изменяется от первоначального распределения до предельного, определяемого известной формулой Нуссельта [14].
Анализ литературы показал, что при ламинарном течении пленки длина ее входного гидродинамического участка не превышает ${{h}_{\infty }}{{\operatorname{Re} }_{{\text{Ж}}}}$ при любом способе подачи жидкости. Этот участок намного меньше размеров реальных регулярных насадок (0.5–1 м). Последнее означает, что при расчете двухфазного массообмена в таких устройствах можно считать, что распределение скорости в жидкой фазе – парабола Нуссельта, т.е. входным участком в пленке можно пренебречь. В дальнейшем находится распределение скорости в газовой фазе, например, аналитическим методом Шлихтинга [15] или численно с помощью уравнений Навье–Стокса [16] при условии равенства скоростей на границе раздела фаз.
На практике расчеты двухфазных процессов переноса массы часто проводят, используя основное уравнение массопереноса и правило аддитивности фазовых сопротивлений [1, 17, 18]. Такие традиционные приближенные методы требуют знания локальных коэффициентов переноса в конкретных условиях, для нахождения которых требуются дополнительные эксперименты. Применимость подобных методик расчета массообмена была проанализирована в теоретических работах [19, 20] в приближении кратковременного контакта фаз в условиях прямотока. При этом заметного отклонения от приближенной методики не было обнаружено.
Условия применимости правила аддитивности фазовых диффузионных сопротивлений для расчета двухфазного массообмена в орошаемом прямоугольном канале для случаев прямо- и противотока при поршневом режиме движения фаз получены в [21] для всего участка активного массообмена, практически, до достижения концентрационного равновесия в системе. Показано, что в случае прямотока на начальном участке (вдали от равновесия) уравнение аддитивности всегда выполняется, что согласуется с [19, 20]. Однако отклонения от точного решения возрастают при увеличении длины. При противоточном движении фаз длина аппарата, полученная с помощью приближенной методики, в общем случае завышена по сравнению с теоретической. Ошибка даже при малых длинах может достигать порядка 30%, что можно объяснить принципиальным различием в распределении поверхностной концентрации в случае прямо- и противотока.
В ряде случаев перенос тепла и массы описывается однотипными уравнениями – конвективной диффузии и теплопередачи с постоянными коэффициентами. Сравни, например, процессы изотермической абсорбции между жидкостью и газом при малых концентрациях растворимого компонента и двухфазный теплообмен между газами. Это связано с тем, что все физико-химические константы, включая вязкости фаз, можно считать постоянными, несмотря на то, что изменения температуры внутри фаз при тепловых процессах значительные [22].
Задачи двухфазного тепло- и массообмена для случаев противоточного и прямоточного движения сред на участке стабилизации потоков (параболическом распределении скоростей в соседних каналах) впервые рассмотрены в [23–26]. Уравнения конвективной диффузии (теплопередачи) в фазах решались методом разделения переменных при условии сопряжения на границе раздела потоков и концентраций (температур). Рассчитаны безразмерные потоки тепла (массы) для ряда конкретных значений определяющих параметров. Однако в этих работах не анализируются распределения концентраций (температур) в зависимости от значений определяющих параметров. Например, в [27, 28] при теоретическом исследовании двухфазного массообмена в противоточной сорбционной колонке, в которой компонент жидкой фазы поглощается твердым сорбентом, было предположено, что концентрация внутри сорбента в поперечном направлении постоянна. Однако условия, при которых имеет место сделанное предположение, не уточняются.
Вопросы о распределениях концентраций в двухфазных пленочных системах при физической абсорбции при поршневых режимах движения жидкости и газа в случаях прямо- и противотока исследованы в [29]. В этой работе впервые введена плоскость абсорбционных параметров и показано, что решение достаточно получить в ограниченной части этой плоскости. Найдены области, в которых на всем участке активного массообмена изменениями концентрации в жидкой или газовой фазах в поперечном направлении можно пренебречь, области, где в той или иной фазе существуют диффузионные пограничные слои, а также диффузионные сопротивления сосредоточены в газе или жидкости. Решения, полученные при упрощенной гидродинамике движения фаз, позволяют представить физическую картину процесса, а также найти безразмерные комплексы, от которых зависят режимы поглощения. В дальнейшем, с помощью численного моделирования, можно уточнить эти приближенные решения или исследовать более сложные задачи [30, 31].
Все перечисленные выше решения по двухфазному тепло- или массообмену получены или методом разделения переменных, или численно [32, 33]. Даже если область изменения определяющих параметров ограничена, то практическое использование таких методов требует проведения большого объема вычислений: нахождения корней характеристических уравнений и т.д.
В работе [34] предложена методика приближенного аналитического решения задач двухфазного массопереноса. В основе этой методики лежит предположение, что распределения концентраций в фазах при переменной концентрации на границе раздела остаются такими же, как при постоянных поверхностных концентрациях. На примере двухфазной задачи абсорбции при поршневых гидродинамических режимах фаз было доказано, что приближенное решение практически не отличается от соответствующего решения, которое получено методом разделения переменных.
Предложенным аналитическим методом решена задача двухфазной абсорбции в орошаемой трубке при прямотоке и реальном распределении скоростей в контактирующих фазах [35].
Целью настоящей работы является получение аналогичного приближенного решения задачи двухфазного массообмена в плоском орошаемом канале.
ПОСТАНОВКА И РЕШЕНИЕ ГИДРОДИНАМИЧЕСКИХ ПРОБЛЕМ
В работе рассматривается абсорбция в жидкость компонента разбавленной газовой смеси в регулярных насадках, состоящих из плоских каналов высоты $2R,$ ширины $b$ ($b \gg R$), в которых тонкая пленка жидкости ($h \ll R$) вертикально стекает по стенкам (рис. 1а). Исследуется случай прямоточного потока газа и жидкости.
Рис. 1.
(а) – схема распределения скорости в фазах и системы координат. (б) – функции ${{F}_{1}}({{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R})$ (кривая 1) и ${{F}_{2}}({{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R})$ (кривая 2), необходимые для расчета ${{\delta }_{{\text{Г}}}}.$
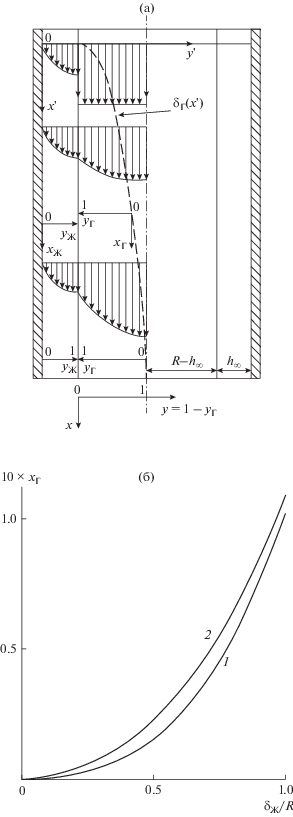
Гидродинамика жидкой пленки. Учитывая, что входной гидродинамический участок не превышает ${{h}_{\infty }}{{\operatorname{Re} }_{{\text{Ж}}}}$ [35] и при ламинарном стекании выполняется неравенство ${{h}_{\infty }}{{\operatorname{Re} }_{{\text{Ж}}}} \ll l$ ($l$ – длина канала), можно предполагать, что массопередача протекает на участке стабилизации пленки и скорость $u_{{\text{Ж}}}^{'}$ – это парабола Нуссельта, которая устанавливается сразу на входе жидкости в канал ($x{\text{'}} = 0$):
(1)
$\begin{gathered} u_{{\text{Ж}}}^{'} = \frac{3}{2}({q \mathord{\left/ {\vphantom {q {{{h}_{\infty }}}}} \right. \kern-0em} {{{h}_{\infty }}}})(2{{y}_{{\text{Ж}}}} - y_{{\text{Ж}}}^{2}), \\ {{y}_{{\text{Ж}}}} = {{y{\text{'}}} \mathord{\left/ {\vphantom {{y{\text{'}}} {{{h}_{\infty }}}}} \right. \kern-0em} {{{h}_{\infty }}}},\,\,\,\,h \cong {{h}_{\infty }} = \sqrt[3]{{\frac{{3{{\nu }^{2}}}}{g}}}\operatorname{Re} _{{\text{Ж}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}, \\ {{y}_{{\text{Г}}}} = (R - y{\text{'}})(R - h). \\ \end{gathered} $Схематическое изображение распределения скоростей в фазах, координат ($x{\text{'}},$ $y{\text{'}}$), ${{y}_{{\text{Ж}}}},$ ${{y}_{{\text{Г}}}}$ показано на рис. 1а. Профиль скорости в газе в отличие от скорости в пленке деформируется по мере удаления от входа в канал. При ламинарном установившемся течении фаз и при слабом гидродинамическом взаимодействии между ними газ не оказывает влияния на жидкость [1].
Гидродинамика газовой фазы. Предположим, что на входе канала ($x{\text{'}} = 0$) устанавливается плоский профиль газа $u_{{\text{Г}}}^{'} = {{U}_{{{\text{Г}}0}}} \geqslant u_{{\text{П}}}^{'},$ где ${{U}_{{{\text{Г}}0}}}$ – константа.
Уравнения гидродинамики с соответствующими начальными и граничными условиями запишем в декартовой системе координат $x{\text{'}},\,\,y{\text{'}}$ следующим образом:
(2)
$\begin{gathered} \frac{{\partial u_{{\text{Г}}}^{'}}}{{\partial x{\text{'}}}} + \frac{{\partial \upsilon _{{\text{Г}}}^{'}}}{{\partial y{\text{'}}}} = 0;\,\,\,\,u_{{\text{Г}}}^{'}\frac{{\partial u_{{\text{Г}}}^{'}}}{{\partial x{\text{'}}}} + \upsilon _{{\text{Г}}}^{'}\frac{{\partial u_{{\text{Г}}}^{'}}}{{\partial y{\text{'}}}} = \\ = - \frac{1}{{{{\rho }_{{\text{Г}}}}}}\frac{{\partial p}}{{\partial x{\text{'}}}} + g + {{\nu }_{{\text{Г}}}}\frac{{{{\partial }^{2}}u_{{\text{Г}}}^{'}}}{{\partial {{y}^{{'2}}}}}, \\ \end{gathered} $(3)
$\begin{gathered} x{\text{'}} = 0{\kern 1pt} :u_{{\text{Г}}}^{'} = {{U}_{{{\text{Г}}0}}};\,\,\,\,y{\text{'}} = R{\kern 1pt} :\frac{{\partial u_{{\text{Г}}}^{'}}}{{\partial y{\text{'}}}} = \upsilon _{{\text{Г}}}^{'} = 0; \\ y{\text{'}} = h{\kern 1pt} :u_{{\text{Г}}}^{'} = u_{{\text{П}}}^{'} = {\text{const}}. \\ \end{gathered} $Очевидно, что пограничный гидродинамический слой ${{\delta }_{{\text{Г}}}}$ существует вблизи поверхности пленки со стороны газа, следовательно, скорость в газе ищем в виде
(4)
$\begin{gathered} u_{{\text{Г}}}^{'} = u_{{\text{П}}}^{'} + ({{U}_{{\text{Г}}}} - u_{{\text{П}}}^{'})(2{{\eta }_{{\text{Г}}}} - \eta _{{\text{Г}}}^{2}), \\ {{\eta }_{{\text{Г}}}} = {{(y{\text{'}} - h)} \mathord{\left/ {\vphantom {{(y{\text{'}} - h)} {{{\delta }_{{\text{Г}}}}}}} \right. \kern-0em} {{{\delta }_{{\text{Г}}}}}} \leqslant 1;\,\,\,\,u_{{\text{Г}}}^{'} = {{U}_{{\text{Г}}}}, \\ {{\delta }_{{\text{Г}}}} \leqslant (y{\text{'}} - h) \leqslant (R - h) \cong R. \\ \end{gathered} $Интегрируя уравнения непрерывности (2) по $y{\text{'}}$ от $h$ до $R,$ получаем
(5)
$\Delta {{U}_{{\text{Г}}}} \equiv {{U}_{{\text{Г}}}} - u_{{\text{П}}}^{'} = {{({{U}_{{{\text{Г}}0}}} - u_{{\text{П}}}^{'})} \mathord{\left/ {\vphantom {{({{U}_{{{\text{Г}}0}}} - u_{{\text{П}}}^{'})} {\left( {1 - \frac{1}{3}{{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R}} \right)}}} \right. \kern-0em} {\left( {1 - \frac{1}{3}{{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R}} \right)}}.$Предполагается, что $h \ll R.$ Из второго уравнения (2) получим соотношение Шлихтинга [15] для нахождения ${{\delta }_{{\text{Г}}}}{\text{:}}$
(6)
$\begin{gathered} \frac{\partial }{{\partial x{\text{'}}}}\left[ {\int\limits_0^{{{\delta }_{{\text{Г}}}}} {u_{{\text{Г}}}^{'}({{U}_{{\text{Г}}}} - u_{{\text{Г}}}^{'})dy} } \right] + \\ + \,\,\left[ {\int\limits_0^{{{\delta }_{{\text{Г}}}}} {({{U}_{{\text{Г}}}} - u_{{\text{Г}}}^{'})dy} } \right]\frac{{d{{U}_{{\text{Г}}}}}}{{dx{\text{'}}}} = {{\nu }_{{\text{Г}}}}{{\left( {\frac{{\partial u_{{\text{Г}}}^{'}}}{{\partial y{\text{'}}}}} \right)}_{{\text{П}}}}. \\ \end{gathered} $Используя равенства (4) и (5), вычислим следующие интегралы:
В результате уравнение (6) принимает вид
(7)
$\begin{gathered} \left( {1 - \alpha } \right)\left[ {\frac{2}{3}\int\limits_0^{{{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R}} {\frac{{ydy}}{{1 - {y \mathord{\left/ {\vphantom {y 3}} \right. \kern-0em} 3}}} + } \int\limits_0^{{{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R}} {{{{\left( {\frac{y}{{1 - {y \mathord{\left/ {\vphantom {y 3}} \right. \kern-0em} 3}}}} \right)}}^{2}}dy} } \right] + \\ + \,\,\frac{5}{3}\alpha \int\limits_0^{{{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R}} {\frac{{ydy}}{{1 - {y \mathord{\left/ {\vphantom {y 3}} \right. \kern-0em} 3}}} = 10{{x}_{{\text{Г}}}}} . \\ \end{gathered} $Интегралы в этом уравнении находятся аналитически с точностью $ \circ {\text{(}}{{y}^{5}}{\text{)}}$ [36]:
Для расчета безразмерной толщины слоя ${{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R}$ как функции $\alpha $ и ${{x}_{{\text{Г}}}}$ получаем уравнение
(8)
${{F}_{1}}\left( {\frac{{{{\delta }_{{\text{Г}}}}}}{R}} \right)(1 - \alpha ) + {{F}_{2}}\left( {\frac{{{{\delta }_{{\text{Г}}}}}}{R}} \right)\alpha = 10{{x}_{{\text{Г}}}},$Функции ${{F}_{1}},$ ${{F}_{2}}$ показаны на рис. 1б.
Скорость $u_{{\text{Г}}}^{'}$ получаем из уравнений (4), (5), (8). При поршневом режиме движения газа ($u_{{\text{П}}}^{'} = {{U}_{{{\text{Г}}0}}},$ $\alpha = 1$) изменения скорости газа не происходит. Начальный профиль скорости заметно деформируется с увеличением xГ при $\alpha \to 0,$ и это может влиять на массообмен, особенно когда он контролируется газовой фазой.
Двухфазная массопередача в орошаемом канале. После нахождения скоростей можно сформулировать двухфазную проблему пленочной абсорбции компонентов газа. При малых концентрациях абсорбция каждого компонента протекает независимо от абсорбции других компонентов. Диффузионные уравнения для любого компонента запишем в виде
(9)
$\begin{gathered} u_{{\text{Г}}}^{'}\frac{{\partial c_{{\text{Г}}}^{'}}}{{\partial x{\text{'}}}} + v_{{\text{Г}}}^{'}\frac{{\partial c_{{\text{Г}}}^{'}}}{{\partial y{\text{'}}}} = {{D}_{{\text{Г}}}}\frac{{{{\partial }^{2}}c_{{\text{Г}}}^{'}}}{{\partial {{y}^{{'2}}}}}, \\ u_{{\text{Ж}}}^{'}\frac{{\partial c_{{\text{Ж}}}^{'}}}{{\partial x{\text{'}}}} = {{D}_{{\text{Ж}}}}\frac{{{{\partial }^{2}}c_{{\text{Ж}}}^{'}}}{{\partial {{y}^{{'2}}}}}. \\ \end{gathered} $Начальные и граничные условия равны
(10)
$\begin{gathered} c_{{\text{Г}}}^{'} = c_{{{\text{Г}}0}}^{'},\,\,\,\,c_{{\text{Ж}}}^{'} = c_{{{\text{Ж}}0}}^{'}\,\,{\text{при }}x{\text{'}} = 0; \\ {{D}_{{\text{Г}}}}{{\left( {\frac{{\partial c_{{\text{Г}}}^{'}}}{{\partial y{\text{'}}}}} \right)}_{{\text{П}}}} = {{D}_{{\text{Ж}}}}{{\left( {\frac{{\partial c_{{\text{Ж}}}^{'}}}{{\partial y{\text{'}}}}} \right)}_{{\text{П}}}},\,\,\,\,Kc_{{{\text{ГП}}}}^{'} = c_{{{\text{ЖП}}}}^{'}; \\ \frac{{\partial c_{{\text{Ж}}}^{'}}}{{\partial y{\text{'}}}} = 0\,\,{\text{при }}y{\text{'}} = 0;\,\,\,\,\frac{{\partial c_{{\text{Г}}}^{'}}}{{\partial y{\text{'}}}} = 0\,\,{\text{при }}y{\text{'}} = R. \\ \end{gathered} $Проблему массопереноса сформулируем в безразмерной форме:
(11)
$\begin{gathered} {{u}_{{\text{Г}}}}\frac{{\partial {{c}_{{\text{Г}}}}}}{{\partial {{x}_{{\text{Г}}}}}} + {{v}_{{\text{Г}}}}\frac{{\partial {{c}_{{\text{Г}}}}}}{{\partial {{y}_{{\text{Г}}}}}} = \frac{{{{\partial }^{2}}{{c}_{{\text{Г}}}}}}{{\partial y_{{\text{Г}}}^{2}}}, \\ \frac{3}{2}(2{{y}_{{\text{Ж}}}} - y_{{\text{Ж}}}^{2})\frac{{\partial {{c}_{{\text{Ж}}}}}}{{\partial {{x}_{{\text{Ж}}}}}} = \frac{{{{\partial }^{2}}{{c}_{{\text{Ж}}}}}}{{\partial y_{{\text{Ж}}}^{2}}}, \\ {{\left( {\frac{{\partial {{c}_{{\text{Г}}}}}}{{\partial {{y}_{{\text{Г}}}}}}} \right)}_{S}} = (\varepsilon {{\beta }^{2}}){{\left( {\frac{{\partial {{c}_{{\text{Ж}}}}}}{{\partial {{y}_{{\text{Ж}}}}}}} \right)}_{S}}, \\ {{c}_{{\text{П}}}} = {{c}_{{{\text{ГП}}}}} = {{c}_{{{\text{ЖП}}}}}\left( {{{y}_{{\text{Г}}}} = {{y}_{{\text{Ж}}}} = 1} \right); \\ \end{gathered} $(12)
$\begin{gathered} {{c}_{{\text{Г}}}} = 1,\,\,\,\,{{c}_{{\text{Ж}}}} = 0\,\,{\text{при }}{{x}_{{\text{Ж}}}} = 0; \\ \frac{{\partial {{c}_{{\text{Г}}}}}}{{\partial {{y}_{{\text{Г}}}}}} = 0\,\,{\text{при }}{{y}_{{\text{Г}}}} = 0;\,\,\,\,\frac{{\partial {{c}_{{\text{Ж}}}}}}{{\partial {{y}_{{\text{Ж}}}}}} = 0\,\,{\text{при }}{{y}_{{\text{Ж}}}} = 0, \\ \end{gathered} $Безразмерные концентрации фаз ${{c}_{{\text{Ж}}}},$ ${{c}_{{\text{Г}}}}$ определим по формулам
Интегральные массовые потоки $I',$ $\sum '$ через границу раздела фаз равны
(13)
$\begin{gathered} I' = bR{{U}_{{{\text{Г}}0}}}c_{{{\text{Г0}}}}^{'} - bR\int\limits_h^R {u_{{\text{Г}}}^{'}c_{{\text{Г}}}^{'}dy{\text{'}}} = \\ = bR{{U}_{{{\text{Г}}0}}}(c_{{{\text{Г0}}}}^{'} - {{c_{{{\text{Ж0}}}}^{'}} \mathord{\left/ {\vphantom {{c_{{{\text{Ж0}}}}^{'}} K}} \right. \kern-0em} K})I = \\ = b\int\limits_0^h {u_{{\text{Ж}}}^{'}c_{{\text{Ж}}}^{'}dy{\text{'}} - b{{c}_{{{\text{Ж}}0}}}q} = bq(Kc_{{{\text{Г}}0}}^{'} - c_{{{\text{Ж0}}}}^{'})\sum = \sum ', \\ \end{gathered} $Баланс массы в безразмерной форме принимает вид
Проблему (11)–(12) можно решить численно, как это было сделано для поршневого режима движения фаз в работе [29]. Однако эту и ряд подобных проблем можно решить приближенным методом, предложенным в [34], предполагая, что безразмерные потоки равны
(15)
$I = {{I}_{{\text{Г}}}}({{x}_{{\text{Г}}}})(1 - {{c}_{{\text{П}}}}(x{\text{'}})),\,\,\,\,\sum = {{\sum }_{{\text{Ж}}}}({{x}_{{\text{Ж}}}}){{c}_{{\text{П}}}}(x{\text{'}}),$Подставляя уравнения (15) в (14) для ${{c}_{{\text{П}}}}(x{\text{'}}),$ $I(x{\text{'}})$ и $\sum (x{\text{'}}),$ получаем зависимости
(16)
$\begin{gathered} {{c}_{{\text{П}}}}(x{\text{'}}) = \frac{{{{I}_{{\text{Г}}}}({{x}_{{\text{Г}}}})}}{{{{I}_{{\text{Г}}}}({{x}_{{\text{Г}}}}) + \varepsilon {{\sum }_{{\text{Ж}}}}({{x}_{{\text{Ж}}}})}} = \\ = \frac{1}{{1 + \varepsilon \left[ {{{{{\sum }_{{\text{Ж}}}}({{x}_{{\text{Ж}}}})} \mathord{\left/ {\vphantom {{{{\sum }_{{\text{Ж}}}}({{x}_{{\text{Ж}}}})} {{{I}_{{\text{Г}}}}({{x}_{{\text{Г}}}})}}} \right. \kern-0em} {{{I}_{{\text{Г}}}}({{x}_{{\text{Г}}}})}}} \right]}},\,\,\,\,\sum = \frac{{{{\sum }_{{\text{Ж}}}}}}{{1 + \varepsilon [{{{{\sum }_{{\text{Ж}}}}} \mathord{\left/ {\vphantom {{{{\sum }_{{\text{Ж}}}}} {{{I}_{{\text{Г}}}}({{x}_{{\text{Г}}}})}}} \right. \kern-0em} {{{I}_{{\text{Г}}}}({{x}_{{\text{Г}}}})}}]}}, \\ I = \frac{{\varepsilon {{\sum }_{{\text{Ж}}}}({{x}_{{\text{Ж}}}})}}{{1 + \varepsilon [{{{{\sum }_{{\text{Ж}}}}({{x}_{{\text{Ж}}}})} \mathord{\left/ {\vphantom {{{{\sum }_{{\text{Ж}}}}({{x}_{{\text{Ж}}}})} {{{I}_{{\text{Г}}}}({{x}_{{\text{Г}}}})}}} \right. \kern-0em} {{{I}_{{\text{Г}}}}({{x}_{{\text{Г}}}})}}]}}. \\ \end{gathered} $В результате решение двухфазных проблем переноса сводится к нахождению потоков ${{I}_{{\text{Г}}}}({{x}_{{\text{Г}}}})$ и ${{\sum }_{{\text{Ж}}}}({{x}_{{\text{Ж}}}}),$ т.е. к решению частных однофазных проблем переноса.
Однофазная проблема массообмена, контролируемого жидкой пленкой (${{c}_{{\text{П}}}} = 1$). В области, где диффузионный пограничный слой еще не пророс на толщину пленки, безразмерная концентрация ${{c}_{{\text{Ж}}}}$ и средняя концентрация ${{\bar {c}}_{{\text{Ж}}}} \cong {{\sum }_{{\text{Ж}}}}$ равны [37]
(17)
$\begin{gathered} {{c}_{{\text{Ж}}}} = {\text{erfc}}\left( {\frac{1}{2}\sqrt {\frac{3}{2}} {{\eta }_{{\text{Ж}}}}} \right),\,\,\,\,{{\eta }_{{\text{Ж}}}} = \frac{{1 - {{y}_{{\text{Ж}}}}}}{{\sqrt {{{x}_{{\text{Ж}}}}} }}; \\ {{{\bar {c}}}_{{\text{Ж}}}} = \int\limits_0^1 {\frac{3}{2}(2{{y}_{{\text{Ж}}}} - y_{{\text{Ж}}}^{2})} {{c}_{{\text{Ж}}}}d{{y}_{{\text{Ж}}}}; \\ \end{gathered} $(18)
$\begin{gathered} {{\sum }_{{\text{Ж}}}} = \sqrt {6{{x}_{{\text{Ж}}}}} \left\{ {\left( {\frac{{1 - {\text{exp}}( - {{A}^{2}})}}{{\sqrt \pi }}} \right) + A{\text{erfc}}(A)} \right. - \frac{8}{9}{{x}_{{\text{Ж}}}} \times \\ \left. {\,\, \times \left[ {\left( {\frac{{1 - {\text{exp}}( - {{A}^{2}})}}{{\sqrt \pi }}} \right) - \frac{{{{A}^{2}}{\text{exp}}( - {{A}^{2}})}}{{\sqrt \pi }} + {{A}^{3}}{\text{erfc(}}A)} \right]} \right\}, \\ A = \frac{1}{2}{{\sqrt {\frac{3}{2}} } \mathord{\left/ {\vphantom {{\sqrt {\frac{3}{2}} } {\sqrt {{{x}_{{\text{Ж}}}}} }}} \right. \kern-0em} {\sqrt {{{x}_{{\text{Ж}}}}} }}. \\ \end{gathered} $Решения (17), (18) имеют место при достаточно малых ${{x}_{{\text{Ж}}}}.$ Концентрация ${{c}_{{\text{Ж}}}}({{y}_{{\text{Ж}}}})$ показана на рис. 2а для ряда значений ${{x}_{{\text{Ж}}}}.$ Диффузионный слой достигает поверхности пленки при ${{x}_{{\text{Ж}}}} \to 0.14$ и концентрация ${{c}_{{\text{Ж}}}}({{y}_{{\text{Ж}}}})$ (17) совпадает с параболической зависимостью ${{c}_{{\text{Ж}}}}({{y}_{{\text{Ж}}}}) \equiv 1 - (1 - y_{{\text{Ж}}}^{2}).$ Функция сЖ ≅ $ \cong 1 - a({{x}_{{\text{Ж}}}})(1 - y_{{\text{Ж}}}^{2})$ при любой $a({{x}_{{\text{Ж}}}})$ удовлетворяет обоим граничным условиям (12): ${{c}_{{\text{П}}}} = 1$ при ${{y}_{{\text{Ж}}}} = 1$ и ${{\partial {{c}_{{\text{Ж}}}}} \mathord{\left/ {\vphantom {{\partial {{c}_{{\text{Ж}}}}} {\partial {{y}_{{\text{Ж}}}}}}} \right. \kern-0em} {\partial {{y}_{{\text{Ж}}}}}} = 0$ при ${{y}_{{\text{Ж}}}} = 0.$ При ${{x}_{{\text{Ж}}}} > 0.14,$ когда решение (17) становится неприменимым, концентрацию в жидкости можно искать в следующем виде: ${{c}_{{\text{Ж}}}} \cong 1 - a({{x}_{{\text{Ж}}}})(1 - y_{{\text{Ж}}}^{2}).$ В этом случае ${{\bar {c}}_{{\text{Ж}}}} = 1 - 0.55a({{x}_{{\text{Ж}}}})$ и $a(0.14) = 1$ (см. (17)).
Рис. 2.
Распределения концентраций в фазах: (а) – концентрация ${{c}_{{\text{Ж}}}}({{y}_{{\text{Ж}}}})$ при сопротивлении переносу в пленке: 1 – ${{x}_{{\text{Ж}}}} = 0.01,$ 2 – 0.05, 3 – 0.10, 4 – 0.14; (б) – концентрация ${{c}_{{\text{Г}}}}({{y}_{{\text{Г}}}})$ при сопротивлении переносу в газе при $\alpha = 0{\text{:}}$ 1 –${{\delta }_{{\text{Г}}}}$/R = 0, 2 – 0.5, 3 – 1.
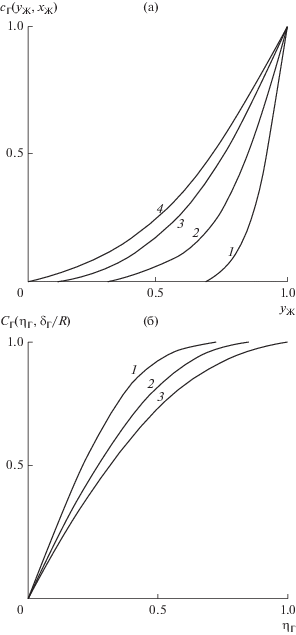
Неизвестную функцию $a({{x}_{{\text{Ж}}}})$ находим с помощью уравнения баланса для жидкой фазы:
(19)
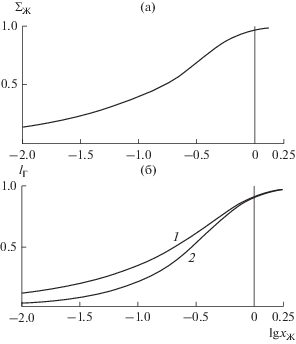
$\begin{gathered} \frac{{\partial {{{\bar {c}}}_{{\text{Ж}}}}}}{{\partial {{x}_{{\text{Ж}}}}}} = {{\left( {\frac{{\partial {{c}_{{\text{Ж}}}}}}{{\partial {{y}_{{\text{Ж}}}}}}} \right)}_{{\text{П}}}}\,\,{\text{или }}\frac{{da({{x}_{{\text{Ж}}}})}}{{d{{x}_{{\text{Ж}}}}}} = - 3.6a({{x}_{{\text{Ж}}}}), \\ a(0.14) = 1. \\ \end{gathered} $Средняя концентрация ${{\sum }_{{\text{Ж}}}} = {{\bar {c}}_{{\text{Ж}}}}$ показана на рис. 3a (см. (18), (19)):
(20)
$\begin{gathered} {{\sum }_{{\text{Ж}}}} \cong \sqrt {\frac{6}{\pi }} \sqrt {{{x}_{{\text{Ж}}}}} \left( {1 - \frac{8}{9}{{x}_{{\text{Ж}}}}} \right)\,\,\,\,({{x}_{{\text{Ж}}}} < 0.14), \\ {{\sum }_{{\text{Ж}}}} = 1 - 0.91\,{\text{exp}}( - 3.6{{x}_{{\text{Ж}}}})\,\,\,\,({{x}_{{\text{Ж}}}} \geqslant 0.14). \\ \end{gathered} $Рис. 3.
Безразмерные потоки при сопротивлении массопереносу в жидкости и газе: (а) – поток ${{\sum }_{{\text{Ж}}}}({{x}_{{\text{Ж}}}});$ (б) – поток ${{I}_{{\text{Г}}}}({{x}_{{\text{Г}}}})$ при $\alpha = 1$ (кривая 1) и при $\alpha = 0$ (кривая 2).
Решение при ${{x}_{{\text{Ж}}}} < 0.14$ получено из (18), так как $A \geqslant 1.64$ и ${\text{erfc}}(A) \ll 1.$ Решение при ${{x}_{{\text{Ж}}}} > 0.14$ – из (19), так как $a = 1.66\,{\text{exp}}( - 3.6{{x}_{{\text{Ж}}}}).$
Проблема однофазной массопередачи, контролируемой газовой фазой. Рассмотрим практически важный случай, когда скорость газа (${{U}_{{{\text{Г}}0}}}$) на входе больше, чем скорость $u_{{\text{П}}}^{'}$ (${{U}_{{{\text{Г}}0}}} \geqslant u_{{\text{П}}}^{'}$). Ниже исследуются два подслучая: скорость в газовой фазе не деформируется ($\alpha = 1,$ ${{U}_{{{\text{Г}}0}}} = u_{{\text{П}}}^{'}$) и скорость испытывает максимальную деформацию ($\alpha \ll 1,$ ${{U}_{{{\text{Г}}0}}} \gg u_{{\text{П}}}^{'}$).
Поршневое движение газа ($\alpha = 1$). Уравнение (11) и соответствующие начальные и граничные условия запишем в следующем виде:
(21)
$\begin{gathered} \frac{{\partial {{c}_{{\text{Г}}}}}}{{\partial {{x}_{{\text{Д}}}}}} = \frac{{{{\partial }^{2}}{{c}_{{\text{Г}}}}}}{{\partial y_{{\text{Г}}}^{2}}};\,\,\,\,{{x}_{{\text{Д}}}} = 0{\kern 1pt} :{{c}_{{\text{Г}}}} = 1; \\ {{y}_{{\text{Г}}}} = 1{\kern 1pt} :{{c}_{{\text{Г}}}} = 0;\,\,\,\,{{y}_{{\text{Г}}}} = 0{\kern 1pt} :\frac{{\partial {{c}_{{\text{Г}}}}}}{{\partial {{y}_{{\text{Г}}}}}} = 0. \\ \end{gathered} $Решение (21) найдено методом разделения переменных [37] и представлено на рис. 3б (кривая 1).
(22)
$\begin{gathered} {{{\bar {c}}}_{{\text{Г}}}} = \int\limits_0^1 {{{c}_{{\text{Г}}}}dy} = \sum\limits_{n = 0}^\infty {\frac{2}{{{{\pi }^{2}}{{{(n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}}^{2}}}}} {\text{exp}}( - {{\pi }^{2}}(n + \\ + \,\,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{{)}^{2}}{{x}_{{\text{Д}}}}),\,\,\,\,{{I}_{{\text{Г}}}} = 1 - {{{\bar {c}}}_{{\text{Г}}}}. \\ \end{gathered} $Предполагается, что ${{x}_{{\text{Д}}}} = {{x{\text{'}}} \mathord{\left/ {\vphantom {{x{\text{'}}} {({{R}^{2}}({{{{U}_{{{\text{Г}}0}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{Г}}0}}}} {{{D}_{{\text{Г}}}}}}} \right. \kern-0em} {{{D}_{{\text{Г}}}}}}))}}} \right. \kern-0em} {({{R}^{2}}({{{{U}_{{{\text{Г}}0}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{Г}}0}}}} {{{D}_{{\text{Г}}}}}}} \right. \kern-0em} {{{D}_{{\text{Г}}}}}}))}} \cong {{x}_{{\text{Г}}}},$ так как для разбавленных газов обычно ${{\nu }_{{\text{Г}}}} \cong {{D}_{{\text{Г}}}}$ [22].
Максимальное изменение скорости (случай ${{U}_{{{\text{Г}}0}}} \gg u_{{\text{П}}}^{'},$ $\alpha \ll 1$). Уравнения переноса в газе (11), принимая во внимание (4), (5), имеют вид
(23)
$\frac{{(2{{\eta }_{{\text{Г}}}} - \eta _{{\text{Г}}}^{2})}}{{1 - {{({{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} {R)}}} \right. \kern-0em} {R)}}} \mathord{\left/ {\vphantom {{({{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} {R)}}} \right. \kern-0em} {R)}}} 3}} \right. \kern-0em} 3}}}\frac{{\partial {{c}_{{\text{Г}}}}}}{{\partial {{x}_{{\text{Г}}}}}} = \frac{{{{\partial }^{2}}{{c}_{{\text{Г}}}}}}{{\partial y_{{\text{Г}}}^{2}}},\,\,\,\,{{\eta }_{{\text{Г}}}} = \frac{{1 - {{y}_{{\text{Г}}}}}}{{{{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R}}}.$Решение уравнения (23) в области ${{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R} < 1$ будем искать в виде ${{c}_{{\text{Г}}}} = {{c}_{{\text{Г}}}}({{\eta }_{{\text{Г}}}},{{x}_{{\text{Г}}}}),$ рассматривая переменную ${{x}_{{\text{Г}}}}$ (или ${{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R}$) как параметр. В общем случае диффузионный пограничный слой ýже, чем гидродинамический (это будет проверено ниже). Решение уравнения (23) внутри гидродинамического слоя равно
(24)
$\begin{gathered} {{c}_{{\text{Г}}}} = \frac{{\int\limits_0^{{{\eta }_{{\text{Г}}}}} {{\text{exp}}\left[ { - B({{x}_{{\text{Г}}}}){{\eta }^{3}} + {3 \mathord{\left/ {\vphantom {3 8}} \right. \kern-0em} 8}B({{x}_{{\text{Г}}}}){{\eta }^{4}}} \right]d\eta } }}{{\int\limits_0^1 {\exp \left[ { - B({{x}_{{\text{Г}}}}){{\eta }^{3}} + {3 \mathord{\left/ {\vphantom {3 8}} \right. \kern-0em} 8}B({{x}_{{\text{Г}}}}){{\eta }^{4}}} \right]d\eta } }} \cong \\ \cong \frac{{Г\left( {\frac{1}{3},t} \right) + \frac{3}{8}\frac{1}{{{{B}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}Г\left( {\frac{5}{3},t} \right)}}{{Г\left( {\frac{1}{3}} \right) + \frac{3}{8}\frac{1}{{{{B}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}Г\left( {\frac{5}{3}} \right)}} \cong \frac{{Г\left( {\frac{1}{3},t} \right)}}{{Г\left( {\frac{1}{3}} \right)}}, \\ \end{gathered} $Расчет концентраций ${{c}_{{\text{Г}}}}({{\eta }_{{\text{Г}}}})$ (24) для ряда величин отношения ${{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R}$ показан на рис. 2б. Диффузионный слой ýже гидродинамического, так как ${{c}_{{\text{Г}}}} \Rightarrow 1$ всегда при ${{\eta }_{{\text{Г}}}} \leqslant 1.$
Среднюю концентрацию ${{\bar {c}}_{{\text{Г}}}}$ в области ${{x}_{{\text{Г}}}} \leqslant 0.1$ ($0 \leqslant {{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R} \leqslant 1$) получим в результате численного интегрирования (24):
(25)
${{\bar {c}}_{{\text{Г}}}} = \int\limits_0^1 {{{c}_{{\text{Г}}}}{{u}_{{\text{Г}}}}d{{y}_{{\text{Г}}}}} \cong \frac{{1 - ({{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R})(0.4 + 0.06({{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R}))}}{{1 - {{({{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R})} \mathord{\left/ {\vphantom {{({{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R})} 3}} \right. \kern-0em} 3}}}.$При ${{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R} \to 1$ (${{x}_{{\text{Г}}}} \to 0.1$) концентрация ${{c}_{{\text{Г}}}}$ совпадает с параболической зависимостью ($1 - y_{{\text{Г}}}^{2}$) (см. рис. 2б). Эта зависимость удовлетворяет граничным условиям (21). Это значит, что в области ${{x}_{{\text{Г}}}} \geqslant 0.1$ концентрацию можно искать в виде ${{c}_{{\text{Г}}}} = a({{x}_{{\text{Г}}}})\left( {1 - y_{{\text{Г}}}^{2}} \right),$ где неизвестная функция $a({{x}_{{\text{Г}}}})$ находится из уравнения материального баланса в газе:
(26)
$\frac{{\partial {{{\bar {c}}}_{{\text{Г}}}}}}{{\partial {{x}_{{\text{Г}}}}}} = \left( {\frac{{\partial {{c}_{{\text{Г}}}}}}{{\partial {{y}_{{\text{Г}}}}}}} \right)\,\,{\text{или }}\frac{{\partial a}}{{\partial {{x}_{{\text{Г}}}}}} = - (2.5)a,\,\,\,\,a\left( {0.1} \right) = 1.$Следовательно,
(27)
$\begin{gathered} {{{\bar {c}}}_{{\text{Г}}}} = \frac{3}{2}\int\limits_0^1 {{{c}_{{\text{Г}}}}} \left( {2{{y}_{{\text{Г}}}} - y_{{\text{Г}}}^{2}} \right)d{{y}_{{\text{Г}}}} \cong 0.94\exp ( - 2.5{{x}_{{\text{Г}}}}), \\ {{x}_{{\text{Г}}}} \geqslant 0.1. \\ \end{gathered} $Безразмерный поток ${{I}_{{\text{Г}}}} = 1 - {{\bar {c}}_{{\text{Г}}}}$ при $\alpha \Rightarrow 0$ показан на рис. 3б (кривая 2). Приближенно можно считать
(28)
$\begin{gathered} {{I}_{{\text{Г}}}} \cong {{\alpha }_{{\text{Г}}}}\sqrt {{{x}_{{\text{Г}}}}} \,\,\left( {{{x}_{{\text{Г}}}} \leqslant 0.1,\,\,{{\alpha }_{{\text{Г}}}} = 0.45} \right), \\ {{I}_{{\text{Г}}}} \cong 1 - 0.94\exp ( - 2.5{{x}_{{\text{Г}}}}),\,\,\,\,{{x}_{{\text{Г}}}} \geqslant 0.1. \\ \end{gathered} $С помощью упомянутых выше решений для газовой и жидкой фаз легко найти концентрацию ${{c}_{{\text{П}}}}(0)$ на входе орошаемого канала (${{x}_{{\text{Г}}}} = {{x}_{{\text{Ж}}}} \to 0$):
(29)
$\begin{gathered} {{c}_{{\text{П}}}}(0) = \frac{1}{{1 + ({{{{\alpha }_{{\text{Ж}}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{{\text{Ж}}}}} {{{\alpha }_{{\text{Г}}}}}}} \right. \kern-0em} {{{\alpha }_{{\text{Г}}}}}})\varepsilon \beta }} \cong \frac{1}{{1 + \varepsilon {{\beta }_{1}}}}, \\ {{\beta }_{1}} = ({{{{\alpha }_{{\text{Ж}}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{{\text{Ж}}}}} {{{\alpha }_{{\text{Г}}}}}}} \right. \kern-0em} {{{\alpha }_{{\text{Г}}}}}})\beta , \\ \end{gathered} $РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Следуя работе [35], решение системы (11)–(12) при любых $\alpha $ будем рассматривать в плоскости гидродинамических переменных $X - Y,$ где $X = \lg \varepsilon ,$ $Y = \lg (\varepsilon {{\beta }_{1}})$ (рис. 4а).
Рис. 4.
(а) – плоскость переменных $X - Y.$ (б) – сравнение численного решения [29] (сплошная кривая) с расчетами по формулам (15), (16) (точки). (в) – сравнение экспериментальных данных при абсорбции СО2 в пленку воды при малых ${{\operatorname{Re} }_{{\text{Ж}}}} \leqslant 30$ (точки) с расчетной зависимостью ${{\sum }_{{\text{Ж}}}}({{x}_{{\text{Ж}}}}){\text{:}}$ а – данные [38] ($l$ = 0.21 м), б – [39] ($l$ = 1.5 м), в – [39] ($l$ = 0.5 м), г – [40] ($l$ = 0.4 м), д – [41] ($l$ = 1.22 м).
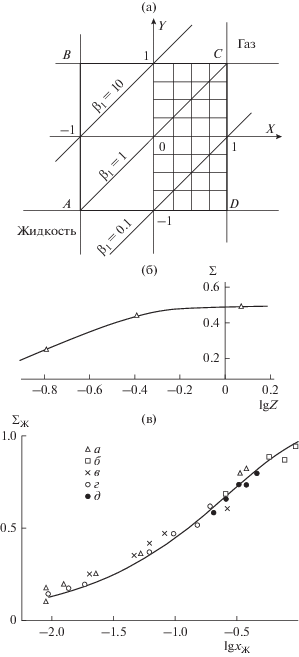
В любой точке этой плоскости безразмерные продольные координаты $Z$ определим следующим образом:
(30)
$\begin{gathered} \sqrt {{{x}_{{\text{Г}}}}} (1 - {{c}_{{\text{П}}}}(0)) = \sqrt Z \,\,\,\,(\lg X \geqslant 0); \\ \sqrt {{{x}_{{\text{Ж}}}}} {{c}_{{\text{П}}}}(0) = \sqrt Z \,\,\,\,(\lg X < 0). \\ \end{gathered} $Следовательно,
(31)
$\begin{gathered} Z = {{{{x}_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{x}_{{\text{Г}}}}} {{{{\left( {1 + \frac{1}{{\varepsilon {{\beta }_{1}}}}} \right)}}^{2}}}}} \right. \kern-0em} {{{{\left( {1 + \frac{1}{{\varepsilon {{\beta }_{1}}}}} \right)}}^{2}}}}\,\,\,\,(\lg X \geqslant 0); \\ Z = {{{{x}_{{\text{Ж}}}}} \mathord{\left/ {\vphantom {{{{x}_{{\text{Ж}}}}} {{{{\left( {1 + \varepsilon {{\beta }_{1}}} \right)}}^{2}}}}} \right. \kern-0em} {{{{\left( {1 + \varepsilon {{\beta }_{1}}} \right)}}^{2}}}}\,\,\,\,(\lg X < 0). \\ \end{gathered} $Предельные значения безразмерных потоков $I$ и $\sum $ при малых и больших значениях $Z$ в любой точке плоскости $X - Y$ равны (см. (15), (16), (28), (30))
(32)
$\begin{gathered} I \to {{\alpha }_{{\text{Г}}}}\sqrt Z ,\,\,\,\,\sum \to {{\alpha }_{{\text{Ж}}}}\sqrt Z \,\,\,\,(Z \to 0); \\ I \to \frac{\varepsilon }{{1 + \varepsilon }},\,\,\,\,\sum \to \frac{1}{{1 + \varepsilon }}\,\,\,\,(Z \to \infty ). \\ \end{gathered} $Преимущество координат $Z,$ определенных выше, в том, что выход функции $I(Z)$ на предельную величину ${\varepsilon \mathord{\left/ {\vphantom {\varepsilon {(1 + \varepsilon )}}} \right. \kern-0em} {(1 + \varepsilon )}}$ в правой половине плоскости $X - Y,$ как и выход $\sum (Z)$ на максимальное значение ${1 \mathord{\left/ {\vphantom {1 {(1 + \varepsilon )}}} \right. \kern-0em} {(1 + \varepsilon )}}$ в левой половине ($X < 0$), происходит на участке $Z$ ∼ 1. Как показано в работе [29], потоки $I(Z)$ и $\sum (Z)$ для наглядности удобно изображать на горизонтальных прямых $Y = {\text{const}}$ ($ - 1 \leqslant Y \leqslant 1$) (рис. 4а), причем для поршневых режимов можно ограничиться расчетами $I(Z)$ в правой половине плоскости $X - Y$ при $0 \leqslant X \leqslant 1,$ так как для безразмерных потоков имеет место условие симметрии: $I(X,Y,Z) = \sum ( - X, - Y,Z)$ при одинаковых $Z.$
Однако при более реальном распределении скоростей, которые предполагаются в данной работе, ограничиться расчетами при $X > 0$, т.е. в правой половине плоскости $X - Y$, нельзя, так как условия симметрии потоков не соблюдаются.
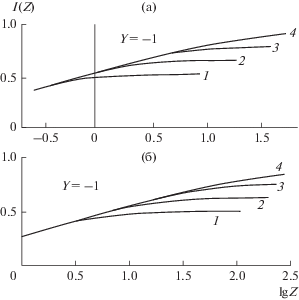
Вычисления потоков $I(Z)$ с помощью уравнений (16) на горизонтальных прямых $Y = 1,$ 0, –1 в правой половине плоскости $X - Y,$ т.е. при $1 \geqslant X \geqslant 0,$ представлены на рис. 5–7 для случаев $\alpha = 1$ и $\alpha \ll 1.$ Подобные вычисления потоков $\sum (Z)$ с помощью (16) можно также выполнить для левой половины плоскости $X - Y$ ($X < 0$). Однако мы этого делать не будем, так как зависимости $\sum (Z)$ в симметричных точках ($X \to - X,$ $Y \to - Y$) из левой половины плоскости $X - Y$ ($X < 0$) качественно совпадают с соответствующими зависимостями $I(Z)$ при $X > 0$ при одинаковых $Z$ и могут быть получены с помощью предложенного приближенного метода. Видно, что влияние параметра $\alpha = {{u_{{\text{П}}}^{'}} \mathord{\left/ {\vphantom {{u_{{\text{П}}}^{'}} {{{U}_{{{\text{Г}}0}}}}}} \right. \kern-0em} {{{U}_{{{\text{Г}}0}}}}}$ на решение в общем случае заметно. Потоки $I(Z)$ (или $\sum (Z)$) при $\alpha = 1$ и $\alpha = 0$ могут различаться в 2.5 раза в случае достаточно малых $Z,$ так как соответствующие коэффициенты ${{\alpha }_{{\text{Г}}}}$ равны ${2 \mathord{\left/ {\vphantom {2 {\sqrt \pi }}} \right. \kern-0em} {\sqrt \pi }}$ и 0.45 соответственно (см. рис. 5–7 и (28)).
Рис. 5.
(а) – безразмерный поток $I(Z)$ в правой половине плоскости $X - Y$ при $Y = 1$ и $\alpha = 1.$ Кривая 1 – $X = 0,$ 2 – 0.25, 3 – 0.5, 4 – 1.0. Кривая 5 – $I = {{I}_{{\text{Г}}}}(Z).$ (б) – то же при $\alpha = 0.$
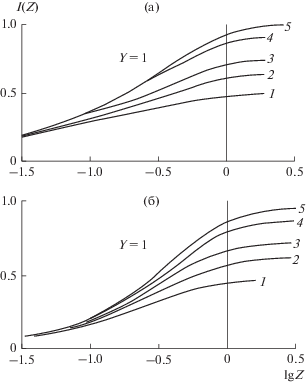
Рис. 6.
(а) – безразмерный поток $I(Z)$ при $Y = 0$ и $\alpha = 1.$ Кривая 1 – $X = 0,$ 2 – 0.25, 3 – 0.5, 4 – 1.0. (б) – то же при $\alpha = 0.$
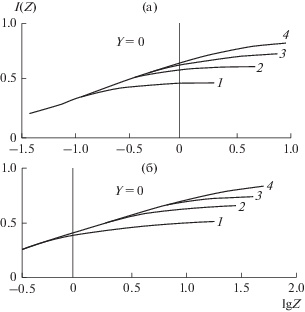
Рис. 7.
(а) – безразмерный поток $I(Z)$ при $Y = - 1$ и $\alpha = 1.$ (б) – поток $I(Z)$ при $Y = - 1,$ $\alpha = 0.$ Обозначения кривых как на рис. 6.
Расчеты показывают, что безразмерные потоки $I(Z)$ ($\sum (Z)$) зависят от обоих параметров X, $Y$ в ограниченной области плоскости $X - Y$ (внутри квадрата ABCD, рис. 4а). Вне этого квадрата имеют место упрощения. Число параметров уменьшается, и решения совпадают с предельными, которые можно получить из общих зависимостей (15), (16) при $\varepsilon {{\beta }_{1}} \to \infty ,$ $\varepsilon {{\beta }_{1}} \to 0$ и $\varepsilon \to \infty ,$ $\varepsilon \to 0$ соответственно. Например, в верхней части плоскости $X - Y$ (практически при $Y \geqslant 1$) выполняется равенство ${{c}_{{\text{П}}}}(0) \cong 0$ (29), изменением концентрации в жидкой фазе в поперечном направлении на входе ($Z = 0$) можно пренебречь, как впрочем и при любом Z, так как в этой области плоскости ${{x}_{{\text{Ж}}}} \to \infty ,$ ${{\sum }_{{\text{Ж}}}}({{x}_{{\text{Ж}}}}) \to 1,$ а следовательно, $\sum \cong {{c}_{{\text{П}}}}$ (см. (16)). В результате потоки $I(Z)$ в правой половине, а также $\sum (Z)$ в левой половине зависят только от параметра $\varepsilon {\text{:}}$
(33)
$\begin{gathered} I = I(Z,X) = \frac{\varepsilon }{{1 + {\varepsilon \mathord{\left/ {\vphantom {\varepsilon {{{I}_{{\text{Г}}}}(Z)}}} \right. \kern-0em} {{{I}_{{\text{Г}}}}(Z)}}}}\,\,\,\,\left( {X > 0} \right), \\ \sum = \sum (Z,X) = \frac{1}{{1 + {\varepsilon \mathord{\left/ {\vphantom {\varepsilon {{{I}_{{\text{Г}}}}({{\varepsilon }^{2}}{{{({{{{\alpha }_{{\text{Ж}}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{{\text{Ж}}}}} {{{\alpha }_{{\text{Г}}}}}}} \right. \kern-0em} {{{\alpha }_{{\text{Г}}}}}})}}^{2}}Z)}}} \right. \kern-0em} {{{I}_{{\text{Г}}}}({{\varepsilon }^{2}}{{{({{{{\alpha }_{{\text{Ж}}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{{\text{Ж}}}}} {{{\alpha }_{{\text{Г}}}}}}} \right. \kern-0em} {{{\alpha }_{{\text{Г}}}}}})}}^{2}}Z)}}}}\,\,\,\,\left( {X < 0} \right). \\ \end{gathered} $В нижней части плоскости $X - Y$ ($Y \leqslant - 1$) изменением концентрации в газе в поперечном направлении пренебрегаем и при любом Z, так как в этой области ${{x}_{{\text{Г}}}} \to \infty ,$ ${{I}_{{\text{Г}}}} \to 1,$ ${{c}_{{\text{П}}}}(0) = 1$ и ${{c}_{{\text{Г}}}} = {{c}_{{\text{П}}}}(Z)$ (16).
Безразмерные потоки $I(Z)$ и $\sum (Z)$ также зависят от $\varepsilon {\text{:}}$
(34)
$\begin{gathered} I = I(Z,X) = \frac{{\varepsilon {{\sum }_{{\text{Ж}}}}({{Z{{{({{{{\alpha }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{{\text{Г}}}}} {{{\alpha }_{{\text{Ж}}}}}}} \right. \kern-0em} {{{\alpha }_{{\text{Ж}}}}}})}}^{2}}} \mathord{\left/ {\vphantom {{Z{{{({{{{\alpha }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{{\text{Г}}}}} {{{\alpha }_{{\text{Ж}}}}}}} \right. \kern-0em} {{{\alpha }_{{\text{Ж}}}}}})}}^{2}}} {{{\varepsilon }^{2}}}}} \right. \kern-0em} {{{\varepsilon }^{2}}}})}}{{1 + \varepsilon {{\sum }_{{\text{Ж}}}}({{Z{{{({{{{\alpha }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{{\text{Г}}}}} {{{\alpha }_{{\text{Ж}}}}}}} \right. \kern-0em} {{{\alpha }_{{\text{Ж}}}}}})}}^{2}}} \mathord{\left/ {\vphantom {{Z{{{({{{{\alpha }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{{\text{Г}}}}} {{{\alpha }_{{\text{Ж}}}}}}} \right. \kern-0em} {{{\alpha }_{{\text{Ж}}}}}})}}^{2}}} {{{\varepsilon }^{2}}}}} \right. \kern-0em} {{{\varepsilon }^{2}}}})}}\,\,\,\,\left( {X > 0} \right), \\ \sum = \sum (Z,X) = \frac{{{{\sum }_{{\text{Ж}}}}(Z)}}{{1 + \varepsilon {{\sum }_{{\text{Ж}}}}(Z)}}\,\,\,\,\left( {X < 0} \right). \\ \end{gathered} $В правой половине плоскости $X - Y$ ($X \geqslant 1$) в жидкой фазе в области Z ~ 1, т.е. на всем участке активного массообмена, существуют диффузионные пограничные слои. Здесь ${{x}_{{\text{Ж}}}} \approx 0,$ следовательно,
(35)
$\begin{gathered} I = I(Z,Y) = \\ = \,\,{{[{{\alpha }_{{\text{Г}}}}(\varepsilon {{\beta }_{1}})\sqrt {{{x}_{{\text{Г}}}}} ]} \mathord{\left/ {\vphantom {{[{{\alpha }_{{\text{Г}}}}(\varepsilon {{\beta }_{1}})\sqrt {{{x}_{{\text{Г}}}}} ]} {[1 + {{\alpha }_{{\text{Г}}}}(\varepsilon {{\beta }_{1}})}}} \right. \kern-0em} {[1 + {{\alpha }_{{\text{Г}}}}(\varepsilon {{\beta }_{1}})}}{{\sqrt {{{x}_{{\text{Г}}}}} } \mathord{\left/ {\vphantom {{\sqrt {{{x}_{{\text{Г}}}}} } {{{I}_{{\text{Г}}}}}}} \right. \kern-0em} {{{I}_{{\text{Г}}}}}}({{x}_{{\text{Г}}}})], \\ {{x}_{{\text{Г}}}} = {{(1 + {1 \mathord{\left/ {\vphantom {1 {\varepsilon {{\beta }_{1}}}}} \right. \kern-0em} {\varepsilon {{\beta }_{1}}}})}^{2}}Z. \\ \end{gathered} $Безразмерный поток зависит только от параметра Y.
В левой половине плоскости $X - Y$($X \leqslant - 1$) в области Z ~ 1 диффузионные пограничные слои существуют в газовой фазе. Здесь ${{x}_{{\text{Г}}}} \approx 0.$ В результате поток также зависит от Y:
(36)
$\begin{gathered} \sum = \sum (Z,Y) = \frac{{{{\sum }_{{\text{Ж}}}}({{x}_{{\text{Ж}}}})}}{{{{1 + (\varepsilon {{\beta }_{1}}){{\sum }_{{\text{Ж}}}}({{x}_{{\text{Ж}}}})} \mathord{\left/ {\vphantom {{1 + (\varepsilon {{\beta }_{1}}){{\sum }_{{\text{Ж}}}}({{x}_{{\text{Ж}}}})} {{{\alpha }_{{\text{Ж}}}}\sqrt {{{x}_{{\text{Ж}}}}} }}} \right. \kern-0em} {{{\alpha }_{{\text{Ж}}}}\sqrt {{{x}_{{\text{Ж}}}}} }}}}, \\ {{x}_{{\text{Ж}}}} = {{(1 + \varepsilon {{\beta }_{1}})}^{2}}Z. \\ \end{gathered} $Таким образом, решение, полученное в данной работе приближенным методом, так же как и численные решения [29], зависит от обоих параметров X и $Y$ только внутри квадрата ABCD (рис. 4а). Вне этого квадрата число параметров уменьшается: выше ВС и ниже АD решение зависит только от X (см. уравнения (33), (34)), в области справа от CD и слева от AB (уравнения (35), (36)) решение зависит только от Y.
В плоскости $X - Y$ имеются области, где потоки, рассматриваемые как функции Z, не зависят ни от X, ни от Y. Во-первых, это верхний правый угол C, где сопротивление лимитируется газовой фазой (${{c}_{{\text{П}}}} \to 0,$ $I(z) \to {{I}_{{\text{Г}}}}({{x}_{{\text{Г}}}}) = {{I}_{{\text{Г}}}}(Z)$), и, соответственно, нижний левый угол A, где массопередача контролируется жидкой фазой (${{c}_{{\text{П}}}} \to 1,$ $\sum (z) \to {{\sum }_{{\text{Ж}}}}({{x}_{{\text{Ж}}}}) = {{\sum }_{{\text{Ж}}}}(Z)$). Безразмерные потоки не зависят от X, $Y$ также в нижнем правом углу D плоскости $X - Y$ ($X \geqslant 1,$ $Y \leqslant - 1$) и в верхнем левом углу B ($X \leqslant - 1,$ $Y \geqslant 1$), где безразмерные потоки равны соответственно
(37)
$I = \frac{{{{\alpha }_{{\text{Г}}}}\sqrt Z }}{{1 + {{\alpha }_{{\text{Г}}}}\sqrt Z }},\,\,\,\,\sum = \frac{{{{\alpha }_{{\text{Ж}}}}\sqrt Z }}{{1 + {{\alpha }_{{\text{Ж}}}}\sqrt Z }}.$Первая формула (37) получена из (34) при $\varepsilon \to \infty $ и из (35) при $\varepsilon {{\beta }_{1}} \to 0.$ В нижнем правом углу плоскости $X - Y$ эти зависимости совпадают между собой. Очевидно, в этой области поперечным изменением концентрации в газе можно пренебречь, а в жидкой фазе на всем участке массообмена существует диффузионный пограничный слой.
Вторая формула (37) получена из (34) при $\varepsilon \to 0$ и из (36) при $\varepsilon {{\beta }_{1}} \to \infty .$
В левом верхнем углу плоскости $X - Y$ диффузионный пограничный слой существует в газе, а поперечным изменением концентрации можно пренебречь в жидкости.
В заключение отметим, что по физическому смыслу предложенный выше метод расчета двухфазного массообмена в регулярных пленочных устройствах применим независимо от гидродинамики контактирующих фаз.
Сравнение точного решения для двухфазной абсорбции в орошаемом плоском канале при поршневых режимах, полученного методом разделения переменных в работе [29], с приближенным решением (15), (16) проведено в [34]. В этом случае ${{\alpha }_{{\text{Г}}}} = {{\alpha }_{{\text{Ж}}}} = {2 \mathord{\left/ {\vphantom {2 {\sqrt \pi }}} \right. \kern-0em} {\sqrt \pi }},$ $\varepsilon {{\beta }_{1}} = \varepsilon \beta ,$ ${{\sum }_{{\text{Ж}}}} = F({{x}_{{\text{Ж}}}}),$ ${{I}_{{\text{Г}}}} = F({{x}_{{\text{Г}}}}),$ где
В качестве примера такое сравнение приведено на рис. 4б в центре гидродинамической плоскости, при $X = Y = 0.$ Подобные сравнения, приведенные в [34] в других точках плоскости $X - Y,$ свидетельствуют о практической идентичности указанных решений.
На рис. 4в представлены экспериментальные данные ряда исследователей [38–41] по абсорбции плохорастворимого газа СО2 в стекающую под действием силы тяжести пленку жидкости при температуре 20°С ($K \cong 1.4$) для безволнового режима движения (${{\operatorname{Re} }_{{\text{Ж}}}} \leqslant 30$). Как видно, экспериментальные точки располагаются вблизи теоретической кривой (20), полученной приближенным методом. Все эксперименты проведены при соблюдении неравенств $\varepsilon \leqslant 0.1,$ $\varepsilon {{\beta }_{1}} \leqslant 0.1,$ т.е. в левом нижнем углу плоскости $X - Y$ (рис. 4а), где сопротивление переносу сосредоточено в пленке.
В диссертации автора [42] приведены эксперименты по абсорбции в воду хорошо растворимого газа NH3 ($K \cong {{10}^{3}}$) при ламинарном течении в трубках (${{R}_{{\text{Г}}}} \leqslant {{10}^{3}}$) при соблюдении неравенств $\varepsilon \geqslant 10,$ $\varepsilon {{\beta }_{1}} \geqslant 10,$ $\alpha \leqslant 0.1.$ Экспериментальные точки располагались вблизи соответствующей теоретической кривой ${{I}_{{\text{Г}}}}({{x}_{{\text{Г}}}})$ для орошаемых трубок.
Указанное выше свидетельствует о достоверности приближенного метода для решения проблем двухфазного массопереноса независимо от гидродинамики.
В работах [43, 44] показано, что такие процессы, как поглощение некоторых неорганических газов (SO2, H2S, HCl) водой, водными растворами кислот, щелочей, солей, первичных аминов и аммиака, в ряде случаев можно свести к решению уравнений конвективной диффузии в газовой и жидкой фазах с тем отличием, что условия для концентраций на фазовой границе являются нелинейными. Все эти задачи были решены при условии поршневого движения газа и жидкости. Однако они могут быть решены предложенным в данной работе, приближенным, аналитическим методом при более реальных распределениях скоростей.
ЗАКЛЮЧЕНИЕ
В настоящей работе исследован двухфазный массообмен в орошаемых плоских каналах, являющихся составной частью регулярных насадок при ламинарном прямоточном течении фаз с учетом торможения газового потока пленкой жидкости. Предложен приближенный аналитический метод для расчета безразмерного потока. Решение двухфазной задачи переноса сведено к решению частных предельных задач для случаев, когда сопротивление массообмену сосредоточено в газовой и жидкой фазах.
Для наглядного представления безразмерных потоков как функции безразмерной длины $Z$ вводится плоскость гидродинамических переменных $X - Y.$ Показано, что решение достаточно получить в ограниченной области этой плоскости ($ - 1 \leqslant X \leqslant 1,$ $ - 1 \leqslant Y \leqslant 1$). Вне этой области имеют место некоторые упрощения: например, сопротивление массообмену сосредоточено в газовой или жидкой фазе, изменениями концентраций в поперечных направлениях в той или иной фазе можно пренебречь или, наоборот, существуют диффузионные пограничные слои в жидкой и газовой фазах на всем участке активного массообмена.
Торможение газа пленкой негативно влияет на процесс массопередачи и в общем случае приводит к уменьшению потока. Это влияние возрастает при уменьшении размеров канала и при увеличении сопротивления массообмену в газовой фазе.
Предложенный в работе метод расчета может быть использован при исследовании широкого класса двухфазных задач переноса, которые сводятся к решению уравнений конвективной диффузии в контактирующих фазах с более сложными условиями на границе раздела.
ОБОЗНАЧЕНИЯ
| $b$ | ширина плоского канала, м |
| $c_{{\text{Ж}}}^{'},$$c_{{\text{Г}}}^{'}$ | концентрация компонента в фазах, моль/м3 |
| ${{c}_{{\text{Ж}}}},$${{c}_{{\text{Г}}}}$ | безразмерная концентрация в фазах |
| ${{D}_{{\text{Ж}}}},$${{D}_{{\text{Г}}}}$ | коэффициенты диффузии, м2/с |
| ${\text{erfc}}(x) = 1 - {\text{erf}}(x),$${\text{erf}}(x)$ | функция ошибок |
| $g$ | ускорение свободного падения, м/с2 |
| h, ${{h}_{\infty }}$ | толщина пленки и ее предельное значение, м |
| I', $\sum '$ | интегральные потоки массы через границу раздела фаз, моль/с |
| I, $\sum $ | безразмерные интегральные потоки |
| ${{I}_{{\text{Г}}}},$${{I}_{{\text{Ж}}}}$ | безразмерные потоки при сопротивлении переносу в газе и жидкости |
| $K$ | константа равновесия на границе раздела |
| $l$ | длина канала, м |
| $p$ | давление, Па |
| $q$ | плотность орошения, м2 с |
| $R$ | полувысота канала, м |
| ${{U}_{{\text{Г}}}},$${{U}_{{{\text{Г}}0}}}$ | скорость газа в ядре потока и на входе в канал, м/с |
| $u_{{\text{Ж}}}^{'}$ | продольная компонента скорости в пленке, м/с |
| $u_{{\text{Ж}}}^{'},$$v_{{\text{Г}}}^{'}$ | продольная и поперечная скорости в газе, м/с |
| ${{u}_{{\text{Г}}}} = {{u_{{\text{Г}}}^{'}} \mathord{\left/ {\vphantom {{u_{{\text{Г}}}^{'}} {{{U}_{{{\text{Г}}0}}},}}} \right. \kern-0em} {{{U}_{{{\text{Г}}0}}},}}$${{v}_{{\text{Г}}}} = {{Rv_{{\text{Г}}}^{'}} \mathord{\left/ {\vphantom {{Rv_{{\text{Г}}}^{'}} {{{\nu }_{{\text{Г}}}}}}} \right. \kern-0em} {{{\nu }_{{\text{Г}}}}}}$ | безразмерные скорости в газе |
| ${{u}_{{\text{Ж}}}} = {{u_{{\text{Ж}}}^{'}} \mathord{\left/ {\vphantom {{u_{{\text{Ж}}}^{'}} {({q \mathord{\left/ {\vphantom {q h}} \right. \kern-0em} h})}}} \right. \kern-0em} {({q \mathord{\left/ {\vphantom {q h}} \right. \kern-0em} h})}}$ | безразмерная продольная скорость в пленке, м/с |
| $u_{{\text{П}}}^{'}$ | скорость жидкости на поверхности пленки, м/с |
| $X = \lg \varepsilon ,$$Y = \lg (\varepsilon {{\beta }_{1}})$ | безразмерные параметры |
| $(x',\,y')$ | декартовая система координат; $x{\text{'}} = 0$ на входе газа и жидкости в канал; $y{\text{'}} = 0$ на стенке, м |
| ${{x}_{{\text{Ж}}}} = {{x{\text{'}}} \mathord{\left/ {\vphantom {{x{\text{'}}} {({{hq} \mathord{\left/ {\vphantom {{hq} {{{D}_{{\text{Ж}}}}}}} \right. \kern-0em} {{{D}_{{\text{Ж}}}}}})}}} \right. \kern-0em} {({{hq} \mathord{\left/ {\vphantom {{hq} {{{D}_{{\text{Ж}}}}}}} \right. \kern-0em} {{{D}_{{\text{Ж}}}}}})}},$${{x}_{{\text{Г}}}} = {{x{\text{'}}} \mathord{\left/ {\vphantom {{x{\text{'}}} {({{R}^{2}}({{{{U}_{{{\text{Г}}0}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{Г}}0}}}} {{{D}_{{\text{Г}}}}}}} \right. \kern-0em} {{{D}_{{\text{Г}}}}}}))}}} \right. \kern-0em} {({{R}^{2}}({{{{U}_{{{\text{Г}}0}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{Г}}0}}}} {{{D}_{{\text{Г}}}}}}} \right. \kern-0em} {{{D}_{{\text{Г}}}}}}))}}$$ \cong {{x{\text{'}}} \mathord{\left/ {\vphantom {{x{\text{'}}} {({{R}^{2}}({{{{U}_{{{\text{Г}}0}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{Г}}0}}}} {{{\nu }_{{\text{Г}}}}}}} \right. \kern-0em} {{{\nu }_{{\text{Г}}}}}}))}}} \right. \kern-0em} {({{R}^{2}}({{{{U}_{{{\text{Г}}0}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{Г}}0}}}} {{{\nu }_{{\text{Г}}}}}}} \right. \kern-0em} {{{\nu }_{{\text{Г}}}}}}))}}$ | безразмерные продольные координаты в фазах |
| ${{y}_{{\text{Ж}}}} = {{y{\text{'}}} \mathord{\left/ {\vphantom {{y{\text{'}}} h}} \right. \kern-0em} h},$${{y}_{{\text{Г}}}} = {{(R - y{\text{'}})} \mathord{\left/ {\vphantom {{(R - y{\text{'}})} {(R - h)}}} \right. \kern-0em} {(R - h)}}$ | безразмерные поперечные координаты |
| $Z$ | безразмерная диффузионная координата |
| $\alpha = {{u_{{\text{П}}}^{'}} \mathord{\left/ {\vphantom {{u_{{\text{П}}}^{'}} {{{U}_{{{\text{Г0}}}}}}}} \right. \kern-0em} {{{U}_{{{\text{Г0}}}}}}}$ | параметр, влияющий на скорость в газе |
| ${{\alpha }_{{\text{Г}}}},$${{\alpha }_{{\text{Ж}}}}$ | коэффициенты в асимптотических зависимостях потоков ${{I}_{{\text{Г}}}} = {{\alpha }_{{\text{Г}}}}\sqrt {{{x}_{{\text{Г}}}}} $ и ΣЖ = ${{\alpha }_{{\text{Ж}}}}\sqrt {{{x}_{{\text{Ж}}}}} $ при малых аргументах |
| $\begin{gathered} {{\beta }^{2}} = \hfill \\ = \,\,{{({{R}^{2}}{{{{U}_{{{\text{Г}}0}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{Г}}0}}}} {{{D}_{{\text{Г}}}}}}} \right. \kern-0em} {{{D}_{{\text{Г}}}}}})} \mathord{\left/ {\vphantom {{({{R}^{2}}{{{{U}_{{{\text{Г}}0}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{Г}}0}}}} {{{D}_{{\text{Г}}}}}}} \right. \kern-0em} {{{D}_{{\text{Г}}}}}})} {({{hq} \mathord{\left/ {\vphantom {{hq} {{{D}_{{\text{Ж}}}})}}} \right. \kern-0em} {{{D}_{{\text{Ж}}}})}}}}} \right. \kern-0em} {({{hq} \mathord{\left/ {\vphantom {{hq} {{{D}_{{\text{Ж}}}})}}} \right. \kern-0em} {{{D}_{{\text{Ж}}}})}}}}, \hfill \\ \end{gathered} $$\beta _{1}^{2} = {{\beta }^{2}}{{({{{{\alpha }_{{\text{Ж}}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{{\text{Ж}}}}} {{{\alpha }_{{\text{Г}}}}}}} \right. \kern-0em} {{{\alpha }_{{\text{Г}}}}}})}^{2}}$ | отношения характерных диффузионных размеров фаз; |
| ${\text{Г}}(\alpha ) = \int\limits_0^\infty {{{t}^{{\alpha - 1}}}{\text{exp}}{{{( - t)}}^{{ - t}}}dt} ,$${\text{Г}}(\alpha ,t)$ = $\int\limits_0^t {{{t}^{{\alpha - 1}}}{\text{exp}}( - t)dt} $ | гамма-функция и неполная гамма-функция |
| ${{\delta }_{{\text{Г}}}}$ | толщина гидродинамического пограничного слоя в газе, м |
| $\varepsilon = {{qK} \mathord{\left/ {\vphantom {{qK} {R{{U}_{{{\text{Г}}0}}}}}} \right. \kern-0em} {R{{U}_{{{\text{Г}}0}}}}}$ | абсорбционный фактор |
| ${{\eta }_{{\text{Г}}}} = {{(y{\text{'}} - h)} \mathord{\left/ {\vphantom {{(y{\text{'}} - h)} {{{\delta }_{{\text{Г}}}}}}} \right. \kern-0em} {{{\delta }_{{\text{Г}}}}}}$$ \cong {{(1 - {{y}_{{\text{Г}}}})} \mathord{\left/ {\vphantom {{(1 - {{y}_{{\text{Г}}}})} {({{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R})}}} \right. \kern-0em} {({{{{\delta }_{{\text{Г}}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{\text{Г}}}}} R}} \right. \kern-0em} R})}}$ | безразмерная координата внутри пограничного слоя в газе |
| $\nu $ | кинематическая вязкость, м2/с |
| $\rho $ | плотность, кг/м3 |
| ${{\operatorname{Re} }_{{\text{Ж}}}} = {q \mathord{\left/ {\vphantom {q {{{\nu }_{{\text{Ж}}}}}}} \right. \kern-0em} {{{\nu }_{{\text{Ж}}}}}},$${{\operatorname{Re} }_{{\text{Г}}}} = {{{{R}^{2}}{{U}_{{{\text{Г}}0}}}} \mathord{\left/ {\vphantom {{{{R}^{2}}{{U}_{{{\text{Г}}0}}}} {{{\nu }_{{\text{Г}}}}}}} \right. \kern-0em} {{{\nu }_{{\text{Г}}}}}}$ | числа Рейнольдса в фазах |
ИНДЕКСЫ
Список литературы
Рамм В.М. Абсорбция газов. М.: Химия, 1976.
Гимбутис П. Теплообмен при гравитационном течении пленки жидкости. Вильнюс: Мо-кслас, 1988.
Воинов Н.А., Николаев Н.А. Пленочные трубчатые газо-жидкостные реакторы. Казань: Отечество, 2008.
Rosen A.N., Kostanyan D.E. Scaling-up effect in chemical engineering // Theor. Found. Chem. Eng. 2002. V. 36. № 4. P. 307. [Розен А.Н., Костанян А.Е. К вопросу о масштабном переходе в химической технологии // Теор. осн. хим. технол. 2002. Т. 36. № 4. С. 339.]
Вертузаев Е.Д. Опыт масштабного перехода при разработке промышленных массообменных аппаратов // Хим. пром-сть. 1990. № 4. С. 223.
Тананайко Ю.Н., Воронцов Е.Г. Методы расчета и исследования пленочных процессов. Киев: Техника, 1975.
Hassan N.A. Laminar flow along a vertical wall // Trans. ASME, Ser. E. 1967. V. 34. № 3. P. 535.
Cerro R.L., Whitaker S. Entrance region flow with a free surface of the falling liquid film // Chem. Eng. Sci. 1971. V. 26. № 10. P. 785.
Воронцов Е.Г., Яхно Д.М. Локальная толщина орошаемой пленки на входном участке // Прикл. мех. тех. физ. 1974. № 4. С. 64.
Stücheli A., Özisik M.N. Hydrodynamic entrance lengths of laminar falling films // Chem. Eng. Sci. 1976. V. 31. № 5. P. 369.
Кулов Н.Н., Муравьев М.Ю., Малюсов В.А., Жаворонков Н.М. Профили скорости в стекающих пленках жидкости // Теор. осн. хим. технол. 1982. Т. 16. № 4. С. 499.
Воронцов Е.Г., Гандзюк Ю.М. Исследование поля скоростей на начальном участке течения пленки // Инж.-физ. ж. 1986. Т. 50. № 6. С. 913.
Айнштейн В.Г., Захаров М.К. Оценка длины участка гидродинамической стабилизации при гравитационном течении пленки жидкости // Теор. осн. хим. технол. 1990. Т. 24. № 3. С. 393.
Nusselt W. Die Oberflächenkondensation des Wasserdampfes // Z. Ver. Dtsch. Ing. 1916. Bd. 60. № 27. S. 541.
Шлихтинг Г. Теория пограничного слоя. М.: Наука, 1974.
Ландау Л.О., Лифшиц Е.М. Гидродинамика. М.: Наука, 1988.
Лыков А.В. Теория теплопроводности. М.: Гостехтеориздат, 1952.
Кутателадзе С.С. Основы теории теплообмена. М.: Атомиздат, 1979.
Szekely J. Notes on the transfer at the interface of two independently stirred liquids // Int. J. Heat Mass Transfer. 1963. V. 6. № 9. P. 833.
King C.J. The additivity of individual phase resistances in mass transfer operations // AIChE J. 1964. V. 10. № 5. P. 671.
Бабак В.Н. О применимости уравнения аддитивности фазовых диффузионных сопротивлений для средних коэффициентов массоотдачи при физической абсорбции // Теор. осн. хим. технол. 1978. Т. 12. № 4. С. 483.
Рид Р., Праусниц Дж., Шервуд Т. Свойства газов и жидкостей. Л.: Химия, 1982.
Позин М.Е. Теория хемосорбции // Ж. прикл. хим. 1948. Т. 21. № 1. С. 58.
Nunge R.J., Gill W.N. An analytical study of laminar counterflow double-pipe heat exchangers // AIChE J. 1966. V. 12. № 2. P. 279.
Nunge R.J., Gill W.N. Analysis of heat or mass transfer in some countercurrent flow // Int. J. Heat Mass Transfer. 1965. V. 8. № 6. P. 873.
Stein R.P. Mathematical and practical aspects of heat transfer in double pipe heat exchangers // Proceedings of the Third International Heat Transfer Conference. New York: American Institute of Chemical Engineers, 1966. V. 1. P. 139.
Сафонов М.С., Потапов Ю.Т. К теории противоточного массо- и теплообмена // Теор. осн. хим. технол. 1968. Т. 2. № 4. С. 565.
Сафонов М.С., Потапов Ю.Т. К расчету противоточного тепло- и массообмена // Теор. осн. хим. технол. 1972. Т. 7. № 4. С. 496.
Бабак В.Н., Бабак Т.Б., Холпанов Л.П., Малюсов В.А., Жаворонков Н.М. Тепло-массообмен между пленкой жидкости и газом в режиме противотока и прямотока при поршневом движении фаз // Теор. осн. хим. технол. 1978. Т. 12. № 1. С. 3.
Kenig E.Ya. Mass transfer-reaction coupling in two-phase multicomponent fluid systems // Chem. Eng. J. 1995. V. 57. P. 189.
Boyadjiev Ch. Mechanism of gas absorption with two-phase absorbents // Int. J. Heat Mass Transfer. 2011. V. 54. P. 3004.
Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Физматгиз, 1966.
Самарский А.А. Теория разностных схем. М.: Наука, 1983.
Babak V.N., Babak T.B., Kholpanov L.P. Unsteady-state mass transfer of gases between two quiescent phases // Theor. Found. Chem. Eng. 2004. V. 38. № 5. P. 462. [Бабак В.Н., Бабак Т.Б., Холпанов Л.П. Нестационарный массоперенос газов между двумя неподвижными фазами // Теор. осн. хим. технол. 2004. Т. 38. № 5. С. 490.]
Babak V.N. Two-phase mass exchange in irrigated tubular packing for the concurrent laminar phase flow // Theor. Found. Chem. Eng. 2015. V. 49. № 5. P. 636. [Бабак В.Н. Двухфазный массообмен в орошаемых трубчатых насадках при прямоточном ламинарном потоке фаз // Теор. осн. хим. технол. 2015. Т. 49. № 5. С. 543.]
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Физматгиз, 1963.
Левич В.Г. Физико-химическая гидродинамика. М.: Гос. изд-во физ.-мат. лит., 1959.
Авдонин Ю.А. Сравнительное исследование массообмена при пленочной ректификации и абсорбции, а также некоторые вопросы гидродинамики пленочного течения жидкости с противотоком газа. Автореф. дис. … канд. техн. наук. М.: Государственный институт азотной промышленности, 1967.
Борисов Г.С. Исследование массообмена в пленке жидкости. Автореф. дис. … канд. техн. наук. М.: Московский институт химического машиностроения, 1964.
Конобеев Б.И. Массообмен в тонких пленках жидкости. Автореф. дис. … канд. хим. наук. М.: Научно-исследовательский физико-химический институт им. Л.Я. Карпова, 1958.
Малюсов В.А. Исследование массообмена в процессе пленочной абсорбции. Автореф. дис. … канд. техн. наук. М.: Научно-исследовательский физико-химический институт им. Л.Я. Карпова, 1951.
Бабак В.Н. Тепломассоперенос в двухфазных системах с фиксированной поверхностью контакта фаз. Автореф. дис. … докт. физ.-мат. наук. Иваново: Ивановский государственный химико-технологический университет, 2014.
Babak V.N. Absorption of gases by aqueous solutions of acids and alkalis // Theor. Found. Chem. Eng. 2005. V. 39. № 2. P. 141. [Бабак В.Н. Поглощение газов водными растворами кислот и щелочей // Теор. осн. хим. технол. 2005. Т. 39. № 2. С. 152.]
Babak V.N. Absorption of organic gases by aqueous solutions of salts, primary amines and ammonia // Theor. Found. Chem. Eng. 2005. V. 39. № 4. P. 367. [Бабак В.Н. Поглощение неорганических газов водными растворами солей, первичных аминов и аммиака // Теор. осн. хим. технол. 2005. Т. 39. № 4. С. 390.]
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


