Теоретические основы химической технологии, 2019, T. 53, № 6, стр. 703-714
Растворимость озона в водных растворах щавелевой кислоты, нитратов калия и натрия: определение анион-специфического параметра для оксалат-иона в модели растворимости газов в растворах электролитов
А. В. Гордеев a, *, А. Ф. Селиверстов a, Б. Г. Ершов a
a Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
Москва, Россия
* E-mail: Gordeev@ipc.rssi.ru
Поступила в редакцию 30.10.2018
После доработки 04.02.2019
Принята к публикации 11.02.2019
Аннотация
Изучена растворимость озона при 25°C в растворах щавелевой кислоты H2C2O4 и нитрата калия KNO3 до концентраций 1 и 2 М соответственно. Найдены значения констант Сеченова для этих растворов электролитов: 0.081 ± 0.010 и 0.082 ± 0.004 M–1 соответственно. Определено значение анион-специфического параметра в модели растворимости газов Weisenberger–Schumpe для оксалат-иона ${{h}_{{{{{\text{C}}}_{2}}{\text{O}}_{4}^{{2 - }}}}}$ = 0.1266 M–1. На основании экспериментальных данных из различных источников определен набор коэффициентов для расчета плотности растворов H2C2O4 в зависимости от температуры в диапазоне от 5 до 100°C и концентрации раствора вплоть до насыщенных при заданной температуре.
ВВЕДЕНИЕ
Оксалат-ионы и другие комплексоны широко используются в радиохимической промышленности и в атомной энергетике в технологиях переработки ядерного топлива и утилизации радиоактивных отходов [1]. В результате возникают значительные по объему жидкие радиоактивные отходы (ЖРО). Наличие комплексонов в растворе в присутствии высокого содержания солей, преимущественно нитратов (вплоть до 300–400 г/л), существенно осложняет очистку ЖРО от радионуклидов. Окислительное разложение оксалат-иона озоном является наиболее эффективным и безотходным способом переработки ЖРО [2, 3]. Технологически процесс разложения оксалатов основан на процессах массопереноса озона из газовой фазы в жидкую в результате реализации различных способов барботажа озоно-кислородной смеси через растворы. Поэтому эффективность разложения оксалатов в значительной степени зависит от растворимости озона в растворах. На растворимость же, в свою очередь, заметно влияют солевой состав системы и температура, которые могут значительно изменяться при реализации технологического процесса. В связи с этим необходимость расчета равновесного содержания озона, на границе газ–жидкость, является весьма актуальной задачей для оптимизации технологического процесса переработки ЖРО. Отметим, что поставленная задача выходит далеко за рамки радиохимических технологий и важна также для практики переработки многих водных стоков с высоким солевым содержанием, включая жидкие промышленные и бытовые отходы.
Ранее рядом исследователей [4–6] была предложена модель расчета растворимости газов в концентрированных растворах. В окончательной редакции [6] разработанная модель позволяла с учетом температурного фактора рассчитывать содержание порядка 20 видов газов в растворах индивидуальных электролитов и их смесей. Эта модель получила название модели Weisenberger–Schumpe. Расчет растворимости газов в ней основывается на использовании хорошо известной эмпирической зависимости Сеченова, связывающей растворимость неэлектролита (в нашем случае газа) с концентрацией электролита в растворе:
(1)
$\lg \left( {\frac{{{{k}_{{\text{H}}}}}}{{k_{{\text{H}}}^{{\text{0}}}}}} \right) = {{K}_{{\text{S}}}}{{c}_{{{\text{sol}}}}}.$Модель Weisenberger–Schumpe предлагает простое и удобное уравнение для расчета константы Сеченова (KS), основанное на использовании индивидуальных параметров ионов hi (i = +, –) и газа hG [7]:
(2)
${{K}_{{\text{S}}}} = \sum\limits_i {\left( {{{h}_{i}} + {{h}_{{\text{G}}}}} \right)} {{n}_{i}},\,\,\,\,{{h}_{{\text{G}}}} = {{h}_{{{\text{G,0}}}}} + {{h}_{t}}\left( {t - 25} \right).$Значения hi для 50 неорганических катионов и анионов, hG,0 и ht для 22 газов были определены в работе [6] на основе обработки более 900 различных констант Сеченова. Отметим, что в рамках модели Weisenberger–Schumpe были найдены значения параметров неорганических ионов, входящих как в состав сильных электролитов (K+, Na+, Cl– и т.д.), так и ионов, склонных к гидролизу или к неполной диссоциации (Al3+, Th4+, ${\text{PO}}_{4}^{{3 - }},$ ${\text{HPO}}_{4}^{{2 - }},$ $~{{{\text{H}}}_{{\text{2}}}}{\text{PO}}_{4}^{ - }$). Вне зависимости от этого, модель Weisenberger–Schumpe позволяет достаточно хорошо (±20%), учитывая значительной разброс в экспериментальных данных, предсказывать значение констант Генри для различных газов в растворах электролитов [6]. Это дает основание предполагать, что модель может быть использована и для описания влияния на растворимость газов не только в растворах неорганических, но и органических кислот и солей, которые склонны к неполной диссоциации. Для распространения действия модели на растворы органических кислот и их солей достаточно на основе экспериментальных данных определить для них значения анион-специфических параметров модели – h–. В частности, для щавелевой кислоты это будет параметр ${{h}_{{{{{\text{C}}}_{{\text{2}}}}{\text{O}}_{{\text{4}}}^{{{\text{2}} - }}}}}$ для аниона ${{{\text{C}}}_{{\text{2}}}}{\text{O}}_{{\text{4}}}^{{{\text{2}} - }}.$
Отметим, что изначально озон не входил в список газов, для которых был определен газоспецифический параметр hG,0 [6]. Наиболее вероятная причина этого связана с отсутствием надежных данных из-за неустойчивости озона в водных растворах и взаимодействия его с растворенным веществом [8]. Это затрудняло использование обычных статических методов определения растворимости. Позднее значение hG,0 для озона было определено отдельно в работе [9] и вошло в обобщенные данные для параметров модели [7]. В работе [10] мы уточнили значение hG,0. Найденное нами значение hG,0 = –0.0152 M–1 было использовано в настоящем исследовании.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Материалы. При приготовлении растворов H2C2O4 использовался дважды перекристаллизованный реагент марки “х. ч.”, что позволило в несколько раз снизить наблюдаемую скорость гибели озона в концентрированных растворах. Растворы готовились на тридистиллированной воде с сопротивлением не менее чем 18 Мом. Концентрации приготовленных растворов уточнялись по плотности, определяемой весовым способом, в соответствии с уравнением (4), представляющим собой зависимость плотности раствора от концентрации и температуры, взятой из [11]. Так как для щавелевой кислоты значения коэффициентов в уравнении (4) в работе [11] отсутствовали, их значения были получены нами в результате обработки экспериментальных данных различных источников (см. раздел “Плотность растворов щавелевой кислоты”). При определении плотности растворов в качестве раствора сравнения использовалась вода. Выражение для определения плотности воды от температуры было взято из работы [11]. При получении озона использовался кислород из баллона марки “о.с.ч.” (99.99%) без предварительной очистки. Однако при определении параметров спектра поглощения озона в чистой воде применялись дополнительные методы очистки кислорода и озоно-кислородной смеси, описанные в разделе “Спектр озона в воде”.
Установка. Схема установки и ее модификация для проведения озонирования, а также методика проведения экспериментов по определению растворимости озона в растворах солей были детально описаны в наших предыдущих работах [10, 12 ]. Особенностью данной установки является возможность определения истинной растворимости озона в условиях, когда его растворение сопровождается заметным разложением (t1/2 > 10 с). Методика основывается на корректировке наблюдаемой концентрации озона в жидкой фазе с учетом соотношения скорости массопереноса озона через поверхность раздела фаз и скоростью его гибели в растворе [13]. Значительная интенсификация процесса насыщения за счет сокращения объема ячейки, а также возможность измерения скорости массопереноса и скорости гибели непосредственно в каждом эксперименте существенно расширяет диапазон исследуемых растворов.
Для уменьшения экспериментальной ошибки и улучшения воспроизводимости измерений в установку, которая была описана в работе [12], был внесен ряд конструкционных изменений [10]. Перед измерением концентрации озона в газовой фазе прибором “Медозон-254/5” озоно-кислородная смесь пропускалась через 3 ловушки Дрекселя. Две первые ловушки были заполнены дистиллированной водой и служили для очистки озона. Третья заполнялась раствором того же состава, как и исследуемый раствор. После прохождения этой ловушки давление паров воды в газовой фазе и над раствором ячейки выравнивалось, что позволяло избегать изменения состава раствора при барботировании. Для улучшения воспроизводимости результатов регистрационный блок установки, часть газовых коммуникаций, включая ловушки Дрекселя и газоанализатор озона “Медозон-254/5”, были помещены в воздушный термостат. Температура в воздушном термостате устанавливалась на уровне температуры ячейки и регулировалась с точностью ±0.1°C.
Для получения высоких концентраций озона, необходимых при изучении растворов щавелевой кислоты, использовался капиллярный озонатор “БИКОЗ-10” с водяным охлаждением и диапазоном изменения концентрации озона на выходе от 100 до 180 мг/л при расходе до 2–5 мл/с. При изучении растворимости озона в растворах KNO3, обладающих значительным поглощением на длине волны регистрации озона (263.2 нм), использовался пластинчатый озонатор “УОТА-60-01” производства ООО “Фирма Медозон”, генерирующий концентрацию озона на выходе в диапазоне от 10 до 80 мг/л и позволяющий устанавливать и поддерживать ее с точностью до 1 мг/л.
Методика эксперимента. Методика проведения эксперимента и обработки результатов были описаны ранее [12, 10 ]. Из-за сильного поглощения оксалат-иона в УФ-области (рис. 1, кривая 3) регистрация поглощения озона осуществлялась на одной из длин волн – 290 или 300 нм, в зависимости от концентрации исследуемого раствора. Поглощение озона в растворах KNO3 регистрировалось на длине волны 263.2 нм, где раствор был наиболее прозрачен (рис. 1, кривая 4). Все измерения растворимости проводились при 25°C. Коэффициенты молярного поглощения при выбранных длинах волн были вычислены из уравнения (3), полученного при изучении поглощения озона в чистой воде.
Рис. 1.
Зависимость поглощения от длины волны. Спектры поглощения воды: (1) – после барботирования озоновой смеси в течение 20 с; (2) – после барботирования Ar в течение 5 мин; (1–0) – общий спектр поглощения озона в растворе; (1–1), (1–2), (1–3), (2–1) – полосы поглощения, входящие в общий спектр, рассчитанные в соответствии с уравнением (3) и с параметрами из табл. 1, (1–0) = (1–1) + (1–2) + (1–3) + (2–1). Амплитуды полос поглощения: (1–1) – a1 = 0.416; (1–2) – a2 = 0.053; (1–3) – a3 = 0.339; (2–1) – a4 = 0.020. Спектры поглощения растворов: (3) – H2C2O4 (0.143 M); (4) – KNO3 (0.1 M). Длины волн, при которых определялось содержание озона в растворах: (а) – λ = 263.2 нм, ε = 2948 M–1 см–1; (б) – λ = 290.0 нм, ε = 907 M–1 см–1; (в) – λ = 300.0 нм, ε = 345 M–1 см–1.
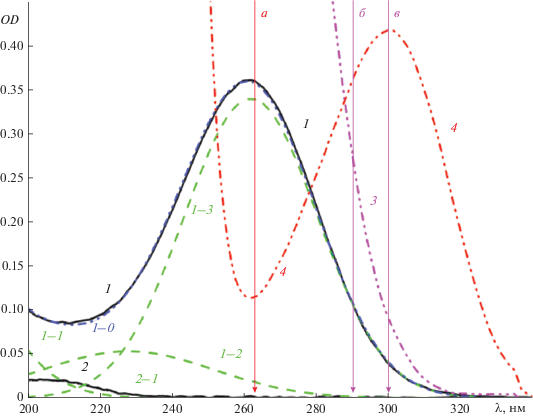
Спектр озона в воде. Спектр поглощения озона представляет собой несимметричный пик с максимумом при 260 нм [14, 15]. Для определения зависимости коэффициента молярного поглощения (ε) растворенного озона от длины волны (λ) была проведена серия экспериментов, в которых определялось влияние концентрации газа и pH среды на форму спектра. Характерные спектры поглощения, получаемые в ходе исследования, приведены на рис. 1 (спектры 1 и 2). Во всех спектрах было учтено исходное поглощение системы с помощью вычитания из регистрируемого спектра исходного спектра ячейки, заполненной водой или раствором кислоты. В соответствии с использованной методикой эксперимента спектры поглощения озона получали путем насыщения свежеприготовленной тридистиллированной воды или водного раствора хлорной кислоты (1.5 М) в кварцевой ячейке в течение 20 с (см. раздел “Установка”). Уровень концентрации озона в растворе регулировался путем задания в генераторе озона “УОТА-60-01” его содержания в озоно-кислородной смеси. После окончания насыщения и регистрации спектра, приблизительно через 4 мин с начала эксперимента, раствор продувался аргоном в течение 5 минуты и затем фиксировался остаточный спектр поглощения (рис. 1, спектр 2). Учитывая, что продуктом разложения озона в воде является кислород и крайне незначительное количество пероксида водорода (≈10–7 M), наблюдаемое остаточное поглощение в чистой воде после продувки аргоном свидетельствует о присутствии посторонних примесей в озоно-кислородной смеси. Для их удаления был предпринят ряд мер по очистке газа, как на входе в озонатор, так и после него. До озонатора кислород из баллона пропускался через поглотитель Зайцева с пористой пластиной, заполненный натровой известью VentiSorb, с целью удаления остаточного CO2. После озонатора озоно-кислородная смесь пропускалась через азотную ловушку, заполненную сухим льдом, а затем через ловушку Дрекселя, заполненную водой. Для очистки аргона использовалась только ловушка с натровой известью VentiSorb и газ подавался в ячейку напрямую, минуя озонатор. В отсутствие описанной системы очистки газа наблюдалось значительное нарастание поглощения при 200 нм, увеличивающееся с увеличением времени озонирования. Более того, pH воды значительно снижался (до 3.5 за 30 мин озонирования) и появлялось заметное количество пероксида водорода (≈10–4 M), который уверенно определялся специфической реакцией с Ti(SO4)2. Возникновение значительного количества пероксида водорода и подкисление раствора можно объяснить гидролизом органических перекисных соединений. Последние возникают в результате окисления присутствующих органических примесей при пропускании через озонатор неочищенного кислорода. В результате в растворе накапливался пероксид водорода и органическая кислота.
В отличие от поглощения озона в газовой фазе, где полосу поглощения Хартли (Hartlay) (200–300 нм) можно описать одной гауссовой кривой [16–18], в воде и водных растворах форма полосы поглощения значительно отличается от кривой Гаусса [14, 15]. Три полосы поглощения с формой нормального распределения Гаусса было использовано нами при описании суммарного спектра поглощения озона в воде (рис. 1, полосы 1–1, 1–2, 1–3). Суммарный коэффициент поглощения рассчитывался по уравнению
(3)
$\varepsilon \left( \lambda \right) = {{\varepsilon }_{{\max }}}\sum\limits_{i = 1}^3 {\left[ {{{a}_{i}}\exp \left( { - \frac{{{{{\left( {\lambda - {{\lambda }_{{\max ,i}}}} \right)}}^{2}}}}{{2\omega _{i}^{2}}}} \right)} \right]} ,\,\,\,\,{{{\text{M}}}^{{ - 1}}}{\text{с}}{{{\text{м}}}^{{ - 1}}}.$К сожалению, однозначно установить положение и ширину всех трех полос на имеющемся экспериментальном материале не представлялось возможным. Полосы поглощения 1–1 и 1–2 на рис. 1 не имели четко выраженных раздельных максимумов и перегибов, а их амплитуды линейно коррелированы между собой, что видно на рис. 2а. Для определения характеристик полосы поглощения 1–3 на рис. 1 имелся лишь небольшой участок его крыла, к тому же, как показал дальнейший анализ, поглощение в этой области имеет составляющую, не связанную с поглощением озона (рис. 2б). Для устранения перечисленных выше неопределенностей мы предположили, что наблюдаемое поглощение озона формируется из поглощения трех частиц: O3, H2O4 и HO2. Схему превращения между этими тремя частицами формально можно представить в виде следующих равновесий:
Рис. 2.
Соотношения между амплитудами полос поглощения (табл. 1), составляющие спектр поглощения озона. (а) – корреляция меду амплитудами пиков при 262 и 228 нм. (б) – корреляция меду амплитудами пиков при 262 и 158.7 нм. Отношения амплитуд: (1) – в чистой воде; (2) – в растворе 1.5 М HClO4; (3) – в растворах HClO4 [14]; (4) – в растворах 0.01 M HClO4 [15]. Сплошные линии – линейные регрессии, описывающие данные (1) и (2).
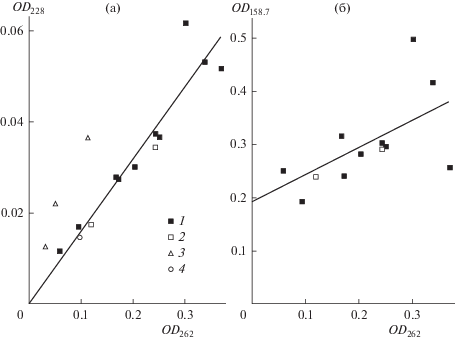
По спектрам, представленным в работах [19, 20], были определены характеристики полосы поглощения HO2 – ее положение (λmax = 228 нм) и полуширина (ω = 23.8 нм). На основании данных по оценке ультрафиолетовых спектров поглощения полиоксидов водорода (HO2, H2O2, H2O4), представленных в работе [21], мы зафиксировали положение максимума для H2O4 при 158.7 нм. Остаточное поглощение в системе после продувки ее аргоном описывалось одной полосой гауссовой формы (рис. 1, спектр 2–1) и учитывалось как дополнительный пик в уравнении (3) с фиксированными параметрами. При этом найденные для этой полосы значения λmax = 204.8 нм и ω = 12.9 нм были постоянными для всех спектров, а значение амплитуды (a) фиксировалось только для текущего спектра. Остальные параметры в уравнении (3), такие как положение максимума полосы Хартли и полуширины полос, определялись при обработке экспериментальных спектров. Значения найденных параметров пиков, моделирующих поглощение озона в воде и кислых растворах, представлены в табл. 1. На рис. 1 для одного из спектров поглощения озона приведен пример такого описания. На рис. 2 показаны соотношения между амплитудами всех трех пиков, полученные при описании спектров. На рис. 2а видно, что как для чистой воды, так и для 1.5 М раствора хлорной кислоты между амплитудами пиков с положениями 262 и 228 нм наблюдается линейная корреляция с коэффициентом 0.159, проходящая через начало координат. Это свидетельствует о том, что поглощение при 228 нм и его интенсивность прямо зависит от содержания озона в растворе и принадлежит либо самому озону, либо частице, находящейся с ним в равновесии, например HO2. Соотношение амплитуд пиков с положением 262 и 158.7 нм также описывается прямой линией с наклоном 0.511. Однако в этом случае она не проходит через начало координат. Это можно объяснить дополнительным поглощением в этой области, которое не связано с присутствием озона в растворе, но которое исчезает при продувке его аргоном. Это дополнительное поглощение в окончательном варианте не учитывалось в суммарном спектре озона, определяемом уравнением (3). Отметим, что влияние полосы поглощения с максимумом при 158.7 нм при λ ≥ 225 нм не превышает 1%.
Таблица 1.
Значения параметров λmax,i, ωi и ai в уравнении (3). εmax = 2972 M–1 см–1
| Параметр | Номер пика в уравнении (3) (i) |
|||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| λmax,i, нм | 158.7 | 228 | 262 | 204.8 |
| ωi, нм | 21 | 23.8 | 18.5 | 12.9 |
| ai после нормировки при λ = 260.8 нм |
0.482 | 0.15 | 0.944 | Определялась отдельно для каждого спектра |
Для предварительной нормировки рассчитываемого спектра озона в соответствии с уравнением (3) значение амплитуды пика 3 на рис. 1 при 262 нм принималось за 1.0, а амплитуды двух других пиков принимались равными углам наклона корреляционных кривых на рис. 2: a1 = 0.511 и a2 = 0.159. В результате расчета поглощения по уравнению (3) в интервале от 200 до 350 нм с использованием найденных значений амплитуд и значения εmax = 1.0 было найдено максимальное значение 1.059, которое соответствовало длине волны λ = 260.8 нм. Именно это значение использовалось для окончательной нормировки. В табл. 1 приведены значения амплитуд пиков для нормированного спектра. Исходя из ранее использованного нами значения коэффициента молярного поглощения озона в воде ε = 2810 M–1 см–1 при λ = 254.2 нм [10, 12 ], величина εmax в уравнении (3) в положении максимума поглощения озона при 260.8 нм составила 2972 M–1 см–1.
Используя уравнение (3) и величины параметров (i = 1–3) из табл. 1, мы определили значения коэффициентов молярного поглощения озона для длин волн, на которых в экспериментах регистрировалось его поглощение в растворах щавелевой кислоты и нитратах: ε263.2 = 2948 M–1 см–1; ε290 = 907 M–1 см–1; ε300 = 345 M–1 см–1.
Плотность растворов. Как было отмечено в разделе “Материалы”, для приготовления растворов и уточнения концентраций использовалась зависимость их плотности от концентрации и температуры растворов, предложенная в [11]:
(4)
$\begin{gathered} \rho = {{\rho }_{{\text{w}}}} + (Ac + Bct + Cc{{t}^{2}} + \\ + \,\,D{{c}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} + E{{c}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}t + {{F{{c}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{t}^{2}})} \mathord{\left/ {\vphantom {{F{{c}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{t}^{2}})} {1000}}} \right. \kern-0em} {1000}},~~{\text{г с}}{{{\text{м}}}^{{ - 3}}}. \\ \end{gathered} $Значения коэффициентов A, B, C, D, E, F были табулированы в [11] для более чем 300 неорганических растворов. Поскольку для H2C2O4 данные в работе отсутствовали, мы определили значения коэффициентов в уравнении (4), используя данные оригинальных работ.
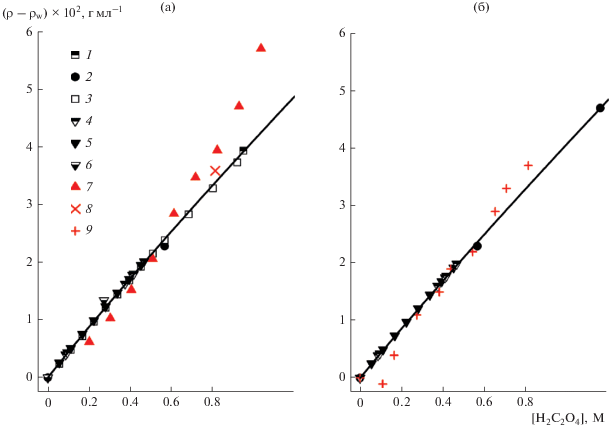
При нахождении коэффициентов в уравнении (4) для H2C2O4 использовались данные работ [22–39]. Наиболее полные зависимости изменения плотности от концентрации щавелевой кислоты (0–30%) и изменения температуры (15–100°C) приведены в [31]. Данные других работ были менее систематическими и относились, как правило, к температурам 20 или 25°C. Поскольку значения плотности концентрированных растворов щавелевой кислоты не сильно отличались от плотности воды, при отборе и дальнейшей обработке данных мы использовали концентрационные зависимости Δρ(t) = ρ(t) – ρw(t). Определение коэффициентов в уравнении (4) для растворов щавелевой кислоты проводилось в два этапа. В начале, на основании предварительного расчета, были исключены данные, отклонение которых от расчетной величины составляло более чем 10%. Следует отметить, что подход при реализации этого этапа не был полностью формальным. Так, были отклонены данные работы [38] для всех четырех температур (20, 30, 40 и 50°C). Причиной стала ярко выраженная нелинейность, представленной в работе, зависимости плотности от концентрации при t = 20°C (рис. 3а, точки 7), которая сильно отличалась от аналогичных зависимостей других восьми авторов (рис. 3а). И хотя при других температурах зависимости из работы [38] явно доминировали по числу точек над другими малочисленными данными из работ [27, 31], мы сочли правильным исключить все данные этой работы из рассмотрения с целью избежать возможного искажения результата.
Аналогично, из-за участков зависимостей плотность–концентрация раствора, на которых плотность растворов была ниже плотности воды, из рассмотрения были исключены данные работы [39], для температур 35 и 45°C. Окончательно при нахождении коэффициентов в уравнении (4) нами были использованы только данные работ [22–31], как в наибольшей степени согласованных и не имеющих внутренних противоречий
Ввиду значительного различия, более чем в 60 раз, между экспериментальными значениями ρ(t) – ρw(t), поиск коэффициентов для уравнения (4) мы проводили с использованием разновидности обобщенного метода наименьших квадратов (МНК) весового МНК. Этот метод, за счет использования весов для каждой точки эксперимента, позволял минимизировать не сумму квадратов ошибки отклонений, а сумму квадратов относительных отклонений. В результате достигалось более равномерное приближение для всех экспериментальных данных. Детали использованного подхода были описаны в работе [10] на примере нахождения параметров ${{h}_{{{\text{ClO}}_{{\text{4}}}^{ - }}}}$ и hG,0 для модели Weisenberger–Schumpe. Найденные коэффициенты для расчета плотности растворов H2C2O4 приведены в табл. 2. Отклонение рассчитываемых значений плотности растворов ρ(t) в диапазоне температур от 5 до 100°C и концентраций вплоть до насыщенных при данной температуре составило не более 0.2%. Отклонение между рассчитанными и экспериментальными значениями величин Δρ(t) = ρ(t) – ρw(t) не превышало 6.5%.
Таблица 2.
Коэффициенты, использованные для расчета плотности растворов по уравнению (4), кг м–3
Определение растворимости озона в растворах щавелевой кислоты. Для определения значения параметра ${{h}_{{{{{\text{C}}}_{{\text{2}}}}{\text{O}}_{{\text{4}}}^{{{\text{2}} - }}}}}$ для ${{{\text{C}}}_{{\text{2}}}}{\text{O}}_{4}^{{2 - }}$ в модели Weisenberger–Schumpe мы использовали уравнение (2). В соответствии с ним константа Сеченова для озона в растворах щавелевой кислоты может быть записана следующим образом:
(5)
${{K}_{{\text{S}}}} = \left( {{{h}_{{{{{\text{H}}}^{ + }}}}} + {{h}_{{\text{G}}}}} \right)2 + \left( {{{h}_{{{{{\text{C}}}_{{\text{2}}}}{\text{O}}_{{\text{4}}}^{{{\text{2}} - }}}}} + {{h}_{{\text{G}}}}} \right).$С учетом того, что в модели Weisenberger–Schumpe для иона H+ параметр ${{h}_{{{{{\text{H}}}^{ + }}}}}$ принимается равным 0, из уравнения (5) получаем уравнение для расчета значения ${{h}_{{{{{\text{C}}}_{{\text{2}}}}{\text{O}}_{{\text{4}}}^{{{\text{2}} - }}}}}{\text{:}}$
(6)
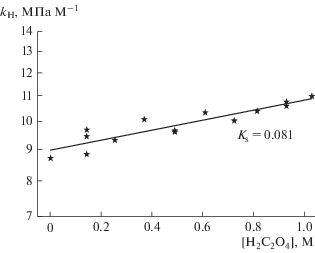
${{h}_{{{{{\text{C}}}_{{\text{2}}}}{\text{O}}_{{\text{4}}}^{{{\text{2}} - }}}}} = {{K}_{{\text{S}}}} - 3{{h}_{{\text{G}}}}.$Значение константы Сеченова KS озона для растворов щавелевой кислоты было определено по углу наклона линейной зависимости константы Генри kH от молярной концентрации в полулогарифмических координатах, показанной на рис. 4. Подставив в уравнение (6) найденное значение константы Сеченова KS = 0.081 ± 0.010 M–1 и значение специфической газовой постоянной для озона, определенное нами в работе [10]: hG,0 = –0.0152 M–1, которое при температуре эксперимента 25°C совпадает с hG (уравнение (2)), находим ${{h}_{{{{{\text{C}}}_{{\text{2}}}}{\text{O}}_{{\text{4}}}^{{{\text{2}} - }}}}}$ = 0.1266 M–1. Данное значение приведено до четвертого знака, аналогично тому, как это сделано в работах [6, 7]. С учетом точности полученных экспериментальных данных значение определенного нами параметра следует записать как ${{h}_{{{{{\text{C}}}_{{\text{2}}}}{\text{O}}_{{\text{4}}}^{{{\text{2}} - }}}}}$ = 0.13 ± 0.01 M–1.
Рис. 4.
Зависимость константы Генри kH Па M–1 для озона от молярной концентрации растворов щавелевой кислоты. Температура 25°C. Точки – экспериментальные значения; линия – линейная аппроксимация экспериментальных точек.
В нашей работе в качестве вспомогательного параметра при определении растворимости озона использовалась константа гибели озона в растворах щавелевой кислоты (kd). Данные кинетики гибели озона, как и кинетики насыщения, фиксировались в каждом эксперименте и использовались для корректировки регистрируемой концентрации озона в растворе. Эта скорректированная концентрация соответствовала концентрации озона на поверхности раздела газ–раствор и принималась за истинную, равновесную концентрацию. Кинетика гибели озона в растворах щавелевой кислоты хорошо описывается реакцией первого порядка от концентрации озона:
(7)
$\frac{{{\text{d}}[{{{\text{O}}}_{3}}]}}{{{\text{d}}\tau }} = - {{k}_{{\text{d}}}}[{{{\text{O}}}_{3}}],\,\,\,\,{{М}^{{ - 1}}}{\text{ми}}{{{\text{н}}}^{{ - 1}}}.$Константа скорости гибели kd при этом оказывается зависимой от концентрации щавелевой кислоты в растворе, что следует из наклона зависимости kd–[H2C2O4] на рис. 5. Представив эту зависимость в виде уравнения
(8)
${{k}_{{\text{d}}}} = {{k}_{{{\text{d,0}}}}} + k{{[{{{\text{H}}}_{{\text{2}}}}{{{\text{C}}}_{{\text{2}}}}{{{\text{O}}}_{4}}]}^{r}},$по углу наклона зависимости lg(kd – kd,0)–lg([H2C2O4]) находим порядок реакции по щавелевой кислоте – r = 0.6. Значение lg(k) = –0.642 и соответственно k = 0.228 мин–1 также определяется из этой зависимости как значение lg(kd – kd,0) при концентрации [H2C2O4] = 1 M, для которой lg([H2C2O4]) = 0. Учитывая, что в наших исследованиях наблюдаемая константа гибели озона в чистой воде kd,0 = 0.036 мин–1, уравнение (7) можно записать следующим образом:
(9)
$\begin{gathered} \frac{{{\text{d}}[{{{\text{O}}}_{3}}]}}{{{\text{d}}\tau }} = - 0.036 \cdot [{{{\text{O}}}_{3}}] - \\ - \,\,0.228 \cdot [{{{\text{O}}}_{3}}]{{[{{{\text{H}}}_{{\text{2}}}}{{{\text{C}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{4}}}}]}^{{0.6}}},\,\,{{{\text{М}}}^{{ - 1}}}{\text{ми}}{{{\text{н}}}^{{ - 1}}}. \\ \end{gathered} $Отметим, что дробный порядок скорости гибели озона по концентрации щавелевой кислоты, скорее всего, указывает на сложный, многоступенчатый механизм взаимодействия озона с ней.
Определение растворимости озона в растворах KNO3 и NaNO3. Значительные количества солей нитратов щелочных металлов, в основном натрия, присутствующих в составе ЖРО, существенно снижают растворимость озона. Это негативно сказывается на эффективности использования озона при окислении щавелевой кислоты. Модель Weisenberger–Schumpe позволяет рассчитать константы Сеченова, а следовательно, и концентрации озона на поверхности раздела фаз в таких растворах. Оценку точности, с которой модель предсказывает значения констант Сеченова для растворов солей нитратов при растворении в них озона, мы провели на примере растворов NaNO3 и KNO3. Используя ион-специфические параметры модели для ионов Na+, K+ и ${\text{NO}}_{3}^{ - },$ определенные ранее при исследовании растворимости других газов в растворах различных солей [6, 7], а также уточненное нами значение параметра hG,0 для озона [10], мы провели проверку соответствия рассчитанных констант Сеченова для озона по модели Weisenberger–Schumpe с экспериментальными данными. Ранее экспериментальное определение растворимости и константы Сеченова для озона в растворах NaNO3 было выполнено в работе [10] при температуре 25°C. Растворимость озона в растворах NaNO3 также была изучена при трех температурах (20, 30 и 40°C) в [40]. Экспериментальные данные вместе с расчетными зависимостями, полученными в соответствии с моделью Weisenberger–Schumpe, представлены на рис. 6а. Расчет константы Генри для температур 20, 25 и 30°C был выполнен по уравнению (1). В нем константы Сеченова для каждой из температур определялись в соответствии с уравнением
(10)
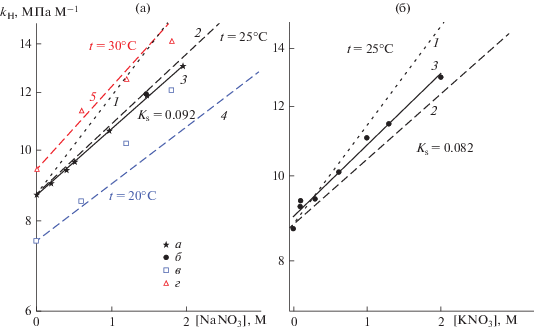
${{K}_{{\text{S}}}} = \left( {{{h}_{{{\text{N}}{{{\text{a}}}^{ + }}}}} + {{h}_{{\text{G}}}}} \right) + \left( {{{h}_{{{\text{NO}}_{{\text{3}}}^{{{\text{2}} - }}}}} + {{h}_{{\text{G}}}}} \right) = 0.1271 + 2{{h}_{{{\text{G,0}}}}}.$Рис. 6.
Зависимость константы Генри для O3 от концентрации электролита в растворе в полулогарифмических координатах: (а) – для NaNO3; (б) – для KNO3. Точки: (а) – t = 25°C, из [10]; (б) – t = 25°C, настоящая работа; (в) – t = 20°C, из [40]; (г) – t = 30°C, из [40]. Линии (точечные) (1) – t = 25°C, расчет по модели Weisenberger–Schumpe c использованием оригинальных параметров модели [7]. Линии (пунктирные) – расчет по модели Weisenberger–Schumpe c использованием нового параметра модели hG,0 = –0.0152 M–1 [10]: (2) – t = 25°C; (4) – t = 20°C; (5) – t = 30°C. Линии (3) – t = 25°C, линейные аппроксимации экспериментальных данных (а) и (б).
Для расчета газоспецифического параметра hG использовалось уравнение
(11)
${{h}_{{\text{G}}}} = {{h}_{{{\text{G,0}}}}} + 1.79 \times {{10}^{{ - 3}}}\left( {t - 25} \right).$На рис. 6 линия 1 соответствует использованию оригинального значения параметра hG,0 = 0.00396 M–1, взятого из работы [7], а линии 2, 4, 5 соответствуют использованию значения hG,0 = –0.0152 M–1, полученного нами в работе [10].
Для расчета константы Сеченова озона для KNO3 при 25°C использовалось уравнение
(12)
${{K}_{{\text{S}}}} = \left( {{{h}_{{{{{\text{K}}}^{ + }}}}} + {{h}_{{\text{G}}}}} \right) + \left( {{{h}_{{{\text{NO}}_{{\text{3}}}^{{{\text{2}} - }}}}} + {{h}_{{\text{G}}}}} \right) = 0.105 + 2{{h}_{{{\text{G,0}}}}}.$Результаты расчетов показаны на рис. 6б. На нем линии 1 и 2, как и на рис. 6а, соответствовали использованию различных значений hG,0 для озона. Из экспериментальных данных, представленных на рис. 6 для NaNO3 и KNO3, значения констант Сеченова, соответствующие углам наклона зависимостей lg(kH)–c, были найдены равными 0.092 ± 0.001 и 0.082 ± 0.004 M–1 соответственно. При определении KS как для растворов нитратов, так и для щавелевой кислоты использовалось значение константы Генри для озона в воде kH,0 = = 8.71 × 106 Па M–1. Оно рассчитывалось как среднее значение kH,0, измеренных для воды с использованием как озонатора “БИКОЗ-10”, так и “УОТА-60-10” [10].
Как для растворов NaNO3, так и для KNO3 более хорошее совпадение рассчитанных и измеренных значений достигается при использовании значения газоспецифического параметра hG,0 = –0.0152 M–1, полученного нами в работе [10].
ЗАКЛЮЧЕНИЕ
В результате выполненного исследования определено значение анион-специфического параметра для ${{{\text{C}}}_{{\text{2}}}}{\text{O}}_{4}^{{2 - }}$ (${{h}_{{{{{\text{C}}}_{{\text{2}}}}{\text{O}}_{{\text{4}}}^{{{\text{2}} - }}}}}$ = 0.1266 M–1) в модели растворимости газов Weisenberger–Schumpe. Таким образом, модель Weisenberger–Schumpe может быть использована для расчета растворимости газов в растворах, содержащих оксалат-ион.
Продемонстрировано хорошее согласие между рассчитанными и измеренными истинными (на поверхности раздела фаз) значениями констант Генри для озона в растворах NaNO3 и KNO3 в широком диапазоне концентраций (до 160 г/л для NaNO3 и до 200 г/л для KNO3). Отметим, что из-за ограничений при постановке эксперимента применимость модели была подтверждена до концентраций нитратов существенно более низких, чем встречаются на практике (до 400 г/л). Тем не менее мы считаем, что модель Weisenberger–Schumpe можно использовать для расчета констант Генри озона в растворах с более высокой концентрацией NaNO3 и KNO3. Такое предположение основано, во-первых, на отсутствии отклонений от закона Сеченова в исследованном концентрационном диапазоне, во-вторых, на хорошем описании моделью констант Генри CO2 в растворах с концентрацией до 5 М [41] и, в третьих, на схожести поведения растворенного озона с поведением других атмосферных газов.
Отмечено, что использование в модели Weisenberger–Schumpe значения газоспецифического параметра –0.0152 М–1 для озона, определенного нами в предыдущей работе [10], дает значительно более хорошее совпадение между расчетными и измеренными значениями, что становится особенно заметно в концентрированных растворах.
В ходе выполнения работы были найдены коэффициенты для эмпирической зависимости плотности щавелевой кислоты от ее молярной концентрации и температуры в соответствии с уравнением (4), предложенным в работе [11]. Анализ спектра озона в воде и кислых растворах показал, что спектр озона в области длин волн выше 225 нм практически не изменяется от его концентрации в растворе и может быть описан двумя кривыми Гаусса с положением максимумов при 228 и 262 нм в соответствии с уравнением (3) и данными табл. 1.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 16-03-00336) и Министерства науки и высшего образования Российской Федерации (регистрационный номер исследовательской работы АААА-А16-116121410087-6).
ОБОЗНАЧЕНИЯ
| A, B, C, D, E, F | коэффициенты в уравнении (4) |
| a | амплитуда пиков поглощения в уравнении (3) |
| c | молярная концентрация электролита, моль (л раствора)–1 |
| h | параметр модели Weisenberger–Schumpe для ионов и газа, M–1 |
| KS | константа Сеченова, M–1 |
| k | константа гибели озона с щавелевой кислотой, мин–1 |
| kd | константа гибели озона в растворе, мин–1 |
| kd, 0 | константа гибели озона в воде, мин–1 |
| kH | константа Генри в растворе, Па M–1 |
| $k_{{\text{H}}}^{0}$ | константа Генри в чистом растворителе, Па M–1 |
| m | моляльная концентрация электролита, моль (кг H2O)–1 |
| n | стехиометрический номер |
| OD | оптическая плотность |
| p | процентная концентрация, % |
| r | порядок реакции |
| t | температура, °C |
| [X] | молярная концентрация вещества X, М |
| ε | молярный коэффициент поглощения, M–1 см–1 |
| λ | длина волны, нм |
| ρ | плотность раствора, г см-3 |
| τ | время, мин |
| ω | полуширина пика, нм |
ИНДЕКСЫ
Список литературы
Seliverstov A.F., Lagunova Y.O., Ershov B.G., Gelis V.M., Basiev A.G. Recovery of radioactive cobalt from aqueous EDTA solutions using concentrated ozone // Radiochemistry. 2009. V. 51. № 3. P. 326. [Селиверстов А.Ф., Лагунова Ю.О., Ершов Б.Г., Гелис В.М., Басиев А.Г. Выделение радиоактивного кобальта из водных растворов ЭДТА с использованием концентрированного озона // Радиохимия. 2009. Т. 51. № 3. С. 286.]
Lagunova Y.O., Seliverstov A.F., Ershov B.G., Basiev A.G. Oxidative decomposition of oxalate ions in water solutions of concentrated ozone // At. Energy (N. Y., NY, U. S.). 2012. V. 113. № 2. P. 112. [Лагунова Ю.О., Селиверстов А.Ф., Ершов Б.Г., Басиев А.Г. Окислительное разложение оксалат-ионов в водных растворах концентрированным озоном // Ат. энерг. 2012. Т. 113. № 2. С. 93.]
Seliverstov A.F., Lagunova Y.O., Ershov B.G., Shashkovskii S.G. Oxidative decomposition of oxalate ion with ozone in aqueous solution // Russ. J. Gen. Chem. 2017. V. 87. № 11. P. 2533. [Селиверстов А.Ф., Лагунова Ю.О., Ершов Б.Г., Шашковский С.Г. Окислительное разложение оксалат-иона озоном в водных растворах // Журн. общ. хим. 2017. Т. 87. № 11. С. 1789.]
van Krevelen D.W., Hoftijzer P.J. On the Solubility of Gases in Aqueous Solutions // Chimie et Industrie: Numero Speciale du XXI Congres Internationale de Chimie Industrielle. Bruxelles, 1948. P. 168.
Onda K., Sada E., Kobayashi T., Kito S., Ito K. Salting-out Parameters of Gas Solubility in Aqueous Salt Solutions // J. Chem. Eng. Jpn. 1970. V. 3. P. 18.
Weisenberger S., Schumpe A. Estimation of Gas Solubilities in Salt Solutions at Temperatures from 273 to 363 K // AIChE J. 1996. V. 42. P. 298.
Sander S.P., Abbatt J., Barker J.R., Burkholder J.B., Friedl R.R., Golden D.M., Huie R.E., Kolb C.E., Kurylo M.J., Moortgat G.K., Orkin V.L., Wine P.H. Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies, Evaluation 17; JPL Publication 10–6. Pasadena: Jet Propulsion Laboratory, 2011.
Hoigné J., Bader H, Haag W.R, Staehelin J. Rate constants of reactions of ozone with organic and inorganic compounds in water–III. Inorganic compounds and radicals // Water Res. 1985. V. 19. № 8. P. 993.
Rischbieter E., Stein H., Schumpe A. Ozone Solubilities in Water and Aqueous Salt Solutions // J. Chem. Eng. Data. 2000. V. 45. № 2. P. 338.
Ershov B.G., Gordeev A.V., Seliverstov A.F. Ozone solubility in aqueous solutions of perchlorates and other electrolytes: Correction of the Weisenberger–Schumpe model parameters for the ${\text{ClO}}_{4}^{ - }$ and O3 // Ozone: Sci. Eng. 2018. https://doi.org/10.1080/01919512.2018.1525278
Novotnỳ P., Söhnel O. Densities of Binary Aqueous Solutions of 306 Inorganic Substances // J. Chem. Eng. Data. 1988. V. 33. № 1. P. 49.
Ershov B.G., Gordeev A.V., Seliverstov A.F. Ozone solubility in aqueous solutions of NaCl, Na2SO4, and K2SO4: application of the Weisenberger–Schumpe model for description of regularities and calculation of the ozone absorption coefficient // Ozone: Sci. Eng. 2017. V. 39. № 2. P. 69.
Roth J.A., Sullivan D.E. Solubility of ozone in water // Ind. Eng. Chem. Fundam. 1981. V. 20. № 2. P. 137.
Alder M.G., Hill G.R. The Kinetics and Mechanism of Hydroxide Ion Catalyzed Ozone Decomposition in Aqueous Solution1 // J. Am. Chem. Soc. 1950. V. 72. № 5. P. 1884.
Kilpatrick M.L., Herrick C.C., Kilpatrick M. The Decomposition of Ozone in Aqueous Solution 1, 2 // J. Am. Chem. Soc. 1956. V. 78. № 9. P. 1784.
Molina L.T., Molina M.J. Absolute absorption cross sections of ozone in the 185 to 350 nm wavelength range // J. Geophys. Res.: Atmos. 1986. V. 91. № 13. P. 14501.
Joens J.A. An assignment of the structured features in the Hartley band absorption spectrum of ozone // J. Chem. Phys. 1994. V. 100. № 5. P. 3407.
O’Keeffe P., Ridley T., Lawley K.P., Donovan R.J. Re-analysis of the ultraviolet absorption spectrum of ozone // J. Chem. Phys. 2001. V. 115. № 20. P. 9311.
Hug G.L. Optical spectra of nonmetallic inorganic transient species in aqueous solution. NSRDSNBS Report 69. Washington, DC: National Bureau of Standards, U.S. Department of Commerce, 1981.
Bielski B.H.J. Reevaluation of the spectral and kinetic properties of HO2 and O2- free radicals // Photochem. Photobiol. 1978. V. 28. № 4–5. P. 645.
Sprague M.K., Irikura K.K. Thermochemistry of HO2 + + HO2 → H2O4: Does HO2 Dimerization Affect Laboratory Studies? // J. Phys. Chem. A. 2015. V. 119. № 27. P. 7052.
Hull C. et al. International critical tables of numerical data, physics, chemistry and technology. National Academies, 1933. V. 3.
Roth W. Über die Absorption des Stickoxyduls in wässrigen Lösungen verschieden dissociierter Stoffe // Z. Phys. Chem. 1897. V. 24. № 1. P. 114.
Masson J.I.O. XI.–The solubility of electrolytes in aqueous solutions. Part II. Solubility of oxalic acid in other acids // J. Chem. Soc., Trans. 1912. V. 101. P. 103.
Livingston J., Morgan R., McKirahan W.W. The Weight of a Falling Drop and the Laws of Tate; XIV. The Drop Weights of Aqueous Solutions of the Salts of Organic Acids // J. Am. Chem. Soc. 1913. V. 35. № 11. P. 1759.
Kohlrausch F. Das ele ktrische Leitungsvermögen der Chlor, Bromund JodWasserstoffsäure, der Schwefel, Phosphor, Oxal, Weinund Essigsäure in wässerigen Lösungen // Ann. Phys. (Berlin, Ger.). 1876. V. 235. № 10. P. 233.
Herz W., Martin E. Zur Kenntnis der inneren Reibung flüssiger Systeme // Z. Anorg. Allg. Chem. 1923. V. 132. № 1. P. 41.
Haynes W.M. Concentrative properties of aqueous solutions: density, refractive index, freezing point depression, and viscosity // CRC Handbook of Chemistry and Physics / Ed. Haynes W.M. Boca Raton, Fla.: CRC, 2012. Section 5. P. 5-123.
Справочник химика. Т. 3. Химическое равновесие и кинетика. Свойства растворов. Электродные процессы / Под ред. Никольского Б.П. М.: Химия, 1965.
Hyvärinen A.P. et al. Surface tensions and densities of oxalic, malonic, succinic, maleic, malic, and cis-pinonic acids // J. Chem. Eng. Data. 2006. V. 51. № 1. P. 255.
Голубев И.Ф., Вагина Э.Н., Церковская К.Н. Плотность и вязкость водных и азотнокислых растворов дикарбоновых кислот // Сборник. Химия и технология продуктов органического синтеза (полупродукты для синтеза полиамидов). М.: Госхимиздат, 1963. С. 57.
Le Blanc M. Optisch-chemische Studien mit Berücksichtigung der Dissociationstheorie // Z. Phys. Chem. 1889. V. 4. № 1. P. 553.
Nicol W.W.J. XXIV. The molecular volumes of salt-solutions.—Part II. Water of crystallization // London, Edinburgh Dublin Philos. Mag. J. Sci. 1884. V. 18. № 112. P. 179.
Loomis E.H. Ueber das specifische Gewicht und das electrische Leitungsvermögen der Normallösungen von Natrium und Kaliumhydroxyd, von Salzsäure, Schwefelsäure, Salpetersäure und Oxalsäure // Ann. Phys. Chem. 1897. V. 60. № 2. P. 547.
Franz B. Die specifischen Gewichte einiger wässrigen Lösungen // Adv. Synth. Catal. 1872. V. 5. № 1. P. 274.
Schulze A. Ueber die Ausdehnung der wichtigsten Titrirflüssigkeiten durch die Wärme // Z. Anal. Chem. 1882. V. 21. № 1. P. 167.
von Traube J. Ueber die Capillaritätsconstanten organischer Stoffe in wässerigen Lösungen // Justus Liebigs Ann. Chem. 1891. V. 265. № 1. P. 27.
Gupta R.R., Singh M. Apparent molar volumes of oxalic acid in water and in aqueous solutions of fructose at 293.15, 303.15, 313.15 and 323.15 K // Indian J. Chem., Sect. A: Inorg., Bio-inorg., Phys., Theor. Anal. Chem. 2007. V. 46. P. 455.
Amutha P.S., Rajkumar X.R. Apparent Molal Volumes and Partial Molar Volumes of Aqueous Solutions of Some Biologically Important Compounds at 308 and 318 K // Asian J. Chem. 2011. V. 23. № 3. P. 1360.
Panich N.M., Ershov B.G. The solubility and kinetics of decomposition of ozone in aqueous solutions of nitrates // Russ. J. Phys. Chem. A. 2008. V. 82. № 8. P. 1262. [Панич Н.М., Ершов Б.Г. Растворимость и кинетика разложения озона в водных растворах нитратов // Ж. физ. хим. 2008. Т. 82. № 8. С. 1423.]
Yasunishi A., Yoshida F. Solubility of carbon dioxide in aqueous electrolyte solutions // J. Chem. Eng. Data. 1979. V. 24. № 1. P. 11.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии