Теоретические основы химической технологии, 2019, T. 53, № 6, стр. 715-720

Конвективная неустойчивость устойчиво стратифицированной среды, обусловленная термодиффузией

Л. Х. Ингель^*

НПО “Тайфун”
Обнинск, Россия

Поступила в редакцию 26.02.2018
После доработки 26.11.2018
Принята к публикации 27.12.2018

DOI: 10.1134/S004035711905004X

Аннотация

В линейном приближении исследуется устойчивость состояния покоя жидкой среды в поле силы тяжести. Плотность среды линейно зависит от температуры и концентрации примеси. В фоновом состоянии примесь распределена однородно, а стратификация температуры устойчивая (плотность убывает с высотой). Поэтому, согласно известным критериям, состояние покоя считается устойчивым. Показано, что даже относительно слабая термодиффузия при отрицательных значениях коэффициента Соре может дестабилизировать устойчиво стратифицированную по плотности среду (найдены нейтральные кривые, относящиеся к монотонной неустойчивости в бесконечном вертикальном слое). Для задачи с нагревом от боковой границы показана возможность эффективной “отрицательной теплоемкости” – понижения температуры среды в области притока тепла.

Ключевые слова: термодиффузия, двухкомпонентная среда, конвективная неустойчивость, температурная стратификация, отрицательная теплоемкость

ВВЕДЕНИЕ

Пусть жидкая среда устойчиво стратифицирована по температуре в поле силы тяжести – температура с высотой растет, плотность убывает. Конвективная устойчивость такой среды, на первый взгляд, не вызывает сомнений. Правда, в двухкомпонентной среде, плотность которой зависит не только от температуры, но и от концентрации примеси, возможно возникновение специфической неустойчивости, связанной с различием скоростей диффузии двух компонентов [1, 2]. Но это возможно только при достаточной неустойчивой фоновой стратификации примеси. В настоящей работе показано, что в двухкомпонентной среде возможно возникновение конвективной неустойчивости и при отсутствии вклада примеси в фоновую стратификацию плотности – при учете даже довольно слабого перекрестного кинетического эффекта – термодиффузии (эффекта Соре) [3–5]. Попутно обращается внимание на нетривиальные особенности отклика рассматриваемой среды на тепловыделение. Проявления термодиффузии, как известно, имеют важное значение для некоторых процессов химической технологии (см., например, [6]).

ФОНОВОЕ СОСТОЯНИЕ И ИСХОДНЫЕ УРАВНЕНИЯ

Согласно обычно используемому приближению, предполагаем, что отклонения плотности среды $\rho {\text{'}}$ линейно зависят от возмущений температуры $T$ и отклонений концентрации примеси $s$ (простейший пример – соленая вода):

$\rho {\text{'}} = {{\rho }_{0}}\left( {1 - \alpha T + \beta s} \right),$

где ${{\rho }_{0}}$ – средняя (отсчетная) плотность среды; $\alpha $ – термический коэффициент расширения среды, $\beta $ – соответствующий коэффициент для концентрации примеси (в случае соленой воды – коэффициент ее соленостного сжатия).

Рассматриваем устойчиво стратифицированную по температуре жидкую среду в бесконечном вертикальном слое ${{ - L} \mathord{\left/ {\vphantom {{ - L} 2}} \right. \kern-0em} 2} < x < {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}$ ($x$ – горизонтальная координата). Задан постоянный фоновый вертикальный градиент температуры ${{\gamma }_{T}} > 0.$ Фоновая стратификация примеси отсутствует, т.е. задано постоянное значение массовой доли примеси $\bar {\mu } = {{\bar {c}} \mathord{\left/ {\vphantom {{\bar {c}} {{{\rho }_{0}}}}} \right. \kern-0em} {{{\rho }_{0}}}},$ где $c$ – концентрация примеси (кг/м³). Поскольку отклонения концентрации примеси удобно измерять в промилле, $c = \bar {c} + c{\text{'}} \approx \bar {c} + {{10}^{{ - 3}}}{{\rho }_{0}}s.$

Линеаризованная система уравнений для возмущений в приближении Буссинеска с учетом термодиффузии имеет вид [3–5]

(1)

$\begin{gathered} \frac{{\partial v}}{{\partial t}} = - \frac{1}{{{{\rho }_{0}}}}\nabla p + \nu {{\nabla }^{2}}v + g\left( {\alpha T - \beta s} \right){{e}_{z}},\,\,\,\,\nabla v = 0, \\ \frac{{\partial T}}{{\partial t}} + {{\gamma }_{T}}v \cdot {{e}_{z}} = \kappa {{\nabla }^{2}}T,\,\,\,\,\frac{{\partial s}}{{\partial t}} = \chi {{\nabla }^{2}}s + {{\chi }_{T}}{{\nabla }^{2}}T. \\ \end{gathered} $

Здесь $v$ – вектор возмущения поля скорости, $t$ – время, $p$ – возмущение давления, ${{e}_{z}}$ – единичный вектор в направлении вертикальной оси z, $g$ – ускорение свободного падения; $\nu $ – кинематический коэффициент вязкости, $\kappa $ – коэффициент температуропроводности, $\chi $ – коэффициент диффузии примеси, ${{\chi }_{T}}$ – соответствующий коэффициент, относящийся к термодиффузии.

Поясним последнее из уравнений (1) (остальные достаточно традиционны [3–5, 7]). В более общем случае уравнение переноса примеси имеет вид [4]

(2)

$\frac{{\partial c}}{{\partial t}} = \nabla \left[ {\chi \nabla c + \chi {{s}_{T}}c\left( {1 - \frac{c}{\rho }} \right)\nabla T} \right],$

где ${{s}_{T}}$ – коэффициент Соре (°C)^–1 [3, 4]. Ограничиваемся здесь случаем, когда в (2) коэффициенты $\chi $ и ${{s}_{T}}$ можно считать постоянными, а вариации фоновой плотности достаточно малы, так что ${c \mathord{\left/ {\vphantom {c \rho }} \right. \kern-0em} \rho } \approx {c \mathord{\left/ {\vphantom {c {{{\rho }_{0}}}}} \right. \kern-0em} {{{\rho }_{0}}}}.$ В этом случае (2) можно переписать в виде

(3)

$\begin{gathered} \frac{{\partial \mu }}{{\partial t}} = \chi {{\nabla }^{2}}\mu + \chi {{s}_{T}}\nabla \left[ {\mu \left( {1 - \mu } \right)} \right]\nabla T + \\ + \,\,\chi {{s}_{T}}\mu \left( {1 - \mu } \right){{\nabla }^{2}}T = 0, \\ \end{gathered} $

где $\mu \approx {c \mathord{\left/ {\vphantom {c {{{\rho }_{0}}}}} \right. \kern-0em} {{{\rho }_{0}}}}.$ Концентрация примеси и температура складываются из фоновых значений и возмущений. При линеаризации по возмущениям первое слагаемое в правой части (3) имеет вид $\chi {{\nabla }^{2}}\mu {\text{'}};$ порядок второго слагаемого – $\chi {{s}_{T}}{{\gamma }_{T}}\left( {1 - 2\bar {\mu }} \right)\nabla \mu {\text{'}}$ (здесь штрихом обозначены возмущения). Отношение абсолютной величины второго слагаемого к первому, как видно из масштабного анализа, порядка $l{{s}_{T}}{{\gamma }_{T}}\left( {1 - 2\bar {\mu }} \right),$ где $l$ – наименьший из рассматриваемых пространственных масштабов возмущений. Ниже будут рассматриваться значения параметров, при которых упомянутое отношение много меньше единицы. Поэтому пренебрегаем вторым слагаемым и приходим к последнему уравнению (1), в котором

(4)

${{\chi }_{T}} = {{10}^{3}}\chi {{s}_{T}}\bar {\mu }\left( {1 - \bar {\mu }} \right),$

где множитель 10³ связан с тем, что возмущение концентрации примеси $s$ здесь измеряется в промилле.

На вертикальных границах $x = \pm L{\text{/}}2$ предполагается выполнение условий непротекания и прилипания, а также отсутствуют температурные возмущения и потоки примеси:

(5)

$w = 0,\,\,\,\,T = 0,\,\,\,\,\frac{{\partial s}}{{\partial x}} = 0\,\,{\text{при }}x = \pm {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}.$

НЕЙТРАЛЬНЫЕ КРИВЫЕ ДЛЯ СИММЕТРИЧНЫХ (ВЕРТИКАЛЬНО-ОДНОРОДНЫХ) ВОЗМУЩЕНИЙ В ВЕРТИКАЛЬНОМ СЛОЕ

Будем исследовать устойчивость состояния покоя по отношению к монотонным вертикально-однородным возмущениям. Ищется решение вида

(6)

$\begin{gathered} \left\{ {w\left( {x,t} \right),T\left( {x,t} \right),s\left( {x,t} \right)} \right\} = \\ = \left\{ {W\left( x \right),\theta \left( x \right),S\left( x \right)} \right\}\exp \left( {\omega t} \right), \\ \end{gathered} $

где $W\left( x \right),\,\,\theta \left( x \right),\,\,S\left( x \right)$ – соответствующие амплитудные функции. При $\omega = 0$ (имея в виду расчет порога неустойчивости) из последних двух уравнений (1) следует уравнение

(7)

$W{{\gamma }_{s}} = \chi {{\nabla }^{2}}S,$

где введено обозначение

(8)

${{\gamma }_{s}} \equiv - \frac{{{{\gamma }_{T}}{{\chi }_{T}}}}{\kappa } = - {{10}^{3}}\frac{\chi }{\kappa }{{\gamma }_{T}}{{s}_{T}}\bar {\mu }\left( {1 - \bar {\mu }} \right).$

Уравнение (7) формально совпадает с линеаризованным стационарным уравнением переноса примеси без учета термодиффузии, но при наличии фоновой вертикальной стратификации примеси с градиентом ${{\gamma }_{s}}$ (‰/м). Тем самым задача о нейтральных кривых формально свелась к известным задачам для двухкомпонентных сред, стратифицированных по обоим компонентам [1, 7, 8]. В частности, в безграничной среде монотонная неустойчивость имеет место при не слишком малых положительных значениях ${{\gamma }_{s}}{\text{:}}$

(9)

$\xi \equiv \frac{\kappa }{\chi }\frac{{\beta {{\gamma }_{s}}}}{{\alpha {{\gamma }_{T}}}} = - {{10}^{3}}\frac{\beta }{\alpha }{{s}_{T}}\bar {\mu }\left( {1 - \bar {\mu }} \right) > 1.$

Но с учетом краевых эффектов, условие неустойчивости, как показано ниже, может быть гораздо мягче. Аналогичная задача без учета термодиффузии, но при наличии фоновой вертикальной стратификации концентрации примеси, рассмотрена в [7]. Поэтому здесь достаточно лишь вкратце напомнить решение. (В промежуточных выкладках [7] содержится ряд опечаток, не отразившихся на окончательных результатах. Ниже приведены исправленные формулы.) Исключая из исходной системы уравнений все неизвестные, кроме $w,$ при $\omega = 0$ приходим к уравнению

(10)

$\frac{{{{d}^{4}}W}}{{d{{x}^{4}}}} = - \frac{1}{{\nu \kappa }}\left( {N_{T}^{2} + \frac{\kappa }{\chi }N_{s}^{2}} \right)W,$

где ${{N}_{T}} = {{\left( {\alpha g{{\gamma }_{T}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ ${{N}_{s}} = {{\left( { - \beta g{{\gamma }_{s}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ – частоты плавучести, обусловленные стратификациями каждого из компонентов. Вводя безразмерную горизонтальную координату $X = \frac{x}{{\left( {{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}} \right)}},$ систему уравнений можно переписать в виде

(11)

$\frac{{{{d}^{4}}W}}{{d{{X}^{4}}}} = - {\text{R}}W,$

(12)

$\frac{{{{d}^{2}}\theta }}{{d{{X}^{2}}}} = \left( {{{{{L}^{2}}{{\gamma }_{T}}} \mathord{\left/ {\vphantom {{{{L}^{2}}{{\gamma }_{T}}} {4\kappa }}} \right. \kern-0em} {4\kappa }}} \right)W,\,\,\,\,\frac{{{{d}^{2}}S}}{{d{{X}^{2}}}} = \left( {{{{{L}^{2}}{{\gamma }_{s}}} \mathord{\left/ {\vphantom {{{{L}^{2}}{{\gamma }_{s}}} {4\chi }}} \right. \kern-0em} {4\chi }}} \right)W.$

Здесь безразмерный параметр

(13)

${\text{R}} = \frac{{{{L}^{4}}}}{{16\nu \kappa }}\left( {N_{T}^{2} + \frac{\kappa }{\chi }N_{s}^{2}} \right) = \frac{{\alpha g{{\gamma }_{T}}{{L}^{4}}}}{{16\nu \kappa }}\left( {1 - \xi } \right)$

с точностью до знака является некоторым аналогом и обобщением числа Рэлея (рассматриваемым стратификациям, устойчивым по известным критериям, соответствует R > 0).

Общее решение уравнения (11) имеет вид

(14)

$W(X) = \sum\limits_{j = 1}^4 {{{C}_{j}}\exp ({{q}_{j}}X),} $

где ${{C}_{j}}$ – постоянные интегрирования, q_j – корни характеристического уравнения:

(15)

${{q}_{j}} = \pm B(1 \pm i),\,\,\,B = \sqrt[4]{{{{\text{R}} \mathord{\left/ {\vphantom {{\text{R}} 4}} \right. \kern-0em} 4}}}.$

Интегрирование уравнений (12) дает

$\theta = {{\theta }_{0}} + {{\theta }_{1}}X + \frac{{{{L}^{2}}{{\gamma }_{T}}}}{{4\kappa }}\sum\limits_{j = 1}^4 {\frac{{{{C}_{j}}}}{{q_{j}^{2}}}} \exp \left( {{{q}_{j}}X} \right),$

$S = {{S}_{0}} + {{S}_{1}}X + \frac{{{{L}^{2}}{{\gamma }_{s}}}}{{4\chi }}\sum\limits_{j = 1}^4 {\frac{{{{C}_{j}}}}{{q_{j}^{2}}}} \exp \left( {{{q}_{j}}X} \right),$

где ${{\theta }_{{0,1}}},$ ${{S}_{{0,1}}}$ – постоянные интегрирования. С учетом краевых условий, для постоянных интегрирования получаем уравнения

$\begin{gathered} \sum\limits_{j = 1}^4 {{{C}_{j}}} \exp \left( { \pm {{q}_{j}}} \right) = 0,\,\,\,\,{{S}_{1}} + \frac{{{{L}^{2}}{{\gamma }_{s}}}}{{4\chi }}\sum\limits_{j = 1}^4 {\frac{{{{C}_{j}}}}{{{{q}_{j}}}}} \exp \left( { \pm {{q}_{j}}} \right) = 0, \\ {{\theta }_{0}} + {{\theta }_{1}} + \frac{{{{L}^{2}}{{\gamma }_{T}}}}{{4\kappa }}\sum\limits_{j = 1}^4 {\frac{{{{C}_{j}}}}{{q_{j}^{2}}}} \exp \left( {{{q}_{j}}} \right) = 0, \\ {{\theta }_{0}} - {{\theta }_{1}} + \frac{{{{L}^{2}}{{\gamma }_{T}}}}{{4\kappa }}\sum\limits_{j = 1}^4 {\frac{{{{C}_{j}}}}{{q_{j}^{2}}}} \exp \left( { - {{q}_{j}}} \right) = 0. \\ \end{gathered} $

Еще одно соотношение следует из того, что разность $\alpha T - \beta s$ в правой части (2) не должна содержать каких-либо слагаемых, помимо экспонент (в противном случае они бы проявились в стационарном решении для w). Следовательно, должно выполняться соотношение

$\alpha {{\theta }_{1}} - \beta {{S}_{1}} = 0.$

Таким образом, имеем однородную линейную систему из семи уравнений с семью неизвестными C_i, θ₀, θ₁, S₁. Условие существования нетривиального решения, соответствующего границе устойчивости – обращение в ноль определителя системы. Как показывают расчеты, это имеет место при следующем соотношении между основными безразмерными параметрами:

(16)

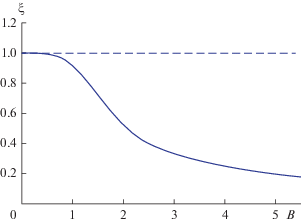
$\begin{gathered} \xi = \frac{{F\left( B \right)}}{B}, \\ F\left( B \right) = \frac{{\exp \left( {4B} \right) - 2\exp \left( {2B} \right)\cos \left( {2B} \right) + 1}}{{\exp \left( {4B} \right) + 2\exp \left( {2B} \right)\sin \left( {2B} \right) - 1}}. \\ \end{gathered} $

На рис. 1 представлена нейтральная кривая $\xi = {{F\left( B \right)} \mathord{\left/ {\vphantom {{F\left( B \right)} B}} \right. \kern-0em} B}$ – нижняя граница области монотонной неустойчивости, обусловленной термодиффузией в сочетании с краевыми эффектами (сплошная линия). Для сравнения штриховая прямая отвечает условию (9). Видно, что при достаточно большой толщине $L$ рассматриваемого слоя, когда велики значения параметров ${\text{R}}$ и B, неустойчивость имеет место даже при малых положительных значениях ξ, т.е. даже при малых по абсолютной величине отрицательных значениях коэффициента Соре ${{s}_{T}}$ и при сильной устойчивой фоновой стратификации плотности (но следует иметь в виду, что с ростом $L$ увеличивается время развития возмущений).

Рис. 1.

Нейтральные кривые при отрицательных значениях коэффициента Соре (нижние границы области неустойчивости; пояснено в тексте).

Проиллюстрируем это на численном примере, отвечающем возможным лабораторным экспериментам. В соленой воде при температурах, близких к 0°C, коэффициент Соре ${{s}_{T}}$ порядка $ - {{10}^{{ - 3}}}$ (°C)^–1 [4]. Пусть фоновая концентрация соли $\bar {\mu } = 0.05,$ фоновая стратификация солености отсутствует, ${{\gamma }_{T}} = 0.1$ К/м, $L = 0.1$ м. Примем характерные для соленой морской воды значения $\nu = {{10}^{{ - 6}}}$ м²/c, $\kappa = 1.4 \times {{10}^{{ - 7}}}$ м²/c, $\chi = 1.5 \times {{10}^{{ - 9}}}$ м²/c, $\alpha = {{10}^{{ - 4}}}$ К^–1, $\beta = 8 \times {{10}^{{ - 4}}}$ (‰)^–1. В этом случае $\xi = 0.38,$ R ≈ 2750, $B \approx 5.1,$ $F{{\left( B \right)} \mathord{\left/ {\vphantom {{\left( B \right)} B}} \right. \kern-0em} B} \approx 0.196,$ ${{\gamma }_{s}} = 0.51 \times {{10}^{{ - 4}}}$ ‰/м. Таким образом, при указанном наборе параметров имеет место неустойчивость, несмотря на устойчивую стратификацию плотности. Отметим, что в выражении (9) отношение коэффициентов обмена $\kappa {\text{/}}\chi $ в итоге сократилось, так что природа рассматриваемой неустойчивости принципиально отличается от известной неустойчивости, обусловленной различием скоростей диффузии тепла и примеси [1, 2]. К сожалению, мы не нашли в литературе экспериментальных данных с геометрией и набором параметров, отвечающих рассмотренной здесь идеализированной постановке задачи, допускающей аналитическое исследование. Для сопоставления теории с экспериментом требуются, с одной стороны, специально ориентированные эксперименты (известны жидкие среды с более сильно выраженным эффектом Соре, чем соленая вода). С другой стороны, реальные экспериментальные установки обычно не обладают такой идеальной симметрией, которая необходима для получения аналитических решений, так что, вероятно, потребуется и численное моделирование.

“ОТРИЦАТЕЛЬНАЯ ТЕПЛОЕМКОСТЬ” СРЕДЫ, ОБУСЛОВЛЕННАЯ ТЕРМОДИФФУЗИЕЙ

Рассмотрим ситуацию, когда среда в области значений параметров ниже порога возникновения рассмотренной неустойчивости нагревается от одной из боковых границ, т.е. одно из краевых условий (5) изменено:

(17)

$\frac{{\partial T}}{{\partial x}} = - Q < 0\,\,{\text{при }}x = {{ - L} \mathord{\left/ {\vphantom {{ - L} 2}} \right. \kern-0em} 2},$

где $Q > 0.$ На первый взгляд, приток тепла, очевидно, должен приводить к повышению температуры вблизи этой границы. Так и обстоит дело при отсутствии эффекта термодиффузии, в чем легко убедиться, например, из простого аналитического решения в предельном случае полуограниченной среды ($L \to \infty $). Правда, возникающие при нагреве восходящие течения приносят снизу более холодные объемы среды, но это лишь частично компенсирует нагрев от боковой границы. Но учет термодиффузии при отрицательном значении коэффициента Соре, как показано выше, эквивалентен существованию неустойчивой стратификации концентрации примеси, ${{\gamma }_{s}} > 0.$ Это обстоятельство должно дополнительно усиливать восходящие движения в области притока тепла, т.е. усиливать приток холодных объемов среды снизу. Возникает вопрос, не может ли это в итоге приводить к понижению температуры в области притока тепла. На рис. 2 представлен пример стационарного горизонтального профиля отклонения температуры. Он получен численно из решения системы уравнений (12) совместно с

$\frac{{{{d}^{2}}W}}{{d{{X}^{2}}}} = \frac{{g{{L}^{2}}}}{{4\nu }}\left( { - \alpha \theta + \beta S} \right),$

Рис. 2.

Пример безразмерного горизонтального профиля температурного возмущения в задаче с притоком тепла от левой границы.

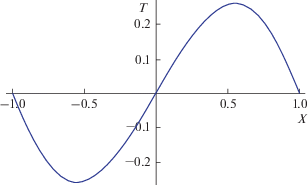
при $L = 0.052$ м и тех же, что и выше значениях остальных параметров. Меньшее, чем использованное ранее, значение $L$ отвечает меньшим значениям безразмерных параметров ${\text{R}},$ $B,$ которые, тем самым находятся несколько ниже порога устойчивости. Видно, что поступление тепла от левой границы действительно приводит к понижению температуры, т.е. проявление термодиффузии делает возможной эффективную “отрицательную теплоемкость” среды. Правее, где имеют место компенсационные нисходящие течения, последние приносят сверху более теплые объемы среды, так что отклонения температуры положительны.

ЗАКЛЮЧЕНИЕ

При отрицательных значениях коэффициента Соре отклонения плавучести, вызванные температурными возмущениями, могут дополнительно усиливаться за счет отклонений концентрации примеси. Такие проявления термодиффузии, как показано выше, в некоторых отношениях эквивалентны наличию неустойчивой фоновой стратификации концентрации примеси. Гидротермодинамике двухкомпонентных сред, стратифицированных по обоим компонентам, присущ целый ряд нетривиальных особенностей [8]. Выше показано, что даже относительно слабая термодиффузия в принципе может приводить к дестабилизации среды, сколь угодно устойчиво стратифицированной по плотности. В задаче с внешними источниками тепла представляется нетривиальной также возможность эффективной “отрицательной теплоемкости” – понижения температуры среды в области притоков тепла.

ОБОЗНАЧЕНИЯ

$\,B$	безразмерный параметр
C_j	постоянные интегрирования, м/с
$c$	концентрация примеси, кг/м³
$\bar {c}$	фоновая концентрация примеси, кг/м³
$c{\text{'}}$	отклонение концентрации примеси, кг/м³
${{e}_{z}}$	безразмерный единичный вектор в направлении вертикальной оси z
$F$	безразмерная функция
$g$	ускорение свободного падения, м/с²
$L$	ширина рассматриваемой области, м
$l$	наименьший из рассматриваемых пространственных масштабов возмущений, м
${{N}_{s}}$	частота плавучести, обусловленная эффективной стратификацией концентрации примеси, с^–1
${{N}_{T}}$	частота плавучести, обусловленная температурной стратификацией, с^–1
$p$	возмущение давления, Па
$Q$	нормированный поток тепла через боковую границу, К/м
q_j	безразмерные корни характеристического уравнения
${\text{R}}$	безразмерный параметр
${{S}_{{0,\,1}}}$	постоянные интегрирования, ‰
$S\left( x \right)$	амплитудная функция отклонения концентрации примеси, ‰;
$s$	отклонение концентрации примеси, ‰
${{s}_{T}}$	коэффициент Соре, (°C)^–1
$T$	отклонение температуры, К
$t$	время, с
$v$	вектор возмущения поля скорости, м/с
$W\left( x \right)$	амплитуда вертикальной скорости, м/с
$w$	вертикальная скорость, м/с
$X$	безразмерная горизонтальная координата
$x$	горизонтальная координата, м
$z$	вертикальная координата, м
$\alpha $	термический коэффициент расширения среды, К^–1
$\beta $	коэффициент, характеризующий влияние концентрации примеси на плотность среды (в случае соленой воды – коэффициент ее соленостного сжатия), (‰)^–1
${{\gamma }_{s}}$	эффективный вертикальной градиент концентрации примеси,‰/м
${{\gamma }_{T}}$	фоновый вертикальный градиент температуры, К/м
$\theta $	амплитудная функция отклонения температуры, К
${{\theta }_{{0,\,1}}}$	постоянные интегрирования, К
$\mu $	массовая доля примеси
$\bar {\mu }$	фоновое значение массовой доли примеси
$\nu $	кинематический коэффициент вязкости, м²/с
$\xi $	безразмерный параметр
$\rho $	плотность среды, кг/м³
${{\rho }_{0}}$	средняя (отсчетная) плотность среды, кг/м³
$\rho {\text{'}}$	отклонение плотности среды, кг/м³
$\chi $	коэффициент диффузии примеси, м²/с
${{\chi }_{T}}$	коэффициент переноса, относящийся к термодиффузии, м²/с
$\omega $	инкремент возмущений, с^–1

ИНДЕКСЫ

0	фоновое значение или номер постоянной интегрирования
$j$	номер постоянной интегрирования
$s$	относится к примеси
$T$	относится к температуре

Список литературы

Тернер Дж. Эффекты плавучести в жидкостях. М.: Мир, 1977.
Radko T. Double-Diffusive Convection. Cambridge: Cambridge University Press, 2013.
Рыжков И.И. Термодиффузия в смесях: уравнения, симметрии, решения и их устойчивость. Новосибирск: СО РАН, 2013.
Angeli C., Leonardi E. The effect of thermodiffusion on the stability of a salinity gradient solar pond // Int. J. Heat Mass Transfer. 2005. V. 48. P. 4633.
Гершуни Г.З., Жуховицкий Е.М. Конвективная устойчивость несжимаемой жидкости. М.: Наука, 1972.
Berezhnoi A.N., Semenov A.V. Thermal diffusion in the helium-xenon gas system // Theor. Found. Chem. Eng. 2005. V. 39. № 2. P. 173. [Бережной А.Н., Семенов А.В. Термодиффузия в газовой смеси гелий–ксенон // Теор. осн. хим. технол. 2005. Т. 39. № 2. С. 186.]
Ingel L.Kh. Convective instability mechanism for a binary mixture at a vertical surface // Tech. Phys. 2009. V. 54. № 2. P. 204 [Ингель Л.Х. Механизм конвективной неустойчивости бинарной смеси у вертикальной поверхности // Ж. тех. физ. 2009. Т. 79. № 2. С. 43.]
Ingel L.Kh., Kalashnik M.V. Nontrivial features in the hydrodynamics of seawater and other stratified solutions // Phys.-Usp. 2012. V. 55. № 4. P. 356. [Ингель Л.Х., Калашник М.В. Нетривиальные особенности гидротермодинамики морской воды и других стратифицированных растворов // Усп. физ. наук. 2012. Т. 182. № 4. С. 379.]

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал