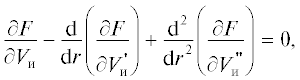Теоретические основы химической технологии, 2019, T. 53, № 6, стр. 617-621
Полуэмпирический метод определения скорости стесненного медленного движения
А. М. Трушин a, Л. В. Равичев a, В. Е. Яшин a, М. А. Носырев a, *, Р. Б. Комляшев a
a Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия
* E-mail: vnissok@list.ru
Поступила в редакцию 20.05.2019
После доработки 29.05.2019
Принята к публикации 03.06.2019
Аннотация
Получены полуэмпирические уравнения для определения скорости медленного стесненного движения сферических частиц в жидкости, с большой точностью соответствующие эмпирическим данным. Показана применимость вариационного принципа минимума интенсивности диссипации энергии при определении скорости стесненного движения.
ВВЕДЕНИЕ
Определение скорости стесненного движения дисперсных частиц, а также решение аналогичной задачи нахождения скорости ожижающего агента в кипящем слое осуществляются аналитическими, полуэмпирическими и эмпирическими методами.
Чисто аналитический подход использовался в ячеечных моделях [1]. К полуэмпирическим относятся методы, основанные на теории эффективной вязкости, а также методы, базирующиеся на определении коэффициентов сопротивления. В ряде работ [2–4] ячеечные модели и модели, основанные на коэффициентах сопротивления, были разработаны с использованием вариационного принципа минимума интенсивности диссипации энергии.
Следует отметить, что аналитические и полуэмпирические методы расчета дают сильные погрешности в области высоких концентраций дисперсной фазы. Исключением является ячеечная модель Хаппеля, погрешность расчета по которой достигает 100%, но при очень больших концентрациях твердой фазы, граничащих с неподвижным слоем, результаты расчета приближаются к экспериментальным данным. Это можно объяснить тем, что несовершенство самой модели компенсируется погрешностью расчета при высоких концентрациях дисперсных частиц.
Сильно концентрированные дисперсные системы встречаются в псевдоожиженных слоях, в процессах осаждения и при всплытии ансамбля пузырьков [5].
Целью данной работы является определение скорости стесненного медленного осаждения сферических частиц, а также доказательство того, что величина скорости стесненного движения является следствием самоорганизации системы дисперсных частиц и может быть определена из вариационного принципа минимума интенсивности диссипации энергии, как это предполагалось в работах [2–4].
СТЕСНЕННОЕ ДВИЖЕНИЕ ЧАСТИЦ ПРИ ВЫСОКИХ КОНЦЕНТРАЦИЯХ ДИСПЕРСНОЙ ФАЗЫ
Рассмотрим идеальный случай движения жидкости в каналах кипящего однородного слоя, принятых условно прямыми с постоянным эквивалентным радиусом Rэ. Примем также условно равной нулю скорость жидкости у поверхности сферических монодисперсных твердых частиц. Градиент давления в псевдоожиженном слое с долей дисперсной фазы φ равен силе тяжести единицы объема кипящего слоя с обратным знаком:
(1)
$\nabla p = - \left[ {{{\rho }_{{\text{т}}}}\varphi + \rho \left( {1 - \varphi } \right)} \right]g.$С учетом этого, баланс внешних и внутренних сил, отнесенных к единице объема жидкости, текущей в каналах псевдоожиженного слоя, выражается следующим уравнением в цилиндрических координатах:
(2)
$\mu \frac{1}{r}\frac{{\text{d}}}{{{\text{d}}r}}\left( {r\frac{{{\text{d}}{{V}_{{\text{и}}}}}}{{{\text{d}}r}}} \right) = - \left( {{{\rho }_{{\text{т}}}} - \rho } \right)\varphi {\kern 1pt} g.$Уравнение (2) служит основой для определения зависимости скорости стесненного движения частиц от доли дисперсной фазы.
Известно, что уравнение Пуазейля–Хагена может быть получено вариационным методом.
Поскольку одной из задач данной статьи является доказательство того, что скорость стесненного медленного движения может быть определена вариационным методом, а также, ввиду того, что движение жидкости по каналам псевдоожиженного слоя имеет некоторые особенности, следует показать применимость принципа минимума интенсивности диссипации энергии в этом случае. Для этого достаточно показать соответствие уравнения (2) функционалу, дающему минимум интенсивности диссипации.
Функционал в виде интенсивности диссипации при ламинарном движении в каналах кипящего слоя длиной L выражается следующим образом:
(3)
$I\left( {{{V}_{{\text{и}}}}} \right) = 2\pi \int\limits_0^{{{R}_{{\text{э}}}}} {\mu {\kern 1pt} L{\kern 1pt} {{V}_{{\text{и}}}}\left( {\frac{{{\text{d}}{{V}_{{\text{и}}}}}}{{{\text{d}}r}} + r\frac{{{{{\text{d}}}^{2}}{{V}_{{\text{и}}}}}}{{{\text{d}}{{r}^{2}}}}} \right)} {\text{d}}r = \min .$Функция Vи(r), дающая экстремум функционалу I(Vи), определяется из уравнения Эйлера–Лагранжа:
где F – подынтегральное выражение функционала.При постоянном расходе жидкости для вариационной задачи (3) имеется дополнительное условие:
(5)
$2\pi \int\limits_0^{{{R}_{{\text{э}}}}} {{{V}_{{\text{и}}}}\left( {{{\rho }_{{\text{т}}}} - \rho } \right)\varphi {\kern 1pt} g} L{\kern 1pt} r\,{\text{d}}r = {\text{const}}.$С учетом дополнительного условия (5) функция F в уравнении (4) заменяется на функцию Ф:
(6)
${\text{Ф}} = \mu {\kern 1pt} L{{V}_{{\text{и}}}}\left( {\frac{{{\text{d}}{{V}_{{\text{и}}}}}}{{{\text{d}}r}} + r\frac{{{{{\text{d}}}^{2}}{{V}_{{\text{и}}}}}}{{{\text{d}}{{r}^{2}}}}} \right) + \lambda {{V}_{{\text{и}}}}\left( {{{\rho }_{{\text{т}}}} - \rho } \right){\kern 1pt} g\varphi {\kern 1pt} Lr,$Из уравнения Эйлера–Лагранжа в данном случае получим следующее дифференциальное уравнение второго порядка:
(7)
$\mu {\kern 1pt} \frac{1}{r}\frac{{\text{d}}}{{{\text{d}}r}}\left( {r\frac{{{\text{d}}{{V}_{{\text{и}}}}}}{{{\text{d}}r}}} \right){\text{ = }} - \frac{\lambda }{2}\left( {{{\rho }_{{\text{т}}}} - \rho } \right)g{\kern 1pt} \varphi .$Для соблюдения баланса внешних и внутренних сил, отнесенных к единице объема жидкости, величина λ в уравнении (7) должна равняться двум, что соответствует полной идентичности уравнений (2) и (7). Таким образом, можно считать, что задача об определении приведенной скорости жидкости в однородном кипящем слое или эквивалентная задача определения скорости стесненного осаждения, основой для решения которых является уравнение (2), может быть решена вариационным методом.
Решение уравнения (2) с последующим определением объемного потока жидкости через поперечное сечение канала кипящего слоя приводит к следующему выражению для средней скорости жидкости, проходящей через слой в идеальном случае:
(8)
${{V}_{{{\text{и}}{\text{.ср}}}}} = R_{{\text{э}}}^{2}\frac{{\left( {{{\rho }_{{\text{т}}}} - \rho } \right)g\varphi }}{{8\mu }} = d_{{\text{э}}}^{2}\frac{{\left( {{{\rho }_{{\text{т}}}} - \rho } \right)g\varphi }}{{32\mu }}.$В случае зернистого слоя сферических частиц с диаметром d эквивалентный диаметр виртуальных цилиндрических каналов определяется по уравнению
Из уравнений (8) и (9) получим
(10)
${{V}_{{{\text{и}}{\text{.ср}}}}} = \frac{{{{d}^{2}}\left( {{{\rho }_{{\text{т}}}} - \rho } \right)g{{{\left( {1 - \varphi } \right)}}^{2}}}}{{72\mu \varphi }}.$Средняя скорость жидкости связана с приведенной скоростью Vи.п следующим соотношением:
С учетом (11) получим
(12)
${{V}_{{{\text{и}}{\text{.п}}}}} = \frac{{{{d}^{2}}\left( {{{\rho }_{{\text{т}}}} - \rho } \right)g{{{\left( {1 - \varphi } \right)}}^{3}}}}{{72\mu {\kern 1pt} \varphi }}.$Следует отметить, что аналогичный подход был использован Козени, Карманом и Блэйком [6] для получения градиента давления в неподвижном зернистом слое на основе уравнения Пуазейля–Хагена.
Переведем уравнение (12) в безразмерную форму:
(13)
${{\operatorname{Re} }_{{\text{и}}}} = \frac{{{\text{Ar}}}}{{72}}\frac{{{{{\left( {1 - \varphi } \right)}}^{3}}}}{\varphi }.$С учетом того, что каналы кипящего слоя извилисты и имеют неравномерное сечение, а также того, что частицы в кипящем слое могут вращаться, действительная скорость Vп отличается от идеальной Vи.п:
С учетом (14) получим уравнение для действительной приведенной скорости:
(15)
$\operatorname{Re} = \frac{{{\text{Ar}}}}{{72K}}\frac{{{{{\left( {1 - \varphi } \right)}}^{3}}}}{\varphi }.$Из аналогии между псевдоожижением и осаждением известно, что истинная скорость стесненного осаждения частиц равна приведенной скорости жидкости в кипящем слое Vп. Ввиду этого уравнение (15) может быть использовано для определения скорости стесненного осаждения.
Ввиду того, что при малых значения Re (медленное течение) действует закон Стокса, для этого случая уравнение (15) можно записать как
Функция f(φ) = (1 – φ)3/(4Kφ) является отношением скорости стесненного и свободного осаждения.
Запишем f(φ) в упрощенном виде:
где A = 1/(4K).Сложность задачи движения жидкости по извилистым каналам переменного сечения требует привлечения экспериментальных данных для определения величины A.
Отношение скорости стесненного и свободного осаждения мелкодисперсных сферических частиц в ламинарной области с достаточной точностью определяется по степенным зависимостям [7]:
(19)
$n = 4.65 + 19.5\frac{d}{{{{d}_{{\text{к}}}}}}\,\,\,\,{\text{при}}\,\,\,\,{{\operatorname{Re} }_{0}} < 0.2,$(20)
$\begin{gathered} n = \left( {4.35 + 17.5\frac{d}{{{{d}_{{\text{к}}}}}}} \right)\operatorname{Re} _{0}^{{ - 0.03}} \\ {\text{при}}\,\,\,0.2 < {{\operatorname{Re} }_{0}} < 2. \\ \end{gathered} $Число Re0 определяется по скорости свободного осаждения.
Поскольку значениям Re < 2 соответствуют значения диаметра частиц, на несколько порядков отличающиеся от диаметра колонн dк, величины 19.5d/dк и 17.5d/dк в расчете n не учитывались.
Величины коэффициентов A, дающих наиболее близкое соответствие уравнений (17) и (18) при Re0 < 0.2, определялись из системы уравнений
(21)
$J = \int\limits_{1 - {{\varphi }_{1}}}^{1 - {{\varphi }_{2}}} {{{{\left( {{{\varepsilon }^{n}} - A\frac{{{{\varepsilon }^{3}}}}{{1 - \varepsilon }}} \right)}}^{2}}} {\text{d}}\varepsilon = \min ,$(22)
$\frac{{{\text{d}}J}}{{{\text{d}}A}} = - 2\int\limits_{1 - {{\varphi }_{1}}}^{1 - {{\varphi }_{2}}} {\left[ {\left( {{{\varepsilon }^{n}} - A\frac{{{{\varepsilon }^{3}}}}{{1 - \varepsilon }}} \right)\left( {\frac{{{{\varepsilon }^{3}}}}{{1 - \varepsilon }}} \right)} \right]{\text{d}}\varepsilon } = 0.$В уравнениях (21) и (22) для удобства расчета использовалась доля жидкой фазы ε = 1 – φ.
Интеграл (17) вычислялся в пределах от φ1 = 0.25 до φ2 = 0.55. Верхнее значение φ2 = 0.55 близко к неподвижному слою. При концентрациях частиц меньших значений φ1 = 0.25, как показывают расчеты, расхождения уравнений (17) и (18) становятся значительными. Это, вероятно, связано с тем, что при низких концентрациях твердой фазы каналы, по которым перемещается жидкость, разрушаются и, соответственно, предлагаемая модель движения дисперсных частиц ограничена интервалом дисперсной фазы от 0.25 до 0.55. Уравнения (16) и (17) применимы для значений Re0 < 0.2, когда закон Стокса дает достаточно малые расхождения с экспериментальными данными. В случае медленного движения (0 < Re0 < 0.2) значение коэффициента A, определенное по уравнению (22), равно 0.16.
Таким образом, для медленного движения сферических частиц соотношение скоростей стесненного и свободного движения в интервале значений доли дисперсной фазы от 0.25 до 0.55 можно определить следующим образом:
Среднее расхождение между величинами, определяемыми по уравнениям (18) и (23), составляет 4.7%.
СТЕСНЕННОЕ ДВИЖЕНИЕ ПРИ НИЗКИХ ЗНАЧЕНИЯХ ДОЛИ ДИСПЕРСНОЙ ФАЗЫ
Скорость стесненного осаждения сферических частиц при низких концентрациях дисперсной фазы в интервале 0 < φ < 0.25 при Re0 < 0.2 может быть определена на основе представления суспензии как ньютоновской жидкости, обладающей большей (эффективной) вязкостью μэф, являющейся функцией доли дисперсной фазы.
Безразмерная эффективная вязкость $\bar {\mu }$, являющаяся отношением вязкости суспензии и вязкости дисперсионной среды, в достаточно широком интервале доли дисперсной фазы (0 < φ < 0.4) может быть определена по следующей экспериментально найденной формуле [8]:
При низких значениях φ формула (24) переходит в известную формулу Эйнштейна.
Сильно приближенное рассмотрение осаждения посторонней сферической частицы в среде с эффективной вязкостью и плотностью суспензии при расчете выталкивающей силы Архимеда приводит к следующему соотношению скоростей стесненного и свободного осаждения сферических частиц в области Re0 < 0.2:
(25)
$f\left( \varphi \right) = \frac{{{{{\left( {1 - \varphi } \right)}}^{2}}}}{{1 + 2.5\varphi + 12.5{{\varphi }^{2}}}}.$При получении уравнения (25) предполагалось, что коэффициент сопротивления при стесненном осаждении в среде с эффективной вязкостью и в дисперсионной среде соответствует закону Стокса.
Из работы [3] следует, что это уравнение дает заниженные результата, что связано с завышенной величиной выталкивающей силы. Следует отметить, что такое выражение силы Архимеда противоречит допущению о равномерности движения частиц при осаждении. Исключение этого противоречия приводит к меньшей зависимости f(φ) от доли сплошной фазы:
В свою очередь, уравнение (26) соответствует заниженным значениям f(φ) по сравнению с эмпирическими данными.
Расчеты показывают, что наименьшее расхождение с эмпирическими данными дает среднее геометрическое из уравнений (25) и (26):
(27)
$f\left( \varphi \right) = \frac{{{{{\left( {1 - \varphi } \right)}}^{{1.5}}}}}{{1 + 2.5\varphi + 12.5{{\varphi }^{2}}}}.$Среднее расхождение между расчетными значениями f(φ), полученными по уравнениям (27) и (18), составляет 1.2%.
Такой же результат можно получить, исходя из взаимосвязи между f(φ) и безразмерной эффективной вязкостью [8]:
В этой формуле используют два значения показателя степени m: m = 1 (формула Кинча) и m = 2 (формула Хоксли). При этом функцию f(φ) рассчитывают по ячеечной модели с целью определения эффективной вязкости. Если принять среднее геометрическое для функции (1 – φ)m при значениях m = 1 и m = 2, то в результате получим формулу (27), при использовании формулы (24) для расчета эффективной вязкости.
Уравнения (25)–(28) получены, исходя из равномерного распределения частиц по объему слоя, в то время как при осаждении доля дисперсной фазы распределена неравномерно вследствие объединения частиц в группы [2–4]. В этом случае истинная доля дисперсной фазы больше средней. Если предположить превышение истинного значения φи над средним φ на 12.5%, то формула (26) преобразуется следующим образом:
(29)
$f\left( \varphi \right) = \frac{{1 - 1.125\varphi }}{{1 + 2.813\varphi + 15.82{{\varphi }^{2}}}}.$Среднее расхождение величин f(φ), рассчитанных по уравнениям (27) и (29), составляет менее 1%. Исходя из этого, можно предположить, что причиной завышенных величин f(φ), рассчитанных по уравнению (26), является объединение частиц в группы при осаждении.
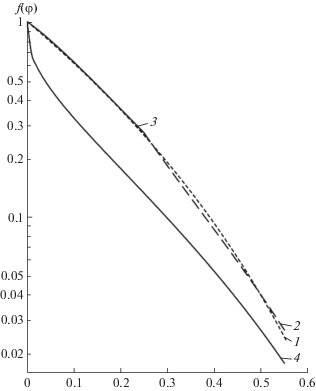
Как показывает рис. 1, где проведено сравнение эмпирического уравнения (18) с полуэмпирическими зависимостями (23) и (27), (29) и теоретическим уравнением Хаппеля [6], полученные полуэмпирические зависимости очень близки к эмпирическому уравнению, в то время как теоретическое уравнение Хаппеля сильно отклоняется как от эмпирических, так и от полуэмпирических зависимостей. С учетом большей точности эмпирического уравнения (18) [9] можно сделать вывод о достаточной обоснованности теоретических подходов при получении полуэмпирических соотношений скоростей стесненного и свободного осаждения.
Рис. 1.
Зависимость соотношения скоростей стесненного и свободного осаждения частиц от доли дисперсной фазы: 1 – формула (18), 2 – формула (23), 3 – формулы (27) и (29), 4 – уравнение Хаппеля.
ЗАКЛЮЧЕНИЕ
Подытоживая изложенное выше, можно заключить, что задача об определении скорости стесненного медленного осаждения решается с использованием уравнения (23) для высоких значений доли дисперсной фазы (0.25 < φ < 0.55) и уравнения (27) или (29) в области низких концентраций дисперсных частиц (0 < φ < 0.25). Можно также заключить, что стесненное медленное движение подчиняется вариационному принципу минимума интенсивности диссипации энергии.
ОБОЗНАЧЕНИЯ
| d | диаметр частиц |
| dэ | эквивалентный диаметр каналов |
| g | ускорение свободного падения |
| K | корректирующий коэффициент |
| Rэ | эквивалентный радиус канала |
| Vи | скорость жидкости в каналах в идеальном случае |
| Vи.п | приведенная скорость жидкости в идеальном случае |
| Vп | приведенная скорость жидкости |
| ε | доля жидкой фазы |
| λ | коэффициент Лагранжа |
| μ | динамический коэффициент вязкости |
| $\bar {\mu }$ | приведенная эффективная вязкость |
| ρ | плотность жидкости |
| ρт | плотность частицы |
| φ | доля дисперсной фазы |
| Re | число Рейнольдса для стесненного движения частиц |
| Re0 | число Рейнольдса для свободного движения частиц |
| Reи | число Рейнольдса в идеальном случае движения в каналах |
Список литературы
Слободов Е.Б., Чепура И.В. К вопросу о ячеечной модели двухфазных сред // Теор. осн. хим. технол. 1982. Т. 16. № 3. С. 331.
Trushin A.M., Dmitriev E.A., Nosyrev M.A., Tarasova T.A., Kuznetsova I.K. Determining the Velocity of the Hindered Motion of Spherical Gas Particles through Liquid in a Gravity Field // Theor. Found. Chem. Eng. 2013. V. 47. № 4. P. 368. [Трушин А.М., Дмитриев Е.А., Носырев М.А., Тарасова Т.А., Кузнецова И.К. Определение скорости стесненного движения сферических газовых частиц в жидкости в поле силы тяжести // Теор. осн. хим. технол. 2013. Т. 47. № 4. С. 434.]
Trushin A.M., Dmitriev E.A., Nosyrev M.A., Khusanov A.E., Kaldybaeva B.M. General method of measurement of velocity of laminar constrained motion of spherical solid and gas particles in liquids // Theor. Found. Chem. Eng. 2013. V. 47. № 6. P. 730. [Трушин А.М., Дмитриев Е.А., Носырев М.А., Хусанов А.Е., Калдыбаева Б.М. Обобщённый метод определения скорости ламинарного стесненного движения сферических твердых частиц в жидкости // Теор. осн. хим. технол. 2013. Т. 47. № 6. С. 668.]
Трушин А.М., Дмитриев Е.А., Носырев М.А. Использование вариационного метода для определения скорости стесненного турбулентного движения дисперсных частиц в жидкости // Теор. осн. хим. технол. 2017. Т. 51. № 2. С. 86.
Носырев М.А., Трушин А.М., Комляшев Р.Б., Кабанов О.В., Кузнецова И.К. Очистка биогаза в микробарботажной колонне // Хим. пром-сть сегодня. 2018. № 3. С. 32.
Протодьяконов И.О., Чесноков Ю.Г. Гидромеханические основы процессов химической технологии. Л.: Химия, 1987.
Швыдкий В.С. Механика жидкости и газа. М.: Академкнига, 2003.
Кутепов А.М., Полянин А.Д., Запрянов З.Д., Вязьмин А.В., Казенин Д.А. Химическая гидродинамика. М.: Бюро Квантум, 1996.
Davidson J.F., Harrison D. Fluidization. London: Academic, 1971.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии