Теоретические основы химической технологии, 2019, T. 53, № 6, стр. 652-663
Оценка необратимости и оптимальная организация интегрированной системы многопоточного теплообмена
А. М. Цирлин a, *, А. А. Ахременков a, **, С. Ю. Бойков b, ***
a Институт программных систем им. А.К. Айламазяна РАН
Переславль-Залесский, Россия
b Ярославский технический университет
Ярославль, Россия
* E-mail: tsirlin@sarc.botik.ru
** E-mail: andrei@svp.polnet.botik.ru
*** E-mail: boykovsy@ystu.ru
Поступила в редакцию 11.12.2018
После доработки 04.02.2019
Принята к публикации 18.02.2019
Аннотация
Предложен алгоритм синтеза структуры и распределения поверхностей в теплообменной системе для случая, когда фиксированы водяные эквиваленты и входные температуры горячих потоков, а для холодных потоков кроме этого заданы и их температуры на выходе. Алгоритм учитывает возможность изменения фазового состояния контактирующих потоков. Минимизации диссипации при заданной суммарной тепловой нагрузке соответствует минимум суммарной поверхности контакта, тесно коррелированной со стоимостью теплообменной системы.
ВВЕДЕНИЕ
Задачи синтеза многопоточных теплообменных систем состоят в том, чтобы организовать тепловые контакты между горячими и холодными потоками (выбрать структуру системы), распределить между двухпоточными теплообменными ячейками тепловые нагрузки, рассчитать коэффициенты теплообмена для каждой ячейки так, чтобы минимизировать некоторый критерий оптимальности и удовлетворить поставленным ограничениям. В большинстве случаев системы теплообмена интегрированы с некоторым технологическим процессом (металлургия, процессы ректификации и др.) [1], в котором потоки, поступающие в технологическую систему, должны иметь определенные температуры, как и отходящие горячие потоки. За счет теплообмена минимизируют затраты тепла, потребляемые технологией.
В большинстве работ (см., например, [2]) критерий оптимальности носит технико-экономический характер, суммируя с выбранными весами капитальные и эксплуатационные затраты, а ограничения определяются характеристиками синтезируемой системы. Так, в процессе многоколонной ректификации технологические требования диктуют температуры и водяные эквиваленты потоков, а в систему теплообмена могут быть включены теплообменные устройства колонн (куб и дефлегматор). Синтез такой системы при большом числе контактирующих потоков является сложной комбинаторной задачей, решаемой численно, в ряде случаев с привлечением эвристических соображений [3, 4].
Использование технико-экономических критериев сопряжено с произволом в выборе коэффициентов, оценивающих эксплуатационные и капитальные затраты, в величине самих этих затрат, зависящих от стоимости материалов, монтажа конструкций и пр. Кроме того, такой критерий предполагает численную процедуру и не дает возможности использовать общие термодинамические закономерности.
В [5] использован эксергетический критерий, сводящийся к минимизации потерь эксергии (работоспособной энергии). Такой подход позволил авторам сравнить несколько различных систем по фактическим потерям эксергии. Никакой процедуры оптимизации или синтеза систем по выбранному критерию при этом не предлагалось.
В практике проектирования технологических систем значительное распространение получил пинч-анализ [6–8]. В нем строят зависимости температур контактирующих потоков от их энтальпии, находят пинч-зону, в которой эти температуры наиболее близки (пинч-температуры). Дальнейшие построения базируются на самых общих качественных соображениях о характере контактов для температур выше и ниже пинча. Никакого термодинамического обоснования и количественной оценки эффективности полученных систем не предлагается.
Потери эксергии равны произведению производства энтропии в системе на абсолютную температуру окружающей среды, поэтому минимуму этих потерь соответствует минимум производства энтропии (необратимости). Этот факт использован в методах оптимизационной термодинамики [9–14]. При этом решают задачи об оптимальном по критерию минимума производства энтропии синтезе термодинамических систем при тех или иных ограничениях.
Такой подход обоснован тем, что производство энтропии при заданной суммарной поверхности теплообмена и структуре системы монотонно возрастает с ростом тепловой нагрузки и, наоборот, при заданной тепловой нагрузке монотонно падает с ростом поверхности теплообмена. Значит, в структуре, найденной по условию минимума необратимости, можно при заданной поверхности обеспечить максимум тепловой нагрузки, а при фиксированной нагрузке – минимум суммарной поверхности контакта, которая коррелирована со стоимостью системы.
В работе [15] рассмотрена задача о предельных возможностях теплообменной системы (“идеальный” теплообмен). Там найдено минимально возможное производство энтропии $\sigma {\text{*}}$ в системе с заданными значениями водяных эквивалентов и входных температур горячих или холодных потоков и заданными суммарной тепловой нагрузкой и суммарным коэффициентом теплообмена. Показано, что для случая, когда поток теплоты пропорционален разности температур (ньютоновской кинетике), эта граница необратимости может быть достигнута, если в каждой точке контакта отношение абсолютных температур потоков одинаково, а их температуры на выходе из системы одинаковы для всех потоков, входные температуры которых фиксированы (горячих или холодных).
Условия идеального теплообмена накладывают весьма жесткие требования на характеристики системы:
– каждая двухпоточная ячейка должна представлять собой противоточный теплообменник;
– отношение водяных эквивалентов горячего и холодного потока в ней должно быть равно отношению в градусах Кельвина температуры холодного потока на выходе из теплообменной ячейки к температуре горячего потока на ее входе (“условия термодинамической согласованности”);
– это отношение и соответствующее ему минимально возможное производство энтропии при фиксированных температурах и водяных эквивалентах горячих потоков связаны с их температурами на входе $T_{i}^{0},$ водяными эквивалентами ${{W}_{i}}$ и суммарным коэффициентом теплообмена $K$ как
(1)
$\left. {\begin{array}{*{20}{l}} {m = 1 - \frac{1}{K}\sum\limits_{i = 1}^n {{{W}_{i}}} (\ln T_{i}^{0} - \ln {{{\bar {T}}}_{ + }}),} \\ {\sigma {\text{*}} = K\frac{{{{{(1 - m)}}^{2}}}}{m}.} \end{array}} \right\}$– температура горячих потоков на выходе должна быть одинакова и, как следует из условий энергетического баланса, равна
(2)
${{\bar {T}}_{ + }} = \frac{{\sum\limits_{i = 1}^k {{{T}_{{i0}}}} {{W}_{i}} - \bar {q} - \sum\limits_z {} }}{{\sum\limits_{i = 1}^k {{{W}_{i}}} }},$– горячие потоки с начальными температурами, меньшими чем ${{\bar {T}}_{ + }},$ в системе теплообмена не участвуют.
Если часть горячих потоков конденсируется в процессе теплообмена, то в выражении для $m$ (1) водяной эквивалент соответствующего слагаемого стремится к бесконечности. Присвоим конденсирующемуся потоку индекс k и найдем предел
при стремлении ${{W}_{k}}$ к бесконечности. С использованием правила Лопиталя для раскрытия неопределенностей находим, что
Здесь учтено, что температура $T_{k}^{0}$ равна температуре конденсации, а тепловая нагрузка – произведению расхода на скрытую теплоту парообразования.
Таким образом, выражение для $m$ при наличии конденсирующихся потоков перепишется в форме
(3)
$m = 1 - \frac{1}{K}\left( {\sum\limits_{i \ne k} {{{W}_{i}}} (\ln T_{i}^{0} - \ln {{{\bar {T}}}_{ + }}) + \sum\limits_k {\frac{{{{g}_{k}}{{r}_{k}}}}{{{{T}_{{bk}}}}}} } \right).$При выводе приведенных выше выражений предполагалось, что все параметры холодных потоков выбирают для заданной нагрузки и величины K по условию минимума необратимости. Между тем во многих случаях нет возможности такого выбора.
В многопоточной системе, интегрированной с технологическим процессом, заданы значения водяных эквивалентов как горячих, так и холодных потоков, а часто заданы их температуры на выходе. Поэтому показателей идеальной теплообменной системы достичь невозможно. Естественно поставить задачу синтеза теплообменной системы с минимальной необратимостью при более жестких ограничениях на характеристики потоков. Условия идеального теплообмена при этом могут служить лишь “путеводной звездой” подобно КПД Карно для тепловых машин, а величина отношения σ* к производству энтропии в спроектированной системе – показателем ее термодинамического совершенства.
Ниже предлагаются расчетные соотношения для оценки снизу минимальной диссипации в системе с перечисленными выше ограничениями и синтез гипотетической системы, в которой такая оценка реализуется.
ПОСТАНОВКА И УСЛОВИЯ ОПТИМАЛЬНОСТИ ЗАДАЧИ СИНТЕЗА СИСТЕМЫ ТЕПЛООБМЕНА
Рассмотрим систему многопоточного теплообмена, содержащую множество горячих (индекс $i$) и холодных потоков (индекс $j$) с заданными водяными эквивалентами ${{W}_{i}},{{W}_{j}}.$ Для каждого из холодных (нагреваемых) потоков заданы его температуры на входе и на выходе системы $T_{j}^{0}$ и ${{\bar {T}}_{j}} > T_{j}^{0}.$
Для горячих (охлаждаемых) потоков кроме водяных эквивалентов заданы их температуры на входе в теплообменник $T_{i}^{0}.$ Если поток меняет свое фазовое состояние, то для него кроме водяных эквивалентов фиксирован расход ${{g}_{i}},{{g}_{j}}$ и теплота парообразования (конденсации) ${{r}_{i}},{{r}_{j}}.$ Температуру окружающей среды будем обозначать как ${{T}_{0}}$.
При этих условиях тепловая нагрузка системы равна суммарной энергии, требующейся на подогрев всех холодных потоков, и определена равенством
(4)
$\bar {q} = \sum\limits_j {{{q}_{j}}} = \sum\limits_j {{{W}_{j}}} ({{\bar {T}}_{j}} - T_{j}^{0}).$Различие в условиях, наложенных на горячие и холодные потоки, обусловлено тем, что для холодных потоков, выходящих из системы с температурой меньшей заданной, требуется подогрев, т.е. дополнительные затраты энергии, а для горячих, если их температуры на выходе оказались больше заданной, нужно охлаждение, которое значительно проще.
Для некоторых из горячих потоков температура на выходе может быть задана, будем отмечать эти потоки индексом z и предполагать, что температуры всех потоков в системе не ниже, чем температура окружающей среды T0.
Производство энтропии равно разнице между суммарной энтропией уходящих потоков и суммарной энтропией входящих. Первоначально будем считать, что все потоки входят и покидают систему в одном и том же фазовом состоянии, изменение давления в системе мало, а теплоемкости постоянны. Тогда изменение энтропии каждого потока равно произведению его водяного эквивалента на логарифм отношения его температур на входе и на выходе в градусах Кельвина [16, 17]. Так что из условий термодинамического баланса по энтропии следует, что
(5)
$\begin{gathered} \sigma = {{\sigma }_{ + }} + {{\sigma }_{ - }} = \sum\limits_i {{{W}_{i}}} (\ln {{{\bar {T}}}_{i}} - \ln T_{i}^{0}) + \\ + \,\,\sum\limits_j {{{W}_{j}}} (\ln {{{\bar {T}}}_{j}} - \ln T_{j}^{0}). \\ \end{gathered} $Первое из этих слагаемых отрицательно, а второе положительно, причем их сумма всегда больше $\sigma {\text{*}} > 0.$ Выражение для расчета производства энтропии при изменении фазового состояния потока будет приведено ниже.
Отметим, что все переменные, определяющие величину прироста энтропии холодных потоков, заданы условиями задачи, так что минимуму производства энтропии соответствует минимум при заданной тепловой нагрузке первого слагаемого по температурам ${{\bar {T}}_{i}}.$
Формальная постановка примет следующий вид:
(6)
$\begin{gathered} {{\sigma }_{ + }} = \sum\limits_i {{{W}_{i}}} (\ln {{{\bar {T}}}_{i}} - \ln T_{i}^{0}) \to {{\min } \mathord{\left/ {\vphantom {{\min } {\sum\limits_i {{{W}_{i}}} (T_{i}^{0} - {{{\bar {T}}}_{i}})}}} \right. \kern-0em} {\sum\limits_i {{{W}_{i}}} (T_{i}^{0} - {{{\bar {T}}}_{i}})}} = \\ = \bar {q} = \sum\limits_j {{{W}_{j}}} ({{{\bar {T}}}_{j}} - T_{j}^{0}). \\ \end{gathered} $Функция Лагранжа этой задачи
Условия ее стационарности по ${{\bar {T}}_{i}}$ приводят к равенству
Сформулируем условия оптимальности: при любых водяных эквивалентах Wi и входных температурах горячих потоков минимуму диссипации соответствует такая организация теплообмена, для которой температуры горячих потоков на выходе одинаковы. Обозначим эту выходную температуру как ${{\bar {T}}_{ + }}.$ Она определена условием энергетического баланса системы (см. (2)).
В более общем случае, когда для некоторых горячих потоков выходная температура ${{\bar {T}}_{z}}$ задана, получим
(7)
${{\bar {T}}_{ + }} = \frac{{\sum\limits_{i = 1}^k {{{T}_{{i0}}}} {{W}_{i}} - \bar {q} - \sum\limits_z {{{{\bar {T}}}_{z}}{{W}_{z}}} }}{{\sum\limits_{i \ne z} {{{W}_{i}}} }}.$Подстановка этого значения выходной температуры горячих потоков в выражение (5) позволяет переписать его и найти производство энтропии в проектируемой системе. При этом для горячих потоков, конденсирующихся при температурах ${{T}_{{bi}}},$ и для холодных, испаряющихся при температурах ${{T}_{{bj}}},$ в правой части равенства (5) добавятся слагаемые, соответствующие снижению энтропии потока при конденсации $ - \frac{{{{g}_{i}}{{r}_{i}}}}{{{{T}_{{bi}}}}}$ и увеличении ее при испарении $\frac{{{{g}_{j}}{{r}_{j}}}}{{{{T}_{{bj}}}}}.$ Получим
(8)
$\begin{gathered} {{\sigma }^{0}} = {{\sigma }_{ + }} + {{\sigma }_{ - }} = \sum\limits_i {{{W}_{i}}} (\ln {{{\bar {T}}}_{ + }} - \ln T_{i}^{0}) - \\ - \,\,\sum\limits_{bi} {\frac{{{{g}_{i}}{{r}_{i}}}}{{{{T}_{{bi}}}}}} + \sum\limits_j {{{W}_{j}}} (\ln {{{\bar {T}}}_{j}} - \ln T_{j}^{0}) + \sum\limits_{bj} {\frac{{{{g}_{j}}{{r}_{j}}}}{{{{T}_{{bj}}}}}} . \\ \end{gathered} $Чтобы сравнить это значение с минимально возможным значением, соответствующим идеальному теплообмену, нужно знать суммарную величину коэффициента теплопереноса в системе, а это, в свою очередь, предполагает выбор контактирующих потоков, их температур и характера гидродинамики в двухпоточных теплообменных ячейках, реализующих этот контакт.
Знание температуры ${{\bar {T}}_{ + }}$ позволяет для каждого из горячих потоков найти его “располагаемую теплоту” ${{q}_{i}}$ и суммарную “располагаемую теплоту” ${{q}_{ + }}$:
Если ${{\bar {T}}_{ + }} < {{T}_{0}},$ то необходимо ввести в систему дополнительный горячий поток так, чтобы это неравенство не имело места. Нетрудно видеть, что для температуры на выходе, определяемой выражением (2), ${{q}_{ + }} = {{q}_{ - }}$.
ЗАВИСИМОСТЬ КОЭФФИЦИЕНТОВ ТЕПЛООБМЕНА ОТ ТЕМПЕРАТУР И ГИДРОДИНАМИКИ ПОТОКОВ
После того как определена структура теплообменной системы и тепловые нагрузки двухпоточных ячеек, нужно найти соответствующие им коэффициенты теплообмена, от которых зависит поверхность контакта. Приведем без вывода формулы для коэффициентов теплообмена, соответствующих различным гидродинамическим режимам ячеек [3]. Так как в этом случае потоков только два, то будем использовать для температур и водяных эквивалентов индекс “+” для горячего и индекс “–” для холодного потоков.
1. Смешение–смешение
Здесь и ниже
Эта величина заведомо не превышает значения каждого из водяных эквивалентов. Если один из потоков меняет свое фазовое состояние (его водяной эквивалент сколь угодно велик), то значение $\bar {W}$ равно водяному эквиваленту второго контактирующего потока.
Если оба потока изменяют свое фазовое состояние (один испаряется, а другой конденсируется), то величина $K$ равна
2. Вытеснение–вытеснение (прямоток)
(11)
$K = \bar {W}\ln \frac{{T_{ + }^{0} - T_{ - }^{0}}}{{{{{\bar {T}}}_{ + }} - {{{\bar {T}}}_{ - }}}}.$3. Смешение–вытеснение
Когда в режиме вытеснения горячий поток, то
(12)
$K = {{W}_{ + }}\ln \frac{{T_{ + }^{0} - T_{ - }^{0} - \frac{{\bar {q}}}{{{{W}_{ - }}}}}}{{T_{ + }^{0} - T_{ - }^{0} - \frac{{\bar {q}}}{{\bar {W}}}}}.$Если при этом холодный поток испаряется при температуре ${{T}_{{b - }}}$, то
(13)
$K = {{W}_{ + }}\ln \frac{{T_{ + }^{0} - {{T}_{{b - }}}}}{{T_{ + }^{0} - {{T}_{{b - }}} - \frac{{{{g}_{ - }}{{r}_{ - }}}}{{{{W}_{ + }}}}}}.$Когда в режиме вытеснения холодный поток, то
(14)
$K = {{W}_{ - }}\ln \frac{{T_{ + }^{0} - T_{ - }^{0} - \frac{{\bar {q}}}{{{{W}_{ + }}}}}}{{T_{ + }^{0} - T_{ - }^{0} - \frac{{\bar {q}}}{{\bar {W}}}}}.$Если при этом горячий поток конденсируется при температуре ${{T}_{{b + }}}$, то
(15)
$K = {{W}_{ - }}\ln \frac{{{{T}_{{b + }}} - T_{ - }^{0}}}{{{{T}_{{b + }}} - T_{ - }^{0} - \frac{{{{g}_{ + }}{{r}_{ + }}}}{{{{W}_{ - }}}}}}.$4. Вытеснение–вытеснение (противоток)
(16)
$K = \frac{1}{A}\ln \frac{{T_{ + }^{0} - {{{\bar {T}}}_{ - }}}}{{\overline {{{T}_{ + }}} - T_{ - }^{0}}}.$Здесь
ПОДГОТОВКА ИСХОДНЫХ ДАННЫХ В СИСТЕМАХ С ИЗМЕНЕНИЕМ ФАЗОВОГО СОСТОЯНИЯ ПОТОКОВ
В общем случае потоки теплоносителя на входе в систему могут иметь различное фазовое состояние: пара (П), жидкости (Ж) или парожидкостной смеси (ПЖ). Такие же состояния могут быть и на выходе.
Если поток не изменяет своего фазового состояния, а меняет только температуру, то будем считать известными его температуру на входе $T_{k}^{0},$ водяной эквивалент ${{W}_{k}}$ и для холодных потоков – температуру на выходе ${{\bar {T}}_{k}}.$ Температура горячих потоков на выходе системы ${{\bar {T}}_{ + }}$ подлежит выбору (см. (2)).
Если холодный поток изменяет свое фазовое состояние так, что на входе он является жидкостью при температуре кипения, а на выходе насыщенным паром (Ж–П) (будем называть его “испаряющимся”). Для него заданы весовой расход ${{g}_{j}}$, температура кипения ${{T}_{{bj}}}$ и теплота парообразования ${{r}_{j}}$.
То же справедливо и для горячих “конденсирующихся” потоков. Они имеют на входе состояние насыщенного пара, а на выходе состояние жидкости при температуре кипения (П–Ж).
Пусть холодный поток на входе в систему представляет собой парожидкостную смесь с заданной весовой долей пара $d_{j}^{0} \geqslant 0,$ а на выходе парожидкостную смесь с долей пара ${{\bar {d}}_{j}} \geqslant d_{j}^{0}.$ Известны расход потока ${{g}_{j}},$ температура кипения ${{T}_{{bj}}}$ и теплота парообразования ${{r}_{j}}.$ Для расчета удобно разбить его на три потока: “испаряющийся” поток с расходом ${{g}_{{je}}} = {{g}_{j}}({{\bar {d}}_{j}} - d_{j}^{0})$ и два “сквозных потока” – паровой и жидкостный с расходами ${{g}_{j}}d_{j}^{0}$ и ${{g}_{j}}(1 - {{\bar {d}}_{j}})$ соответственно. Оба этих потока не меняют свою температуру и фазовое состояние и при расчете прироста энтропии и тепловой нагрузки могут не учитываться.
Аналогично может быть рассмотрен и горячий поток, с той разницей, что весовая доля пара у него на выходе меньше, чем на входе. И он может быть представлен как “конденсирующийся” поток и два “сквозных”, которые в расчетах не участвуют.
В том случае, когда на вход системы подается холодный поток в форме жидкости с температурой $T_{j}^{0} < {{T}_{{bj}}},$ которая нагревается до температуры кипения ${{T}_{{bj}}}$, а затем полностью либо частично испаряется, и возможно нагревается до температуры перегретого пара, он может быть представлен в виде трех потоков: двух “нагревающихся” и одного “испаряющегося”. Причем “нагревающиеся” потоки в силу различия теплоемкостей пара и жидкости имеют разные водяные эквиваленты. Если же он испаряется не полностью, то последний поток также разбивается на два: “испаряющийся” и “сквозной”, причем последний в расчетах не участвует.
Аналогично горячий поток, поступающий в форме перегретого пара, может быть представлен как “охлаждающийся” до температуры кипения ${{T}_{{bi}}}$ и полностью либо частично “конденсирующийся” и “охлаждающийся” поток от температуры кипения до конечной температуры в жидком состоянии. Если поток конденсируется не полностью, то из него выделяют “сквозной” поток, не изменяющий своей энтальпии и энтропии. При этом жидкостный “охлаждающийся” поток отсутствует.
Таким образом, первым шагом является подготовка исходных данных, при которой от фактических потоков и их характеристик переходят к расчетным потокам. Они могут быть двух типов: не изменяющие своего фазового состояния (нагреваемые и охлаждаемые) и изменяющие его при температуре кипения (испаряющиеся и конденсирующиеся). Сквозные потоки в расчете не участвуют. Для расчета суммарной тепловой нагрузки следует использовать выражение
(18)
$\sum\limits_{jh} {{{W}_{{jh}}}} ({{\bar {T}}_{{jh}}} - T_{{jh}}^{0}) + \sum\limits_{bj} {{{g}_{{bj}}}} {{r}_{{be}}} = \bar {q}.$Здесь первая сумма в левой части равенства берется по всем “нагреваемым” расчетным потокам, а вторая – по всем “испаряющимся”.
ЗАВИСИМОСТЬ ТЕМПЕРАТУР КОНТАКТА ОТ ТЕПЛОВОЙ НАГРУЗКИ И РАСЧЕТНАЯ СИСТЕМА ТЕПЛООБМЕНА
По мере движения горячих потоков от одной ячейки контакта к следующей их температура изменяется за счет отдачи части теплового потока. На выходе системы отданный ими поток теплоты равен $\bar {q}$, а температура ${{\bar {T}}_{ + }}$. Обозначим через $q$ отданную тепловую нагрузку в некотором промежуточном состоянии горячих потоков. По мере охлаждения горячих потоков она меняется от нуля до $\bar {q}$.
Будем называть этот поток текущей тепловой нагрузкой. Для каждого промежуточного значения текущей тепловой нагрузки температуры горячих потоков, отдавших эту теплоту, и температуры холодных, получающих эту теплоту чтобы достигнуть заданных температур на выходе, не фиксированы. Согласно полученным выше условиям оптимальности температуры горячих потоков на выходе участка системы с текущей тепловой нагрузкой $q$ и температуры холодных на его входе должны быть одинаковы.
Этот факт позволяет перейти к объединенным эквивалентным потокам, имеющим температуры T+(q) и T–(q). Каждая из них с ростом текущей тепловой нагрузки снижается. Число потоков, объединенных в эквивалентный поток, следовательно, и его водяной эквивалент зависят от этих температур, а значит, и от $q$.
Требование минимальной диссипации предполагает выполнение “принципа противотока”: холодные потоки с более высокими температурами (нагретые) должны контактировать с горячими потоками, имеющими также более высокую температуру.
При охлаждении горячего потока с самой высокой входной температурой (первого) до температуры $T_{2}^{0}$ первый и второй потоки объединяются в расчетный эквивалентный, так что их водяные эквиваленты суммируются. Аналогичное объединение происходит с третьим потоком и т.д. до тех пор, пока температура эквивалентного горячего потока не опустится до заранее рассчитанной по формулам (2), (7) ${{\bar {T}}_{ + }}$. Если в числе горячих потоков оказывается при некоторой температуре ${{T}_{{bi}}}$ конденсирующийся поток, то температура эквивалентного потока постоянна и равна ${{T}_{{bi}}}$ до тех пор, пока эквивалентный поток не передаст теплоту конденсации ${{q}_{{bi}}} = {{g}_{{bi}}}{{r}_{i}}.$ Зависимость температуры эквивалентного горячего потока от отданной им тепловой нагрузки ${{T}_{ + }}(q)$ будем называть температурой контакта горячих потоков.
Холодные потоки упорядочим по величине их температуры на выходе, так что $j = 1$ соответствует потоку с самой высокой выходной температурой. Для холодных потоков величина $q$ равна текущей потребной тепловой нагрузке, т.е. той теплоте, которую они должны получить, чтобы удовлетворить условиям, наложенным на их температуры и фазовые состояния на выходе. Чем больше $q$, тем ниже соответствующая этому значению температура T– эквивалентного холодного потока. Состав этого потока, а значит, и его водяной эквивалент изменяются с изменением текущей тепловой нагрузки.
При снижении с ростом $q$ температуры первого холодного потока возможны два события:
1. Его температура опустится до заданной температуры на выходе второго холодного потока.
2. Его температура опустится до его начальной температуры.
В первом случае первый холодный поток объединяют со вторым в один эквивалентный. Во втором случае его исключают из системы и переходят к нагреву второго потока. Такая процедура продолжается до достижения эквивалентным холодным потоком самой низкой заданной температуры холодных потоков на входе в систему. Число потоков, входящих в эквивалентный холодный поток, меняется, как за счет добавления потоков с более низкими температурами на выходе, так и за счет исключения из него потоков с самыми высокими температурами на входе. Но каждому значению $q$ соответствует значение ${{T}_{ - }}(q)$ температуры контакта холодных потоков.
Зависимости текущих температур контакта эквивалентных потоков могут быть вычислены из условий энергетического баланса, подобных выражениям (2), (7). Для эквивалентного горячего потока:
(19)
${{T}_{ + }}(q) = \frac{{\sum\limits_{i = 1}^{{{S}_{ + }}({{T}_{ + }})} {{{W}_{i}}} T_{i}^{0} - q}}{{\sum\limits_{i = 1}^{{{S}_{ + }}({{T}_{ + }})} {{{W}_{i}}} }},$Аналогично для температуры контакта эквивалентного холодного потока имеем
(20)
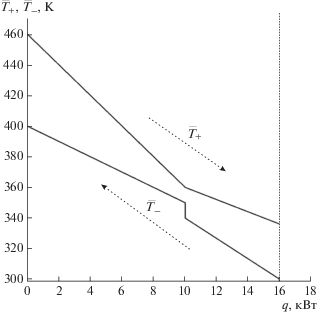
${{T}_{ - }}(q) = \frac{{\sum\limits_{j \in {{S}_{ - }}({{T}_{ - }})} {{{W}_{j}}} {{{\bar {T}}}_{j}} - q}}{{\sum\limits_{j \in {{S}_{ - }}({{T}_{ - }})} {{{W}_{j}}} }},$Вид зависимостей температур контакта от текущей тепловой нагрузки показан на рис. 1. Они монотонно уменьшаются с ростом $q$, причем ${{T}_{ + }}(q) > {{T}_{ - }}(q).$ На каждой из этих кривых выделены точки (узлы), в которых либо изменяется состав потоков, входящих в эквивалентный поток, либо происходит процесс конденсации/испарения. В последнем случае на кривых появляются горизонтальные участки. На этих участках контактирует только поток, меняющий фазовое состояние. Наклон участков охлаждения и нагрева равен $\frac{1}{{\sum\limits_k {{{W}_{k}}} }},$ где $k$ – индекс потоков, входящих в эквивалентный поток при текущей тепловой нагрузке. Так что если состав горячих потоков не изменяется, то с приближением к величине $\bar {q}$ наклон зависимости ${{T}_{ + }}(q)$ на участках охлаждения не увеличивается.
На кривой ${{T}_{ - }}(q)$ могут быть и вертикальные разрывы, если температура потока $T_{j}^{0} > {{\bar {T}}_{{j - 1}}}.$ Если для всех холодных потоков температура на выходе больше, чем ближайшая к ней более высокая входная температура, то кривые температур эквивалентных потоков кусочно-гладкие.
Интервал $\delta {{q}_{\nu }}$ от одного из узлов на любой из кривых контакта до ближайшего узла на той же или на другой кривой характеризуется одинаковым составом и фазовым состоянием контактирующих потоков. Будем называть его интервалом однородности.
РАСЧЕТ КОЭФФИЦИЕНТА ТЕПЛООБМЕНА ДЛЯ КАЖДОГО ИНТЕРВАЛА ОДНОРОДНОСТИ
Для каждого такого интервала величиной $\delta {{q}_{\nu }}$ возможны три сочетания контактирующих потоков:
1. Оба эквивалентных потока меняют свои фазовые состояния.
2. Горячий эквивалентный поток охлаждается, а холодный нагревается.
3. Один из потоков изменяет свое фазовое состояние, а другой охлаждается либо нагревается.
Кривые температур контакта предоставляют все данные для расчета коэффициента теплообмена ячейки, в которой осуществляется этот контакт. Действительно:
– водяные эквиваленты ${{W}_{ + }},{{W}_{ - }}$ равны сумме водяных эквивалентов потоков, которые входят в состав эквивалентных контактирующих потоков;
– температуры эквивалентных потоков на входе и выходе интервала однородности известны;
– тепловая нагрузка такой расчетной ячейки равна $\delta {{q}_{\nu }}.$
В зависимости от того, какое из перечисленных сочетаний контакта реализуется, можно выбрать тип гидродинамики ячейки и найти ${{K}_{\nu }}$ по формулам (10), когда оба потока меняют свое фазовое состояние, по формулам (13) и (15), когда фазовое состояние меняет один из эквивалентных потоков, и, наконец, по формулам (16), (17), когда оба потока не изменяют своего фазового состояния. Коэффициент теплообмена в случае, когда один поток кипит или испаряется, а другой в режиме перемешивания, оказывается больше, чем в том случае, когда второй поток в режиме вытеснения, поэтому эту величину коэффициента теплообмена используют только в случае, когда режим перемешивания диктуется технологическими соображениями.
Найдя для каждого $\nu $-го интервала однородности коэффициент теплообмена ${{K}_{\nu }}$ и просуммировав эти коэффициенты по всем интервалам, получим суммарный коэффициент $K$, которого можно достичь, организовав противоточный теплообмен эквивалентных потоков. В свою очередь, знание тепловой нагрузки $\bar {q}$ и суммарного коэффициента теплообмена позволяет рассчитать минимально возможное производство энтропии $\sigma {\text{*}}$ по формуле (1) и оценить степень термодинамического совершенства построенной системы как $\eta = \frac{{\sigma {\text{*}}}}{{{{\sigma }^{0}}}},$ где величина ${{\sigma }^{0}}$ найдена согласно (8).
О ФИЗИЧЕСКОЙ РЕАЛИЗАЦИИ РАССЧИТАННОЙ СИСТЕМЫ
Построенная выше теплообменная система с минимальной необратимостью, в которой выполнены ограничения по водяным эквивалентам, температурам и фазовым состояниям потоков, предполагает объединение потоков в два эквивалентных. Если горячие потоки представляют собой потоки воды и водяного пара, то такое объединение можно реализовать за счет их слияния. Если же эти потоки не однородны и слияние невозможно, то контакту эквивалентного горячего потока, имеющего водяной эквивалент ${{W}_{ + }} = \sum\limits_i {{{W}_{i}}} ,$ c потоком, имеющим водяной эквивалент ${{W}_{ - }} = \sum\limits_j {{{W}_{j}}} ,$ соответствует их теплообмен в двухпоточных ячейках, число которых равно большему из числа потоков, входящих в эквивалентный горячий или эквивалентный холодный, при этом отношение водяных эквивалентов в каждой такой ячейке должно быть одинаково и равно $\frac{{{{W}_{ - }}}}{{{{W}_{ + }}}}.$ Если на интервале однородности один из потоков изменяет свое фазовое состояние, то второй эквивалентный поток на этом интервале контактирует только с ним. При этом в корпусе одного теплообменника может содержаться несколько двухпоточных ячеек, когда один холодный поток нагревается несколькими горячими, каждый из которых проходит по своему змеевику. Таким образом, расчетная система определяет порядок и структуру контактов, которой при введенных ограничениях соответствует минимум необратимости.
Алгоритм расчета поясняют приведенные ниже примеры.
ПРИМЕРЫ
1. Четырехпоточный теплообменник. Рассмотрим систему с двумя горячими и двумя холодными потоками. Исходные данные представлены в табл. 1.
Таблица 1.
Исходные данные
| № | $T_{i}^{0}$, K | ${{W}_{i}}$, Вт/К | $T_{j}^{0}$, K | ${{\bar {T}}_{j}}$, K | ${{W}_{j}}$, Вт/К | ${{q}_{j}}$, Вт |
|---|---|---|---|---|---|---|
| 1 | 460 | 100 | 350 | 400 | 200 | 10 000 |
| 2 | 360 | 150 | 300 | 340 | 150 | 6000 |
Поскольку все потоки не меняют своего фазового состояния, то таблица расчетных потоков будет иметь аналогичный вид.
1. Потребная теплота:
2. Температура горячих потоков на выходе согласно выражению (2):
(21)
${{\bar {T}}_{ + }} = \frac{{100 \times 460 + 150 \times 360 - 16000}}{{100 + 150}} = 336\,\,{\text{K}}.$3. Производство энтропии в системе, где нет потоков, меняющих свое фазовое состояние, согласно (8):
(22)
$\begin{gathered} {{\sigma }^{0}} = \sum\limits_i {{{W}_{i}}} (\ln {{{\bar {T}}}_{ + }} - \ln T_{i}^{0}) + \sum\limits_j {{{W}_{j}}} (\ln {{{\bar {T}}}_{j}} - \ln T_{j}^{0}) = \\ = 100\ln \frac{{336}}{{460}} + 150\ln \frac{{336}}{{360}} + 200\ln \frac{{400}}{{350}} + \\ + \,\,150\ln \frac{{340}}{{300}} = 3.76\,\,{{{\text{Вт}}} \mathord{\left/ {\vphantom {{{\text{Вт}}} {\text{К}}}} \right. \kern-0em} {\text{К}}}. \\ \end{gathered} $4. Расчет узловых точек и интервалов однородности на кривых температур эквивалентных потоков.
Значение ${{T}_{ + }}(0) = T_{{1 + }}^{0} = 460\,\,{\text{K}}{\text{.}}$ Ближайшая узловая точка на этой кривой соответствует температуре $T_{{2 + }}^{0}$ и равна 360 K, а соответствующее ей значение теплоты, переданной первым горячим потоком (только он участвует в теплообмене), $q = {{q}_{1}}$ = ${{W}_{1}}(460 - 360)100 \times 100 = 10\,000$ Вт. Конечное значение температуры ${{T}_{ + }}(\bar {q})$ согласно (24) равно 336 К. После первой узловой точки в теплообмене участвуют оба горячих потока, их водяной эквивалент ${{W}_{{2 + }}} = 100 + 150 = 250$ Вт/К.
Начальное значение кривой ${{T}_{ - }}(0) = {{\bar {T}}_{{1 - }}}.$ Ближайшая узловая точка соответствует максимальному значению из температур $T_{{1 - }}^{0}$ и ${{\bar {T}}_{{2 - }}}.$ В нашем примере эта температура равна $T_{{1 - }}^{0} = 350\,\,{\text{K}}{\text{.}}$ Соответствующее значение тепловой нагрузки равно ${{q}_{2}} = {{W}_{{1 - }}}({{\bar {T}}_{{1 - }}} - T_{{1 - }}^{0})$ = $200 \times 50 = 10\,000$ Вт. После этой точки первый из холодных потоков не участвует в теплообмене. Кривая ${{T}_{ - }}(q)$ испытывает вертикальный скачок до 340 К.
Следующая узловая точка соответствует температуре ${{\bar {T}}_{{2 - }}} = 340\;\;{\text{K}}$. На участке от $q = 10\,000$ Вт до $q = 16\,000$ Вт в теплообмене участвует только второй холодный поток.
Зависимости T+(q), T−(q) показаны на рис. 1.
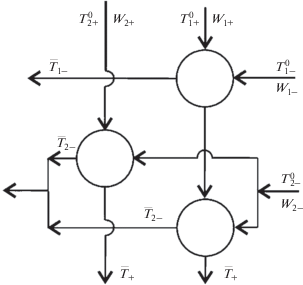
Таким образом, можно выделить два интервала однородности на оси абсцисс: от нуля до $q = 10\,000$ Вт и от $q = 10\,000$ Вт до $q = 16\,000$ Вт. На первом интервале контактируют первый горячий и первый холодный поток, на втором оба горячих и второй холодный поток. Возможная схема теплообмена представлена на рис. 2.
5. Найдем величины коэффициентов теплообмена для каждого из интервалов однородности в предположении противоточного теплообмена по формулам (16), (17).
Для первого интервала:
Для второго интервала:
6. Знание суммарного коэффициента теплообмена $K = {{K}_{1}} + {{K}_{2}} = 578$ ${\text{Вт/К}}$ позволяет рассчитать минимально возможное производство энтропии $\sigma {\text{*}}$ по формуле (1) и оценить степень термодинамического совершенства построенной системы:
Система состоит из трех двухпоточных ячеек. Первый горячий поток проходит через две ячейки последовательно, а второй только через третью. Второй холодный поток разветвляется между второй и третьей ячейками так, чтобы отношения водяных эквивалентов горячего и холодного потока в каждой из этих ячеек были одинаковы. Так что
(23)
$\begin{gathered} {{W}_{{21}}} = {{W}_{{2 - }}}\frac{{{{W}_{{1 + }}}}}{{{{W}_{{1 + }}} + {{W}_{{2 + }}}}} = 150\frac{{100}}{{100 + 150}} = 60\,\,{{{\text{Вт}}} \mathord{\left/ {\vphantom {{{\text{Вт}}} {\text{К}}}} \right. \kern-0em} {\text{К}}}, \\ {{W}_{{22}}} = {{W}_{{2 - }}}\frac{{{{W}_{{2 + }}}}}{{{{W}_{{1 + }}} + {{W}_{{2 + }}}}} = 150\frac{{150}}{{100 + 150}} = 90\,\,{{{\text{Вт}}} \mathord{\left/ {\vphantom {{{\text{Вт}}} {\text{К}}}} \right. \kern-0em} {\text{К}}}. \\ \end{gathered} $В каждой ячейке реализуется противоточный теплообмен.
2. Четырехпоточный теплообменник с конденсацией. Рассмотрим систему из примера 1 с одним изменением: первый горячий поток поступает в виде насыщенного пара при температуре конденсации со следующими характеристиками:
Поскольку один горячий поток в процессе теплообмена конденсируется, то таблица расчетных горячих потоков будет иметь вид, приведенный в табл. 2.
Таблица 2.
Расчетные горячие потоки
| № | $T_{{j + }}^{0},$ K | W, Вт/К | ${{g}_{{i + }}}$, кг/с | ${{r}_{{i + }}}$ кДж/кг |
|---|---|---|---|---|
| 1 | 460 | – | 0.012 | 833 |
| 2 | 460 | 36.2 | – | – |
| 3 | 360 | 150 | – | – |
Расчеты будем проводить в той же последовательности, как в примере 1.
1. Потребная теплота:
2. Температура горячих потоков на выходе согласно выражению (2):
(24)
${{\bar {T}}_{ + }} = - \frac{{833 \times 12 + 36.2 \times 460 + 150 \times 360 - 16000}}{{36.2 + 150}} = 347.6\,\,{\text{K}}.$3. Производство энтропии в системе с учетом конденсирующегося потока согласно (8) равно
(25)
$\begin{gathered} {{\sigma }^{0}} = - \frac{{{{g}_{1}}r)1}}{{T_{{1 + }}^{0}}} + \sum\limits_i {{{W}_{i}}} (\ln {{{\bar {T}}}_{ + }} - \ln T_{i}^{0}) + \\ + \,\,\sum\limits_j {{{W}_{j}}} (\ln {{{\bar {T}}}_{j}} - \ln T_{j}^{0}) = - \frac{{10000}}{{460}} + \\ + \,\,36.2\ln \frac{{347.6}}{{460}} + 150\ln \frac{{347.6}}{{360}} + \\ + \,\,200\ln \frac{{400}}{{350}} + 150\ln \frac{{340}}{{300}} = 8.04\,\,{{{\text{Вт}}} \mathord{\left/ {\vphantom {{{\text{Вт}}} {\text{К}}}} \right. \kern-0em} {\text{К}}}. \\ \end{gathered} $4. Расчет узловых точек и выделение интервалов однородности на кривых температур эквивалентных потоков.
Значение ${{T}_{ + }}(0) = T_{{1 + }}^{0} = 460\,\,{\text{K}}{\text{.}}$ Ближайшая узловая точка на этой кривой соответствует концу горизонтального участка конденсации, соответствующая ей точка на оси абсцисс равна 10 000 Вт. В теплообмене участвует только конденсирующийся поток и первый холодный.
На следующем интервале конденсат с водяным эквивалентом ${{W}_{{1 + }}} = 36.2$ контактирует с холодным потоком, пока температура конденсата не опустится до 360 К. При этом он передает теплоту равную $\delta q = $ 3620 Вт, нагревая холодный поток на 24.1 К, с 315.9 до 340 К.
На последнем интервале горячие потоки объединяются, так что их суммарный водяной эквивалент оказывается равным W+ = 36.2 + 150 = = 186.2 Вт/К. Они охлаждаются до ${{\bar {T}}_{ + }}$ = 347.6 К, нагревая холодный поток с 300 до 315.9 К.
Начальное значение кривой ${{T}_{ - }}(0) = {{\bar {T}}_{{1 - }}}.$ Ближайшая узловая точка соответствует начальной температуре первого из холодных потоков 350 К. При $q = 10\,000$ температура контакта холодного потока снижается до 340 К и далее второй холодный поток контактирует на втором интервале с одним, а на последнем, третьем с двумя горячими, причем его водяные эквиваленты в соответствии с формулой (23) равны
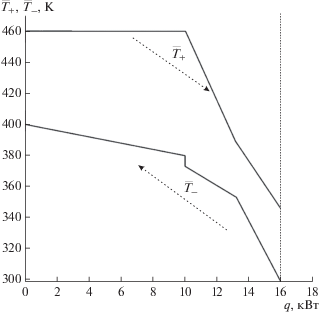
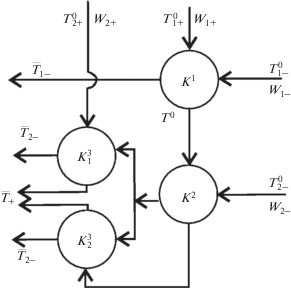
Зависимости ${{T}_{ + }}(q),{{T}_{ - }}(q)$ показаны на рис. 3. Структура системы теплообмена показана на рис. 4. В первом теплообменнике реализуется режим конденсации для горячего и вытеснения для холодного потоков, а в последующих ячейках режим вытеснения с противотоком.
5. Найдем величины коэффициентов теплообмена для каждого из интервалов однородности с учетом конденсации на первом и противоточного теплообмена на втором и третьем интервалах однородности по формулам (15)–(17).
Для первого интервала:
Для второго интервала:
Для третьего интервала:
Зависимость температур контактов от тепловой нагрузки показана на рис. 3.
6. Знание суммарного коэффициента теплообмена $K = {{K}_{1}} + {{K}_{2}}$ + ${{K}_{3}} = 228\,\,{{{\text{Вт}}} \mathord{\left/ {\vphantom {{{\text{Вт}}} {\text{К}}}} \right. \kern-0em} {\text{К}}}$ позволяет рассчитать минимально возможное производство энтропии $\sigma {\text{*}}$ по формуле (3) и оценить степень термодинамического совершенства построенной системы:
СРАВНЕНИЕ С ПИНЧ-АНАЛИЗОМ
Построенные выше зависимости температур контактирующих потоков от текущей тепловой нагрузки весьма близки к используемым в пинч-анализе зависимостям температур эквивалентных горячего и холодного потоков от их энтальпии [6–8]. Основное отличие заключается в том, что в работе все построения базируются на термодинамическом критерии минимума диссипативных потерь и результаты синтеза количественно оцениваются сравнением с минимально возможными потерями.
Следствием этого является и разница в методике построения и виде диаграмм:
1. От исходных потоков мы переходим к расчетным потокам, что дает возможность рассматривать случаи, когда поток поступает в форме парожидкостной смеси.
2. Не выделяются специально источники “внешнего” подогрева и охлаждения, так как реально это дополнительные потоки, равноправные со всеми остальными потоками системы и влияющие на ее оптимальную организацию не только при конечных, но и при всех промежуточных температурах. Так, дополнительный поток подогрева в виде пара конденсируется и участвует в дальнейшем теплообмене в соответствии с общим алгоритмом. “Сдвиги” пинч-диаграмм вдоль оси абсцисс не имеют смысла при таком подходе.
3. Введенные интервалы однородности определяют не только то, какие горячие потоки с какими холодными должны контактировать при этих температурах, но и гидродинамику двухпоточных теплообменников, их коэффициенты теплопередачи, выбор водяных эквивалентов потоков при их расщеплении. При этом смешение потоков с различающимися температурами отсутствует.
4. Во многих случаях выходные температуры всех или части горячих потоков не фиксированы, поэтому полученное выше по критерию минимальной диссипации условие равенства таких свободных температур дает ограничение снизу на температуру горячих потоков, пригодных для использования в системе.
Соотношения, полученные в работах об “идеальном теплообмене” [15], позволяют не только количественно оценить термодинамическое совершенство синтезированной системы, но и сформулировать общие рекомендации, выполнять которые желательно при синтезе:
1. Отношение температур эквивалентных потоков в градусах Кельвина желательно приблизить к константе. Это значит, что желательно минимальную разность температур (пинч-зона) достичь вблизи холодного конца теплообменной системы.
2. На участке однородности, где не происходит изменения фазового состояния ни одного из потоков, отношение водяных эквивалентов горячего и холодного потоков желательно сделать близким к обратной величине отношения их температур в градусах Кельвина, т.е. желательно, чтобы W_- был больше, чем W_+. В этом случае отношение температур для теплообменника с противотоком будет близко к константе по ходу контакта.
ЗАКЛЮЧЕНИЕ
Предложен алгоритм расчета минимальной необратимости для теплообменных систем с фиксированными температурами, водяными эквивалентами и фазовым состоянием потоков на входе в систему и заданной тепловой нагрузкой. Алгоритм приводит к решению за конечное число шагов. Он позволяет найти структуру и распределение тепловых нагрузок и поверхностей теплообмена между двухпоточными ячейками в системе, где найденная оценка может быть реализована. При этом каждый поток может контактировать с несколькими. Результаты можно рассматривать как развитие и термодинамическое обоснование пинч-анализа.
Побудительным мотивом к изложенным исследованиям послужило знакомство авторов с интересными работами [1, 2, 4].
ОБОЗНАЧЕНИЯ
Список литературы
Ostrovskii G.M., Ziyatdinov N.N., Emel’yanov I.I. Synthesis of Optimal Systems of Simple Distillation Columns with Heat Recovery // Dokl. Chem. 2015. V. 461. P. 89. [Островский Г.М., Зиятдинов Н.Н., Емельянов И.И. Синтез оптимальных систем простых ректификационных колонн с рекуперацией тепла // Докл. Акад. наук. 2015. Т. 461. № 2. С. 189.]
Ziyatdinov N.N., Ostrovskii G.M., Emel’yanov I.I. Designing a Heat Exchange System upon the Reconstruction and Synthesis of Optimal Systems of Distillation Columns // Theor. Found. Chem. Eng. 2016. V. 50. № 2. P. 178. [Зиятдинов Н.Н., Островский Г.М., Емельянов И.И. Построение системы теплообмена при реконструкции и синтезе оптимальных систем ректификационных колонн // Теор. осн. хим. технол. 2016. Т. 50. № 2. С. 184.]
Kafarov V.V., Meshalkin V.P., Perov V.L. Mathematical Foundations of Computer Aided Design of Chemical Plants. Moscow: Khimiya, 1979.
Ziyatdinov N.N., Emel’yanov I.I., Tuen L.Q. Method for the Synthesis of Optimum Multistage Heat Exchange Network // Theor. Found. Chem. Eng. 2018. V. 52. № 6. P. 943. [Зиятдинов Н.Н., Емельянов И.И., Туен Л.К. Метод синтеза оптимальных многостадийных систем теплообмена // Теор. осн. хим. технол. 2018. Т. 52. № 6. С. 1.]
Brodjanskiy V.M., Fratsher V., Mikhalek K. Exergy Methods and Its Applications. Moscow: Energoatomizdat, 1988.
Linnhoff B. Pinch analysis-A state-of-the-art overview: Techno-economic analysis // Chem. Eng. Res. Des. 1993. V. 71. № 5. P. 503.
Linnhoff B., Vredeveld D.R. Pinch technology has come of age // Chem. Eng. Prog. 1984. V. 88. № 7. P. 33.
Смит Р., Клеменш Й., Товяжинский Л.Л. и др. Основы интеграции тепловых процессов. Харьков: НТУ “ХПИ”, 2000.
Berry R.S., Kasakov V.A., Sieniutycz S., Szwast Z., Tsirlin A.M. Thermodynamic Optimization of Finite Time Processes. Chichester: Wiley, 1999.
Tsirlin A.M., Mironova W.A., Amelkin S.A., Kazakov V.A. Finite-time thermodynamics: Conditions of minimal dissipation for thermodynamic processes with given rate // Phys. Rev. E. 1998. V. 58. P. 215.
Цирлин А.М. Оптимальное управление необратимыми процессами тепло- и массопереноса // Изв. Акад. наук СССР. Тех. киберн. 1991. Т. 2. С. 171.
Andresen B., Gordon J.M. Optimal heating and cooling strategies for heat exchanger design // J. Appl. Phys. 1992. V. 71. № 1. P. 76.
Salamon P., Nitzan A., Andresen B., Berry R.S. Minimum entropy production and the optimization of heat engines // Phys. Rev. 1980. V. 21. P. 2115.
Цирлин А.М., Ахременков А.А., Григоревский И.Н. Минимальная необратимость, оптимальное распределение поверхности и тепловой нагрузки теплообменных систем // Теор. осн. хим. технол. 2008. Т. 42. С. 1.
Tsirlin A.M. Ideal heat exchange system // J. Eng. Phys. Thermophys. 2017. V. 90. № 5. P. 1035.
Kondepudi D., Prigogine I. Modern Thermodynamics: From Heat Engines to Dissipative Structures. New York: Wiley, 1998.
Цирлин А.М., Ахременков А.А. Оптимальный теплообмен при изменении фазового состояния хладагента // Теор. осн. хим. технол. 2018. Т. 52. № 5. С. 1.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии