Теоретические основы химической технологии, 2020, T. 54, № 1, стр. 10-16

Теоретический анализ релаксационных процессов в акрилатных латексных полимерах

Т. Р. Асламазова^a, *, В. А. Котенев^a, Н. Ю. Ломовская^a, В. А. Ломовской^a, А. Ю. Цивадзе^a

^a Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
Москва, Россия

Поступила в редакцию 25.05.2019
После доработки 12.06.2019
Принята к публикации 22.07.2019

DOI: 10.31857/S0040357120010029

Аннотация

Проведен анализ диссипативных процессов, протекающих в высокоэластичных латексных полимерах, на основе теоретического расчета релаксационной микрогетерогенности структур полимера. Микрогетерогенность оценивали графически из зависимости соотношения интенсивностей диссипации λ/λ_max от температурного соотношения (Т – Т_max)/Т_max. Интенсивность процесса α-релаксации определяли на спектре внутреннего трения, полученном с применением метода динамической релаксационной спектроскопии.

Ключевые слова: микрогетерогенность, диссипативные процессы, релаксация, латексный полимер, эластичность

ВВЕДЕНИЕ

Особенность строения полимера обусловлена наличием двух видов структурных элементов (звеньев цепей и самих цепей), значительно различающихся подвижностью. В случае высокоэластичного полимера это проявляется в перегруппировке звеньев, т.е. изменении конформации цепей при изменении температуры. Анализ релаксационной подвижности звеньев цепей и/или самих цепей с привлечением метода релаксационной спектроскопии, основанного на анализе реакции отдельных структурно-кинетических элементов полимерных систем на внешнее воздействие, выводящее их или всю систему из состояния механического и термодинамического равновесия [1‒4], может дать представление о структуре образующихся частиц и полимера. Вследствие больших размеров подвижность полимерной цепи невелика. Поэтому изменение температуры вызывает в случае высокоэластичного полимера главным образом перегруппировку звеньев, т.е. изменение конформации цепей. Отсюда следует, что введение активных к функциональным группам полимера ингредиентов композиционной системы может вызвать изменение конформации полимерных цепей.

Цель работы – с привлечением динамической механической релаксационной спектроскопии выявить возможность качественного анализа изменения релаксационной микронеоднородности латексных полимеров различной эластичности при их наполнении высокодисперсным наполнителем; продемонстрировать вероятность оценки ширины непрерывных спектров времен релаксации путем сопоставления температурных зависимостей приведенных спектров внутреннего трения с температурной зависимостью изменения дискретного времени релаксации α-процесса; рассмотреть корреляцию между температурно-частотными изменениями модуля сдвига систем в режиме свободных колебаний систем и степенью их релаксационной микронеоднородности. Для выполнения этой задачи привлечены пленкообразующие акрилатные латексы, отличающиеся, помимо сомономерного состава, входящими в их состав функциональными группами.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Для проведения исследования были привлечены два высокоэластичных акрилатных полимера: (мет)акрилатный полимер с температурой стеклования 5°С и метил(мет)акрилатный латекс с температурой стеклования 15°С, содержащий в своем составе метакриловую кислоту, далее именуемые АК1 и АК2 соответственно.

Пленки готовили отливом латексных пленок на тефлоновой подложке с последующим высушиванием на воздухе, а затем в вакуумном шкафу – до постоянного веса. Из полученных пленок вырезались образцы прямоугольного сечения размером 60 × 5 × 0.5 мм.

Для выяснения природы релаксационных диссипативных процессов в полимерах снимались температурные зависимости спектров внутреннего трения λ в широком интервале температур от –150 до +50^оС в режиме свободных затухающих крутильных колебаний при частоте f ≈ 1 Гц на горизонтальном крутильном маятнике [1‒4].

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

На рис. 1 представлены характерные кривые спектра внутреннего трения в обоих исследуемых латексных полимерах АК1 и АК2, а также температурно-частотная зависимость процесса диссипации, которая указывает на релаксационный характер диссипативных процессов, протекающих в системах. Аналогичные зависимости получены для латексных полимеров, наполненных высокодисперсным порошком железа.

Рис. 1.

Спектр внутреннего трения (1, 2) и температурная зависимость частоты колебательного процесса f (3, 4) в ненаполненных латексных полимерах АК1 (1, 3) и АК2 (2, 4).

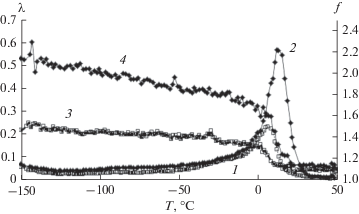
Из рис. 1 следует существенное различие в интенсивности процесса α-релаксации АК1 и АК2, коррелирующей с их температурой стеклования, и спада частотной зависимости, ответственного за их дефект модуля и упругие свойства полимеров.

С целью выяснения релаксационной микрогетерогенности далее проведен теоретический анализ диссипативных процессов, протекающих в высокоэластичных латексных полимерах при температуре стеклования в сопоставлении с экспериментальными данными.

Релаксационную микронеоднородность полимеров определяют путем сопоставления нормированных интенсивностей диссипативных потерь λ и температурного изменения в нормированном интервале температур дискретного времени релаксации τ_i [5, 6]. Этому соответствует соотношение λ/λ_max = f[(Т–Т_max)/Т_max], где λ_max и Т_max – интенсивность и температура максимума диссипативных потерь соответственно. При таком анализе качественно сопоставляются непрерывные спектры времен релаксации без применения какой-либо функции релаксации. Для этого необходимо знать энергию активации процесса U_α, дискретное время релаксации в максимуме интенсивности диссипативных потерь на спектре внутреннего трения и предэкспоненциальный коэффициент в уравнении Аррениуса, которое описывает температурную зависимость дискретного времени релаксации τ_i = f(T).

В работе [7] с использованием данных по энергии активации процесса α-релаксации (14 ккал/моль) и предэкспоненциального коэффициента в уравнении, описывающем температурную зависимость дискретного времени релаксации (~5 × 10^–12 с), проведен качественный анализ релаксационных спектров процессов, протекающих в акрилатных полимерах.

С учетом этих результатов [7, 8] было целесообразно привлечь к анализу релаксационной микронеоднородности полимерной структуры температурную зависимость дискретного времени релаксации τ_i = f(T) в рамках феноменологической модели стандартного линейного тела (модель Зинера) и соотношения Деборы [6].

Для полимерных систем характерным является процесс размораживания сегментальной подвижности макромолекул (α-процесс релаксации), исследуемый в настоящей работе. Другие релаксационные процессы различной степени межмолекулярной кооперативности здесь не рассматриваются, хотя они и наблюдаются на спектре внутреннего трения в области более низких значений температуры [7]. Максимумы потерь рассчитываются для одного дискретного времени релаксации τ_i. В процессе релаксации участвуют кинетические единицы одной структуры и природы, но различающиеся временами релаксации от τ_i. Это обусловливается различными стерическими и конформационными положениями релаксирующей единицы. Наличие совокупности времен релаксации для единиц, участвующих в одном релаксационном процессе, позволяет рассматривать данный процесс с привлечением не только дискретного времени релаксации τ_i, но и непрерывного спектра времен релаксации Н(τ), где τ – переменное время релаксации.

Описание непрерывного спектра времен релаксации Н(τ) для любого диссипативного процесса, имеющего релаксационный механизм и обнаруживаемого на спектре внутреннего трения λ = f(T) и температурной зависимости частоты свободных затухающих крутильных колебаний, возбуждаемых в исследуемой системе, т.е. f = f(T), обусловливает необходимость проведения теоретического анализа с применением той или иной функции φ(t), которая и определяет возникновение Н(τ).

Феноменологически описать реакцию исследуемой системы, приводящую к возникновению области локальной неупругости и, как следствие этого, появлению пика диссипативных потерь на спектре λ = f(T), возможно в виде обобщенной модели Максвелла [9, 10], состоящей из n-го количества элементарных максвелловских элементов, каждый из которых будет характеризоваться своим локальным временем релаксации и описывать реакцию каждого отдельного элемента одной структурно-кинетической подсистемы, состоящей из n-го количества элементарных элементов.

Совокупность всех локальных (в рамках одной структурно-кинетической подсистемы) времен релаксации τ_i и дает непрерывный спектр времен релаксации Н(τ) того или иного релаксационного процесса (α-релаксации), т.е.

(1)

$H(\tau ) = \sum\limits_{i = 1}^n {{{\tau }_{i}}} .$

Время релаксации τ_i определяется из дифференциального уравнения Максвелла, которое имеет вид

(2)

$\dot {\sigma }(t) + \frac{\sigma }{\tau } = G\dot {\varepsilon }(t),$

где $\dot {\sigma }(t) = \frac{{d\sigma }}{{dt}}$ – скорость изменения напряжения; $\dot {\varepsilon }(t) = \frac{{d\varepsilon }}{{dt}}$ – скорость изменения деформации; τ – время релаксации; G – модуль сдвига.

Для соотношения (2) время релаксации определяется в виде

(3)

$\tau = \frac{\eta }{G},$

где η – вязкостные характеристики элементарной ветви Максвелла.

Для определения вида функции φ(t) рассматривается статический режим исследования для внешнего воздействия:

(4)

$\varepsilon (t) = 0(t\angle {{t}_{0}}),\,\,\,\,\varepsilon (t) = {{\varepsilon }_{0}} = {\text{const}}(t \geqslant {{t}_{0}}),$

где ε₀ ‒ амплитуда деформации, ε(t) – текущая деформация.

Следует отметить, что соотношение (2) не учитывает зависимость τ = f(T), поэтому для описания спектра внутреннего трения λ = f(T) и непрерывного спектра времен релаксации Н(τ), а следовательно, и всей температурной области неупругости следует учитывать температурную зависимость времени α-релаксации каждой подсистемы:

(5)

${{\tau }_{i}} = {{\tau }_{{{{o}_{i}}}}}\exp \frac{{{{U}_{i}}}}{{RT}}.$

Кроме того, если для процесса изотермической релаксации модели Максвелла [9, 10] используется в качестве ядра релаксации уравнение Больцмана–Вольтерра [9, 11], функция релаксации в виде

(6)

$\varphi (t) = \exp \left[ { - \left( {\frac{t}{\tau }} \right)} \right],$

то использование (6) требует теоретического анализа ее применения при различных температурах и в динамическом режиме

(7)

$\varepsilon (t) = {{\varepsilon }_{o}}{{e}^{(}}^{{i\omega t - \delta )}},$

где ω ‒ круговая частота. По-видимому, это приводит к существенному изменению дифференциального уравнения (2).

Рассмотрим теоретическую возможность использования функции (6) в динамическом режиме, что позволит перейти к анализу температурно-частотной зависимости с учетом ширины непрерывного спектра времен релаксации Н(τ) и оценить релаксационную микронеоднородность композита в температурном интервале.

Соотношение (6), где t > 0, должно удовлетворять следующим условиям:

(8)

$\begin{gathered} 1)\,\,\,\,\mathop {\lim }\limits_{x \to 0} \varphi (t) = 1, \hfill \\ 2)\,\,\,\,\mathop {\lim }\limits_{x \to 0} \varphi (t) = \mathop {\lim }\limits_{p \to \infty } p\bar {\varphi }(p), \hfill \\ 3)\,\,\,\,\mathop {\lim }\limits_{t \to \infty } \varphi (t) = 0 \equiv {\text{const,}} \hfill \\ {\text{4)}}\,\,\,\,\mathop {\lim }\limits_{t \to \infty } \varphi (t) = \mathop {\lim }\limits_{p \to \infty } p\bar {\varphi }(p), \hfill \\ \end{gathered} $

где р ‒ комплексная плоскость, $\bar {\varphi }$ – преобразование Лапласа.

Преобразование Лапласа для функции Максвелла (соотношение (6)) имеет следующий вид:

(9)

$\bar {\varphi }(p) = \wedge \left[ {\varphi (t)} \right] = \frac{1}{{p + \frac{1}{\tau }}} = \frac{\tau }{{p\tau + 1}}.$

Разложение функции (6) в ряд имеет вид

(10)

$\varphi (t) = \exp \left[ { - \frac{t}{\tau }} \right] = \sum\limits_{n = 0}^\infty {\frac{{{{{( - 1)}}^{n}}}}{{n!}}{{{\left( {\frac{t}{\tau }} \right)}}^{n}}} ,$

где $ - \infty \angle \frac{t}{\tau }\angle + \infty .$

Преобразование Лапласа для разложения (10) имеет вид

(11)

$\begin{gathered} \bar {\varphi }(p) = \sum\limits_{n = 0}^\infty {\frac{{{{{( - 1)}}^{n}}}}{{n!}}\frac{1}{{{{\tau }^{n}}}} \wedge \left[ {{{t}^{n}}} \right]} = \tau \sum\limits_{n = 0}^\infty {\frac{{{{{( - 1)}}^{n}}}}{{{{{(pr)}}^{{n + 1}}}}}} = \\ = \tau \left[ {{{{(p\tau )}}^{{ - 1}}} - {{{(pr)}}^{{ - 2}}} + {{{(pr)}}^{{ - 3}}} - ...} \right]. \\ \end{gathered} $

Ряд (11) сходится к ряду (10), откуда следует

(12)

$\bar {\varphi }(p) = \tau \frac{{{{{(pr)}}^{{ - 1}}}}}{{1 + {{{(pr)}}^{{ - 1}}}}} = \frac{\tau }{{p\tau + 1}}.$

Из соотношений (10)–(12) следует, что ряд (12) сходится к соотношению (11) при условии, что ${{\left| {pr} \right|}^{{ - 1}}} < 1$ или при $\left| p \right| > \frac{1}{\tau }$ на комплексной плоскости р вне круга радиуса ${1 \mathord{\left/ {\vphantom {1 \tau }} \right. \kern-0em} \tau }$.

Для анализа сходимости ряда (11) внутри круга r < 1/t рассматривается обращение этого ряда в виде

(13)

${{ \wedge }^{{ - 1}}}\left[ {\bar {\varphi }(p)} \right] = \sum\limits_{n = 0}^\infty {\frac{{{{{( - 1)}}^{n}}}}{{n!}}{{{\left( {\frac{t}{\tau }} \right)}}^{n}}} .$

Полученный ряд (13) сходится при любых значениях t/τ и его суммой является экспонента $\exp \left[ {\frac{t}{\tau }} \right],$ т.е.

(14)

${{ \wedge }^{{ - 1}}}\left[ {\bar {\varphi }(p)} \right] = \varphi (t) = \exp \left[ { - \frac{t}{\tau }} \right].$

Из этого следует, что функция Максвелла может быть использована при описании температурной зависимости дефекта модуля [4, 12], который и характеризует релаксационную неоднородность элементов структуры, соответствующих диссипативному процессу α-релаксации.

Далее мы сопоставили нормированные к единице интенсивности диссипативных потерь λ/λ_max в зависимости от параметра (Т – Т_max)/Т_max.

С целью выяснения эффекта наполнителя на релаксационную микронеоднородность в зависимости от высокоэластичности полимера далее строили зависимости соотношения текущей интенсивности к максимально достигаемой интенсивности диссипативных потерь λ/λ_max от соотношения (Т – Т_max)/Т_max. Полученные кривые представлены на рис. 2.

Рис. 2.

(а, б) – зависимость λ/λ_max от (Т – Т_max)/Т_max для ненаполненных (1) и наполненных (2) полимеров: (а) – АК1; (б) – АК2. (в, г) – сопоставление релаксационной микронеоднородности ненаполненных (в) и наполненных (г) полимеров АК1 (1) и АК2 (2).

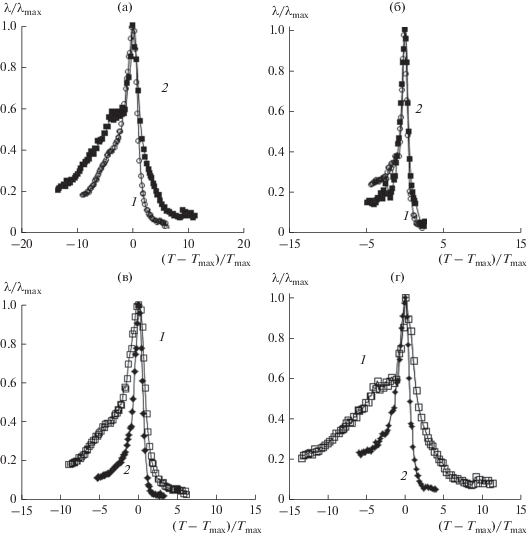
На рис. 2а и 2б представлено сопоставление изменения микрогетерогенности релаксационной структуры АК1 и АК2 при введении высокодисперсного наполнителя. Видно, что микрогетерогенность обоих полимеров возрастает в присутствии наполнителя, указывая на некоторое разрушение межмолекулярных связей. Как следует из рис. 2б, полимер АК2, который содержит в своем составе функциональные карбоксильные группы, характеризуется более однородной релаксационной структурой, что можно связать с образованием водородных связей, препятствующих разрушению релаксационной структуры при введении наполнителя.

На рис. 2в и 2г сопоставлена релаксационная микрогетерогенность структуры наполненных полимеров различной эластичности АК1 и АК2, имеющих Т_ст = 5 и 15°С соответственно. Видно ее существенное изменение в зависимости от температуры стеклования и функциональности полимерного материала. Так, при сопоставлении ненаполненных полимеров (рис. 2в) микрогетерогенность структуры АК1 выше, чем АК2, что связано с большей подвижностью макроцепей высокоэластичного полимера АК1. Из сопоставления микрогетерогенности наполненных полимеров следует, что при ее росте в обоих случаях эффект более выражен для АК1.

Таким образом, ширина температурной области релаксационной микронеоднородности и величина дефекта модуля [4, 12] в этой области, характеризующая упругие свойства полимерной системы, коррелируют с высокоэластичностью полимера.

С целью применения функции Максвелла к описанию релаксационной микронеоднородности полимеров в качестве примера на рис. 3 представлена экспериментальная температурная зависимость частоты колебательного процесса в ненаполненном и наполненном полимере АК2.

Рис. 3.

Экспериментальные (1, 2) и теоретические (3, 4) температурно-частотные зависимости в ненаполненном (1, 3) и наполненном (2, 4) полимере АК2.

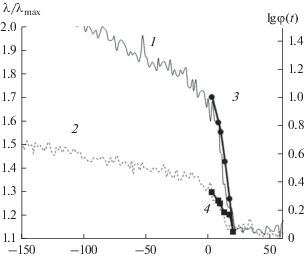
Теоретические точки, наложенные на экспериментальные кривые, получены на основании рассмотрения функции релаксации Максвелла (14) с учетом аномального спада модуля сдвига от G₁ до G₂, характеризующего дефект модуля полимера ∆G в области температуры стеклования в следующем виде:

(15)

$\begin{gathered} \exp \left[ { - \frac{t}{{{{\tau }_{0}}\exp \frac{U}{{R{{T}_{i}}}}}}} \right] = \Delta G(t) = \hfill \\ = \,\,\frac{{{{G}_{1}} - {{G}_{2}}}}{{{{G}_{1}}}} = \frac{{f_{1}^{2} - f_{2}^{2}}}{{f_{1}^{2}}}, \hfill \\ \end{gathered} $

где период колебания частицы на дне потенциальной ямы τ₀ ~ 10^–12 с.

С учетом того, что период колебательного процесса $\theta $ в эксперименте может быть представлен в виде

(16)

$t \equiv \theta \to \frac{1}{f},$

уравнение (15) преобразуется в следующий вид

(17)

$\exp \left[ { - \frac{1}{{f{{\tau }_{0}}\exp \frac{U}{{R{{T}_{i}}}}}}} \right] = \Delta G(T) = \frac{{{{G}_{1}} - {{G}_{2}}}}{{{{G}_{1}}}}.$

Принимаем, что при температуре, соответствующей начальной точке аномального участка изменения модуля сдвига G₁, и соответствующей ей величине частоты колебательного процесса $f_{1}^{2}$, функция релаксация имеет следующее значение:

(18)

$\begin{gathered} \exp \left[ { - \frac{t}{{{{\tau }_{0}}\exp \frac{U}{{R{{T}_{i}}}}}}} \right] = \Delta G(t) = \\ = \frac{{{{G}_{1}} - {{G}_{2}}}}{{{{G}_{1}}}} = \frac{{f_{1}^{2} - f_{2}^{2}}}{{f_{1}^{2}}}. \\ \end{gathered} $

При температуре, соответствующей конечной точке аномального участка изменения модуля сдвига G₁, и соответствующей ей величине частоты колебательного процесса $f_{2}^{2}$, функция релаксация имеет следующее значение:

(19)

На основании уравнений (17)–(19) рассчитаны начальная точка G₁ и конечная точка G₂ аномального участка изменения модуля сдвига G и показана их локализация на экспериментальных кривых рис. 3, на котором обнаружено хорошее соответствие экспериментальных и теоретических результатов.

ЗАКЛЮЧЕНИЕ

Показана возможность качественного анализа изменения релаксационной микронеоднородности латексных полимеров различной эластичности при введении высокодисперсного порошка железа. Продемонстрирована вероятность оценки ширины непрерывных спектров времен релаксации путем сопоставления температурных зависимостей приведенных спектров внутреннего трения с температурной зависимостью изменения дискретного времени релаксации α-процесса. Рассмотрена корреляция между экспериментально установленными температурно-частотными изменениями модуля сдвига систем в режиме свободных колебаний систем и степенью их релаксационной микронеоднородности, теоретически оцененной с привлечением функции релаксации Максвелла.

Исследование физико-химических свойств и структуры латексных полимеров выполнялось при финансовой поддержке программы ПРАН “Физико-химических основы высокоэффективных методов получения многослойных наночастиц и пленочных нанокомпозитов с выраженными функциональными свойствами (в т.ч. защитными, механическими и т.д.)”.

ОБОЗНАЧЕНИЯ

f	частота колебательного процесса
G	модуль сдвига
G₁	начальная точка аномального участка изменения модуля сдвига
G₂	конечная точка аномального участка изменения модуля сдвига
∆G	дефект модуля сдвига
Н(τ)	непрерывный спектр времен релаксации
h	постоянная Планка
k	постоянная Больцмана
р	комплексная плоскость
R	универсальная газовая постоянная
Т	температура
U_a	энергия активации процесса
δ	сдвиг фаз напряжение–деформация в динамическом режиме,
ε(t)	текущая деформация
$\dot {\varepsilon }(t) = \frac{{d\varepsilon }}{{dt}}$	скорость изменения деформации
ε₀	амплитуда деформации
η	вязкостные характеристики элементарной ветви Максвелла
휃	экспериментальный период колебательного процесса
λ	логарифмический декремент
$\dot {\sigma }(t) = \frac{{d\sigma }}{{dt}}$	скорость изменения напряжения
τ	время релаксации
τ_i	дискретное время релаксации
τ₀	предэкспоненциальный коэффициент, период колебания частицы на дне потенциальной ямы
φ(t)	функция релаксации Максвелла
$\bar {\varphi }$	преобразование Лапласа
Ω	круговая частота

ИНДЕКСЫ

ст	стеклование
max	максимальные значения внутреннего трения и температуры

Список литературы

Бартенев Г.М. Структура и релаксационные свойства эластомеров. М.: Химия, 1979.
Тагер А.А. Физикохимия полимеров. М.: Научный мир, 2007.
Lomovskoy V.A., Abaturova N.A., Lomovskaya N.Y., Khlebnikova O.A., Galushko T.B. Relaxation phenomena in acetylcellulose // Inorg. Mater.: Appl. Res. 2010. № 1. Р. 29. [Ломовской В.А., Абатурова Н.А., Ломовская Н.Ю., Хлебникова О.В., Галушко Т.Б. Релаксационные явления в ацетилцеллюлозе // Материаловедение. 2010. № 1. С. 29.]
Valishin A.A., Gorshkov A.A., Lomovskoy V.A. Modulus defect of solid solution of H₂ in Pd // Mech. Solids (Engl. Transl.). 2011. V. 46. № 2. Р. 299. [Валишин А.А., Горшков А.А., Ломовской В.А. Дефект модуля упругости твердого раствора водорода в палладии // Изв. Акад. наук. Мех. тверд. тела. 2011. № 2. С. 169.]
Bartenev G.M., Lomovskoy V.A., Lomovskaya N.Yu. The effect of thermal degradation of poly(methylmethacrylate) on the glass transition and relaxation time spectra // Polym. Sci., Ser. A. 1994. V. 36. № 9. P. 1273. [Бартенев Г.М., Ломовской В.А., Ломовская Н.Ю. Влияние термодеструкции на стеклование и спектры времен релаксации полиметилметакрилата // Высокомол. соедин. Сер. А. 1994. Т. 36. № 9. С. 1529.]
Petrukhin A.A., Lomovskoy V.A. Deborah number and relaxation processes in polymethacrylate // Inorg. Mater.: Appl. Res. 2001. № 3. P. 3. [Петрухин А.А., Ломовской В.А. Число Деборы и релаксационные процессы в полиметилметакрилате // Материаловедение. 2001. № 3. С. 3.]
Nekhoda A.P., Rostishlvili V.G., Irzhak T.F., Irzhak V.I. The effect of preliminary history on α- and β-transitions in polymers // Polym. Sci., Ser. В. 1988. V. 30. № 10. Р. 692. [Нехода А.Р., Ростиашвили В.Г., Иржак Т.Ф., Иржак В.И. Влияние температурной предыстории на α- и β-переходы в полимерах // Высокомол. соедин. Сер. Б. 1988. Т. 30. № 10. С. 768.]
Aslamazova T.R., Lomovskoi V.A., Tsivadze A.Yu. Relaxation phenomena in latex polymers modified with water-soluble phthalocyanine // Polym. Sci., Ser. A. 2013. V. 55. № 12. Р. 729. [Асламазова Т.Р., Ломовской В.А., Цивадзе А.Ю. Релаксационные явления в латексных полимерах, модифицированных водорастворимым фталоцианином // Высокомол. соедин. Сер. А. 2013. № 12. С. 1427.]
Работнов Ю.Н. Ползучесть элементов. M.: Наука, 1966.
Slonimskii G.L., Askadskii A.A., Pavlov V.I. Investigation of the effect of the type of supermolecular and chemical structure on the strength and elasticity of polymer glasses // Polym. Sci., Ser. A. 1967. V. 9. № 2. P. 408. [Слонимский Г.Л., Аскадский А.А., Павлов В.И. Исследование эффекта типа супрамолекулярной и химической структуры на прочность и эластичность полимерных стекол // Высокомол. соедин. Сер. А. 1967. Т. 9. № 2. С. 367.]
Ржаницин A.Р. Теория ползучести. M.: Литература по строительству, 1968.
Aslamazova T.R., Lomovskoi V.A., Kotenev V.A., Tsivadze A.Yu. Selection of a Relaxation Function to Describe the Dissipative α-Relaxation Process in Latex Polymers // Prot. Met. Phys. Chem. Surf. 2019. V. 55. № 1. Р. 94. [Асламазова Т.Р., Ломовской В.А., Котенев В.А., Цивадзе А.Ю. Выбор функции релаксации для описания диссипативного процесса α-релаксации в латексном полимере // Физикохим. поверхн. защ. матер. 2019. Т. 55. № 1. С. 65.]

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал