Теоретические основы химической технологии, 2020, T. 54, № 1, стр. 17-29
Проектирование химико-технологических систем при учете объединенных мягких ограничений
Т. В. Лаптева a, *, Н. Н. Зиятдинов a, И. И. Емельянов a
a Казанский национальный исследовательский технологический университет
Казань, Россия
* E-mail: tanlapteva@yandex.ru
Поступила в редакцию 02.08.2019
После доработки 06.08.2019
Принята к публикации 09.09.2019
Аннотация
Предлагается метод решения задач проектирования оптимальных химико-технологических систем при учете неполноты и неточности исходной информации, представленных в форме одноэтапных задач оптимизации с объединенными вероятностными ограничениями. Объединенные вероятностные ограничения гарантируют требуемый уровень вероятности выполнения, в отличие от отдельных вероятностных ограничений, которые дают лишь оценку уровня выполнения. Однако вычисление объединенных вероятностных ограничений значительно сложнее в сравнении с отдельными вероятностными ограничениями. В работе предлагается способ решения задач проектирования оптимальных химико-технологических систем при учете объединенных вероятностных ограничений, позволяющий исключить операцию прямого вычисления ограничений. Способ предполагает преобразование задачи стохастического программирования в последовательность задач детерминированного нелинейного программирования и позволяет значительно сократить время решения задачи. Эффективность предлагаемого подхода проиллюстрирована на модельных примерах.
ВВЕДЕНИЕ
Известно, что химико-технологические системы (ХТС) в процессе работы испытывают влияние внешних и внутренних факторов, что отражается на функционировании ХТС. Эксплуатация ХТС в изменяющихся условиях работы требует учета таких изменений при проектировании новых ХТС. В современной теории оптимизации ХТС такие задачи решают на основе постановок задач оптимизации с учетом неопределенности в исходной информации [1], когда изменения в условиях функционирования ХТС представляют через изменения ряда параметров ее математической модели. Обычно считается, что изменение значений таких параметров происходит независимо от нашего желания и предполагается случайная природа таких параметров. Однако, исходя из имеющихся исторических данных, можно прогнозировать диапазон изменения этих параметров за выбранный период функционирования создаваемой ХТС. В ряде случаев имеющейся информации достаточно для определения закона распределения значений неопределенных параметров и его характеристик.
Общий вид задачи проектирования оптимальной ХТС при учете изменения неопределенных параметров можно записать в виде [1, 2]
где $H = \{ d,z:{{h}_{q}}(d,z) \leqslant 0,q = 1,...,p\} ,$ ограничения (2) есть математическая формулировка проектных требований к работе ХТС, $d$ – вектор конструктивных параметров размерности ${{n}_{d}}$, $z$ – ${{n}_{z}}$-вектор переменных, характеризующих режим работы ХТС, $f(d,z,\theta )$ – функция оценки эффективности работы ХТС. $\theta $ – ${{n}_{\theta }}$-вектор неопределенных параметров, $\theta \in T$, область неопределенности $T = \{ \theta :\theta _{i}^{L} \leqslant {{\theta }_{i}} \leqslant \theta _{i}^{U},$$i = 1,...,{{n}_{\theta }}\} $ формируется из выявленных диапазонов изменения значений неопределенных параметров ${{\theta }_{i}}$, $i = 1,...,{{n}_{\theta }}.$ Предполагается непрерывная дифференцируемость функций $f(d,z,\theta )$ и ${{g}_{j}}(d,z,\theta ),$ $j = 1,...,m.$Задача (1)–(2) не может быть решена, поскольку неизвестны точные значения параметров $\theta $.
Задачи проектирования оптимальных ХТС при учете неопределенности в исходной информации в зависимости от природы и полноты информации на разных этапах жизненного цикла ХТС, возможности ее уточнения и желания проектировщика решают на основе постановок одно- или двухэтапных задач оптимизации [2]. Случайная природа экзогенной и эндогенной неопределенности [3] по-разному учитывается в критерии и ограничениях задачи оптимизации. Это приводит к использованию постановок задач робастной оптимизации [4], стохастической оптимизации [5] либо оптимизации с учетом мягких ограничений [6].
Задачи робастной оптимизации предполагают выполнение требований к работе ХТС при любых изменениях условий функционирования ХТС. Такие ограничения называют жесткими [7]. Мягкие ограничения [8] предполагают выполнение требований к работе ХТС в среднем или с заданной вероятностью. При использовании последних требуется весьма высокий уровень вероятности выполнения таких ограничений, или малый уровень риска. Методы решения двухэтапных задач оптимизации с жесткими ограничениями и одноэтапных задач с вероятностными ограничениями предложены во многих работах [9–11]. В данной работе будут рассмотрены постановки задач оптимизации с мягкими ограничениями в форме вероятностных ограничений.
Вероятностные ограничения впервые были введены в работе [12], после чего значительные исследования свойств таких ограничений были сделаны в [13]. Исследователей в основном привлекали задачи с отдельными вероятностными ограничениями, которые можно представить в виде
(3)
$\begin{gathered} {\text{Pr\{ }}{{g}_{j}}(d,z,\theta ) \leqslant 0\} \geqslant {{\alpha }_{j}},\,\,\,\,j = 1,...,m, \\ Pr\{ {{g}_{j}}(d,z,\theta ) \leqslant 0\} = \int\limits_{{{\Omega }_{j}}} {\rho (\theta )d\theta } , \\ \end{gathered} $Вычисление значений ограничений вида (3) в процессе решения задачи оптимизации требует проведения процедуры многомерного интегрирования на каждом шаге метода оптимизации, а область интегрирования ${{\Omega }_{j}}$ вида (4) не является выпуклой в большинстве задач [14]. При этом еще в работе [15] анализировались объединенные вероятностные ограничения, имеющие вид
(5)
$\begin{gathered} {\text{Pr\{ }}{{g}_{j}}(d,z,\theta ) \leqslant 0;j = 1,...,m\} \geqslant \alpha , \\ Pr\{ {{g}_{j}}(d,z,\theta ) \leqslant 0;j = 1,...,m\} = \int\limits_{{{\Omega }_{\alpha }}} {\rho (\theta )d\theta } \geqslant \alpha , \\ \end{gathered} $(6)
${{\Omega }_{\alpha }} = \{ \theta :{{g}_{j}}(d,z,\theta ) \leqslant 0;j = 1,...,m;\theta \in T\} .$Ограничения вида (5) являются еще более сложными в вычислительном смысле, поскольку часто невычислимы впрямую и приводят к овражистым областям и жестким задачам [16].
Сравнивая два типа ограничений вида (3) и вида (5), рассмотрим особенности получаемого решения. Требование выполнения ограничений (3) не предполагает выполнение всех $m$ ограничений на одной и той же области, позволяя иметь различные области ${{\Omega }_{j}},$ $j = 1,...,m.$ Необходимо обеспечить лишь требуемый уровень вероятности выполнения ограничений. В силу того, что
возможна ситуация, в которой часть ограничений с номерами из множества $\bar {J}$, $\bar {J} \subset \{ 1,...,m\} ,$ выполняется в некоторой точке ${{\theta }^{{\bar {t}}}} \in T,$
а часть ограничений в этой точке выполняться не будет.
Поскольку такая точка области неопределенности характеризует момент этапа функционирования ХТС, то мы можем получить ситуацию, когда, получив заданный уровень вероятности выполнения ограничений после решения задачи оптимизации с ограничениями вида (3), часть ограничений будут выполняться в указанный момент этапа функционирования ХТС, а часть – нет. Получается, что мы не можем гарантировать требуемый уровень вероятности выполнения ограничений, а получаем лишь оценку решения задачи [17].
С другой стороны, объединенные ограничения (5) в формализованной постановке уже предполагают обеспечение уровня выполнения вероятности выполнения ограничений при их одновременном выполнении в одной и той же подобласти области неопределенности. Это гарантирует обеспечение требуемого уровня вероятности выполнения ограничений. Гарантия одновременного выполнения объединенных ограничений привлекла активное внимание к таким ограничениям в последнее десятилетие.
Проблема решения задач оптимизации с объединенными вероятностными ограничениями состоит в том, что на каждом шаге оптимизационного метода требуется вычислять многомерные интегралы в левой части (5) для получения значения уровня вероятности выполнения ограничений, кроме того области выполнения ограничений невыпуклы [14]. На решение возникающих проблем направлены методы, которые можно разделить на три группы: методы, предлагающие модификации квадратурных формул для многомерного интегрирования с заданной точностью; методы, основанные на идее статистических испытаний; методы, предоставляющие легко вычислимые аппроксимации левых частей ограничений.
Первая группа методов предполагает использование особенностей решаемой задачи для получения специальных квадратурных формул, позволяющих эффективно получать значения многомерных интегралов с заданной точностью [18–20]. Однако до сих пор использование этой группы методов приводит к резкому росту числа узлов в области интегрирования при увеличении ее размерности и требовании высокой точности. Вторая группа методов включает методы статистических испытаний или выборочной аппроксимации [21]. Группа методов развивает идею метода Монте-Карло, предлагая его модификации, позволяющие ускорить сходимость метода без потери точности [22, 23]. Здесь следует выделить активно использующиеся квази-Монте-Карло методы, которые используют последовательности с так называемым низким несоответствием, например последовательности Соболя. Эти последовательности могут рассматриваться как псевдослучайные для многих известных распределений. Обзор таких методов приведен в работе [24]. Другим направлением в этой области являются методы, использующие вероятностные метрики, которые позволяют оценивать ошибку решения, получаемого при помощи статистических испытаний [25, 26]. Третьим направлением в этой области являются методы, подгоняющие моменты генерируемого набора под характеристики исходного [27]. Сравнение методов статистических испытаний дано в части 16 книги [28]. Поскольку все перечисленные методы группы базируются на генерации дискретного распределения согласно некоторым требованиям и алгоритму, то в литературе используется их общее название методы выборочной аппроксимации или аппроксимации выборочного среднего (SAA) [29]. Оригинальная идея метода была предложена А. Немировским и А. Шапиро в работе [23]. В работе авторы разработали метод решения двухэтапной задачи оптимизации с мягкими ограничениями для случая биафинных зависимостей от переменных $d,z$ и параметров $\theta $ в левых частях ограничений. Адаптацию SAA-метода к решению двухэтапных задач линейной оптимизации с квантильным критерием предложили авторы [30]. В работе [31] метод модифицирован и комбинирован с декомпозиционным алгоритмом Бендерса для решения двухэтапной задачи оптимизации с бинарными параметрами первого этапа и непрерывными на втором этапе жизненного цикла системы. Однако SAA-метод в свою очередь использует генерацию случайных чисел для моделирования исходного распределения и вычисления ограничений. Это может привести к значительным отклонениям от реального распределения, либо потребует больших вычислительных затрат для достижения приемлемой точности [14].
Методы третьей группы включают способы сведения имеющихся ограничений к хорошо известным и легко вычисляемым, а также способы сведения вероятностных ограничений к детерминированному виду. Среди первых способов следует упомянуть использование неравенства Чебышева [32], неравенства Хефдинга [33]. Выпуклая аппроксимация объединенных вероятностных ограничений предложена в [34], где авторы рассмотрели задачу линейной оптимизации. Использование неравенства Бонферрони для сведения объединенных вероятностных ограничений к отдельным вероятностным показано в работах [23, 35]. Аппроксимации ограничений предложены в работе [37] для задач многоэтапной линейной оптимизации. Вычисление ограничений для разных типов непрерывных и дискретных распределений значений неопределенных параметров рассмотрено в [38]. В работе [39] представлена выпуклая аппроксимация объединенных ограничений для частных случаев функций ограничений. Эти аппроксимации позволяют упростить вычисление многомерных интегралов при получении значений левых частей вероятностных ограничений. В то же время разрабатываются методы, сводящие вероятностные ограничения к детерминированному виду, что позволяет полностью исключить операции многомерного интегрирования. Первоначально такие методы предлагались для отдельных вероятностных ограничений, однако уже в 1997 K. Маранас рассмотрел способ преобразования объединенного вероятностного ограничения к детерминированному виду для линейного вида ограничений. В работах Г.М. Островского с соавторами сформулирована двухэтапная задача оптимизации с мягкими ограничениями [40, 41] и предложен метод ее решения, предполагающий преобразование вероятностных ограничений к детерминированному виду. Однако все перечисленные работы либо предполагают использование отдельных вероятностных ограничений, либо рассчитаны на узкий класс функций ограничений, либо дискретные распределения.
В настоящей работе будет предложен новый метод решения задач оптимизации с объединенными ограничениями для случая, когда неопределенные параметры являются независимыми случайными величинами. Также будем предполагать, что неопределенные параметры ${{\theta }_{i}}$ имеют нормальное распределение со средним ${{\mu }_{i}}$ и дисперсией $\sigma _{i}^{2}$. Будем рассматривать вероятностные ограничения с неопределенностью только в левой части ограничений.
ФОРМУЛИРОВАНИЕ ЗАДАЧ ОПТИМИЗАЦИИ С ОБЪЕДИНЕННЫМИ МЯГКИМИ ОГРАНИЧЕНИЯМИ
Задача проектирования оптимальных ХТПС в постановке одноэтапной задачи оптимизации с отдельными вероятностными ограничениями в стратегии оптимальности в среднем может быть сформулирована в виде [41]
(8)
$\Pr \{ \theta \in \Omega \} \equiv \int\limits_\Omega {\rho (\theta )d\theta } \geqslant \alpha ,$В задаче (7)–(8) уровень вероятности выполнения ограничений (8) задается проектировщиком в предположении $0 \leqslant \alpha \leqslant 1$, (10) – математическое ожидание функции $f(d,z,\theta ).$
Если рассматривать объединенные вероятностные ограничения и учет информации с этапов проектирования и функционирования в жизни ХТС, то в общем виде задача проектирования оптимальных ХТПС в постановке двухэтапной задачи оптимизации с объединенными вероятностными ограничениями (ДЭЗОВО) в стратегии оптимальности в среднем имеет вид [42]
(11)
$\mathop {\min }\limits_{d,z(\theta ) \in H} \int\limits_T {f(d,z(\theta ),\theta )\rho (\theta )d\theta } ,$(13)
$Pr\{ {{g}_{j}}(d,z(\theta ),\theta ) \leqslant 0;j = 1,...,m\} = \int\limits_{{{\Omega }_{T}}} {\rho (\theta )d\theta } ,$(14)
${{\Omega }_{T}} = \{ \theta :{{g}_{j}}(d,z(\theta ),\theta ) \leqslant 0;j = 1,...,m;\theta \in T\} .$Будем далее предполагать, что решение задачи (11)–(12) существует и обозначим его как $d*,z*(\theta ).$
Учитывая, что левую часть ограничения (12) можно переписать в виде (13), (14), задачу (11)–(12) можно переписать в следующем виде:
(15)
$\mathop {\min }\limits_{d,z(\theta ) \in H} \int\limits_T {f(d,z(\theta ),\theta )\rho (\theta )d\theta } ,$(16)
$\Pr \{ \theta \in {{\Omega }_{T}}\} \equiv \int\limits_{{{\Omega }_{T}}} {\rho (\theta )d\theta } \geqslant \alpha ,$(17)
${{\Omega }_{T}} = \{ \theta :{{g}_{j}}(d,z(\theta ),\theta ) \leqslant 0;j = 1,...,m;\theta \in T\} .$В случае, когда управляющие переменные $z(\theta )$ не зависят от параметров $\theta $, т.е. $z(\theta ) = z = {\text{const}},$ $\forall \theta \in T$, задача (15)–(16) преобразуется в одноэтапную задачу оптимизации с объединенными вероятностными ограничениями (ОЭЗОВО) вида
(19)
$\Pr \{ \theta \in {{\Omega }_{O}}\} \equiv \int\limits_{{{\Omega }_{O}}} {\rho (\theta )d\theta } \geqslant \alpha ,$Предполагая, что решение задачи (18)–(19) существует, обозначим его как $d*,z{\text{*}}.$
Сложности решения ДЭЗОВО и ОЭЗОВО состоят в следующем:
а) вычисление многомерных интегралов в (15), (18) и (16), (19) для получения точных значений критерия и ограничений задач на каждой итерации метода оптимизации;
б) в задаче (15)–(16) поисковые переменные $z(\theta )$ являются функциями неопределенных параметров, имеющие неизвестный вид.
Далее будем рассматривать решение ОЭЗОВО (18)–(19).
Предлагаемый подход будет основан на следующих операциях:
а) Построение области $\tilde {\Omega } \subset T$ для аппроксимации области ${{\Omega }_{O}}$. Область $\tilde {\Omega }$ будет строиться таким образом, чтобы исключить операции многомерного интегрирования при вычислении значений левых частей ограничений (19). Область $\tilde {\Omega }$ будет уточняться на каждой итерации решения ОЭЗОВО, для чего будет разработана процедура уточнения аппроксимации области ${{\Omega }_{O}}$.
б) Аппроксимация ${{E}_{{{\text{ap}}}}}[f(d,z,\theta )]$ критерия ОЭЗОВО, имеющего вид матожидания $E[f(d,z,\theta )]$. Будем использовать аппроксимацию, предложенную ранее в [43], которая позволяет избежать многомерного интегрирования в (18).
Тогда на некоторой итерации с номером $k$ будем решать следующую задачу:
АППРОКСИМАЦИЯ КРИТЕРИЯ ОЭЗОВО
Для исключения операции многомерного интегрирования при получении значения критерия задачи (18)–(19) в [45] мы предложили аппроксимацию критерия задачи на основе кусочно-линейной зависимости. Пусть на $k$-й итерации область неопределенности $Т$ разбита на подобласти $T_{q}^{{(k)}}$, $q = 1,...,{{Q}^{{(k)}}},$ такие, что выполняются условия
(22)
$\begin{gathered} T_{{{{q}_{1}}}}^{{(k)}} \cap T_{{{{q}_{2}}}}^{{(k)}} = \emptyset ,\,\,\,\,{{q}_{1}} = 1,..,{{Q}^{{(k)}}}, \\ {{q}_{2}} = 1,..,{{Q}^{{(k)}}},\,\,\,\,{{q}_{1}} \ne {{q}_{2}}, \\ \end{gathered} $(23)
$\begin{gathered} T_{q}^{{(k)}} = \{ \theta :\theta _{i}^{{(k)L,q}} \leqslant {{\theta }_{i}} \leqslant \theta _{i}^{{(k)U,q}},i = 1,...,{{n}_{\theta }}\} , \\ q = 1,..,{{Q}^{{(k)}}}. \\ \end{gathered} $Аппроксимируем функцию $f(d,z,\theta )$ зависимостью $\bar {f}(d,z,\theta ,{{\theta }^{q}}),$ которую построим на основе разложения функции $f(d,z,\theta )$ в ряд Тейлора по неопределенным параметрам $\theta $ в точках ${{\theta }^{q}} \in T_{q}^{{(k)}},$ $q = 1,...,{{Q}^{{(k)}}},$ оставив линейную часть разложения. В [45] показано, что для критерия вида (10) может быть использована аппроксимация ${{E}_{{{\text{ap}}}}}[f(d,z,\theta )]$:
(24)
$\begin{gathered} {{E}_{{{\text{ap}}}}}[f(d,z,\theta )] = \sum\limits_{q = 1}^{{{Q}^{{(k)}}}} {\left( {{{a}_{q}}f(d,z,{{\theta }^{q}}) + \frac{{^{{^{{}}}}}}{{_{{_{{}}}}}}} \right.} \\ \left. { + \,\,\sum\limits_{i = 1}^{{{n}_{\theta }}} {\frac{{\partial f(d,z,{{\theta }^{q}})}}{{\partial {{\theta }_{i}}}}(E[{{\theta }_{i}};T_{q}^{{(k)}}] - {{a}_{q}}\theta _{i}^{q})} } \right), \\ \end{gathered} $(26)
$E[{{\theta }_{i}};T_{q}^{{(k)}}] = \int\limits_{T_{q}^{{(k)}}} {{{\theta }_{i}}\rho (\theta )d\theta } .$Используя сведения о независимости неопределенных параметров, мы можем вычислять (25) на основе зависимости [43]
(27)
${{a}_{q}} = \prod\limits_{i = 1}^{{{n}_{\theta }}} {[\Phi (\tilde {\theta }_{i}^{{(k)U,q}}) - \Phi (\tilde {\theta }_{i}^{{(k)L,q}})]} ,$(28)
$\begin{gathered} \tilde {\theta }_{i}^{{(k)L,q}} = \frac{{\theta _{i}^{{(k)L,q}} - E[{{\theta }_{i}}]}}{{{{\sigma }_{i}}}},\,\,\,\,\tilde {\theta }_{i}^{{(k)U,q}} = \frac{{\theta _{i}^{{(k)U,q}} - E[{{\theta }_{i}}]}}{{{{\sigma }_{i}}}}, \\ q = 1,..,{{Q}^{{(k)}}},\,\,\,\,i = 1,...,{{n}_{\theta }}, \\ \end{gathered} $Также интеграл правой части выражения (26) будем вычислять в виде
(29)
$\begin{gathered} E[{{\theta }_{i}};T_{q}^{{(k)}}] = \prod\limits_{r = 1}^{i - 1} {[\Phi (\tilde {\theta }_{r}^{{(k)U,q}}) - \Phi (\tilde {\theta }_{r}^{{(k)L,q}})]} \times \\ \times \,\,\int\limits_{\theta _{i}^{{(k)L,q}}}^{\theta _{i}^{{(k)U,q}}} {{{\theta }_{i}}\rho (\theta )d\theta } \prod\limits_{r = i + 1}^{{{n}_{\theta }}} {[\Phi (\tilde {\theta }_{r}^{{(k)U,q}}) - \Phi (\tilde {\theta }_{r}^{{(k)L,q}})]} . \\ \end{gathered} $В выражениях (26) и (29) остались формулы одномерного интеграла, который будет необходимо вычислять на каждой итерации метода
(30)
${{I}_{{i,q}}} = \int\limits_{\theta _{i}^{{(k)L,q}}}^{\theta _{i}^{{(k)U,q}}} {{{\theta }_{i}}\rho (\theta )d\theta } .$Аппроксимировав функцию нормального стандартного распределения $\Phi (\xi )$, а также одномерного интеграла, мы исключим операции интегрирования при получении значения (18).
ПОСТРОЕНИЕ АППРОКСИМАЦИИ $\tilde {\Omega }$ ДЛЯ ОЭЗОВО
Рассмотрим некоторую итерацию с номером $k$. Пусть мы получили решение задачи (18)–(19). Тогда нам известен набор областей ${{\Omega }_{j}}$, ${{\Omega }_{j}} \ne \emptyset ,$ $j = 1,...,m,$ вида
(31)
${{\Omega }_{j}} = \{ \theta :{{g}_{j}}(d,z,\theta ) \leqslant 0,\,\,\theta \in T\} ,\,\,\,\,j = 1,...,m.$Очевидно, что искомая область ${{\Omega }_{O}}$ может быть получена как
Рассмотрим отдельную область ${{\Omega }_{j}}$. Ее границу можно описать уравнением
Выразим из (33) параметр ${{\theta }_{{{{n}_{\theta }}}}}$ как функцию остальных параметров уравнения (33). При известных значения переменных $d,z$ и параметров ${{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{{{{n}_{\theta }} - 1}}}$ всегда можно получить числовое значение параметра ${{\theta }_{{{{n}_{\theta }}}}}$ из уравнения
Введем новые функции вида
(34)
$\begin{gathered} {{{\bar {g}}}_{j}}(d,z,{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{{{{n}_{\theta }}}}}) = \\ = \left\{ {\begin{array}{*{20}{c}} {{{\theta }_{{{{n}_{\theta }}}}} - {{\varphi }_{j}}(d,z,{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{{{{n}_{\theta }} - 1}}}),\,\,\,\,\frac{{\partial {{g}_{j}}}}{{\partial {{\theta }_{{{{n}_{\theta }}}}}}} \geqslant 0;} \\ \vdots \\ {{{\varphi }_{j}}(d,z,{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{{{{n}_{\theta }} - 1}}}) - {{\theta }_{{{{n}_{\theta }}}}},\,\,\,\,\frac{{\partial {{g}_{j}}}}{{\partial {{\theta }_{{{{n}_{\theta }}}}}}} \leqslant 0.} \end{array}} \right. \\ \end{gathered} $Очевидно, что приведенные выше рассуждения можно распространить на все области ${{\Omega }_{j}}$, $j = 1,...,m$. Тогда, используя вид (34) функций ${{\bar {g}}_{j}}(d,z,{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{{{{n}_{\theta }}}}}),$ можно представить искомую область ${{\Omega }_{O}}$ в виде
(35)
$\begin{gathered} {{\Omega }_{O}} = \{ \theta :{{{\bar {g}}}_{j}}(d,z,{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{{{{n}_{\theta }}}}}) \leqslant 0, \\ j = 1,...,m,\,\,\theta _{i}^{L} \leqslant {{\theta }_{i}} \leqslant \theta _{i}^{U},\,\,i = 1,...,{{n}_{\theta }}\} . \\ \end{gathered} $Введем на итерации с номером $k$ некоторое разбиение области неопределенности на подобласти $R_{l}^{{(k)}} = \{ \theta :\theta _{i}^{{(k)L,l}}$ ≤ ${{\theta }_{i}} \leqslant \theta _{i}^{{(k)U,l}},$ $i = 1,...,{{n}_{\theta }}\} $, $l = 1,...,{{N}^{{(k)}}},$ такие, что выполняются условия
(37)
$\begin{gathered} \left( {R_{{{{q}_{1}}}}^{{(k)}}} \right) \cap \left( {R_{{{{q}_{2}}}}^{{(k)}}} \right) = \emptyset ,\,\,\,\,{{q}_{1}} = 1,..,{{N}^{{(k)}}}, \\ {{q}_{2}} = 1,..,{{N}^{{(k)}}},\,\,\,\,{{q}_{1}} \ne {{q}_{2}}, \\ \end{gathered} $Рассмотрим новую область ${{\Omega }^{{l,(k)}}} = R_{l}^{{(k)}} \cap {{\Omega }_{O}},$ $l = 1,...,{{N}^{{(k)}}}.$ Учитывая (32), (36), (37), можно представить область ${{\Omega }_{O}}$ в виде
Рассмотрим далее способ аппроксимации подобластей ${{\Omega }^{{l,(k)}}}$. Для этого введем обозначения вектора $\bar {\theta } = ({{\theta }_{1}},...,{{\theta }_{{{{n}_{\theta }} - 1}}})$ и области $\bar {R}_{l}^{{(k)}}$ в пространстве переменных $\bar {\theta }$:
(38)
$\begin{gathered} \bar {R}_{l}^{{(k)}} = \{ \theta :\theta _{i}^{{(k)L,l}} \leqslant {{\theta }_{i}} \leqslant \theta _{i}^{{(k)U,l}},i = 1,...,{{n}_{\theta }} - 1\} , \\ l = 1,...,{{L}^{{(k)}}}, \\ \end{gathered} $Для описания аппроксимации подобластей ${{\Omega }^{{l,(k)}}}$ рассмотрим поведение функций gj(d, z, θ1, θ2, …, ${{\theta }_{{{{n}_{\theta }}}}}).$ Рассмотрим случай, когда выполняется
(40)
$\frac{{\partial {{g}_{j}}(d,z,\theta )}}{{\partial {{\theta }_{{{{n}_{\theta }}}}}}} \geqslant 0,\,\,\,\,j = 1,...,m.$В этом случае область ${{\Omega }^{{l,(k)}}}$ можно представить в виде
(41)
$\begin{gathered} {{\Omega }^{{l,(k)}}} = \{ \theta :{{\theta }_{{{{n}_{\theta }}}}} - {{\varphi }_{j}}(d,z,{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{{{{n}_{\theta }} - 1}}}) \leqslant 0, \\ j = 1,...,m,\bar {\theta } \in \bar {R}_{l}^{{(k)}}\} . \\ \end{gathered} $Будем аппроксимировать на итерации $k$ функции ${{\varphi }_{j}}(d,z,{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{{{{n}_{\theta }} - 1}}}),$ $j = 1,...,m,$ кусочно-линейными зависимостями
(42)
$\bar {\varphi }_{j}^{{(k)}}(d,z,\bar {\theta }) = \{ \varphi _{{j,l}}^{{(k)}},\,\,{\text{если}}\,\,\bar {\theta } \in \bar {R}_{l}^{{(k)}}\} ,\,\,\,\,j = 1,...,m,$Тогда для аппроксимации областей ${{\Omega }^{{l,(k)}}},$ l = 1, …, L(k), можно ввести области ${{\tilde {\Omega }}^{{l,(k)}}},$ $l = 1,...,{{L}^{{(k)}}},$ вида
Поскольку выполняются условия (37) и (39), то область ${{\Omega }_{O}}$ можно аппроксимировать областью $\tilde {\Omega }$ вида
(43)
$\begin{gathered} \tilde {\Omega } = {{{\tilde {\Omega }}}^{{1,(k)}}} \cup {{{\tilde {\Omega }}}^{{2,(k)}}} \cup ... \cup {{{\tilde {\Omega }}}^{{{{L}^{{(k)}}},(k)}}}, \\ {{\Omega }^{{q,(k)}}} \cap {{\Omega }^{{s,(k)}}} = \emptyset ,\,\,\,\,q = 1,..,{{L}^{{(k)}}},\,\,\,\,s = 1,..,{{L}^{{(k)}}}, \\ q \ne s. \\ \end{gathered} $Введем переменную
Тогда можно записать, что условие ${{\theta }_{{{{n}_{\theta }}}}} \leqslant y_{l}^{{(k)}}$ равносильно условию ${{\theta }_{{{{n}_{\theta }}}}} - \varphi _{{j,l}}^{{(k)}} \leqslant 0,$ $j = 1,...,m.$
Запишем вероятностную меру области ${{\tilde {\Omega }}^{{l,(k)}}},$ учитывая (44):
(45)
$\begin{gathered} \Pr \{ \theta \in {{{\tilde {\Omega }}}^{{l,(k)}}}\} = \left( {\prod\limits_{i = 1}^{{{n}_{\theta }} - 1} {[\Phi (\tilde {\theta }_{i}^{{(k)U,l}}) - \Phi (\tilde {\theta }_{i}^{{(k)L,l}})]} } \right) \times \\ \times \,\,[\Phi (\tilde {y}_{l}^{{(k)}}) - \Phi (\tilde {\theta }_{i}^{{(k)L,l}})], \\ \end{gathered} $(46)
$\begin{gathered} \tilde {\theta }_{i}^{{(k)L,l}} = \frac{{\theta _{i}^{{(k)L,l}} - E[{{\theta }_{i}}]}}{{{{\sigma }_{i}}}},\,\,\,\,\tilde {\theta }_{i}^{{(k)U,l}} = \frac{{\theta _{i}^{{(k)U,l}} - E[{{\theta }_{i}}]}}{{{{\sigma }_{i}}}}, \\ l = 1,..,{{L}^{{(k)}}},\,\,\,\,i = 1,...,{{n}_{\theta }},\,\,\,\,\tilde {y}_{l}^{{(k)}} = \frac{{y_{l}^{{(k)}} - E[{{\theta }_{{{{n}_{\theta }}}}}]}}{{{{\sigma }_{{{{n}_{\theta }}}}}}}. \\ \end{gathered} $Учитывая (45) и (43), можно записать
(47)
$\begin{gathered} \Pr \{ \theta \in {{{\tilde {\Omega }}}^{{(k)}}}\} = \Pr \{ \theta \in {{{\tilde {\Omega }}}^{{1,(k)}}}\} + \\ + \,\,\Pr \{ \theta \in {{{\tilde {\Omega }}}^{{2,(k)}}}\} + ... + \Pr \{ \theta \in {{{\tilde {\Omega }}}^{{{{L}^{{(k)}}},(k)}}}\} . \\ \end{gathered} $Подставим выражения (24), (45) и (47) в задачу (18)–(19). Учтя дополнительные поисковые переменные в новой постановке, получим задачу
(48)
$f_{1}^{{(k)}} = \mathop {\min }\limits_{d,z \in H,y_{l}^{{(k)}}} E_{{{\text{ap}}}}^{{(k)}}[f(d,z,\theta )],$(50)
$y_{l}^{{(k)}} = \mathop {\min }\limits_{j = 1,...,m} \varphi _{{j,l}}^{{(k)}},\,\,\,\,l = 1,..,{{L}^{{(k)}}}.$Задача (48)–(50) дает $1$оценку искомого решения задачи (15)–(16), но при этом содержит недифференцируемую функцию в правой части (50). Заменим ограничение (50). Введем ограничение вида
(51)
$y_{l}^{{(k)}} \leqslant \mathop {\min }\limits_{j = 1,...,m} \varphi _{{j,l}}^{{(k)}},\,\,\,\,l = 1,..,{{L}^{{(k)}}}.$Рассмотрим решение задачи (48), (49), (51). В силу монотонного возрастания функции $\Phi (\xi )$ при возрастании значения $y_{l}^{{(k)}}$ значение $\Phi (\tilde {y}_{l}^{{(k)}})$ также будет возрастать. Следовательно, допустимая область задачи (48), (49), (51) будет увеличиваться при росте $y_{l}^{{(k)}}$. Поскольку целевая функция задачи (48), (49), (51) не зависит от $y_{l}^{{(k)}},$ то, при росте допустимой области задачи, значение целевой функции не будет возрастать, а может уменьшиться. Тогда метод решения задачи (48), (49), (51) будет увеличивать значение $y_{l}^{{(k)}}$ до тех пор, пока не выполнится условие (50). Тогда мы получим задачу (48)–(50).
Очевидно, что ограничение (51) эквивалентно ограничению
(52)
$y_{l}^{{(k)}} \leqslant \varphi _{{j,l}}^{{(k)}},\,\,\,\,j = 1,...,m,\,\,\,\,l = 1,..,{{L}^{{(k)}}}.$Подставив (52) в задачу (48)–(50) вместо (50), получим новый вид задачи, дающей оценку решения задачи (18)–(19):
(53)
$\begin{gathered} f_{1}^{{(k)}} = \mathop {\min }\limits_{d,z \in H,y_{l}^{{(k)}}} E_{{{\text{ap}}}}^{{(k)}}[f(d,z,\theta )], \\ \sum\limits_{l = 1}^{{{L}^{{(k)}}}} {A_{l}^{{(k)}}} [\Phi (\tilde {y}_{l}^{{(k)}}) - \Phi (\tilde {\theta }_{i}^{{(k)L,l}})] \geqslant \alpha , \\ y_{l}^{{(k)}} \leqslant \varphi _{{j,l}}^{{(k)}},\,\,\,\,j = 1,...,m,\,\,\,\,l = 1,..,{{L}^{{(k)}}}, \\ \end{gathered} $Задача (53) содержит только непрерывно дифференцируемые функции и является обычной задачей нелинейного программирования.
Рассмотрим теперь случай, когда $\frac{{\partial {{g}_{j}}(d,z,\theta )}}{{\partial {{\theta }_{{{{n}_{\theta }}}}}}} \leqslant 0,$ $j = 1,...,m.$ В этом случае область ${{\Omega }^{{l,(k)}}}$ можно представить в виде
Повторив проведенные выше рассуждения для нового случая, введем области
Тогда, введя переменные $v_{l}^{{(k)}} = \mathop {\max }\limits_{j = 1,...,m} \varphi _{{j,l}}^{{(k)}},$ l = 1, …, L(k),получим вероятностную меру области ${{\tilde {\Omega }}^{{l,(k)}}}$ в виде
Повторив рассуждения, аналогичные рассуждениям при замене ограничения (50) на ограничение (51), а далее, на ограничение (52), получим вид задачи оценки решения задачи (18)–(19):
(54)
$\begin{gathered} f_{1}^{{(k)}} = \mathop {\min }\limits_{d,z \in H,y_{l}^{{(k)}}} E_{{{\text{ap}}}}^{{(k)}}[f(d,z,\theta )], \\ \sum\limits_{l = 1}^{{{L}^{{(k)}}}} {A_{l}^{{(k)}}} [\Phi (\tilde {y}_{l}^{{(k)}}) - \Phi (\tilde {\theta }_{i}^{{(k)L,l}})] \geqslant \alpha , \\ v_{l}^{{(k)}} \geqslant \varphi _{{j,l}}^{{(k)}},\,\,\,\,j = 1,...,m,\,\,\,\,l = 1,..,{{L}^{{(k)}}}. \\ \end{gathered} $Рассмотрим теперь случай, когда $\frac{{\partial {{g}_{j}}(d,z,\theta )}}{{\partial {{\theta }_{{{{n}_{\theta }}}}}}}$ ≥ 0, $j \in {{J}_{1}},$ $\frac{{\partial {{g}_{j}}(d,z,\theta )}}{{\partial {{\theta }_{{{{n}_{\theta }}}}}}} \leqslant 0,$ $j \in {{J}_{2}},$ ${{J}_{1}} \cup {{J}_{2}} = \{ 1,...,m\} ,$ ${{J}_{1}} \cap {{J}_{2}} = \emptyset .$ Тогда будем использовать переменные
Проведя рассуждения, аналогичные выполненным выше, получим вид задачи, дающей оценку решения задачи (18)–(19):
(55)
$\begin{gathered} f_{1}^{{(k)}} = \mathop {\min }\limits_{d,z \in H,y_{l}^{{(k)}}} E_{{{\text{ap}}}}^{{(k)}}[f(d,z,\theta )], \\ \sum\limits_{l = 1}^{{{L}^{{(k)}}}} {A_{l}^{{(k)}}} [\Phi (\tilde {y}_{l}^{{(k)}}) - \Phi (\tilde {v}_{l}^{{(k)}})] \geqslant \alpha , \\ v_{l}^{{(k)}} \geqslant \kappa _{{j,l}}^{{(k)}},\,\,\,\,j \in {{J}_{2}},\,\,\,\,y_{l}^{{(k)}} \leqslant \varphi _{{j,l}}^{{(k)}}, \\ j \in {{J}_{1}},\,\,\,l = 1,..,{{L}^{{(k)}}}. \\ \end{gathered} $Очевидно, что задачу (55) можно использовать, если выполняется условие
Замечание. Следует заметить, $1$что в ходе решения задачи производная $\frac{{\partial {{g}_{j}}(d,z,\theta )}}{{\partial {{\theta }_{{{{n}_{\theta }}}}}}}$ может менять знак. Это влечет недифференцируемость функций $\Phi (\tilde {y}_{l}^{{(k)}}),\Phi (\tilde {v}_{l}^{{(k)}}),$ создает сложности применения методов оптимизации, использующих производные, при решении задач. Однако в работе [46] показано, что при использовании гладких функций в критерии и в левых частях ограничений в точке решения, метод нелинейного программирования может продолжать работу из точки, в которой произошла смена знака производной.
СПОСОБ УТОЧНЕНИЯ АППРОКСИМАЦИЙ
Решение задач (53), (54), (55) проводится для заданного разбиения области неопределенности $T_{q}^{{(k)}}$, $q = 1,...,{{Q}^{{(k)}}},$ вида (23), а также заданных областей ${{\tilde {\Omega }}^{{l,(k)}}},$ $l = 1,...,{{L}^{{(k)}}},$ вида (38). Для уточнения получаемой оценки значения критерия задачи (15)–(16) необходимо уточнять аппроксимации, использованные при построении задач (53), (54), (55). Следовательно, необходимо уточнять аппроксимацию функции $f(d,z,\theta )$ зависимостью $\bar {f}(d,z,\theta ,{{\theta }^{q}}),$ $q = 1,...,{{Q}^{{(k)}}},$ а также аппроксимацию области ${{\Omega }_{O}}$ областями ${{\tilde {\Omega }}^{{l,(k)}}},$ $l = 1,...,{{L}^{{(k)}}}.$ Для этого будем проводить разбиение областей $T_{q}^{{(k)}},$ $q = 1,...,{{Q}^{{(k)}}},$ и $\bar {R}_{l}^{{(k)}},$ $l = 1,...,N_{j}^{{(k)}},$ на подобласти. Можно предложить различные способы разбиения, например на каждой новой итерации разбивать все имеющиеся области пополам. Очевидно, что это должно улучшать используемые аппроксимации. Однако качество аппроксимации в разных областях различно, и, разбивая все области, мы будем подвергать разбиению и те области, качество аппроксимации в которых уже высоко. При этом быстрое увеличение числа областей $\bar {R}_{l}^{{(k)}},$ $l = 1,...,N_{j}^{{(k)}},$ приведет к быстрому росту числа поисковых переменных $y_{l}^{{(k)}}$, $v_{l}^{{(k)}}$ и ограничений задачи, что приведет к росту размерности решаемой задачи. Поэтому будем на каждой новой итерации разбивать только одну из областей $T_{q}^{{(k)}},$ $q = 1,...,{{Q}^{{(k)}}},$ и одну из областей $\bar {R}_{l}^{{(k)}},$ $l = 1,...,N_{j}^{{(k)}}.$
Рассмотрим далее принцип выбора областей для разбиения. Пусть на итерации с номером $k$ мы решили одну из задач (53), (54), (55) и получили решение ${{d}^{{(k)}}},{{z}^{{(k)}}}$.
Для уточнения аппроксимации $\bar {f}(d,z,\theta ,{{\theta }^{q}})$ на каждой новой итерации с номером $k$ будем разбивать некоторую область $T_{s}^{{(k)}}$ с номером $s$ из набора $T_{q}^{{(k)}}$, $q = 1,...,{{Q}^{{(k)}}}.$ Для выбора такой области будем оценивать качество аппроксимации функции $f(d,z,\theta )$ зависимостями $\bar {f}(d,z,\theta ,{{\theta }^{q}})$ в каждой из областей $T_{q}^{{(k)}}$, $q = 1,...,{{Q}^{{(k)}}}$ и будем выбирать область, которой соответствует наихудшее качество аппроксимации:
Разбивать найденную область $T_{s}^{{(k)}}$ будем по центру ребра, соответствующего неопределенному параметру, выбираемому последовательно из набора $\{ {{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{{{{n}_{\theta }}}}}\} .$
Для уточнения аппроксимации области ${{\Omega }_{O}}$ областями ${{\tilde {\Omega }}^{{l,(k)}}},$ $l = 1,...,{{L}^{{(k)}}},$ будем разбивать некоторую область $\bar {R}_{p}^{{(k)}}$ с номером $p$ из набора $\bar {R}_{l}^{{(k)}},$ $l = 1,...,N_{j}^{{(k)}}.$ Для выбора такой области будем оценивать качество аппроксимации функции ${{\varphi }_{j}}(d,z,{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{{{{n}_{\theta }} - 1}}})$ зависимостями ${{\varphi }_{j}}(d,z,\theta _{1}^{{(k),l,{\text{mid}}}},...,$ $\theta _{{{{n}_{\theta }} - 1}}^{{(k),l,{\text{mid}}}})$ ($\theta _{i}^{{(k),l,{\text{mid}}}}$ = = $0.5(\theta _{i}^{{(k),U,l}} - \theta _{i}^{{(k),L,l}})$, $i = 1,...,{{n}_{\theta }} - 1$) в каждой из областей $\bar {R}_{l}^{{(k)}},$ $l = 1,...,N_{j}^{{(k)}}$ и будем выбирать область, которой соответствует наихудшее качество аппроксимации. Номер области $\bar {R}_{p}^{{(k)}}$ с наихудшим качеством аппроксимации будем находить решением задачи
Разбивать найденную область $\bar {R}_{p}^{{(k)}}$ будем по центру ребра, соответствующего неопределенному параметру, выбираемому последовательно из набора $\{ {{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{{{{n}_{\theta }} - 1}}}\} .$
ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ
Для демонстрации эффективности предложенного метода были решены ОЭЗО с вероятностными ограничениями при разных уровнях вероятности и размерах области неопределенности для ХТС, описанной в [45]. Задача решалась в двух постановках: в виде ОЭЗО с отдельными ограничениями (7)–(8) и в виде ОЭЗО с объединенными ограничениями (18)–(19). Задача проектирования оптимальной ХТС в постановке (7)–(8) была решена методом, предложенным в работе [44], назовем его метод 1, а также методом, предложенными в [2], назовем его метод 2. Задача проектирования оптимальной ХТС в постановке (18)–(19) была решена методом, предложенным в данной работе.
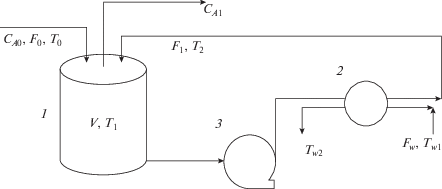
Пример. Рассматривается технологическая система (рис. 1), состоящая из реактора и теплообменника, с рециклом [45].
Математическая модель ХТС включает уравнения материального и теплового балансов реактора и уравнения теплопередачи и теплового баланса теплообменника. В [45] была предложена аппроксимация уравнения теплопередачи, благодаря чему часть переменных состояния выражены как функции остальных параметров. Математическая модель ХТС приняла вид
Значения параметров состояния модели приведены в табл. 1.
Таблица 1.
Параметры математической модели примера
| Параметр | Значение | Параметр | Значение |
|---|---|---|---|
| $\rho {{c}_{p}}$, кДж/(м3 К) | 167.4 | U, кДж/(м2 ч К) | 1635 |
| ${{\rho }_{w}}{{c}_{{pw}}}$, кДж/(м3 К) | 4.190 | ${{T}_{0}}$, К | 333 |
| ${{F}_{0}}$, ${{{{{\text{м}}}^{3}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{3}}} {\text{ч}}}} \right. \kern-0em} {\text{ч}}}$ | 45.36 | ${{T}_{{w1}}}$, К | 300 |
| ${{C}_{{A0}}}$, ${{{\text{кмоль}}} \mathord{\left/ {\vphantom {{{\text{кмоль}}} {{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м}}}^{{\text{3}}}}}}$ | 32.04 | ${E \mathord{\left/ {\vphantom {E R}} \right. \kern-0em} R}$, К | 560 |
| ${{k}_{R}}$, м3/(кмоль ч) | 9.81 | $\Delta H$, кДж/кмоль | –23 260 |
Вектор неопределенных параметров состоит из пяти величин ${{F}_{0}},{{T}_{0}},{{T}_{{w1}}},{{k}_{R}},U$. Область неопределенности задается в виде интервалов изменения неопределенных параметров относительно их номинальных значений: $\{ {{\theta }_{i}}:\theta _{i}^{N}(1 - \gamma {{\sigma }_{i}})$ ≤ ≤ ${{\theta }_{i}} \leqslant \theta _{i}^{N}(1 + \gamma {{\sigma }_{i}})\} ,$ $i = 1,...,5.$ Параметр $\gamma $ задает размер области неопределенности. Номинальные значения $\theta _{i}^{N}$ неопределенных параметров и разброс ${{\sigma }_{i}}$ приведены табл. 2. Предполагается статистическая взаимная независимость неопределенных параметров.
Таблица 2.
Характеристики неопределенных параметров
| $\theta _{i}^{{}}$ | $\theta _{i}^{N}$ | ${{\sigma }_{i}}$ |
|---|---|---|
| ${{F}_{0}}$, м3/ч | 45.36 | 0.1 |
| ${{T}_{0}}$, К | 333 | 0.02 |
| ${{T}_{{w1}}}$, К | 300 | 0.03 |
| ${{k}_{R}}$, м3/(кмоль ч) | 9.81 | 0.1 |
| $U$, кДж/(м2 ч К) | 1635 | 0.1 |
Целевая функция имеет вид суммарных затрат
В задаче четыре поисковые переменные: конструктивные $d$ – объем реактора $V$ и поверхность теплообмена в теплообменнике $A$; управляющие $z$ – температуры ${{T}_{1}}$ и ${{T}_{{w2}}}$. Предъявляемые к системе требования имеют вид ограничений:
(57)
$0,9 - {{({{C}_{{A0}}} - {{C}_{{A1}}})} \mathord{\left/ {\vphantom {{({{C}_{{A0}}} - {{C}_{{A1}}})} {{{C}_{{A0}}}}}} \right. \kern-0em} {{{C}_{{A0}}}}} \leqslant 0,$Ограничения (57)–(61) косвенно зависят от неопределенных параметров и считаются вероятностными.
Результаты решения задачи проектирования оптимальной ХТС без учета неопределенности в исходной информации, т.е. в номинальной точке, приведены в табл. 3 и соответствуют размеру области неопределенности, равному 0.
Таблица 3.
Результаты решения задачи проектирования ХТС в форме ОЭЗО с отдельными вероятностными ограничениями
| γ | α | Метод 2 | Метод 1 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| f2 | V | A | t, с | f1 | V | A | t, с | ||
| 0 | 9374 | 5.48 | 7.88 | 0.01 | – | – | – | – | |
| 1 | 0.5 | 9878 | 5.63 | 7.44 | 10 | 9379 | 5.48 | 7.87 | 2.9 |
| 0.75 | 9957 | 5.79 | 7.48 | 11 | 9608 | 5.64 | 7.70 | 3.38 | |
| 0.95 | 10 132 | 6.04 | 7.62 | 12.59 | 9983 | 5.84 | 7.68 | 3.85 | |
| 1.5 | 0.5 | 9941 | 5.7 | 7.68 | 65 | 9386 | 5.48 | 7.86 | 2.73 |
| 0.75 | 10 019 | 5.95 | 7.98 | 70 | 9750 | 5.72 | 7.66 | 2.32 | |
| 0.95 | 10 155 | 6.35 | 8.07 | 73 | 10113 | 6.03 | 7.64 | 14 | |
| 2.5 | 0.5 | – | – | – | – | 9409 | 5.48 | 7.82 | 2.19 |
| 0.95 | – | – | – | – | 10 824 | 6.42 | 8.61 | 10 | |
Значения критерия $f$ задачи проектирования оптимальной ХТС в постановке (7)–(8), полученные методами 1 и 2 для разных размеров области неопределенности и вероятности ${{\alpha }_{j}}$, ($j = 57,\;58,\;59,\;60,\;61$), даны в табл. 3. При этом уровень вероятности выполнения ограничения (61) задавался равным 0.95 для обеспечения сходимости материально-теплового баланса ХТС.
Значения критерия $f$ оценки критерия оптимальности задачи проектирования оптимальной ХТС в постановке (18)–(19), полученные предложенным данной работе методом для разных размеров области неопределенности и уровня вероятности $\alpha $ выполнения объединенных ограничений, приведены в табл. 4.
Таблица 4.
Результаты решения задачи проектирования ХТС в форме ОЭЗО с объединенными вероятностными ограничениями
| γ | α | f | V | A | t, с |
|---|---|---|---|---|---|
| 1.0 | 0.5 | 9937 | 5.76 | 7.41 | 0.3 |
| 0.75 | 10 038 | 5.85 | 7.54 | 0.35 | |
| 0.95 | 10 168 | 5.97 | 7.84 | 0.3 | |
| 1.5 | 0.5 | 10 014 | 5.81 | 7.49 | 0.3 |
| 0.75 | 10 155 | 6.15 | 7.84 | 0.3 | |
| 0.95 | 10 268 | 6.23 | 8.02 | 0.35 | |
| 2.5 | 0.5 | 10 093 | 5.91 | 7.81 | 0.3 |
| 0.95 | 10 833 | 6.89 | 8.75 | 0.5 |
Анализируя представленные результаты, следует отметить, что решение задачи с объединенными ограничениям во всех случаях дает значение критерия большее, чем при решении задачи с отдельными объединенными ограничениями, что определяется необходимостью выполнения ограничений на одной общей области. Эта особенность подтверждает работоспособность предложенного метода. При этом видно, что значения критерия в табл. 4, полученные для задачи (18)–(19) незначительно превышают значения критерия в табл. 3, представленные для метода 2 решения задачи (7)–(8), но значительно превышают значения, полученные методом 1. Это можно объяснить малой достигнутой точностью аппроксимации ограничений при использовании метода 1, т.е. для метода 1 следовало бы провести большее число итераций.
Отметим, что, в сравнении с методом 1 и методом 2, предлагаемый метод находит решение за очень малое время. Кроме того, метод работоспособен на больших размерах области неопределенности, в отличие от метода 2.
Несомненным достоинством предлагаемого в данной работе метода является гарантирование соблюдения требуемого уровня вероятности выполнения ограничений в любой момент этапа функционирования проектируемой ХТС, а также малое время, затрачиваемое на получение решения.
ЗАКЛЮЧЕНИЕ
В статье предложен подход к решению задач проектирования гибких ХТС, представленных в форме одноэтапных задач оптимизации с объединенными вероятностными ограничениями. Сложность решения таких задач состоит в невозможности вычисления получаемых многомерных интегралов в левых частях ограничений известными методами для многих нелинейных функций, формализующих требования к работе ХТС. В случаях, когда такое вычисление возможно, требуется проводить операции многомерного интегрирования на каждой итерации метода при прямом решении задач.
Предлагаемый в работе метод предполагает решение последовательности задач, дающих оценку критерия искомой задачи. Для построения таких задач предлагается использование аппроксимаций подынтегральных функций, что позволяет освободиться от многомерного интегрирования в критерии задачи и приводит объединенные вероятностные ограничения к набору детерминированных.
К достоинствам предлагаемого метода можно отнести высокую скорость получения результата, а также итоговые форму, размер и местоположение области выполнения ограничений в области неопределенности. Это позволит более полно оценить работоспособность спроектированной ХТС в разные моменты этапа ее функционирования.
ОБОЗНАЧЕНИЯ
| Обозначения теоретической части | |
| $a$ | коэффициент в аппроксимации подынтегральной функции |
| $d$ | конструктивные поисковые переменные |
| $E$ | математическое ожидание |
| $f$ | функция оценки эффективности работы ХТС |
| $g$ | функция ограничения |
| $H$ | допустимая область изменения поисковых переменных |
| h | ограничения, не зависящие от неопределенных параметров |
| I | одномерный интеграл |
| $k$ | номер итерации |
| $L$ | количество подобластей в области Ω |
| $m$ | количество вероятностных ограничений |
| $N$ | количество подобластей в области Ω |
| $n$ | размерность вектора |
| $\Pr $ | вероятность |
| $p$ | число ограничений, не зависящих от неопределенных параметров |
| Q | количество подобластей в области T |
| $R$ | аппроксимация области Ω |
| $S$ | диапазон изменения неопределенного параметра |
| $T$ | область неопределенности |
| $z$ | управляющие поисковые переменные |
| $\alpha $ | уровень вероятности |
| $\theta $ | неопределенные параметры |
| $\xi $ | случайная величина |
| $\rho $ | плотность вероятности |
| $\sigma $ | среднеквадратичное отклонение |
| $\Phi $ | функция стандартного нормального распределения |
| $\phi $ | аппроксимируемая гиперповерхность, полученная для вероятностного ограничения |
| Ω | область выполнения ограничений |
| $\tilde {\Omega }$ | аппроксимация области Ω |
| Индексы теоретической части | |
| ${\text{ap}}$ | аппроксимация |
| $i$ | индекс |
| $j$ | номер ограничения |
| $l$ | номер подобласти |
| $L$ | левая граница области |
| $O$ | одноэтапная задача оптимизации |
| $q$ | номер подобласти |
| r | номер подобласти |
| $s$ | номер подобласти |
| $T$ | двухэтапная задача оптимизации |
| $U$ | правая граница области |
| Обозначения вычислительного эксперимента | |
| $A$ | поверхность теплообмена в теплообменнике, м2 |
| $C$ | концентрация реагента, кмоль/м3 |
| $с$ | теплоемкость, ${{{\text{кДж}}} \mathord{\left/ {\vphantom {{{\text{кДж}}} {({\text{кг}}\,{\text{K)}}}}} \right. \kern-0em} {({\text{кг}}\,{\text{K)}}}}$ |
| ${\text{conv}}$ | конверсия реагента A |
| $E$ | энергия активации, Дж/кмоль |
| $\Delta H$ | теплота реакции, кДж/кмоль |
| $F$ | расход потока, м3/ч |
| ${{k}_{R}}$ | предэкспоненциальный множитель уравнения Аррениуса, ${{{{{\text{м}}}^{3}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{3}}} {({\text{кмоль}}\,{\text{ч)}}}}} \right. \kern-0em} {({\text{кмоль}}\,{\text{ч)}}}}$ |
| $Q$ | количество тепла, кДж |
| $R$ | универсальная газовая постоянная, Дж/кмоль К |
| $T$ | температура, К |
| $t$ | время решения задачи, с |
| $U$ | полный коэффициент теплопередачи, ${\text{кДж/(}}{{{\text{м}}}^{2}}\,{\text{ч}}\,{\text{K)}}$ |
| $V$ | объем реактора, м3 |
| $\gamma $ | параметр, определяющий размер области неопределенности |
| $\rho $ | плотность, кг/м3 |
| Индексы вычислительного эксперимента | |
| 1 | реактор |
| 2 | теплообменник |
| N | номинальное значение |
| $p$ | рецикловый поток |
| $w$ | вода |
Список литературы
Henrion R., Moller A. Optimization of a continuous distillation process under random inflow rate // Comput. Math. Appl. 2003. V. 45. P. 247.
Ostrovsky G.M., Lapteva T.V., Ziyatdinov N.N., Silvestrova A.S. Design of chemical engineering systems with chance constraints // Theor. Found. Chem. Eng. 2017. V. 51. № 6. P. 961. [Островский Г.М., Лаптева Т.В., Зиятдинов Н.Н., Сильвестрова А.С. Проектирование оптимальных химико-технологических систем при учете вероятностных ограничений // Теор. осн. хим. технол. 2017. Т. 51. № 6. С. 618.]
Goel V., Grossmann I.E. A Class of stochastic programs with decision dependent uncertainty // Math. Prog. 2006. V. 108. № 2–3. P. 335.
Ben-Tal A., Ghaoui L.E., Nemirovski A. Robust Optimization. Princeton Series in Applied Mathematics. Princeton, N.J.: Princeton Univ. Press, 2009.
Pflug G.C., Pichler A. Multistage Stochastic Optimization. New York: Springer, 2014.
Calfa B.A., Grossmann I.E., Agarwal A., Bury S.J., Wassick J.M. Data-Driven Individual and Joint Chance-Constrained Optimization via Kernel Smoothing // Comput. Chem. Eng. 2015. V. 78. P. 51.
Ostrovsky G.M., Ziyatdinov N.N., Lapteva T.V., Pervukhin I.D. Flexibility analysis of chemical technology systems // Theor. Found. Chem. Eng. 2007. V. 41. № 3. P. 235. [Островский Г.М., Зиятдинов Н.Н., Лаптева Т.В., Первухин И.Д. Оценка гибкости химико-технологических систем // Теор. осн. хим. технол. 2007. Т. 41. № 3. С. 249.]
Finger M., Le Bras R., Gomes C.P., Selman B. Solutions for Hard and Soft Constraints Using Optimized Probabilistic Satisfiability // Theory and Applications of Satisfiability Testing – SAT 2013. Lecture Notes in Computer Science / Eds. Järvisalo M., Van Gelder A. Berlin: Springer-Verlag, 2013.
Powell W.B. Approximate Dynamic Programming: Solving the Curses of Dimensionality. Wiley Series in Probability and Statistics. Hoboken, N.J.: Wiley, 2011.
Grossmann I.E., Apap R.M., Calfa B.A., García-Herreros P., Zhang Q. Recent advances in mathematical programming techniques for the optimization of process systems under uncertainty // Comput. Chem. Eng. 2016. V. 91. P. 3.
Schwarm A.T., Nikolaou M. Chance-constrained model predictive control // AIChE J. 1999. V. 45. № 8. P. 1743.
Charnes A., Cooper W.W., Symonds G.H. Cost horizons and certainty equivalents: an approach to stochastic programming of heating oil // Manage. Sci. 1958. V. 4. P. 235.
Prékopa A. Stochastic Programming. New York: Springer, 1995.
Zhuangzhi L., Zukui L. Optimal robust optimization approximation for chance constrained optimization problem // Comput. Chem. Eng. 2015. V. 74. P. 89.
Jagannathan R. Chance-constrained programming with joint constraints // Oper. Res. 1974. V. 22. № 2. P. 358.
Ackooij van W., Sagastizábal C. Constrained bundle methods for upper inexact oracles with application to joint chance constrained energy problems // SIAM J. Optim. 2014. V. 2. № 24. P. 733.
Javier O., Xavier M., Mohamed G., Yongdong L. Optimal Design and Placement of Piezoelectric Actuators using Genetic Algorithm: Application to Switched Reluctance Machine Noise Reduction. INTECH, 2011.
Bernardo F.P. Performance of cubature formulae in probabilistic model analysis and optimization // J. Comput. Appl. Math. 2015. V. 280. P. 110.
Klöppel M., Geletu A., Hoffmann A., Li P. Using sparse-grid methods to improve computation efficiency in solving dynamic nonlinear chance-constrained optimization problems // Ind. Eng. Chem. Res. 2011. V. 50. P. 5693.
Acevedo J., Pistikopoulos E.N. Stochastic optimization based algorithms for process synthesis under uncertainty // Comput. Chem. Eng. 1998. V. 22. P. 647.
Кнопов П.С., Норкин В.И. Об условиях сходимости метода эмпирических средних в стохастическом программировании // Киберн. сист. анал. 2018. Т. 54. № 1. С. 51.
Calafiore G.C., Campi M.C. The scenario approach to robust control design // IEEE Trans. Autom. Control. 2006. V. 51. P. 742.
Nemirovski A., Shapiro A. Scenario approximations of chance constraints // Probabilistic and Randomized Methods for Design under Uncertainty / Eds. Calafiore G., Dabbene F. London: Springer-Verlag, 2006. P. 3.
Robert C.P., Casella G. Monte Carlo Integration // Introducing Monte Carlo Methods with R. Springer Series in Use R! New York: Springer-Verlag, 2010. Ch. 3. P. 61.
Heitsch H., Roomisch W. A note on scenario reduction for two-stage stochastic programs // Oper. Res. Lett. 2007. V. 35. № 6. P. 731.
Pennanen T., Koivu M. Epi-convergent discretizations of stochastic programs via integration quadratures // Numer. Math. 2005. V. 100. № 1. P. 141.
Mehrotra S., Papp D. Generating moment matching scenarios using optimization techniques // SIAM J. Optim. 2013. V. 23. № 2. P. 963.
Dempster M.A., Medova E.A., Yong Y.S. Comparison of sampling methods for dynamic stochastic programming // Stochastic Optimization Methods in Finance and Energy. New York: Springer, 2011.
Löhndorf N. An empirical analysis of scenario generation methods for stochastic optimization // Eur. J. Oper. Res. 2016. V. 255. P. 121.
Ivanov S.V., Kibzun A.I. Sample average approximation in the two-stage stochastic linear programming problem with quantile criterion // Proc. Steklov Inst. Math. 2018. V. 303. № 1. P. 115.
Bidhandi H.M., Patrick J. Accelerated sample average approximation method for two-stage stochastic programming with binary first-stage variables // Appl. Math. Modell. 2017. V. 41. P. 582.
Xu H., Caramanis C., Mannor S. Optimization under probabilistic envelope constraints // Oper. Res. 2012. V. 60. № 3. P. 682.
Bertsimas D., Sim M. The price of robustness // Oper. Res. 2004. V. 52. P. 35.
Hong L.J., Yang Y., Zhang L. Sequential convex approximations to joint chance con-strained programs: a Monte Carlo approach // Oper. Res. 2011. V. 59. P. 617.
Bertsimas D., Gupta V., Kallus N. Data-driven robust optimization; https://arxiv.org/abs/1401.0212
Chen W., Sim M., Sun J., Teo C.P. From CVaR to uncertainty set: Implications in joint chance-constrained optimization // Oper. Res. 2010. V. 58. № 2. P. 470.
Li Z., Ding R., Floudas C.A. A Comparative Theoretical and Computational Study on Robust Counterpart Optimization: I. Robust Linear and Robust Mixed Integer Linear Optimization // Ind. Eng. Chem. Res. 2011. V. 50. P. 10567.
Li Z., Floudas C.A. A Comparative Theoretical and Computational Study on Robust Counterpart Optimization: III. Improving the Quality of Robust Solutions // Ind. Eng. Chem. Res. 2014. V. 53. P. 13112.
Hu Z., Hong L.J., So A.M.-C. Ambiguous probabilistic programs; http://www.optimization-online.org/ DB_FILE/ 2013/09/ 4039.pdf
Ostrovsky G.M., Ziyatdinov N.N., Lapteva T.V., Zaitsev I.V. Two-stage optimization problem with chance constraints // Chem. Eng. Sci. 2011. V. 66. P. 3815.
Ostrovsky G.M., Ziyatdinov N.N., Lapteva T.V. Optimal design of chemical processes with chance constraints // Comput. Chem. Eng. 2013. V. 59. P. 74.
Baker K., Toomey B. Efficient relaxations for joint chance constrained AC optimal power flow // Electr. Power Syst. Res. 2017. № 148. P. 230.
Ostrovsky G.M., Ziyatdinov N.N., Lapteva T.V. One-Stage Optimization Problem with Chance Constraints // Chem. Eng. Sci. 2010. V. 65. P. 2373.
Ostrovsky G.M., Ziyatdinov N.N., Lapteva T.V. Optimization problem with normally distributed uncertain parameters // AIChE J. 2013. V. 59. № 7. C. 2471.
Ostrovsky G.M., Lapteva T.V., Ziyatdinov N.N. Optimal design of chemical processes under uncertainty // Theor. Found. Chem. Eng. 2014. V. 48. № 5. P. 583. [Островский Г.М., Лаптева Т.В., Зиятдинов Н.Н. Проектирование оптимальных химико-технологических систем в условиях неопределенности // Теор. осн. хим. технол. 2014. Т. 48. № 5. С. 527. ]
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. М.: Мир, 1985.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии