1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 54, № 1, 2020

Теоретические основы химической технологии, 2020, T. 54, № 1, стр. 30-37

Анализ теплофизических и химико-технологических свойств отходов горно-обогатительных комбинатов

В. П. Мешалкин a, С. В. Панченко b, В. И. Бобков b, *, М. И. Дли b

a Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия

b Национальный исследовательский университет “МЭИ” в г. Смоленске,
Смоленск, Россия

* E-mail: vovabobkoff@mail.ru

Поступила в редакцию 06.09.2019
После доработки 17.09.2019
Принята к публикации 28.09.2019

Полный текст (PDF)

Аннотация

Представлены результаты системного анализа объемов, физико-химических, гранулометрических, литологических и теплофизических характеристик отходов апатит-нефелиновых руд, хранящихся в отвалах (хвостохранилищах) горно-обогатительных комбинатов, для оценки экономического потенциала их использования в системах комплексной энергоресурсоэффективной экологически безопасной переработки, включающих обжиговые машины конвейерного типа и рудно-термические печи. Полученные результаты позволяют сформулировать основные технические, технологические, экономические и экологические требования к сложным химико-энерготехнологическим системам переработки отходов апатит-нефелиновых руд на горно-обогатительных комбинатах, а также определять степень вариабельности характеристик партий отходов из различных отвалов.

Ключевые слова: химико-энерготехнологическая система, техногенное сырье, переработка отходов, тепломассообмен, теплопроводность, теплоемкость, температуропроводность, моделирование

ВВЕДЕНИЕ

Системный анализ теплофизических и химико-технологических свойств фосфоросодержащих техногенных отходов, скопившихся в хвостохранилищах горно-обогатительных и металлургических предприятий, главным образом основывается на экспериментальных исследованиях [1]. Полученные методами монотонного нагрева образцов данные обрабатываются на базе решения обратной коэффициентной задачи теплопроводности для совокупного определения теплофизических и химико-технологических свойств отходов, таких как теплоемкость, теплопроводность и температуропроводность, и кинетических констант химико-технологических реакций с использованием специально разработанного программного обеспечения [2, 3]. Системное представление свойств фосфоросодержащих отходов базируется на выявлении главных структурных составляющих [4, 5]. Зависимость их свойств от температуры, с учетом реагирующих включений и полупродуктов, представлена в виде многочленов.

Все это дало возможность сформировать процедуры расчета теплофизических характеристик (ТФХ) фосфоросодержащих отходов переработки апатит-нефелиновых руд, различного состава в самом широком диапазоне температур обработки, с учетом протекания неизотермических химико-технологических реакций [6, 7].

Системный анализ результатов показывает, что начальная теплопроводность и ее изменение при нагреве сильно варьируется для отходов различных месторождений апатит-нефелиновых руд и пород [8, 9]. Термически активируемые химико-энерготехнологические процессы сильно влияют на зависимость ТФХ от температуры [10, 11].

ЭКСПЕРИМЕНТАЛЬНЫЙ МЕТОД ИССЛЕДОВАНИЯ АКУСТИЧЕСКИХ КОЛЕБАНИЙ

Наличие потока теплоты в фосфоросодержащих отходах переработки апатит-нефелиновых руд обеспечивает неравновесное перераспределение фононов и отличие от равновесного состояния при заданном градиенте температуры определяет теплопроводность. Так как фононы характеризуют энергию колебаний узлов решетки и являются квазичастицами, они определяют характеристики среды. Таким образом, ТФХ твердых тел определяются параметрами фононов. Фононы в твердых телах ассоциируются с “фононным газом”, причем температуропроводность и теплопроводность описываются уравнениями [12, 13]

(1)
$a = \frac{1}{3}{{W}_{f}}{{l}_{f}} = \frac{1}{3}W_{f}^{2}{{{\tau }}_{f}},$
(2)
$\lambda = \frac{1}{3}{{c}_{v}}{{W}_{f}}{{l}_{f}} = \frac{1}{3}{{c}_{v}}W_{f}^{2}{{{\tau }}_{f}}.$
Здесь ${{c}_{v}}$ – объемная теплоемкость тела, ${{W}_{f}}$ – скорость упругой волны, ${{l}_{f}}$ – длина свободного пробега фононов, ${{{\tau }}_{f}}$ – время релаксации фононов.

Такие зависимости обоснованно применимы для аморфных, полукристаллических и кристаллических твердых тел. Это описывается квантово-механической теорией взаимодействия фононов. Длина свободного пробега фононов ${{l}_{f}}$ зависит от рассеяния на границах кристаллов, дефектов решетки, состояния аморфности структур, а также от рассеяния на других фононах. Причем последний механизм является основным при высоких температурах. Рассеяние фононов на фононах приводит к зависимости, где ${{l}_{f}} \propto {{T}^{{ - 1}}}$ [14, 15].

Согласно экспериментальным исследованиям акустических колебаний, для некоторых составляющих отходов переработки апатит-нефелиновых руд получены значения ${{l}_{f}}$ и ${{{\tau }}_{f}}$ (табл. 1).

Таблица 1.  

Некоторые значения длины пробега и времени релаксации фононов составляющих отходов переработки апатит-нефелиновых руд

Порода ${{l}_{f}} \times {{10}^{9}}$, м ${{{\tau }}_{f}} \times {{10}^{{13}}}$, c
Кристаллический кварц 9.6 (± 0.3) 1.7 (± 0.06)
Породы кристаллического фундамента 7.7 (± 0.3) 1.1 (± 0.05)
Песчаник 5.7 (± 0.3) 2.9 (± 0.2)
Карбонатные отложения 5.0 (± 0.3) 1.5 (± 0.1)
Глины 3.9 (± 0.35) 2.2 (± 0.25)
Аморфный кварц 4.2 (± 0.15) 0.75 (± 0.03)

В зависимости от структуры и размеров кристаллических зерен в породах меняется длина пробега фононов и время релаксации. Таким образом, ТФХ также зависят от кристаллических образований и структуры [13]. Так как длина пробега фононов является одним из основных параметров, определяющих ТФХ материала, то, соответственно, с возрастанием длины пробега увеличивается теплопроводность и температуропроводность отходов. Так, например, для глинистых образований ${\lambda } \approx 1.01$ Вт/(м К) и $а \approx 5 \times {{10}^{{ - 7}}}$ м2/с, а для кристаллических образований ${\lambda } \approx 3.5$ Вт/(м К) и $а \approx 14 \times {{10}^{{ - 7}}}$ м2/с.

Теплоемкость твердых тел кристаллической структуры хорошо описывается формулой Дебая

(3)
${{c}_{v}} = 3RD({T \mathord{\left/ {\vphantom {T {{{{\theta }}_{{\text{D}}}}}}} \right. \kern-0em} {{{{\theta }}_{{\text{D}}}}}}),$
где ${{{\theta }}_{{\text{D}}}}$ – температура Дебая, R – универсальная газовая постоянная, D(x) – функция Дебая [16].

Для основных составляющих отходов горно-обогатительных комбинатов апатит-нефелиновых руд для температур, превышающих температуру Дебая $\left( {Т \geqslant 500{\kern 1pt} - {\kern 1pt} 1000\,\,{\text{K}}} \right)$, скорость звука и теплоемкость меняются несущественно, и, значит, теплопроводность обратно пропорциональна температуре $\lambda = {1 \mathord{\left/ {\vphantom {1 Т}} \right. \kern-0em} Т}.$

Таким образом, теплопроводность кристаллических тел при высоких и нормальных температурах обратно пропорциональна температуре, что связано с соответствующим уменьшением длины пробега фононов, и, соответственно, температуропроводность аморфных тел слабо зависит от температуры [14]. ТФХ поликристаллических тел, в зависимости от размеров кристаллических зерен, имеют промежуточные значения между кристаллическими и аморфными веществами.

С повышением температуры теплопроводность и температуропроводность для кристаллов и поликристаллических твердых тел приближается к значению аморфных тел и при температуре плавления их разность будет наименьшей.

В табл. 2 представлены данные по значениям коэффициентов теплопроводности техногенного сырья из отвалов горно-обогатительных комбинатов апатит-нефелиновых руд различной структуры. Результаты отражают основные тенденции, характерные для подобных материалов в зависимости от минерального состава и структуры составляющих [17, 18].

Таблица 2.  

Зависимость коэффициента теплопроводности отходов переработки апатит-нефелиновых руд от их структуры

Структура λ, Bт/(м К) при T = 293 К Варьирование λ в интервале температур 273–773 К, %
Чистые монокристаллы ≥ 10 –60
Зернистые 2.7–3.5 –20…–15
Офитовая 2.5–3.0 –15…–5
Микрозернистая 2.1–2.6 –5–5
Микрокристаллическая 1.6–2.1   5–15
Аморфная 1.5–1.9  15–20

В табл. 3 представлены данные по фосфоросодержащим отходам обогащения апатит-нефелиновых руд. Здесь в зависимости от содержания P2O5 меняется тип этого техногенного сырья, его минеральный состав и, соответственно, теплопроводность и плотность. Это показывает наличие закономерности в зависимости ТФХ от минерального состава [19, 20]. Поэтому отыскание обобщенной зависимости от минерального состава и структуры составляющих является весьма актуальной проблемой дальнейших исследований [21, 22]. Конечно, базой построения обобщенных зависимостей от химического состава и температуры являются экспериментальные исследования [23–25].

Таблица 3.  

Плотность и теплопроводность фосфоритов различного минералогического состава

Порода Содержание Р2О5, % ρ×10-3, кг/м3 λ, Вт/(м К)
Фосфатизированные (кремни) 0–10 2.4–2.7 7.0–1.0
Доломиты 10–15 2.75–2.85 4.0–2.5
Фосфориты:
карбонатные 18–25 2.75–2.92 3.0–2.0
высококачественные 25–30 2.9–3.01 2.5–1.8
От высококачественных до субмономинеральных 30–35 2.96–3.10 2.2–1.6
Сланцевые породы – 3.0 - 3.2 1.7

СТРУКТУРНЫЙ АНАЛИЗ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЙ

Так как минералогический состав фосфоросодержащего техногенного сырья из отвалов горно-обогатительных комбинатов в основном представлен фторкарбонатапатитом Сa10P5СО24F2, доломитом CaMg(CO3)2, кальцитом CaCO3, кварцитом и халцедоном SiO2, а также прочими примесями, количество составляющих, которые влияют на ТФХ, следует считать конечным, что дает право обозначить наиболее значимые факторы. Зернистая структура этих составляющих в цементирующем носителе позволяет использовать для описания теплопроводности структурные модели. Основная компонента, определяющая структуру модели расчета коэффициента теплопроводности фосфоросодержащих отходов, фосфат, представленный оолитами окатанной формы размером 0.05–0.5 мм.

Типы структур в фосфоросодержащем техногенном сырье:

• матричная с изолированными включениями фосфата;

• переходная от матричной к взаимопроникающей;

• взаимопроникающая инвариантная;

• матричная с изолированными включениями карбонатов и кремнезема.

Для первой структуры характерны фосфатизированные кремни и доломиты с небольшим содержанием (5–12%) фосфатного вещества, бедные фосфоритные, кремнисто-карбонатные, перлитоморфно-кремнистые, забалансовые и метаморфизированные руды с содержанием P2О5 около 20%, что соответствует 50% фосфатного вещества. Структурный анализ образцов показывает, что увеличение объемной доли фосфата до 50% не приводит к заметному точечному контактированию оолитов между собой. Основная масса оолитов имеет простое строение с размерами 0.04–0.3 мм. Если цементирующий материал представлен карбонатной массой от мелкозернистой до криптокристаллической структуры, то теплопроводность таких фосфоросодержащих отходов можно рассчитать по модели трехкомпонентной смеси с замкнутыми включениями или переходом к бинарным системам по самосогласованному методу.

Дальнейшее увеличение объемной доли оолитов в фосфоросодержащих отходах до 60% приводит к точечному контактированию включений с последующим смыканием изолированных объемов. При этом структура подобна структуре с взаимопроникающими компонентами и ее можно отнести к переходной. К такому типу структур также относятся карбонатно-кремнистые и частично высококачественные фосфориты. Поскольку структура с взаимопроникающими компонентами по отношению к свойствам компонент инвариантна, для ориентировочных расчетов допускается иметь объемную долю фосфата 70%, т.е. P2O5 – 29%. Среднее арифметическое между адиабатным и изотермическим дроблением дает возможность определить эффективную теплопроводность на основе комбинированного подхода для любых соотношений теплопроводностей компонент.

В фосфоритах с большой концентрацией фосфата наблюдается следующее:

• появляется фосфат-цемент и последующее слияние оолитов фосфатного вещества;

• нарушается непрерывность доминирующей компоненты (цемента);

• происходит переход структуры от взаимопроникающих компонент к изолированным включениям и смена доминирующей компоненты.

К этому типу структуры относятся почти все высококачественные фосфориты.

Для оценки коэффициента теплопроводности отходов переработки апатит-нефелиновых месторождений следует использовать модель трехкомпонентной смеси, где цементом служит фосфатное вещество.

Использование моделей для расчета теплопроводности в широком диапазоне температур переработки отходов возможно лишь при известных значениях коэффициентов теплопроводности их составляющих. К ним необходимо отнести фосфатизированные кремни, кремнитные, высококачественные и мономинеральные фосфориты. Моделирование теплопроводности высококарбонатных фосфоритов требует дальнейших исследований из-за изменения структуры реагирующего материала и соотношения компонент в результате реакций диссоциации доломита при нагревании.

Следует учитывать перестройку структуры во взаимопроникающую с изолированными включениями, с появлением контактов между вкраплениями и последующим ростом поперечного сечения в диапазоне изменения объемной доли вкраплений 0.125–0.5, что характерно для хаотических систем.

Так, например, теплопроводность в бинарной системе, для случая когда один компонент находится в окружении другого компонента, с изолированными включениями описывается уравнением

(4)
$\begin{gathered} {{{{\bar {\lambda }}}}_{i}} = {{{\lambda }}_{i}}\left[ {1 - {{v_{i}^{ * }} \mathord{\left/ {\vphantom {{v_{i}^{ * }} {\left( {{{{(1 - {{{{{\lambda }}_{i}}} \mathord{\left/ {\vphantom {{{{{\lambda }}_{i}}} {{\lambda }_{i}^{ * }}}} \right. \kern-0em} {{\lambda }_{i}^{ * }}})}}^{{ - 1}}}} \right.}}} \right. \kern-0em} {\left( {{{{(1 - {{{{{\lambda }}_{i}}} \mathord{\left/ {\vphantom {{{{{\lambda }}_{i}}} {{\lambda }_{i}^{ * }}}} \right. \kern-0em} {{\lambda }_{i}^{ * }}})}}^{{ - 1}}}} \right.}}} \right. - \\ \left. {\left. { - \,\,(1 + v_{i}^{ * })(1 - \sqrt[3]{{v_{i}^{ * }}}){{{(1 - \sqrt[3]{{v_{i}^{ * }}})}}^{{ - 1}}}} \right)} \right], \\ \end{gathered} $
где ${{{\bar {\lambda }}}_{i}}$ – теплопроводность двухкомпонентной системы с учетом принятой структуры; ${{{\lambda }}_{i}}$ – теплопроводность i-го компонента с концентрацией vi; ${\lambda }_{i}^{ * }$ – теплопроводность второго компонента-окружения c концентрацией $v_{i}^{ * } = 1 - {{v}_{i}}.$

Для взаимопроникающих компонент при комбинированном дроблении зависимость более сложная:

(5)
$\begin{gathered} {{{{\bar {\lambda }}}}_{i}} = {{{\lambda }}_{i}}\left[ {\frac{{{{c}^{2}} + ({{{{{\lambda }}_{i}}} \mathord{\left/ {\vphantom {{{{{\lambda }}_{i}}} {{\lambda }_{i}^{ * }}}} \right. \kern-0em} {{\lambda }_{i}^{ * }}})c\left( {1 - c} \right)}}{{({{{{{\lambda }}_{i}}} \mathord{\left/ {\vphantom {{{{{\lambda }}_{i}}} {{\lambda }_{i}^{ * }}}} \right. \kern-0em} {{\lambda }_{i}^{ * }}})c\left( {1 - c} \right) + 1 - c + {{c}^{2}}}}} \right. + \\ \left. { + \,\,({{{{{\lambda }}_{i}}} \mathord{\left/ {\vphantom {{{{{\lambda }}_{i}}} {{\lambda }_{i}^{ * }}}} \right. \kern-0em} {{\lambda }_{i}^{ * }}})\frac{{c\left( {1 - c} \right) + ({{{{{\lambda }}_{i}}} \mathord{\left/ {\vphantom {{{{{\lambda }}_{i}}} {{\lambda }_{i}^{ * }}}} \right. \kern-0em} {{\lambda }_{i}^{ * }}}){{{\left( {1 - c} \right)}}^{2}}}}{{c\left( {1 - c} \right) + ({{{{{\lambda }}_{i}}} \mathord{\left/ {\vphantom {{{{{\lambda }}_{i}}} {{\lambda }_{i}^{ * }}}} \right. \kern-0em} {{\lambda }_{i}^{ * }}})(1 - c + {{c}^{2}})}}} \right], \\ \end{gathered} $
где c – положительный корень кубического уравнения $2{{с}^{3}} - 3{{с}^{2}} + 1 = v_{i}^{ * },$ с = 0.5 + Аcos(φ/3), 270° < < φ < 360°; при $0 \leqslant v_{i}^{ * } \leqslant 0.5,$ A = –1 и φ = arccos(1 – ‒ $2v_{i}^{ * }$); при $0.5 < v_{i}^{ * } \leqslant 1,$ A = 1 и φ = arccos($2v_{i}^{ * }$ – 1).

В свою очередь для реагирующих включений, представляющих собой крупно- или среднекристаллические зерна карбоната размером 0.001–0.2 мм, объемная доля исходного непрореагировавшего материала (доломита) при нагреве будет изменяться с появлением продуктов реакции смеси CaO и MgO или ортосиликатов кальция и магния в кремнисто-карбонатных рудах.

Объемная доля непрореагировавшего карбоната ${{v}_{{c0}}}$ может быть выражена через степень реагирования η: ${{v}_{{c0}}} = {{\left[ {1 + \left( {{{\eta } \mathord{\left/ {\vphantom {{\eta } {\left( {1 - {\eta }} \right)}}} \right. \kern-0em} {\left( {1 - {\eta }} \right)}}} \right)\left( {{{{{{\rho }}_{0}}} \mathord{\left/ {\vphantom {{{{{\rho }}_{0}}} {{{{\rho }}_{r}}}}} \right. \kern-0em} {{{{\rho }}_{r}}}}} \right)} \right]}^{{ - 1}}},$ где ${{{\rho }}_{0}}$, ${{{\rho }}_{r}}$ – плотности исходного и обожженного материала соответственно. При этом реагирующий материал будет представлять собой матричную структуру изолированных включений непрореагировавшего материала в цементе, состоящем из продуктов реакции. Теплопроводность такого типа системы следует определять с использованием метода расчета многокомпонентной системы путем последовательного сведения к двухкомпонентной, таким образом можно рассчитать теплопроводность композиционного материала с реагирующими включениями. Следовательно, для описания теплопроводности отходов различных апатит-нефелиновых месторождений необходимо иметь зависимость теплопроводности компонент, составляющих композит, химический или минералогический состав и результаты по реакции диссоциации карбонатов.

Теплопроводность отдельных составляющих в структуре отходов апатит-нефелиновых месторождений получена по экспериментальным данным для широкого диапазона минералогического состава отходов методом нелинейных наименьших квадратов. Вычислены коэффициенты теплопроводности вещества, кремнезема, непрореагировавшего и обожженного карбоната. Зависимость теплопроводности компонент от температуры хорошо описывается многочленами второй степени в диапазоне 400–1300 К ${\lambda } = \sum {{{b}_{i}}{{T}^{{i - 1}}}} .$

Из-за сложности экспериментального определения теплопроводности в зоне химического реагирования для обработки использовались данные экстраполяции для образцов с непрореагировавшими карбонатными включениями.

Удельную теплоемкость композиционного материала ${{с}_{р}}$ можно определить по аддитивной модели ${{с}_{р}} = \sum {{{m}_{i}}} {{с}_{р}}_{i},$ где ${{m}_{i}}$ – массовая доля компонента; ${{с}_{р}}_{i}$ – удельные теплоемкости компонент.

Коэффициенты для описания теплоемкости компонент получены путем обработки экспериментальных значений различных типов фосфоросодержащих отходов апатит-нефелиновых руд с различным компонентным составом и с учетом модификационных превращений α- в β-кварц (табл. 4).

Таблица 4.  

Коэффициенты многочленов для описания теплопроводности, Вт/(м К), и удельной теплоемкости, кДж/(кг К), компонентов, определяющих ТФХ фосфоросодержащих отходов апатит-нефелиновых месторождений

Компоненты Теплопроводность Удельная теплоемкость
b1 b2 × 102 b3 × 105 s1 s2 × 102 s3 × 106
Фосфатное вещество 2.82 –0.3 0.14 0.788 0.061 –0.25
Кремнистая составляющая 12.6 –1.75 0.95 0.394 0.150 –0.41
4.150 –0.572 2.72
Карбонаты до реакции 7.85 –1.08 0.49 0.410 –0.155 –0.4
Обожженный карбонат 1.52 –0.13 0.049 1.943 –1.580 0.98

1 До температуры модификационного превращения α- в β-кварц (T = 850 К). 2 Для температур выше 850 К.

Многочлен имеет вид ${{с}_{р}} = \sum {{{s}_{i}}} {{T}^{{i - 1}}}$.

Полученные значения теплоемкости всех составляющих практически совпадают с известными зависимостями в пределах 14%. Что касается теплоемкости доломита после термического разложения, то ее значения значительно отличаются от теплоемкости CaO и MgO, поскольку эти окислы вступают в твердофазные реакции с кварцем SiO2, образуя силикатные расплавы.

Расчет теплоемкости фосфоритов в зоне температур реакций декарбонизации можно проводить полагая, что доля прореагировавшего компонента пропорциональна степени реагирования реакции диссоциации карбонатов:

(6)
${\rho }{{c}_{p}}\left( {T,{\eta }} \right) = {\rho }{{c}_{{p0}}}(T) + \left( {{\rho }{{c}_{{p0}}}(T) - {\rho }{{c}_{{pr}}}(T)} \right)\left( {1 - {\eta }} \right),$
где ${\rho }{{c}_{{p0}}}$, ${\rho }{{c}_{{pr}}}$ – объемные теплоемкости исходного и обожженного материала.

Теплоемкость исходного материала в зоне реагирования определялась экстраполяцией экспериментальных значений.

Эффективную теплоемкость ${\rho }{{c}_{{pe}}}$ в зоне термического разложения MgCO3 и CaCO3 можно вычислить из теплового баланса, где учтено влияние реагирующих компонент:

(7)
${\rho }{{c}_{{pe}}}\left( {{{dT} \mathord{\left/ {\vphantom {{dT} {d{\tau }}}} \right. \kern-0em} {d{\tau }}}} \right) = {\rho }{{c}_{p}}\left( {{{dT} \mathord{\left/ {\vphantom {{dT} {d{\tau }}}} \right. \kern-0em} {d{\tau }}}} \right) + \sum\limits_{i = 1}^2 {{{Q}_{i}}} {{{\rho }}_{i}}\left( {{{d{{{\eta }}_{i}}} \mathord{\left/ {\vphantom {{d{{{\eta }}_{i}}} {d{\tau }}}} \right. \kern-0em} {d{\tau }}}} \right).$
Здесь Q1 = 1.21 Дж/моль и Q2 = 1.74105 Дж/моль – тепловые эффекты реакций диссоциации карбонатов CaCO3 и MgCO3 соответственно.

Плотность фосфоритов, как композиционных материалов, рассчитывалась по формуле

(8)
${\rho } = \sum {{{v}_{i}}{{{\rho }}_{i}}} ,$
где ρi – плотность i-го компонента.

Для отдельных составляющих можно найти значения плотностей на основе анализа плотности от различного содержания компонент. Зависимость плотности образцов от содержания P2O5 носит явный характер для карбонатных, карбонатно-кремнистых и высококачественных фосфоритов, асимптотически приближаясь к значению плотности 3.1 г/см3 для субмономинерального фосфорита (табл. 3).

Наименьшая плотность фосфатизированных сланцев объясняется различной пористостью образцов.

Анализ этих данных позволяет выделить плотности минералов или основных компонент, содержащихся в отвалах горно-обогатительных комбинатов из отходов апатит-нефелиновых руд:

Вещество ρ, г/см3
Оолиты, цемент 3.1
Доломит, кальцит 2.8–2.85
Кремнезем 2.5–2.6

В общем случае корреляция свойств от содержания P2O5 и минерального состава вполне определенна и подтверждает правильность поиска закономерностей для обобщенного описания. Таким образом, по химическому составу отходов (процентному содержанию простейших окислов, среди которых P2O5, CaO, MgO, CO2, SiO2, Al2O3, F, K2O, Na2O, Fe2O3, FeO) можно, используя основные связи между массовыми долями минеральных составляющих и химическим составом, определить основные ТФХ.

Эффективная теплопроводность многокомпонентных систем рассчитывалась на основе самосогласованного метода, т.е. многократного использования бинарных структур с применением следующего алгоритма.

1. Исходные данные: химический состав отходов обогащения руд, структура (содержание фосфатного, карбонатного и кремнистого вещества), температура, степень реагирования.

2. Определение минерального состава, т.е. массовых долей основных компонент.

3. Расчет плотности i -х компонент при заданной температуре ρi(T).

4. Определение объема отдельных компонент и объемных долей.

5. Цикл по (i = 1, …, n)-компонентам. Пересчет объемных долей для окружения i-го компонента.

6. Расчет теплопроводности среды, окружающей i-й компонент, по слоистой модели со структурой компонент, параллельной потоку тепла.

Определение структуры композиции, где i -й компонент находится в смеси из остальных n – 1 по соответствующему критерию, и присвоение признака данной структуры (1 – слоистая со слоями, параллельными тепловому потоку; 2 – слоистая со слоями, перпендикулярными тепловому потоку; 3 – с взаимопроникающими компонентами; 4 – с изолированными включениями, когда теплопроводность вкраплений меньше теплопроводности окружения; 5 – с изолированными включениями, когда теплопроводность включения больше теплопроводности окружения).

7. Определение теплопроводности двухкомпонентной системы ${{{\bar {\lambda }}}_{i}}$ с учетом принятой структуры, состоящей из i-го компонента с теплопроводностью λi и концентрацией vi и второго компонента-окружения с теплопроводностью ${\lambda }_{i}^{ * }$ и концентрацией $v_{i}^{ * } = 1 - {{v}_{i}}.$

8. Определение теплопроводности как композитной системы:

${{{\lambda }}_{f}} = \sum\limits_{i = 1}^n {{{{\lambda }}_{i}}{{({{{{\bar {\lambda }}}}_{i}} - {\lambda }_{i}^{ * })} \mathord{\left/ {\vphantom {{({{{{\bar {\lambda }}}}_{i}} - {\lambda }_{i}^{ * })} {({{{\lambda }}_{i}} - {\lambda }_{i}^{ * })}}} \right. \kern-0em} {({{{\lambda }}_{i}} - {\lambda }_{i}^{ * })}}} $

9. Конец цикла.

10. Вывод результатов.

Особый интерес для анализа представляет область температур химического реагирования. На рис. 1 и 2 представлены результаты расчета теплопроводности и теплоемкости материалов из отвалов горно-обогатительных комбинатов апатит-нефелиновых месторождений по разработанному алгоритму в диапазоне температур, включающих высокотемпературную зону диссоциации карбонатных составляющих.

Рис. 1.

Экспериментальные значения теплоемкости отходов из отвалов апатит-нефелиновых руд и рассчитанные на основе обобщенных зависимостей.

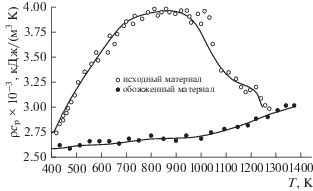
Рис. 2.

Экспериментальные значения теплопроводности отходов из отвалов апатит-нефелиновых руд и рассчитанные на основе обобщенных зависимостей в температурном диапазоне эндотермической реакции диссоциации карбонатов.

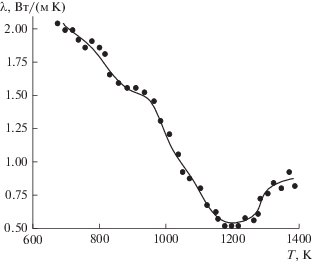
Необходимо отметить достаточную для практического использования при переработке таких отходов сопоставимость расчетных и экспериментальных данных.

ЗАКЛЮЧЕНИЕ

Использование разработанных моделей в композиционных структурах оказывается вполне удовлетворительным и позволяет учесть реагирование отдельных компонентов. Особое внимание необходимо уделять корректному определению структуры отходов апатит-нефелиновых руд, так как это существенно влияет на результаты второго этапа в оценке теплопроводности многокомпонентных систем.

Научно обоснован подход к обобщению теплофизических свойств для широкого спектра отходов горно-обогатительных комбинатов. Очевидно он будет справедлив и для химико-технологических характеристик.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 18-29-24094 MK).

ОБОЗНАЧЕНИЯ

a температуропроводность, м2/с
${{с}_{р}}$ удельная массовая теплоемкость, Дж/(кг К)
${{c}_{v}}$ объемная теплоемкость, Дж/(м3 К)
${{l}_{f}}$ длина свободного пробега фононов, м
m массовая доля компонента в многокомпонентной системе
R универсальная газовая постоянная, равная 8.31446261815324 Дж/(моль К)
Т температура, К
ν концентрация компонента в многокомпонентной системе
${{W}_{f}}$ скорость распространения волны, м/с
η степень реагирования в реакции диссоциации карбонатов
${{{\theta }}_{{\text{D}}}}$ температура Дебая, К
λ теплопроводность, Вт/(м К)
ρ плотность, кг/м3
${\tau }$ время, с
${{{\tau }}_{f}}$ время релаксации фононов, c

ИНДЕКСЫ

i порядковый номер компонента в многокомпонентной системе

Список литературы

  1. Bobkov V.I., Borisov V.V., Dli M.I., Meshalkin V.P. Study of the Thermal Characteristics of Phosphate Raw Materials in the Annealing Temperature Range // Theor. Found. Chem. Eng. 2017. V. 51. № 3. З. 307. [Бобков В.И., Борисов В.В., Дли М.И., Мешалкин В.П. Исследование тепловых характеристик фосфатного сырья в диапазоне температур обжига // Теор. осн. хим. технол. 2017. Т. 51. № 3. С. 295.]

  2. Леонтьев Л.И. Физико-химические особенности комплексной переработки железо-содержащих руд и техногенных отходов // ХХ Менделеевский съезд по общей и прикладной химии. Екатеринбург, 2016. С. 92.

  3. Elgharbi S., Horchani-Naifer K., Férid M. Investigation of the structural and mineralogical changes of Tunisian phosphorite during calcinations // J. Therm. Anal. Calorim. 2015. V. 119. № 1. P. 265.

  4. Panchenko S.V., Shirokikh T.V. Thermophysical processes in burden zone of submerged arc furnaces // Theor. Found. Chem. Eng. 2014. V. 48. № 1. P. 77. [Панченко С.В., Широких Т.В. Теплофизические процессы в шихтовой зоне электротермических рудовосстановительных реакторов // Теор. осн. хим. технол. 2014. Т. 48. № 1. С. 83.]

  5. Luis P., Van der Bruggen B. Exergy analysis of energy-intensive production processes: advancing towardsa sustainable chemical industry // J. Chem. Technol. Biotechnol. 2014. V. 89. № 9. P. 1288.

  6. Bobkov V.I., Borisov V.V., Dli M.I., Meshalkin V.P. Intensive Technologies for Drying a Lump Material in a Dense Bed // Theor. Found. Chem. Eng. 2017. V. 51. № 1. P. 72. [Бобков В.И., Борисов В.В., Дли М.И., Мешалкин В.П. Интенсивные технологии сушки кускового материала в плотном слое // Теор. осн. хим. технол. 2017. Т. 51. № 1. С. 72.]

  7. Meshalkin V.P., Bobkov V.I., Dli M.I., Khodchenko S.M. Computer-aided modeling of the chemical process of drying of a moving dense multilayer mass of phosphorite pellets // Dokl. Chem. 2017. V. 475. № 2. P. 188. [Мешалкин В.П., Бобков В.И., Дли М.И., Ходченко С.М. Компьютерное моделирование химико-технологического процесса сушки движущейся плотной многослойной массы фосфоритовых окатышей // Докл. Акад. наук. 2017. Т. 475. № 4. С. 410.]

  8. Meshalkin V.P., Bobkov V.I., Dli M.I., Khodchenko S.M. Computer modeling of the chemical-power engineering process of roasting of a moving multilayer mass of phosphorite pellets // Dokl. Chem. 2017. V. 477. № 2. P. 282. [Мешалкин В.П., Бобков В.И., Дли М.И., Ходченко С.М. Компьютерное моделирование химико-энерготехнологического процесса обжига движущейся многослойной массы фосфоритовых окатышей // Докл. Акад. наук. 2017. Т. 477. № 5. С. 559.]

  9. Meshalkin V.P., Bobkov V.I., Dli M.I., Khodchenko S.M. Optimizing the energy efficiency of the chemical and energy engineering process of drying of a moving dense multilayer mass of phosphorite pellets // Dokl. Chem. 2017. V. 477. № 2. P. 286. [Мешалкин В.П., Бобков В.И., Дли М.И., Ходченко С.М. Оптимизация энергоэффективности химико-энерготехнологического процесса сушки движущейся плотной многослойной массы фосфоритовых окатышей // Докл. Акад. наук. 2017. Т. 477. № 6. С. 667.]

  10. Буткарев А.А., Буткарев А.П., Ащеулов В.Н., Жомирук П.А., Лазебная Ю.П. Оптимизация работы тракта эксгаустера обжиговой машины ОК-108 АО ССГПО для увеличения производства окатышей // Сталь. 2015. № 3. С. 12.

  11. Зайнуллин Л.А., Дружинин Г.М., Буткарев А.А. Инновационные разработки ОАО ВНИИМТ для энергосбережения и экологии в металлургии // Черн. металл. 2014. № 7 (1375). С. 79.

  12. Берман Р. Теплопроводность твердых тел. М.: Мир, 1979. [Berman R. Thermal Conduction in Solids (Oxford Studies in Physics). Oxford: Oxford Univ. Press, 1976.]

  13. Рейсленд Дж. Физика фононов. М.: Мир, 1975. [Reissland J.A. The Physics of Phonons. New York: Wiley, 1973.]

  14. Миснар А. Теплопроводность твердых тел, жидкостей, газов и их композиций. М.: Мир, 1968. [Missenard A. Conductivite thermique des solides, liquides, gaz et de leurs melanges. Paris: Editions eyrolle, 1965.]

  15. Дучков А.Д., Соколова К.С. Геотермические исследования в Сибири. Новосибирск: Наука, 1974.

  16. Леванов А.В., Антипенко Э.Е. Определение термодинамических свойств статистическими методами. Реальные газы. Жидкости. Твердые тела. М.: МГУ им. М.В. Ломоносова, 2006.

  17. Melamud S.G., Yur’ev B.P. Oxidation of iron ore at moderate and high temperatures // Steel Transl. 2016. V. 46. № 6. P. 384.

  18. Акбердин А.А., Ким А.С., Султангазиев Р.Б. Планирование численного и физического эксперимента при моделировании технологических процессов // Изв. высш. учебн. завед. Черн. металл. 2018. Т. 61. № 9. С. 737.

  19. Швыдкий В.С., Фатхутдинов А.Р., Девятых Е.А., Девятых Т.О., Спирин Н.А. К математическому моделированию слоевых металлургических печей и агрегатов. Сообщение 2 // Изв. высш. учебн. завед. Черн. металл. 2018. Т. 60. № 1. С. 19.

  20. Bokovikov B.A., Bragin V.V., Shvydkii V.S. Role of the thermal-inertia zone in conveyer roasting machines // Steel Transl. 2014. V. 44. № 8. P. 595.

  21. Bragin V.V., Bokovikov B.A., Naidich M.I., Gruzdev A.I., Shvydkii V.S. Relation between the productivity and fuel consumption in roasting machines // Steel Transl. 2014. V. 44. № 8. P. 590.

  22. Швыдкий В.С., Ярошенко Ю.Г., Спирин Н.А., Лавров В.В. Математическая модель процесса обжига рудоугольных окатышей на конвейерной машине // Изв. высш. учебн. завед. Черн. металл. 2018. Т. 60. № 4. С. 329.

  23. Новичихин А.В., Шорохова А.В. Процедуры управления поэтапной переработкой железорудных отходов горнопромышленных районов // Изв. высш. учебн. завед. Черн. металл. 2018. Т. 60. № 7. С. 565.

  24. Леонтьев Л.И., Григорович К.В., Костина М.В. Фундаментальные исследования как основа создания новых материалов и технологий в области металлургии. Часть 1 // Изв. высш. учебн. завед. Черн. металл. 2018. Т. 61. № 1. С. 11.

  25. Гурин И.А., Лавров В.В., Спирин Н.А., Никитин А.Г. Веб-технологии построения информационно-моделирующих систем технологических процессов в металлургии // Изв. высш. учебн. завед. Черн. металл. 2017. Т. 60. № 7. С. 573.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал