Теоретические основы химической технологии, 2020, T. 54, № 2, стр. 257-264
Потери давления вдоль канала трубчатой мембраны в процессе ультрафильтрации жидких сред
С. В. Федосов a, В. А. Масленников a, Ю. П. Осадчий a, А. В. Маркелов a, *
a Ивановский государственный политехнический университет
Иваново, Россия
* E-mail: aleksandr203.37@mail.ru
Поступила в редакцию 04.09.2017
После доработки 14.12.2018
Принята к публикации 11.02.2019
Аннотация
Представлены результаты исследования потери давления при ультрафильтрации жидких сред на трубчатом мембранном модуле. В основу решения системы дифференциальных уравнений, предложенных С.-Т. Хвангом и К. Каммермейером, для определения потери давления по длине узкого канала был положен метод функционального преобразования Лапласа. Показано, что потери напора зависят от площади, пористости и радиуса пор мембраны, вязкости и объемного потока разделяемой жидкости. Полученное уравнение позволяет учесть потери напора при инженерных расчетах ультрафильтрационных аппаратов трубчатого типа.
ВВЕДЕНИЕ
Баромембранные процессы, к которым относится и ультрафильтрация, активно используются в качестве ресурсосберегающих технологий для восстановления физико-химических свойств отработанных технических жидкостей [1–4].
К одной из основных задач при разработке методик инженерного расчета баромембранных аппаратов относится расчет гидравлического сопротивления движению жидкости вдоль мембранного канала. Такой расчет необходим с целью определения напора, создаваемого насосом для подачи исходного раствора в аппарат с заданным давлением [5]. Кроме того, перепад давления влияет на гидромеханику, производительность и качество процесса разделения [6, 7].
Давление Р, развиваемое насосом баромембранного аппарата, должно создавать движущую силу процесса разделения – перепад рабочего давления через мембрану ΔР и преодолевать гидравлические сопротивления основному потоку ΔРf и потоку пермеата в дренажных слоях ΔРР, а также компенсировать потери давления на трение и местные сопротивления в трубопроводе и арматуре $\sum {\Delta {{Р}_{{{\text{МС}}}}}} $и подъем раствора на определенную геометрическую высоту РGН [7]:
(1)
${{Р}_{{}}} = \Delta Р - \Delta {{P}_{{\text{f}}}} - \Delta {{Р}_{{\text{p}}}} - \sum {\Delta {{Р}_{{{\text{МС}}}}} - {{Р}_{{{\text{GН}}}}}} .$Течению жидкости в каналах с проницаемыми стенками были посвящены ряд работ отечественных и зарубежных авторов.
В работах [8, 9] проведено экспериментальное исследование перехода от ламинарного течения к турбулентному в канале с плоскопараллельными стенками, одна из которых была пористой. Исследователями были сделаны выводы, что наличие пористой стенки приводит к увеличению массового расхода и уменьшению коэффициента трения по сравнению с их значениями для канала со сплошными стенками и, кроме того, переход к турбулентному режиму в канале с пористыми стенками происходит при меньшем значении числа Рейнольдса.
В работах [10–12] приведены данные по расчету потерь напора при течении вязкой жидкости в прямоугольной щели без отбора расхода на стенках, выполненному на основе уравнения Дарси.
В работе [14] были исследованы потери давления при турбулентном течении жидкости через трубчатый мембранный модуль с поперечным потоком.
Для потоков, выходящих через некоторое число выпусков, были составлены уравнения энергетического баланса, основанные на уравнении Бернулли. Для потока, выходящего из первого выпуска:
(2)
$\frac{{{{P}_{{{\text{K}}1}}}}}{{\rho }} + \frac{{V_{1}^{2}}}{2} - {{E}_{{{\text{turb}}}}} - {{E}_{{{\text{fric}}}}} = \frac{{{{P}_{{\text{P}}}}}}{{\rho }} + \frac{{u_{1}^{2}}}{2}.$В данной формуле потери энергии на преодоление сил трения Еfric определяются по выражению
Потери энергии на преодоления гидродинамического сопротивления определяются из выражения
(4)
${{E}_{{{\text{turb}}}}} = \frac{{V_{1}^{2}}}{2}{{\left( {1 - \frac{{{{d}^{2}}}}{{{{D}^{2}}}}} \right)}^{2}}.$После подстановки выражений (3) и (4) в уравнение (2) определяется скорость выхода потока через первый выпуск u1:
(5)
${{u}_{1}} = \sqrt {\frac{{\frac{{{{P}_{{{\text{K}}1}}} - {{P}_{{\text{P}}}}}}{{\rho }} + \frac{{V_{1}^{2}}}{2}}}{{\frac{1}{2}{{{\left( {\frac{{{{D}^{2}}}}{{{{d}^{2}}}} - 1} \right)}}^{2}} + \frac{1}{2} + \frac{{fe}}{{2d}}}}} .$Используя уравнения (2)–(5) и данные экспериментальных исследований, определяются потери давления на первом выпуске PК1 [14]. На следующем шаге рассчитывается давление перед вторым выходом РК2.
Согласно предложенной методике [14], изменение давления может зависеть от внезапного расширения потока в пространстве после первого выхода, трения вдоль стенок, изменения скорости от точки к точке и как результат потери энергии на расширение [14]:
(6)
${{E}_{{{\text{exp}}}}} = \frac{1}{2}{\rho }V_{1}^{{'2}}{{\left( {1 - \frac{{S_{1}^{'}}}{S}} \right)}^{2}}.$Потери энергии на трение вдоль трубчатого модуля [15]:
где ψ = 0.184Re–0.2 для турбулентного режима [14].Давление РК2 находится из выражения [14]
(8)
${{P}_{2}} = {{P}_{1}} + \frac{1}{2}{\rho }(V_{1}^{2} - V_{2}^{2}) - {{E}_{{{\text{wall}}}}} - {{E}_{{{\text{exp}}}}}.$Аналогичным методом находится давление Р3 и т.д.
Приведенная выше методика позволяет найти потери давления при турбулентном течении жидкости через трубчатый мембранный модуль с поперечным потоком.
В отечественной практике при расчете перепада рабочего давления ΔР принято учитывать потери напора на преодоление гидравлического сопротивления потоку разделяемого раствора в каналах мембранных аппаратов ΔРa и потоку в дренажном слое ΔРd, используя уточненную формулу Дарси–Вейсбаха [3, 15]:
(10)
$\Delta {{P}_{{\text{d}}}} = {\lambda }\frac{{{{{\delta }}_{{\text{d}}}}}}{d}\frac{{{\rho }{{u}^{{'2}}}}}{2}{{\chi }_{{\text{2}}}}.$Ю.И. Дытнерский [13] полагал, что гидравлическое сопротивление потоку разделяемого раствора в трубчатом мембранном модуле определяется по общепринятым формулам движения жидкости по гладким трубам с ламинарным, переходным или турбулентным режимами течения. Сопротивление в дренажном канале ввиду малого пути пермеата, равного толщине пористой трубки, также не велико. Поэтому в аппаратах с трубчатыми мембранами давление практически полностью обусловлено перепадом давления через мембрану, а вклад остальных составляющих можно не учитывать. Указанные сопротивления нужно учитывать только для аппаратов плоскокамерного типа и волоконных мембранных модулей.
С.-Т. Хванг и К. Каммермейер [6] говорят о потере напора вследствие гидравлического сопротивления в активном и дренажном слоях мембраны, но рассматривают расчет только для половолоконных аппаратов.
Анализируя отечественные и зарубежные работы в области расчета баромембранных ультрафильтрационных аппаратов, можно сделать вывод о том, что проницание пермеата через пористую перегородку приводит к возникновению гидравлического сопротивления. Методика расчета потерь давления, предложенная в [14], достаточно сложна и трудно применяема для практических расчетов баромембранных аппаратов. Метод, который используется в отечественной практике [3, 10–12, 15], очень неточен и может использоваться для предварительных, грубых расчетов таких аппаратов.
Мнение о том, что потери напора в активном и дренажном слоях трубчатых мембранных модулей можно не учитывать [6, 13], хорошо подходит для расчета установок с низкой производительностью и небольшой длиной трубчатых элементов. Современные ульрафильтрационные мембраны имеют достаточно высокую удельную производительность и большую площадь разделения. В таких аппаратах проницание пермеата через пористую перегородку дополнительно увеличивает потери давления в фазе высокого и низкого давления. Движущая сила проницания уменьшается и эффективность модуля падает, что особенно важно когда требуется высокое значение проницания при низком соотношении давлений, а также в длинных тонких мембранных каналах.
Таким образом, целью данной работы является определение закономерности потери напора вдоль трубчатого мембранного канала от площади, пористости и радиуса пор мембраны, вязкости и объемного потока разделяемого раствора и его влияния на удельную производительность мембран, физико-химические свойства очищаемой жидкости и технологические параметры аппаратов для ультрафильтрации жидкостей.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
Движущей силой процесса фильтрования является разность давлений ΔР в мембранном модуле [4–7].
Трубчатый мембранный элемент представляет собой тонкий канал, в котором разделяемая жидкость имеет высокую скорость потока, что обеспечивает движение в режиме идеального вытеснения.
Поэтому давление уменьшается вдоль канала и эффективность модуля снижается. Основной причиной потери давления является гидродинамическое сопротивление у стенок канала. Кроме того, проницание молекул через мембрану дополнительно увеличивает потерю давления в фазе высокого давления над мембраной РН [6].
Эффект потери давления становится важным, особенно когда используется длинный тонкий мембранный канал. Для очень длинного канала потери напора могут быть так велики, что давление в сбросном потоке Рк и в пермеате Рр станут равными и проницаемость прекратится [6].
Для нахождения потери давления по длине канала мембраны необходимо решить систему дифференциальных уравнений, представляющих два модифицированных уравнения материальных балансов и уравнения сохранения количества движения.
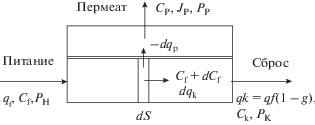
Известные специалисты в области мембранных процессов С.-Т. Хванг и К. Каммермейер предлагают решение системы дифференциальных уравнений для определения потери напора по длине узкого канала (рис. 1), записанную в безразмерной форме [6], которая состоит из уравнения баланса массопереноса по элементу поверхности dS:
(11)
$ - d{{J}_{{\text{k}}}} = d{{J}_{{\text{p}}}} = ds \times р - \pi ({{C}_{{\text{f}}}} - {{C}_{{\text{p}}}}),$(12)
$ - d({{J}_{{\text{k}}}}{{C}_{{\text{k}}}}) = {{C}_{{\text{p}}}}d{{J}_{{\text{p}}}} = \varphi ds({{C}_{{\text{f}}}} - {{C}_{{\text{p}}}}),$Рис. 1.
Ультрафильтрационный модуль трубчатого типа: Cf, Cp, СК – концентрации асфальто-смолистых примесей соответственно на входе в мембранный модуль, в пермеате и на выходе в концентрате; qf, qp, qK – объемный поток соответственно разделяемой жидкости в трубке, пермеата и концентрата; PH, PP, PK – давление на входе в мембранный модуль и на выходе в пермеате и концентрате соответственно.
и уравнения сохранения количества движения:
Здесь безразмерный перепад давления через мембрану определяется по формуле [6]
и является переменной искомой величиной, так как давление концентрата на сбросе будет изменяться вследствие гидравлического сопротивления в трубчатом канале, пористом и дренажном слоях.
Параметр, отражающий величину потери давления вдоль канала мембраны в безразмерном виде, определяется по формуле [6]
(15)
${{A}_{{\text{p}}}} = \frac{{8\mu q_{{\text{f}}}^{'}}}{{\pi {{r}^{4}}n\Delta Р}}\frac{1}{{2\pi r{{n}_{{{\text{tr}}}}}}}\frac{{{{q}_{{{\text{ftr}}}}}{{C}_{{\text{в}}}}L}}{{G\Delta Р}}.$Безразмерная площадь мембраны s определяется по выражению
Безразмерная объемная скорость потока:
в сбросном потоке
в потоке пермеата
Для упрощения процедуры анализа и последующего поиска аналитического решения перепишем уравнения (11)–(13) в следующем виде:
Здесь принято, что В величина постоянная и равная
Применим к уравнениям (20) и (23) прямое преобразование Лапласа [16]. При этом используем теорему дифференцирования оригинала:
В этом случае для уравнения (20) запишем
А для выражения (23) будем иметь
Выражаем из обеих записей величину р(ξ) и приравниваем правые части из получаемых выражений:
(28)
$\frac{{{{р}_{0}}}}{\xi } + {{A}_{{\text{p}}}}\frac{1}{\xi }{{J}_{{\text{p}}}}(\xi ) = {{J}_{{\text{p}}}}(\xi )\varsigma - {{J}_{{\text{p}}}}(0) + \frac{B}{\xi }.$Решая уравнение (28) относительно функции Jp(ξ), получаем
(29)
${{J}_{{\text{p}}}}(\xi ) = \frac{{{{p}_{{\text{0}}}} - B}}{{{{\xi }^{2}} - {{A}_{{\text{p}}}}}} + \frac{{{{J}_{{\text{p}}}}(0)\xi }}{{{{\xi }^{2}} - {{A}_{{\text{p}}}}}}.$Перепишем выражение (29) следующим образом:
(30)
$\begin{gathered} {{J}_{{\text{p}}}}(\xi ) = {{J}_{{\text{p}}}}(0)\left\{ {\frac{\xi }{{{{\xi }^{2}} - (\sqrt {{{A}_{{\text{p}}}}{{)}^{2}}} }}} \right\} + \\ + \,\,\frac{{({{p}_{0}} - B)}}{{\sqrt {{{A}_{{\text{p}}}}} }}\left\{ {\frac{{\sqrt {{{A}_{{\text{p}}}}} }}{{{{\xi }^{2}} - (\sqrt {{{A}_{{\text{p}}}}{{)}^{2}}} }}} \right\}. \\ \end{gathered} $Перевод в область оригиналов осуществляем с помощью таблиц обратного преобразования Лапласа [16]:
Для первого слагаемого правой части запишем
(32)
$\frac{{({{p}_{0}} - B)}}{{\sqrt {{{A}_{{\text{p}}}}} }}{{L}^{{ - 1}}}\left\{ {\frac{{\sqrt {{{A}_{{\text{p}}}}} }}{{{{\xi }^{2}} - (\sqrt {{{A}_{{\text{p}}}}{{)}^{2}}} }}} \right\} = \frac{{({{p}_{0}} - B)}}{{\sqrt {A{}_{{\text{p}}}^{{}}} }}{\text{sh}}(\sqrt {{{A}_{{\text{p}}}}} s).$Для второго слагаемого запишем
(33)
${{J}_{{\text{p}}}}(0){{L}^{{ - 1}}}\left[ {\frac{\xi }{{{{\xi }^{2}} - (\sqrt {{{A}_{{\text{p}}}}{{)}^{2}}} }}} \right] = {\text{ch}}(\sqrt {{{A}_{{\text{p}}}}} s){{J}_{p}}(0).$Искомое решение в области оригиналов будет
(34)
${{J}_{{\text{p}}}}(s) = {{J}_{{\text{p}}}}(0){\text{ch}}(\sqrt {{{A}_{{\text{p}}}}} s) + \frac{{({{p}_{0}} - В)}}{{\sqrt {{{A}_{{\text{p}}}}} }}{\text{sh}}(\sqrt {{{A}_{{\text{p}}}}} s).$Из граничного условия следует, что при s = 0 Jp(0) = 0. Поэтому первое слагаемое правой части (34) можно принять равным нулю. С учетом этого и подставляя (34) в (27), запишем
(35)
$\begin{gathered} p(\xi )\xi - {{p}_{0}} = {{A}_{{\text{p}}}}\frac{{({{p}_{0}} - B)}}{{{{\xi }^{2}} - {{{(\sqrt {{{A}_{{\text{p}}}}} )}}^{2}}}} + \\ + \,\,{{J}_{p}}(0)\left. {\left. {\frac{\xi }{{{{\xi }^{2}} - (\sqrt {{{A}_{{\text{p}}}}{{)}^{2}}} }}} \right\}} \right] \\ \end{gathered} $или
(36)
$p(\xi ) = \frac{{{{р}_{0}}}}{\xi } + {{A}_{{\text{p}}}}\frac{{({{p}_{0}} - B)}}{{\xi [{{\xi }^{2}} - (\sqrt {{{A}_{{\text{p}}}}{{)}^{2}}]} }}.$Табличной функции преобразования для второго слагаемого правой части (36) не существует.
В этом случае возможно применение теоремы Бореля для свертки изображений:
(37)
${{f}_{1}}(\xi ){{f}_{2}}(\xi ) = \int\limits_0^s {{{f}_{1}}(s - \varpi ){{f}_{2}}(\varpi )d\varpi } .$Запишем уравнение (36) в удобном для преобразования виде:
(38)
$p(\xi ) = \frac{{{{р}_{0}}}}{\xi } + {{A}_{{\text{p}}}}\frac{{({{p}_{0}} - B)}}{{\xi [{{\xi }^{2}} - (\sqrt {{{A}_{{\text{p}}}}{{)}^{2}}]} }}\frac{{\sqrt {{{А}_{{\text{р}}}}} }}{{\sqrt {{{А}_{{\text{р}}}}} }}.$Выполним следующие преобразования:
(39)
${{f}_{1}}(s - \varpi ) = {{L}^{{ - 1}}}\left[ {\frac{{\sqrt {{{A}_{{\text{p}}}}} }}{{{{\xi }^{2}} - (\sqrt {{{A}_{{\text{p}}}}{{)}^{2}}} }}} \right] = {\text{sh}}[\sqrt {{{A}_{{\text{p}}}}} (s - \varpi )];$Подставим выражения (39) и (40) в (37) и проинтегрируем его в интервале [0, s]:
(41)
$\begin{gathered} \int\limits_0^s {{{f}_{1}}(s - \varpi ){{f}_{2}}(\varpi )d\varpi } = \int\limits_0^s {{\text{sh}}[\sqrt {{{A}_{{\text{p}}}}} (s - \varpi )]d\varpi = } \\ = - \frac{1}{{\sqrt {{{A}_{{\text{p}}}}} }}[{\text{c}}{{{\text{h}}}^{2}}(\sqrt {{{A}_{{\text{p}}}}} s) - {\text{s}}{{{\text{h}}}^{2}}(\sqrt {{{A}_{{\text{p}}}}} s)] + {\text{ch}}(\sqrt {{{A}_{{\text{p}}}}} s)\frac{1}{{\sqrt {{{A}_{{\text{p}}}}} }}. \\ \end{gathered} $Левое слагаемое в квадратных скобках правой части выражения (41) подчиняется соотношению между гиперболическими функциями [17]
(42)
$[{\text{c}}{{{\text{h}}}^{2}}(\sqrt {{{A}_{{\text{p}}}}} s) - {\text{s}}{{{\text{h}}}^{2}}(\sqrt {{{A}_{{\text{p}}}}} s)] = 1.$С учетом равенства (42) выражение (41) примет вид
(43)
$\int\limits_0^s {{{f}_{1}}(s - \varpi ){{f}_{2}}(\varpi )d\varpi } = \frac{1}{{\sqrt {{{A}_{{\text{p}}}}} }}[{\text{ch}}(\sqrt {{{A}_{{\text{p}}}}} s) - 1].$Подстановка (43) во второе слагаемое (36) дает для него решение относительно оригиналов:
(44)
$\begin{gathered} {{L}^{{ - 1}}}\left[ {\frac{{\sqrt {{{A}_{{\text{p}}}}} }}{{\xi \{ {{\xi }^{2}} - (\sqrt {{{A}_{{\text{p}}}}{{)}^{2}}\} } }}} \right] = \\ = - \frac{{{{A}_{{\text{p}}}}}}{{\sqrt {{{A}_{{\text{p}}}}} }}({{р}_{0}} - В)\frac{1}{{\sqrt {{{A}_{{\text{p}}}}} }}[{\text{ch}}(\sqrt {{{A}_{{\text{p}}}}} s) - 1]. \\ \end{gathered} $Первое слагаемое (36) в области оригиналов будет иметь следующий вид:
Окончательно полное решение уравнения (36) относительно оригиналов для определения потерь давления в зависимости от изменения поверхности разделения примет вид
Для решения полученного уравнения необходимо задаться граничными условиями: p0 = 0 – изменение перепада давления в начальный период; ${{J}_{р}}(0)$ = 0 – расход пермеата без учета потерь давления; 0 < s < 1 – изменение активной поверхности мембраны; $B = \pi ({{C}_{{\text{f}}}} - {{C}_{{\text{p}}}})$ – постоянная, характеризующая влияние осмотического давления, которая, как правило, при разделении методом ультрафильтрации не учитывается [13].
Тогда с учетом приведенных выше условий уравнение (46) примет следующий вид:
Подставим в уравнение (47) выражения (14), (15), (16) и получим размерную форму для расчета потери давления:
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Проведем сравнительный расчет потерь давления по методу, приведенному в отечественной литературе [15], и по методу, предлагаемому авторами.
Рассчитаем гидравлическое сопротивление ультрафильтрационной установки для разделения сточных вод, содержащих дисперсии акрилатов, с использованием трубчатых полисульфонамидных мембран [17, 18]. Исходные данные приведены в табл. 1.
Таблица 1.
Исходные данные для расчета гидравлических сопротивлений
| Параметр | Значение |
|---|---|
| Удельная производительность мембраны ПСА-300 Gi, м3/(м2 с) при начальном давлении РН: | |
| 0.15 МПа | 2.86 × 10–5 |
| 0.20 МПа | 3.55 × 10–5 |
| 0.25 МПа | 3.77 × 10–5 |
| 0.30 МПа | 3.50 × 10–5 |
| 0.35 МПа | 3.44 × 10–5 |
| 0.40 МПа | 3.33 × 10–5 |
| Подача исходного раствора qf , м3/с | 9.3 × 10–4 |
| Объемная скорость потока в единичном модуле $q_{{\text{f}}}^{'}$, м3/c | 1.86 × 10-4 |
| Объемная скорость потока в единичном трубчатом элементе qftr, м3/c | 0.26 × 10-4 |
| Диаметр трубчатого канала dк, м | 12 × 10–3 |
| Радиус трубчатого канала r, м | 6 × 10–3 |
| Число трубчатых элементов в мембранном модуле n | 35 |
| Общее число трубчатых элементов nftr | 210 |
| Кинематическая вязкость раствора ν, м2/с | 1.1 × 10–6 |
| Динамическая вязкость раствора μ, Па с | 1.27 × 10–3 |
| Плотность раствора ρ, кг/м3 | 1154 |
| Концентрация растворителя Св, кг/кг | 0.997 |
| Высота дренажного слоя δd, м | 0.5 × 10–3 |
| Коэффициент гидравлического сопротивления χ2 | 100 |
| Толщина активного слоя мембраны l, м | 1 × 10–6 |
| Длина единичного модуля L, м | 2 |
Разделение акриловых дисперсий проводилось на установке УР-30, в которой мембранные трубчатые модули соединены параллельно-последовательно по формуле 5 × 6 [17].
Проведем расчет потерь давления в аппарате по методу, приведенному в отечественной литературе, по формулам (9), (10).
Для ламинарного и переходного режима течения в гладкой трубе коэффициент трения можно определить по наиболее часто используемой формуле [19]
где Re – критерий Рейнольдса для данного процесса фильтрования (Re = 7000–10 000).Получим
Коэффициент местного сопротивления χ1 зависит от вида сепарирующей сетки. В рассматриваемой ульрафильтрационной установке нет сеток, поэтому этот коэффициент можно не учитывать:
Выражение для расчета потерь в дренажном слое (10) можно записать в виде
(50)
$\Delta {{P}_{{\text{d}}}} = 12\frac{{{\nu }{{G}_{i}}{{L}^{2}}}}{{{\delta }_{{\text{d}}}^{{\text{3}}}}}{{\chi }_{{\text{2}}}}.$Отсюда
Полные потери напора в мембранном модуле для начального давления РН = 0.25 МПа составят
Давление на выходе из ультрафильтрационной установки:
Расчет потери давления по методу, предлагаемому авторами работы, для начального давления РН = 0.25 МПа:
Расчеты для остальных значений давления на выходе из баромембранной установки выполняются аналогично и представлены в табл. 2.
Таблица 2.
Сравнительный расчет потерь давления в мембранных аппаратах трубчатого типа
| Давление
на входе Рн, МПа |
Перепад давления ΔР, МПа |
Площадь мембраны S, м2 |
Удельная произво-дительность мембраны G × 105, м3/(м2 с) |
Давление
на выходе
(по методу
в литературе) Ркл, МПа |
Давление на выходе (по предлагае-мому методу) Ркр, МПа |
Давление
на выходе (опытные данные) Рко, МПа |
|---|---|---|---|---|---|---|
| 0.25 | 0.15 | 15 | 2.86 | 0.0786 | 0.1986 | 0.20 |
| 0.30 | 0.20 | 15 | 3.55 | 0.0360 | 0.2137 | 0.23 |
| 0.35 | 0.25 | 15 | 3.77 | 0.0350 | 0.2350 | 0.27 |
| 0.40 | 0.30 | 15 | 3.50 | 0.0980 | 0.2726 | 0.30 |
| 0.45 | 0.35 | 15 | 3.44 | 0.1510 | 0.3040 | 0.33 |
| 0.50 | 0.40 | 15 | 3.33 | 0.2060 | 0.3388 | 0.35 |
Сравнительный анализ потерь давления приведен в табл. 2 и на рис. 2.
Рис. 2.
Сравнительный анализ расчетных и экспериментальных данных потери давления в баромембранном трубчатом аппарате: 1 – расчетные значения по методике, изложенной в отечественной литературе; 2 – расчет по предлагаемому методу; 3 – экспериментальные данные.

Эксперимент подтвердил влияние величины удельной производительности на потери давления. Потери давления, рассчитанные по методу, принятому в отечественной практике, на 40–60% ниже значений, полученных в результате эксперимента.
ЗАКЛЮЧЕНИЕ
Выполненный анализ позволил получить закономерности влияния величины удельной производительности мембран на потери давления установки ультрафильтрации трубчатого типа с учетом физико-химических свойств очищаемой жидкости и технологических параметров установки и мембран.
Эксперимент подтвердил влияние величины производительности мембраны на потери давления. Экспериментальные исследования на опытно-промышленной установке ультрафильтрации показали, что предложенное авторами уравнение по расчету гидравлического сопротивления хорошо согласуется с опытными данными.
Полученное выражение (48) для определения потерь давления по длине мембранного канала можно использовать в инженерных расчетах при проектировании аппаратов по разделению ультрафильтрацией жидких дисперсных сред.
ОБОЗНАЧЕНИЯ
| Ар | параметр, отражающий величину потери давления вдоль канала мембраны в безразмерном виде |
| B | постоянная, характеризующая влияние осмотического давления |
| C | концентрации примесей, кг/кг |
| ${{C}_{{\text{B}}}}$ | концентрация растворителя, кг/кг |
| D | диаметр трубчатого модуля, м |
| d | диаметр выходного отверстия (поры), м |
| Е | энергия течения жидкости в трубке, Дж |
| е | толщина пластины, м |
| f | коэффициент Дарси |
| G | удельная проницаемость мембраны по растворителю, м3/(Па м2 с) |
| g | доля исходного потока, перешедшая в пермеат |
| J | безразмерный объемный поток |
| L | длина единичного трубчатого модуля, м |
| $l$ | толщина активного слоя мембраны, м |
| n | число трубчатых элементов в одном мембранном модуле |
| ntr | общее число трубчатых элементов в установке |
| Р | давление, Па |
| ΔР | перепад рабочего давления, Па |
| р | безразмерный перепад рабочего давления, Па |
| Q | массовый расход очищаемой технической жидкости, кг/с |
| q | объемная скорость потока, м3/с |
| qftr | объемная скорость потока в единичном трубчатом элементе, м3/с |
| r | радиус трубчатого элемента, м |
| S | площадь разделения трубчатого модуля, м2 |
| S ' | площадь сечения трубчатого модуля, м2 |
| s | безразмерная площадь разделения трубчатого модуля |
| u | скорость выходящего потока, м/с |
| v | скорость потока в модуле, м/с |
| V' | средняя скорость потока, м/с |
| λ | коэффициент потерь на трение по длине |
| µ | коэффициент динамической вязкости, (Н с)/м2 |
| ξ | комплексная переменная прямого преобразования Лапласа |
| ρ | плотность жидкости, кг/м3 |
| φ | селективность мембраны по примесям |
| χ1 | коэффициент гидравлического сопротивления сетки в канале, χ1 = 5–10 [1] |
| χ2 | коэффициент гидравлического сопротивления, зависящий от вида и пористости дренажного материала, χ2 = 100–200 [1] |
| Ψ | коэффициент потерь на трение вдоль гладкой стенки при турбулентном режиме |
| $\varpi $ | параметр в диапазоне [0;s] |
| Re | число Рейнольдса |
ИНДЕКСЫ
| 0 | начальное значение |
| 1 | первое входное отверстие (выпуск) |
| 2 | второе выходное отверстие |
| 3 | третье выходное отверстие |
| 4 | четвертое выходное отверстие |
| атм | атмосферное давление при нормальных условиях |
| d | дренаж |
| f | вход в мембранный модуль |
| GH | потери давления на подъем столба жидкости |
| р | пермеат |
| к | концентрат |
| мс | потери на трение и местные сопротивления |
| н | начальные показатели |
| ' | относится к единичному мембранному модулю |
Список литературы
Свитцов А.А. Введение в мембранные технологии. М.: ДеЛи принт, 2007.
Игнатович Э. Химическая техника. Процессы и аппараты. М.: Техносфера, 2007.
Родионов А.И., Кузнецов Ю.П., Соловьев Г.С. Защита биосферы от промышленных выбросов. Основы проектирования технологических процессов. М.: Химия, 2005.
Дытнерский Ю.И. Процессы и аппараты химической технологии. Часть I. Теоретические основы процессов химической технологии. Гидромеханические и тепловые процессы и аппараты. М.: Химия, 1995.
Лейси Р.Е., Леб С. Технологические процессы с применением мембран. М.: Мир, 1972.
Хванг С.-Т., Каммермейер К. Мембранные процессы разделения. М.: Химия, 1981.
Дытнерский Ю.И., Борисов Г.С. Брыков В.П. Основные процессы и аппараты химической технологии. М.: Химия, 1991.
Биверс Г., Спэрроу Е. Экспериментальное исследование течения в канале с пористой стенкой // Теор. осн. инж. расчетов. 1970. Т. 92. № 4. С. 146.
Sparrow E., Beavers G. Channel and tube flows with surface mass transfer and velocity slip // Phys. Fluids. 1971. V. 15. № 7. P. 1312.
Емцев Б.Т. Техническая гидромеханика. М.: Машиностроение, 1987.
Попов Д.Н. Нестационарные гидромеханические процессы. М.: Машиностроение, 1982.
Картвелишвили Н.А. Нетрадиционные задачи гидравлики. М.: Энергоатомиздат, 1985.
Дытнерский Ю.И. Баромембранные процессы. Теория и расчет. М.: Химия, 1986.
Darcovich K., Toll F., Paynot F. Inlet Plenum Pressure Drop Calculation for a Cross-Flow Module // Can. J. Chem. Eng. 1999. V. 77. № l. P. 119.
Романков П.Г., Фролов В.Ф., Флисюк О.М. Методы расчета процессов и аппаратов химической технологии. СПб.: Химия, 1993.
Корн Г., Корн Т. Справочник по математике. М.: Наука, 1970.
Осадчий Ю.П., Блиничев В.Н. Баромембранная очистка сточных вод, содержащих пигменты и кислотные красители // Технол. текст. пром-сти. 2007. № 5. С. 64.
Осадчий Ю.П., Блиничев В.Н. Опыт использования мембранной очистки сточных вод в текстильной промышленности // Технол. текст. пром-сти. 1992. № 7. С. 87.
Amanbaev T.R. Dynamics of a suspension in the presence of liquid filtration, disperse phase sedimentation, and precipitate formation processes // Theor. Found. Chem. Eng. 2016. V. 50. № 3. P. 303. [Аманбаев Т.Р. Динамика суспензии при наличии процессов фильтрации жидкости, седиментации дисперсной фазы и осадкообразования // Теор. осн. хим. технол. 2016. Т. 50. № 3. С. 311.]
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


