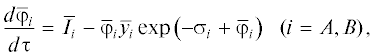Теоретические основы химической технологии, 2020, T. 54, № 2, стр. 236-243
Моделирование механохимических и структурных превращений в бинарной порошковой смеси
О. В. Лапшин *
Томский научный центр СО РАН
Томск, Россия
* E-mail: ovlap@mail.ru
Поступила в редакцию 28.12.2018
После доработки 22.07.2019
Принята к публикации 12.09.2019
Аннотация
На основе построенной математической модели исследована макрокинетика формирования частиц механокомпозитов в механообрабатываемой порошковой смеси. Выявлены области различных режимов процесса, позволяющих получать конечный продукт с заданными характеристиками.
ВВЕДЕНИЕ
Механическая обработка (МО) реакционноспособной гетерогенной системы – этап многих технологических процессов, а также эффективный способ управления химическим превращением. В настоящее время метод МО используется для стимулирования различных твердофазных реакций и позволяет получать многие химические вещества [1–5].
В процессе МО происходит активация реагентов за счет создания новой высокодефектной структуры в них, характеризуемой повышенным запасом избыточной энергии. Наряду с активацией, в ходе МО происходит значительное диспергирование реагентов, а также осуществляется образование межфазной поверхности путем агломерации реагентов в слоистые частицы-механокомпозиты, которые непрерывно измельчаются, агломерируются и образуют новые частицы с еще более сложной внутренней структурой [6].
В этом случае скорость структурных превращений в механокомпозитах во многом будет определяться их слоистостью, которую можно отождествить с толщиной чередующихся внутренних слоев, состоящих из входящих в механокомпозиты разнородных компонентов.
В свою очередь химические превращения при МО можно разделить на механически активированные и механохимические [7, 8]. Механически активированные химические превращения являются термическими, инициируются возникающими при МО структурными дефектами, от которых сильно зависят. В отличие от них механохимические превращения обусловлены действием механических сил, протекают при низкой температуре и являются атермическими. На этой стадии под действием деформации при начальной температуре происходит перемешивание твердых компонентов на молекулярном или кластерном уровне. Она предшествует стадии образования непосредственно продукта реакции. Механохимические процессы, обусловливающие частичное или полное растворение одного компонента в другом еще на стадии механообработки, присущи многим конденсированным системам, например, Ni–Al, Nb–Si, Mg–MoO3, Mg–Tf, Al–Ti, Al–Fe и др. [9–15].
На современном этапе развития исследований немаловажное значение приобретают задачи моделирования и управления физико-химическими процессами в реакционных средах. Достаточно отметить, что этой проблеме посвящены тематики многих научных симпозиумов и конференций (например, [16, 17]). В большинстве случаев моделирование хоть и не дает точных количественных оценок, но позволяет осуществлять целенаправленный поиск оптимальных химико-технологических режимов, тем самым сокращая число проводимых экспериментов.
Цель настоящей работы – построение в макроскопическом приближении математической модели механохимических и структурных превращений в бинарной порошковой смеси при ее механической обработке и оценка динамики параметров, определяющих этот процесс.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Рассмотрим бинарную порошковую смесь металлических компонентов А и В, массовая доля компонента А в смеси – ${{c}_{0}}$. Плотности компонентов А и В: ${{\rho }_{A}}$ и ${{\rho }_{B}}$ соответственно. В ходе механической обработки в энергонапряженной мельнице компоненты измельчаются, активируются и образуют в результате агломерации механокомпозиты АВ. Пусть более твердым является компонент А, компонент В измельчается лучше. В механокомпозите между компонентами А и В через сформированную межфазную поверхность осуществляется образование продукта механохимического превращения F, массовая доля компонента А в котором – $c{\text{*}}.$
Не умаляя общности дальнейшего анализа, примем следующие упрощения:
1. Для моделирования процесса в макроскопическом приближении предполагается осредненное его описание в масштабе всего измельчителя – аппарата, в котором смесь реагентов подвергается интенсивному механическому воздействию.
2. Частицы компонентов А, В и механокомпозитов АВ имеют сферическую форму, измельчаются независимо друг от друга.
3. Соблюдается равенство плотностей всех конденсированных веществ. Такое приближение позволяет не учитывать движение вещества за счет химического превращения, что существенно упрощает математические выкладки.
4. Процесс механической обработки порошковой смеси рассматривается в изотермическом приближении, без учета диссипации тепла от работы измельчителя.
Согласно [7], величина выхода продукта, обусловленная механохимическим превращением, пропорциональна межфазной поверхности, формирующейся в механокомпозитах в результате механической обработки порошковой смеси. Тогда можно записать следующее уравнение:
где $\alpha $ – полнота механохимического превращения, определенная как отношение массы продукта к массе смеси в целом; $D = {{tW} \mathord{\left/ {\vphantom {{tW} V}} \right. \kern-0em} V}$ – доза поглощенной порошковой смесью энергии в результате работы энергонапряженной мельницы; $t$ – время; $W$ – мощность мельницы; $V$ – объем смеси; $m$ – коэффициент; $F(S)$ – функция реакционной поверхности или величина относительной внутренней межфазной поверхности в механокомпозите.С учетом принятых выше допущений динамику механической обработки бинарной порошковой смеси опишем следующими уравнениями:
– измельчения, определяющего величину удельных поверхностей частиц компонентов А и В, и механокомпозитов АВ [18]
(2)
$\frac{{d{{s}_{i}}}}{{dt}} = \left( {1 - \frac{{{{s}_{i}}}}{{{{s}_{{mi}}}}}} \right){{k}_{i}}\,\,\,\,\left( {i = A,B} \right),$(3)
$\begin{gathered} \frac{{d({{s}_{{AB}}})}}{{dt}} = \left( {1 - \frac{{{{s}_{{AB}}}}}{{{{s}_{{mAB}}}}}} \right){{k}_{{AB}}} + \\ + \,\,\left[ {\frac{{{{s}_{A}}{{s}_{B}}{{\mu }_{A}}{{\mu }_{B}}(\lambda {{\mu }_{A}} + {{\mu }_{B}})}}{{{{\mu }_{{AB}}}({{s}_{A}}{{\mu }_{B}} + \lambda {{s}_{B}}{{\mu }_{A}})}} - \frac{{{{s}_{{AB}}}({{\mu }_{A}} + {{\mu }_{B}})}}{3}} \right]q, \\ \end{gathered} $– изменения относительных объемов компонентов А и В при агломерации [18]
(4)
$\begin{gathered} \frac{{d{{\mu }_{i}}}}{{dt}} = - \left[ {\mu _{i}^{2}{{\mu }_{j}} + {{\mu }_{i}}{{\mu }_{{AB}}}\left( {{{\mu }_{A}} + {{\mu }_{B}}} \right)} \right]\frac{{\lambda q}}{{\lambda {{\mu }_{A}} + {{\mu }_{B}}}} \\ (i,j = A,B;\,\,\,i \ne j), \\ \end{gathered} $– изменения относительной межфазной поверхности в механокомпозитах [19]
(5)
$\frac{{dF(S)}}{{dt}} = P({{v}_{A}},{{v}_{B}})\frac{{{{s}_{{AB}}}}}{{{{s}_{{mAB}}}}} - \frac{{F(S)}}{{{{\mu }_{{AB}}}}}\frac{{d{{\mu }_{{AB}}}}}{{dt}},$– механохимического превращения, полученного из (1)
– скорости избыточной энергии в реагентах и продукте F [20, 21]
(7)
$\frac{{d{{\varphi }_{i}}}}{{dt}} = {{I}_{i}} - {{\varphi }_{i}}{{y}_{i}}\exp \left( { - \frac{{{{U}_{i}} - {{\varphi }_{i}}}}{{RT}}} \right)\,\,\,\,(i = A,B),$(8)
$\begin{gathered} \frac{{d{{\varphi }_{F}}}}{{dt}} = {{I}_{F}} + \frac{1}{\alpha }\left[ {{{A}_{1}}c{\text{*}}{{\varphi }_{A}} + {{B}_{1}}(1 - c{\text{*}}){{\varphi }_{B}} - {{\varphi }_{F}}} \right] \times \\ \times \,\,\frac{{d\alpha }}{{dt}} - {{\varphi }_{F}}{{y}_{F}}\exp \left( { - \frac{{{{U}_{F}} - {{\varphi }_{F}}}}{{RT}}} \right). \\ \end{gathered} $В (2)–(8) введены обозначения: ${{V}_{i}}$, ${{s}_{i}} = {{{{S}_{i}}} \mathord{\left/ {\vphantom {{{{S}_{i}}} {{{V}_{i}}}}} \right. \kern-0em} {{{V}_{i}}}},$ ${{S}_{i}}$ – объем, удельная и абсолютная поверхности i-го компонента; ${{s}_{{mA}}},$ ${{s}_{{mB}}},$ ${{s}_{{mAB}}}$ – максимально достижимые величины удельных поверхностей в процессе измельчения; ${{\mu }_{i}} = {{{{V}_{i}}} \mathord{\left/ {\vphantom {{{{V}_{i}}} V}} \right. \kern-0em} V}$ – относительный объем i-го компонента в смеси; $\omega = {W \mathord{\left/ {\vphantom {W V}} \right. \kern-0em} V}$ – удельная мощность мельницы; ${{k}_{A}} = k_{A}^{'}\omega ,$ ${{k}_{B}} = k_{B}^{'}\omega ,$ ${{k}_{{AB}}} = k_{{AB}}^{'}\omega $ – коэффициент измельчения компонентов А, В и АВ соответственно;  $q = q{\kern 1pt} '\omega $ – константа скорости агломерации; $k_{A}^{'},$ $k_{B}^{'},$ $k_{{AB}}^{'},$ $q{\kern 1pt} '$ – коэффициенты, зависящие от физико-химических свойств участвующих в измельчении
и агломерации компонентов; $\lambda $ – коэффициент, учитывающий различие реологических свойств компонентов А и В, величина
которого изменяется в пределах от 0 (агломераты из разнородных частиц не образуются)
до 1 (равное участие ${\text{в}}$ образовании агломератов обоих компонентов в предельном случае одинаковых реологических
свойств); $P({{v}_{A}},{{v}_{B}}) = {{K}_{{AB}}}{{v}_{A}}{{v}_{B}}$ – вероятность образования межфазной поверхности между А и В, которая пропорциональна
произведению их объемов (${{v}_{A}}$ и ${{v}_{B}}$) в агломерате [19, 20]; ${{K}_{{AB}}} = K_{{AB}}^{'}\omega $ – коэффициент пропорциональности, линейным образом зависящий от мощности мельницы
(чем интенсивнее механообработка, тем выше вероятность образования разнородных контактов
между компонентами смеси); ${{\varphi }_{i}},$ ${{I}_{i}} = {{a}_{i}}\omega $ – величина избыточной энергии и скорость ее накопления в i-м компоненте; ${{a}_{i}}$ – коэффициент; ${{y}_{i}}$, ${{U}_{i}}$ – предэкспоненциальный множитель и энергия активации релаксации избыточной энергии
в i-м компоненте; ${{A}_{1}}$, ${{B}_{1}}$ – коэффициенты (причем, если ${{A}_{1}} = {{B}_{1}} = 1$ – продукт полностью наследует содержащиеся в реагентах структурные дефекты (а вместе
с ними и избыточную энергию), при ${{A}_{1}} = {{B}_{1}} = 0$ продукт не наследует структурные дефекты реагентов). Отметим, что на практике избыточную
энергию можно отождествить с относительным уширением пиков рентгеновской дифракции
$\Delta {{h}_{i}} = \frac{{{{H}_{i}} - {{H}_{{i0}}}}}{{{{H}_{{i0}}}}}$ (где ${{H}_{{i0}}},$ ${{H}_{i}}$ – уширение пиков рентгеновской дифракции i-м компоненте, находящемся в нормальном и активированном (содержащем структурные несовершенства)
состояниях соответственно) [22]. В [20, 21] было принято, что количество запасенной избыточной энергии пропорционально относительному
уширению $\Delta {{h}_{i}}$, т.е. ${{\varphi }_{i}} = {{K}_{i}}\Delta {{h}_{i}}$ (где ${{K}_{i}}$ – коэффициент). Конечная полнота механохимического превращения ${{\alpha }_{k}}$ в (6) будет определяться соотношением
$q = q{\kern 1pt} '\omega $ – константа скорости агломерации; $k_{A}^{'},$ $k_{B}^{'},$ $k_{{AB}}^{'},$ $q{\kern 1pt} '$ – коэффициенты, зависящие от физико-химических свойств участвующих в измельчении
и агломерации компонентов; $\lambda $ – коэффициент, учитывающий различие реологических свойств компонентов А и В, величина
которого изменяется в пределах от 0 (агломераты из разнородных частиц не образуются)
до 1 (равное участие ${\text{в}}$ образовании агломератов обоих компонентов в предельном случае одинаковых реологических
свойств); $P({{v}_{A}},{{v}_{B}}) = {{K}_{{AB}}}{{v}_{A}}{{v}_{B}}$ – вероятность образования межфазной поверхности между А и В, которая пропорциональна
произведению их объемов (${{v}_{A}}$ и ${{v}_{B}}$) в агломерате [19, 20]; ${{K}_{{AB}}} = K_{{AB}}^{'}\omega $ – коэффициент пропорциональности, линейным образом зависящий от мощности мельницы
(чем интенсивнее механообработка, тем выше вероятность образования разнородных контактов
между компонентами смеси); ${{\varphi }_{i}},$ ${{I}_{i}} = {{a}_{i}}\omega $ – величина избыточной энергии и скорость ее накопления в i-м компоненте; ${{a}_{i}}$ – коэффициент; ${{y}_{i}}$, ${{U}_{i}}$ – предэкспоненциальный множитель и энергия активации релаксации избыточной энергии
в i-м компоненте; ${{A}_{1}}$, ${{B}_{1}}$ – коэффициенты (причем, если ${{A}_{1}} = {{B}_{1}} = 1$ – продукт полностью наследует содержащиеся в реагентах структурные дефекты (а вместе
с ними и избыточную энергию), при ${{A}_{1}} = {{B}_{1}} = 0$ продукт не наследует структурные дефекты реагентов). Отметим, что на практике избыточную
энергию можно отождествить с относительным уширением пиков рентгеновской дифракции
$\Delta {{h}_{i}} = \frac{{{{H}_{i}} - {{H}_{{i0}}}}}{{{{H}_{{i0}}}}}$ (где ${{H}_{{i0}}},$ ${{H}_{i}}$ – уширение пиков рентгеновской дифракции i-м компоненте, находящемся в нормальном и активированном (содержащем структурные несовершенства)
состояниях соответственно) [22]. В [20, 21] было принято, что количество запасенной избыточной энергии пропорционально относительному
уширению $\Delta {{h}_{i}}$, т.е. ${{\varphi }_{i}} = {{K}_{i}}\Delta {{h}_{i}}$ (где ${{K}_{i}}$ – коэффициент). Конечная полнота механохимического превращения ${{\alpha }_{k}}$ в (6) будет определяться соотношением
Отметим, что при $c* = {{c}_{0}}$ (смесь рассчитана на получение продукта F) следует очевидное равенство ${{\alpha }_{k}} = 1.$
Вычислим входящие в функцию $P({{v}_{A}},{{v}_{B}})$ величины ${{v}_{A}}$ и ${{v}_{B}}$, являющиеся объемными долями компонентов А и В в механокомпозите. С учетом того, что механохимическое превращение осуществляется только в механокомпозите, в конечном итоге соотношение для величин ${{v}_{A}}$ и ${{v}_{B}}$ можно записать в виде
(9)
$\begin{gathered} {{v}_{A}} = \frac{{{{\mu }_{{0A}}} - {{\mu }_{A}} - c{\text{*}}\alpha }}{{{{\mu }_{{AB}}}}}, \\ {{v}_{B}} = \frac{{{{\mu }_{{0B}}} - {{\mu }_{B}} - (1 - c*)\alpha }}{{{{\mu }_{{AB}}}}}. \\ \end{gathered} $В силу допущения № 3 связь между объемами компонентов в механообрабатываемой смеси можно представить следующей зависимостью:
(10)
${{\mu }_{A}} + {{\mu }_{B}} + {{\mu }_{{AB}}} = 1,\,\,\,\,\frac{{\left( {1 - {{c}_{0}}} \right)}}{{{{c}_{0}}}}{{\mu }_{{0A}}} = {{\mu }_{{0B}}}.$Соотношение для эффективной (осредненной) избыточной энергии, содержащейся в единице объема порошковой смеси, запишем в виде
(11)
$\varphi = {{\varphi }_{A}}{{\mu }_{A}} + {{\varphi }_{B}}{{\mu }_{B}} + {{\varphi }_{F}}{{\mu }_{F}}.$Так как составляющие смесь частицы сферические, то их размеры связаны с удельными поверхностями следующими соотношениями:
(12)
$\begin{gathered} {{r}_{A}} = {3 \mathord{\left/ {\vphantom {3 {{{s}_{A}}}}} \right. \kern-0em} {{{s}_{A}}}},\,\,\,\,{{r}_{B}} = {3 \mathord{\left/ {\vphantom {3 {{{s}_{B}},}}} \right. \kern-0em} {{{s}_{B}},}}\,\,\,\,{{r}_{{AB}}} = {3 \mathord{\left/ {\vphantom {3 {{{s}_{{AB}}}}}} \right. \kern-0em} {{{s}_{{AB}}}}}, \\ {{r}_{{mA}}} = {3 \mathord{\left/ {\vphantom {3 {{{s}_{{mA}}}}}} \right. \kern-0em} {{{s}_{{mA}}}}},\,\,\,\,{{r}_{{mB}}} = {3 \mathord{\left/ {\vphantom {3 {{{s}_{{mB}}}}}} \right. \kern-0em} {{{s}_{{mB}}}}},\,\,\,\,{{r}_{{mAB}}} = {3 \mathord{\left/ {\vphantom {3 {{{s}_{{mAB}}}}}} \right. \kern-0em} {{{s}_{{mAB}}}}}. \\ \end{gathered} $В (12) величины ${{r}_{{mA}}},$ ${{r}_{{mB}}},$ ${{r}_{{mAB}}}$ – минимальные значения размеров частиц, достижимые при измельчении.
В [19] была определена относительная толщина слоя в структуре слоистого механокомпозита
где $r{\text{*}}$ – размерная толщина слоя. В (13) параметр $F(S)$ находится из уравнения (5) без учета влияния на величины ${{v}_{A}}$ и ${{v}_{B}}$ механохимического превращения. Таким образом, толщина чередующихся внутренних слоев $d$, состоящих из входящих в механокомпозит разнородных компонентов, будет характеризовать степень слоистости его структуры.Начальные условия:
(14)
$\begin{gathered} t = 0{\kern 1pt} :{{s}_{A}} = {{s}_{{0A}}},\,\,\,\,{{s}_{B}} = {{s}_{{0B}}},\,\,\,\,{{\mu }_{A}} = {{\mu }_{{0A}}}, \\ {{\mu }_{B}} = {{\mu }_{{0B}}},\,\,\,\,{{\mu }_{{AB}}} = 0,\,\,\,\,{{\varphi }_{A}} = {{\varphi }_{B}} = {{\varphi }_{F}} = 0, \\ \alpha = 0. \\ \end{gathered} $Зависимости (1)–(14) в макроскопическом приближении описывают динамику механохимических и структурных превращений в ходе механической обработки бинарной порошковой смеси.
ИССЛЕДОВАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
С целью сокращения числа параметров, выделения основных из них, удобства анализа и вычислений будем использовать безразмерные величины. Для этого введем параметр $t* = 1{\text{/}}\omega m$ – характерное время механохимического превращения компонентов, применив который безразмерные величины запишем в виде $\tau = {t \mathord{\left/ {\vphantom {t {t{\text{*}}}}} \right. \kern-0em} {t{\text{*}}}} = t\omega m;$ ${{\bar {s}}_{i}} = {{{{s}_{i}}} \mathord{\left/ {\vphantom {{{{s}_{i}}} {{{s}_{{mi}}}}}} \right. \kern-0em} {{{s}_{{mi}}}}};$ ${{\bar {\varphi }}_{i}} = {{{{\varphi }_{i}}} \mathord{\left/ {\vphantom {{{{\varphi }_{i}}} {RT}}} \right. \kern-0em} {RT}};$ ${{\bar {k}}_{i}} = {{k}_{i}}t* = {{k_{i}^{'}} \mathord{\left/ {\vphantom {{k_{i}^{'}} {({{s}_{{mi}}}m)}}} \right. \kern-0em} {({{s}_{{mi}}}m)}},$ $\bar {q} = qt* = {{q{\kern 1pt} '} \mathord{\left/ {\vphantom {{q{\kern 1pt} '} m}} \right. \kern-0em} m},$ ${{\bar {K}}_{{AB}}} = {{K}_{{AB}}}t* = {{K_{{AB}}^{'}} \mathord{\left/ {\vphantom {{K_{{AB}}^{'}} m}} \right. \kern-0em} m},$ ${{\bar {I}}_{i}} = {{{{I}_{i}}t{\text{*}}} \mathord{\left/ {\vphantom {{{{I}_{i}}t{\text{*}}} {RT}}} \right. \kern-0em} {RT}} = {{{{a}_{i}}} \mathord{\left/ {\vphantom {{{{a}_{i}}} {(mRT)}}} \right. \kern-0em} {(mRT)}},$ ${{\bar {y}}_{i}} = {{y}_{i}}t* = {{{{y}_{i}}} \mathord{\left/ {\vphantom {{{{y}_{i}}} {(\omega m)}}} \right. \kern-0em} {(\omega m)}}$ – отношение характерных времен измельчения компонентов, их агломерации, образования разнородных контактов, накопления и релаксации избыточной энергии к характерному времени механохимического превращения. Дополнительно обозначим: ${{\sigma }_{i}} = {{{{U}_{i}}} \mathord{\left/ {\vphantom {{{{U}_{i}}} {RT}}} \right. \kern-0em} {RT}},$ ${{\bar {s}}_{{0i}}} = {{{{s}_{{0i}}}} \mathord{\left/ {\vphantom {{{{s}_{{0i}}}} {{{s}_{{mi}}}}}} \right. \kern-0em} {{{s}_{{mi}}}}},$ ${{\chi }_{B}} = {{{{s}_{{mAB}}}} \mathord{\left/ {\vphantom {{{{s}_{{mAB}}}} {{{s}_{{mB}}}}}} \right. \kern-0em} {{{s}_{{mB}}}}},$ ${{\chi }_{A}} = {{{{s}_{{mAB}}}} \mathord{\left/ {\vphantom {{{{s}_{{mAB}}}} {{{s}_{{mA}}}}}} \right. \kern-0em} {{{s}_{{mA}}}}}.$
В безразмерных величинах основные уравнения и соотношения записанной выше математической модели принимают вид
(15)
$\frac{{d{{{\bar {s}}}_{i}}}}{{d\tau }} = \left( {1 - {{{\bar {s}}}_{i}}} \right){{\bar {k}}_{i}}\,\,\left( {i = A,B} \right),$(16)
$\begin{gathered} \frac{{d({{{\bar {s}}}_{{AB}}})}}{{d\tau }} = \left( {1 - {{{\bar {s}}}_{{AB}}}} \right){{{\bar {k}}}_{{AB}}} + \\ + \,\,\left[ {\frac{{{{{\bar {s}}}_{A}}{{{\bar {s}}}_{B}}{{\mu }_{A}}{{\mu }_{B}}(\lambda {{\mu }_{A}} + {{\mu }_{B}})}}{{{{\mu }_{{AB}}}({{{\bar {s}}}_{A}}{{\mu }_{B}}{{\chi }_{B}} + \lambda {{{\bar {s}}}_{B}}{{\mu }_{A}}{{\chi }_{A}})}} - \frac{{{{{\bar {s}}}_{{AB}}}({{\mu }_{A}} + {{\mu }_{B}})}}{3}} \right]\bar {q}, \\ \end{gathered} $(17)
$\begin{gathered} \frac{{d{{\mu }_{i}}}}{{d\tau }} = - \left[ {\mu _{i}^{2}{{\mu }_{j}} + {{\mu }_{i}}{{\mu }_{{AB}}}\left( {{{\mu }_{A}} + {{\mu }_{B}}} \right)} \right]\frac{{\lambda \bar {q}}}{{\lambda {{\mu }_{A}} + {{\mu }_{B}}}} \\ \left( {i,j = A,B;\,\,\,\,i \ne j} \right), \\ \end{gathered} $(18)
$\frac{{dF(S)}}{{d\tau }} = {{\bar {K}}_{{AB}}}{{v}_{A}}{{v}_{B}}{{\bar {s}}_{{AB}}} - \frac{{F(S)}}{{{{\mu }_{{AB}}}}}\frac{{d{{\mu }_{{AB}}}}}{{d\tau }},$(21)
$\begin{gathered} \frac{{d{{{\bar {\varphi }}}_{F}}}}{{d\tau }} = {{{\bar {I}}}_{F}} + \frac{1}{\alpha }\left[ {{{A}_{1}}c{\text{*}}{{{\bar {\varphi }}}_{A}} + {{B}_{1}}(1 - c{\text{*}}){{{\bar {\varphi }}}_{B}} - {{{\bar {\varphi }}}_{F}}} \right] \times \\ \times \,\,\frac{{d\alpha }}{{d\tau }} - {{{\bar {\varphi }}}_{F}}{{{\bar {y}}}_{F}}\exp \left( { - {{\sigma }_{F}} + {{{\bar {\varphi }}}_{F}}} \right), \\ \end{gathered} $(22)
$\bar {\varphi } = {{\bar {\varphi }}_{A}}{{\mu }_{A}} + {{\bar {\varphi }}_{B}}{{\mu }_{B}} + {{\bar {\varphi }}_{F}}{{\mu }_{F}}.$(23)
$\begin{gathered} \tau = 0{\kern 1pt} :\,\,\,\,{{{\bar {s}}}_{A}} = {{{\bar {s}}}_{{0A}}},\,\,\,\,{{{\bar {s}}}_{B}} = {{{\bar {s}}}_{{0B}}},\,\,\,\,{{\mu }_{A}} = {{\mu }_{{0A}}}, \\ {{\mu }_{B}} = {{\mu }_{{0B}}},\,\,\,\,{{\mu }_{{AB}}} = 0,\,\,\,\,{{{\bar {\varphi }}}_{A}} = {{{\bar {\varphi }}}_{B}} = {{{\bar {\varphi }}}_{F}} = 0, \\ \alpha = 0. \\ \end{gathered} $Дополнительно сформулируем следующие допущения: продукт F не наследует структурные дефекты реагентов (${{A}_{1}} = {{B}_{1}} = 0$); ${{\chi }_{A}} = {{\chi }_{B}} = 1$; на стадии механообработки скорость релаксации структурных дефектов пренебрежимо мала по сравнению со скоростью их накопления, что имеет место при достаточно большой величине мощности мельницы (в этом случае в (20) и (21) можно положить ${{\bar {y}}_{i}} = {{{{y}_{i}}} \mathord{\left/ {\vphantom {{{{y}_{i}}} {(\omega m)}}} \right. \kern-0em} {(\omega m)}} \approx 0$). Также положим, что радиусы частиц находятся из соотношения ${{\bar {r}}_{i}} = {3 \mathord{\left/ {\vphantom {3 {{{{\bar {s}}}_{i}}}}} \right. \kern-0em} {{{{\bar {s}}}_{i}}}}$ ($i = A,\,B,\,AB$). Значения остальных исходных параметров, не варьировавшихся в процессе численных расчетов, были следующие: ${{\mu }_{{0A}}} = {{\mu }_{{0B}}} = 0.5,$ ${{c}_{0}} = 0.5,$ $c* = 0.3,$ ${{\bar {k}}_{A}} = 0.5,$ ${{\bar {k}}_{B}} = 1,$ ${{\bar {k}}_{{AB}}} = 0.8,$ ${{\bar {K}}_{{AB}}} = 5,$ ${{\bar {I}}_{A}} = {{\bar {I}}_{B}} = {{\bar {I}}_{F}} = 0.5.$
РЕШЕНИЕ ЗАДАЧИ И АНАЛИЗ РЕЗУЛЬТАТОВ
На рис. 1 и 2 представлена динамика механохимических и структурных превращений при механической обработки порошковой смеси в энергонапряженной мельнице. Как следует из рис. 1, с увеличением времени механической обработки происходит измельчение частиц и, в соответствии с этим, рост величины их удельных поверхностей (кривые 1, 2). Так как дробление компонента В осуществляется быстрее, то в процессе МО достигается большая величина поверхности его частиц. Значения ${{\bar {s}}_{A}}$ и ${{\bar {s}}_{B}}$ увеличиваются до полной агломерации компонентов в механокомпозиты. Удельная поверхность ${{\overline s }_{{AB}}}$ измельчающихся в результате МО механокомпозитов растет, асимптотически приближаясь к единице (кривая 3).
Рис. 1.
Динамика величины удельных поверхностей компонентов А (1), В (2), агломератов АВ (3), а также межфазной поверхности $F(S)$ с учетом (4) и без учета (4') механохимического превращения в процессе МО при $\bar {q} = 1.$
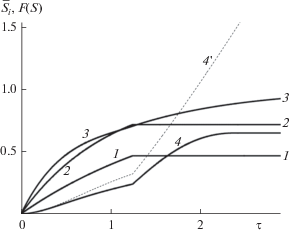
Рис. 2.
Зависимости величин объемных долей компонентов А (1) и В (2), глубины химического превращения (3), избыточной энергии в агломератах (4) от времени МО при $\bar {q} = 1.$
В условиях МО происходит изменение не только внешней, но и внутренней (межфазной) поверхности $F(S)$ в механокомпозитах (кривые 4 и 4'). В ходе циклов измельчение–агломерация внутренняя структура механокомпозитов усложняется, повышается однородность распределения компонентов в них. Сначала величина $F(S)$ увеличивается, а затем, по мере образования продукта механохимического превращения, практически не изменяется (кривая 4). Последнее можно объяснить тормозящим действием образующихся продуктов механохимической реакции на скорость роста межфазной поверхности.
Если механокомпозиты состоят только из чистых компонентов А и В (при МО механохимического превращения нет), то с продлением работы мелющего устройства межфазная поверхность продолжает непрерывно возрастать (кривая 4 '), усложняя внутреннюю структуру агломератов АВ, повышая степень их слоистости даже после того, как будет достигнут предел измельчения частиц.
Динамику фазового состава, а также избыточной энергии в образующихся в результате МО механокомпозитах демонстрирует рис. 2. С продлением времени механообработки доли компонентов А и В в механокомпозите (кривые 1 и 2) сначала практически не изменяются и остаются равными их соотношению в исходной смеси. Затем, по мере образования продукта $F$ (кривая 3), доли компонентов начинают уменьшаться. При достижении максимально возможной полноты механохимического превращения происходит исчерпание компонента В, после чего объемная доля А не меняется.
Динамика избыточной энергии в механокомпозитах при МО носит немонотонный характер (рис. 2, кривая 4). Как видно из рисунка, на начальных этапах работы мельницы дефектность структуры в механокомпозитах повышается, вследствие чего происходит рост величины накопленной в них избыточной энергии ${{\bar {\varphi }}_{{AB}}}$. Затем, по мере образования продукта механохимического превращения, наблюдается частичная нормализация дефектной структуры механокомпозита и некоторое снижение величины ${{\bar {\varphi }}_{{AB}}}$. После завершения формирования фазы F, с продлением механообработки, запас избыточной энергии в механокомпозите снова растет.
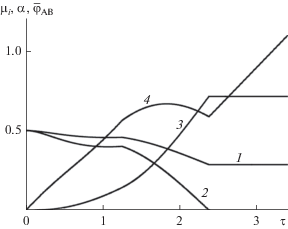
Диаграмма в координатах константа скорости агломерации ($\bar {q}$)–время механической обработки (${{\tau }_{m}}$), определяющая различные сценарии механохимических и структурных превращений в бинарной порошковой смеси, показана на рис. 3. Отметим, что на практике для одной и той же системы А–В уменьшить действие агломерации (и тем самым снизить нежелательное протекание химической реакции между компонентами) можно путем проведения МО в различных инертных средах: например, жидкой [15]. Нередко варьировать константу скорости агломерации удается через введение в реакционную смесь добавки-пассиватора. Такой добавкой, к примеру, могут являться растворимые соли, которые после механообработки отмываются от продуктов [23].
Рис. 3.
Диаграмма константа скорости агломерации ($\bar {q}$) – время механической обработки (${{\tau }_{m}}$). Обозначения разъяснены в тексте.
На диаграмме линии 1–4 являются геометрическим местом точек, выражающих следующие характеристики механообрабатываемой порошковой смеси: ${{\mu }_{{AB}}} = \mu _{{AB}}^{*},$ $\alpha = \alpha {\text{*,}}$ ${{\bar {r}}_{i}} = \bar {r}*,$ $\bar {\varphi } = \bar {\varphi }{\text{*}}$ соответственно. Величины $\mu _{{AB}}^{*},$ $\alpha {\text{*}}$, $\bar {r}{\text{*}}$ и $\bar {\varphi }{\text{*}}$ задаются дополнительно исходя из конкретных требований к конечному продукту механообработки. В данном случае полагалось: $\mu _{{AB}}^{*} = 1,$ $\alpha * = {{\alpha }_{k}},$ $\bar {r}* = \max ({{\bar {r}}_{i}}) = 0.99$ ($i = A,B,AB$), $\bar {\varphi }* = 1.5.$
Из диаграммы следует, что в зоне режимов МО, соответствующих точкам, расположенным выше линии 1, будет наблюдаться полная агломерация порошковой смеси в механокомпозиты. Точки выше линии 2 характеризуют режимы МО, способствующих образованию наибольшего количества продукта механохимического превращения F.
При режимах МО, соответствующих точкам ($\bar {q}$, ${{\tau }_{m}}$) над линиями 3 и 4, происходит максимальное измельчение порошковой смеси и достаточная степень ее активации.
Области параметров механического воздействия, расположенные ниже линии 3, не представляют значительного практического интереса, так как здесь продукт механообработки является неизмельченным и малоактивированным.
На диаграмме имеются шесть основных областей, определяющих режимы МО, при которых порошковая смесь подвергается существенной механообработке. Области I и II отвечают режимам МО, способствующим высокой степени измельчения исходных компонентов, но их агломерация недостаточна. Причем в I продукт – неактивированный, а в II – активированный.
В областях III и IV порошковая смесь является полностью агломерированной, тонко помолотой и состоит из неактивированных (III) и активированных (IV) слоистых частиц механокомпозитов, в которых доля продукта F невелика.
В областях V и VI доля продукта механохимического превращения в полностью агломерированной и предельно измельченной порошковой смеси максимальна. В V механокомпозиты недостаточно активированы, в VI степень их активации высока.
Отметим, что на основе построенных подобного типа диаграмм можно находить области существования режимов, оптимальных для получения модифицированных частиц различного назначения.
Если необходимо сформировать максимальное количество малоразмерных, высокоактивных механокомпозитов с развитой межфазной поверхностью, практически не содержащих продукта механохимического превращения – этому случаю будет соответствовать узкая область параметров механообработки IV. Такие реакционноспособные частицы можно использовать, например, для последующего синтеза материалов вне механореактора [12–14, 23–25].
Высокоактивные мелкодисперсные механокомпозиты, в которых доля продукта механохимического превращения значительна (область режимов механообработки VI), применяют в последующих технологических циклах для изготовления катализаторов, нанокомпозитов, упрочняющих покрытий и т.д. [9, 26, 27].
ЗАКЛЮЧЕНИЕ
Предложена в макроскопическом приближении математическая модель механохимических и структурных превращений в условиях механической обработки бинарной порошковой смеси. Модель позволяет вычислять основные параметры процесса: объемные доли исходных компонентов и механокомпозитов, размеры и степень дефектности частиц, глубину механохимического превращения.
Показано, что варьирование величин параметров механической обработки может существенно влиять на динамику механохимических и структурных превращений, а также на характеристики конечных продуктов в порошковой смеси. Определены области параметров МО, при которых возможно получение малоразмерных частиц механокомпозитов с различным фазовым составом и сложной внутренней структурой.
ОБОЗНАЧЕНИЯ
| ${{c}_{0}}$ | массовая доля компонента А в смеси |
| ${{c}_{*}}$ | массовая доля компонента А в продукте механического смешения F |
| $D$ | доза поглощенной порошковой смесью энергии в результате работы энергонапряженной мельницы |
| $d$ | степень слоистости механокомпозита |
| $F(S)$ | функция реакционной поверхности |
| ${{H}_{{i0}}}$, ${{H}_{i}}$ | уширение пиков рентгеновской дифракции в i-м компоненте, находящемся в нормальном и активированном (содержащем структурные несовершенства) состояниях соответственно |
| $\Delta {{h}_{i}}$ | относительное уширение пиков рентгеновской дифракции |
| ${{k}_{A}}$, ${{k}_{B}}$, ${{k}_{{AB}}}$ | коэффициент измельчения компонентов А, В, АВ соответственно |
| $k_{A}^{'},$$k_{B}^{'}$, $k_{{AB}}^{'}$, $q{\kern 1pt} '$, $\lambda $, $m$, ${{K}_{{AB}}}$, ${{A}_{1}}$, ${{B}_{1}}$, ${{K}_{i}}$, ${{\sigma }_{i}}$, ${{a}_{i}}$, ${{\chi }_{B}}$, ${{\chi }_{A}}$ | коэффициенты |
| $P({{v}_{A}},{{v}_{B}})$ | вероятность образования межфазной поверхности между А и В |
| $q$ | константа скорости агломерации |
| ${{r}_{A}}$, ${{r}_{B}}$, ${{r}_{{AB}}}$ | размеры частиц А, B и AB соответственно |
| ${{r}_{{mA}}}$, ${{r}_{{mB}}}$, ${{r}_{{mAB}}}$ | минимальные значения размеров частиц |
| ${{r}_{*}}$ | размерная толщина слоя в механокомпозите |
| ${{s}_{{0A}}}$, ${{s}_{{0B}}}$, ${{\mu }_{{0A}}}$, ${{\mu }_{{0B}}}$ | начальные значения величин ${{s}_{A}}$, ${{s}_{B}}$, ${{\mu }_{A}}$ и ${{\mu }_{B}}$ соответственно |
| ${{s}_{{mA}}}$, ${{s}_{{mB}}}$, ${{s}_{{mAB}}}$ | максимально достижимые величины удельных поверхностей в процессе измельчения |
| $t$ | время |
| $t{\text{*}}$ | характерное время механохимического смешения компонентов |
| $V$ | объем смеси |
| ${{V}_{i}}$, ${{s}_{i}}$, ${{S}_{i}}$ | объем, удельная и абсолютная поверхности i-го компонента |
| $W$ | мощность мельницы |
| ${{y}_{i}}$, ${{U}_{i}}$ | предэкспоненциальный множитель и энергия активации релаксации избыточной энергии в i-м компоненте |
| $\alpha $ | полнота механохимического превращения |
| ${{\alpha }_{k}}$ | конечная полнота механохимического превращения |
| ${{\mu }_{i}}$ | относительный объем i-го компонента в смеси |
| $\mu _{{AB}}^{*}$, $\alpha {\text{*}}$, $\bar {r}{\text{*}}$, $\bar {\varphi }{\text{*}}$ | требуемые значения параметров ${{\mu }_{{AB}}}$, $\alpha $, ${{\bar {r}}_{i}}$, $\bar {\varphi }$, достигаемые в процессе механообработки |
| ${{v}_{A}}$, ${{v}_{B}}$ | объемные доли компонентов А и В в механокомпозите |
| ${{\rho }_{A}}$, ${{\rho }_{B}}$ | плотности компонентов А и В соответственно |
| $\tau $, ${{\bar {s}}_{i}}$, ${{\bar {\varphi }}_{i}}$, $\bar {\varphi }$, ${{\bar {k}}_{i}}$, $\bar {q}$, ${{\bar {K}}_{{AB}}}$, ${{\bar {I}}_{i}}$, ${{\bar {y}}_{i}}$, ${{\bar {s}}_{{0i}}}$ | безразмерные аналоги размерных параметров $t$, ${{s}_{i}}$, ${{\varphi }_{i}}$, $\varphi $, ${{k}_{i}}$, $q$, ${{K}_{{AB}}}$, ${{I}_{i}}$, ${{y}_{i}}$, ${{s}_{{0i}}}$ соответственно |
| ${{\tau }_{m}}$ | безразмерное время механической обработки |
| φ | эффективная (осредненная) избыточная энергия |
| ${{\varphi }_{i}}$, ${{I}_{i}}$ | величина избыточной энергии и скорость ее накопления в i-м компоненте |
| $\omega $ | удельная мощность мельницы |
ИНДЕКСЫ
Список литературы
Авакумов Е.Г. Механические методы активации химических процессов. Новосибирск: Наука, 1986.
Heinicke G. Tribochemistry. Berlin: Akad.-Verlag, 1984.
Бутягин Ю.П. Проблемы и перспективы развития механохимии // Усп. хим. 1994. Т. 63. № 12. С. 1031.
Болдырев В.В. Исследования по механохимии твердых веществ // Вестн. РФФИ. 2004. Т. 37. № 3. С. 38.
Болдырев В.В. Механохимия в Сибири // Вестн. Росс. акад. наук. 2018. Т. 88. № 3. С. 258.
Механокомпозиты – прекурсоры для создания материалов с новыми свойствами / Отв. ред. Ломовский О.И. Новосибирск: СО РАН, 2010.
Фундаментальные основы механической активации, механосинтеза и механохимических технологий / Под ред. Аввакумова Е.Г. Новосибирск: СО РАН, 2009.
Бутягин П.Ю., Ющенко В.С. Молекулярная динамика деформационного перемешивания в смесях твердых веществ // Кинет. катал. 1988. Т. 29. № 5. С. 1249.
Кузьмич Ю.В., Колесникова И.Г., Серба В.И., Фрейдин Б.М. Механическое легирование. М.: Наука, 2005.
Шкодич Н.Ф., Кочетов Н.А., Рогачев А.С., Ковалев Д.Ю., Сачкова Н.В. О влиянии механической активации на СВС-составы Ni–Al и Ti-Allow // Изв. высш. учебн. завед. Цветн. металл. № 5. 2006. С. 44.
Korchagin M.A., Lyakhov N.Z. Self-propagating high-temperature synthesis in mechanoactivated compositions // Russ. J. Phys. Chem. B. 2008. V. 2. № 1. P. 77.
Korchagin M.A., Grigor’eva T.F., Bokhonov B.B., Sharafutdinov M.R., Barinova A.P., Lyakhov N.Z. Solid state combustion in mechanically activated SHS systems. I. Effect of Activation Time on Process Parameters and Combustion Product Composition // Combust., Explos., Shock Waves. 2003. V. 32. № 1. P. 43.
Korchagin M.A., Grigorieva T.F., Barinova A.P., Lyakhov N.Z. The effect of mechanical treatment on the rate and limits of combustion in SHS processes // Int. J. Self-Propag. High-Temp. Synth. 2000. V. 9. № 3. P. 307.
Шкода О.А., Лапшин О.В. Механохимическая активация и термическая обработка низкокалорийной порошковой смеси Nb + 2Si. I. Эксперимент // Изв. высш. учебн. завед. Физ. 2018. № 11. С. 3.
Dolgoborodov A.Yu. Mechanically activated oxidizer-fuel energetic composites // Combust., Explos., Shock Waves. 2015. V. 51. № 1. P. 86.
Кошелева М.К., Рудобашта С.П. Международная научно-техническая конференция “Повышение эффективности процессов и аппаратов в химической и смежной областях промышленности” // Теор. осн. хим. технол. 2017. Т. 51. № 2. С. 235.
Ziyatdinov N.N. Modeling and Optimization of Chemical Engineering Processes and Systems // Theor. Found. Chem. Eng. 2017. V. 51. № 6. P. 889. [Зиятдинов Н.Н. Моделирование и оптимизация химико-технологических процессов и систем // Теор. осн. хим. технол. 2017. Т. 51. № 6. С. 613.] https://doi.org/10.1134/S0040579517060197
Лапшин О.В., Смоляков В.К. Динамика структурных превращений при измельчении бинарной смеси // Физ. мезомех. 2011. Т. 14. № 2. С. 77.
Лапшин О.В., Смоляков В.К. Формирование слоистой структуры механокомпозитов при измельчении бинарной смеси // Хим. физ. мезоскопия. 2013. Т. 15. № 2. С. 272.
Смоляков В.К., Лапшин О.В. Макроскопическая кинетика механохимического синтеза. Томск: ИОА СО РАН, 2011.
Smolyakov V.K., Lapshin O.V., Boldyrev V.V. Mathematical simulation of mechanochemical synthesis in macroscopic approximation // Theor. Found. Chem. Eng. 2008. V. 42. № 1. P. 54. [Смоляков В.К., Лапшин О.В., Болдырев В.В. Математическая модель механохимического синтеза в макроскопическом приближении // Теор. осн. хим. технол. 2008. Т. 42. № 1. С. 57.]
Болдырев В.В. Экспериментальные методы в механохимии твердых неорганических веществ. Новосибирск: Наука, 1983.
Tsuzuki T., McCormick P. Mechanochemical synthesis of nanoparticles // J. Mater. Sci. 2004. V. 39. P. 5143.
Reddy B.S.B., Das K., Das S. A review on the synthesis of in situ aluminum based composites by thermal, mechanical, and mechanical-thermal activation of chemical reactions // J. Mater. Sci. 2007. V. 42. P. 9366.
Schoenitz M., Ward T., Dreizin E.L. Fully dense nanocomposite energetic powders prepared by arrested reactive milling // Proc. Combust. Inst. 2005. V. 30. P. 2071.
Корчагин М.А., Кинеловский С.А., Ляхов Н.З. Кумулятивное напыление покрытий нанокомпозитными порошками // II Всероссийская конференция по наноматериалам “НАНО 2007”. Новосибирск, 2007. С. 374.
Reddy B.S.B., Rajasekhar K., Venu M., Dilip J.J.S., Das S., Das K. Mechanical activation-assisted solid-state combustion synthesis of in situ aluminum matrix hybrid (Al3Ni/Al3O2) nanocomposites // J. Alloys Compd. 2008. V. 465. P. 97. https://doi.org/10.1016/j.jallcom.2007.10.098
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии