1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 54, № 2, 2020

Теоретические основы химической технологии, 2020, T. 54, № 2, стр. 228-235

Моделирование виброкипящего слоя частиц силикагеля с использованием метода дискретных элементов

Н. С. Орлова a, *, Е. С. Каменецкий a

a Южный математический институт – филиал Владикавказского научного центра РАН
Владикавказ, Россия

* E-mail: norlova.umi.vnc@gmail.com

Поступила в редакцию 25.05.2019
После доработки 12.11.2019
Принята к публикации 15.11.2019

Полный текст (PDF)

Аннотация

С использованием программного обеспечения LIGGGHTS с открытым исходным кодом, в котором реализован метод дискретных элементов, проведено трехмерное моделирование виброкипящего слоя относительно крупных частиц силикагеля. Рассматривалось виброкипение относительно тонких слоев. В вычислительных экспериментах в процессе виброкипения наблюдалась волнообразная поверхность и отдельные всплески над поверхностью. Численные расчеты среднего по времени распределения объемной доли частиц по высоте виброкипящего слоя сравнивались с экспериментальными данными. Представлена зависимость средней степени расширения виброкипящего слоя (отношения средней высоты виброкипящего слоя к начальной высоте) от безразмерного параметра, учитывающего начальную высоту слоя, амплитуду и частоту колебаний полки, на которой располагается слой частиц. По результатам экспериментальных и расчетных значений средней степени расширения слоя построены графики линейной регрессии. Получено, что с увеличением значения безразмерного параметра средняя степень расширения виброкипящего слоя растет.

Ключевые слова: метод дискретных элементов, LIGGGHTS, виброкипение, численные расчеты, сравнение с экспериментом, крупные частицы

ВВЕДЕНИЕ

Как известно, одним из наиболее эффективных методов поглощения различных газообразных соединений являются кипение и виброкипение адсорбента. Кроме того, кипящий и виброкипящий слои широко используются в процессах сушки дисперсного материала и процессах каталитического синтеза порошковых материалов [1–8]. В связи с этим много работ посвящено теоретическому и экспериментальному исследованию кипения и виброкипения [1–24] (в том числе работы с использованием методов математического моделирования [4, 7, 8, 10–21]).

Следует отметить, что состояние кипящего слоя достигается путем воздействия на слой частиц газового потока, состояние виброкипения – путем воздействия на слой частиц внешних вибраций. Под термином “виброкипящий слой” часто также подразумевают состояние дисперсной среды, в которое она переходит при комбинированном воздействии газового потока и вибраций [16, 17, 21–23].

Для моделирования процесса виброкипения используются в основном континуальный и дискретный подходы. В рамках континуального подхода твердая фаза (т.е. фаза твердых частиц) представляется в виде континуума, и для описания твердой фазы используются такие же уравнения, как для газовой фазы [7, 8, 10–12, 16–19]. Кроме того, в уравнениях учитывается межфазный обмен. При использовании такого подхода необходимо учитывать отношение размера ячейки к размеру частиц [7, 8], поэтому моделирование виброкипения тонких слоев представляется практически невыполнимой задачей. Модели на основе континуального подхода лучше использовать для описания виброкипения относительно толстых слоев мелких частиц [7, 8]. Более подробное описание моделей виброкипения, основанных на континуальном подходе, представлено в работах [7, 8, 10–12, 16–19].

В рамках дискретного подхода слой частиц представляется в виде совокупности отдельных частиц. Решаются уравнения движения для каждой частицы с учетом ее взаимодействия с другими частицами, поэтому расчеты с использованием моделей, основанных на дискретном подходе, являются достаточно трудоемкими (особенно когда рассматривается большое количество частиц). Реализация таких моделей требует использования мощных вычислительных ресурсов. В связи с этим дискретный подход целесообразно использовать для описания виброкипения тонких слоев. В работах [20–24] представлено исследование моделей на основе дискретного подхода.

Трехмерное моделирование процесса виброкипения представляет собой сложную задачу, поэтому в настоящее время часто используются готовые пакеты для решения прикладных задач, включающие встроенные решатели. Например, известны решатели коммерческого пакета ANSYS (Analysis System) [16] и свободно распространяемого пакета OpenFOAM (Open Source Field Operation and Manipulation) [18, 19], предназначенные для моделирования процесса виброкипения. В этих решателях реализованы модели на основе континуального подхода.

Целью настоящей работы является верификация и исследование модели виброкипящего слоя на основе метода дискретных элементов. В работе представлены результаты трехмерного моделирования виброкипения относительно тонких слоев с использованием программного обеспечения LIGGGHTS с открытым исходным кодом [25], в котором реализован метод дискретных элементов (Open Source Discrete Element Method Particle Simulation Code). В связи с тем, что рассматривается воздействие только вибраций на слой частиц (без дополнительного продувания газовым потоком) и исследуется виброкипение относительно тонких слоев, в модели не учитывается влияние газовой фазы на движение частиц. Для верификации модели на основе метода дискретных элементов использовались экспериментальные данные по виброкипению относительно крупных частиц силикагеля (средний диаметр 4 мм) [13]. Использовались слои с начальной толщиной 6, 15 и 20 мм.

МЕТОД ДИСКРЕТНОГО ЭЛЕМЕНТА

В рамках метода дискретного элемента движение каждой отдельной частицы описывается с учетом ее взаимодействия с соседними частицами [26]. Используются следующие уравнения [24, 27]:

(1)
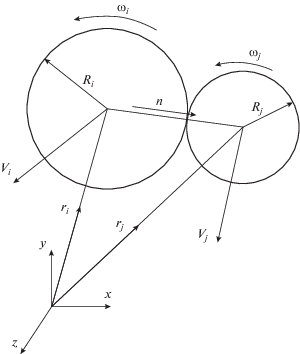
$\left\{ \begin{gathered} {{m}_{i}}\frac{{{\text{d}}{{{\mathbf{V}}}_{i}}}}{{{\text{d}}t}} = {{m}_{i}}{\mathbf{b}} + \sum\limits_{j = 1}^k {{{{\mathbf{F}}}_{{ij}}}} ; \hfill \\ {{I}_{i}}\frac{{{\text{d}}{{{\mathbf{\omega }}}_{i}}}}{{{\text{d}}t}} = \sum\limits_{j = 1}^k {\left( {{{{\mathbf{T}}}_{{ij}}} + {{{\mathbf{M}}}_{{ij}}}} \right)} ; \hfill \\ \end{gathered} \right.$
где ${{m}_{i}}$ – масса частицы; i – индекс частицы, относительно которой рассматривается система уравнений (1); ${{{\mathbf{V}}}_{i}}$ – вектор линейной скорости центра масс; ${{I}_{i}}$ – момент инерции; ${{{\mathbf{\omega }}}_{i}}$ – вектор угловой скорости; ${\mathbf{b}}$ – вектор массовой силы; ${{{\mathbf{F}}}_{{ij}}}$ – внешняя сила, действующая на частицу i через контакт с частицей j; j – индекс частицы, находящейся в контакте с частицей i; k – число частиц в контакте с частицей i; ${{{\mathbf{T}}}_{{ij}}}$ – внешний крутящий момент, связанный с контактным взаимодействием частиц i и j; ${{{\mathbf{M}}}_{{ij}}}$ – момент сопротивления качению.

В методе дискретного элемента каждая частица представляется в виде сферы радиусом ${{R}_{i}}.$ На рис. 1 схематически представлено взаимодействие между частицами i и j (где ${{{\mathbf{r}}}_{i}},{{{\mathbf{r}}}_{j}}$ – радиус-векторы; ${\mathbf{n}}$ –вектор нормали вдоль линии, соединяющей центры частиц i и j).

Рис. 1.

Две взаимодействующие сферические частицы i и j.

Взаимодействие между частицами описывается с использованием модели Герца–Миндлина [28]. В рамках модели предполагается, что частицы при контакте не деформируются, а перекрывают друг друга на величину ${\xi ,}$ образуя пятно контакта. Нормальная и тангенциальная составляющие ${{{\mathbf{F}}}_{{{\text{n}}{\kern 1pt} {\text{'}}ij}}},$ ${{{\mathbf{F}}}_{{{\text{t}}{\kern 1pt} {\text{'}}ij}}}$ суммарной силы взаимодействия между двумя частицами рассчитываются по формулам [24, 26–28]

(2)
${{{\mathbf{F}}}_{{{\text{n}}{\kern 1pt} {\text{'}}ij}}} = {{k}_{{\text{n}}}}{{{\xi }}_{{\text{n}}}}{\mathbf{n}} - {{{\gamma }}_{{\text{n}}}}{{{\mathbf{V}}}_{{\text{n}}}};$
(3)
${{{\mathbf{F}}}_{{{\text{t}}{\kern 1pt} {\text{'}}ij}}} = - \min \left\{ {{{k}_{{\text{t}}}}{{{\xi }}_{{\text{t}}}}{\mathbf{t}} - {{{\gamma }}_{{\text{t}}}}{{{\mathbf{V}}}_{{\text{t}}}};{{{\mu }}_{{\text{s}}}}{{{\mathbf{F}}}_{{\text{n}}}}} \right\},$
где ${{k}_{{\text{n}}}}$– коэффициент упругости при контактном взаимодействии; ${{k}_{{\text{t}}}}$ – коэффициент сдвига при контактном взаимодействии; ${{{\gamma }}_{{\text{n}}}}$ – коэффициент демпфирования в нормальном направлении к контакту; ${{{\gamma }}_{{\text{t}}}}$ – коэффициент демпфирования в тангенциальном направлении к контакту; ${{{\xi }}_{{\text{n}}}}$ – относительное нормальное перекрытие частиц при контактном взаимодействии; ${{{\xi }}_{{\text{t}}}}$ – относительное тангенциальное перекрытие частиц; ${{{\mathbf{V}}}_{{\text{n}}}}$– нормальная составляющая относительной скорости в точке контакта частиц; ${{{\mathbf{V}}}_{{\text{t}}}}$ – тангенциальная составляющая относительной скорости в точке контакта частиц; ${{{\mu }}_{{\text{s}}}}$– коэффициент трения скольжения; ${\mathbf{t}}$ – единичный тангенциальный вектор. Коэффициент упругости рассчитывается с использованием модуля упругости (модуля Юнга) и коэффициента Пуассона. Более подробно выражение для коэффициента упругости, а также выражения для остальных коэффициентов представлены в работах [24, 26–28].

Крутящий момент рассчитывается по формуле

(4)
${{{\mathbf{T}}}_{{ij}}} = \left( {{{R}_{i}}{\mathbf{n}}} \right) \times {{{\mathbf{F}}}_{{{\text{t}}{\kern 1pt} {\text{'}}ij}}}.$

Момент сопротивления качению, возникающий при относительном движении частиц, определяется выражением

(5)
${{{\mathbf{M}}}_{{ij}}} = - {{{\mu }}_{{\text{r}}}}{{k}_{{\text{n}}}}{{{\xi }}_{{\text{n}}}}R{\text{*}}\frac{{{{{\mathbf{\omega }}}_{i}}}}{{\left| {{{{\mathbf{\omega }}}_{i}}} \right|}},$
где ${{{\mu }}_{{\text{r}}}}$ – коэффициент трения качения; $R{\text{*}}$ – приведенный радиус частиц [24, 26–28].

После интегрирования системы уравнений (1) с учетом (2)–(5) рассчитываются скорости и перемещения каждой частицы.

УСЛОВИЯ ВЫЧИСЛЕНИЙ

Размеры расчетной области соответствовали размерам экспериментальной установки (высота – 0.4 м, ширина – 0.4 м, толщина – 0.4 м). Рассчитывалось 2 с процесса виброкипения. Учитывалось столкновение частиц с колеблющейся полкой. Коэффициент восстановления в случае столкновений частиц с полкой, изготовленной из стали, принимался равным 0.5 [7, 8, 13]. В табл. 1 представлены значения входных параметров задачи.

Таблица 1.  

Значения входных параметров задачи

Параметр Значение
Плотность материала частиц, кг/м3 650
Диаметр частиц, м 0.004
Коэффициент восстановления частица–частица 0.15
Коэффициент восстановления частица–полка 0.5
Модуль Юнга, Н/м2 7 × 1010
Коэффициент Пуассона 0.17
Коэффициент трения скольжения 0.12
Начальная высота слоя, м 0.006–0.02
Шаг по времени, с 1 × 10–4

Начальные условия – упакованные под действием сил тяжести частицы, находящиеся на полке. В начальный момент времени задавались координаты всех частиц и их начальные скорости, равные нулю.

Следует отметить, что при проведении расчетов не учитывались краевые эффекты (взаимодействие частиц с границами расчетной области), поскольку исследовалось поведение слоя гранулированного материала в расчетной области относительно больших размеров, а влияние стенок сказывается только вблизи них. Кроме того, предполагалось, что влияние момента сопротивления качению на движение частиц пренебрежимо мало по сравнению с влиянием крутящего момента, поэтому в расчетах коэффициент трения качения принимался равным нулю.

При проведении вычислительных экспериментов задавалось число частиц N = 20 000 (соответствует толщине слоя Н = 6 мм), N = 50 000 (соответствует толщине слоя Н = 15 мм) и N = 65 000 (соответствует толщине слоя Н = 20 мм). Распараллеливание расчетов проводилось на четырех ядрах с частотой процессора 3.1 ГГц. Время, затрачиваемое на расчет одного варианта, составляло от примерно 10 до 50 ч в зависимости от задаваемого числа частиц.

СРАВНЕНИЕ РАСЧЕТОВ С ЭКСПЕРИМЕНТАЛЬНЫМИ ДАННЫМИ

По результатам вычислительных экспериментов были построены средние по времени графики изменения объемной доли частиц αav по высоте слоя. Использовалась методика, которая применялась ранее для обработки экспериментальных данных [10, 13, 19] и результатов вычислительных экспериментов [24].

Следует отметить, что в известной литературе не представлены значения модуля Юнга (упругости) и коэффициента Пуассона для твердых частиц силикагеля. Как известно, силикагель представляет собой синтетический диоксид кремния, в природе это обычный кварц. Поэтому в качестве значений модуля Юнга, коэффициента Пуассона, а также коэффициента трения были взяты справочные данные для частиц кварца [29–32]. В действительности для частиц силикагеля эти значения могут несколько отличаться. В связи с этим были проведены дополнительные расчеты при разных комбинациях значений модуля Юнга, коэффициента Пуассона и коэффициента трения. Значения этих параметров меняли (увеличивали и уменьшали) в пределах примерно 10% от справочных значений, представленных в табл. 1. При обработке полученных расчетов выяснилось, что изменение этих параметров практически не влияет на среднюю степень расширения виброкипящего слоя (отношение средней высоты виброкипящего слоя к его начальной высоте) и среднее по времени распределение объемной доли частиц по его высоте. Поэтому далее представлены результаты расчетов, полученные при значениях параметров, которые представлены в табл. 1.

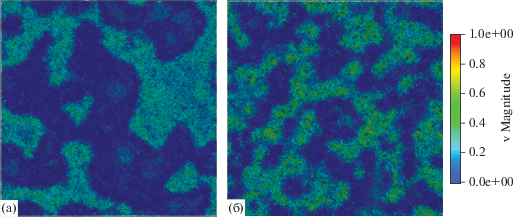
В результате предыдущих исследований было установлено, что в процессе виброкипения наблюдается волнообразная поверхность и отдельные всплески над поверхностью слоя частиц [7, 8, 10, 18, 19]. В вычислительных экспериментах, полученных с использованием метода дискретных элементов, также наблюдается волнообразная поверхность в процессе виброкипения и отдельные всплески над поверхностью. Это видно из рис. 2, на котором представлено распределение скорости частиц (вид сверху) для случая, когда амплитуда колебаний А = 2 мм, частота колебаний f = 30 (рис. 2а) и 36 Гц (рис. 2б). Начальная толщина слоя была равна Н = 15 мм. С использованием свободно распространяемого пакета ParaView v.5.5 осуществлялась визуализация данных. Синим цветом окрашены частицы с минимальной скоростью, зеленым цветом – частицы с максимальной скоростью. Остальные частицы имеют скорость, значения которой лежат в диапазоне между минимальной и максимальной скоростями. Видно, что при большем значении частоты колебаний количество всплесков больше, и максимальная скорость частиц тоже больше. В предыдущих работах [10, 18, 19], посвященных теоретическому и экспериментальному исследованиям процесса виброкипения, уже отмечалось, что с увеличением частоты колебаний увеличивается количество всплесков гранулированного материала.

Рис. 2.

Виброкипящий слой. Вид сверху. Частота колебаний: (а) – 30; (б) – 36 Гц.

На рис. 3 приведено сравнение расчетов среднего по времени распределения объемной доли частиц (αav) с экспериментальными данными, полученными при амплитуде колебаний А = 1.5 мм и частоте колебаний f = 28 Гц. Начальная толщина слоя была равна Н = 6 мм. На рис. 4 представлены результаты сравнения для случая, когда А = 2 мм, f = = 36 Гц, Н = 15 мм, а на рис. 5 – когда А = 1.5 мм, f = 30 Гц, Н = 20 мм.

Рис. 3.

Изменение объемной доли частиц в зависимости от высоты слоя при А = 1.5 мм, f = 28 Гц и Н = 6 мм: 1 – экспериментальные данные; 2 – результаты расчетов.

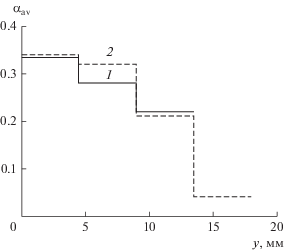
Рис. 4.

Изменение объемной доли частиц в зависимости от высоты слоя при А = 2 мм, f = 36 Гц и Н = 15 мм: 1 – экспериментальные данные; 2 – результаты расчетов.

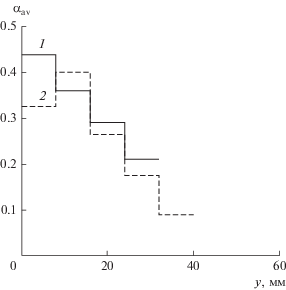
Рис. 5.

Изменение объемной доли частиц в зависимости от высоты слоя при А = 1.5 мм, f = 30 Гц и Н = 20 мм: 1 – экспериментальные данные; 2 – результаты расчетов.

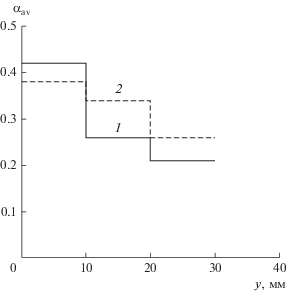
Из приведенных рисунков видно, что в целом результаты расчетов среднего по времени распределения объемной доли частиц удовлетворительно описывают экспериментальные данные. Таким же образом было проведено сравнение результатов расчетов с экспериментальными данными, полученными для слоя с начальной толщиной Н = 6 мм при значениях амплитуды и частоты колебаний: А = 1.5 мм и f = 24 Гц; А = 2 мм и f = 36 Гц. В этих случаях также наблюдалось удовлетворительное совпадение расчетных кривых с экспериментальными. На всех графиках площадь области, ограниченной расчетной кривой, примерно совпадает с площадью области, ограниченной экспериментальной кривой, что свидетельствует о качественном совпадении результатов.

Было проведено сравнение результатов моделирования с экспериментальными данными средней степени расширения виброкипящего слоя (отношения средней высоты виброкипящего слоя к начальной высоте Hav/H). На рис. 6 приведена зависимость средней степени расширения от безразмерного параметра $\Lambda = {{2\pi Af} \mathord{\left/ {\vphantom {{2\pi Af} {{{{\left( {Hg} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {{{{\left( {Hg} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}},$ который учитывает не только амплитуду и частоту колебаний, но и начальную высоту слоя. Параметр $\Lambda $ использовался в работах [7–10] для анализа режимов виброкипения.

Рис. 6.

Зависимость средней степени расширения виброкипящего слоя от безразмерного параметра Λ: 1 – экспериментальные значения; 2 – расчетные значения; 3 – график линейной регрессии, построенный по экспериментальным значениям; 4 – график линейной регрессии, построенный по расчетным значениям.

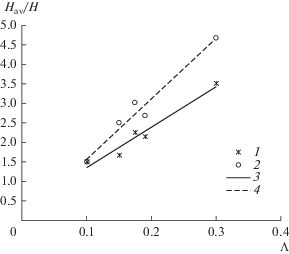
Из рис. 6 видно, что расчетные данные завышены по отношению к экспериментальным. Так как расчетные и экспериментальные значения средней высоты виброкипящего слоя, представленные на рис. 6, были взяты из графиков среднего по времени распределения объемной доли частиц по высоте, разницу между расчетными и экспериментальными данными можно объяснить неточностью значений средней высоты, которая в свою очередь связана с методикой определения средних значений объемной доли частиц.

С увеличением значения безразмерного параметра растет средняя степень расширения виброкипящего слоя за исключением случая, когда $\Lambda = 0.19$ (что соответствует комбинации значений амплитуды А = 2 мм, частоты f = 36 Гц и начальной высоты Н = 15 мм). Это наблюдается как в расчетных данных, так и в экспериментальных. Такое отклонение можно объяснить тем, что параметр $\Lambda $ (несмотря на тот факт, что он учитывает значение начальной толщины слоя) не является универсальным. Как указано в [7, 8, 10], одному значению этого параметра могут соответствовать разные режимы виброкипения.

Следует обратить внимание, что значения $\Lambda = 0.15;$ 0.175 и 0.3 были получены для случаев, когда начальная толщина слоя была равна Н = 6 мм. Завышенное значение средней степени расширения виброкипящего слоя (как в экспериментах, так и в расчетах) при $\Lambda = 0.175$ по отношению к соответствующему значению, полученному при $\Lambda = 0.19,$ можно объяснить тем, что во втором случае (Н = 15 мм) использовался слой гораздо толще. Как известно [7, 8], чем тоньше слой, тем выше степень его расширения в процессе виброкипения.

Значение $\Lambda = 0.1$ соответствует комбинации значений амплитуды А = 1.5 мм, частоты f = 30 Гц и начальной высоты Н = 20 мм. В этом случае рассматривалось виброкипение достаточно толстого слоя при малом значении амплитуды колебаний и среднем (в рамках исследуемого диапазона частот) значении частоты колебаний. В связи с этим степень расширения виброкипящего слоя при таких параметрах ниже, чем в остальных случаях, представленных на рис. 6. Следует отметить, что в предыдущих работах [7, 8, 10, 18, 19] было установлено, что c увеличением амплитуды и частоты колебаний растет степень расширения виброкипящего слоя. При этом амплитуда колебаний оказывает более существенное влияние на степень расширения, чем частота. Частота колебаний влияет на количество всплесков. Чем больше частота колебаний, тем больше всплесков наблюдается над поверхностью слоя [18, 19].

Как указывалось ранее, расчетные данные средней степени расширения виброкипящего слоя завышены по отношению к экспериментальным, т.е. средняя высота виброкипящего слоя в расчетах несколько выше, чем в экспериментальных данных (как показано на рис. 3 и 4). Но если учитывать тот факт, что при значении αav < 0.1 в верхней части виброкипящего слоя наблюдаются единичные частицы [7, 8, 10], то можно заключить, что средние значения высоты виброкипящего слоя в расчетах и экспериментах близки. Также важно отметить, что при больших значениях параметра $\Lambda $ наблюдается большее количество единичных частиц. Единичные частицы сложно зафиксировать при обработке кадров видеосъемки проводимых экспериментов в отличие от результатов визуализации численных расчетов. Поэтому разница между экспериментальными и расчетными данными средней степени расширения виброкипящего слоя на рис. 6 незначительно увеличивается с ростом значения параметра $\Lambda $.

ЗАКЛЮЧЕНИЕ

В результатах моделирования виброкипения тонких слоев частиц силикагеля, полученных с использованием свободно распространяемого пакета LIGGGHTS на основе метода дискретных элементов, так же как и в экспериментах, наблюдается волнообразная поверхность слоя. Получено удовлетворительное совпадение результатов расчетов среднего по времени распределения объемной доли частиц по высоте виброкипящего слоя с экспериментальными данными. Таким образом, можно сделать вывод, что модель на основе метода дискретных элементов, реализованная в пакете LIGGGHTS, позволяет качественно описать процесс виброкипения относительно тонких слоев крупных частиц.

На основе полученных результатов моделирования проведено исследование зависимости средней степени расширения виброкипящего слоя (отношения средней высоты виброкипящего слоя к начальной высоте) от безразмерного параметра, учитывающего начальную высоту слоя, амплитуду и частоту колебаний полки, на которой располагался слой частиц. По результатам экспериментальных и расчетных значений средней степени расширения слоя построены графики линейной регрессии. Получено, что с увеличением значения безразмерного параметра средняя степень расширения виброкипящего слоя растет.

ОБОЗНАЧЕНИЯ

А амплитуда колебаний полки, мм
${\mathbf{b}}$ вектор массовой силы, м/с2
${{{\mathbf{F}}}_{{ij}}}$ внешняя сила, действующая на частицу i через контакт с частицей j, H
f частота колебаний полки, Гц
$g$ ускорение свободного падения, м/с2
H начальная высота слоя частиц (толщина засыпки), мм
Hav средняя высота виброкипящего слоя, мм
$I$ момент инерции, кг м2
${{k}_{{\text{n}}}}$ коэффициент упругости при контактном взаимодействии, Н/м2
${{k}_{{\text{t}}}}$ коэффициент сдвига при контактном взаимодействии, Н/м2
${{{\mathbf{M}}}_{{ij}}}$ момент сопротивления качению, H м
$m$ масса частицы, кг
N число частиц, задаваемое в вычислительных экспериментах
$R$ радиус частицы, м
${\mathbf{r}}$ радиус-вектор, м
${{{\mathbf{T}}}_{{ij}}}$ внешний крутящий момент, связанный с контактным взаимодействием частиц i и j, H м
${\mathbf{V}}$ вектор линейной скорости центра масс, м/с
${{{\alpha }}_{{{\text{av}}}}}$ среднее по времени значение объемной доли частиц
${\gamma }$ коэффициент демпфирования, кг/с
$\Lambda $ безразмерный параметр
${{{\mu }}_{{\text{r}}}}$ коэффициент трения качения
${{{\mu }}_{{\text{s}}}}$ коэффициент трения скольжения
${\xi }$ относительное перекрытие частиц, м
${\mathbf{\omega }}$ вектор угловой скорости, рад/с

ИНДЕКСЫ

аv средний
i, j индексы частиц
n нормальный
r качение
s скольжение
t тангенциальный

Список литературы

  1. Членов В.А., Михайлов Н.В. Виброкипящий слой. М.: Наука, 1972.

  2. Членов В.А., Михайлов Н.В. Сушка сыпучих материалов в виброкипящем слое. М.: Стройиздат, 1967.

  3. Вибрации в технике. Справочник в 6-ти т. Т. 4. Вибрационные процессы и машины / Под ред. Лавендела Э.Э. М.: Машиностроение, 1981.

  4. Kovenskii V.I. Numerical calculation of parameters of an ensemble of particles in a perfectly mixed fluidized-bed reactor // Theor. Found. Chem. Eng. 2014. V. 48. № 1. P. 13. [Ковенский В.И. Численный расчет параметров ансамбля частиц в реакторе идеального смешения с кипящим слоем // Теор. осн. хим. технол. 2014. Т. 48. № 1. С. 15.]

  5. Kovenskii V.I. Self-sustained oscillations of a fluidized bed // Theor. Found. Chem. Eng. 2016. V. 50. № 6. P. 1015. [Ковенский В.И. Автоколебания кипящего слоя // Теор. осн. хим. технол. 2016. Т. 50. № 6. С. 619.]

  6. Нагиев А.Г., Нагиев Г.А., Гулиева Н.А. О структуре пространства состояний тепловой модели реакционно-регенерационных систем с кипящим слоем катализатора и принципах визуализации управления // Теор. осн. хим. технол. 2019. Т. 53. № 1. С. 31.

  7. Орлова Н.С. Разработка и исследование математических моделей виброкипящего слоя. Дис. … канд. техн. наук. Таганрог: Южный федеральный университет, 2013.

  8. Орлова Н.С. Разработка и исследование математических моделей виброкипящего слоя. Saarbrücken: Lambert Academic, 2013.

  9. Goldshtein A., Shapiro M., Moldavsky L., Fichman M. Mechanics of collisional motion of granular materials. Part 2. Wave propagation through vibrofluidized granular layers // J. Fluid Mech. 1995. V. 287. P. 349.

  10. Орлова Н.С. Сравнение результатов экспериментального исследования виброкипящего слоя с расчетами по гидродинамической модели гранулярного газа // Инж.-физ. журн. 2014. Т. 87. № 2. С. 429.

  11. Орлова Н.С. Сравнение расчетов по двухжидкостной модели виброожиженного слоя с экспериментальными данными // Инж.-физ. журн. 2012. Т. 85. № 6. С. 1202.

  12. Орлова Н.С. Тестирование двух моделей виброожиженного слоя // Изв. высш. учебн. завед. Сев.-Кавк. рег. Тех. науки. 2012. № 2. С. 42.

  13. Свердлик Г.И., Рево А.А., Каменецкий Е.С., Орлова Н.С. Сравнение результатов экспериментов и математического моделирования виброожиженного слоя // Изв. высш. учебн. завед. Сев.-Кавк. рег. Тех. науки. 2011. № 1. С. 24.

  14. Martin T.W., Huntley J.M., Wildman R.D. Hydrodynamic model for a vibrofluidized granular bed // J. Fluid Mech. 2005. V. 535. P. 325.

  15. Русанов С.А. Моделювання гiдродинамiки виброкиплячого шару з розробкою утилiзатора тепла сипких матерiалiв. Дис. … канд. техн. наук. Херсон: Херсонский национальный технический университет, 2008.

  16. Acosta-Iborra A., Hernandez-Jimenez F., de Vega M., Briongos J.V. A novel methodology for simulating vibrated fluidized bed using two-fluid models // Chem. Eng. Sci. 2012. V. 198–199. P. 261.

  17. Cano-Pleite E., Hernandez-Jimenez F., Acosta-Iborra A. Compressible-gas two-fluid modeling of isolated bubbles in a vertically vibrated fluidized bed and comparison with experiments // Chem. Eng. J. 2015. V. 271. P. 287.

  18. Орлова Н.С., Качалкина Я.Н. Исследование режимов виброкипящего гранулированного слоя с использованием пакета OpenFOAM // Тр. Инст. сист. програм. Росс. акад. наук. 2014. Т. 26. № 5. С. 143.

  19. Каменецкий Е.С., Орлова Н.С., Тагиров А.М., Волик М.В. Трехмерное моделирование виброкипящего слоя с использованием двухжидкостной модели гранулярного газа // Инж.-физ. журн. 2016. Т. 89. № 6. С. 1480.

  20. Hashemnia K., Pourandi S. Study the effect of vibration frequency and amplitude on the quality of fluidization of a vibrated granular flow using discrete element method // Powder Technol. 2018. V. 327. P. 335.

  21. Tatemoto Y., Mawatari Y., Yasukawa T., Noda K. Numerical simulation of particle motion in vibrated fluidized bed // Chem. Eng. Sci. 2004. V. 59. P. 437.

  22. Tatemoto Y., Mawatari Y., Noda K. Numerical simulation of cohesive particle motion in vibrated fluidized bed // Chem. Eng. Sci. 2005. V. 60. P. 5010.

  23. Xiang L., Shuyan W., Huilin L., Goudong L., Juhui Ch., Yikun L. Numerical simulation of particle motion in vibrated fluidized beds // Powder Technol. 2010. V. 197. P. 25.

  24. Каменецкий Е.С., Орлова Н.С., Волик М.В., Минасян Д.Г. Тестирование модели виброкипящего слоя, использующей метод дискретного элемента // Изв. высш. учебн. завед. Сев.-Кавк. рег. Естеств. науки. 2017. № 4-1. С. 18.

  25. CFDEM®project. https://www.cfdem.com/liggghtsr-open-source-discrete-element-method-particle-simulation-code. Cited 15 January 2019.

  26. Pöschel T. Computational Granular Dynamics Models and Algorithms. Berlin: Springer, 2005.

  27. Карвацкий А.Я., Лазарев Т.В. Оценка метода дискретного элемента для прогнозирования поведения сыпучих сред на примере нефтяного кокса // Хим. нефтегазов. машиностр. 2014. № 3. С. 32.

  28. Makse H.A., Gland N., Johnson D.L., Schwartz L. Granular packings: Nonlinear elasticity, sound propagation, and collective relaxation dynamics // Phys. Rev. E. 2004. V. 70. P. 061302.

  29. Анурьев В.И. Справочник конструктора-машиностроителя в 3 т. Т. 1 / Под ред. Жестковой И.Н. М.: Машиностроение, 2001.

  30. Таблицы физических величин. Справочник / Под ред. Кикоина И.К. М.: Атомиздат, 1976.

  31. Строительный портал. http://okvsk.ru/inzhenernaya-geologiya/853-soprotivlenie-sdvigu-razdelnozernistyh-porod.html. Дата обращения: 15.01.2019.

  32. База данных материалов Total Materia. https:// www.totalmateria.com. Дата обращения: 15.01.2019.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал