Теоретические основы химической технологии, 2020, T. 54, № 2, стр. 208-219
Динамика подвижных концентрационных фронтов в реакционных системах газ–жидкость. Анализ и численный эксперимент
В. В. Дильман a, *, Л. М. Мусабекова b, А. М. Бренер b, **, А. Т. Калбаева b, С. Д. Куракбаева b
a Институт общей и неорганической химии им. Н.С. Курнакова РАН
Москва, Россия
b Южно-Казахстанский государственный университет им. М.О. Ауезова
Шымкент, Республика Казахстан
* E-mail: viktor.dilman@yandex.ru
** E-mail: amb_52@mail.ru
Поступила в редакцию 02.08.2019
После доработки 02.10.2019
Принята к публикации 07.10.2019
Аннотация
Разработана математическая модель процесса хемосорбции с движущимся фронтом мгновенной необратимой реакции при малых числах Рейнольдса в системе газ–жидкость до и после момента времени формирования фронта реакции. Получено аналитическое решение модели для периода времени до образования подвижного фронта хемосорбции с учетом влияния продукта реакции на динамику процесса хемосорбции. Разработанная модель, в отличие от известных ранее результатов, учитывает влияние диффузионного переноса продукта реакции на кинетические характеристики хемосорбции и различные стадии формирования и движения концентрационного фронта. Представлены результаты обработки и анализа результатов численного эксперимента. Построены зависимости характерных глубин и времен проникновения улавливаемого компонента от всех управляющих параметров процесса. Получены числа Шервуда, рассчитаны коэффициенты ускорения абсорбции и коэффициенты массоотдачи улавливаемого компонента в жидкой фазе.
ВВЕДЕНИЕ
В процессах хемосорбции может формироваться сложная картина распределения реагентов и продуктов реакции в жидком слое абсорбента. При этом возникают концентрационные фронты, разделяющие слой на области с различными соотношениями диффузионных и кинетических сопротивлений [1–3].
Такие состояния нестационарны, так как концентрационные фронты могут перемещаться со скоростями, изменяющимися во времени. Несмотря на немалое количество работ в этой области [1–7], проблема учета различных стадий формирования подвижных концентрационных фронтов при расчете интегральной эффективности хемосорбционного процесса остается актуальной [7, 8].
Имеющиеся численные и экспериментальные результаты недостаточно информативны и не позволяют сделать однозначные выводы, открывающие перспективы создания общих инженерных методов расчета [1]. Поэтому известные методики расчета таких процессов основаны, как правило, на вычислении различных поправок к кинетическим зависимостям, полученным для физической абсорбции, т.е. без учета химической реакции [9–11]. Тем более не учитывается при таких расчетах возможная неравномерность движения концентрационных фронтов. Актуальность этой проблемы возрастает в связи с развитием микрореакторных технологий [13].
Классической и по сей день наиболее эффективной является пленочная модель [9–12]. При использовании этой модели расчет числа Шервуда при хемосорбции осуществляется через коэффициенты ускорения. Эта методика хорошо адаптирована к практическим расчетам и широко применяется в инженерной практике. В то же время для использования пленочной модели (для надежной оценки ее параметров) нужно знать характерные масштабы длины и времени, которые в рамках самой модели не определяются.
Пока что трудно предложить более надежную альтернативу такому подходу, и в предлагаемой работе авторы не претендуют на это. Однако интерпретация поправочных параметров с учетом неравномерности движения концентрационного фронта нуждается в уточнении и является актуальной задачей.
Проблема оценки влияния неравномерности движения концентрационных фронтов на интенсивность массопереноса не исчезает даже при описании абсорбции, сопровождающейся необратимой быстрой (в предельном случае – мгновенной) химической реакцией [1, 14, 15]. В этом случае также можно выделить несколько различных стадий процесса [1].
Приближение мгновенной химической реакции можно использовать для систем, в которых скорость химической реакции в жидкой фазе достаточно велика по сравнению со скоростью диффузионного переноса, и можно считать, что абсорбирующийся компонент и активный реагент не присутствуют одновременно в одной области жидкого слоя. Известным примером такого процесса является хемосорбция диоксида серы водно-щелочными растворами. Этот процесс имеет широкое применение в системах очистки промышленных газовых выбросов [1, 10]. Другие примеры ситуаций, когда приближение мгновенной химической реакции в жидком слое в процессе хемосорбции является корректным, можно найти в книгах [9, 10].
В данной статье обобщаются и интерпретируются некоторые результаты авторов в указанной области исследований [13–16]. Цель работы и ее новизна заключаются в том, что, в отличие от известных работ [1–4], процесс абсорбции, сопровождающейся необратимой мгновенной химической реакцией, описывается с учетом влияния продукта реакции на динамику процесса абсорбции, а также рассматриваются различные стадии формирования подвижного концентрационного фронта. Учет влияния продукта реакции на кинетику процесса хемосорбции является принципиальным для систем, в которых скорость диффузионного переноса активного реагента и образующихся продуктов реакции в жидкой фазе не отличаются на порядки. Именно такая ситуация реализуется, в частности, и для процессов улавливания диоксида серы водно-щелочными растворами, где коэффициенты диффузии SO2 и ионов ${\text{SO}}_{{\text{3}}}^{{{\text{2}}--}}$ имеют один порядок [1, 14]. Примеры и анализ различных возникающих ситуаций приводятся в [10, 17].
В данной работе дан анализ построенной математической модели для стадий формирования, ускорения и стабилизированного движения концентрационного фронта и проведено ее численное исследование. Предложена также интерпретация полученных результатов в рамках пленочной модели.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ХЕМОСОРБЦИИ С ДВИЖУЩИМСЯ ФРОНТОМ РЕАКЦИИ
Рассмотрим процесс абсорбции, сопровождающейся мгновенной химической реакцией. Представим общую схему реакции в условном виде [2]
Компонент В является активным компонентом, изначально присутствующим в глубине жидкости в растворенном виде. Компонент А диффундирует из глубины газовой фазы к поверхности раздела жидкой и газовой фаз и до определенного момента не может проникнуть вглубь жидкого слоя, поскольку уже на поверхности раздела жидкой и газовой фаз происходит мгновенная химическая реакция и образуется продукт реакции Е. При этом газовый компонент растворяется и реагирует с нелетучими компонентами в жидкости.
Как только происходит исчерпывание компонента В вблизи поверхности раздела, фронт реакции начинает перемещаться с некоторой скоростью в глубину слоя жидкости. В этот момент времени концентрации улавливаемого компонента и активного компонента абсорбента на поверхности фронта реакции равны нулю, и диффузия этих компонентов в жидком слое определяет скорость процесса. Скорость перемещения фронта реакции не постоянна и изменяется во времени.
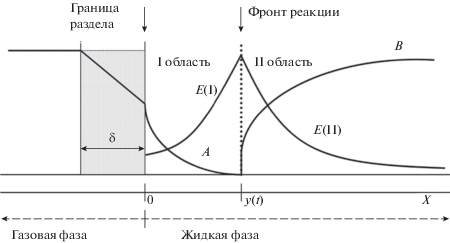
Рассмотрим временные стадии процесса хемосорбции (рис. 1) [1, 14].
1. В момент времени 0 < t < t* концентрация компонента А на границе раздела равна нулю, концентрация компонента В уменьшается, фронт реакции неподвижен и совпадает с поверхностью раздела жидкой и газовой фаз.
2. В некоторый момент времени t = t* концентрация компонента В на границе раздела газа с жидкостью становится равной нулю [14], “включается” мгновенная реакция, в результате чего образуется продукт реакции Е и фронт реакции начинает перемещаться в слой жидкой фазы.
3. В момент времени t > t* возникают три зоны: зона физической абсорбции, где компонент А растворяется в жидкой фазе, зона фронта реакции, где образуется продукт реакции, и зона диффузии активного компонента В и продукта реакции Е.
Для моделирования диффузионных процессов используем представление о практических коэффициентах диффузии. Такой подход при описании многокомпонентной диффузии в жидкой фазе предпочтительнее с позиций упрощенного инженерного расчета, чем использование уравнений Максвелла–Стефана, поскольку дает явное выражение для потоков компонентов через их градиенты [17]. При малых концентрациях химически активной примеси В в растворе, что реализуется во многих хемосорбционных процессах, практические коэффициенты диффузии можно считать постоянными [6, 9], так как их зависимость от концентраций компонентов является достаточно слабой в широком диапазоне концентраций.
Математическая модель динамики хемосорбции на стадии формирования подвижного реакционного фронта при t < t*. Описанная в работах [1, 3] модель возникновения подвижного концентрационного фронта в подобной системе не учитывает влияние продукта реакции E на скорость диффузии компонента В в слое жидкости. Вместе с тем такое влияние может оказаться существенным для кинетики процесса, особенно в моменты времени, близкие ко времени исчерпывания компонента В в поверхностной зоне [15].
C учетом перекрестных диффузионных потоков получаем
(2)
$\begin{gathered} {{j}_{B}} = - {{D}_{{BB}}}\frac{{\partial {{C}_{B}}}}{{\partial X}} - {{D}_{{BE}}}\frac{{\partial {{C}_{E}}}}{{\partial X}}, \\ {{j}_{E}} = - {{D}_{{EB}}}\frac{{\partial {{C}_{B}}}}{{\partial X}} - {{D}_{{EE}}}\frac{{\partial {{C}_{E}}}}{{\partial X}}. \\ \end{gathered} $Поскольку рассматривается начальный период процесса абсорбции, когда фронт реакции еще совпадает с межфазной границей и в слое жидкости отсутствуют источники массы, то в жидкой фазе при Х > 0 (X = 0 –поверхность раздела фаз) справедливы законы сохранения масс компонентов В и Е [18, 19].
Из уравнений потоков и законов сохранения получаем уравнения конвективной диффузии компонентов В и Е, справедливые при Х > 0, t > 0:
(3)
$\begin{gathered} {{D}_{{BB}}}\frac{{{{\partial }^{2}}{{C}_{B}}}}{{{{\partial }^{2}}X}} + {{D}_{{BE}}}\frac{{{{\partial }^{2}}{{C}_{E}}}}{{{{\partial }^{2}}X}} = \frac{{\partial {{C}_{B}}}}{{\partial t}}, \\ {{D}_{{EB}}}\frac{{{{\partial }^{2}}{{C}_{B}}}}{{{{\partial }^{2}}X}} + {{D}_{{EE}}}\frac{{{{\partial }^{2}}{{C}_{E}}}}{{{{\partial }^{2}}X}} = \frac{{\partial {{C}_{E}}}}{{\partial t}}. \\ \end{gathered} $При записи системы (3) учтено, что в начальной стадии процесса, т.е. до начала движения фронта реакции вглубь жидкой фазы, концентрация компонента А в жидкой фазе равна нулю, а потому равна нулю и равновесная концентрация $С_{А}^{*}$ в газовой фазе. Компоненты В и Е предполагаются нелетучими.
Уравнения конвективной диффузии компонентов А и В, справедливые при Х > 0, t > t*:
(4)
$\begin{gathered} {{D}_{{AA}}}\frac{{{{\partial }^{2}}{{C}_{A}}}}{{{{\partial }^{2}}X}} + {{D}_{{AE}}}\frac{{{{\partial }^{2}}{{C}_{E}}}}{{{{\partial }^{2}}X}} = \frac{{\partial {{C}_{A}}}}{{\partial t}}, \\ {{D}_{{EA}}}\frac{{{{\partial }^{2}}{{C}_{A}}}}{{{{\partial }^{2}}X}} + {{D}_{{EE}}}\frac{{{{\partial }^{2}}{{C}_{E}}}}{{{{\partial }^{2}}X}} = \frac{{\partial {{C}_{E}}}}{{\partial t}}. \\ \end{gathered} $Отсюда следуют выражения для граничных условий для компонентов В и Е при Х = 0:
(5)
$\begin{array}{*{20}{c}} {{{D}_{{BB}}}\frac{{\partial {{C}_{B}}}}{{\partial X}} + {{D}_{{BE}}}\frac{{\partial {{C}_{E}}}}{{\partial X}} = \alpha {{C}_{{A\infty }}},} \\ {{{D}_{{EB}}}\frac{{\partial {{C}_{B}}}}{{\partial X}} + {{D}_{{EE}}}\frac{{\partial {{C}_{E}}}}{{\partial X}} = - 2\alpha {{C}_{{A\infty }}},} \end{array}\,\,\,\,{\text{при}}\,\,\,\,t > 0,$Система (5) соответствует моменту времени, когда на свободной поверхности происходит химическая реакция и образуется вещество Е.
Граничные условия для компонента Е при X = = ∞, t > 0:
Граничные условия в момент времени, когда происходит мгновенная необратимая реакция, в результате чего образуется продукт реакции при X = y(t), t > t* для компонентов А и В:
Баланс потоков компонентов А, В и Е:
(9)
${{j}_{A}} + {{j}_{B}} = {{j}_{E}} = {{j}_{{{{E}_{1}}}}} + {{j}_{{{{E}_{2}}}}} = 2{{j}_{A}} = 2{{j}_{B}}.$Граничные условия:
Отсюда следуют соотношения
(11)
$\begin{gathered} 2\left( {{{D}_{{BB}}}\frac{{\partial {{C}_{B}}}}{{\partial X}} + {{D}_{{BE}}}\frac{{\partial {{C}_{E}}}}{{\partial X}}} \right) = \\ = \left( {{{D}_{{EE}}}\frac{{\partial {{C}_{E}}}}{{\partial X}} + {{D}_{{EA}}}\frac{{\partial {{C}_{A}}}}{{\partial X}} + \frac{{\partial {{C}_{B}}}}{{\partial X}}} \right), \\ {{D}_{{BB}}}\frac{{\partial {{C}_{B}}}}{{\partial X}} + {{D}_{{BE}}}\frac{{\partial {{C}_{E}}}}{{\partial X}} = - \left( {{{D}_{{AA}}}\frac{{\partial {{C}_{A}}}}{{\partial X}} + {{D}_{{AE}}}\frac{{\partial {{C}_{E}}}}{{\partial X}}} \right). \\ \end{gathered} $Соответственно, для компонента Е справедливо
(12)
$\begin{gathered} {{D}_{{EE}}}\frac{{\partial {{C}_{E}}}}{{\partial X}} + {{D}_{{EA}}}\frac{{\partial {{C}_{A}}}}{{\partial X}} = 2\alpha {{C}_{{A\infty }}}, \\ {{D}_{{EE}}}\frac{{\partial {{C}_{E}}}}{{\partial X}} + {{D}_{{EB}}}\frac{{\partial {{C}_{B}}}}{{\partial X}} = - 2\alpha {{C}_{{A\infty }}}. \\ \end{gathered} $Полученные системы уравнений (5), (6) с граничными условиями (9)–(10) решаются помощью преобразования Лапласа. В результате получаем следующую систему уравнений:
(13)
$\begin{gathered} {{D}_{{BB}}}\frac{{{{\partial }^{2}}{{{\tilde {C}}}_{B}}}}{{{{\partial }^{2}}X}} + {{D}_{{BE}}}\frac{{{{\partial }^{2}}{{{\tilde {C}}}_{E}}}}{{{{\partial }^{2}}X}} = p{{{\tilde {C}}}_{B}} - C{}_{{B\infty }}, \\ {{D}_{{EB}}}\frac{{{{\partial }^{2}}{{{\tilde {C}}}_{B}}}}{{{{\partial }^{2}}X}} + {{D}_{{EE}}}\frac{{{{\partial }^{2}}{{{\tilde {C}}}_{E}}}}{{{{\partial }^{2}}X}} = p{{{\tilde {C}}}_{{A\infty }}}. \\ \end{gathered} $Концентрация компонента Е в глубине жидкой фазы предполагается равной нулю. Тогда, с учетом граничных условий, получаем
(14)
$\begin{gathered} {{D}_{{BB}}}\frac{{\partial {{{\tilde {C}}}_{B}}}}{{\partial X}} + {{D}_{{BE}}}\frac{{\partial {{{\tilde {C}}}_{E}}}}{{\partial X}} = \frac{{\alpha {{C}_{{A\infty }}}}}{p}, \\ {{D}_{{EB}}}\frac{{{{\partial }^{2}}{{{\tilde {C}}}_{B}}}}{{{{\partial }^{2}}X}} + {{D}_{{EE}}}\frac{{{{\partial }^{2}}{{{\tilde {C}}}_{E}}}}{{{{\partial }^{2}}X}} = - \frac{{2\alpha {{C}_{{A\infty }}}}}{p}. \\ \end{gathered} $Введем следующие обозначения:
(15)
$\begin{gathered} {{y}_{1}} = {{C}_{B}},\,\,\,\,{{y}_{2}} = {{C}_{E}},\,\,\,\,{{a}_{{11}}} = {{D}_{{BB}}},\,\,\,\,{{a}_{{12}}} = {{D}_{{BE}}}, \\ {{a}_{{22}}} = {{D}_{{EE}}},\,\,\,\,{{a}_{{21}}} = {{D}_{{EB}}},\,\,\,\,b = {{C}_{{B\infty }}}. \\ \end{gathered} $Решение полученной системы уравнений представим в виде
(16)
${{y}_{1}} = {{C}_{1}}{{e}^{{{{l}_{1}}x}}} + {{C}_{2}}{{e}^{{{{l}_{2}}x}}} + \frac{b}{p},\,\,\,\,{{y}_{2}} = {{C}_{3}}{{e}^{{{{l}_{1}}x}}} + {{C}_{4}}{{e}^{{{{l}_{2}}x}}}.$Используя новые обозначения, получаем выражения для изображений:
(17)
${{\tilde {C}}_{B}} = {{C}_{1}}\exp ( - \sqrt {{{S}_{1}}p} X) + {{C}_{2}}\exp ( - \sqrt {{{S}_{2}}p} X) + \frac{{{{C}_{{B\infty }}}}}{p},$(18)
${{\tilde {C}}_{E}} = {{C}_{1}}{{\lambda }_{1}}\exp ( - \sqrt {{{S}_{1}}p} X) + {{C}_{2}}{{\lambda }_{2}}\exp ( - \sqrt {{{S}_{2}}p} X).$Здесь
(19)
$\begin{gathered} {{\lambda }_{{1,2}}} = \frac{{ - {{d}_{2}} \pm \sqrt {d_{2}^{2} + 4{{d}_{1}}} }}{{2{{D}_{{BE}}}}}, \\ {{S}_{{1,2}}} = \frac{1}{{{{D}_{{BE}}}{{\lambda }_{{1,2}}} + {{D}_{{BB}}}}} = \frac{2}{{{{D}_{{EE}}} \pm \sqrt {d_{2}^{2} + 4{{d}_{1}}} }}, \\ \end{gathered} $После ряда преобразований находим значения постоянных коэффициентов${{C}_{1}},$ ${{C}_{2}}{\text{:}}$
(21)
$\begin{gathered} {{C}_{1}} = \frac{{\alpha {{C}_{{A\infty }}}\left( {2{{T}_{2}} + {{T}_{1}}} \right)}}{{p\sqrt {{{S}_{1}}p} \left( {{{R}_{2}} - {{R}_{1}}} \right)}}, \\ {{C}_{2}} = - \frac{{\alpha {{C}_{{A\infty }}}\left( {2{{T}_{2}}{{R}_{1}} + {{T}_{1}}{{R}_{2}}} \right)}}{{p\sqrt {{{S}_{2}}p} \left( {{{R}_{2}} - {{R}_{1}}} \right)}}. \\ \end{gathered} $Здесь
(22)
$\begin{gathered} {{R}_{1}} = \frac{{{{D}_{{BB}}} + {{\lambda }_{1}}{{D}_{{BE}}}}}{{{{D}_{{BB}}} + {{\lambda }_{2}}{{D}_{{BE}}}}},\,\,\,\,{{R}_{2}} = \frac{{{{D}_{{EB}}} + {{\lambda }_{1}}{{D}_{{EE}}}}}{{{{D}_{{EB}}} + {{\lambda }_{2}}{{D}_{{EE}}}}}, \\ {{T}_{1}} = \frac{1}{{{{D}_{{BB}}} + {{\lambda }_{2}}{{D}_{{BE}}}}},\,\,\,\,{{T}_{2}} = \frac{1}{{{{D}_{{EB}}} + {{\lambda }_{2}}{{D}_{{EE}}}}}. \\ \end{gathered} $Отсюда следует
(23)
$\begin{gathered} {{{\tilde {C}}}_{B}} = \frac{{\alpha {{C}_{{A\infty }}}}}{{p\sqrt p \left( {{{R}_{2}} - {{R}_{1}}} \right)}}\left[ {\frac{{2{{T}_{2}} + {{T}_{1}}}}{{\sqrt {{{S}_{1}}} }}\exp \left( { - \sqrt {{{S}_{1}}p} X} \right) - } \right. \\ \left. { - \,\,\frac{{2{{T}_{2}}{{R}_{1}} + {{T}_{1}}{{R}_{2}}}}{{\sqrt {{{S}_{2}}} }}\exp \left( { - \sqrt {{{S}_{2}}p} X} \right)} \right] + \frac{{{{C}_{{B\infty }}}}}{p}, \\ \end{gathered} $(24)
$\begin{gathered} {{{\tilde {C}}}_{E}} = \frac{{\alpha {{C}_{{A\infty }}}}}{{p\sqrt p \left( {{{R}_{2}} - {{R}_{1}}} \right)}}\left[ {\frac{{2{{T}_{2}} + {{T}_{1}}}}{{\sqrt {{{S}_{1}}} }}{{\lambda }_{1}}\exp \left( { - \sqrt {{{S}_{1}}p} X} \right) - } \right. \\ \left. { - \,\,\frac{{2{{T}_{2}}{{R}_{1}} + {{T}_{1}}{{R}_{2}}}}{{\sqrt {{{S}_{2}}} }}{{\lambda }_{2}}\exp \left( { - \sqrt {{{S}_{2}}p} X} \right)} \right]. \\ \end{gathered} $Используя формулу
(25)
$\left[ {{{p}^{{ - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{e}^{{ - k\sqrt p }}}} \right] \div 2\sqrt {\frac{t}{\pi }} \exp \left( { - \frac{{{{k}^{2}}}}{{4t}}} \right) - k \cdot {\text{erfc}}\left( {\frac{k}{{2\sqrt t }}} \right),$находим оригиналы изображений и получаем следующие выражения для искомых концентраций активного компонента абсорбента В и продукта реакции Е в слое жидкости в течение времени, предшествующего образованию подвижного фронта реакции:
(26)
$\begin{gathered} {{{\tilde {C}}}_{B}} = \frac{{\alpha {{C}_{{A\infty }}}}}{{\left( {{{R}_{2}} - {{R}_{1}}} \right)}}\frac{{2{{T}_{2}} + {{T}_{1}}}}{{\sqrt {{{S}_{1}}} }} \times \\ \times \,\,\left[ {2\sqrt {\frac{t}{\pi }} \exp \left( { - \frac{{{{Х}^{2}}{{S}_{1}}}}{{4t}}} \right) - Х{\text{erfc}}\left( {\frac{{Х\sqrt {{{S}_{1}}} }}{{2\sqrt t }}} \right)} \right] - \\ - \,\,\frac{{\alpha {{C}_{{A\infty }}}}}{{\left( {{{R}_{2}} - {{R}_{1}}} \right)}}\frac{{2{{T}_{2}}{{R}_{1}} + {{T}_{1}}{{R}_{2}}}}{{\sqrt {{{S}_{2}}} }} \times \\ \times \,\,\left[ {2\sqrt {\frac{t}{\pi }} \exp \left( { - \frac{{{{Х}^{2}}{{S}_{2}}}}{{4t}}} \right) - Х{\text{erfc}}\left( {\frac{{Х\sqrt {{{S}_{2}}} }}{{2\sqrt t }}} \right)} \right] + {{C}_{{B\infty }}}, \\ \end{gathered} $(27)
$\begin{gathered} {{{\tilde {C}}}_{E}} = \frac{{\alpha {{C}_{{A\infty }}}}}{{\left( {{{R}_{2}} - {{R}_{1}}} \right)}}\frac{{2{{T}_{2}} + {{T}_{1}}}}{{\sqrt {{{S}_{1}}} }}{{\lambda }_{1}} \times \\ \times \,\,\left[ {2\sqrt {\frac{t}{\pi }} \exp \left( { - \frac{{{{Х}^{2}}{{S}_{1}}}}{{4t}}} \right) - Х{\text{erfc}}\left( {\frac{{Х\sqrt {{{S}_{1}}} }}{{2\sqrt t }}} \right)} \right] - \\ - \,\,\frac{{\alpha {{C}_{{A\infty }}}}}{{\left( {{{R}_{2}} - {{R}_{1}}} \right)}}\frac{{2{{T}_{2}}{{R}_{1}} + {{T}_{1}}{{R}_{2}}}}{{\sqrt {{{S}_{2}}} }}{{\lambda }_{2}} \times \\ \times \,\,\left[ {2\sqrt {\frac{t}{\pi }} \exp \left( { - \frac{{{{Х}^{2}}{{S}_{2}}}}{{4t}}} \right) - Х{\text{erfc}}\left( {\frac{{Х\sqrt {{{S}_{2}}} }}{{2\sqrt t }}} \right)} \right]. \\ \end{gathered} $Концентрацию компонентов на межфазной границе находим из полученных выражений, принимая в них Х = 0:
(28)
$\begin{gathered} {{C}_{{BS}}} = \frac{{2\alpha {{C}_{{A\infty }}}}}{{\left( {{{R}_{2}} - {{R}_{1}}} \right)}} \times \\ \times \,\,\left( {\frac{{2{{T}_{2}} + {{T}_{1}}}}{{\sqrt {{{S}_{1}}} }} - \frac{{2{{T}_{2}}{{R}_{1}} + {{T}_{1}}{{R}_{2}}}}{{\sqrt {{{S}_{2}}} }}} \right)\sqrt {\frac{t}{\pi }} + {{C}_{{B\infty }}}, \\ \end{gathered} $(29)
$\begin{gathered} {{C}_{{ES}}} = \frac{{2\alpha {{C}_{{A\infty }}}}}{{\left( {{{R}_{2}} - {{R}_{1}}} \right)}} \times \\ \times \,\,\left( {{{\lambda }_{1}}\frac{{2{{T}_{2}} + {{T}_{1}}}}{{\sqrt {{{S}_{1}}} }} - {{\lambda }_{2}}\frac{{2{{T}_{2}}{{R}_{1}} + {{T}_{1}}{{R}_{2}}}}{{\sqrt {{{S}_{2}}} }}} \right)\sqrt {\frac{t}{\pi }} . \\ \end{gathered} $Фронт реакции становится подвижным и начинает перемещаться в слой жидкости в тот момент времени, когда концентрация вещества В на межфазной границе становится равной нулю:
(30)
$t{\text{*}} = \frac{{{{C}_{{B\infty }}}^{2}\pi {{{\left( {{{R}_{2}} - {{R}_{1}}} \right)}}^{2}}}}{{4{{\alpha }^{2}}{{C}_{{A\infty }}}^{2}{{{\left( {\frac{{2{{T}_{2}}{{R}_{1}} + {{T}_{1}}{{R}_{2}}}}{{\sqrt {{{S}_{2}}} }} - \frac{{2{{T}_{2}} + {{T}_{1}}}}{{\sqrt {{{S}_{1}}} }}} \right)}}^{2}}}}.$В этот момент времени достигается максимальная концентрация продукта реакции Е на межфазной поверхности:
(31)
$\begin{gathered} {{C}_{{ES}}} = \\ = \frac{{{{C}_{{B\infty }}}\left[ {{{\lambda }_{1}}\sqrt {{{S}_{2}}} \left( {2{{T}_{2}} + {{T}_{1}}} \right) - {{\lambda }_{2}}\sqrt {{{S}_{1}}} \left( {2{{T}_{2}}{{R}_{1}} + {{T}_{1}}{{R}_{2}}} \right)} \right]}}{{\left[ {\sqrt {{{S}_{2}}} \left( {2{{T}_{2}} + {{T}_{1}}} \right) - \sqrt {{{S}_{1}}} \left( {2{{T}_{2}}{{R}_{1}} + {{T}_{1}}{{R}_{2}}} \right)} \right]}}. \\ \end{gathered} $Полученные выражения ${{C}_{B}}(Х,t*)$ и ${{C}_{E}}(Х,t*)$ используются как начальные данные для вычисления профилей концентраций компонентов А, В и Е с учетом влияния продукта реакции для периода времени абсорбции $t > t{\text{*}}.$
Алгоритм и схема численного решения задачи для периода времени абсорбции $t > t{\text{*}}.$ При $t > t{\text{*}}$ фронт реакции становится подвижным [1, 14]. Соответствующее этой стадии процесса распределение концентраций компонентов в жидкой фазе показано на рис. 1. При $t > t{\text{*}}$ проблема не имеет аналитического решения [1]. Поэтому был поставлен и осуществлен численный эксперимент на основе специально разработанной адаптивной версии метода Кранка–Никольсона [1, 15], метода раздельных прогонок [14] для определения профилей концентрации компонентов А, В, Е, а также модифицированного итерационного метода [14, 20] для контроля профиля концентрации продукта реакции.
Необходимо отметить, что в данной работе не учитывали возможное влияние скачка концентраций при переходе через концентрационный фронт на гидродинамическую картину. Этот вопрос подлежит специальному исследованию в тех случаях, когда физические характеристики жидкости или газа существенно зависят от концентраций примесей [21, 22].
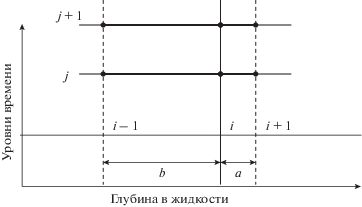
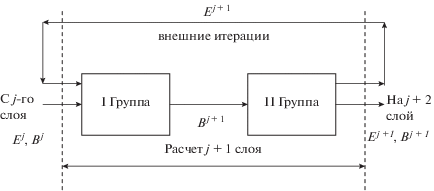
Схема численного эксперимента на основе метода раздельных прогонок показана на рис. 2 и 3.
Обозначим $B_{i}^{j} = B({{x}_{i}},{{t}_{j}}),$ $E_{i}^{j} = E({{x}_{i}},{{t}_{j}})$ соответственно для концентраций компонентов В и Е. Тогда получаем
(32)
$\begin{gathered} {{D}_{{BB}}}\left[ {aB_{{i - 1}}^{{j + 1}} - \left( {a + b + \frac{\delta }{{{{D}_{{BB}}}}}} \right)B_{i}^{{j + 1}} + bB_{{i + 1}}^{{j + 1}}} \right] + \\ + \,\,{{D}_{{BE}}}\left[ {aE_{{i - 1}}^{j} - (a + b)E_{i}^{j} + bE_{{i + 1}}^{j}} \right] = \\ = {{D}_{{BB}}}\left[ { - bB_{{i + 1}}^{j} + \left( {a + b - \frac{\delta }{{{{D}_{{BB}}}}}} \right)B_{i}^{j} - aB_{{i - 1}}^{j}} \right] + \\ + \,\,{{D}_{{BE}}}\left[ { - bE_{{i + 1}}^{j} + (a + b)E_{i}^{j} - aE_{{i - 1}}^{j}} \right]. \\ \end{gathered} $(33)
$\begin{gathered} {{D}_{{AA}}}\left[ {aA_{{i - 1}}^{{j + 1}} - \left( {a + b + \frac{\delta }{{{{D}_{{AA}}}}}} \right)A_{i}^{{j + 1}} + bA_{{i + 1}}^{{j + 1}}} \right] + \\ + \,\,{{D}_{{AE}}}\left[ {aE_{{i - 1}}^{j} - (a + b)E_{i}^{j} + bE_{{i + 1}}^{j}} \right] = \\ = {{D}_{{AA}}}\left[ { - bA_{{i + 1}}^{j} + \left( {a + b - \frac{\delta }{{{{D}_{{AA}}}}}} \right)A_{i}^{j} - aA_{{i - 1}}^{j}} \right] + \\ + \,\,{{D}_{{AE}}}\left[ { - bE_{{i + 1}}^{j} + (a + b)E_{i}^{j} - aE_{{i - 1}}^{j}} \right]. \\ \end{gathered} $(34)
$\begin{gathered} {{D}_{{EA}}}\left[ {aA_{{i - 1}}^{{j + 1}} - (a + b)A_{i}^{{j + 1}} + bA_{{i + 1}}^{{j + 1}}} \right] + \\ + \,\,{{D}_{{EE}}}\left[ {aE_{{i - 1}}^{{j + 1}} + \left( {a + b + \frac{\delta }{{{{D}_{{EE}}}}}} \right)E_{i}^{{j + 1}} - bE_{{i + 1}}^{{j + 1}}} \right] = \\ = {{D}_{{EA}}}\left[ { - bA_{{i + 1}}^{j} + (a + b)A_{i}^{j} - aA_{{i - 1}}^{j}} \right] + \\ + \,\,{{D}_{{EE}}}\left[ { - bE_{{i + 1}}^{j} + \left( {a + b - \frac{\delta }{{{{D}_{{EE}}}}}} \right)E_{i}^{j} - aE_{{i - 1}}^{j}} \right]. \\ \end{gathered} $Для численного решения этой модели соответственно для области I (компоненты А и Е) и II (компоненты В и Е) применяем метод раздельных прогонок (рис. 3).
Так как неизвестны значения концентраций компонентов А и В для второй области, для которой начинается расчет, берем в качестве начальных приближений рассчитанные значения концентраций из предыдущего раздела без учета влияния продукта реакции. Итерационный цикл заканчивается при достижении условия сходимости.
ОБРАБОТКА И АНАЛИЗ РЕЗУЛЬТАТОВ ЧИСЛЕННОГО ЭКСПЕРИМЕНТА
Для каждого численного эксперимента проведены расчеты с различными значениями следующих параметров: парциального давления улавливаемого компонента в газовой фазе pА от 9.322 × 102 до 13.322 × 102 Па; концентрации компонента В∞ в глубине слоя жидкости от 6.073 до 10.073 моль/м3; главных коэффициентов диффузии DBB, DEE, DAA от 1 × 10–9 до 4 × 10–9 м2/с; перекрестных коэффициентов диффузии от 1 × 10–11 до 4 × 10–11 м2/с; коэффициента диффузии улавливаемого компонента DA от 0.7 × 10–9 до 4.7 × 10–9 м2/с; коэффициента диффузии абсорбента DВ от 1.1 × 10–9 до 5.1 × 10–9 м2/с; коэффициента диффузии продукта реакции DЕ от 0.04 × 10–9 до 2.1 × 10–9 м2/с; константы Генри Н от 7.18 до 207.18 (м3 Па/моль); коэффициента массоотдачи α от 0.034 × 10–5 до 34 × × 10–5 моль/(м2 с Па).
Оценка влияния параметров процесса на поверхностные концентрации реагентов. Некоторые характерные результаты численных экспериментов проиллюстрированы на рис. 4–6.
Рис. 4.
Зависимость поверхностной концентрации продукта реакции Еs от времени абсорбции t при изменении концентрации компонента В: а – CB = 6 моль/м3, б – 7, в – 8, г – 9, д – CB = 10 моль/м3.
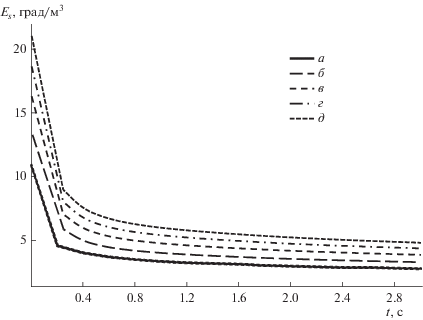
Рис. 5.
Зависимость поверхностной концентрации продукта реакции Еs от времени абсорбции t при изменении коэффициента диффузии улавливаемого компонента DA: а – DA = 0.73 × 10–9 м2/с, б – 1.73 × 10–9, в – 2.73 × 10–9, г – 3.73 × × 10–9, д – DA = 4.73 × 10–9 м2/с.
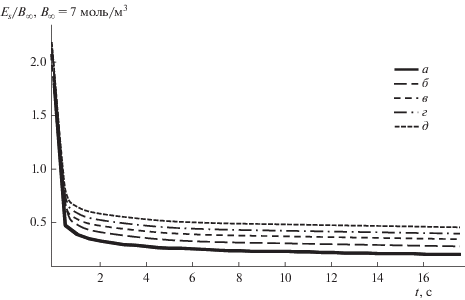
Рис. 6.
Зависимость поверхностной концентрации продукта реакции Еs от времени абсорбции t при изменении коэффициента диффузии DB: а – DВ = 1.1 × 10–9 м2/c, б – 2.1 × 10–9, в – 3.1 × 10–9, г – 4.1 × 10–9, д – DВ = 5.1 × 10–9 м2/c.
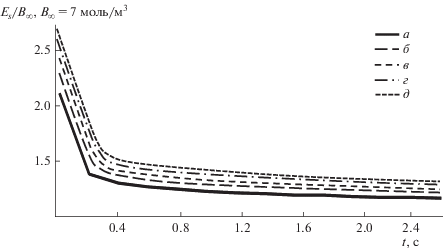
Численный эксперимент показал, что в начальный момент времени поверхностная концентрация продукта реакции имеет максимальное значение, а затем с течением времени медленно уменьшается до нуля. С возрастанием концентрации компонента В и коэффициентов диффузии компонентов А и В наблюдается возрастание концентрации продукта реакции на поверхности пленки ES, причем при изменении коэффициента диффузии компонента А начальное значение концентрации ES одинаково для всех кривых. Как видно из рис. 6 и 7, с увеличением коэффициента диффузии продукта реакции, главных и всех коэффициентов диффузии наблюдается монотонное убывание поверхностной концентрации продукта реакции, причем при изменении главных и всех коэффициентов диффузии начальное значение концентрации продукта реакции на поверхности фронта реакции одинаково для всех кривых.
Рис. 7.
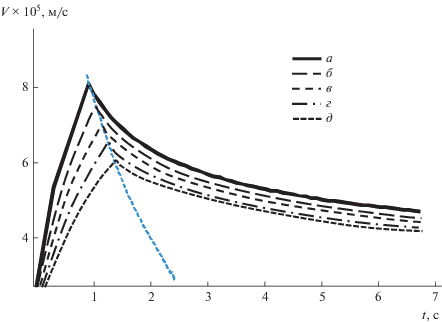
Зависимость скорости перемещения фронта реакции V от времени абсорбции t при изменении концентрации компонента В: а – CB = 6 моль/м3, б – 7, в – 8, г – 9, д – CB = 10 моль/м3.
При этом наибольшее влияние на поверхностную концентрацию продукта реакции оказывает коэффициент диффузии DE. Перекрестные коэффициенты диффузии, константа Генри Н, коэффициент массоотдачи α и парциальное давление pA слабо влияют на концентрацию продукта реакции ES.
В результате численного эксперимента была выделена первая стадия процесса хемосорбции с движущимся фронтом реакции, когда концентрация компонента А на границе раздела фаз быстро возрастает. Затем рост концентрации улавливаемого компонента на границе раздела фаз практически прекращается, что соответствует установлению равновесной концентрации.
С возрастанием концентрации активного компонента абсорбента В, коэффициента диффузии компонентов А, Е и константы Генри Н уменьшается концентрация компонента А на границе раздела фаз, причем при значении коэффициента диффузии продукта реакции DEЕ ≥ 0.06 × 10–9 кривые практически не меняются.
Численный эксперимент показывает, что с возрастанием парциального давления и коэффициента массоотдачи в газовой фазе растет концентрация компонента А на границе раздела фаз, причем при значении коэффициента массоотдачи α > 5.34 × 10–5 моль/(м2 с Па) кривые практически не меняются.
Оценка влияния параметров процесса на скорость перемещения фронта реакции. Наиболее принципиальным результатом численного эксперимента можно считать обнаружение того, что в начальный период времени на стадии процесса t > t* скорость перемещения фронта реакции быстро возрастает, а начиная с некоторого момента эта скорость начинает уменьшаться и медленно стремится к нулю. На рис. 7 ясно видны два характерных участка. По первому участку до момента t = tp, соответствующего максимальной скорости перемещения фронта реакции, была сделана оценка характерной глубины проникновения фронта реакции.
Второй участок начинается от момента времени проникновения t = tp и известен из литературных источников: движение фронта реакции на этом участке хорошо описывается с помощью пленочной модели по закону V ≈${1 \mathord{\left/ {\vphantom {1 {\sqrt t }}} \right. \kern-0em} {\sqrt t }}.$
С возрастанием концентрации В, коэффициента диффузии DB, константы Генри Н наблюдается уменьшение V от значений 5.8 × 10–5 до 8 × × 10–5 м/с при изменении В и DB, для константы Генри от 5 × 10–5 до 11 × 10–5 м/с; увеличении tp от 1 до 1.4 с для концентрации компонента В, от 1 до 1.2 с для коэффициента диффузии DB и от 0.6 до 1.7 с для константы Генри Н.
Аналогичные результаты наблюдаются с возрастанием парциального давления компонента А, коэффициента массоотдачи α, коэффициентов диффузии DA, DE, главных и всех коэффициентов диффузии, т.е. наблюдается возрастание скорости перемещения и уменьшение времени проникновения. Перекрестные коэффициенты диффузии не оказывают заметного влияния на изменение скорости V.
ВЛИЯНИЕ ПАРАМЕТРОВ МОДЕЛИ НА ХАРАКТЕРНЫЕ ВРЕМЕНА И ГЛУБИНЫ ПРОНИКНОВЕНИЯ ФРОНТА РЕАКЦИИ
В результате численного эксперимента появляется возможность определить характерные пространственные и временные масштабы пленочной модели, а именно, без априорного задания толщины пленки можно предложить в качестве оценки этой величины характерные значения глубины проникновения компонента А в жидкую фазу абсорбента на границе первой стадии продвижения фронта реакции.
Концепция расчета. Характерные глубины и времена проникновения рассчитываются по максимальной скорости перемещения фронта реакции (рис. 8, 9). Обработав проведенные численные эксперименты, рассчитали глубины и времена проникновения от физико-химических свойств модели. При этом были обнаружены следующие закономерности.
Рис. 8.
Зависимость характерной глубины проникновения hp от коэффициента диффузии активного компонента абсорбента DB (а) и коэффициента массоотдачи улавливаемого компонента в газовой фазе α (б).
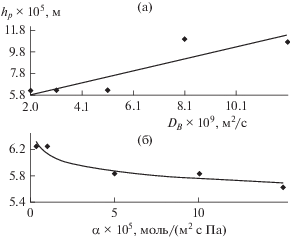
Рис. 9.
Зависимость характерного времени проникновения tp от коэффициента массоотдачи улавливаемого компонента в газовой фазе α.
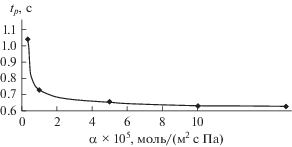
Как видно из рис. 8, с возрастанием коэффициента диффузии компонента В и безразмерных главных коэффициентов диффузии наблюдается возрастание характерной глубины проникновения.
Численные исследования показали также, что с возрастанием безразмерного коэффициента диффузии компонента Е и коэффициента массоотдачи компонента А в газовой фазе характерная глубина проникновения убывает. С возрастанием безразмерных коэффициентов диффузии компонентов А, Е, коэффициента диффузии компонента В, парциального давления, коэффициента массоотдачи компонента А в газовой фазе, безразмерных главных коэффициентов диффузии характерное время проникновения фронта реакции убывает.
Численный эксперимент показывает, что с ростом коэффициента массоотдачи α время проникновения на характерную глубину вначале быстро убывает, затем при дальнейшем возрастании α время проникновения фронта реакции стабилизируется.
Рассчитанные характерные глубины проникновения используются при расчете модифицированного числа Шервуда ShM, а времена проникновения для расчета коэффициента массоотдачи αL для двух стадий процесса хемосорбции.
В основу методики расчета была положена апробированная схема Шервуда на основе представления о коэффициентах ускорения массоотдачи при хемосорбции. Коэффициент ускорения определяется следующим образом [9, 11]:
где(36)
${{r}_{0}} = {{{{D}_{A}}} \mathord{\left/ {\vphantom {{{{D}_{A}}} {{{D}_{B}}}}} \right. \kern-0em} {{{D}_{B}}}},\,\,{{S}_{0}} = {{{{B}_{\infty }}} \mathord{\left/ {\vphantom {{{{B}_{\infty }}} {{{A}_{S}}}}} \right. \kern-0em} {{{A}_{S}}}},$(37)
${{r}_{1}} = {{{{D}_{Е}}} \mathord{\left/ {\vphantom {{{{D}_{Е}}} {{{D}_{B}}}}} \right. \kern-0em} {{{D}_{B}}}},\,\,\,{{S}_{1}} = {{{{B}_{\infty }}} \mathord{\left/ {\vphantom {{{{B}_{\infty }}} {{{Е}_{{fr}}}.}}} \right. \kern-0em} {{{Е}_{{fr}}}.}}$Характерное модифицированное число Шер-вуда:
(38)
${\text{S}}{{{\text{h}}}_{М}} = {{{{D}_{A}}} \mathord{\left/ {\vphantom {{{{D}_{A}}} {(\alpha {{h}_{p}})}}} \right. \kern-0em} {(\alpha {{h}_{p}})}}.$Были рассчитаны и построены зависимости коэффициента ускорения от основных параметров процесса [14]. Численный эксперимент демонстрирует, что с возрастанием коэффициента диффузии компонента В наблюдается уменьшение коэффициента ускорения, при возрастании коэффициентов диффузии компонентов А и Е наблюдается возрастание коэффициента ускорения. При изменении коэффициента диффузии улавливаемого компонента для различных фиксированных значений концентрации абсорбента B = 6–8 моль/м3 получили зависимости коэффициента ускорения от безразмерной концентрации и безразмерного коэффициента диффузии улавливаемого компонента на границе раздела фаз, модифицированного числа Шервуда, а также зависимость числа Шервуда от безразмерной концентрации компонента А на границе раздела фаз.
С возрастанием концентрации компонента В коэффициент ускорения абсорбции Ω возрастает, в то время как число Шервуда не изменяется. C возрастанием коэффициента диффузии улавливаемого компонента DA коэффициент ускорения абсорбции Ω и число Шервуда возрастают, а безразмерная концентрация улавливаемого компонента на границе раздела фаз AS/B∞ убывает.
Зная характерные глубины и времена проникновения для двух стадий, можно найти коэффициент массоотдачи (полный) улавливаемого компонента в жидкой фазе:
а) при t < tp
(39)
${{\alpha }_{L}} \approx {{{{D}_{A}}} \mathord{\left/ {\vphantom {{{{D}_{A}}} {{{h}_{p}}}}} \right. \kern-0em} {{{h}_{p}}}},$б) при t > tp
(40)
${{{\alpha }}_{L}} = \frac{{\sqrt {{{4{{D}_{A}}} \mathord{\left/ {\vphantom {{4{{D}_{A}}} {\pi t}}} \right. \kern-0em} {\pi t}}} }}{{{\text{erf}}{{{\left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon {{{D}_{A}}}}} \right. \kern-0em} {{{D}_{A}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}.$Вторая стадия начинается от момента условного времени проникновения t = tp, известного из литературных источников. Движение концентрационного фронта на этом участке хорошо описывается с помощью пленочной модели [9] по закону V ≈ ${1 \mathord{\left/ {\vphantom {1 {\sqrt t }}} \right. \kern-0em} {\sqrt t }}.$
При t = tp фронт реакции проходит расстояние
где $\varepsilon $ – контрольный параметр пленочной модели [9, 14]. Отсюда очевидна связь контрольного параметра с рассчитываемой в численном эксперименте скоростью перемещения фронта реакции на второй стадии процесса:В результате обработки всего массива данных численного эксперимента удалось получить следующие зависимости для расчета основных характеристик процесса хемосорбции с подвижным фронтом реакции. Начальный участок для периода $t < {{t}_{p}}{\text{:}}$
1. Характерное время проникновения:
(43)
${{t}_{p}} = 13.6{{\left( {1 + 0.018\frac{{{{C}_{B}}{\text{(}}0{\text{)}}H}}{P}} \right)}^{{0.786}}}{{\left( {\frac{{{{D}_{A}}}}{{{{D}_{B}}}}} \right)}^{{ - 3.44}}}.$2. Характерная глубина проникновения:
(44)
${{h}_{p}} = 7.72 \times {{10}^{{ - 5}}}{{\left( {1 + \frac{{{{D}_{E}}}}{{{{D}_{B}}}}} \right)}^{{ - 0.18}}}{{\left( {\frac{{{{D}_{A}}}}{{{{D}_{B}}}}} \right)}^{{0.781}}}.$3. Зависимость концентрации улавливаемого компонента на межфазной поверхности от времени:
(45)
$\frac{{{{C}_{{AS}}}}}{{{{C}_{B}}{\text{(}}0{\text{)}}}} = {{\left( {2.371 - \frac{{{{C}_{B}}{\text{(}}0{\text{)}}H}}{P}} \right)}^{{0.802}}}{{\left( {\frac{t}{{{{t}_{p}}}}} \right)}^{{0.408}}}.$4. Зависимость концентрации продукта реакции на межфазной поверхности от времени
(46)
$\frac{{{{C}_{{ES}}}}}{{{{C}_{{ES}}}{\text{(}}0{\text{)}}}} = {\text{exp}}\left( { - {{{\left[ {\frac{{{{D}_{E}}}}{{{{D}_{A}}}}} \right]}}^{{0.45}}}{{{\left[ {\frac{t}{{{{t}_{p}}}}} \right]}}^{{0.652}}}} \right).$5. Среднее значение коэффициента массоотдачи в жидкой фазе в начальной фазе подвижного фронта реакции:
(47)
$\begin{gathered} {{{{\bar {\alpha }}}}_{L}} = \frac{1}{{{{t}_{p}}}}\int\limits_0^{{{t}_{p}}} {\alpha \left( {\frac{P}{{{{C}_{{AS}}}}} - H} \right)dt} = \\ = {\alpha }\left[ {2.451\frac{P}{{{{C}_{B}}}}{{{\left( {2.371 - \frac{{{{C}_{B}}H}}{P}} \right)}}^{{ - 0.802}}} - H} \right]. \\ \end{gathered} $6. Характерное число Шервуда в начальной фазе движения фронта реакции:
Предложенная методика апробирована для расчета числа Шервуда в процессе хемосорбции на двух системах: хемосорбции SO2 в растворе Na2SO3 и водной абсорбции СО2. Для первой системы получены результаты, хорошо согласующиеся с опытными данными [13, 14]. Во втором случае можно говорить лишь о качественном согласии с опытом и только для низких концентраций диоксида углерода. Это можно объяснить тем, что процесс водной абсорбции СО2 не является необратимым.
ЗАКЛЮЧЕНИЕ
По результатам работы можно сделать следующие выводы.
Получено выражение для расчета времени формирования подвижного фронта реакции с учетом диффузии продукта реакции. В результате численного эксперимента установлено существование двух стадий хемосорбции с подвижным фронтом реакции.
Показано, что первая стадия сопровождается ростом скорости движения фронта реакции и найдены максимальные значения скорости движения фронта реакции.
В результате численного эксперимента определены характерные времена и глубины проникновения улавливаемого компонента и получены оценки характерных масштабов пленочной модели. Разработана методика инженерного расчета с учетом двух стадий процесса хемосорбции в случае мгновенной химической реакции в жидкой фазе. Поскольку параметры расчетных соотношений (43)–(48) получены в результате численного эксперимента в широком диапазоне изменения физических характеристик, можно предполагать, что предложенная методика и соответствующая программа расчета могут быть полезны для инженерных расчетов. Необходимо отметить, что более убедительная верификация и уточнение управляющих параметров модели потребуют дополнительных исследований.
ОБОЗНАЧЕНИЯ
| a, b | безразмерные параметры неравномерной сетки |
| C | концентрация реагентов, кмоль/м3 |
| DAA, DBB, DEE | главные коэффициенты диффузии для компонентов А, В, Е, м2/с |
| DAE, DEA, DBE, DEB | перекрестные коэффициенты диффузии для компонентов А, В, Е, м2/с |
| H | константа Генри, (м3 Па)/кмоль |
| hp | характерная глубина проникновения фронта реакции, м |
| jA, jB, jE | потоки компонентов А, В и Е |
| pA | парциальное давление улавливаемого компонента А в газовой фазе, Па |
| t | временная координата, с; |
| t* | время формирования фронта реакции, с |
| tp | характерное время проникновения, с |
| V | скорость перемещения фронта реакции, м/с |
| x | ось координат, нормальная к поверхности раздела жидкой и газовой фаз и направленная вглубь жидкого слоя, м |
| α, αL | коэффициенты массоотдачи в газовой и жидкой фазах соответственно, кмоль/(м2 с атм) |
| $\kappa $ | безразмерный параметр, зависящий от модели жидкого состояния |
| Ω | безразмерный коэффициент ускорения абсорбции |
ИНДЕКСЫ
Список литературы
Baetens D., Van Keer R., Hosten L.H. Gas-liquid reaction: absorption accompanied by an instantaneous, irreversible reaction // Moving Boundaries IV: Computational Modelling of Free and Moving Boundary Problems / Eds. Van Keer R., Brebbia C.A. Southampton: Computational Mechanics Publications, 1997. P. 185.
Callery O., Healy M.G. Predicting the propagation of concentration and saturation fronts in fixed-bed filters // Water Res. 2017. V. 123. P. 556.
Anger T., Racz Z. Concentration profiles and reaction fronts in A + B → C type processes: Effect of background ions // Phys. Rev. E. 2000. V. 61. № 4. P. 3583.
Seader J.D., Henley E.J. Separation Process Principles. N.Y.: Wiley, 2006.
Górak A., Stankiewicz A. Intensified reaction and separation systems // Annu. Rev. Chem. Biomol. Eng. 2011. V. 2. P. 431.
Kenig E.Y., Gorak A. Reactive absorption // Integrated Chemical Processes: Synthesis, Operation, Analysis, and Control / Eds. Sundmacher K., Kienle A., Seidel-Morgenstern A. Weinheim: Wiley-VCH, 2005. P. 265.
Cencini M., Lopez C., Vergni D. Reaction-Diffusion Systems: Front Propagation and Spatial Structures // Lect. Notes Phys. 2003. V. 636. P. 187.
Inomoto O., Müller S.C., Kobayashi R., Hauser M.J.B. Acceleration of chemical reaction fronts // Eur. Phys. J.: Spec. Top. 2018. V. 227. P. 493.
Астарита Дж. Массопередача с химической реакцией. Л.: Химия, 1971.
Froment G.F., Bischoff K.B., De Wilde J. Chemical Reactors Analysis and Design. N.Y.: Wiley, 2011.
Данквертс П.В. Газожидкостные реакции. М.: Химия, 1973.
Берд Р., Стьюарт В., Лайтфут Е. Явления переноса. М.: Химия, 1974.
Jensen K.F. Flow chemistry – Microreaction technology comes of age // AIChE J. 2017. V. 63. № 3. P. 858.
Musabekova L.M., Brener A.M. Methods for Calculating the Process of Chemisorption in Systems with a Moving Front of Instantaneous Irreversible reaction // Heat Transfer Res. 2007. V. 38. № 2. P. 135.
Мусабекова Л.М., Бренер А.М. Методология расчета процесса хемосорбции в системах с движущимся фронтом мгновенной необратимой реакции // Труды 5-го Минского международного форума по тепло- и массообмену ММФ. Минск, 2004. Т. 1. С. 319.
Musabekova L.M., Kalbayeva A.T., Dilman V.V., Zhumataev N.S., Kurakbayeva S.D., Tauasarov B.R. Modeling of dynamical reaction-diffusion systems with multistage and non-perfect kinetics // News Natl. Acad. Sci. Repub. Kaz., Ser. Geol. Tech. Sci. 2019. № 1(433). P. 120.
Dil'man V.V. Stefan–Maxwell concentration relationships for three-component diffusion in gas mixtures // Theor. Found. Chem. Eng. 2010. V. 44. № 3. P. 254. [Дильман В.В. Концентрационные зависимости трехкомпонентной диффузии Стефана–Максвелла в газовых смесях // Теор. осн. хим. технол. 2010. Т. 44. № 3. С. 270.]
Мусабекова Л.М., Бренер А.М. Методология расчета процесса хемосорбции с движущимся фронтом реакции // Сб. трудов 16 Международной научной конференции “Математические методы в технике и технологиях”. СПб., 2003. Т. 3. С. 212.
Brener A.M., Musabekova L.M. Autowave regimes of heat and mass transfer in the non-isothermal through-reactors // Advanced Computational Methods in Heat Transfer IX (WIT Transactions on Engineering Sciences. V. 53) / Eds. Sundén B., Brebbia C.A. Southampton: WIT Press, 2006. P. 181.
Jarrige N., Malham J.B., Martin J., Rakotomalala N., Salin D., Talon L. Numerical simulations of a buoyant autocatalytic reaction front in tilted Hele-Shaw cells // Phys. Rev. E. 2010. V. 81. P. 066311.
Guzman R., Vasquez D.A. Surface tension driven flow on a thin reaction front // Eur. Phys. J.: Spec. Top. 2016. V. 225. P. 2573.
Finlayson B.A. Introduction to Chemical Engineering Computing. Hoboken, N.J.: Wiley, 2012.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии