Теоретические основы химической технологии, 2020, T. 54, № 2, стр. 220-227
Математическое моделирование процесса десублимации UF6 в емкости с горизонтальным оребрением
А. А. Орлов a, А. Ф. Цимбалюк a, Р. В. Малюгин b, *
a Томский политехнический университет
Томск, Россия
b ТО СургутНИПИнефть ПАО Сургутнефтегаз
Тюмень, Россия
* E-mail: malyugin@tpu.ru
Поступила в редакцию 05.11.2018
После доработки 12.09.2019
Принята к публикации 16.09.2019
Аннотация
Приведены результаты численного моделирования нестационарного процесса десублимации UF6 в вертикальную погружную емкость объемом 6.0 × 10–2 м3 с горизонтальным оребрением с использованием разработанной и программно реализованной двухмерной математической модели. Описаны выявленные закономерности процесса десублимации UF6 при изменении давления и температуры газообразного UF6 в коллекторе, температуры хладагента, количества, расположения и геометрии ребер емкости. Показано, что увеличение количества ребер, изменение режима тепло- и массообмена, увеличение диаметра центрального отверстия в горизонтальных ребрах позволяют существенно увеличить среднюю производительность емкости и уменьшить время ее заполнения.
ВВЕДЕНИЕ
На предприятиях по обогащению урана Российской Федерации происходит модернизация разделительного оборудования [1–5], сопровождающаяся увеличением их разделительных мощностей и нагрузки на цеха конденсационно-испарительных установок, в которых происходит десублимация UF6 [6]. В связи с этим актуальны работы, направленные на исследование и интенсификацию процесса десублимации UF6, проектирование коллекторов десублимации UF6 повышенной производительности и совершенствование конструкций емкостей.
Возможности применения экспериментальных подходов для решения задач, стоящих перед обогатительными предприятиями России, ограничены [6–8]. В связи с этим перспективным является теоретическое исследование нестационарного процесса десублимации UF6 в транспортные емкости, что позволит определить закономерности протекания данного процесса, провести его оптимизацию и выработать обоснованные рекомендации по повышению производительности работы коллекторов десублимации.
Ранее нами были проведены исследования динамики заполнения емкостей с гладкими внутренними стенками различного объема десублимированным UF6 при изменении давления в коллекторе и температуры хладагента с использованием двухмерной математической модели нестационарного процесса десублимации UF6 [9]. Результаты представлены в табл. 1.
Таблица 1.
Средняя производительность емкостей с гладкими внутренними стенками различного объема при изменении давления в коллекторе и температуры хладагента
| P, мм рт.ст. | TC, °С | Средняя производительность емкостей q, г/с | ||||
|---|---|---|---|---|---|---|
| V = 1.0 м3 | V = 2.0 м3 | V = 2.5 м3 | V = 3.0 м3 | V = 4.0 м3 | ||
| 60 | –15 | 2.253 | 3.433 | 3.926 | 4.376 | 5.253 |
| –20 | 2.605 | 3.970 | 4.538 | 5.058 | 6.071 | |
| –25 | 2.955 | 4.502 | 5.146 | 5.736 | 6.882 | |
| 70 | –15 | 2.415 | 3.681 | 4.210 | 4.693 | 5.632 |
| –20 | 2.769 | 4.219 | 4.823 | 5.376 | 6.451 | |
| –25 | 3.120 | 4.753 | 5.433 | 6.055 | 7.265 | |
| 80 | –15 | 2.560 | 3.901 | 4.461 | 4.973 | 5.968 |
| –20 | 2.915 | 4.440 | 5.076 | 5.657 | 6.788 | |
| –25 | 3.266 | 4.975 | 5.686 | 6.337 | 7.603 | |
Расчеты показали, что при уменьшении температуры хладагента с минус 15 до минус 25°С и давлении в коллекторе 60 мм рт. ст. средняя производительность емкостей с гладкими внутренними стенками объемом 1.0–4.0 м3 увеличивается на 23.7%, при давлении 70 мм рт. ст. – на 22.5%, при давлении 80 мм рт. ст. – на 21.5%.
Наибольшие значения средней производительности для всех емкостей с гладкими внутренними стенками получены при температуре хладагента минус 25°С. Показано, что увеличение давления с 60 до 80 мм рт. ст. при данной температуре позволяет повысить среднюю производительность емкостей объемом 1.0–4.0 м3 на 31%.
Расчеты динамики заполнения емкостей с вертикальным оребрением проводились нами с использованием упрощенной трехмерной математической модели процесса десублимации [10].
Установлено [10], что увеличение давления в коллекторе с 60 до 80 мм рт. ст. и понижение температуры хладагента с минус 15 до минус 25°С позволяет повысить среднюю производительность емкостей объемом 1.0–4.0 м3 с вертикальным оребрением примерно на 43.3–45.3% (табл. 2), а увеличение количества ребер с 12 до 20 – на 41.5–65.7%. Уменьшение толщины ребер на 1.0 × × 10–3 м повышает эффективность работы емкостей на 0.4–0.6%. Увеличение ширины вертикальных ребер в 1.33–2.0 раза при сохранении постоянной площади их теплообменной поверхности приводит к увеличению средней производительности емкостей объемом 1.0–4.0 м3 на 8.6–39.3% соответственно. Увеличение отношения высоты емкостей к их радиусу до предельного значения позволяет повысить их среднюю производительность на 1.13–2.97%.
Таблица 2.
Средняя производительность емкостей с вертикальным оребрением различного объема при изменении давления в коллекторе и температуры хладагента
| P, мм рт. ст. | Th, °С | Средняя производительность емкостей q, г/с | ||
|---|---|---|---|---|
| V = 2.0 м3 | V = 3.0 м3 | V = 4.0 м3 | ||
| 60 | –15 | 6.16 | 9.19 | 12.04 |
| –20 | 7.13 | 10.61 | 13.92 | |
| –25 | 8.08 | 12.04 | 15.78 | |
| 70 | –15 | 6.58 | 9.80 | 12.85 |
| –20 | 7.54 | 11.23 | 14.71 | |
| –25 | 8.49 | 12.65 | 16.57 | |
| 80 | –15 | 6.94 | 10.34 | 13.58 |
| –20 | 7.9 | 11.76 | 15.41 | |
| –25 | 8.85 | 13.35 | 17.26 | |
Полученные результаты показали возможность существенного повышения эффективности процесса десублимации UF6 в вертикальных емкостях с гладкими внутренними стенками, поэтому представляло интерес провести аналогичные исследования для вертикальной емкости с горизонтальным оребрением.
В данной статье приведены результаты расчетов средней производительности погружной емкости с горизонтальным оребрением при изменении давления и температуры газообразного UF6 в коллекторе, температуры хладагента, количества, расположения и геометрии ребер емкости.
ОБЪЕКТ ИССЛЕДОВАНИЯ
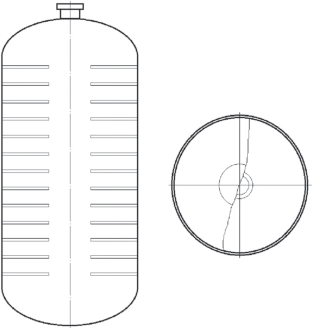
В качестве объекта исследования выступала вертикальная погружная емкость объемом 6.0 × 10–2 м3 с горизонтальным оребрением, представленная на рис. 1. Емкость изготовлена из стали марки 16ГС, имеет 13 ребер толщиной 2.0 × 10–3 м, диаметр центрального отверстия ребра составляет 6.0 × 10–2 м, расстояние между ребрами равно 4.0 × 10–2 м, расстояние от дна емкости до нижнего ребра 1.76 × × 10–1 м, радиус емкости 1.5 × 10–2 м, высота 8.48 × × 10–1 м, толщина стенки емкости 6.0 × 10–3 м.
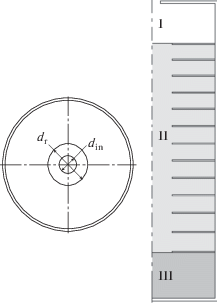
Объем емкости разбивали на несколько подобластей, каждую из которых рассматривали отдельно, с использованием метода Multiblock [11–16]. Схема разбиения емкости на подобласти представлена на рис. 2. Подобласть I соответствует объему емкости между ее верхней стенкой и первым горизонтальным ребром. Подобласть II соответствует объему емкости с оребрением. Подобласть III – объему между донной торцевой стенкой емкости и нижним краем последнего горизонтального ребра. В каждой подобласти находили совместное (с учетом соседней/соседних подобластей) решение уравнений тепло- и массообмена [17, 18].
ОПИСАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
При построении математической модели нестационарного процесса десублимации UF6 был принят ряд допущений [10, 17, 18].
Режим течения газообразного UF6 в рассматриваемой задаче является вязким и дозвуковым, с числами Маха существенно меньше единицы (M $ \ll $ 1). Расчет числа Рейнольдса показал, что Re ≈ 500, в связи с чем течение газообразного UF6 в емкости считали ламинарным.
Полученные нами вектора скорости движения газообразного UF6 в емкости в различные моменты времени [19], а также изотермы в газообразном UF6 и стенке емкости [20] дают представление о характере течения газа. Они показывают, что течение газа имеет вид расширяющейся струи, при этом внутри емкости отсутствуют зоны вихревого течения газообразного UF6.
В связи с осевой симметрией задачи, отсутствием зон вихревого течения газообразного UF6 и малым порядком смешанных производных компонент скорости вместо системы полных уравнений Навье–Стокса при построении математической модели мы посчитали возможным использовать дивергентную форму системы уравнений Прандтля [21–23]:
(1)
$\left\{ \begin{gathered} \frac{\partial }{{\partial \tau }}\left( {r{{\rho }_{{UF}}}} \right) + \frac{\partial }{{\partial r}}\left( {r{{\rho }_{{UF}}}u} \right) + \frac{\partial }{{\partial z}}\left( {r{{\rho }_{{UF}}}{v}} \right) = 0, \hfill \\ \frac{\partial }{{\partial \tau }}\left( {r{{\rho }_{{UF}}}u} \right) + \frac{\partial }{{\partial r}}\left( {r{{\rho }_{{UF}}}{{u}^{2}}} \right) + \frac{\partial }{{\partial z}}\left( {r{{\rho }_{{UF}}}u{v}} \right) = \hfill \\ = - \frac{{\partial rP}}{{\partial r}} + \frac{\partial }{{\partial r}}\left( {{{\mu }_{{UF}}}\frac{{\partial ru}}{{\partial r}}} \right) + \frac{\partial }{{\partial z}}\left( {{{\mu }_{{UF}}}\frac{{\partial ru}}{{\partial z}}} \right) + \frac{{{{\rho }_{{UF}}}u{v}}}{r}, \hfill \\ \frac{\partial }{{\partial \tau }}\left( {r{{\rho }_{{UF}}}{v}} \right) + \frac{\partial }{{\partial r}}\left( {r{{\rho }_{{UF}}}{v}u} \right) + \frac{\partial }{{\partial z}}\left( {r{{\rho }_{{UF}}}{{{v}}^{2}}} \right) = \hfill \\ = - \frac{{\partial rP}}{{\partial z}} + \frac{\partial }{{\partial r}}\left( {{{\mu }_{{UF}}}\frac{{\partial r{v}}}{{\partial r}}} \right) + \frac{\partial }{{\partial z}}\left( {{{\mu }_{{UF}}}\frac{{\partial r{v}}}{{\partial z}}} \right) + \hfill \\ + \,\,\frac{{{{\rho }_{{UF}}}{{{v}}^{2}}}}{r} + r{{\rho }_{{UF}}}g, \hfill \\ \frac{\partial }{{\partial \tau }}\left( {r{{с}_{{pUF}}}{{\rho }_{{UF}}}T} \right) + \frac{\partial }{{\partial r}}\left( {r{{с}_{{pUF}}}{{\rho }_{{UF}}}Tu} \right) + \hfill \\ + \,\,\frac{\partial }{{\partial z}}\left( {r{{с}_{{pUF}}}{{\rho }_{{UF}}}T{v}} \right) = \frac{\partial }{{\partial r}}\left( {{{\lambda }_{{UF}}}\frac{{\partial r{{\rho }_{{UF}}}T}}{{\partial r}}} \right) + \hfill \\ + \,\,\frac{\partial }{{\partial z}}\left( {{{\lambda }_{{UF}}}\frac{{\partial r{{\rho }_{{UF}}}T}}{{\partial z}}} \right). \hfill \\ \end{gathered} \right.$Для расчета температуры стенок емкости использовали уравнение теплопроводности:
(2)
${{с}_{{st}}}{{\rho }_{{st}}}\frac{\partial }{{\partial \tau }}\left( {rT} \right) = \frac{\partial }{{\partial r}}\left( {{{\lambda }_{{st}}}\frac{{\partial rT}}{{\partial r}}} \right) + \frac{\partial }{{\partial z}}\left( {{{\lambda }_{{st}}}\frac{{\partial rT}}{{\partial z}}} \right),$Теплофизические свойства газообразного UF6 рассчитывали по следующим температурным зависимостям [24, 25]:
Во входном патрубке задавали давление равным давлению в коллекторе и температуру газообразного UF6, на оси симметрии – условия симметрии, на боковой и донной стенках емкости – скорость движения фронта фазового перехода, которая вычислялась из решения задачи Стефана, описывающей процесс десублимации.
На внешней и внутренней поверхностях емкости задавали граничные условия первого рода: равенство температуры внешней поверхности стенки емкости температуре хладагента и равенство температуры границы раздела фаз равновесной температуре фазового перехода, которая зависит от давления над поверхностью раздела фаз.
С учетом сделанного допущения, что все тепло, выделяющееся при фазовом переходе, отводится хладагентом, условие Стефана на поверхности раздела газообразной и твердой фаз UF6 можно записать как равенство количества тепла, отводимого хладагентом через стенку емкости и слой десублимата, и количества тепла, выделяемого в результате фазового перехода UF6 из газообразного состояния в твердое [26]:
(3)
$\begin{gathered} {{{v}}_{w}}\left( \tau \right){{\rho }_{u}}{{L}_{{UF}}} = \frac{{{{\lambda }_{u}}r}}{{{{l}_{w}}\left( \tau \right)}}\frac{{\partial T}}{{\partial n}}, \\ {{L}_{{UF}}} = - 16\,700 + 624.176T - 0.9131335{{T}^{2}} + \\ + \,\,{{16\,267\,677.3} \mathord{\left/ {\vphantom {{16\,267\,677.3} T}} \right. \kern-0em} T}\,\,\,\left[ {{{{\text{Дж}}} \mathord{\left/ {\vphantom {{{\text{Дж}}} {{\text{кг}}}}} \right. \kern-0em} {{\text{кг}}}}} \right]. \\ \end{gathered} $Давление в емкости в начальный момент заполнения считали равным 4 мм рт. ст. Система уравнений (1)–(3) решалась численно с использованием алгоритма SIMPLE [27–31].
Разработанная двухмерная математическая модель нестационарного процесса десублимации UF6 в вертикальные погружные емкости была программно реализована на языке FORTRAN-90 в среде Microsoft Developer Visual Studio.
РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ
Исследование влияния параметров, задающих режим процесса десублимации (давление и температура газообразного UF6 в коллекторе, температура хладагента), на среднюю производительность рассматриваемой емкости при ее заполнении десублимированным UF6 до 70% свободного объема проводили при изменении температуры газообразного UF6 в коллекторе от 20 до 40°С, рабочего давления в коллекторе от 60 до 80 мм рт. ст. и температуры хладагента от минус 15 до минус 25°С.
На рис. 3 представлены расчетные зависимости средней производительности емкости при температуре газообразного UF6 30°С от давления в коллекторе при различной температуре хладагента.
Рис. 3.
Зависимость средней производительности емкости от давления в коллекторе при различных температурах хладагента: 1 – минус 25°С, 2 – минус 20°С, 3 – минус 15°С.
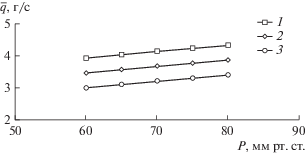
Из рис. 3 видно, что повышение давления в коллекторе от 60 до 80 мм рт. ст. и понижение температуры хладагента от минус 15 до минус 25°С приводит к линейному увеличению средней производительности емкости. Это объясняется тем, что с повышением давления в коллекторе увеличивается температура фазового перехода UF6 и охлаждение газообразного UF6 до этой температуры происходит быстрее [24]. Кроме того, при увеличении разницы между температурой хладагента и температурой фазового перехода UF6 происходит увеличение величины теплового потока и, соответственно, повышение скорости десублимации. Аналогичные зависимости получены для емкости при других температурах газообразного UF6 (табл. 3).
Таблица 3.
Средняя производительность емкости при изменении давления в коллекторе и температуры хладагента
| P, мм рт.ст. | TC, °С | Средняя производительность емкостей q, г/с | ||
|---|---|---|---|---|
| TUF = 20°С | TUF = 30°С | TUF = 40°С | ||
| 60 | –15 | 2.36 | 2.31 | 2.27 |
| –20 | 2.73 | 2.67 | 2.62 | |
| –25 | 3.09 | 3.03 | 2.97 | |
| 70 | –15 | 2.52 | 2.48 | 2.43 |
| –20 | 2.89 | 2.84 | 2.79 | |
| –25 | 3.26 | 3.19 | 3.14 | |
| 80 | –15 | 2.67 | 2.62 | 2.57 |
| –20 | 3.04 | 2.98 | 2.93 | |
| –25 | 3.41 | 3.34 | 3.28 | |
Показано, что уменьшение температуры газообразного UF6 на 10°С приводит к увеличению средней производительности емкости примерно на 2%.
При уменьшении температуры хладагента с минус 15 до минус 25°С и давлении в коллекторе 60 мм рт. ст. средняя производительность емкости увеличивается на 23.67%, при давлении 70 мм рт. ст. – на 22.52%, при давлении 80 мм рт. ст. – на 21.57%.
Наибольшее значение средней производительности данной емкости наблюдается при температуре хладагента минус 25°С. Показано, что увеличение давления с 60 до 80 мм рт. ст. при температуре хладагента минус 25°С позволяет повысить среднюю производительность емкости на 9.44%.
Увеличение давления в коллекторе выше 80 мм рт. ст. нецелесообразно, так как для предотвращения десублимации газообразного UF6 в трубопроводах коллектора нужно будет осуществлять их подогрев, что усложнит технологию и увеличит ее себестоимость. Понижение температуры хладагента (насыщенного раствора CaCl2) ниже минус 25°С также нежелательно, поскольку это приведет к значительному увеличению его вязкости [32].
Дальнейшие исследования влияния геометрии горизонтального оребрения емкости на эффективность ее работы проводили при давлении в коллекторе 80 мм рт. ст., температуре хладагента минус 25°C, температуре газообразного UF6 30°C. Количество ребер в емкости считали равным 13.
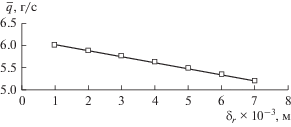
При оценке влияния толщины горизонтальных ребер на среднюю производительность емкости толщина ребер изменялась от 1.0 × 10–3 до 7.0 × 10–3 м. Зависимость средней производительности емкости от толщины горизонтальных ребер представлена на рис. 4.
Из рис. 4 видно, что с уменьшением толщины горизонтальных ребер на 1.0 × 10–3 м происходит возрастание средней производительности емкости примерно на 3.78%. На разделительных производствах используют горизонтальные ребра толщиной 2.0 × 10–3 м. Уменьшение толщины ребер до 1.0 × 10–3 м нецелесообразно, так как может привести к их деформации в процессе десублимации на них UF6. Увеличение толщины ребер приведет к снижению средней производительности емкости, увеличению веса емкости и уменьшению ее свободного объема.
Далее было исследовано влияние на среднюю производительность емкости расстояния между горизонтальными ребрами. Расчеты показали, что при изменении расстояния между ребрами от 2.5 × 10–2 до 6.5 × 10–2 м средняя производительность емкости линейно увеличивается с 5.99 до 6.05 г/с (менее чем на 0.8%).
В связи с незначительным влиянием толщины горизонтальных ребер и расстояния между ними на среднюю производительность емкости эти параметры можно исключить из рассмотрения при оптимизации геометрии емкости.
Дальнейшие исследования [17] показали, что увеличение диаметра центрального отверстия в горизонтальных ребрах с 6.0 × 10–2 до 6.8 × 10–2 м позволяет повысить среднюю производительность емкости на 17.57%.
Для исследования влияния количества горизонтальных ребер на среднюю производительность емкости нами был проведен расчет динамики ее заполнения десублимированным UF6 при изменении количества ребер от 4 до 20. В расчетах верхнее и нижнее ребра находились на расстоянии 7.0 × 10–2 м от верхнего и нижнего краев цилиндрической части емкости соответственно, а остальные ребра располагались между ними на одинаковом расстоянии, диаметр центрального отверстия ребер был равен 6.0 × 10–2 м, толщина ребер 2.0 × 10–3 м. Минимальное расстояние между ребрами составляло 2.5 × 10–3 м, максимальное ограничивалось высотой цилиндрической части емкости с учетом отступа верхнего и нижнего ребер от краев.
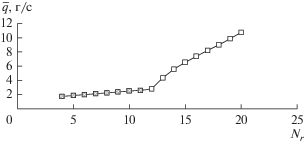
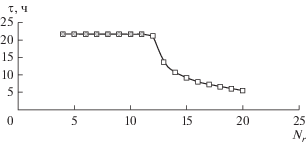
Зависимости средней производительности емкости, степени и времени ее заполнения от количества горизонтальных ребер представлены на рис. 5, 6 и 7 соответственно. Точками с серой заливкой отмечены участки расчетных кривых, на которых происходит “перемерзание” отверстия верхнего ребра емкости, вследствие чего она не заполняется до 70% ее объема.
Из рис. 5 видно, что средняя производительность емкости на участке 4 ≤ Nr ≤ 11 линейно увеличивается с 1.73 до 2.59 г/с, при этом степень ее заполнения десублимированным UF6 изменяется с 44.0 до 66.11% (рис. 6), поскольку происходит “перемерзание” отверстия верхнего ребра емкости. Расчет показал, что “перемерзание” при 4 ≤ ≤ Nr ≤ 11 всегда происходит через 21.65 ч (рис. 7). Это можно объяснить тем, что “перемерзает” только верхнее ребро, которое не меняет своего положения в емкости. На участке с 11 < Nr ≤ 20 “перемерзание” прекращается. Наблюдается линейное увеличение средней производительности емкости с 2.59 до 10.74 г/с (в 4.14 раза). При этом время заполнения емкости до 70% ее свободного объема нелинейно уменьшается с 21.65 до 5.53 ч. Средняя производительность емкости с 13 ребрами составляет 4.33 г/с, время ее заполнения 13.72 ч. Увеличение количества ребер с 13 до 20 позволяет повысить среднюю производительность емкости до 10.74 г/с и уменьшить время ее заполнения примерно в 2.5 раза. Добавление каждого дополнительного ребра уменьшает свободный объем емкости на 1.3 × 10–4 м3, увеличивает массу емкости и затраты металла на ее изготовление. Максимальное количество ребер ограничивается техническими возможностями изготовления емкости (минимальным расстоянием между ребрами).
Таким образом, результаты исследований процесса десублимации UF6 на примере емкости с горизонтальным оребрением объемом 6.0 × 10–2 м3 показали, что существенное влияние на среднюю производительность емкости оказывают два фактора – количество горизонтальных ребер и диаметр центрального отверстия в них. Толщина горизонтальных ребер и расстояние между ними слабо влияют на среднюю производительность емкости.
Исследование влияния отношения высоты емкости с горизонтальным оребрением объемом 6.0 × 10–2 м3 к ее радиусу не проводились, в связи с ограничениями, накладываемыми на минимальный радиус емкости, который должен позволить разместить два патрубка (входной и отсосный) с клапанами под защитным колпаком.
ЗАКЛЮЧЕНИЕ
С помощью двухмерной математической модели нестационарного процесса десублимации газообразного UF6 в вертикальные погружные емкости с горизонтальным оребрением установлены следующие закономерности процесса десублимации UF6. Изменение режима тепло- и массообмена (повышение давления в коллекторе до 80 мм рт. ст. и понижение температуры хладагента до минус 25°С) позволяет повысить среднюю производительность емкости примерно на 30.85%. Толщина ребер и расстояние между ними не оказывают существенного влияния на эффективность работы емкости. Увеличение количества ребер в емкости с 13 до 20 позволяет повысить ее среднюю производительность примерно в 2.5 раза.
Полученные результаты вносят вклад в развитие теории процесса десублимации UF6 и показывают возможность существенного повышения эффективности технологического процесса десублимации на разделительных предприятиях отрасли.
ОБОЗНАЧЕНИЯ
| c | теплоемкость, Дж/(кг К) |
| d | диаметр, м |
| H | высота емкости, м |
| h | расстояние между ребрами, м |
| g | ускорение свободного падения, м/с2 |
| L | теплота фазового перехода, Дж/кг |
| N | количество горизонтальных ребер в емкости |
| n | нормаль к поверхности фазового перехода |
| P | давление, мм рт. ст. |
| q | средняя производительность емкости, г/с |
| R | радиус емкости, м |
| r, z | основная цилиндрическая система координат, начало которой находится на оси симметрии входного отверстия |
| S | площадь теплообменной поверхности, м2 |
| T | температура, К |
| u, v | проекции вектора скорости, м/с |
| δ | толщина стенки емкости, м |
| λ | коэффициент теплопроводности, Дж/(с м К) |
| μ | коэффициент динамической вязкости, Па с |
| ρ | плотность газа, кг/м3 |
| τ | время заполнения емкости, ч |
| M | число Маха |
| Re | число Рейнольдса |
ИНДЕКСЫ
Список литературы
Камчатова Е.Ю. Инновационный потенциал атомной энергетики // Вестн. унив. (Гос. унив. упр.). 2017. № 11. С. 27.
Гергерт А.П., Молостова И.И., Рябов Д.К. Развитие алюминиевого сплава 1960 для газовых центрифуг // Цветн. мет. 2013. № 9. С. 33.
Александров О.Е. Два подхода к оптимизации газовой центрифуги // Перспект. матер. 2010. № 8. С. 29.
Belyntsev A.M., Sergeev G.S., Gromov O.B., Bychkov A.A., Ivanov A.V., Kamordin S.I., Mikheev P.I., Nikonov V.I., Petrov I.V., Seredenko V.A., Starovoitov S.P., Fomin S.A., Frolov V.G., Kholin V.F. Intensification of evaporation of uranium hexafluoride // Theor. Found. Chem. Eng. 2013. V. 47. № 4. P. 499. [Белынцев А.М. Сергеев Г.С., Грормов О.Б., Бычков А.А., Иванов А.В., Камордин С.И., Михеев П.И., Никонов В.И., Петров И.В., Середенко В.А., Старовойтов С.П., Фомин С.А., Фролов В.Г., Холин В.Ф. Интенсификация испарения гексафторида урана // Хим. технол. 2011. Т. 12. № 11. С. 675.]
Turaev N.S., Zherin I.I. Chemistry and Technology of Uranium. Moscow: Ore & Metals, 2006.
Orlov A.A., Tsimbalyuk A.F., Malyugin R.V. Desublimation for purification and transporting UF6: process description and modeling // Sep. Purif. Rev. 2017. V. 46. № 1. P. 81.
Gubanov S.M., Krainov A.Yu., Mazur R.L. Theoretical and experimental modeling of the cooling of uranium hexafluoride vapor desublimation tanks // Theor. Found. Chem. Eng. 2016. V. 50. № 5. P. 766. [Губанов С.М., Крайнов А.Ю., Мазур Р.Л. Теоретическое и экспериментальное моделирование охлаждения емкостей для десублимации паров гексафторида урана // Теор. осн. хим. технол. 2016. Т. 50. № 5. С. 589.]
Gubanov S.M., Krainov A.Yu., Mazur R.L., Durnovtsev M.I. Theoretical modeling of cooling of containers for the desublimation of hydrogen fluoride // Theor. Found. Chem. Eng. 2017. V. 51. № 3. P. 352. [Губанов С.М., Крайнов А.Ю., Мазур Р.Л., Дурновцев М.И. Теоретическое моделирование охлаждения емкостей для десублимации паров фтористого водорода // Теор. осн. хим. технол. 2017. Т. 51. № 3. С. 343.]
Орлов А.А., Малюгин Р.В., Котельникова А.А. Влияние режима тепло- и массообмена на динамику заполнения емкостей с гладкими внутренними стенками десублимированным UF6 // Изотопы: технологии, материалы и применение: Материалы V Международной конференции молодых ученых, аспирантов и студентов. Томск: Графика, 2018. С. 30.
Орлов А.А., Цимбалюк А.Ф., Малюгин Р.В. Математическое моделирование процесса десублимации UF6 в емкости с горизонтальным оребрением // Теор. осн. хим. технол. 2020. Т. 54. № 1. С. 1.
Martins M.M., Vaz Jr. M., Zdanski P.S.B. A note on a derivative scheme for the finite volume method applied to incompressible viscous fluid // Continuum Mech. Thermodyn. 2018. V. 30. P. 943.
Darwish M., Geahchan W., Moukalled F. Fully implicit method for coupling multiblock meshes with nonmatching interface grids // Numer. Heat Transfer, Part B. 2017. V. 71. № 2. P. 109.
Fang W.-Z., Gou J.-J., Chen L., Tao W.-Q. A multi-block lattice Boltzmann method for the thermal contact resistance at the interface of two solids // Appl. Therm. Eng. 2018. V. 138. P. 122.
Khorrami Z., Banihashem M.A. Improving multi-block sigma-coordinate for 3D simulation of sediment transport and steep slope bed evolution // Appl. Math. Modell. 2019. V. 67. P. 378.
Wang S., Nissen A., Kreiss G. Convergence of finite difference methods for the wave equation in two space dimensions // Math. Comput. 2018. V. 314. № 87. P. 2737.
Hassanzadeh R., Tokgoz N. Thermal-hydraulic characteristics of nanofluid flow in corrugated ducts // J. Eng. Thermophys. 2017. V. 26. № 4. P. 498.
Orlov A.A., Tsimbalyuk A.F., Malyugin R.V., Leontieva D.A., Kotelnikova A.A. Effect of tank geometry on its average performance // AIP Conf. Proc. 2018. V. 1938. Article number 020009.
Orlov A.A., Tsimbalyuk A.F., Malyugin R.V., Glazunov A.A. Dynamics of UF6 desublimation with the influence of tank geometry for various coolant temperature // MATEC Web Conf. 2016. V. 72. Article number 01079.
Орлов А.А., Цимбалюк А.Ф., Малюгин Р.В. Математическая модель процесса десублимации гексафторида урана // Вопр. ат. науки тех. Сер.: Мат. модел. физ. процессов. 2016. № 2. С. 75.
Орлов А.А., Цимбалюк А.Ф., Малюгин Р.В., Котельникова А.А. Естественная конвекция газообразного UF6 в вертикальной цилиндрической емкости // Изв. высш. учебн. завед. Физ. 2018. Т. 61. № 12/2. С. 79.
Годунов С.К., Забродин А.В., Иванов М.Я., Крайко А.Н. Численное решение многомерных задач газовой динамики. М.: Наука, 1976.
Шлихтинг Г. Теория пограничного слоя. М.: Наука, 1974.
Мажукин А.В., Мажукин В.И. Динамическая адаптация в параболических уравнениях // Ж. вычисл. мат. мат. физ. 2007. Т. 47. № 11. С. 1913.
Llewellyn D.R. Some physical properties of uranium hexafluoride // J. Chem. Soc. 1953. P. 28.
Katz J.J., Rabinowiych E. The Chemistry of Uranium. Part I. The Element, Its Binary and Related Compounds. N.Y.: McGraw-Hill, 1961.
Orlov A.A., Tsimbalyuk A.F., Malyugin R.V. Mathematical modeling of process of obtaining the solid uranium hexafluoride // Key Eng. Mater. 2016. V. 683. P. 533.
Patankar S.V. Numerical Heat Transfer and Fluid Flow. N.Y.: Hemisphere, 1980.
Hu M.-H., Wu J.-S., Chen Y.-S. Development of parallelized 2D/2D-axisymmetric Navier-Stokes equations and multigrid method // Comput. Fluids. 2011. V. 45. № 1. P. 241.
Corcione M., Cianfrini M., Quintino A. Enhanced natural convection heat transfer of nanofluids in enclosures with two adjacent walls heated and the two opposite walls cooled // Int. J. Heat Mass Transfer. 2015. V. 88. P. 902.
Mamourian M., Milani Shirvan K., Ellahi R., Rahimi A.B. Optimization of mixed convection heat transfer with entropy generation in a wavy surface square lid-driven cavity by means of Taguchi approach // Int. J. Heat Mass Transfer. 2016. V. 102. P. 544.
Xiao H., Wang J., Liu Z., Liu W. A consistent SIMPLE algorithm with extra explicit prediction – SIMPLEC // Int. J. Heat Mass Transfer. 2018. V. 120. P. 1255.
Grigoras C.G., Muntianu G., Gavrila L. Mathematical modelling of CaCl2 aqueous solutions thermophysical properties // Sci. Study Res.: Chem. Chem. Eng., Biotechnol., Food Ind. (Univ. Bacau). 2016. V. 17. № 4. P. 417.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии