Теоретические основы химической технологии, 2020, T. 54, № 2, стр. 192-201

Механизм интенсификации гетерогенной реакции восстановления с выделением пузырьков газа

В. П. Мешалкин^a, С. В. Панченко^b, М. И. Дли^b, В. И. Бобков^b, *, М. В. Черновалова^c

^a Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия

^b Филиал Национального исследовательского университета “МЭИ” в г. Смоленске
Смоленск, Россия

^c Национальный исследовательский университет “МЭИ”
Москва, Россия

^* E-mail: vovabobkoff@mail.ru

Поступила в редакцию 24.10.2019
После доработки 28.10.2019
Принята к публикации 12.11.2019

DOI: 10.31857/S0040357120020104

Полный текст (PDF)

Аннотация

Для оценки степени интенсификации гетерогенных реакций восстановления и растворения решалась задача описания гидродинамики, массообмена и экранирования реакционной поверхности при формировании и действии газофазных продуктов в виде пузырьков. Рассмотрены теоретические положения по формированию пузырьков газа при гетерогенной реакции твердое тело–жидкость–газ. На основе аналогии с теплогидравликой кипения и барботажа получены теоретические зависимости для скорости роста пузырьков при наличии микроподслоя жидкого реагента. Аналитические зависимости, полученные в данной работе, качественно соотносятся с эмпирическими соотношениями других авторов. В связи со сложностью рассматриваемых проблем количественная интерпретация во главу угла не ставилась, но введением незначительных поправок может быть достигнуто количественное совпадение. С учетом особенностей гидродинамики газожидкостных сред исследована динамика гетерогенной реакции твердое тело–жидкость–газ при массообмене жидкого реагента и твердого восстановителя. Получены соотношения для оценки концентраций реагента и доли поверхности, экранированной выделяющимися пузырьками. Оценки показывают, что влияние экранирования незначительно. Видимо поэтому в технических расчетах реакций с выделением пузырьков экранирование не принимается во внимание. Исследована устойчивость протекания реакции и получено, что в равновесии формируются газожидкостные структуры, обеспечивающие чередование экранированных и неэкранированных участков реакционной поверхности, что обеспечивает наличие градиента газосодержания, провоцирующего движение слоев жидкого реагента и интенсивное перемешивание. Анализ критериальных уравнений для массообмена на реакционной поверхности дает зависимость, качественно и частично количественно характеризующую процессы массообмена и совпадающую с полученной экспериментально. Результаты работы могут быть использованы для формирования режимов, обеспечивающих оптимальное функционирование технологических реакторов.

Ключевые слова: гетерогенные реакции восстановления, газофазные продукты, массообмен, экранирование реакционной поверхности, скорость роста пузырьков, динамика гетерогенной реакции жидкость–твердое тело–газ, критериальные уравнения массообмена, интенсификации гетерогенных реакций

ВВЕДЕНИЕ

Задачи гетерогенного реагирования с выделением газовой фазы в виде пузырьков возникают в теории зажигания, горения и взрыва, в процессах растворения, процессах восстановления, протекающих в системах газ–жидкость–твердое тело с выделением вторичных газов, для описания массо- и теплообменных процессов при хлорировании и переработке железоуглеродистых, медноникелевых и других цветных металлов и расплавов [1–3]. Способам интенсификации тепло- и массообмена в такого рода системах уделяется особое внимание [4–9]. Интерес к изучению взаимодействия газа и жидкости возрастает в связи с особенностями поведения таких систем и расширением их сферы приложения [10–14].

В наших работах [15–17] показана роль теплогидравлики в интенсификации целевых процессов восстановления рудных материалов, где скорость массообмена принималась значительной.

В представленной работе рассмотрен механизм реагирования с учетом практически полного набора факторов, влияющих на скорость целевых процессов.

При выделении газовой фазы в процессе реакции происходит интенсивное перемешивание и тепломассообмен интенсифицируется [3]. В то же время процесс образования газовых пузырьков, который экранирует часть поверхности, тормозит доступ жидкой фазы реагента к поверхности и препятствует массообмену. Эти процессы следует изучать и вносить соответствующие поправки в описание скорости реагирования. При кипении процесс экранирования экспериментально рассмотрен в [18]. Считается, что определенная доля поверхности занята образующимися пузырьками, хотя с учетом особенностей образования пузырька с формированием микроподслоя эта доля невелика, что подтверждено экспериментально. Аналогия барботажа и кипения с возникновением повторяющихся зон пузырьков и вихрей жидкости показана в [3].

При рассмотрении процессов тепломассообмена при протекании гетерогенных реакций с образованием газовой фазы в виде пузырьков естественным является аналогия с процессами кипения и барботажа. В кипении большинство явлений, сопровождающих этот процесс, базируется на гидродинамическом подходе. Отмечено, что механизм переноса энергии осуществляется в основном за счет перемешивания жидкости пузырьками газа (более 90%), а не процессами испарения [3]. Именно поэтому коэффициенты энергообмена при кипении и барботаже идентичны. Процессы массопереноса при гетерогенном реагировании иногда называют “химическим кипением”.

Самоинтенсификация процесса реагирования при барботировании пузырьков газообразных продуктов реакции заключается в перемешивании жидкой фазы, увлекаемой пузырьками в виде присоединенной массы. Массообмен на поверхности реагирования при обтекании интенсифицируется за счет воздействия на пограничный слой, когда доставка реагента осуществляется вынужденной конвекцией более эффективно по сравнению с молекулярной диффузией.

Гетерогенные взаимодействия сопровождаются образованием в зоне реакции на границах раздела новой газообразной фазы – продуктов хемосорбции применительно к растворению твердого тела и продуктов восстановительных процессов. На поверхности твердой частицы, погруженной в спокойную жидкость, протекает в диффузионной области быстрая реакция вида ТВ + В = Ж + Г, где ТВ — исходное твердое вещество; В – реагент жидкой фазы; Ж – жидкий продукт реакции (раствор); Г – газообразный продукт реакции (пузырьки). Процесс массопереноса включает следующие стадии: а) диффузию молекул жидкого реагента из объема ванны к поверхности твердого тела; б) протекание быстрой химической реакции на контактной границе, в результате которой концентрация жидкого реагента стремится к нулю и возникают в стехиометрических соотношениях газ и жидкий продукт (их концентрации максимальны на межфазной поверхности); в) диффузию газа и жидкого продукта реакции от зоны реакции в объем жидкости.

ДИНАМИКА ВЗАИМОДЕЙСТВИЯ ЖИДКОСТИ И ПУЗЫРЬКОВ ГАЗА В ГЕТЕРОГЕННОЙ РЕАКЦИИ

Условием гетерогенного реагирования жидкой и твердой фаз при образовании газообразной является непосредственный контакт реагирующих фаз. В случае образования пузырьков газа происходит экранирование твердой поверхности и механизм протекания реакции усложняется. Для протекания реакции необходима подача реагента к основанию пузырька. По аналогии с парообразованием [19] рассмотрим модель формирования пузырька при протекании реакции твердого восстановителя и жидкого окисла [20].

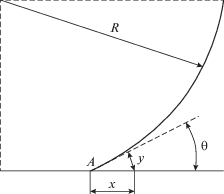
Согласно этой модели, между пузырьком и поверхностью нагрева возникает тонкий слой жидкости, подпитываемый из внешнего объема продуктами реагирующей жидкости в виде газа, поступающего в пузырек. Этот эффект теоретически рассмотрен для кипения Д.А. Лабунцовым [19] и обнаружен весьма тонкими экспериментами [18, 21]. Схема формирования зоны локального реагирования с образованием газовой фазы приведена на рис. 1.

Рис. 1.

Схема формирования локальной плотности массового потока газовой фазы.

В условиях протекания реакции на поверхности нагрева существует весьма тонкий слой жидкости, толщина которого имеет порядок Δ ~ γ_gD_lΔc/j_g. В этом случае основным источником газа, определяющим рост пузырька на поверхности реагирования, являются продукты реакции, отводимые к основанию пузырька через тонкий слой жидкости.

В соответствии с принятой моделью удельный массовый поток газа к элементу поверхности пузырька у его основания (рис. 1)

(1)

${{j}_{g}} = {{{{\gamma }_{g}}{{D}_{l}}\Delta c} \mathord{\left/ {\vphantom {{{{\gamma }_{g}}{{D}_{l}}\Delta c} y}} \right. \kern-0em} y},$

где Δс = с₀ – с – разность концентраций жидкого реагента в объеме и на поверхности контакта с твердым реагентом-восстановителем; γ_g –стехиометрический коэффициент; D_l – коэффициент диффузии жидкого реагента к поверхности твердого восстановителя; у – толщина микрослоя жидкой фазы.

Массовый поток газа к основанию пузырька составит величину

${{J}_{g}} = \int {{{j}_{g}}d{{s}_{A}}} = 2\pi R\cos \frac{{{{{\theta }}_{0}}}}{2}{{\gamma }_{g}}{{D}_{l}}\Delta c\int\limits_{{{y}_{A}}}^{\delta } {\frac{{dy}}{y}} ,$

где ds_A = 2πrdr = 2πrdx – приращение площади пятна, r = Rsinθ₀ = 2Rsin(θ₀/2)cos(θ₀/2) = 2Rsin(θ₀/2) – текущий радиус пятна, cos(θ₀/2) ≈ 1; dr = x – приращение радиуса пятна, на рис. 1 приращение радиуса обозначено через х; y = y_A + 2xsin(θ₀/2) – толщина микрослоя; у_А — наименьшая величина слоя жидкости в окрестности точки А, при которой справедлив закон Фика (величина имеет порядок межмолекулярных расстояний в жидкости, т.е. 10^–6–10^–7 мм).

Интеграл равен

(2)

${{J}_{g}} = 2\pi R\cos \frac{{{{\theta }_{0}}}}{2}{{\gamma }_{g}}{{D}_{l}}\Delta c\ln \frac{\delta }{{{{y}_{A}}}}.$

Из уравнения массового баланса следует

(3)

${{{\rho }}_{g}}\frac{{dV}}{{d{\tau }}} = \int\limits_S {{{j}_{g}}d{{s}_{A}}} .$

Так как

$V = \frac{4}{3}{\pi }{{R}^{3}}{{\left( {{\text{l}} + {\text{cos}}{{{\theta }}_{0}}} \right)}^{{\text{2}}}}\left( {{\text{2}} - {\text{ cos}}{{{\theta }}_{0}}} \right),$

то

(4)

$\frac{{dR}}{{d{\tau }}} = \frac{{{\xi }{{{\gamma }}_{g}}{{D}_{l}}\Delta c}}{{{{{\rho }}_{g}}R}},\,\,\,\,{\tau } = 0,R = 0,$

где

(5)

${\xi } = \frac{{{\text{2cos(}}{{{{{\theta }}_{0}}} \mathord{\left/ {\vphantom {{{{{\theta }}_{0}}} 2}} \right. \kern-0em} 2})}}{{{{{\left( {{\text{l}} + {\text{cos}}{{{\theta }}_{0}}} \right)}}^{{\text{2}}}}\left( {{\text{2}} - {\text{cos}}{{{\theta }}_{0}}} \right)}}\ln \frac{{\delta }}{{{{y}_{A}}}}.$

Для условий 0 < θ₀ < π/2 и δ ≈ 10^–1 мм ξ имеет порядок 10.

Интегрируя уравнение (4) с начальным условием τ = 0, R = 0, имеем

(6)

$\begin{gathered} R = {{\left( {\frac{{2{\xi }{{{\gamma }}_{g}}{{D}_{l}}\Delta c}}{{{{{\rho }}_{g}}}}{\tau }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{с}_{b}}{{{\tau }}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ {{c}_{b}} = {{\left( {\frac{{2{\xi }{{{\gamma }}_{g}}{{D}_{l}}\Delta c}}{{{{{\rho }}_{g}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}. \\ \end{gathered} $

Результаты экспериментальной проверки аналогичного уравнения для процесса кипения дают лучшее по сравнению с другими моделями соответствие с опытными данными.

Основные закономерности роста пузырька описываются этой моделью правильно. Заметим, что модель тонкого слоя реагента физически единственно возможная для реагирования на твердой поверхности, поскольку наличие контакта реагента с реагирующей поверхностью обязательно.

Преобразуем (4) введением безразмерного критерия

(7)

$\frac{{dR}}{{d{\tau }}} = \frac{1}{R}\left( {\frac{{{\xi }{{D}_{g}}\Delta c}}{{{{c}_{0}}}}} \right)\left( {\frac{{{{{\gamma }}_{g}}{{c}_{0}}}}{{{{{\rho }}_{g}}}}\frac{{{{D}_{l}}}}{{{{D}_{g}}}}} \right) = \frac{1}{R}\left( {\frac{{{\xi }{{D}_{g}}\Delta c}}{{{{c}_{0}}}}} \right){\text{J}}{{{\text{a}}}_{D}},$

где ${\text{J}}{{{\text{a}}}_{D}} = \frac{{{{{\gamma }}_{g}}{{c}_{0}}}}{{{{{\rho }}_{g}}}}\frac{{{{D}_{l}}}}{{{{D}_{g}}}}$ – безразмерный критерий Якоба для диффузионных процессов.

ПРОВЕРКА АДЕКВАТНОСТИ МОДЕЛИ ДЛЯ МАССООБМЕННЫХ ПРОЦЕССОВ

На основе полученной модели для массообменных процессов в изотермической среде получим соотношение для отрывного диаметра пузыря в этих условиях и сопоставим результаты с данными эксперимента. Рост газового пузыря на поверхности нагрева происходит до определенного размера, при котором пузырь отрывается от поверхности. Отрывной диаметр пузыря можно определить из условия равновесия сил, действующих на пузырь в момент отрыва. Здесь следует учитывать архимедовы силы, силы поверхностного натяжения, удерживающие пузырь на поверхности, силы гидродинамического вязкостного сопротивления и силы инерции жидкости, окружающей пузырь, вызванные ростом пузыря. Строгого решения этой задачи, учитывающего все силы, действующие на пузырь, в настоящее время нет.

При росте пузыря на горизонтальной поверхности, помещенной в большом объеме, уравнение равновесия сил в момент отрыва в первом приближении можно записать в следующем виде:

(8)

$\begin{gathered} \frac{{\pi }}{6}d_{{b0}}^{3}g({{{\rho }}_{l}} - {{{\rho }}_{g}}) = \frac{{\pi }}{8}{\zeta }d_{{b0}}^{2}{{{\rho }}_{l}}\left( {\frac{{dR}}{{d{\tau }}}} \right)_{{{{R}_{0}}}}^{2} + {\varphi }({\theta })\pi {{d}_{{b0}}}{\sigma } + \\ + \,\,\frac{1}{6}{\pi }d_{{b0}}^{3}\left( {{{{\rho }}_{g}} + \frac{1}{2}{{{\rho }}_{l}}} \right)\frac{{{{d}^{2}}R}}{{d{{{\tau }}^{2}}}}, \\ \end{gathered} $

где d_b0 = 2R₀ – отрывной диаметр пузыря; R – текущий радиус пузыря; ζ – коэффициент гидродинамического сопротивления росту пузыря; φ(θ) – некоторая функция краевого угла смачиваемости; 1/2ρ_l – присоединенная масса жидкости в нестационарном движении сферы.

Из уравнения для скорости роста пузырька следует

$\frac{{{{d}^{2}}R}}{{d{{{\tau }}^{2}}}} = - \frac{1}{R}{{\left( {\frac{{dR}}{{d{\tau }}}} \right)}^{2}},$

т.е. при ρ_l$ \gg $ ρ_g инерционная сила, так же как и гидродинамическое сопротивление, пропорциональна квадрату скорости роста пузырька.

Если не учитывать влияние сил поверхностного натяжения и инерционных сил, то можно получить зависимость отрывного диаметра от критерия Якоба и сопоставить с результатами, которые получены экспериментально

(9)

${{d}_{{b0}}} = {\varepsilon Ja}_{D}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}},\,\,\,\,{\varepsilon } = {{\left( {3{\zeta }\frac{{{{{\rho }}_{l}}}}{{g({{{\rho }}_{l}} - {{{\rho }}_{g}})}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{{\left( {\frac{{{\xi }{{D}_{g}}\Delta c}}{{{{c}_{0}}}}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}.$

Для значений величин (Mg + H₂SO₄, H₂) ζ = 0.5; ρ_g = 0.09 кг/м³; ρ_l = 1830 кг/м³; D_g = 7.2 × 10^–9 м²/с теоретическое значение углового коэффициента составляет ε = 0.26 × 10^–4, экспериментальное значение углового коэффициента составляет ε_e = = 0.63 × 10^–4. Результаты сравнения представлены на рис. 2.

Рис. 2.

Зависимость отрывного диаметра пузырька от критерия Якоба. Точки − эксперимент [22]; линия − теоретические результаты данной работы.

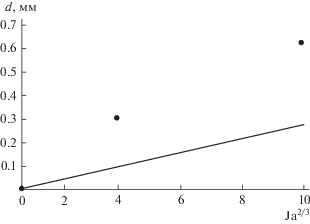
Для такого типа систем, когда неопределенности вносятся самим явлением и способом описания, такое расхождение результатов не является столь существенным. Таким образом, предложенная модель отражает основные гидродинамические закономерности, присущие протеканию гетерогенных процессов с образованием газовой фазы в виде пузырьков.

ИССЛЕДОВАНИЕ ПРОЦЕССА ГЕТЕРОГЕННОГО РЕАГИРОВАНИЯ И УСТОЙЧИВОСТИ ЭКРАНИРОВАНИЯ РЕАКЦИОННОЙ ПОВЕРХНОСТИ ГАЗОВЫМИ ПУЗЫРЬКАМИ

Рассмотрим процесс гетерогенного реагирования на стадии формирования реакционной поверхности, когда пузырьки растут на поверхности и за счет неустойчивости существования фаз, движущихся с предельной относительной скоростью (неустойчивость Гельмгольца) покидают поверхность реагирования, препятствуя поступлению жидкого реагента на поверхность реакции.

С единицы реагирующей поверхности твердого реагента-восстановителя отрываются N пузырьков: N = f/S₀, где f – частота отрыва пузырьков, S₀ – площадь поверхности реагирования. Плотность потока газовой фазы – массы продукта реакции с единицы поверхности:

(10)

$j = {{{{{\rho }}_{g}}{{V}_{{\text{b}}}}f} \mathord{\left/ {\vphantom {{{{{\rho }}_{g}}{{V}_{{\text{b}}}}f} {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}} = {{{{{\rho }}_{g}}\frac{{{\pi }{{d}_{{b0}}}^{3}}}{6}f} \mathord{\left/ {\vphantom {{{{{\rho }}_{g}}\frac{{{\pi }{{d}_{{b0}}}^{3}}}{6}f} {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}}.$

Определение потока газовой фазы требует знания частоты отрыва пузырьков и отрывного диаметра пузырька.

По И.Г. Маленкову жидкость совершает колебательное движение из-за выделения пузырьков и их регулярного отрыва в результате периодического смещения окружающей жидкости [23]. Периодичность повторения обусловлена инерционностью жидкой среды, что в свою очередь связано с инерционностью газовой фазы. Появление пузырьков возмущает жидкость, которая колеблется с частотой f, и возмущение распространяется в жидкость с некоторой скоростью υ, которая определяется размерами пузырьков и свойствами жидкости. Было установлено, что пузырьки, двигаясь в жидкости, возбуждают волны длиной λ = πd₀. Как следует из этого выражения, расстояние между пузырьками в каждой последовательности пропорционально размеру и сохраняется неизменным при любых условиях процесса.

Полагая fλ = υ_b, где υ_b – скорость всплывания пузырька, можно записать

$f{{d}_{0}} = \frac{1}{{\pi }}{{{\upsilon }}_{b}}.$

И.Г. Маленков получил нелинейное уравнение относительно диаметра:

$f{{d}_{0}} = \frac{1}{{{\pi }\left( {1 - {{{\varphi }}_{g}}} \right)}}{{\left[ {\frac{{g{{d}_{0}}\left( {{{{\rho }}_{l}} - {{{\rho }}_{g}}} \right)}}{{2\left( {{{{\rho }}_{l}} + {{{\rho }}_{g}}} \right)}} + \frac{{2g{\sigma }}}{{{{d}_{0}}\left( {{{{\rho }}_{l}} + {{{\rho }}_{g}}} \right)}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$

Исходя из формулы Франк-Каменецкого для скорости подъема пузырька

${{{\upsilon }}_{b}} = 1.5{{\left[ {\frac{{g{\sigma }\left( {{{{\rho }}_{l}} - {{{\rho }}_{g}}} \right)}}{{{{{\rho }}_{l}}^{2}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}},$

Н. Зубер ранее получил [24]

$f{{d}_{0}} = 0.59{{\left[ {\frac{{{\sigma }g\left( {{{{\rho }}_{l}} - {{{\rho }}_{g}}} \right)}}{{{\rho }_{l}^{2}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}.$

Эти соотношения аналогичны, но, главное, они получены из одинаковых теоретических положений. Характерные значения:$f{{d}_{0}}$ ≈ $100{\kern 1pt} - {\kern 1pt} 2000\,\,{\text{мм/с}}$ → → $0.1{\kern 1pt} - {\kern 1pt} 2\,\,{\text{м/с}}{\text{.}}$

Жидкий реагент диффундирует к поверхности из объема. Движение пузырьков газа, с одной стороны, как экранирование играет роль сдерживающего фактора для развития реакции, с другой стороны, одновременно вызывает движение жидкости за счет перемешивания.

Нестационарный процесс, описывающий массовый баланс по жидкой и газовой фазе, можно представить системой дифференциальных уравнений:

(11)

$\frac{{dc}}{{dt}} = {{{\beta }}_{l}}\frac{{{{S}_{0}}}}{V}S({{c}_{0}} - c) - k\frac{{{{S}_{0}}}}{V}Sc{{{\gamma }}_{m}},$

(12)

$\frac{{dS}}{{dt}} = \frac{{{{j}_{g}}}}{{{{{\rho }}_{g}}}}{\chi }(1 - S) - \frac{1}{{{{{\rho }}_{g}}}}kSc{{{\gamma }}_{g}}{\chi ,}$

где c – концентрация реагента на поверхности реагирования; S = S_r/S₀ – доля неэкранированной (доступной) поверхности для реагента; S_r – поверхность, на которой протекает реакция; S₀ – общая поверхность твердого реагента; j_g – массовый поток газовых пузырьков с единицы поверхности в секунду; β_l –коэффициент массообмена; χ – коэффициент пересчета объема газа в площадь сечения, занимаемую пузырьками; c₀ – концентрация реагента в объеме; γ_m – стехиометрический коэффициент для жидкого реагента; γ_g – стехиометрический коэффициент для газофазного продукта реакции; k –истинная константа скорости химической реакции на реагирующей твердой поверхности; ρ_g – плотность газа.

Для стационарных условий можно получить значения доступной поверхности и концентрации реагента:

(13)

$c = \frac{{{{{\beta }}_{l}}{{c}_{0}}}}{{{{{\beta }}_{l}} + k{{{\gamma }}_{m}}}},\,\,\,\,S = \frac{{{{j}_{g}}}}{{{{j}_{g}} + k{{{\gamma }}_{g}}\frac{{{{{\beta }}_{l}}{{c}_{0}}}}{{{{{\beta }}_{l}} + k{{{\gamma }}_{m}}}}}}.$

Асимптотические значения при интенсивном массообмене, вызванном перемешиванием жидкой фазы пузырьками:

${{{\beta }}_{g}} \to \infty ;\,\,\,\,c \to {{c}_{0}};\,\,\,\,S \to \frac{{{{j}_{g}}}}{{{{j}_{g}} + k{{{\gamma }}_{g}}{{c}_{0}}}}.$

При интенсивном массообмене, β_g → ∞, доступная поверхность определяется концентрацией реагента, тормозится кинетикой и возможностями отвода газовой фазы из зоны реакции (от реакционной поверхности).

В стационарных условиях скорость реакции выражается зависимостью

${{{\omega }}_{r}} = kSc = k\frac{{{{{\beta }}_{l}}{{c}_{0}}}}{{{{{\beta }}_{l}} + k{{{\gamma }}_{m}}}}\frac{{{{j}_{g}}}}{{{{j}_{g}} + k{{{\gamma }}_{g}}\frac{{{{{\beta }}_{l}}{{c}_{0}}}}{{{{{\beta }}_{l}} + k{{{\gamma }}_{m}}}}}}$

или

(14)

${{{\omega }}_{r}} = kSc = \frac{{k{{{\beta }}_{l}}{{c}_{0}}{{j}_{g}}}}{{{{j}_{g}}k{{{\gamma }}_{m}} + {{{\beta }}_{l}}({{j}_{g}} + k{{{\gamma }}_{g}}{{c}_{0}})}}.$

Асимптотики:

$\begin{gathered} {{{\beta }}_{g}} \to \infty ,\,\,\,\,{{{\omega }}_{r}} \to \frac{{{{j}_{g}}k{{c}_{0}}}}{{({{j}_{g}} + {{{\gamma }}_{g}}k{{c}_{0}})}}, \\ {{c}_{0}} \to \infty ,\,\,\,\,{{{\omega }}_{r}} \to {{{{j}_{g}}} \mathord{\left/ {\vphantom {{{{j}_{g}}} {{{{\gamma }}_{g}}}}} \right. \kern-0em} {{{{\gamma }}_{g}}}}. \\ \end{gathered} $

Скорость реакции увеличивается с ростом коэффициента массопереноса и стремится к асимптотическому значению. Торможение реакции определяется возможностью отвода газов от реакционной поверхности.

Зависимости, полученные в работе, качественно соотносятся с экспериментальными данными, полученными различными авторами.

Исследование на устойчивость системы уравнений сводится к анализу возмущенной системы уравнений, где используются представления функций в виде

(15)

$с = {{с}_{e}} + {{x}_{1}},\,\,\,\,S = {{S}_{e}} + {{x}_{2}},$

где x₁, x₂ – малые отклонения концентрации и доли свободной поверхности от равновесных.

Тогда систему уравнений можно переписать в линеаризованной форме, где пренебрегли величинами второго порядка малости:

(16)

$\frac{{d{{x}_{1}}}}{{dt}} = {{a}_{{11}}}{{x}_{1}} + {{a}_{{12}}}{{x}_{2}},\,\,\,\,\frac{{d{{x}_{2}}}}{{dt}} = {{a}_{{21}}}{{x}_{1}} + {{a}_{{22}}}{{x}_{2}},$

где

$\begin{gathered} {{a}_{{11}}} = - {{S}_{e}}({{{\beta }}_{l}} + k{{{\gamma }}_{m}}),\,\,\,\,{{a}_{{12}}} = {{{\beta }}_{g}}({{c}_{0}} - {{c}_{e}}), \\ {{a}_{{21}}} = - k{{{\gamma }}_{g}}{\chi }{{S}_{e}},\,\,\,\,{{a}_{{22}}} = - ({{j}_{g}}{\chi } + k{{{\gamma }}_{g}}{{c}_{e}}). \\ \end{gathered} $

Из теории устойчивости следует, что заключение о типе устойчивости системы можно делать, не решая системы уравнений, анализируя характеристический многочлен, определяющий корни характеристического уравнения. При условии, что знаки комплексов известны:

(17)

$G = {{a}_{{11}}}{{a}_{{22}}} - {{a}_{{12}}}{{a}_{{21}}} > 0,\,\,\,\,F = {{a}_{{11}}} + {{a}_{{22}}} < 0,$

следует, что система имеет устойчивый узел, т.е. при малых отклонениях от равновесия система приходит в устойчивое равновесное состояние. Таким образом, формируется структура чередующихся газовых образований и доступных участков поверхности, что для барботажа и процесса кипения экспериментально показано в работе [3].

ЗАВИСИМОСТЬ КОЭФФИЦИЕНТА МАССООТДАЧИ ОТ ПАРАМЕТРОВ ГЕТЕРОГЕННОЙ ХИМИЧЕСКОЙ РЕАКЦИИ

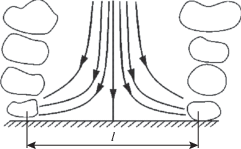
Интенсивность перемешивания пропорциональна объему и количеству пузырей, образующихся на поверхности реагирования. Согласно модели, предложенной С.С. Кутателадзе и А.И. Леонтьевым [25] для процессов кипения, интенсивность теплообмена в этих условиях определяется циркуляцией жидкости в ячейках между действующими центрами парообразования. По аналогии с этими процессами при химическом реагировании твердое тело–жидкость–газ в окрестности действующих центров газообразования основная масса жидкости в пристенном слое увлекается растущими на поверхности реагирования и поднимающимися в объем пузырями. На место увлеченной жидкости поступают свежие порции из основного объема, возникает интенсивная циркуляция жидкости, приводящая к увеличению массоотдачи. Течение жидкости между центрами газообразования можно отождествить с обтеканием лобовой части тупоносого тела, а конвективный массообмен рассчитать по формулам конвективной массоотдачи (рис. 3).

Рис. 3.

Схема процесса массообмена при гетерогенном реагировании [25].

Расход подтекающей жидкости пропорционален количеству газа, образующегося на поверхности реагирования, и имеет порядок

(18)

${{j}_{l}} = {{j}_{g}}(1 + {\varsigma }),$

где j_g – массовый поток газа, образующийся в процессе реагирования; ${\varsigma }$ – коэффициент, учитывающий увлеченную в циркуляцию массу жидкости. При грибообразных пузырях ${\varsigma }$ = 10.

Из баланса массы следует

(19)

${{\upsilon }_{l}} = ({{{{j}_{g}}} \mathord{\left/ {\vphantom {{{{j}_{g}}} {{{{\rho }}_{l}}}}} \right. \kern-0em} {{{{\rho }}_{l}}}})\frac{{(1 + {\varsigma })}}{{1 - {{{\varphi }}_{g}}}},$

где υ_l – скорость жидкости, подтекающей к стенке; φ_g – объемное газосодержание пристенного двухфазного слоя.

Конвективный массообмен в окрестности лобовой точки определяется по уравнению [25]

(20)

${\text{S}}{{{\text{h}}}_{l}}~ = {{{{{\beta }}_{l}}{{d}_{p}}} \mathord{\left/ {\vphantom {{{{{\beta }}_{l}}{{d}_{p}}} {{{D}_{l}}}}} \right. \kern-0em} {{{D}_{l}}}} = {\text{ }}0.68~\operatorname{Re} _{l}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}{\text{S}}{{{\text{c}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},$

где в качестве характерного размера принимается размер реагирующих частиц, среднее расстояние между центрами газообразования или характерный масштаб капиллярно-гравитационного взаимодействия (число Лапласа или капиллярная постоянная).

Без внимания на газофазные процессы гетерогенное реагирование протекает на поверхности с доставкой жидкого реагента в тонком диффузионном слое, что может быть представлено пенетрационной моделью, описанной ниже.

Из решения уравнения диффузии для полуограниченной области:

(21)

$\frac{{\partial c}}{{\partial {\tau }}} = D\frac{{{{\partial }^{2}}c}}{{\partial {{x}^{2}}}}.$

С начальными условиями: τ = 0, c = c₀.

С условиями на границе: х = 0, c = c₁, х → ∞, c = = const, dc/dx = 0.

Решение, например, с использованием преобразования Лапласа, получается в виде

$с - {{с}_{1}} = ({{с}_{0}} - с{}_{1}){\text{erf}}\left( {\frac{x}{{2\sqrt {D{\tau }} }}} \right),$

где ${\text{erf}}(z) = \frac{2}{{\sqrt {\pi } }}\int\limits_z^\infty {\exp ( - {{z}^{2}})dz} .$

Градиент концентрации:

$ - {{\left( {\frac{{\partial с}}{{\partial x}}} \right)}_{{x = 0}}} = \frac{{{{с}_{1}} - с{}_{0}}}{{\sqrt {{{D}_{l}}{\pi \tau }} }}.$

Поток реагента:

${{j}_{c}} = - D{{\left( {\frac{{\partial с}}{{\partial x}}} \right)}_{{x = 0}}} = ({{с}_{1}} - {{с}_{0}})\sqrt {\frac{{{{D}_{l}}}}{{{\pi \tau }}}} .$

Средний поток за время омывания поверхности ${{\tau }_{*}}$:

${{\bar {j}}_{c}} = \frac{1}{{{\tau *}}}\int\limits_0^{{\tau }*} {{{j}_{c}}d{\tau }} = 2({{с}_{1}} - {{с}_{0}})\sqrt {\frac{{{{D}_{l}}}}{{{\pi \tau *}}}} .$

Время реагирования принимается равным времени обтекания поверхности реагирования: ${\tau }* = \frac{{{{d}_{p}}}}{{{{\upsilon }_{l}}}}.$

По определению коэффициент массоотдачи: ${{{\beta }}_{l}} = \frac{{{{{\bar {j}}}_{c}}}}{{{{с}_{1}} - {{с}_{0}}}},$ тогда

${{{\beta }}_{l}} = 2\sqrt {\frac{{{{D}_{l}}}}{{{\pi }{{{\tau }}_{*}}}}} = \frac{2}{{\sqrt {\pi } }}\sqrt {{{D}_{l}}\frac{{{{\upsilon }_{l}}}}{{{{d}_{p}}}}} ,$

откуда следует критериальное уравнение массообмена:

(22)

$\begin{gathered} \frac{{{{{\beta }}_{l}}{{d}_{p}}}}{{{{D}_{l}}}} = \frac{2}{{\sqrt {\pi } }}\sqrt {\frac{{{{\upsilon }_{l}}{{d}_{p}}}}{{{{{\nu }}_{l}}}}} \sqrt {\frac{{{{{\nu }}_{l}}}}{{{{D}_{l}}}}} , \\ {\text{S}}{{{\text{h}}}_{l}} = \frac{2}{{\sqrt {\pi } }}{{\operatorname{Re} }^{{0.5}}}{\text{S}}{{{\text{c}}}^{{0.5}}} = 1.13{{\operatorname{Re} }^{{0.5}}}{\text{S}}{{{\text{c}}}^{{0.5}}}. \\ \end{gathered} $

Здесь наблюдается аналогия для массообмена к свободной поверхности раздела расплав–газ с учетом движения расплава в поверхностном слое, когда используется модель Маклина–Крауса [4]:

(23)

$\frac{{dc}}{{dt}} = {{{\beta }}_{g}}\frac{{{{S}_{0}}}}{V}({{c}_{0}} - c) = \frac{2}{{\sqrt {\pi } }}\sqrt {{{D}_{l}}\frac{{{{\upsilon }_{l}}}}{{{{d}_{p}}}}} \frac{{{{S}_{0}}}}{V}({{c}_{0}} - c).$

Из экспериментов [22] следует зависимость, которая по структуре не отличается от теоретической и полуэмпирической:

(24)

${\text{S}}{{{\text{h}}}_{l}} = {\text{N}}{{{\text{u}}}_{d}} = 3.1\operatorname{Re} _{l}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}{\text{S}}{{{\text{c}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\,\,{\text{Sc}} = 300{\kern 1pt} - {\kern 1pt} 12\,000,$

где ${\text{R}}{{{\text{e}}}_{l}}$ = ${{{{{\gamma }}_{g}}{{{\beta }}_{l}}{{c}_{0}}{{l}_{{\sigma }}}} \mathord{\left/ {\vphantom {{{{{\gamma }}_{g}}{{{\beta }}_{l}}{{c}_{0}}{{l}_{{\sigma }}}} {({{{\rho }}_{g}}{{\nu }_{l}})}}} \right. \kern-0em} {({{{\rho }}_{g}}{{\nu }_{l}})}},$ ${{l}_{{\sigma }}} = {{({{\sigma } \mathord{\left/ {\vphantom {{\sigma } {({{{\rho }}_{l}} - {{{\rho }}_{g}})}}} \right. \kern-0em} {({{{\rho }}_{l}} - {{{\rho }}_{g}})}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ – линейный масштаб капиллярно-гравитационного взаимодействия (число Лапласа или капиллярная постоянная); ${{\upsilon }_{g}} = {{{{j}_{g}}} \mathord{\left/ {\vphantom {{{{j}_{g}}} {{{{\rho }}_{g}}}}} \right. \kern-0em} {{{{\rho }}_{g}}}}$ ~ ${{{{{\gamma }}_{g}}{{{\beta }}_{l}}{{c}_{0}}} \mathord{\left/ {\vphantom {{{{{\gamma }}_{g}}{{{\beta }}_{l}}{{c}_{0}}} {{{{\rho }}_{g}}}}} \right. \kern-0em} {{{{\rho }}_{g}}}}$ ~ ${{{{{\gamma }}_{g}}k{{c}_{0}}} \mathord{\left/ {\vphantom {{{{{\gamma }}_{g}}k{{c}_{0}}} {{{{\rho }}_{g}}}}} \right. \kern-0em} {{{{\rho }}_{g}}}}$ – средняя скорость газообразования.

ПРОВЕРКА АДЕКВАТНОСТИ КРИТЕРИАЛЬНОЙ ЗАВИСИМОСТИ, ПОЛУЧЕННОЙ АНАЛИТИЧЕСКИ

Для значений величин (Mg + H₂SO₄, H₂) ρ_g = = 0.09 кг/м³; ρ_l = 1830 кг/м³; D_l = 7.2 × 10^–9 м²/с теоретические значения коэффициента массоотдачи рассчитаны по аналитической зависимости (22), а экспериментальные значения взяты из [22]. Экспериментальные значения имеют ярко выраженный максимум, что, впрочем, не отражено в критериальных зависимостях. Расчеты по полуэмпирической модели (20) незначительно разнятся с экспериментом.

Результаты сравнения представлены на рис. 4.

Рис. 4.

Зависимость коэффициента массоотдачи от концентрации реагента в растворе. Точки − эксперимент [22]; линия − теоретические результаты данной работы.

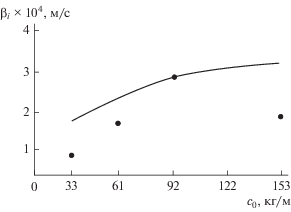
Следует отметить, что для многофазных систем сопоставимость результатов в области возрастания вполне удовлетворительная с соблюдением общей закономерности. Во всей области концентраций наблюдается расхождение, связанное с отсутствием экстремума в критериальных зависимостях. Вопрос наличия гидродинамического кризиса требует дальнейшего рассмотрения.

ЗАКЛЮЧЕНИЕ

Проведен анализ процессов гетерогенного реагирования с образованием газовой фазы. По аналогии с кипением предложен механизм образования газовой фазы в виде пузырьков, которые участвуют в перемешивании жидкого реагента и интенсифицируют целевые процессы. На основе предложенной модели получены соотношения для параметров пузырьков, коррелирующие с экспериментальными данными.

Рассмотрен процесс гетерогенного реагирования с учетом гидродинамических особенностей формирования реакционной поверхности, когда пузырьки за счет неустойчивости существования фаз, движущихся с предельной относительной скоростью (неустойчивость Гельмгольца), покидают поверхность реагирования, препятствуя поступлению жидкого реагента на поверхность реакции. Доля экранированной поверхности несущественна и представляет собой чередование зон жидкой и газовой фаз. Теоретическое рассмотрение массообмена при протекании гетерогенной реакции дает возможность записать критериальное соотношение, адекватное экспериментальным данным без учета гидродинамического кризиса. Модель подслоя при образовании пузырьков газа на реагирующей поверхности обнаруживает удовлетворительное качественное и количественное совпадение. Анализ динамики гетерогенной реакции с учетом неравнодоступности реакционной поверхности за счет образования пузырьков показал незначительное влияние пузырьков на экранирование поверхности реагирования. Полученные теоретически критериальные соотношения для коэффициентов массообмена обнаруживают приемлемое совпадение с экспериментальными данными лишь на участке возрастания и не учитывают влияние гидродинамических кризисов.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 18-29-24094).

ОБОЗНАЧЕНИЯ

a₁₁, a₁₂, a₂₁, a₂₂	коэффициенты линеаризованной системы уравнений
с	концентрация реагента на поверхности, кг/м³
с₀	концентрация реагента в объеме, кг/м³
с_b	константа в выражении для радиуса пузырька
с_e	равновесная концентрация, кг/м³
Δс	разность концентраций жидкого реагента в объеме и на поверхности контакта с твердым реагентом-восстановителем, кг/м³
D_g	коэффициент диффузии газа в жидком реагенте, м²/с
D_l	коэффициент диффузии жидкого реагента к поверхности твердого восстановителя, м²/с
d₀	начальный диаметр, м
d_b0	отрывной диаметр пузырька, м
d_p	характерный размер частицы, м
F, G	комплексы системы уравнений
f	частота отрыва, 1/с
g	ускорение свободного падения, м/с²
J_g	массовый поток газа к основанию пузырька, кг/с
j_g	плотность массового потока газа с единицы поверхности в секунду, кг/(м³ с)
k	истинная константа скорости химической реакции на реагирующей твердой поверхности
l_σ	линейный масштаб капиллярно-гравитационного взаимодействия (число Лапласа или капиллярная постоянная), м
R	текущий радиус пузырька, м
r	текущий радиус пятна, м
dr	приращение радиуса пятна, м
S	доля неэкранированной (доступной) поверхности для реагента
S₀	общая площадь поверхности реагирования, м²
S_e	равновесное значение доли доступной поверхности
S_r	поверхность, на которой протекает реакция, м²
ds_A	приращение площади пятна, м²
V	объем, м³
V_b	объем пузырька, м³
x	приращение радиуса пятна, м
x₁	малое отклонение концентрации от равновесной
x₂	малое отклонение доли свободной поверхности от равновесной
у	толщина микрослоя жидкой фазы, м
у_А	наименьшая величина слоя жидкости в окрестности точки А, м
z	переменная
β_l	коэффициент массообмена, м/с
γ_g	стехиометрический коэффициент для газофазного продукта реакции
γ_m	стехиометрический коэффициент для жидкого реагента
δ	толщина диффузионного слоя, м
ε	теоретическое значение углового коэффициента
ε_е	экспериментальное значение углового коэффициента
ζ	коэффициент гидродинамического сопротивления росту пузырька
θ	угол смачиваемости, град
θ₀	угол смачиваемости между поверхностью реагирования и поверхностью пузырька в точке касания в момент отрыва пузырька, град
λ	длина волны, образующейся в результате движения пузырьков в жидкости, м
ν_l	кинематическая вязкость жидкости, м²/с
ξ	доля объема пузырька
ρ_g	плотность газа, кг/м³
ρ_l	плотность жидкости, кг/м³
σ	коэффициент поверхностного натяжения, Н/м
$\varsigma $	доля присоединенной массы
τ	время, с
υ	скорость, м/с
υ_b	средняя скорость пузырьков, м/с
υ_g	скорость газа, м/с
υ_l	скорость жидкости, подтекающей к стенке, м/с
φ_g	объемное газосодержание пристенного двухфазного слоя;
φ(θ)	некоторая функция краевого угла смачиваемости
χ	коэффициент пересчета объема газа в площадь сечения, занимаемую пузырьками, м²/м³
ω_r	скорость химической реакции, кг/с
Ja_D	число Якоба для диффузионных процессов
Nu_d	диффузионное число Нуссельта
Re_l	число Рейнольдса для жидкости
Sc	число Шмидта
Sh_l	число Шервуда

ИНДЕКСЫ

0	начальный
A	тип реагента
B	жидкий реагент
b	пузырек
D	диффузия
e	эксперимент, равновесный
g	газ
l	жидкость
m	средний
p	частица
r	реакция

Список литературы

Сурин В.А., Назаров Ю.Н. Массо- и теплообмен, гидрогазодинамика металлургической ванны. М.: Металлургия, 1993.
Аксельруд Г.А., Молчанов А.Д. Растворение твердых веществ. М.: Химия, 1977.
Кутателадзе С.С., Накоряков В.Е. Тепломассообмен и волны в газожидкостных системах. Новосибирск: Наука, 1984.
Шалимов А.Г., Готин В.Н., Тулин Н.А. Интенсификация процессов специальной электрометаллургии. М.: Металлургия, 1988.
Keil F.J. Process intensification // Rev. Chem. Eng. 2018. V. 34. № 2. P. 135.
Zhenga Z., Chena Y., Zhana X., Gaoa M., Wang Z. Mass transfer intensification in a novel airlift reactor assembly with helical sieve plates // Chem. Eng. J. 2018. V. 342. P. 61.
Zhang X., Guo K., Qi W., Zhang T., Liu C. Gas Holdup, Bubble Behaviour, and Mass Transfer Characteristics in a Two-Stage Internal Loop Airlift Reactor with Different Screens // Can. J. Chem. Eng. 2017. V. 95. P. 1202.
Utikar R.P., Ranade V.V. Intensifying Multiphase Reactions and Reactors: Strategies and Examples // ACS Sustainable Chem. Eng. 2017. V. 5. № 5. P. 3607.
Powell J.B. Application of multiphase reaction engineering and process intensification to the challenges of sustainable future energy and chemicals // Chem. Eng. Sci. 2017. V. 157. P. 15.
Пахомов М.А., Терехов В.И. Моделирование влияния пузырьков на структуру течения и теплоперенос в турбулентном полидисперсном восходящем двухфазном потоке за внезапным расширением трубы // Теплофиз. выс. темп. 2018. Т. 56. № 1. С. 50.
Елизаров Д.В., Шавалеев Р.Р., Елизаров В.И. Математическое моделирование и управление процессом массопереноса в аппаратах с непрерывным контактом фаз // Теор. осн. хим. технол. 2018. Т. 52. № 3. С. 260.
Лаптев А.Г., Карпеев С.В., Лаптева Е.А. Моделирование и модернизация тарельчатых колонн при проведении реакционно-массообменных процессов // Теор. осн. хим. технол. 2018. Т. 52. № 1. С. 3.
Губайдуллин Д.А., Снигерев Б.А. Численное моделирование турбулентного восходящего потока газожидкостной пузырьковой смеси в вертикальной трубе. Сравнение с экспериментом // Теплофиз. выс. темп. 2018. Т. 56. № 1. С. 61.
Räsänen M., Eerikäinen T., Ojamo H. Characterization and hydrodynamics of a novel helix airlift reactor // Chem. Eng. Process. Process Intensif. 2016. V. 108. P. 44.
Meshalkin V.P., Panchenko S.V., Dli M.I., Panchenko D.S. Analysis of the thermophysical processes and operating modes of electrothermic reactor using a computer model // Theor. Found. Chem. Eng. 2018. V. 52. № 2. P. 166. [Мешалкин В.П., Панченко С.В., Дли М.И., Панченко Д.С. Анализ теплофизических процессов и режимов работы электротермического реактора с использованием компьютерной модели // Теор. осн. хим. технол. 2018. Т. 52. № 2. С. 141.]
Panchenko S.V., Shirokikh T.V. Thermal hydraulics of moving dispersive layer of process units // Theor. Found. Chem. Eng. 2016. V. 50. № 2. P. 217. [Панченко С.В., Широких Т.В. Теплогидравлика движущегося дисперсного слоя технологических агрегатов // Теор. осн. хим. технол. 2016. Т. 50. № 2. С. 223.]
Meshalkin V.P., Menshikov V.V., Panchenko S.V., Panchenko D.S., Kazak A.S. computer-aided simulation of heat- and mass-transfer processes in an ore-reduction electrothermal reactor // Theor. Found. Chem. Eng. 2015. V. 49. № 5. P. 606. [Мешалкин В.П., Панченко С.В., Панченко Д.С., Меньшиков В.В., Казак А.С. Компьютерное моделирование тепломассообменных процессов в рудовосстановительном электротермическом реакторе // Теор. осн. хим. технол. 2015. Т. 49. № 5. С. 510.]
Torikai K., Yamazaki T. Dry state in a contact area of a boiling bubble on a heating surface // Bull. Jpn. Soc. Mech. Eng. 1967. V. 10. № 38. P. 349.
Лабунцов Д.А. Физические основы энергетики. Избранные труды по теплообмену, гидродинамике, термодинамике. М.: МЭИ, 2000.
Панченко С.В. Массообмен при протекании гетерогенной реакции с выделением газообразных продуктов // Математические методы в технике и технологиях – ММТТ-29: сборник трудов ХХIХ Междунар. науч. конф. Самара: Самарский гос. техн. ун-т, 2016. Т. 10. С. 74.
Cooper M.G., Lloyd A.J.P. The microlayer in nucleate pool boiling // Int. J. Heat Mass Transfer. 1969. V. 12. № 8. P. 895.
Аксельруд Г.А., Гумницкий Я.М., Маллик С. Исследование химического кипения в области пузырькового режима // Инж.-физ. ж. 1987. Т. 53. № 2. С. 205.
Маленков И.Г. Частота отрыва как функция размера паровых пузырьков // Прикл. мех. тех. физ. 1978. № 6. С. 130.
Zuber N. Hydrodynamic Aspects of Boiling Heat Transfer. PhD Dissertation. Los Angeles: Univ. of California, 1959.
Теория тепломассообмена / Под ред. Леонтьева А.И. М.: Высшая школа, 1980.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал