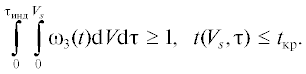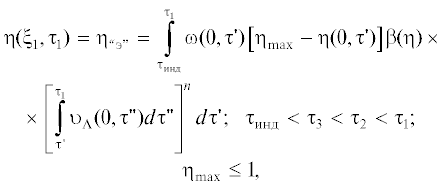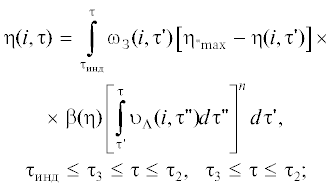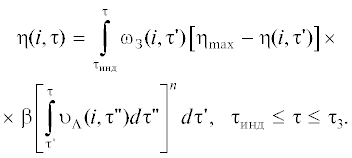Теоретические основы химической технологии, 2020, T. 54, № 3, стр. 309-324
Математическое описание фазовых и формально аналогичных им превращений для инженерных расчетов
Ю. А. Таран *
МИРЭА – Российский технологический университет
Москва, Россия
* E-mail: aj_@mail.ru
Поступила в редакцию 03.12.2019
После доработки 21.01.2020
Принята к публикации 24.01.2020
Аннотация
Применительно к фазовым и формально аналогичным им превращениям предложены пригодные для инженерных расчетов математические описания последовательных, объемных и объемно-последовательных превращений со структурной перестройкой исходной системы в рамках предложенной формальной аналогии данных процессов. Для конкретизации рассмотренных моделей они даны применительно к кристаллизации расплавов. Обсуждены возможные методы их решения.
ВВЕДЕНИЕ
Формальная аналогия процессов со структурной перестройкой исходной системы [1–3] основана на расширенном толковании понятия фазы, как системы, обладающей определенной структурой, и фазового превращения, как процесса перестройки исходной структуры фазы. Скорости этих процессов зависят от величины термодинамического стимула (движущей силы кинетики превращения). Последняя определяет максимально возможную скорость фазового превращения, которая может быть меньше, если контролируется явлениями переноса субстанции (теплоты, вещества, количества движения) [4–7].
Тогда под понятие фазового превращения подпадают как классические фазовые превращения: кристаллизация–плавление, десублимация–сублимация, конденсация–испарение, обратимые полиморфные превращения и т.д. [3–6, 8, 9], так и формально аналогичные им процессы гранулирования порошков – дробления, коалесценции (коагуляции) – диспергирования (эмульгирования); вплоть до зарождения и роста “пятен турбулентности” [1–3, 10, 12]. Таким образом, для инженерного расчета процесса, т.е. для определения динамики степени превращения, распределения новообразований и сопутствующих им явлений, например, усадочной пористости и др., а также полей температур, концентраций и скоростей достаточно информации о зависимости скоростей зарождения и роста центров превращения от термодинамического стимула и уравнений переноса субстанции с условиями однозначности. Такого рода формальная аналогия полезна, так как для классических фазовых превращений модельные представления, предложения по аппаратурно-технологическому оформлению и инженерскому расчету хорошо разработаны [4–9, 13–15], чего не скажешь о вышеназванных формально аналогичных им процессах [16–19]. Косвенным подтверждением правомерности упомянутой аналогии служит многолетнее успешное использование уравнения Колмогорова–Аврами для описания изопотенциальных процессов как классических фазовых превращений (кристаллизации, конденсации, десублимации, полиморфных превращений) [4–9, 13–18], так и реакционных процессов, гранулирования порошков, коалесценции (коагуляции) и др. [1–3, 10–12, 20, 21]. Колмогоров же получил это уравнение, используя понятия о скоростях зарождения и роста точек на числовой оси и аппарата математической статистики [22].
Целью работы является предложение единого подхода к определению значимых для инженерных расчетов параметров (изменение во времени степени превращения, структуры новообразований и сопутствующих им явлений, например, усадочной пористости, полей температур, концентраций и скоростей) для процессов со структурной перестройкой исходной системы, включающих как классические фазовые превращения (кристаллизация – плавление, энантиотропные полиморфные превращения и т.д.) так и другие процессы (гранулирование порошка – истирание гранул, коалесценция (коагуляция) – диспергирование (эмульгирование), зарождение и рост “бляшек” отложений – растворение при промывке и многих других). Аксиоматикой для решения такой задачи можно считать факт, что превращение “старой” фазы в новую не может происходить иначе, как за счет зарождения в “старой” фазе новообразований, их роста (т.е. кинетики процесса) и явлений переноса субстанции (вещества и энергии).
Процесс фазового и формального аналогичного ему превращения может проходить по последовательному, объемному и объемно-последовательному механизмам [5, 13, 14, 23–28]. Для конкретизации рассматриваемых моделей они даны применительно к кристаллизации расплавов. Для начала процесса необходимо получение как минимум одного центра “новой” фазы в метастабильном (для кристаллизации расплавов переохлажденном) объеме Vs “старой” фазы:
Если  $t({{V}_{s}},{\tau }) \leqslant {{t}_{{{\text{кр}}}}},$ ${{{\omega }}_{3}}(t)$ = $f[{{t}_{{{\text{кр}}}}} - t({{V}_{s}},{\tau })]$ то процесс фазового превращения вероятнее всего протекает по нестационарному последовательному
(одномерному) механизму. Иначе
$t({{V}_{s}},{\tau }) \leqslant {{t}_{{{\text{кр}}}}},$ ${{{\omega }}_{3}}(t)$ = $f[{{t}_{{{\text{кр}}}}} - t({{V}_{s}},{\tau })]$ то процесс фазового превращения вероятнее всего протекает по нестационарному последовательному
(одномерному) механизму. Иначе 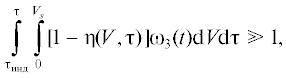 $t({{V}_{s}},{\tau }) \leqslant {{t}_{{{\text{кр}}}}},$ ${{{\omega }}_{3}}(t)$ = $f[{{t}_{{{\text{кр}}}}} - t({{V}_{s}},{\tau })]$ по нестационарному объемному (трехмерному) механизму. В промежутке между этими неравенствами
по объемно-последовательному (трехмерному, вырождающемуся в одномерный) механизму.
$t({{V}_{s}},{\tau }) \leqslant {{t}_{{{\text{кр}}}}},$ ${{{\omega }}_{3}}(t)$ = $f[{{t}_{{{\text{кр}}}}} - t({{V}_{s}},{\tau })]$ по нестационарному объемному (трехмерному) механизму. В промежутке между этими неравенствами
по объемно-последовательному (трехмерному, вырождающемуся в одномерный) механизму.
Допущения для последовательного фазового превращения: полагали систему однокомпонентной, фазы несжимаемыми, термокапиллярную гравитационную конвекцию отсутствующей, игнорировали анизотропию роста граней кристаллов, их устойчивость, трансформацию формы, влияние кривизны поверхности растущих кристаллов на равновесную температуру превращения, неустойчивость плоской границы превращения, дендритный рост в переохлажденной зоне, влияния на ход кристаллизации “дрейфа” кристаллов с подсасыванием к межфазной границе потоком расплава, явления газовыделения и кавитации, захвата газовых пузырьков растущими кристаллами, распределение пор по размерам и его изменение, распределение термонапряжений в кристаллической фазе. Кроме вышеизложенных допущений для последовательной кристаллизации при описании объемной кристаллизации игнорировали еще захват газовых пузырьков при образовании распределенной пористости, процессы перекристаллизации в переходной зоне. Для объемно-последовательной кристаллизации дополнительно игнорировали еще и “дрейф” кристаллов с расплавом в переходную зону и изменение распределения между захватываемым и фильтруемым количествами расплава.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ ПОСЛЕДОВАТЕЛЬНОГО МЕХАНИЗМА ФАЗОВОГО ПРЕВРАЩЕНИЯ
Из-за разности плотностей фаз возникает сосредоточенная внешняя усадка. Когда “старая” фаза (расплав) замкнута в “новой” (кристаллическая корка), возникает сосредоточенная внутренняя усадка (усадочная полость), форму которой определяют из условий минимума поверхностной энергии: ${{{{S}_{{\text{П}}}}({\tau }){\sigma }({\tau })} \mathord{\left/ {\vphantom {{{{S}_{{\text{П}}}}({\tau }){\sigma }({\tau })} {{{V}_{{\text{П}}}}}}} \right. \kern-0em} {{{V}_{{\text{П}}}}}}({\tau }) \to \min .$ Текущий и максимальный ее объем соответственно равны:
(2)
$\begin{gathered} {{V}_{{\text{П}}}}(\tau ) = {{V}_{{\rm K}}}(\tau )\frac{{{{\rho }_{{\text{{\rm K}}}}}({{t}_{{{\text{{\rm K}{\rm P}}}}}}) - {{\rho }_{{\text{ж}}}}({{t}_{{{\text{{\rm K}{\rm P}}}}}})}}{{{{\rho }_{{\text{ж}}}}({{t}_{{{\text{{\rm K}{\rm P}}}}}})}}; \\ {{V}_{{\text{П}}}} = V\frac{{{{\rho }_{{\text{{\rm K}}}}}({{t}_{{{\text{{\rm K}{\rm P}}}}}}) - {{\rho }_{{\text{б}}}}({{t}_{{{\text{{\rm K}{\rm P}}}}}})}}{{{{\rho }_{{\rm K}}}({{t}_{{{\text{{\rm K}{\rm P}}}}}})}}. \\ \end{gathered} $В условиях “прилипания” расплава к фазовой границе это вызывает конвективный (Стефановский) поток с объемной (dVп/dτ) и линейной скоростями υП = 1/SП(τ)(dVп/dτ). Термическая усадка приводит к уменьшению объема гранулы (кристаллической фазы), либо к образованию в ней распределенной усадочной пористости объемом Vпр(τ) в виде трещин:
(3)
$\begin{gathered} {{V}_{{{\text{пр}}}}}(\tau ) = {{V}_{{\text{к}}}}(\tau )\frac{{\langle {{\rho }_{{\text{к}}}}\rangle - {{\rho }_{{\text{к}}}}({{t}_{{{\text{кр}}}}})}}{{\langle {{\rho }_{{\text{к}}}}\rangle }}, \\ {{\left\langle \rho \right\rangle }_{K}} = \frac{1}{{{{V}_{K}}(\tau )}}\int\limits_0^{{{V}_{{\text{к}}}}} {{{\rho }_{K}}(t)dV} ;\,\,\,\,t = f({{V}_{{\text{к}}}},\tau ). \\ \end{gathered} $При полиморфном превращении берут плотности “соседних” модификаций.
В случае кондуктивного переноса теплоты в j-фазной среде используется уравнение
(4)
${{с}_{j}}{{\rho }_{j}}{{\nabla }_{\tau }}t = {{\nabla }_{}}({{\lambda }_{j}}{{\nabla }_{}}t),\,\,{{\xi }_{}}(i,\tau ) \leqslant i \leqslant {{\xi }_{{ + 1}}}(i,\tau ),$j = к1, к2, к3……ж – индексы, обозначающие вид фаз;
с начальным:
Возможныe граничныe на внешней поверхности условия І–ІV рода:
(5)
$\begin{gathered} {{\lambda }_{j}}{{\nabla }_{n}}t(0,\tau ) = {{t}_{{\text{с}}}}(0,\tau ) \vee {{q}_{{\text{с}}}}(0,\tau ) \vee {{\alpha }_{{\text{с}}}}\left( \tau \right)[t\left( {0,\tau } \right)-- \\ - \,\,{{t}_{{\text{с}}}}\left( \tau \right)] \vee {{\lambda }_{{{\text{ст}}}}}{{\nabla }_{n}}t\left( {0,\tau } \right), \\ \tau < {{\tau }_{{{\text{инд}}}}},\,\,j = {\text{ж}},\,\,\tau > {{\tau }_{{{\text{инд}}}}},\,\,j = {{K}_{1}}, \\ \end{gathered} $n – нормаль к изотерме (межфазной поверхности).
Возможные граничные условия на подвижных границах:
(6)
$\begin{gathered} {{t}_{j}}\left( {{{\xi }_{j}},\tau } \right) = {{t}_{{j + 1}}}\left( {{{\xi }_{j}},\tau } \right);~\,\,\,\,{{\lambda }_{j}}{{\nabla }_{n}}~t\left( {{{\xi }_{j}},\tau } \right) - \\ - \,\,\{ {{\lambda }_{{j + 1}}}{{\nabla }_{n}}t{\text{(}}{{\xi }_{j}},\tau {v}{{\alpha }_{с}}\left( \tau \right)\left[ {t\left( {{{\xi }_{1}},\tau } \right) - t\left( {{{i}_{n}},\tau } \right)} \right]{\text{\} }} = \\ = {{L}_{j}}{{\rho }_{j}}\frac{{d{{\xi }_{j}}}}{{d\tau }} = ~{{L}_{j}}{{\rho }_{j}}{{\upsilon }_{{{\Lambda }j}}};~\,\,\,\,{{\upsilon }_{{{\Lambda }j}}} = ~{{f}_{2}}\left[ {{{t}_{{{\text{кр}}}}} - t\left( {{{\xi }_{j}},\tau } \right)} \right], \\ \end{gathered} $Lj – справочное значение скрытой теплоты превращения, включающее собственно теплоту превращения $\left( {L_{j}^{'}} \right)$ и теплоту изменения теплоемкости фаз.
Условие на границе усадочной полости:
Перенос теплоты при фазовом превращении (в данном случае кристаллизации) описывается системой (4)–(7). Параметрами кинетики превращения являются зависимости скоростей зарождения ω3 и роста υΛ центров превращения (в данном случае кристаллизации) от термодинамического стимула (в данном случае переохлаждения расплава ΔtS): ω3 = f1(ΔtS); υΛ = f2(ΔtS), которые теоретически могут быть лишь оценены с погрешностью до порядка [4–5, 13, 26], а для инженерных расчетов определяются с инструментальной погрешностью экспериментально [1–3, 12, 20, 21]. С их помощью по уравнению (1) оценивают продолжительность индукционного периода τинд, предшествующего превращению, и оценивают возможный механизм превращения. Условие (6) связывает температуру на фронте превращения с линейной скоростью роста поли-(моно)кристаллического фронта υΛ (обобщенная задача Стефана). Последовательное превращение может проходить с плоским и разрушенным фронтом. Необходимо контролировать устойчивость межфазной границы по соотношению подводимого и отводимого теплового потока [3, 5, 13, 29] и вероятности появления в переохлажденной зоне расплава у межфазной границы центра превращения, что при игнорировании ''занесения'' в нее центра кристаллизации нужно оценивать по уравнению сходному с (1). С учетом упомянутых упрощений и оговорок, фиксации краевых условий и коэффициентов система (1)–(7) замкнута, но может быть решена лишь численными методами [3, 26, 30], прежде всего методом конечных разностей [31, 32]. Практика решения инженерных задач на основе данного математического описания [3, 20, 21] показала, что их удобно и экономично решать, аппроксимируя математическое описание на основе уравнений (1)–(7) устойчивым неявным конечно-разностным аналогом, нелинейным относительно значений сеточной функции на искомом временном слое. Решение носит итерационный характер, когда на каждом шаге по времени в ходе каждой итерации комплексно уточняются значения термодинамических параметров, граничных условий, размеры объекта, форма и размеры усадочных полостей, кинетические параметры, положения межфазных границ, которые отслеживаются с помощью “подвижных” узлов и использования для решения многомерных задач “локально-одномерной” разностной схемы с итерационным уточнением значений сеточных функций и другой важной при инженерных расчетах информацией в соседних с “локально-одномерной” схемой узлах [2, 3, 33]. Это делает предполагаемый алгоритм более экономичным (по сравнению с известными факторизованными и аддитивными схемами [31, 33], исключая поперечную прогонку и расчеты на дробных шагах по времени) и универсальным, сочетающим четкое выделение положений фазовых фронтов с возможностью решения многомерных многофронтов ых задач [2, 3, 33].
ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ ПРИ АНАЛИЗЕ ПОСЛЕДОВАТЕЛЬНОГО МЕХАНИЗМА ФАЗОВОГО ПРЕВРАЩЕНИЯ И ИХ ОБСУЖДЕНИЕ
В качестве примера приведем некоторые результаты решения нами практических задач с использованием вышеизложенного математического описания и алгоритма его реализации. Приведем результаты расчета процесса кристаллизации и охлаждения капель расплава в восходящем потоке воздуха в грануляционных башнях (рис. 1). Для подтверждения адекватности результата вычислительного эксперимента ходу реального процесса использовали сравнение расчета с термограммами, полученными нами скоростным термическим анализом СТА, разработанным в [18] и усовершенствованным в [3]. Лучшее согласование с экспериментом дают результаты расчета с учетом изменения коэффициента теплоотдачи по поверхности обдуваемой гранулы (рис. 2а). Игнорирование этого фактора, при незначительной ошибке во времени полной кристаллизации капли, вносит существенную погрешность в динамику фазовых фронтов, усадочной полости и температурных полей (рис. 2б). Пример расчета процесса кристаллизации капель расплава на охлаждаемой поверхности ленточного кристаллизатора (рис. 3) также демонстрирует применимость предлагаемого математического описания и алгоритма его реализации для решения практических и инженерных задач.
Рис. 1.
Положение межфазных границ и изотерм в капле расплава NH4NO3 (А2), падающей в башне в различные моменты времени (Н = 30 м; tжн = 175°С; Ri = 1 мм; tсн = 45°С; ωн = 4 м/с; φ = 0.2 мас. %). Цифры у кривых – значения температур в °С.
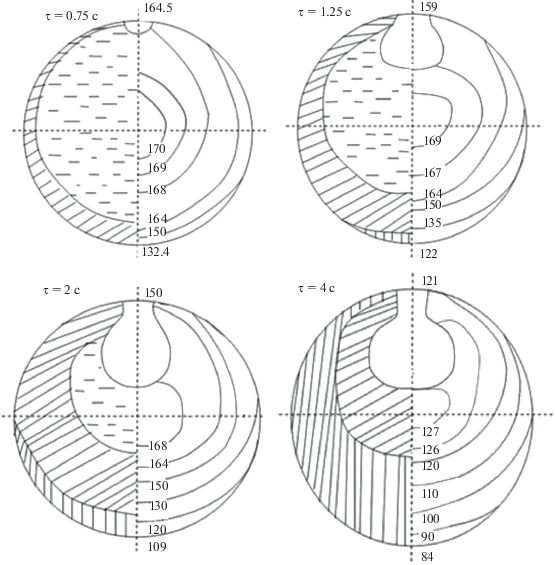
Рис. 2.
(а) – изменение во времени температур в центре (1), в лобовой (3), в кормовой (2) и на поверхности (4) (при αс = const) частях гранулы NH4NO3 (А2). Сплошные линии – эксперимент СТА [18], штриховые – расчет при αс = var, штрихпунктирные – расчет при αс = const (tжн = 178°С; Ri = 1.3 мм; tсн = 40°С; ωн = 5.5 м/с; φ = 0.2 мас. %). (б) – расчет положений в различные моменты времени межфазных границ и изотерм при αс = var переменной (сплошные линии) и αс = const постоянной (штриховые линии) интенсивности отвода тепла по поверхности гранулы NH4NO3, падающей в башне (Н = 30 м; tжн = 175°С; Ri = 1 мм; tсн = 45°С; ωн = 4 м/с; φ = 0.2 мас. %). Цифры у кривых – значения температур в °С.
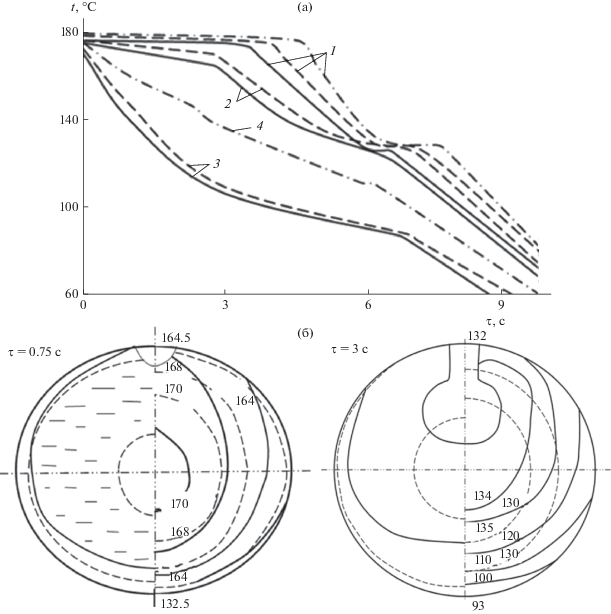
Рис. 3.
Зависимость положения межфазной границы (заштрихована кристаллическая фаза модификация I(β) – косая редкая штриховая; III(γ) – двойная косая штриховая; II(α)– косая частая штриховая) и изотерм (цифры у кривых – значения температуры в °С) при кристаллизации капли расплава К1 (KNO3 ГОСТ 19790-74) с содержанием KNO3 99.9–99.8% на стальной ленте ленточного кристаллизатора в различные моменты времени (R = 1.5 мм; δст = 1 мм; λст = 16 Вт/(м К); ε = 0.7; αc' = 15 Вт/(м2 К); αc = 250 Вт/(м2 К); tc = 20°С; tжн = 345°С).
Приведенное в качестве примера математическое описание легко видоизменяется для инженерных расчетов процессов с фазовыми превращениями, включая обратимые полиморфные превращения [2, 3, 10, 20, 21, 33], что касается формально аналогичных им процессов, то аналогом рассмотренного примера при гранулировании порошков является рост одиночной гранулы [3, 21] или рост одиночной капли макроэмульсии в коалесцирующей (микроэмульсии) [2, 3].
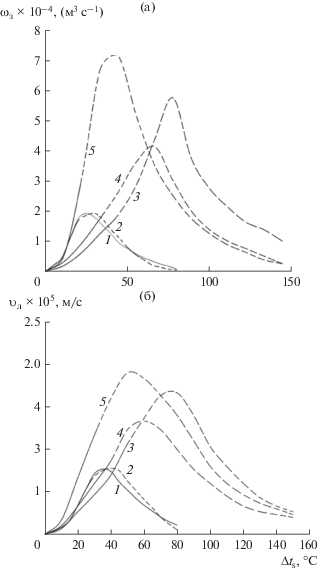
Наличие формальной аналогии зависимостей кинетических параметров, (скоростей зарождения и роста центров превращения) от термодинамического стимула, позволило создать обобщенную методику их экспериментального определения для различных видов превращений со структурной перестройкой исходной системы, экспериментально подтвердить аналогию вида этих зависимостей, объяснить это явление и использовать его на практике [1–3, 10–12, 20, 21] (рис. 4). Сказанное фрагментарно будет представлено ниже.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ ОБЪЕМНОГО МЕХАНИЗМА ФАЗОВОГО ПРЕВРАЩЕНИЯ
Процессы объемного фазового превращения могут быть изопотенциальными, (протекающими при постоянном термодинамическом стимуле – переохлаждение, пересыщение, “недонасыщение” гранулируемого объема порошка механической энергий и др.), и неизопотенциальными, (протекающими при переменном термодинамическом стимуле). В последнем случае процесс превращения контролируется кинетикой образования и роста “новой” фазы и явлениями переноса в двухфазной среде [34, 35]. Рассмотрим изопотенциальное объемное превращение, контролируемое кинетическими параметрами (скоростями зарождениями и роста центров превращения) [1–3, 10, 12, 21, 23, 27].
Процесс зарождения центров новой фазы является случайным процессом [1–7, 36]. Скорость зарождения центров превращения можно по аналогии с теорией кристаллизации [36], трактовать как
где V – объем исходной фазы (расплава, порошка при гранулировании, микроэмульсии при коалесценции и т.д.); M(τ) – наиболее вероятное число центров “новой” фазы, возникших по времени τ.Объем VK изотропно растущего с линейной скоростью υᴧ новообразования равен
(9)
${{V}_{{\text{к}}}} = \beta {{\left[ {\int\limits_{{{{\tau }}_{{{\text{инд}}}}}}^{{{{\tau }}_{{\text{к}}}}} {{{\upsilon }_{{\Lambda }}}(\tau {\kern 1pt} ')d\tau {\kern 1pt} '} } \right]}^{n}},$Механизм зарождения и роста центров фазовых превращений рассматривается рядом научных направлений физического и физико-химического профиля, но не позволяет количественно, с достаточной для инженерных расчетов точностью определить значения ${{\omega }_{3}}$ и ${{\upsilon }_{{\Lambda }}}{\text{\;}}$ [3–5, 13]. То же можно сказать о кинетических параметрах процессов, формально-аналогичных фазовому превращению, в частности, о коалесценции в микроэмульсиях [2, 19], гранулировании порошков [1–3, 10, 12, 21] и др. В инженерно-технологических расчетах часто нужно знать лишь динамику степени превращения $\eta \left( \tau \right) = {{{{V}_{{\text{к}}}}\left( \tau \right)} \mathord{\left/ {\vphantom {{{{V}_{{\text{к}}}}\left( \tau \right)} V}} \right. \kern-0em} V}$ (отношение объема “новой” фазы ${{V}_{{\text{к}}}}\left( \tau \right)$ к исходному объему “старой” фазы V) и структуру ${{V}_{{\text{к}}}}\left( \tau \right)$ (распределение по объему и форме новообразований и пор). Эти параметры во многом определяют физико-механические, физико-химические и потребительские свойства продукта [1–3, 8, 13, 14, 23, 24, 28, 37, 38].
Если плотности фаз неизменны, рост поверхности новообразований изотропен, претерпевающая превращение двухфазная среда идеально перемешана (изопотенциальное объемное превращение) или поля температур, концентраций, давлений и т.д. определяются из решения задач переноса субстанции в фазах, известны зависимости скоростей зарождения ${{\omega }_{3}}$ и роста ${{\upsilon }_{{\Lambda }}}{\text{\;}}$ центров новообразований от движущей силы процесса (в частности, пересыщения, переохлаждения, разности кинетических энергий, диссипируемой в гранулируемом слое порошка или диспергируемой эмульсии и т.д.), после истечения индукционного периода ${{\tau }_{{{\text{инд}}}}},$ предшествующего началу превращения, число образовавшихся центров dN, объем “новой” фазы d${{V}_{{\text{к}}}}$ и степень превращения dη и η равны:
(11)
$\begin{gathered} d{{V}_{{\text{к}}}} = {{{v}}_{{\text{к}}}}dN = \\ = \beta {{\left[ {\int\limits_{\tau }^{{{{\tau }}_{{\text{к}}}}} {{{\upsilon }_{{\Lambda }}}(\tau {\kern 1pt} ')d\tau {\kern 1pt} '} } \right]}^{n}}{{\omega }_{3}}(\tau )\left[ {V - {{V}_{{\text{к}}}}(\tau )} \right]d\tau , \\ \end{gathered} $(12)
$d\eta = \beta {{\left[ {\int\limits_{\tau }^{{{{\tau }}_{{\text{к}}}}} {{{\upsilon }_{{\Lambda }}}(\tau {\kern 1pt} ')d\tau {\kern 1pt} '} } \right]}^{n}}{{\omega }_{3}}(\tau )\left[ {1 - \eta (\tau )} \right]d\tau ,$(13)
$\eta ({{\tau }_{{\text{к}}}}) = \int\limits_{{{{\tau }}_{{{\text{инд}}}}}}^{{{{\tau }}_{{\text{к}}}}} {\beta {{{\left[ {\int\limits_{\tau }^{{{{\tau }}_{{\text{к}}}}} {{{\upsilon }_{{\Lambda }}}(\tau {\kern 1pt} ')d\tau {\kern 1pt} '} } \right]}}^{n}}{{\omega }_{3}}(\tau )\left[ {1 - \eta (\tau )} \right]d\tau } .$Используя разностные аналоги этих уравнений, можно решать задачи с переменной в пространственно-временном континууме движущей силой кинетических процессов (не изопотенциальное объемное превращение), определяя не только динамику степени превращения и структуры новообразования на каждом шаге по времени, но и поля температур, скоростей, концентраций в фазах. Если $\beta ,$ ${{\omega }_{3}},$ ${{\upsilon }_{{\Lambda }}}$ = const, а τинд и η(τ) → 0, то из (13) получаем известное уравнение Колмогорова–Аврами [22]:
(14)
$\begin{gathered} \eta ({{\tau }_{{\text{к}}}}) \cong 1 - \exp \left( { - \beta \frac{1}{{{\text{п}} + 1}}{{\omega }_{3}}\upsilon _{{\Lambda }}^{{\text{п}}}\tau _{{\text{к}}}^{{{\text{п}} + 1}}} \right) = \\ = 1 - \exp ( - \kappa {{\tau }^{{{\text{п}} + 1}}}), \\ \end{gathered} $Зависимости (10)–(14) описывают объемные фазовые превращения при “гомогенном” зародышеобразовании в “старой” фазе, в частности, с использованием модификаторов І рода [3, 5, 23, 27, 29, 33]. При “гетерогенном” зародышеобразовании (в том числе, на модификаторах ІІ рода при кристаллизации, конденсации, десублимации) [3, 23, 27, 33], при формально аналогичных им превращениях в случае гранулирования порошков на внешнем ретуре [1–3, 21] или в случае эмульгирования на внешних включениях, десорбируемых микропузырьках [2, 19], или при различных технологиях микрокапсулирования [2, 3, 37, 38] степень превращения η определяется зависимостью [1–3, 20, 21]
(15)
$\begin{gathered} \eta ({{\tau }_{{\text{к}}}}) = {{N}_{{{\text{уд}}}}}\beta \left[ {{{{\left( {r + \int\limits_0^{{{{\tau }}_{{\text{к}}}}} {{{\upsilon }_{{\Lambda }}}(\tau {\kern 1pt} ')d\tau {\kern 1pt} '} } \right)}}^{n}} - {{r}^{n}}} \right] + \\ + \,\,{{\int\limits_{{{{\tau }}_{{{\text{инд}}}}}}^{{{{\tau }}_{{\text{к}}}}} {\beta \left[ {\int\limits_{\tau }^{{{{\tau }}_{{\text{к}}}}} {{{\upsilon }_{{\Lambda }}}(\tau {\kern 1pt} ')d\tau } } \right]} }^{n}}{{\omega }_{3}},\,\,\,\,\left[ {1 - \eta (\tau )} \right]d\tau . \\ \end{gathered} $При ${{N}_{{{\text{уд}}}}}$ = 0 уравнение (15) при β ≠ ωз, ${{\upsilon }_{{\Lambda }}}$ = const, η, τинд → 0 переходит в (14). При исключении “гомогенного” зародышеобразования, т.е. в процессе, протекающем только на внешних структурах [1–3, 10, 21], уравнение (15) трансформируется в зависимость (16), в том числе для гетерогенного зародышеобразования (аналог уравнения Колмогорова–Аврами при β, ωз, ${{\upsilon }_{{\Lambda }}}$ = const, η, τинд → 0 имеет вид (17)):
(16)
$\eta ({{\tau }_{{\text{к}}}}) = {{N}_{{{\text{уд}}}}}\beta \left[ {{{{\left( {r + \int\limits_0^{{{{\tau }}_{{\text{к}}}}} {{{\upsilon }_{{\text{л}}}}(\tau {\kern 1pt} ')d\tau {\kern 1pt} '} } \right)}}^{n}} - {{r}^{n}}} \right],$(17)
$\begin{gathered} \eta ({{\tau }_{{\text{к}}}}) \cong 1 - \\ - \,\,\exp \left\{ { - \beta \left[ {{{N}_{{{\text{уд}}}}}\left[ {{{{(r + {{\upsilon }_{{\text{л}}}}{{\tau }_{{\kappa }}})}}^{n}} - {{r}^{n}}} \right] + \frac{{{{\omega }_{{\text{з}}}}\upsilon _{{\text{л}}}^{n}}}{{n + 1}}\tau _{{\text{к}}}^{{n + 1}}} \right]} \right\}. \\ \end{gathered} $В случае если максимальная степень превращения ηmax < 1, как это имеет место при кристаллизации ВМС, полимеров, обратимых полиморфных превращениях, конденсации, десублимации, формально аналогичных им: гранулировании порошков, коалесценции и др. [1–3, 10, 12, 39, 40], то в уравнениях (12)–(15) вместо 1 подставляют ηmax, определяемую из термодинамических соображений или экспериментов [1–3, 7, 8, 10, 12, 19, 39, 40].
ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ ПРИ АНАЛИЗЕ ОБЪЕМНОГО МЕХАНИЗМА ФАЗОВОГО ПРЕВРАЩЕНИЯ И ИХ ОБСУЖДЕНИЕ
Расчеты с использованием разностных аналогов полученных уравнений (12)–(16) позволяют на каждом шаге по времени учитывать изменение значений кинетических параметров и формы новообразований, в том числе за счет эффекта “стесненности”, взаимовлияния растущих центров, введением в систему уравнений переноса теплоты, массы, количества движения и поверхностных явлений решать задачи неизопотенциальных объемных превращений с эффектами коагуляции, коалесценции, дробления, истирания и т.д. Некоторые задачи и оценки названных эффектов приведены нами в работах [1–3, 12, 13, 20, 21, 33, 41, 42]. На каждом шаге по времени в расчетах получают не только степень превращения, но и фракционный состав новообразований по размеру, форме, результату взаимодействия, вероятности взаимодействия и вкладу каждой из этих фракций в общую степень превращения [3, 21, 41, 42].
Для адекватного реальности расчета процесса, в общем случае не изопотенциального объемного фазового и формально аналогичного ему превращения, необходимо знать:
– зависимости величин скоростей зарождения и роста центров превращения от величины термодинамического стимула (в линейном приближении разности концентраций, температур, давлений, поверхностных энергий, электрических потенциалов, недонасыщения (пересыщения) механической энергии гранулируемой (коагулируемой), коалесцирующей (диспергируемой) фазы и т.д. [2, 6, 7, 34]).
– скорости образования и роста областей взаимодействия (разрушения) новообразований (коллектива новообразований) от величины термодинамических стимулов;
– зависимости, описывающие явления переноса субстанции.
Выше упоминалось, что теоретические зависимости, количественно (с достаточной для инженерных расчетов точностью) описывающие связь величин скоростей зарождения и роста центров новообразований с термодинамическим стимулом, отсутствуют. Имеющиеся пригодны лишь для качественных ориентировочных оценок. Предлагаемая методика экспериментального определения кинетических параметров основана на вероятностном характере процесса зародышеобразования центров превращения и известном факте [3–6, 13, 20, 21, 36, 41, 42], что число положительных событий много меньше числа элементарных актов. Поэтому вероятность образования K центров превращения ко времени τ описывается распределением Пуассона [36]. Образования одного и более центров K ≥ 1 – уравнением (19) и может быть экспериментально определена через эмпирическую функцию ожидания начала превращения (появления первого центра (20)):
(18)
${\rm P}(\kappa ,\tau ) = \frac{{{\rm M}{{{(\tau )}}^{{\text{к}}}}}}{{{\rm K}!}}\exp [ - {\rm M}(\tau )],$(19)
${\rm P}(\kappa ,\tau ) = 1 - \exp \left[ { - {\rm M}(\tau )} \right],\,\,\,\,K \geqslant {\text{1,}}$(20)
${\rm P}(\kappa ,\tau ) = F(\tau ) = \frac{{n(\tau )}}{{{{n}_{\sum }} + 1}},\,\,\,\,K \geqslant {\text{1}},$(21)
${{\omega }_{{\text{з}}}} = - \frac{1}{V}\frac{{d\{ \ln \left[ {1 - F(\tau )} \right]\} }}{{d\tau }},\,\,\,\,{{\omega }_{3}} = - \frac{1}{V}\frac{{\Delta \ln \left[ {1 - F(\tau )} \right]}}{{\Delta \tau }}.$При определении скорости зародышеобразования на практике [1–3, 10, 11, 20, 21, 41] используют конечные приращения $\Delta ~{\text{ln}}~\left[ {1 - F\left( \tau \right)} \right]$ и $\Delta \tau ,$ поэтому при систематической погрешности определения этих параметров не точная фиксация времени появления первого центра новообразования не критична. Подробности этой универсальной методики и практики ее применения изложены в работах [1–3, 10, 11, 20, 21, 41, 43].
Получив обработкой экспериментальных данных зависимости ${{\omega }_{3}}\left( {\Delta {{t}_{s}}} \right)$ и η(τ), по уравнению (1), с изложенными рекомендациями, оценивают механизм превращения. С использованием разностных аналогов выражений (12), (15) для степени превращения η(τ) при “гомогенном” и “гетерогенном” зарождении, оценивают по уравнениям (22), (23) вклад в степень превращения растущего первого зародыша (последний член суммы):
(22)
$\begin{gathered} \eta ({{\tau }_{{\text{к}}}}) = \frac{4}{3}\pi \left[ {{{{\sum\limits_{i = 1}^{{{N}_{1}}} {\left[ {\sum\limits_{j = 1}^{{{N}_{2}}} {{{\upsilon }_{{{\Lambda }j}}}\Delta {{\tau }_{j}}} } \right]} }}^{3}}{{\omega }_{{{\text{з}}i}}}} \right. \times \\ \times \,\,\left. {\left[ {{{\eta }_{{\max }}} - \eta \left( {\sum\limits_{i = 1}^{{{N}_{1}}} {\Delta {{\tau }_{i}}} } \right)} \right]\Delta {{\tau }_{i}} + \frac{1}{V}{{{\left[ {\sum\limits_{i = 1}^{{{N}_{1}}} {{{\upsilon }_{{{\Lambda }i}}}\Delta {{\tau }_{i}}} } \right]}}^{3}}} \right], \\ \end{gathered} $(23)
$\begin{gathered} \eta ({{\tau }_{{\text{к}}}}) = {{{\rm N}}_{{{\text{уд}}}}}\frac{4}{3}\pi \left[ {{{{\left( {r + \sum\limits_{{\text{к}} = 1}^{{{N}_{3}}} {{{\upsilon }_{{{\Lambda к}}}}\Delta {{\tau }_{{\text{к}}}}} } \right)}}^{3}} - {{r}^{3}}} \right] + \\ + \,\,\frac{4}{3}\pi \left[ {\sum\limits_{i = 1}^{{{N}_{1}}} {{{{\left[ {\sum\limits_{j = 1}^{{{N}_{2}}} {{{\upsilon }_{{{\Lambda }j}}}\Delta {{\tau }_{j}}} } \right]}}^{3}}{{\omega }_{i}}} } \right.\left[ {{{\eta }_{{\max }}} - \eta \left( {\sum\limits_{i = 1}^{{{N}_{1}}} {\Delta {{\tau }_{i}}} } \right)} \right] \times \\ \times \,\,\left. {\Delta {{\tau }_{i}} + \frac{1}{V}{{{\left[ {\sum\limits_{i = 1}^{{{N}_{1}}} {{{\upsilon }_{{{\Lambda }i}}}\Delta {{\tau }_{i}}} } \right]}}^{3}}} \right] \\ \end{gathered} $Решением инверсной задачи на каждом шаге по времени можно, используя выражения (22), (23), зная ${{\omega }_{3}}\left( {\Delta {{t}_{s}}} \right)$ и η(τ), получить не только зависимость линейной скорости роста новообразований от термодинамического стимула υΛ($\Delta {{t}_{s}}$), учесть влияние на нее “стесненности” роста υΛ($\Delta {{t}_{s}},$ η), а в общем случае, с привлечением дополнительной информации, учесть изменение фактора формы $\beta $ роста новообразования и анизотропию роста его поверхности (граней) υΛ($\Delta {{t}_{s}},$ η, $~\beta $). Разумеется, при обоснованности упрощающих допущений, можно использовать более простые зависимости (12, 15, 16, 17 и др.). Подробности методики и практики решения подобных задач даны в [1–3, 10, 11, 20, 21, 41, 43]
Истоки дискретного во времени решения задач объемного (трехмерного) превращения даны в работe [43]. Затем они использованы в работах [44–46] и др. [47–49]. Зависимости, описывающие явления переноса вещества и энергии подробно обсуждены в [7, 9, 29, 50] и мы на них не останавливаемся.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ ОБЪЕМНО-ПОСЛЕДОВАТЕЛЬНОГО МЕХАНИЗМА ФАЗОВОГО ПРЕВРАЩЕНИЯ
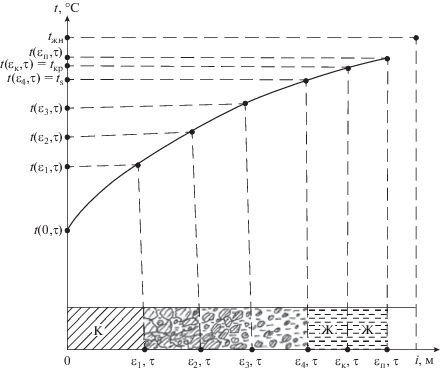
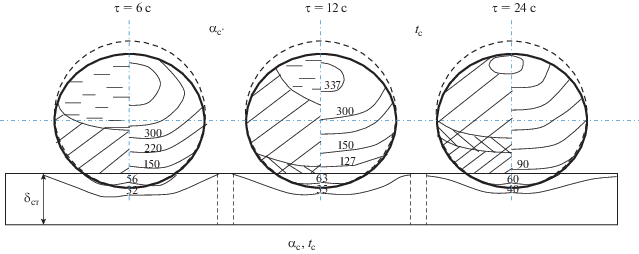
Объемно-последовательное (трехмерное, вырождающееся в одномерное) фазовое превращение проиллюстрируем математическим описанием кристаллизации однокомпонентного расплава. Процесс происходит в интервале температур, в котором существует движущаяся двухфазная (кристаллы–расплав), трехфазная (кристаллы–расплав–газ) переходная зона (рис. 5) [3, 13, 14, 23, 24, 27]. Она состоит из кристаллической фазы с распределенной усадочной пористостью, ограниченной движущейся границей ${{\xi }_{1}}\left( \tau \right);$ трехфазной зоны: строящегося кристаллического каркаса с захваченными областями расплава с внутренними усадочными порами, ограниченной движущимися границами ${{\xi }_{1}}\left( \tau \right)$ – ${{\xi }_{2}}\left( \tau \right);$ двухфазной зоны: расплав–растущие стесненно кристаллы с границами ${{\xi }_{2}}\left( \tau \right)$ – ${{\xi }_{3}}\left( \tau \right);$ двухфазной зоны: расплав–растущие нестесненно кристаллы с границами ${{\xi }_{3}}\left( \tau \right)$ – ${{\xi }_{4}}\left( \tau \right);$ (в зону ${{\xi }_{2}}\left( \tau \right)$ – ${{\xi }_{4}}\left( \tau \right)$ возможна фильтрация расплава за счет разности плотности фаз, за счет термокапиллярного течения и термогравитационной конвекции); однофазной зоны переохлажденного расплава с границами ${{\xi }_{4}}\left( \tau \right)$ – ${{\xi }_{{\kappa }}}\left( \tau \right);$ однофазной зоны перегретого расплава ${{\xi }_{{\text{к}}}}\left( \tau \right)$ – ${{\xi }_{n}}\left( \tau \right),$ где ${{\xi }_{n}}$(τ) – граница сосредоточенной усадочной поры (рис. 5). Плотность переходной зоны ${{\rho }_{{{\text{nз}}}}}$ и коэффициент объемной пористости ${{\varepsilon }_{{v}}}$ = $\varepsilon _{{v}}^{p}$ + $\varepsilon _{{v}}^{c}$ (пористость подразделяется на сосредоточенную $\varepsilon _{{v}}^{c}$ и распределенную $\varepsilon _{{v}}^{p}$) определяются зависимостями
(24)
$\rho _{{{\text{ПЗ}}}}^{'} = \frac{{{{V}_{{\text{П}}}}{{\rho }_{{\text{Г}}}} + {{V}_{{{\text{ПЗ}}}}}{{\rho }_{{{\text{ПЗ}}}}}}}{{{{V}_{{\text{П}}}} + {{V}_{{{\text{ПЗ}}}}}}} \approx \frac{1}{{{{\varepsilon }_{{v}}} + 1}}{{\rho }_{{{\text{ПЗ}}}}},$(25)
$\begin{gathered} {{\varepsilon }_{{v}}} = \frac{{{{\rho }_{{{\text{ПЗ}}}}} - {{\rho }_{{\text{ж}}}}({{t}_{{{\text{жн}}}}})}}{{{{\rho }_{{\text{ж}}}}({{t}_{{{\text{жн}}}}})}} \cong \eta \frac{{{{\rho }_{{\text{к}}}}({{t}_{{{\text{кр}}}}})}}{{{{\rho }_{{\text{ж}}}}({{t}_{{{\text{жн}}}}})}} \times \\ \times \,\,\left[ {1 + {{\beta }_{{\text{к}}}}({{t}_{{{\text{кр}}}}} - t)} \right] - \eta , \\ \end{gathered} $(26)
$\begin{gathered} \varepsilon _{{v}}^{P} = {{\varepsilon }_{{v}}} - \varepsilon _{{v}}^{c} = \frac{{{{\rho }_{{\kappa }}}({{t}_{{{\text{кр}}}}})}}{{{{\rho }_{{\text{ж}}}}({{t}_{{{\text{жн}}}}})}} \times \\ \times \,\,\left\{ {{{\eta }_{{\max }}}\left[ {1 + {{\beta }_{{\text{к}}}}[{{t}_{{{\text{кp}}}}} - t({{\xi }_{2}},\tau )]} \right] - \eta ({{\xi }_{2}},\tau )} \right. \times \\ \left. { \times \,\,\left[ {1 + \beta [{{t}_{{{\text{кр}}}}} - t({{\xi }_{2}},\tau )]} \right]} \right\} - {{\eta }_{{\max }}} + \eta ({{\xi }_{2}},\tau ). \\ \end{gathered} $Сосредоточенная пористость (усадочная раковина закрытого или открытого типа) формируется, пока возможна фильтрация расплава в переходную зону (как правило, до η ≤ 0.6 [2, 3, 5, 13, 23]. Нами [3, 41] и др. [3, 16–18] для гранул карбамида, аммиачной селитры, серы, KNО3 экспериментально получены значения, лежащие в диапазоне (0.55 ≤ η(${{\xi }_{2}}\tau $) ≤ 0.7). Затем формируется распределенная усадочная пористость.
В зоне 0–${{\xi }_{1}}\left( \tau \right)$ процесс кристаллизации закончен, но в кристаллической фазе могут проходить энантиотропные полиморфные превращения, для математического описания которых применена система уравнений и алгоритм ее решения, которые будут изложены ниже (надо лишь помнить, что в фазах отсутствуют конвективные потоки, формируется лишь распределенная усадка, а явления переноса идут на молекулярном уровне). Перенос теплоты в кристаллической фазе (без полиморфизма) описывается уравнением:
(27)
$с_{{\text{к}}}^{'}\rho _{{\text{к}}}^{'}{{\nabla }_{{\tau }}}t = {{\nabla }_{i}}\left[ {\lambda _{{\text{к}}}^{'}{{\nabla }_{i}}t} \right],\,\,\,\,0 \leqslant i \leqslant {{\xi }_{1}}(\tau );\,\,\,\,\tau > 0,$С помощью такого же уравнения можно рассчитывать динамику превращения в любой точке пространства, занятого первоначально расплавом от момента прохождения через эту точку фронта ${{\xi }_{2}}$($\tau $) до момента “прихода” туда фронта ${{\xi }_{1}}\left( \tau \right).$ Перенос теплоты в зоне ${{\xi }_{1}}\left( \tau \right)$–${{\xi }_{2}}\left( \tau \right)$ описывается уравнением с распределенным объемным источником, а введением эффективной теплоемкости $с_{{\text{э}}}^{'}$ сводится к виду, пригодному для использования конечно-разностных схем “сквозного счета” со “сглаживанием” фазовых фронтов [31, 32]:
(29)
$с_{{{\text{ПЗ}}}}^{'}\rho _{{{\text{ПЗ}}}}^{'}{{\nabla }_{{\tau }}}t = {{\nabla }_{i}}[\lambda _{{{\text{ПЗ}}}}^{'}{{\nabla }_{i}}t] + L{{\rho }_{K}}{{\nabla }_{{\tau }}}\eta ,\,\,\,\,{\text{или}}$(30)
$\begin{gathered} \left( {с_{{{\text{ПЗ}}}}^{'}\rho _{{{\text{ПЗ}}}}^{'} - L{{\rho }_{K}}{{\nabla }_{t}}\eta } \right){{\nabla }_{{\tau }}}t = {{\nabla }_{i}}[\lambda _{{{\text{ПЗ}}}}^{'}{{\nabla }_{i}}t]; \\ с_{{\text{Э}}}^{'}\rho _{{{\text{ПЗ}}}}^{'}{{\nabla }_{{\tau }}}t = {{\nabla }_{i}}[\lambda _{{{\text{ПЗ}}}}^{'}{{\nabla }_{i}}t], \\ \end{gathered} $Динамика образования усадочной пористости за счет разности плотностей фаз и термической усадки определяется уравнением:
(31)
$\begin{gathered} \varepsilon _{{v}}^{p}(i,\tau ) = {{\varepsilon }_{{v}}} - \varepsilon _{{v}}^{c} = \frac{{{{\rho }_{{\text{к}}}}({{t}_{{{\text{кp}}}}})}}{{{{\rho }_{{\text{ж}}}}({{t}_{{{\text{жн}}}}})}} \times \\ \times \,\,\left\{ {\eta (i,\tau )\left[ {1 + {{\beta }_{{{\text{ПЗ}}}}}\left( {{{t}_{{{\text{кр}}}}} - t(i,\tau )} \right)} \right] - \eta ({{\xi }_{2}},{{\tau }_{2}}) \times } \right. \\ \left. { \times \,\,\left[ {1 - {{\beta }_{{{\text{ПЗ}}}}}\left( {{{t}_{{{\text{кр}}}}} - t({{\xi }_{2}},{{\tau }_{2}})} \right)} \right]} \right\} - \eta (i,\tau ) + \eta ({{\xi }_{2}},{{\tau }_{2}}), \\ \eta ({{\xi }_{2}},\tau ) \leqslant \eta (i,\tau ) \leqslant {{\eta }_{{\max }}}, \\ \end{gathered} $При определении η(i, τ) по уравнению сходному с (28) фактор формы растущих кристаллов $\beta \left( \eta \right)$ из-за “врастания” кристаллов друг в друга изменяется c изменением $\eta ~\left( {i,\tau } \right)~$ на каждом шаге по времени и может быть определен расчетно [73–76] или экспериментально и аппроксимирован, например полиномом $\beta \left( \eta \right)$ = $\beta - {{a}_{1}}\eta - {{a}_{2}}{{\eta }^{2}}....$
В зону не полностью сросшихся кристаллов ${{\xi }_{2}}\left( \tau \right)$ – ${{\xi }_{3}}\left( \tau \right)$ за счет разности плотностей фаз и термокапиллярной конвекции идет фильтрация расплава ${{\omega }_{i}}$ c переменной на каждом шаге пространства времени скоростью, а перенос теплоты описывается конвективным уравнением с объемными распределенными источниками:
(32)
$\begin{gathered} с_{{{\text{ПЗ}}}}^{'}\rho _{{{\text{ПЗ}}}}^{'}{{\nabla }_{{\tau }}}t + {{c}_{{\text{ж}}}}{{\rho }_{{\text{ж}}}}{{\omega }_{i}}{{\nabla }_{i}}t = {{\nabla }_{i}}\left[ {\lambda _{{{\text{ПЗ}}}}^{'}{{\nabla }_{i}}t} \right] + \\ + \,\,L{{\rho }_{{\text{к}}}}{{\nabla }_{{\tau }}}\eta \,\,\,\,{\text{или}} \\ \left( {с_{{{\text{ПЗ}}}}^{'}\rho _{{{\text{ПЗ}}}}^{'} - L{{\rho }_{{\text{к}}}}{{\nabla }_{t}}\eta } \right){{\nabla }_{{\tau }}}t + \\ + \,\,{{c}_{{\text{ж}}}}{{\rho }_{{\text{ж}}}}{{\omega }_{i}}{{\nabla }_{i}}t = {{\nabla }_{i}}\left[ {\lambda _{{{\text{ПЗ}}}}^{'}{{\nabla }_{i}}t} \right]; \\ \end{gathered} $(33)
$с_{{\text{Э}}}^{'}\rho _{{{\text{ПЗ}}}}^{'}{{\nabla }_{{\tau }}}t + {{c}_{{\text{ж}}}}{{\rho }_{{\text{ж}}}}{{\omega }_{i}}{{\nabla }_{i}}t = {{\nabla }_{i}}\left[ {\lambda _{{{\text{ПЗ}}}}^{'}{{\nabla }_{i}}t} \right].$Фильтрация расплава в переходную зону на участках ${{\xi }_{1}}\left( \tau \right) \leqslant i$ ≤ ${{\xi }_{3}}\left( \tau \right)$ и ${{\xi }_{3}}\left( \tau \right) \leqslant {{\xi }_{4}}\left( \tau \right)$ приводит к образованию сосредоточенной усадочной полости, динамика изменения коэффициента которой $\varepsilon _{{v}}^{c}$ и степени превращения η($i,\tau $) на участках ξ2(τ) – ξ3(τ) и ${{\xi }_{3}}\left( \tau \right)$ – ${{\xi }_{4}}\left( \tau \right)$ определяются зависимостями
(34)
$\begin{gathered} \varepsilon _{{v}}^{c} = \eta (i,\tau )\left\{ {\frac{{{{\rho }_{{\text{к}}}}({{t}_{{{\text{кp}}}}})}}{{{{\rho }_{{\text{ж}}}}({{t}_{{{\text{жн}}}}})}}\left[ {1 + {{\beta }_{{{\text{ПЗ}}}}}({{t}_{{{\text{кр}}}}} - t)} \right] - 1} \right\}; \\ 0 \leqslant \eta (i,\tau ) \leqslant \eta ({{\xi }_{2}},\tau ), \\ \end{gathered} $Граница зоны “стесненного” роста определяется ориентировочно величиной $\eta \left( {{{\xi }_{{3,~}}}\tau } \right)$ ≈ 0.3–0.4 [3, 23] или может быть уточнена вычислительным экспериментом [43–46].
Скорость течения расплава “всасываемого” в переходную зону определяется уравнением неразрывности:
(37)
$\begin{gathered} \left\{ {{{\rho }_{{\text{к}}}}({{t}_{{{\text{кp}}}}})\left[ {1 + {{\beta }_{{{\text{ПЗ}}}}}({{t}_{{{\text{кр}}}}} - t)} \right] - {{\rho }_{{\text{ж}}}}({{t}_{{{\text{жн}}}}})} \right\} \times \\ \times \,\,{{\nabla }_{{\tau }}}\eta = {{\nabla }_{i}}({{\rho }_{{\text{ж}}}}\omega ). \\ \end{gathered} $В практических расчетах использован разностный аналог уравнения (37), с помощью которого на каждом шаге по времени по рассчитанному изменению степени превращения в каждой точке участка переходной зоны определяют изменение скорости течения в окрестности этой точки.
Границы переохлажденной зоны ${{\xi }_{4}}\left( \tau \right)$ – ${{\xi }_{k}}\left( \tau \right)$ определяли совместным решением уравнения конвективного переноса теплоты и взаимосвязанных уравнений расчета объема переохлажденного расплава ${{V}_{{{\text{ж}}s}}}$ и времени ожидания появления первого центра кристаллизации ${{\tau }_{{{\text{инд}}}}}{\text{:}}$
(38)
${{с}_{{\text{ж}}}}{{r}_{{\text{ж}}}}[{{\nabla }_{\tau }}t + {{\omega }_{i}}{{\nabla }_{i}}t] = {{\nabla }_{i}}[{{\lambda }_{{\text{ж}}}}{{\nabla }_{i}}t];\,\,{{\xi }_{4}}(\tau ) \leqslant i \leqslant {{\xi }_{{\text{к}}}}(\tau ),$(40)
$\int\limits_{{{{\tau }}_{{{\text{кр}}}}}}^{{{{\tau }}_{{{\text{инд}}}}}} {\int\limits_0^{{{V}_{{{\text{ж}}s}}}({\tau })} {{{\omega }_{3}}(i,\tau {\kern 1pt} ')d{{V}_{{\text{ж}}}}d\tau {\kern 1pt} ' = 1;\,\,\,\,d{{V}_{{\text{ж}}}}} } = \prod\limits_{(i)} {di} ,$Результатами итерационного решения системы (38)–(40) являются положения границ переходной зоны ${{\xi }_{4}}\left( {{{\tau }_{{{\text{инд}}}}}} \right)$ – ${{\xi }_{{\text{к}}}}\left( {{{\tau }_{{\text{к}}}}} \right)$ и поле температур в ней (т.е. ${{t}_{s}}$).
Систему уравнений (24)–(40) необходимо дополнить уравнениями зависимости скоростей зарождения и роста новообразований от термодинамического стимула (в данном случае от переохлаждения $\Delta {{t}_{s}}$) с заменой переохлаждения на температурное поле t(i, τ), а далее на пространственно-временные координаты ($i,\tau $):
Взаимосопряженность уравнений кинетики возникновения и роста новообразований с уравнениями переноса энергии, а в многокомпонентных системах и массы позволяет в каждой точке пространства–времени рассчитать динамику превращения, структуру и форму новообразований и сопутствующих им усадочных явлений. Расчет возможен лишь численно, итерационно с коррекцией коэффициентов в ходе итераций на каждом шаге по времени:
Система (24)–(42) замыкается краевыми условиями:
– начальными:
(43)
$t\left( {i,0} \right) = {{t}_{{{\text{жн}}}}} \geqslant {{t}_{{{\text{кр}}}}};\,\,\,\,\eta \left( {i,0} \right){\text{ }}0;\,\,\,\,{{\varepsilon }_{{v}}},\,\,\varepsilon _{{v}}^{p},\,\,\varepsilon _{{v}}^{c} = 0;$– граничными:
(45)
$\left. {\begin{array}{*{20}{c}} {t({{\xi }_{1}} - 0,\tau ) = t({{\xi }_{1}} + 0,\tau );} \\ {\lambda _{{\text{к}}}^{'}{{\nabla }_{i}}t({{\xi }_{1}},\tau ) - \lambda _{{{\Pi З}}}^{'}{{\nabla }_{i}}t({{\xi }_{1}},\tau ) = L{{\rho }_{{\text{к}}}}(1 - {{\eta }_{{\max }}}){{\nabla }_{{\tau }}}{{\xi }_{1}};} \\ {{{\nabla }_{{\tau }}}{{\xi }_{1}} = {{\upsilon }_{{\Lambda }}} = f(\Delta {{t}_{s}}) = f[{{t}_{{{\text{кр}}}}} - t({{\xi }_{1}},\tau )];\,\,\,\,{{h}_{{\max }}} \leqslant 1} \end{array}} \right\}\,\,\,\,i = {{\xi }_{1}}(\tau ),$(46)
$\left. {\begin{array}{*{20}{c}} {t({{\xi }_{2}} - 0,\tau ) = t({{\xi }_{2}} + 0,\tau );} \\ {\lambda _{{{\text{ПЗ1}}}}^{'}{{\nabla }_{i}}t({{\xi }_{2}},\tau ) - \lambda _{{{\Pi З2}}}^{'}{{\nabla }_{i}}t({{\xi }_{2}},\tau );} \\ {{{\omega }_{i}}({{\xi }_{2}},\tau ) = 0;\,\,\,\,\eta (({{\xi }_{2}},\tau ) \sim 0.6 = {\text{const}};} \end{array}} \right\}\,\,\,\,i = {{\xi }_{2}}(\tau ),$(47)
$\left. {\begin{array}{*{20}{c}} {t({{\xi }_{3}} - 0,\tau ) = t({{\xi }_{3}} + 0,\tau );} \\ {\lambda _{{{\Pi З2}}}^{'}{{\nabla }_{i}}t({{\xi }_{3}},\tau ) = \lambda _{{{\Pi З}}}^{'}{{\nabla }_{i}}t({{\xi }_{3}},\tau ) + {{\omega }_{i}}({{\xi }_{3}},\tau ){{\rho }_{{\text{ж}}}}{{c}_{{\text{ж}}}}t({{\xi }_{3}},\tau );} \\ {{{\rho }_{{\text{ж}}}}{{\omega }_{i}}({{\xi }_{3}},\tau ) = {{G}_{с}}({{\xi }_{3}},\tau ) = {{\rho }_{{\text{ж}}}}({{t}_{{{\text{жн}}}}})\int\limits_{{{х}_{2}}}^{{{х}_{3}}} {\int\limits_{{{у}_{2}}}^{{{у}_{3}}} {\int\limits_{{{z}_{2}}}^{{{z}_{3}}} {\frac{{d\varepsilon _{{\nu }}^{c}}}{{d\tau }}dxdydz;\,\,\,\,i = x,y,z;} } } } \\ {\eta ({{\xi }_{3}},\tau )\sim 0.3 - 0.4 = {\text{const}};} \end{array}} \right\}\,\,\,\,i = {{\xi }_{4}}(\tau ),$(48)
$\left. {\begin{array}{*{20}{c}} {t({{\xi }_{4}} - 0,\tau ) = t({{\xi }_{4}} + 0,\tau ) = {{t}_{s}} < {{t}_{{{\text{кр}}}}};} \\ {\lambda _{{{\Pi З3}}}^{'}{{\nabla }_{i}}t({{\xi }_{4}},\tau ) = {{\lambda }_{{\text{ж}}}}{{\nabla }_{i}}t({{\xi }_{4}},\tau ) + {{\omega }_{i}}({{\xi }_{4}},\tau ){{\rho }_{{\text{ж}}}}{{c}_{{\text{ж}}}}t({{\xi }_{4}},\tau );} \\ {{{\rho }_{{\text{ж}}}}{{\omega }_{i}}({{\xi }_{4}},\tau ) = {{\rho }_{{\text{ж}}}}({{t}_{{{\text{жн}}}}})\int\limits_{(i)} {\frac{{d\varepsilon _{{v}}^{c}}}{{d\tau }}di} = {{\rho }_{{\text{ж}}}}({{t}_{{{\text{жн}}}}})\int\limits_{{{x}_{3}}}^{{{x}_{4}}} {\int\limits_{{{y}_{3}}}^{{{y}_{4}}} {\int\limits_{{{z}_{3}}}^{{{z}_{4}}} {\frac{{d\varepsilon _{{v}}^{c}}}{{d\tau }}dxdydz} ;\,\,\,\,i = x,y,z;} } } \\ {\eta ({{\xi }_{4}},\tau ) = 0;} \end{array}} \right\}\,\,\,\,i = {{\xi }_{4}}(\tau ),$(49)
$\left. {\begin{array}{*{20}{c}} {t({{\xi }_{{\text{к}}}} - 0,\tau ) = t({{\xi }_{{\text{к}}}} + 0,\tau ) = {{t}_{{{\text{кр}}}}} = {\text{const}};} \\ {{{\omega }_{i}}({{\xi }_{{\text{к}}}},\tau ) = {{\omega }_{i}}({{\xi }_{4}},\tau );\,\,\,\eta ({{\xi }_{{\text{к}}}},\tau ) = 0;} \end{array}} \right\}\,\,i = {{\xi }_{{\text{к}}}}(\tau ),$(50)
$\left. {\begin{array}{*{20}{c}} {t({{\xi }_{\Pi }},\tau ) = \left\{ {\begin{array}{*{20}{c}} {{{t}_{{{\text{жн}}}}};} \\ {t(\tau );} \end{array}\,\,\,\,{{\lambda }_{j}}{{\nabla }_{i}}t({{\xi }_{\Pi }},\tau ) = \left\{ {\begin{array}{*{20}{c}} {{{q}_{1}}(\tau );} \\ {0;} \end{array}} \right.\,\,\,\,j = {\text{ж}},{\text{ПЗ}},{\text{ж}}} \right.} \\ {{{V}_{\Pi }}({{\xi }_{\Pi }},\tau ) = V\varepsilon _{{v}}^{c}({{\xi }_{2}},\tau );\,\,\,\,\sigma \frac{{{{S}_{\Pi }}({{\xi }_{{\Pi ,}}}\tau )}}{{{{V}_{\Pi }}({{\xi }_{\Pi }},\tau )}} \to {\text{мин}};\,\,\,\,d{{\xi }_{\Pi }}(\tau ) = \frac{{d{{V}_{\Pi }}({{\xi }_{\Pi }},\tau )}}{{d{{S}_{\Pi }}({{\xi }_{\Pi }},\tau )}}} \end{array}} \right\}\,\,\,\,i = {{\xi }_{{\text{П}}}}(\tau ),$ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ ПРИ АНАЛИЗЕ ОБЪЕМНО-ПОСЛЕДОВАТЕЛЬНОГО МЕХАНИЗМА ФАЗОВОГО ПРЕВРАЩЕНИЯ И ИХ ОБСУЖДЕНИЕ
Приведенное математическое описание включает описание последовательного и объемного превращений, в качестве частных случаев, но, при этом, исключается априорный субъективный выбор моделей превращения [2, 3].
Неявный нелинейный разностный аналог системы уравнений (24)–(50) удобно решается по предложенному алгоритму [2, 3, 33] итерационно, с явным выделением положения фазовых фронтов и “ловлей” их в узлах сетки, в пространственных ячейках которых находятся на данном шаге по времени фазовые фронты, с решением многомерных задач на “локально-одномерных” сетках по алгоритму последовательного формирования переходной зоны [2, 3].
В расчетах по известным предложенным математическим описаниям, которые проводились нами, игнорировали: термодиффузию, термокапиллярную, концентрационную, гравитационную конвекции, анизотропию роста граней кристаллов, их устойчивость и трансформацию формы кристалла, влияние кривизны поверхности растущих кристаллов на равновесную температуру превращения, неустойчивость плоской границы превращения и дендритный рост в переохлажденной зоне, влияние на ход кристаллизации “дрейфа” кристаллов в переходную зону с фильтруемым расплавом, явления газовыделения, кавитации, захвата газовых пузырьков растущими кристаллами и при порообразовании, изменение распределения пор по размерам, распределение термонапряжений в кристаллической фазе, процессы перекристаллизации в переходной зоне. Однако следует заметить, что предложенная математическая модель может быть дополнена математическим описанием большинства этих явлений, равно как и распространена на другие процессы фазовых и формально аналогичных им превращений, т.е. является достаточно удобной и универсальной оболочкой для оценочных инженерных расчетов процессов с фазовыми и формально аналогичными им превращениями.
ЗАКЛЮЧЕНИЕ
Предложена расширенная трактовка фазы как системы, обладающей определенной структурой, и фазового превращения как процесса перестройки структуры исходный “старой” фазы. Отмечено, что вышеназванный процесс может происходить не иначе, как за счет зарождения в “старой” фазе “новой” фазы и роста центров новообразований. Кинетика этого процесса определяется значениями скоростей зарождения и роста центров новообразований от термодинамического стимула, а также явлениями переноса субстанции (вещества и энергии, чаще всего механической и тепловой). Это позволило считать формально аналогичными процессы со структурной перестройкой в исходной системы, такие как классические процессы фазового превращения (кристаллизация – плавление, энантиотропные полиморфные превращения и т.д.), и ранее не считавшиеся таковыми процессы: (гранулирование порошка – истирание гранул, коалесценция (коагуляция) – диспергирование (эмульгирование)).
Наличие отмеченной формальной аналогии позволяет пользоваться подходами и моделями, взятыми из хорошо изученных процессов (например, кристаллизация – плавление) при работе с менее изученными процессами, например, гранулирование порошков – истирание гранул и др., том числе с классическими фазовыми превращениями, такими, как энантиотропные полиморфные превращения.
Показано, что для формально аналогичных фазовых превращений с единых позиций, зная кинетические параметры (скорости зарождении и роста центров новообразований от термодинамического стимула) и грамотно описав явления переноса, можно определить значимые для инженерных расчетов зависимости: изменение во времени степени превращения, структуры новообразований и сопутствующих превращению явлений: например, усадочной пористости, полей температур, концентраций и скоростей.
Показано, что процесс фазового или формально аналогичного ему превращения может протекать в рамках последовательного (одномерного), объемного (трехмерного) и объемно-последовательного (трехмерного, вырождающегося в одномерный) процесса, описания которых даны на примере одного из наиболее изученных классических фазовых превращений, кристаллизация–плавление. Разработки для этого процесса можно использовать для изучения других фазовых превращений со структурной перестройкой исходной системы.
Рассмотрено использование для численных расчетов разностного алгоритма численного решения задач с четким выделением фазовых фронтов “ловлей их подвижные узлы пространственно-временной сетки” и экономичный алгоритм итерационного решения нелинейных многомерных разностных задач на “локально одномерной сетке”.
ОБОЗНАЧЕНИЯ
| H | высота башни (аппарата), м |
| i | пространственная координата, м |
| j | номера фаз (название фаз) |
| Nуд | число частиц |
| n | параметр роста новообразования (n = 3 – трехмерный рост, n = 2 – двухмерный, n = 1 – одномерный) |
| q | удельный поток тепла, Вт/м2 |
| R | радиус гранулы, м |
| t | температура, °C |
| V | объем, м3 |
| α | коэффициент теплоотдачи, Вт/(м2 К); угол, град |
| β | фактор формы |
| ∆ | приращение физической величины |
| δ | толщина (линейный размер), м |
| δст | толщина стенки кристаллизатора |
| εv = Vn/V | коэффициент объемной пористости |
| η | степень превращения |
| λ | коэффициент теплопроводности, Вт/(м К) |
| с | теплоемкость, Дж/кг |
| ξ | координата подвижной межфазной границы, м |
| ρ | плотность, кг/м3 |
| σ | поверхностное натяжение, Дж/м2 |
| τ | время, с |
| υΛ | линейная скорость роста центров превращения, м/с |
| ωз | скорость зародышеобразования, [м3 × с]–1 |
| ∇ | дифференциальный оператор Гамильтона |
| $ \vee $ | или |
| $ \wedge $ | и |
ИНДЕКСЫ
| А2 | аммиачная селитра + 0.35% заводской магнезиальной добавки |
| г | газовая фаза |
| ж | жидкость (расплав) |
| з | зарождение |
| инд | индукционный |
| к | кристаллическая фаза, конечное значение параметра |
| кр | кристаллизация |
| н | начальное значение параметра |
| п | порошок, полость |
| пр | распределенная пористость |
| ПЗ | переходная зона |
| П1 | полиуретан на основе гексаметилендиизоцианата и триэтиленгликоля |
| П2 | полиуретан на основе гексаметилендиизоцианата и диэтиленгликоля |
| П3 | полиуретан на основе гексаметилендиизоцианата и тетраэтиленгликоля |
| с | среда, охлаждающая (нагревающая) среда |
| ст | стенка |
| э | эффективный |
| n | нормаль |
Список литературы
Taran A.L., Nosov G.A. Formal analogy between the granulation kinetics of fine powders and the phase-transition kinetics // Theor. Found. Chem. Eng. 2001.V. 35. № 5. Р. 494. [Таран А.Л., Носов Г.А. Формальная аналогия кинетики гранулообразования в мелкодисперсных материалах и фазового превращения // Теорет. основы хим. технологии. 2001. Т. 35. № 5. С. 523.]
Таран Ю.А., Таран А.В. Под общей редакцией Тарана А.Л. Теория и практика изучения кинетики фазовых и формально аналогичных им превращений. Монография. М.: Московский технологический университет (МИРЭА), 2016. 246 c. ISBN 978-5-600-01695-8.
Таран А.Л., Теория и практика процессов гранулирования расплавов и порошков. Дис. … докт. техн. наук. М.: МИТХТ, 2001.
Зельдович Я.Б. Избранные труды. Химическая физика и гидродинамика. М.: Наука, 1984.
Любов Б.Я. Теория кристаллизации в больших объемах. М.: Наука, 1975.
Румер Ю.Б., Рывкин М.Ш. Термодинамика, статистическая физика и кинетика. М.: Наука,1977.
Чернов А.А. Процессы кристаллизации // Современная кристаллография. М.: Наука, 1980, т. 3, С. 3.
Горелик А.Г., Амитин А.В. Десублимация в химической промышленности. М.: Химия, 1986.
Дильман В.В., Полянин А.Д. Методы модельных уравнений и аналогий в химической технологии. М.: Химия, 1988.
Taran A.L., Nosov G.A., Kholin A.YU., Myasnikov S.K. Kinetics of crystallization of binary melts of eutectic-forming substances theoretical foundations of chemical engineering // Theor. Found. Chem. Eng. 2004. V. 38. № 2. Р. 164. [Таран А.Л., Носов Г.А., Холин А.Ю., Мясников С.К. Кинетика кристаллизации бинарных расплавов эвтектикообразующих веществ // Теорет. основы хим. технологии. 2004. Т. 38. № 2. С. 176.]
Pokusaev B.G., Karlov S.P., Vyaz’min A.V., Nekrasov D.A. Laws of the Formation and Diffusion Properties of Silica and Agarose Gels // Theor. Found. Chem. Eng. 2018. V. 52, № 2. P. 222. [Покусаев Б.Г., Карлов С.П., Вязьмин А.В., Некрасов Д.А. Закономерности формирования и диффузионные свойства силикатных и агарозных гелей // Теорет. основы хим. технологии. 2018. Т. 52. № 2. С. 200.]
Taran A.L. Experimental determination of the nucleation and growth rates of first-order phase transition centers // Theor. Found. Chem. Eng. 2004. V. 38. № 5. Р. 530. [Таран А.Л. Методика экспериментального определения скоростей и зарождения и роста центров фазовых превращений первого рода // Теорет. основы хим. технологии. 2004. Т. 38. № 5. С. 561.].
Борисов В.Т. Теория двухфазной зоны металлического слитка. М.: Металлургия, 1987.
Соболев В.В. О механизмах формирования структуры при быстрой кристаллизации // Изв. АНСССР. Металлы.1986. №1. С.79.
Liu B., Wang Y., Sun H. Macroscopic kinetics of melt crystallization of ammonium nitrate // J. Cryst. Growth. 2018. Vol. 509. № 1. P. 29.
Горловский Д.М., Альтшулер Л.Н., Кучерявый В.И. Технология карбамида. Л.: Химия, 1981.
Производство аммиачной селитры в агрегатах большой единичной мощности / Под ред. Олевского В.М., М.: Химия, 1990.
Казакова Е.А. Гранулирование и охлаждение азотсодержащих удобрений. М.: Химия, 1980.
Неппер Д. Стабилизация коллоидных дисперсий полимерами. М.: Мир, 1986.
Таран Ю.А., Козлов А.В., Таран А.Л. Влияние образования отложений в порах фильтровальной перегородки на процесс фильтрации // Тонкие химические технологии. 2019. Т. 14. №2. С. 15.
Морозов Р.В. Разработки в технологии гранулирования аммиачной селитры методом “fattening”. Дисс… канд. техн. наук. М.: МИРЭА, 2019.
Колмогоров А.Н. Избранные труды. Математика и механика. М.: Наука, 1985.
Баландин Г.Ф. Основы теории формирования отливки. М.: Машиностроение, Ч1, 1976, Ч2, 1979.
Polyanin A.D., Vyazmin A.V. Differential-difference heat-conduction and diffusion models and equations with a finite relaxation time // Theor. Found. Chem. Eng. 2013. V. 47, № 3. P. 217. [Вязьмин А.В., Полянин А.Д. Дифференциально-разностные модели и уравнения теплопроводности и диффузии с конечным временем релаксации. Теор. основы хим. технол. 2013. Т. 47. № 3. С. 271–278.]
Иванова Т. Б., Васькин В.В. Обобщённая модель кинетики образования новой фазы // Вестник Удмуртск. Ун-та. Матем. Мех. Компьют. Науки. 2009. Вып. 2. С. 110.
Асеев Д.Л., Александров Д.В. Нелинейная динамика затвердевания бинарного расплава с неравновесной двухфазной зоной. ДАН. 2006. Т.408. № 5. С. 609.
Коверда В.П., Скрипов В.П. Метастабильное состояние и фазовый переход жидкость – кристалл в дисперсных системах // Изв. АНСССР. Расплавы. 1987. Т.1. Вып. 4. С. 3.
Олемский А.И. Фрактальная кинетика перестройки кристаллической структуры // Физика металлов и металловедение. 1989. Т. 68. № 1. С. 56.
Соболев В.В. Условия формирования дендритной структуры при затвердевании расплавов // Изв. АНСССР. Металлы. 1987. №3. С. 76.
Рубинштейн Л.И. Проблема Стефана. Рига: Зинатне, 1967.
Самарский А.А. Теория разностных схем. М.: Наука, 1983.
Мареев В.В., Станкова Е.Н. Основы методов конечных разностей // Изд-во С.-Петерб. ун-та, 2012. С. 64.
Таран А.Л., Долгалёв Е.В., Таран Ю.А. Решение многомерных задач с фазовыми превращениями на локально-одномерном разностном аналоге // Сб. тр. ХХ Международной научной конференции “Математические методы в технике и технологиях ММТТ-20”, Ярославль, 2007. С. 150.
Протодьяконов И.О., Марцулевич Н.А., Марков А.В. Явления переноса в химической технологии. Л.: Химия, 1981.
Нигматулин Р.И. Динамика многофазных сред. Ч.1. М.: Наука, 1987.
Кидяров Б.И. Кинетика образования кристаллов из жидкой фазы. Новосибирск: Наука, 1979.
Маковская Ю.В. Моделирование процесса инкапсуляции в псевдоожиженном слое и прогнозирование качества покрытий. Дисс. … канд. техн. наук. М.: РХТУ им. Д.И. Менделеева, 2011.
Devassine M., Henry F., Guerin P., Briand X. Coating of fertilizers by degradable polymers // International Journal of Pharmaceutics. 2002. № 242. P. 399.
Годовский Ю.К. Теплофизика полимеров. М.: Химия, 1982.
Нанонаука и нанотехнологии. Энциклопедия систем жизнеобеспечения / Гл. соред. О. О. Аваделькарим и др. М.: ИД Магистр-пресс и др., 2009.
Таран Ю.А., Таран А.Л. Аппаратурно-технологическое оформление реконструкции существующих производств гранулированных продуктов с целью повышения их качественных показателей // ХНГМ. 2015. № 9. С. 3.
Таран Ю.А., Соловьев А.А., Калинин С.А. Установка для оптических методов изучения кинетики кристаллизации и формально аналогичных превращений // Химическая технология. 2019. Т. 20. № 6. С. 276.
Миркин И.Л. Аналитическое исследование процесса кристаллизации // Проблемы теоретического металловедения. Труды Моск. института стали. 1938. Вып. 10. С. 3.
Черепанова Т.А. Общий подход к моделированию роста кристаллов на ЭВМ методом Монте-Карло // Рост кристаллов. Минск: АНБССР, 1980. С. 143.
Кояло И.Э. Расчет общей задачи кристаллизации с учетом зарождения и динамики роста кристаллов в объеме переохлажденного расплава // Уч. записки Латв. гос. университета. 1975. С. 68.
Богданов Н.М., Коверда В.П., Скоков В.Н., Дик А.А., Скрипов В.П. Спонтанная взрывная кристаллизация ультрадисперсных порошков аморфного германия // ДАН СССР. 1987. Т. 293. Вып. 3. С. 595.
Кудинов В.А., Карташов Э.М., Калашников В.В. Аналитические решения задач тепломассопереноса и термоупругости для многослойных конструкций. М.: Высшая школа, 2005.
Абашева Э.Р. Исследование и моделирование процессов кристаллизации с применением клеточных автоматов. Дис. … канд. техн. наук. М.: РХТУ им. Д.И. Менделеева, 2007.
Bandman O. Cellular-neural automaton: a hybrid model for reaction-diffusion simulation // FGCS. 2000. V. 18. P. 737.
Кольцова Э.М., Третьяков Ю.Д., Гордеев Л.С., Вергетел А.А. Нелинейная динамика и термодинамика необратимых процессов в химии и химической технологии. М.: Химия, 2001.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии