Теоретические основы химической технологии, 2020, T. 54, № 4, стр. 409-420

Повышение эффективности коагуляции субмикронных частиц при ультразвуковом воздействии

В. Н. Хмелёв^a, А. В. Шалунов^a, Р. Н. Голых^a, *

^a Бийский технологический институт (филиал) Алтайского государственного технического университета им. И.И. Ползунова
Бийск, Россия

^* E-mail: grn@bti.secna.ru

Поступила в редакцию 02.11.2019
После доработки 20.12.2019
Принята к публикации 13.01.2020

DOI: 10.31857/S0040357120030069

Полный текст (PDF)

Аннотация

Представлены результаты исследований процесса коагуляции субмикронных частиц (размером менее 1–2.5 мкм) при различных условиях ультразвукового воздействия с целью выявления возможности повышения эффективности коагуляции. Анализ особенностей процесса коагуляции как при синусоидальном воздействии, так и при ударно-волновом (импульсном) воздействии позволил установить, что ударно-волновое воздействие обеспечивает до 20 раз более высокую скорость коагуляции субмикронных частиц по сравнению с синусоидальным воздействием при одинаковой суммарной энергии воздействия. Показано, что причиной ускорения процесса являются нелинейные эффекты, возникающие при ударно-волновом воздействии и влияющие на скорость коагуляции частиц (изменение площади сечения столкновения, локальное уплотнение среды, взаимная диффузия газа, окружающего частицу, при переходном режиме обтекания между свободномолекулярным и сплошным).

Ключевые слова: ультразвук, ударная волна, коагуляция, субмикронные частицы, скорость, уравнение Смолуховского, нелинейные эффекты

ВВЕДЕНИЕ

Аэрозоли, формирующиеся в атмосфере за счет антропогенного воздействия человека, техногенных аварий, террористических актов, а также естественных процессов, являются глобальной проблемой. Человечество вынуждено непрерывно бороться с туманами, смогом, пылью, аэрозолями вредных, ядовитых и радиоактивных веществ [1–4].

Наибольшую опасность представляют аэрозоли тонкодисперсных частиц (размером менее 1–2.5 мкм). Такие частицы имеют высокие суммарную поверхность (более 55% от суммарной поверхности частиц, выбрасываемых в атмосферу) и счетную концентрацию (более 95% от суммарной счетной концентрации даже при незначительной массовой доле (менее 1% от суммарной доли аэрозолей, содержащихся в атмосфере).

Благодаря малым размерам и массе такие аэрозоли могут длительное время удерживаться в воздухе и способны легко проникать в альвеолы легких человека, вызывая необратимые изменения организма.

На сегодняшний день одним из наиболее эффективных способов улавливания аэрозольных частиц, движущихся через газоходы и проникающих в атмосферу, является предварительное объединение частиц в агломераты (коагуляция) под действием синусоидальных ультразвуковых колебаний высокой интенсивности для дальнейшего улавливания укрупненных частиц традиционными методами (инерционное или гравитационное осаждение, фильтрация сквозь пористый материал и т.д.).

На сегодняшний день эффективность ультразвуковой коагуляции многократно доказана для частиц размером более 2.5 мкм. Многими авторами указываются режимы коагуляции [2–5], при которых достигается наибольшая степень укрупнения, и предлагается специальное оборудование [3–11], позволяющее коагулировать частицы, как на открытом пространстве, так и в замкнутом объеме. При этом ультразвуковые излучатели устанавливаются в технологические камеры газоочистных аппаратов и повышают их эффективность без изменения конструкций.

Однако существующее оборудование оказывается недостаточно эффективным для коагуляции частиц размером менее 2.5 мкм и особенно менее 1 мкм. Это обусловлено особенностью синусоидального ультразвукового воздействия, при котором происходит вовлечение субмикронных частиц в колебательное движение в пределах областей между зонами с минимумами колебательной скорости [5, 7, 12] и практически полным отсутствием их соударений в пределах этих областей. При таком воздействии площадь сечения столкновения частиц размером 1 мкм в 100 раз меньше, чем для частиц 20 мкм [13–15].

Необходимость решения проблемы требует исследования процесса взаимодействия субмикронных частиц при различных условиях ультразвукового воздействия для выявления новых нелинейных эффектов, способных увеличить вероятности коагуляции таких частиц.

ПОСТАНОВКА ЗАЛАЧИ ИССЛЕДОВАНИЙ

Ввиду сложности экспериментального исследования [16] путем обеспечения различных условий ультразвукового воздействия целесообразно проведение теоретического анализа процесса коагуляции субмикронных частиц.

В качестве действующего фактора коагуляции следует рассмотреть воздействие не только в синусоидальном режиме, но и воздействие с измененным профилем акустического возмущения, когда энергия возмущения не равномерно распределена во времени, а сконцентрирована в узкой временной области, малой по сравнению с периодом возмущений. Это воздействие является воздействием в ударно-волновом режиме. Целесообразность такого воздействия обусловлена наличием экспериментальных данных [17, 18], свидетельствующих о возможном ускорении коагуляции аэрозолей, хотя и полученных при воздействии в звуковом диапазоне (период акустических возмущений более 1/20 000 с).

Поскольку на практике создать ударные волны сжатия или разряжения при отсутствии сопутствующих периодов разрежения или сжатия невозможно, следует рассмотреть случаи воздействия при различных соотношениях между длительностями фазы разрежения (${{\tau }_{d}}$) и следующей за ней фазой сжатия (${{\tau }_{с}}$) $\frac{{{{\tau }_{d}}}}{{{{\tau }_{c}}}},$ включая предельные соотношения – 0 (волна сжатия имеет нулевую амплитуду) или +∞ (волна разрежения имеет нулевую амплитуду).

Конечная цель исследований заключается в выявлении эффективных условий воздействия, обеспечивающих коагуляцию различных частиц и выявлении зависимостей скорости коагуляции от влияющих факторов, определяемых согласно следующему выражению:

(1)

$\begin{gathered} \frac{1}{{{{D}_{{30}}}}}\frac{{\partial {{D}_{{30}}}}}{{\partial t}} = \frac{\partial }{{\partial t}}\left( {\ln {{D}_{{30}}}} \right) = \\ = \frac{\partial }{{\partial t}}\left( {\ln \sqrt[3]{{\frac{{\sum\limits_{i = 1}^\infty {\left\langle {{{n}_{i}}{{D}_{i}}^{3}} \right\rangle } }}{{\sum\limits_{i = 1}^\infty {\left\langle {{{n}_{i}}} \right\rangle } }}}}} \right) = - \frac{{\frac{\partial }{{\partial t}}\left( {\sum\limits_{i = 1}^\infty {\left\langle {{{n}_{i}}} \right\rangle } } \right)}}{{3\sum\limits_{i = 1}^\infty {\left\langle {{{n}_{i}}} \right\rangle } }}, \\ \end{gathered} $

где D₃₀ – среднеобъемный диаметр частиц, м; n_i – счетная концентрация частиц размером D_i, м^–3; знак “〈 〉” означает усреднение концентрации частиц по длине ультразвукового возмущения.

Для исследования процесса коагуляции субмикронных частиц целесообразно применять вероятностный подход, предложенный Смолуховским [19], максимально развитый на сегодняшний день в [7, 12], подтвержденный экспериментально [9, 10, 13] и позволяющий исследовать эволюцию частиц при заданной вероятности столкновения частиц, описываемую уравнением

(2)

$\begin{gathered} \frac{{\partial {{n}_{k}}}}{{\partial t}}({\mathbf{r}},t) + \left( {{{{\mathbf{u}}}_{k}},\nabla } \right){{n}_{k}}({\mathbf{r}},t) = \\ = \frac{1}{2}\sum\limits_{i = 1}^{k - 1} {{{\beta }_{{i,k - i}}}{{n}_{i}}({\mathbf{r}},t){{n}_{{k - i}}}({\mathbf{r}},t) - {{n}_{k}}({\mathbf{r}},t)} \sum\limits_{i = 1}^N {{{\beta }_{{i,k}}}{{n}_{i}}({\mathbf{r}},t)} , \\ \end{gathered} $

где n_k – концентрация частиц с условным диаметром ${{d}_{0}}\sqrt[3]{k},$ м^–3; u_k – усредненная скорость движения частиц диаметром ${{d}_{0}}\sqrt[3]{k};$ ${{\beta }_{{i,k}}}$ – вероятность столкновения частиц с диаметрами ${{d}_{0}}\sqrt[3]{i}$ и ${{d}_{0}}\sqrt[3]{k},$ м³/с.

Для определения вероятности парного столкновения субмикронных частиц при ультразвуковом воздействии необходимо рассматривать газовую фазу изотропной [14, 15], а характерное время теплопереноса больше времени изменения возмущения давления, т.е. считать процесс адиабатическим.

Диапазон выбранных интенсивностей ультразвукового воздействия обусловлен ограничениями, связанными с волновым сопротивлением газа, и особенностями ультразвуковых излучателей, для которых средний уровень давления в дальнем поле не превышает 150 дБ, а в фокусе 160 дБ [3, 6, 9]. При этом формируются импульсы длительностью от 2 мкс (такова минимальная длительность импульса, реализуемая в имеющихся устройствах) при усредненных за период интенсивностях до 0.06 Вт/см² (среднеквадратичное значение ультразвукового давления не превышает 500 Па, максимальное мгновенное возмущение не более 5000 Па).

При длительности скачка уплотнения более 2 мкс сила, которую необходимо приложить для ускорения газового потока, составит

$\begin{gathered} {{f}_{{V\max }}}\sim \frac{{{{p}_{A}}}}{{\rho c\tau }}\sim \frac{{{{p}_{{RMS}}}}}{{\rho c\tau }}\sqrt {\frac{T}{\tau }} = \frac{{{{p}_{{RMS}}}}}{{\rho c\tau }}\sqrt {\frac{1}{{\tau f}}} = \\ = \frac{{{\text{500}}\,\,{\text{Па}}}}{{1.22\,\,\frac{{{\text{кг}}}}{{{{{\text{м}}}^{{\text{3}}}}}} \times 343\,\,\frac{{\text{м}}}{{\text{с}}}}}\sqrt {\frac{1}{{{{\tau }^{3}} \times 22000\,\,{{{\text{с}}}^{{ - 1}}}}}} < \\ < 3\frac{{МН}}{{{{{\text{м}}}^{{\text{3}}}}}} = 3\,\,\frac{{{\text{кН}}}}{{{\text{д}}{{{\text{м}}}^{{\text{3}}}}}}. \\ \end{gathered} $

При исследовании ультразвуковой коагуляции рассматривался монодисперсный и полидисперсный аэрозоль с заданной исходной счетной концентрацией, размером частиц 0.1–0.5 мкм, обычно не улавливаемый известными устройствами.

Очевидно, что при ультразвуковой коагуляции таких частиц необходимо учитывать изменение площади сечения столкновения за счет движения молекул газовой фазы, а также изменение концентрации частиц при больших изменениях давления газовой фазы за счет инерционности частиц и взаимную диффузию молекул газа на длине свободного пробега.

Далее представлена методология и результаты исследований по определению скорости коагуляции частиц в зависимости от условий ультразвукового воздействия, свойств и характеристик этих дисперсных частиц.

МЕТОДОЛОГИЯ ИССЛЕДОВАНИЙ ВЛИЯНИЯ УЛЬТРАЗВУКОВОГО ВОЗДЕЙСТВИЯ НА СКОРОСТЬ КОАГУЛЯЦИИ ЧАСТИЦ

Как следует из уравнения (2), скорость коагуляции частиц определяется их концентрацией и изменяется при ультразвуковом воздействии за счет столкновений, вероятность которых определяется площадью эквивалентного сечения столкновения и силами взаимодействия частиц:

(3)

$\frac{1}{{{{D}_{{30}}}}}\frac{{\partial {{D}_{{30}}}}}{{\partial t}} = - \frac{{\frac{\partial }{{\partial t}}\left( {\sum\limits_{i = 1}^\infty {\left\langle {{{n}_{i}}} \right\rangle } } \right)}}{{3\sum\limits_{i = 1}^\infty {\left\langle {{{n}_{i}}} \right\rangle } }} = \frac{{\left\langle {{{\beta }_{{1.1}}}n} \right\rangle }}{6};\,\,\,\,n = \frac{N}{V},$

где 〈 〉 – знак усреднения за период изменения давления; V – выделенный объем облака, размеры которого малы по сравнению с протяженностью воздействия, но велики по сравнению с расстоянием между частицами, м³; N – количество частиц в выделенном объеме V; n – исходная счетная концентрация частиц, м^–3; ${{\beta }_{{1.1}}}$ – вероятность столкновения частиц, м³/с.

Скорость коагуляции характеризует увеличение среднего объемного диаметра частиц в единицу времени.

Вероятность столкновения частиц определяется выражением [7]

(4)

$\beta [p]\left( t \right) = {{\beta }_{{\text{H}}}}[p]\left( t \right) + {{\beta }_{{\text{O}}}}[p]\left( t \right),$

где ${{\beta }_{{\text{H}}}}[p]\left( t \right)$ – компонента гидродинамического взаимодействия, м³/с; ${{\beta }_{{\text{O}}}}[p]\left( t \right)$ – компонента ортокинетического взаимодействия, м³/с.

Компоненты вероятности столкновения определяются согласно выражениям

(5)

${{\beta }_{H}}[p] = \frac{1}{T}\int\limits_0^T {\int\limits_\Omega {\frac{{{{f}_{{21}}}[p]\left( {t,{\mathbf{n}}} \right)}}{{12{{\pi }^{2}}\mu d}}S[p]\left( t \right)d\Omega \left( {\mathbf{n}} \right)} dt} ;$

(6)

$S[p]\left( t \right) = \pi {{\left( {d + \sqrt {{{\sigma }_{r}}} \left[ p \right]\left( t \right)} \right)}^{2}};$

(7)

${{\beta }_{O}}[p] = \frac{1}{T}\int\limits_0^T {\left| {\frac{{p{\kern 1pt} '\left( {t + cl} \right)}}{{{{\rho }_{0}}c}} - \frac{{p{\kern 1pt} '\left( t \right)}}{{{{\rho }_{0}}c}}} \right|S[p]\left( t \right)dt} ,$

где ${{f}_{{21}}}[p]\left( {t,{\mathbf{n}}} \right)$ – сила взаимодействия частиц, Н; $S[p]\left( t \right)$ – площадь сечения столкновения, м²; n – единичный вектор, обозначающий направление линии центров частиц, относительно волнового вектора ультразвукового поля; ${{\sigma }_{r}}$ – дисперсия (квадрат неопределенности) пространственного положения частицы, м; l – расстояние между частицами, м; c – скорость распространения ультразвуковых колебаний в несущей газовой фазе.

Из сравнения двух компонент следует, что ${{\beta }_{{\text{O}}}}[p]\left( t \right) \ll {{\beta }_{{\text{H}}}}[p]\left( t \right),$ т.е. гидродинамическое взаимодействие является определяющим. Ортокинетическое взаимодействие незначительно, поскольку каждая частица вне зависимости от размера в равной степени вовлекается в колебательное движение.

Вероятность гидродинамического взаимодействия пропорциональна площади сечения столкновения. Согласно имеющимся данным [20, 21], площадь сечения столкновения субмикронных частиц изменяется за счет влияния броуновского движения. При учете броуновского движения площадь сечения столкновения увеличивается за счет дисперсии σ_r пространственного положения частицы:

(8)

$S[p]\left( t \right) = \pi {{\left( {d + \sqrt {{{\sigma }_{r}}} \left[ p \right]\left( t \right)} \right)}^{2}}.$

Очевидно, что соударения движущихся молекул газовой фазы с частицами (рис. 1) приводят к изменению площади сечения столкновения согласно выражению (8) и схеме на рис. 2.

Рис. 1.

Схематичное изображение процесса соударения молекул газовой фазы с субмикронной частицей и изменения скорости частицы в результате элементарного акта соударения (v – случайная скорость движения молекул газовой фазы; u – случайная составляющая скорости движения частицы, обусловленная тепловым соударением молекул газовой фазы с частицей; U – детерминированная составляющая скорости движения, вызванная увлечением частицы в колебательное движение газового потока.)

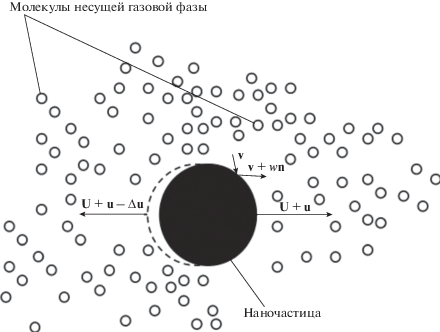
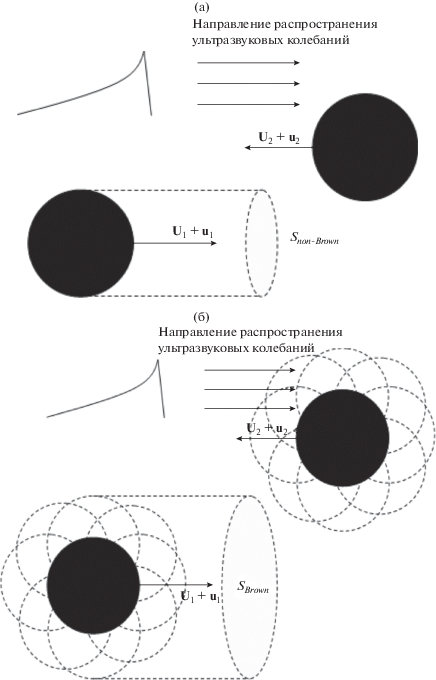
Рис. 2.

Влияние броуновского движения на площадь сечения столкновения: (а) – площадь сечения столкновения без учета броуновского движения; (б) площадь сечения столкновения с учетом броуновского движения

Дисперсия положения частицы определяется методом Монте-Карло с учетом случайной генерации времен соударения молекулы с частицей, скоростей молекулы в момент соударения и положений точки поверхности частицы, в которой происходит соударение молекулы с ней.

Генерация перечисленных параметров происходит с учетом следующих предположений:

– скорость частицы после соударения молекулы с ней определяется законом сохранения импульса;

– соударения являются абсолютно упругими;

– соударения равновероятны во всех возможных направлениях, поскольку наиболее вероятная скорость произвольно выбранной молекулы газа многократно превышает скорость движения частицы, поскольку масса отдельной частицы много больше массы отдельной молекулы газа.

Пространственное положение частицы в результате последовательности элементарных актов соударения частица–молекула газовой фазы определяется согласно следующему выражению:

${{{\mathbf{r}}}_{{i + 1}}} = {{{\mathbf{r}}}_{i}} + {{{\mathbf{u}}}_{i}}\left( {{{t}_{{i + 1}}} - {{t}_{i}}} \right),$

где t_i – момент времени возникновения i-го элементарного акта соударения молекулы с частицей, c; u_i – скорость частицы в результате i-го элементарного акта соударения с молекулой, м/с; r_i – вектор координат частицы в момент возникновения i-го элементарного акта соударения, м.

Скорость частицы в результате i-го элементарного акта соударения определяется согласно закону сохранения импульса:

${\mathbf{v}} - {\mathbf{u}} \to {\mathbf{v}} - {\mathbf{u}} + w{\mathbf{n}}$ – изменение скорости соударяющейся молекулы в системе отсчета центра масс частицы;

${\mathbf{v}} \to {\mathbf{v}} + w{\mathbf{n}}$ – изменение скорости соударяющейся молекулы в лабораторной системе отсчета;

$m(v + wn) + M{{u}_{{{\text{new}}}}} = mv + Mu$ – закон сохранения импульса для системы частица–соударяющаяся молекула;

${{{\mathbf{u}}}_{{{\text{new}}}}} = {\mathbf{u}} - \frac{m}{M}w{\mathbf{n}}$ – общее выражение для изменения скорости частицы в результате i-го элементарного акта соударения.

Неизвестная величина $w$ определяется из закона сохранения энергии

$\begin{gathered} \frac{{M{{{\left( {{\mathbf{u}} - \frac{m}{M}w{\mathbf{n}}} \right)}}^{2}}}}{2} + \frac{{m{{{\left( {{\mathbf{v}} + w{\mathbf{n}}} \right)}}^{2}}}}{2} = \frac{{M{{{\mathbf{u}}}^{2}}}}{2} + \frac{{m{{{\mathbf{v}}}^{2}}}}{2}; \\ {{{\mathbf{u}}}_{{i + 1}}} = {{{\mathbf{u}}}_{i}} + \frac{{2\frac{m}{M}}}{{1 + \frac{m}{M}}}\left( {{{{\mathbf{v}}}_{i}} - {{{\mathbf{u}}}_{i}},{{{\mathbf{n}}}_{i}}} \right){{{\mathbf{n}}}_{i}}, \\ \end{gathered} $

где M – масса частицы, кг; m – масса молекулы газовой фазы, кг.

При генерации времен, скоростей соударения молекулы с частицей, положений точки поверхности, в которой возникает соударение, предполагается, что функция распределения скоростей при произвольном выборе молекулы подчиняется закону Максвелла:

$f\left( {{{{\mathbf{u}}}_{i}},{\mathbf{n}},{{{v}}_{n}}} \right)d{{{v}}_{n}} = \sqrt {\frac{\rho }{{2\pi p}}} {{e}^{{ - \frac{{\rho {{{\left| {{\mathbf{v}} - {\mathbf{u}}} \right|}}^{2}}}}{{2p}}}}}.$

Генерация скоростей, времен и положений точки поверхности, в которой возникает соударение, происходит до тех пор, пока не будут равны функции распределения положений отдельной частицы в результате следующего и предыдущего элементарных актов соударений:

(9)

${{F}_{{i + 1}}}\left( {\mathbf{r}} \right) = {{F}_{i}}\left( {\mathbf{r}} \right) = F\left( {\mathbf{r}} \right).$

Проведенные предварительные расчеты показали, что время, достаточное для реализации условия (9), много меньше характерного времени изменения давления. Это позволяет при определении мгновенного эффективного сечения столкновения частиц считать давление постоянным.

Изложенный подход позволил установить зависимости эффективного сечения столкновения от амплитуды колебаний для различных ультразвуковых воздействий:

1. Непрерывного синусоидального

$p{\kern 1pt} '\left( t \right) = {{p}_{A}}\sin \left( {2\pi \frac{t}{T}} \right).$

2. Ударно-волнового (импульсного)

$p{\kern 1pt} '\left( t \right) = {{p}_{A}}{{e}^{{ - \frac{{t - \left\lfloor {\frac{t}{T}} \right\rfloor T}}{\tau }}}},$ которое можно условно разделить на импульсы сжатия при ${{p}_{A}} > 0$ и импульсы разрежения при ${{p}_{A}} < 0,$ где T – период акустических возмущений, с; p_A – амплитуда ультразвуковых возмущений, Па; τ – характерная длительность импульса, с.

В частности, для непрерывного синусоидального $p{\kern 1pt} '\left( t \right)$ = ${{p}_{A}}\sin \left( {2\pi \frac{t}{T}} \right)$ воздействия эффективное сечение столкновения изменяется незначительно (увеличение менее чем на 10%). Для импульсного ударно-волнового воздействия $p{\kern 1pt} '\left( t \right)$ = ${{p}_{A}}{{e}^{{ - \frac{{t - \left\lfloor {\frac{t}{T}} \right\rfloor T}}{\tau }}}},$ при формировании преимущественной фазы сжатия ${{p}_{A}} > 0$ изменение площади столкновения даже для самых мелких частиц (100–200 мкм) не превышает 35–40%, и только при формировании преимущественной фазы разряжения в ультразвуковом воздействии $\left( {{{p}_{A}} < 0} \right)$ площадь столкновения возрастает до 2 раз при энергиях, обеспечиваемых современными излучателями [3, 4].

Полученные данные о величине площади столкновения позволили перейти к исследованию процесса гидродинамического взаимодействия, которое, согласно [5], определяется радиационным давлением ультразвукового воздействия, отраженного от соседней частицы:

(10)

${{f}_{{21}}} = \int\limits_S {\left( { - p + \rho {\mathbf{u}}\left( {{\mathbf{u}},{\mathbf{n}}} \right)} \right){\mathbf{n}}dS} ,$

где f₂₁ – сила взаимодействия между частицами, Н; p – возмущение давления газа вблизи частицы, создаваемое соседней частицей, Па; u – возмущение скорости газа вблизи частицы, создаваемое соседней частицей, м; n – вектор нормали к поверхности частицы.

Поскольку рассматриваемые частицы являются субмикронными, а расстояние между ними сопоставимо с длиной свободного пробега молекул газовой фазы, для расчета поля отраженных ультразвуковых воздействий было применены квазигазодинамические уравнения, учитывающие взаимную диффузию газовой фазы и неравновесность протекания процесса изменения давления в газовой фазе [22]:

(11)

$div\left( {{{{\mathbf{j}}}_{m}} \otimes {\mathbf{u}}} \right) + \nabla p = div\Pi ;$

(12)

$div\left( {{{{\mathbf{j}}}_{m}}} \right) = 0;$

(13)

${{{\mathbf{j}}}_{m}} = \rho {\mathbf{u}} - \tau \left( {div\left( {\rho {\mathbf{u}} \otimes {\mathbf{u}}} \right) + \nabla p} \right);$

(14)

$\begin{gathered} \Pi = \tau {\mathbf{u}} \otimes \left[ {\rho \left( {{\mathbf{u}},\nabla } \right){\mathbf{u}} + \nabla p} \right] + \\ + \,\,\tau I\left[ {\left( {{\mathbf{u}},\nabla } \right)p + \gamma pdiv{\mathbf{u}}} \right], \\ \end{gathered} $

где j_m – плотность потока массы газовой фазы, кг/(м² с); u – скорость движения молекул газовой фазы, м/с; ρ – плотность газовой фазы, кг/м³; τ – время релаксации, необходимое для перехода газовой фазы в равновесное состояние, c; Π – тензор напряжений в газовой фазе, Па.

Решение представленной системы уравнений позволило определить поля возмущений давления и скорости газа вокруг отдельной частицы при заданном ультразвуковом воздействии (синусоидальном или с преимущественными фазами сжатия или разряжения) и произвести расчет силы радиационного давления на соседнюю частицу со стороны найденных полей возмущений.

Поскольку процесс распространения ультразвукового воздействия является адиабатическим, система уравнений (11)–(14) преобразуется:

(15)

$div\left( {{{{\mathbf{j}}}_{m}} \otimes {\mathbf{u}}} \right) + \nabla p = div\Pi ;$

(16)

$div\left( {{{{\mathbf{j}}}_{m}}} \right) = 0;$

(17)

$\begin{gathered} {{{\mathbf{j}}}_{m}} = {{\rho }_{{rel}}}{{\left( {\frac{p}{{{{p}_{{rel}}}}}} \right)}^{{\frac{1}{\gamma }}}}\nabla \varphi - {{\tau }_{{rel}}}\frac{\tau }{{{{\tau }_{{rel}}}}} \times \\ \times \,\,\left( {div\left( {{{\rho }_{{rel}}}{{{\left( {\frac{p}{{{{p}_{{rel}}}}}} \right)}}^{{\frac{1}{\gamma }}}}\nabla \varphi \otimes \nabla \varphi } \right) + \nabla p} \right); \\ \end{gathered} $

(18)

$\begin{gathered} \Pi = \tau {\mathbf{u}} \otimes \left[ {{{\rho }_{{rel}}}{{{\left( {\frac{p}{{{{p}_{{rel}}}}}} \right)}}^{{\frac{1}{\gamma }}}}\left( {{\mathbf{u}},\nabla } \right){\mathbf{u}} + \nabla p} \right] + \\ + \,\,\tau I\left[ {\left( {{\mathbf{u}},\nabla } \right)p + \gamma pdiv{\mathbf{u}}} \right]. \\ \end{gathered} $

Далее система дополняется граничным условием на поверхности частицы (19), от которой происходит отражение, и условиями (20), (21) на расстоянии, превосходящем расстояния между соседними частицами:

(19)

${\mathbf{u}} = 0;$

(20)

$p = {{p}_{{rel}}} + {{P}_{A}}\left( t \right);$

(21)

${\mathbf{u}} = \frac{{\mathbf{k}}}{k}\frac{{{{P}_{A}}\left( t \right)}}{{\rho c}},$

где ${{p}_{{rel}}}$ – статическое давление в газе в отсутствие ультразвуковых возмущений, Па; P_A – давление ультразвукового воздействия, Па; k – волновой вектор поля, м^–1.

Распределение возмущений давления вблизи частицы сферической формы будет состоять из трех составляющих:

$p = {{p}_{{rel}}} + {{P}_{A}}\left( t \right) + {{p}_{{refl}}},$

где ${{p}_{{refl}}}$ – давление в ультразвуковых воздействиях, отраженных от частицы, Па.

Поскольку размеры частиц много меньше длины ультразвукового воздействия, вклад в радиационное давление на поверхность соседней частицы будет вносить давление ${{p}_{{refl}}},$ так как остальные составляющие гораздо слабее зависят от координаты и интеграл по составляющим ${{P}_{A}}$ и ${{p}_{{rel}}}$ равен нулю.

В реальных газодисперсных системах расстояние между частицами превышает длину свободного пробега молекул газа (70 нм) и определение полей возмущений скорости и давления основано на асимптотическом разложении по степеням времени релаксации газа $\tau $ (времени, необходимого для перехода в равновесное состояние и принятия микроскопических параметров ансамбля молекул, соответствующих параметрам газа) и амплитуде внешнего ультразвукового воздействия:

$\begin{gathered} {\mathbf{u}} = \sum\limits_{n = 0}^\infty {{{{\mathbf{u}}}_{n}}\frac{{{{\tau }^{n}}}}{{\tau _{{rel}}^{n}}}} = \sum\limits_{n,m = 0}^\infty {{{{\mathbf{u}}}_{{n,m}}}\frac{{{{\tau }^{n}}{{U}^{m}}}}{{\tau _{{rel}}^{n}{{c}^{m}}}}} ; \\ p = \sum\limits_{n = 0}^\infty {{{p}_{n}}\frac{{{{\tau }^{n}}}}{{\tau _{{rel}}^{n}}}} = \sum\limits_{n,m = 0}^\infty {{{p}_{{n,m}}}\frac{{{{\tau }^{n}}{{U}^{m}}}}{{\tau _{{rel}}^{n}{{c}^{m}}}}} ; \\ \rho = \sum\limits_{n = 0}^\infty {{{\rho }_{n}}\frac{{{{\tau }^{n}}}}{{\tau _{{rel}}^{n}}}} = \\ = {{\rho }_{{rel}}}{{\left( {1 + \left( {\frac{{\sum\limits_{n,m = 0,(n,m)! = (0,0)}^\infty {{{p}_{{n,m}}}\frac{{{{\tau }^{n}}{{U}^{m}}}}{{\tau _{{rel}}^{n}{{c}^{m}}}}} }}{{{{p}_{{rel}}}}}} \right)} \right)}^{{\frac{1}{\gamma }}}}. \\ \end{gathered} $

Исходя из представленных асимптотических разложений, система уравнений сохранения массы и импульса раскладывается на несколько уравнений по степеням времени релаксации:

$\begin{gathered} div\left( {{{\rho }_{0}}{{{\mathbf{u}}}_{0}} \otimes {{{\mathbf{u}}}_{0}}} \right) + \nabla {{p}_{0}} = div{{\Pi }_{0}};\,\,\,\,div\left( {{{\rho }_{0}}{{{\mathbf{u}}}_{0}}} \right) = 0; \hfill \\ \left\{ \begin{gathered} div\left( {{{\rho }_{0}}{{{\mathbf{u}}}_{0}} \otimes {{{\mathbf{u}}}_{1}}} \right) + div\left( {\left( {{{\rho }_{0}}{{{\mathbf{u}}}_{1}} + {{\rho }_{1}}{{{\mathbf{u}}}_{0}} + {{\tau }_{{rel}}}\frac{{\partial \left( {{{\rho }_{0}}{{{\mathbf{u}}}_{0}}} \right)}}{{\partial t}}} \right) \otimes {{{\mathbf{u}}}_{0}}} \right) + \nabla {{p}_{1}} = div{{\Pi }_{1}} \hfill \\ div\left( {{{\rho }_{0}}{{{\mathbf{u}}}_{1}} + {{\rho }_{1}}{{{\mathbf{u}}}_{0}} + {{\tau }_{{rel}}}\frac{{\partial \left( {{{\rho }_{0}}{{{\mathbf{u}}}_{0}}} \right)}}{{\partial t}}} \right) = 0 \hfill \\ \end{gathered} \right., \hfill \\ \end{gathered} $

а также по степеням времени и скорости:

$\begin{gathered} \left\{ \begin{gathered} {{\rho }_{{0.0}}}\left( {{{{\mathbf{u}}}_{{0.0}}},\nabla } \right){{{\mathbf{u}}}_{{0.0}}} + \nabla {{p}_{{0.0}}} = 0 \hfill \\ div\left( {{{{\mathbf{u}}}_{{0.0}}}} \right) = 0 \hfill \\ \end{gathered} \right.;\,\,\,\left\{ \begin{gathered} {{\rho }_{{0.1}}}\left( {{{{\mathbf{u}}}_{{0.1}}},\nabla } \right){{{\mathbf{u}}}_{{0.1}}} + \nabla {{p}_{{0.3}}} = 0 \hfill \\ div\left( {{{\rho }_{{0.0}}}{{{\mathbf{u}}}_{{0.3}}}} \right) + div\left( {{{\rho }_{{0.2}}}{{{\mathbf{u}}}_{{0.1}}}} \right) = 0 \hfill \\ \end{gathered} \right.; \\ \left\{ \begin{gathered} \nabla {{p}_{{0.1}}} = 0 \hfill \\ div\left( {{{{\mathbf{u}}}_{{0.1}}}} \right) = 0 \hfill \\ \end{gathered} \right.;\,\,\,\,\left\{ \begin{gathered} \nabla {{p}_{{1.0}}} = 0 \hfill \\ div\left( {{{\rho }_{{0.0}}}{{{\mathbf{u}}}_{{1.0}}} + {{\rho }_{{1.0}}}{{{\mathbf{u}}}_{{0.0}}}} \right) = 0 \hfill \\ \end{gathered} \right.; \\ \left\{ \begin{gathered} {{\rho }_{{0.0}}}\left( {{{{\mathbf{u}}}_{{0.1}}},\nabla } \right){{{\mathbf{u}}}_{{0.1}}} + \nabla {{p}_{{0.2}}} = 0 \hfill \\ div\left( {{{{\mathbf{u}}}_{{0.2}}}} \right) = 0 \hfill \\ \end{gathered} \right.;\,\,\,\,\left\{ \begin{gathered} \nabla {{p}_{{1.1}}} = 0 \hfill \\ div\left( {{{\rho }_{{0.0}}}{{{\mathbf{u}}}_{{1.1}}}} \right) = 0 \hfill \\ \end{gathered} \right.; \\ \left\{ \begin{gathered} 2{{\rho }_{{rel}}}{{\tau }_{{rel}}}\frac{\partial }{{\partial t}}\left( {\left( {{{{\mathbf{u}}}_{{0.1}}},\nabla } \right){{{\mathbf{u}}}_{{0.1}}}} \right) + \nabla {{p}_{{1.2}}} = 0 \hfill \\ {{{\mathbf{u}}}_{{1,2}}} = 0 \hfill \\ \end{gathered} \right.; \\ \left\{ \begin{gathered} div\left( {\left( {{{\rho }_{1}}{{{\mathbf{u}}}_{0}} + {{\tau }_{{rel}}}\frac{{\partial \left( {{{\rho }_{{0.1}}}{{{\mathbf{u}}}_{{0.1}}}} \right)}}{{\partial t}}} \right) \otimes {{{\mathbf{u}}}_{{0.1}}}} \right) + \nabla {{p}_{{1.3}}} = div\left( { - {{\tau }_{{rel}}}{{\rho }_{{0.1}}}{{{\mathbf{u}}}_{{0.1}}} \otimes \frac{{\partial {{{\mathbf{u}}}_{{0.1}}}}}{{\partial t}} - {{\tau }_{{rel}}}I\frac{{\partial {{p}_{{0.3}}}}}{{\partial t}}} \right) \hfill \\ div\left( {{{\rho }_{0}}{{{\mathbf{u}}}_{1}} + {{\rho }_{1}}{{{\mathbf{u}}}_{0}} + {{\tau }_{{rel}}}\frac{{\partial \left( {{{\rho }_{0}}{{{\mathbf{u}}}_{0}}} \right)}}{{\partial t}}} \right) = 0 \hfill \\ \end{gathered} \right.. \\ \end{gathered} $

Подстановка найденной силы взаимодействия частиц f₂₁ в выражение для вероятности столкновения позволила рассчитать скорость коагуляции частиц в зависимости от параметров акустических возмущений:

$\frac{1}{{{{D}_{{30}}}}}\frac{{\partial {{D}_{{30}}}}}{{\partial t}} = \frac{{\left\langle {n\int\limits_\Omega {\frac{{{{f}_{{21}}}[p]\left( {t,{\mathbf{n}}} \right)}}{{12{{\pi }^{2}}\mu d}}S[p]\left( t \right)d\Omega \left( {\mathbf{n}} \right)} } \right\rangle }}{6}.$

Полученные зависимости скорости коагуляции представлены в следующем разделе.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ ПРОЦЕССА КОАГУЛЯЦИИ ЧАСТИЦ ПРИ УЛЬТРАЗВУКОВЫХ ВОЗДЕЙСТВИЯХ

Результаты определения скорости коагуляции представлены на рис. 3. Как следует из представленных зависимостей, ультразвуковое воздействие в виде импульсов (как с преимущественной фазой сжатия, так и разрежения) ускоряет процесс коагуляции по сравнению с синусоидальным ультразвуковым воздействием. При этом скорость коагуляции возрастает при уменьшении длительности фаз разряжения или сжатия, даже когда среднеквадратичное значение звукового давления сохраняется (суммарная введенная энергия).

Рис. 3.

Зависимости скорости коагуляции от среднеквадратичного значения давления при различных размерах частиц и условиях воздействия: (а) – 100; (б) – 300; (в) – 500 нм.

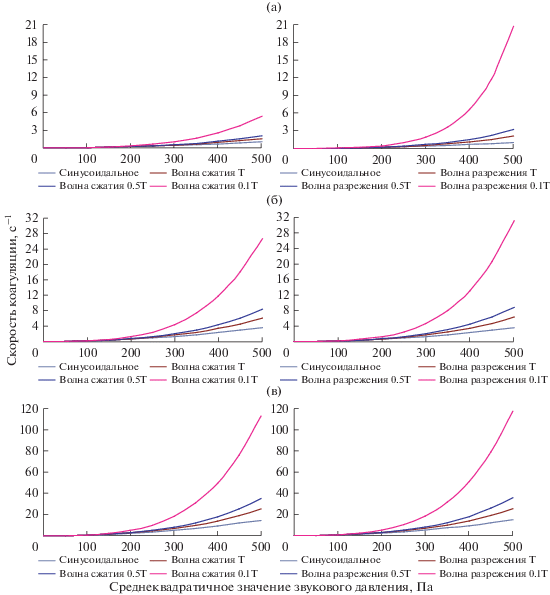
Это обусловлено нелинейными эффектами (конвективный перенос, изменение площади сечения столкновения при броуновском движении), возникающими при резком изменении мгновенного значения звукового давления.

В этих и последующих зависимостях величина T (период акустических возмущений) равна 1/22 000 с.

Полученные данные показывают эффективность коагуляции с помощью импульсного ультразвукового воздействия при сохранении величины вводимой энергии. Установлено, что ударно-волновое воздействие с преимущественной фазой сжатия увеличивает скорость коагуляции до 5 раз для субмикронных частиц с размерами диапазона 100–500 нм лишь за счет изменения условий ультразвукового воздействия. Воздействие с преимущественной фазой разрежения за счет дополнительного увеличения площади сечения столкновения (изменяется неопределенность положения частицы) увеличивает скорость коагуляции частиц размером 500 нм до 8 раз, а частиц размером 100 нм до 20 раз по сравнению с синусоидальным воздействием. Это подтверждает наибольшую эффективность ударно-волнового воздействия для частиц малых размеров.

Поскольку невозможна реализация импульсного воздействия только с фазой разряжения (или сжатия), следует считать, что максимальный эффект ускорения коагуляции (в 10 раз и более) на практике будет обеспечиваться при последовательном воздействии колебаниями, в которых длительность фазы сжатия меньше фазы разрежения.

Зависимости скорости укрупнения от отношения длительности фазы разрежения к длительности фазы сжатия ${{{{\tau }_{d}}} \mathord{\left/ {\vphantom {{{{\tau }_{d}}} {{{\tau }_{c}}}}} \right. \kern-0em} {{{\tau }_{c}}}}$ представлены на рис. 4.

Рис. 4.

Зависимости скорости коагуляции от отношения длительности фазы разрежения к длительности фазы сжатия ${{{{\tau }_{d}}} \mathord{\left/ {\vphantom {{{{\tau }_{d}}} {{{\tau }_{c}}}}} \right. \kern-0em} {{{\tau }_{c}}}}{\text{:}}$ (а) – среднеквадратичное значение давления 200 Па; (б) – среднеквадратичное значение давления 500 Па.

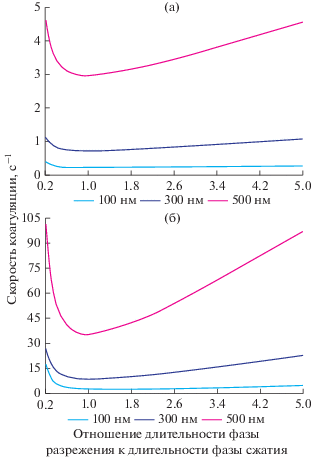
Как следует из представленных зависимостей, максимальная скорость коагуляции достигается, когда в ультразвуковом воздействии длительность фазы сжатия преобладает над длительностью фазы разрежения (амплитуда фазы разрежения выше, чем фазы сжатия).

Далее с учетом выявленного значения скорости коагуляции устанавливалось влияние акустического возмущения на фракционный состав полидисперсного аэрозоля. Уравнение Смолуховского [7] после подстановки полученных выражений для вероятности столкновения (5), (7) позволяет построить гистограммы исходного аэрозоля и аэрозолей после различных ультразвуковых воздействий (рис. 5).

Рис. 5.

Изменение фракционного состава частиц с исходным модальным размером 100 нм при различных среднеквадратичных значениях давления и условиях ультразвукового воздействия: (а) – 200 Па; (б) – 500 Па.

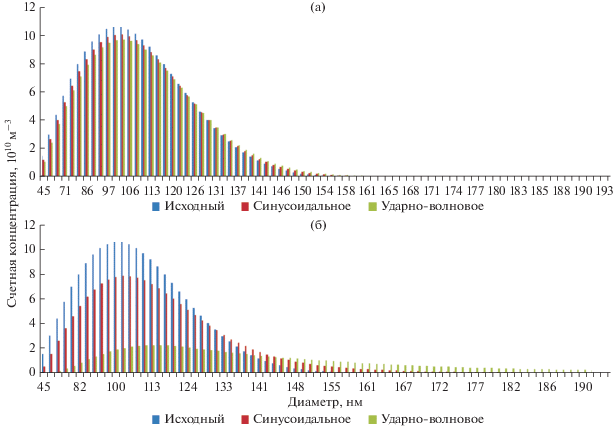
Время воздействия в обоих модельных случаях составляло 10 мин, начальная концентрация (суммарная по всем типоразмерам частиц) – 2 × × 10¹¹ г/м³, частота воздействия – 22 кГц, для ударно-волнового (импульсного) воздействия отношение длительности фазы разрежения к длительности фазы сжатия – 0.2.

Начальное распределение аэрозоля по размерам (счетные концентрации частиц каждого размера) подчиняется закону Рэлея.

Из представленных гистограмм следует, что с увеличением диаметра частиц повышается эффективность коагуляции. При этом добавка к массовой доле, обусловленная ударно-волновым воздействием, наиболее существенна для частиц с исходным модальным размером 100 нм.

Представленные гистограммы подтверждают повышенную эффективность специальных условий воздействия по сравнению с синусоидальным даже для полидисперсных аэрозолей. При этом (для модального размера исходных частиц – 100 нм, RMS – 500 Па) наблюдается увеличение количественной доли крупной фракции (частиц, диаметр которых превышает модальный диаметр более чем на 30%) до 9 раз, в то время как при синусоидальном ультразвуковом воздействии доля крупной фракции увеличивается не более чем в 3 раза.

На основе полученных гистограмм были построены зависимости среднеобъемно-поверхностного диаметра аэрозольных частиц от времени при различных среднеквадратичных значениях звукового давления и условий ультразвукового воздействия.

Рис. 6.

Зависимости D32 от времени при различных среднеквадратичных значениях давления, условиях ультразвукового воздействия и начальных модальных диаметрах частиц: (а) – 100 нм; (б) – 300 нм; (в) – 500 нм.

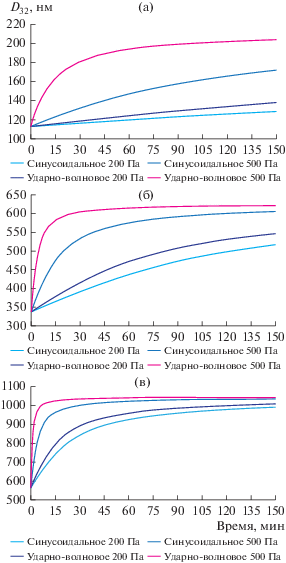
Представленные зависимости свидетельствуют о сокращении времени достижения максимального размера частиц при использовании ударно-волнового воздействия. Например, для частиц размером 100 нм при синусоидальном воздействии максимальный диаметр не достигается даже за 150 мин, в то время как при ударно-волновом воздействии за 60 мин достигается диаметр, составляющий более 95% от максимального.

ЗАКЛЮЧЕНИЕ

Проведенные исследования подтвердили эффективность коагуляции субмикронных частиц при синусоидальном и ударно-волновом воздействии и позволили выявить условия воздействия, обеспечивающие максимальную эффективность коагуляции.

Показана возможность ускорения коагуляции частиц размером до 1 мкм до 20 раз при использовании ударно-волнового ультразвукового воздействия в сравнении с синусоидальным.

Ускорение процесса коагуляции при ударно-волновом ультразвуковом воздействии на газовые среды может быть обеспечено разработанными источниками ультразвукового воздействия при создании специальных условий распространения колебаний (распространение между источниками и отражателями с регулированием фазы отражения, формирование последовательностей различных по частоте импульсов с учетом дисперсии скорости распространения в газовой среде, фокусированием и интерференцией колебаний, излучаемых многочастотными и пространственно распределенными излучателями и др.) или изменением условий распространения потока газа с субмикронными частицами (прерывателями потока, изменениями плотности потока, изменением направления движения потока и т.п.).

Результаты исследований лягут в основу создания и применения нового класса устройств для улавливания субмикронных частиц в условиях современных высокотехнологичных производств и решения проблемы защиты окружающей среды и человека.

Исследование выполнено при финансовой поддержке Российского научного фонда в рамках научного проекта № 19-19-00121.

ОБОЗНАЧЕНИЯ

〈 〉	усреднение за период изменения давления
c	скорость распространения ультразвуковых колебаний в несущей газовой фазе, м/с
D	средний диаметр частиц, м
d₀	наименьший диаметр частиц, м
f	частота возмущений давления, c^–1
${{f}_{{21}}}[p]\left( {t,{\mathbf{n}}} \right)$	сила взаимодействия частиц
${{f}_{{V\max }}}$	сила, которую необходимо приложить для ускорения газового потока, Н
${{{\mathbf{j}}}_{m}}$	плотность потока массы газовой фазы, кг/(м² с)
l	расстояние между частицами, м
M	масса частицы, кг
m	масса молекулы газовой фазы, кг
N	количество частиц в выделенном объеме V
n	исходная счетная концентрация частиц, м^–3
n	единичный вектор, обозначающий направление линии центров частиц, относительно волнового вектора ультразвукового поля
n_k	концентрация частиц с условным диаметром ${{d}_{0}}\sqrt[3]{k},$ м^–3
${{p}_{A}}$	амплитуда акустических возмущений, Па
${{p}_{{RMS}}}$	среднеквадратичное значение давления, Па
r_i	вектор координат частицы в момент возникновения i-го элементарного акта соударения, м
$S[p]\left( t \right)$	площадь сечения столкновения, м²
T	период возмущений давления, с
t_i	момент времени возникновения i-го элементарного акта соударения молекулы с частицей, c
u	возмущение скорости газа вблизи частицы, создаваемое соседней частицей, м
u_i	скорость частицы в результате i-го элементарного акта соударения с молекулой, м/с
V	выделенный объем облака, размеры которого малы по сравнению с протяженностью воздействия, но велики по сравнению с расстоянием между частицами, м³
${{\beta }_{{i,k}}}$	вероятность столкновения частиц с диаметрами ${{d}_{0}}\sqrt[3]{i}$ и ${{d}_{0}}\sqrt[3]{k},$ м³/с
${{\beta }_{{\text{H}}}}[p]\left( t \right)$	компонента гидродинамического взаимодействия, м³/с
${{\beta }_{{\text{O}}}}[p]\left( t \right)$	компонента ортокинетического взаимодействия, м³/с
Π	тензор напряжений в газовой фазе, Па
$\rho $	плотность газовой фазы, кг/м³
${{\sigma }_{r}}$	дисперсия (квадрат неопределенности) пространственного положения частицы, м
$\tau $	характерная длительность импульса ударной волны, с

ИНДЕКСЫ

21	направление взаимодействия от 2 к 1-й частице
30	средний объемный
32	средний объемно-поверхностный
A	амплитудное значение
H	гидродинамическое взаимодействие
i	номер элементарного акта соударения молекулы с частицей
i, j	номера мер, участвующих в столкновении – частиц с диаметрами ${{d}_{0}}\sqrt[3]{i}$ и ${{d}_{0}}\sqrt[3]{j}$
k	номер меры – частицы с условным диаметром ${{d}_{0}}\sqrt[3]{k}$
O	ортокинетическое взаимодействие
RMS	среднеквадратичное значение

Список литературы

Oren I., Haddad N., Finkelstein R. Invasive pulmonary aspergillosis in neutropenic patients during hospital construction: before and after chemoprophylaxis and institution of HEPA filters // Am. J. Hematol. 2001. P. 257.
Тимошенко В.И., Чернов Н.Н. Осаждение и осадконакопление промышленных дымов. Ростов-на-Дону: Ростиздат, 2004.
Khmelev V.N., Shalunov A.V., Golykh R.N., Dorovskikh R.S., Nesterov V.A., Khmelev S.S., Shalunova K.V. Efficiency Increase of Wet Gas Cleaning from Dispersed Admixtures by the Application of Ultrasonic Fields // Arch. Acoust. 2016. V. 40. № 4. P. 757.
Khmelev V.N., Shalunov A.V., Tsyganok S.N., Golykh R.N., Shalunova K.V. Experimental Investigations of the Effectiveness of Acoustic Vibration Influence of Ultrasonic Frequency on Fogs // Rom. J. Acoust. Vib. 2017. V. 14. № 2. P. 69.
Физические основы ультразвуковой технологии / Под ред. Розенберга Л.Д. М.: Наука, 1970.
Riera E., Gallego-Juarez J., Mason T. Airborne ultrasound for the precipitation of smokes and powders and the destruction of foams // Ultrason. Sonochem. 2006. V. 13. P. 107.
Sheng C.D., Shen X.L. Modelling acoustic agglomeration processes using direct simulation Monte Carlo method // J. Aerosol Sci. 2006. V. 37. № 1. P. 16.
Mizuno A. Electrostatic precipitation // IEEE Trans. Dielectr. Electr. Insul. 2000. P. 615.
Riera E., Cardoni A., Gallego-Juárez J.A., Acosta V.M., Blanco A., Rodríguez G., Blasco M., Herranz L.E. Recent advances in the development and application of power plate transducers in dense gas extraction and aerosol agglomeration processes // 43rd Ann. Symp. of the Ultras. Ind. Assoc. 2015. P. 67.
Jajarmi R.I. Acoustic Separation and Electrostatic Sampling of Submicron Particles Suspended in Air. Stockholm: Royal Institute of Technology, 2016.
Crook B. Non-inertial samplers: biological perspectives // Bioaerosols Handbook / Ed. Cox C.S., Wathes C.M. Boca Raton, Fla.: CRC, 1995. P. 269.
Sheng C.D., Shen X.L. Simulation of acoustic agglomeration processes of poly-disperse solid particle // Aerosol Sci. Technol. 2007. V. 41. № 1. P. 1.
Мюллер Г.В. Теория коагуляции полидисперсных систем // Коагуляция коллоидов / Под ред. Рабиновича А.И., Васильева П.С. М.: ОНТИ, 1936. С. 7.
Протодьяконов И.О., Цибаров В.А., Чесноков Ю.Г. Кинетическая теория газовзвесей. Л.: Изд-во Ленингр. ун-та, 1985.
Цибаров В.А. Кинетический метод в теории газовзвесей. СПб.: Изд-во Санкт-Петербург. ун-та, 1997.
Кузнецов Г.В., Стрижак П.А., Шлегель Н.Е. Взаимодействие капель воды и суспензий при их столкновениях в газовой среде // Теор. осн. хим. технол. 2019. Т. 53. № 5. С. 546.
Shuster K., Fichman M., Goldshtein A., Gutfinger C. Agglomeration of submicrometer particles in weak periodic shock waves // Phys. Fluids. 2002. V. 14. № 5. P. 1802.
Goldshtein A., Shuster K., Vainshtein P., Fichman M., Gutfinger C. Particle motion in resonance tubes // J. Fluid Mech. 1998. V. 360. № 1. P. 1.
Smoluchowski M.V. Drei Vorträge über Diffusion, Brownsche Molekularbewegung und Koagulation von Kolloidteilchen // Phys. Z. 1916. V. 17. P. 557.
Michaelides E.E. Brownian movement and thermophoresis of nanoparticles in liquids // Int. J. Heat Mass Transfer. 2015. V. 81. P. 179.
Yang H., Cornaglia M., Trouillon R., Lehnert T., Gijs M.A.M. Study of constrained Brownian motion of nanoparticles near an interface using optical tweezers // Proc. SPIE 9379: Complex Light and Optical Forces IX, 93790W. Society of Photo-Optical Instrumentation Engineers (SPIE): San Francisco, 2015.
Елизарова Т.Г. Математические модели и численные методы в динамике жидкости и газа. Подходы, основанные на системах квазигазодинамических и квазигидродинамических уравнений. М.: МГУ, 2005.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал