Теоретические основы химической технологии, 2020, T. 54, № 4, стр. 431-439
Анализ взаимных преобразований структур диаграмм трехкомпонентных систем путем образования бинарных граничных тангенциальных азеотропов
Т. В. Челюскина a, *, А. В. Полковниченко a, Д. Д. Модурова a
a МИРЭА – Российский технологический университет (Институт тонких химических технологий
им. М.В. Ломоносова)
Москва, Россия
* E-mail: cheluskina@mitht.ru
Поступила в редакцию 16.12.2019
После доработки 20.01.2020
Принята к публикации 07.02.2020
Аннотация
Рассмотрены взаимные преобразования структур диаграмм парожидкостного равновесия трехкомпонентных систем, не имеющих тройных азеотропов и содержащих моноазеотропные и биазеотропные бинарные составляющие, через образование бинарного граничного тангенциального азеотропа при изменении внешних условий. Выявлены особенности возникновения биазеотропии на границах концентрационного симплекса в трехкомпонентных системах, относящихся к различным типам структур диаграмм парожидкостного равновесия.
ВВЕДЕНИЕ
Одним из наиболее распространенных методов разделения органических веществ в химической технологии является ректификация, характеризующаяся высокими удельными затратами энергии [1–3]. Разработка различных схем ректификационного разделения многокомпонентных смесей и сравнение энергетических затрат на их реализацию возможны только при наличии достоверных данных о фазовом равновесии жидкость–пар, а также при условии правильности их интерпретации. Рассмотрение эволюции фазовых диаграмм представляется весьма удобным инструментом разработки принципиальных технологических схем и предварительного проектирования [4]. Открытие же би- и триазеотропии резко повышает роль качественных методов исследования [5].
Любые преобразования диаграммы фазового равновесия жидкость–пар происходят в соответствии с теорией тангенциальной азеотропии [6–10], которая определяет механизмы возникновения (исчезновения) азеотропов различной компонентности. Топологическая структура фазовых диаграмм жидкость–пар при изменении внешних условий может трансформироваться или оставаться неизменной. Структуры, которые существуют в некотором диапазоне внешних условий без изменения, называются грубыми. Переход от одной грубой структуры к другой осуществляется через тонкую структуру, существующую при единственном наборе внешних параметров [6, 11]. Явление тангенциальной азеотропии [12] встречается в практике ректификации и не может не учитываться в связи с проблемой получения особо чистых веществ ректификационными методами.
Анализ взаимных преобразований структур диаграмм фазового равновесия (СДФР), с точки зрения механизма изменения топологической структуры последних, позволяет устанавливать общие закономерности трансформации зеотропных, моно- и биазеотропных систем; создавать наиболее благоприятные условия для разделения таких смесей за счет изменения их СДФР.
Ранее нами были рассмотрены взаимные преобразования диаграмм дистилляционных линий трехкомпонентных систем, не имеющих тройных азеотропов и содержащих зеотропные, моноазеотропные и биазеотропные бинарные составляющие, через стадию образования бинарного внутреннего тангенциального азеотропа при изменении внешних условий [13].
Целью настоящей работы является изучение взаимных преобразований структур диаграмм парожидкостного равновесия (ПЖР) трехкомпонентных систем, не имеющих тройных азеотропов и содержащих моно- и биазеотропные бинарные составляющие, через образование бинарного граничного тангенциального азеотропа (ГТА) за счет изменения внешних условий (давления, температуры).
РАСЧЕТНО-АНАЛИТИЧЕСКАЯ ЧАСТЬ
Нами проведен анализ преобразований СДФР систем классов 3.1.0, 3.2.0 и 3.3.0 по классификации [11] (табл. 1) с образованием различных типов диаграмм биазеотропных систем первой группы по классификации [14], через возникновение бинарного ГТА. Так как в этом случае появление бинарной биазеотропии может происходить только в моноазеотропной бинарной составляющей, класс 3.0.0 исключен из рассмотрения. Возможность одновременного появления ГТА на разных сторонах концентрационного треугольника маловероятна и поэтому не рассматривается. Основные свойства бинарного граничного тангенциального азеотропа приведены в работе [6]; типы и условия существования граничных тангенциальных азеотропов в трехкомпонентных системах – в работах [15–17].
Таблица 1.
Количество моноазеотропных бинарных составляющих в трехкомпонентных системах разного типа
| № | Класс | Тип и подтип диаграммы | Количество моноазеотропных бинарных составляющих |
|---|---|---|---|
| 1 | 3.1.0 | 1а | 1 |
| 2 | 1б | ||
| 3 | 2 | ||
| 4 | 3.2.0 | 1 | 2 |
| 5 | 2а | ||
| 6 | 2б | ||
| 7 | 2в | ||
| 8 | 3.3.0 | 1а | 3 |
| 9 | 1б | ||
| 10 | 2 |
На рис. 1–10 показаны термодинамически непротиворечивые механизмы взаимных преобразований структур диаграмм фазового равновесия моно- и биазеотропных трехкомпонентных систем. Всем подтипам СДФР систем с бинарной биазеотропной составляющей присвоена буква латинского алфавита с учетом обозначений, принятых нами ранее в работе [13].
Рис. 1.
Взаимные преобразования СДФР систем классов 3.1.0-1а и 3.[2.0.0].0-2а через образование ГТА на составляющей 1–2 в вершине 1.
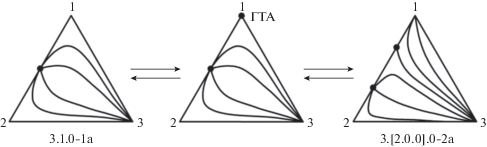
Рис. 2.
Взаимные преобразования СДФР систем классов 3.1.0-1б и 3.[2.0.0].0-1 через образование ГТА на составляющей 1–3 в вершине 3.
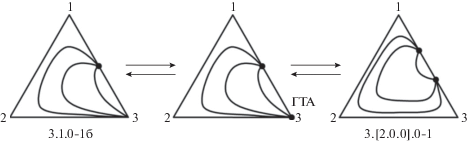
Рис. 3.
Взаимные преобразования СДФР систем классов 3.1.0-2 и 3.[2.0.0].0-2а через образование ГТА на составляющей 2–3 в вершине 2.
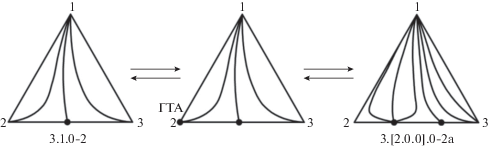
Рис. 4.
Взаимные преобразования СДФР систем классов 3.2.0-1 и 3.[2.1.0].0-3 через образование ГТА на составляющей 1–2 в вершинах: (а) – 1; (б) – 2.
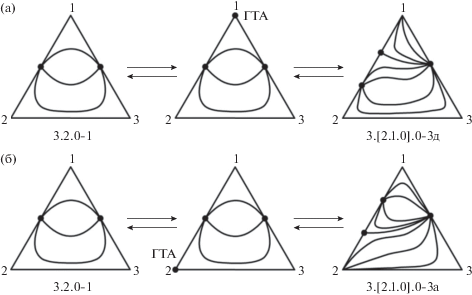
Рис. 5.
Взаимные преобразования СДФР систем классов 3.2.0-2а и 3.[2.1.0].0-3, 3.[2.1.0].0-4 через образование ГТА на составляющей: (а, б) – 1–2; (в) – 1-3.
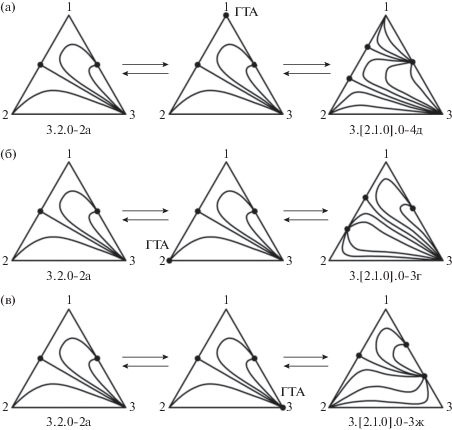
Рис. 6.
Взаимные преобразования СДФР систем классов 3.2.0-2б и 3.[2.1.0].0-3, 3.[2.1.0].0-4 через образование ГТА на составляющей: (а, б) – 1–2; (в, г) – 1-3.
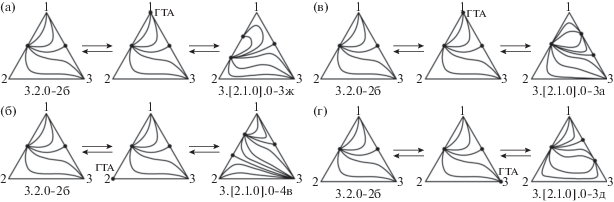
Рис. 7.
Взаимные преобразования СДФР систем классов 3.2.0-2в и 3.[2.1.0].0-3, 3.[2.1.0].0-4 через образование ГТА на составляющей: (а, б) – 1–2; (в, г) – 1-3.
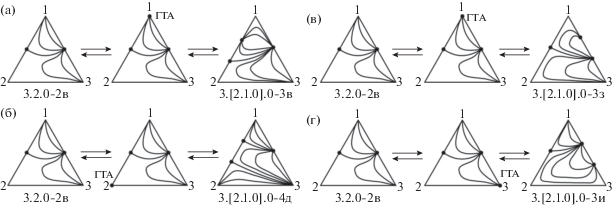
Рис. 8.
Взаимные преобразования СДФР систем классов 3.3.0-1а и 3.[2.1.1].0-5, 3.[2.1.1].0-6 через образование ГТА на составляющей 1–2 в вершинах: (а) – 1; (б) – 2.
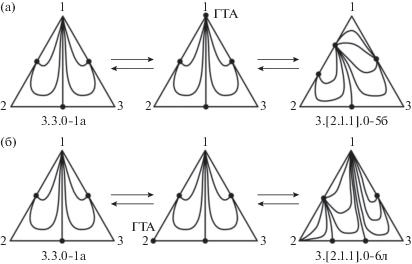
Рис. 9.
Взаимные преобразования СДФР систем классов 3.3.0-1б и 3.[2.1.1].0-5, 3.[2.1.1].0-6 через образование ГТА на составляющей: (а, б) – 1-2; (в, г) – 2-3; (д, е) – 1-3.
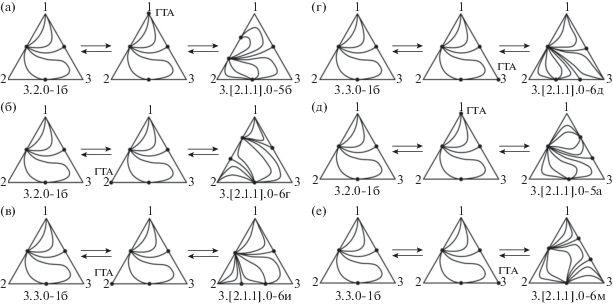
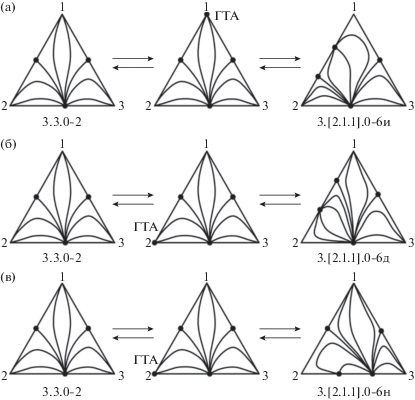
Рис. 10.
Взаимные преобразования СДФР систем классов 3.3.0-2 и 3.[2.1.1].0-6 через образование ГТА на составляющей: (а, б) – 1–2; (в,) – 2-3.
Начнем рассмотрение с трехкомпонентных систем, содержащих одну моноазеотропную бинарную составляющую (рис. 1–3). В диаграммах таких систем многовариантность, связанная с возможностью возникновения биазеотропии на той или иной моноазеотропной бинарной составляющей, отсутствует. Следовательно, мы имеем предопределенный элемент СДФР, на котором это возможно.
Рассмотрим появление ГТА в бинарной моноазеотропной составляющей системы класса 3.1.0-1а (рис. 1). В этом случае граничный тангенциальный азеотроп представляет собой сложное односегментное седло. При изменении внешних условий происходит бифуркация [18] сложной особой точки – граничного тангенциального азеотропа – с образованием двух простых особых точек: точки типа узел, соответствующей компоненту 1, и точки типа седло, соответствующей бинарному азеотропу. Таким образом, структура диаграммы класса 3.1.0-1а взаимосвязана только с одной СДФР, содержащей бинарную биазеотропную составляющую, класса 3.[2.0.0].0-2а.
На рис. 2 представлен механизм возникновения биазеотропии через стадию образования граничного тангенциального азеотропа в системе класса 3.1.0-1б. Здесь на стороне 1-3 может быть реализован ГТА, являющийся сложным односегментным узлом. Возникновение же граничного тангенциального азеотропа типа сложное односегментное седло невозможно, так как такой вариант противоречит условию образования ГТА: азеотроп с минимумом температуры кипения появляется (исчезает) в вершине, соответствующей легколетучему компоненту, а азеотроп с максимумом температуры кипения – в вершине, соответствующей тяжелолетучему компоненту [6, 15]. Таким образом, при изменении внешних условий возможен только один механизм взаимного преобразования СДФР, согласно которому ГТА имеет тип сложного односегментного узла, бифуркация которого приводит к образованию системы класса 3.[2.0.0].0-1.
На рисунке 3 представлен механизм возникновения биазеотропии в системе класса 3.1.0-2. Граничный тангенциальный азеотроп типа сложный односегментный узел появляется в одной из вершин моноазеотропной бинарной составляющей. При изменении внешних условий происходит бифуркация сложной особой точки и образуется система класса 3.[2.0.0].0-2а.
Таким образом, анализ рис. 1–3 показал, что каждому из классов 3.1.0-1а, 3.1.0-1б и 3.1.0-2 соответствует лишь одна СДФР трехкомпонентных биазеотропных систем. Причем возникновение биазеотропии через стадию образования ГТА и в системе класса 3.1.0-1а, и в системе класса 3.1.0-2 приводит к образованию идентичных структур диаграмм, принадлежащих к классу 3.[2.0.0].0-2а. Следует отметить, что данная особенность не характерна для взаимных преобразований СДФР через стадию образования внутреннего тангенциального азеотропа [13].
Взаимное преобразование структур диаграмм ПЖР классов 3.1.0-2 и 3.[2.0.0].0-2а через стадию образования бинарного ГТА (рис. 3) наглядно иллюстрируют результаты проведенного с использованием программного комплекса Aspen Plus® V.9.0 вычислительного эксперимента по математическому моделированию парожидкостного равновесия трехкомпонентной системы, образованной смесью метилэтилкетон-перфторбензол и диметилсульфоксидом, при значениях давления от 300 мм рт. ст. (система биазеотропна) до 760 мм рт. ст. (система моноазеотропна) через стадию образования ГТА при 604 мм рт. ст. [19].
На рис. 4–7 представлены механизмы возникновения биазеотропии через образование ГТА в системе класса 3.2.0. Отметим, что из-за увеличения числа особых точек на границе концентрационного симплекса данной системы появляется многовариантность механизмов взаимного преобразования диаграмм классов 3.2.0 и 3.[2.1.0].0.
Проанализируем рис. 4. Диаграмма ПЖР системы класса 3.2.0-1 включает две моноазеотропные бинарные составляющие, которые содержат узловые азеотропы. При этом возникновение биазеотропии через стадию образования ГТА на обеих моноазеотропных бинарных составляющих происходит по двум механизмам. Если ГТА реализуется в вершине, расположенной на контуре концентрационного треугольника между двумя особыми точками типа узел, образуется структура диаграммы ПЖР системы класса 3.[2.1.0].0-3д (рис. 4а); если в вершинах, расположенных между узловой и седловидной особыми точками, то – 3.[2.1.0].0-3а (рис. 4б). В обоих случаях граничный тангенциальный азеотроп представляет собой сложное односегментное седло, которое при изменении внешних условий бифурцирует с образованием двух простых особых точек седловидного и узлового типа. Следует отметить, что СДФР биазеотропных систем, представленные на рис. 4, принадлежат одному и тому же классу и типу, но различаются подтипами. Таким образом, при изменении внешних условий возможны взаимные преобразования СДФР моноазеотропной системы класса 3.2.0-1 и двух топологически различных структур биазеотропных трехкомпонентных систем.
На рис. 5 представлены три возможных механизма возникновения биазеотропии в системе класса 3.2.0-2а. При изменении внешних условий граничный тангенциальный азеотроп может появиться либо на бинарной составляющей, содержащей седловидный азеотроп, либо на стороне концентрационного симплекса, содержащей узловой азеотроп. В первом случае, если граничный тангенциальный азеотроп является сложным односегментным седлом (рис. 5а), после прохождения стадии бифуркации ГТА образуется система класса 3.[2.1.0].0-4д; если же граничный тангенциальный азеотроп представляет собой сложный односегментный узел (рис. 5б), реализуются взаимные преобразования диаграмм дистилляционных линий классов 3.2.0-2а и 3.[2.1.0].0-3г. Согласно третьему механизму, биазеотропия возникает в концентрационном треугольнике на стороне, которая содержит узловой азеотроп (рис. 5в). ГТА в этом случае является сложным односегментным узлом, и реализуются взаимные преобразования диаграмм дистилляционных линий классов 3.2.0-2а и 3.[2.1.0].0-3ж. Отметим, что для системы класса 3.2.0-2а, по аналогии с системой класса 3.1.0-1б, возникновение ГТА типа сложного односегментного седла на стороне концентрационного симплекса, содержащей узловой азеотроп, невозможно из-за особенности образования граничного тангенциального азеотропа, отмеченной ранее. В отличие от случаев, рассмотренных нами выше, структура диаграммы ПЖР системы 3.2.0-2а при изменении внешних условий может трансформироваться в СДФР биазеотропных систем разных типов (рис. 5а – 3.[2.0.0].0-4 и рис. 5б, 5в – 3.[2.1.0].0-3).
Рисунки 6 и 7 демонстрируют взаимосвязь СДФР, включающих две моноазеотропные составляющие, с четырьмя топологически различными структурами диаграмм ПЖР с биазеотропной бинарной составляющей. В структурах диаграмм классов 3.2.0-2б (рис. 6) и 3.2.0-2в (рис. 7) одна из моноазеотропных бинарных составляющих содержит узловой азеотроп, другая – седловидный. При этом биазеотропия может появиться через образование ГТА на обеих моноазеотропных бинарных составляющих в каждой из вершин концентрационного треугольника. На рис. 6 приведены взаимные преобразования структуры диаграммы класса 3.2.0-2б и структур диаграмм классов 3.[2.1.0].0-3а, 3.[2.1.0].0-3д, 3.[2.1.0].0-3ж, 3.[2.1.0].0-4в; а на рис. 7 – взаимные преобразования структуры диаграммы класса 3.2.0-2в и структур диаграмм классов 3.[2.1.0].0-3в, 3.[2.1.0].0-3з, 3.[2.1.0].0-3и, 3.[2.1.0].0-4д. Отметим, что СДФР биазеотропных систем, представленные на этих рисунках, принадлежат одному классу, но различаются типами и подтипами.
Анализ рис. 4–7 показал, что структуры диаграмм ПЖР трехкомпонентных систем с двумя бинарными моноазеотропными составляющими связаны со СДФР жидкость–пар биазеотропных систем классов 3.[2.1.0].0-3 и 3.[2.1.0].0-4 различных подтипов. Образование СДФР класса 3.[2.1.0].0-3 возможно при возникновении ГТА любого типа: сложного односегментного седла или сложного односегментного узла. А структуры диаграмм, принадлежащих к классу 3.[2.1.0].0-4, образуются только в тех случаях, когда граничный тангенциальный азеотроп представляет собой сложное односегментное седло.
Перейдем к исследованию взаимных преобразований СДФР систем классов 3.3.0 и 3.[2.1.1].0-5, 3.[2.1.1].0-6 (рис. 8–10). В системе класса 3.3.0 биазеотропия может возникать через образование граничного тангенциального азеотропа в любой из трех бинарных моноазеотропных составляющих концентрационного симплекса.
Механизмы появления биазеотропии в системе класса 3.3.0-1а рассмотрены на рис. 8. В данном случае, если граничный тангенциальный азеотроп представляет собой сложный односегментный узел, при изменении внешний условий реализуется преобразование СДФР систем классов 3.3.0-1а и 3.[2.1.1].0-5б (рис. 8а), если – сложное односегментное седло, то – 3.3.0-1а и 3.[2.1.1].0-6л (рис. 8б). Таким образом, СДФР системы класса 3.3.0-1а взаимосвязана с двумя топологически различными структурами диаграмм ПЖР с биазеотропной бинарной составляющей. Стоит отметить, что, по аналогии с системами класса 3.1.0-1б и 3.2.0-2а, в системе класса 3.3.0-1а появление граничного тангенциального азеотропа типа сложное односегментное седло невозможно на стороне, содержащей узловой азеотроп.
Проанализируем рис. 9. Видно, что при изменении внешних условий СДФР моноазеотропной системы класса 3.3.0-1б может трансформироваться в шесть топологически различных СДФР биазеотропных систем. Классы 3.[2.1.1].0-5а (рис. 9д) и 3.[2.1.1].0-5б (рис. 9а) реализуются, когда ГТА является сложным односегментным узлом. Если он появляется на бинарной составляющей, содержащей седловидный азеотроп, то при изменении внешних условий образуется диаграмма ПЖР системы класса 3.[2.1.1].0-5а, если же на стороне концентрационного симплекса, содержащей азеотроп типа узел, то – СДФР системы класса 3.[2.1.1].0-5б. В тех случаях, когда граничный тангенциальный азеотроп представляет собой сложное односегментное седло, при изменении внешних условий возможно образование структур диаграмм ПЖР систем, принадлежащих к классу 3.[2.1.1].0-6, четырех различных подтипов. Появление ГТА на стороне, содержащей азеотроп типа седло, приводит к образованию структуры 3.[2.1.1].0-6м (рис. 9е); а на стороне, содержащей узловой азеотроп, связанный сепаратрисой с азеотропом седловидного типа, – 3.[2.1.1].0-6г (рис. 9б). В случае, когда ГТА возникает на бинарной составляющей, имеющей узловой азеотроп, не связанный сепаратрисой с какой-либо особой точкой концентрационного симплекса, возможна трансформация структуры диаграммы ПЖР системы класса 3.3.0-1б в СДФР систем классов 3.[2.1.1].0-6д (рис. 9г) и 3.[2.1.1].0-6и (рис. 9в). Здесь образование определенной структуры (3.[2.1.1].0-6д или 3.[2.1.1].0-6и) зависит от типов простых особых точек на контуре концентрационного треугольника, между которыми расположен граничный тангенциальный азеотроп.
На рис. 10 представлены взаимные преобразования СДФР систем классов 3.3.0-2 и 3.[2.1.1].0-6. Диаграмма ПЖР системы класса 3.3.0-2 образована тремя моноазеотропными бинарными составляющими, две из которых содержат азеотропы типа седло, а третья – узловой азеотроп. Во всех случаях ГТА представляет собой сложный односегментный узел. При реализации граничного тангенциального азеотропа на стороне концентрационного симплекса, содержащей азеотроп типа седло, возможны два варианта возникновения биазеотропии в системе класса 3.3.0-2. Если ГТА появляется в вершине, расположенной на контуре концентрационного треугольника между простыми особыми точками седловидного типа, то при изменении внешних условий образуется диаграмма ПЖР системы класса 3.[2.1.1].0-6и (рис. 10а); если в вершине, расположенной между простыми особыми точками седловидного и узлового типа, то – СДФР системы класса 3.[2.1.1].0-6д (рис. 10б). Появление же ГТА на бинарной составляющей, содержащей узловой азеотроп, приводит к образованию структуры 3.[2.1.1].0-6н (рис. 10в). Таким образом, СДФР моноазеотропной трехкомпонентной системы класса 3.2.0-2 связана с тремя топологически различными структурами диаграмм фазового равновесия жидкость–пар трехкомпонентных биазеотропных систем. Стоит отметить, что СДФР систем, содержащих бинарную биазеотропную составляющую, принадлежат одному и тому же классу и типу, но различаются подтипами.
Рассмотренные нами варианты взаимных преобразований СДФР через стадию образования бинарного граничного тангенциального азеотропа характеризуются тем, что структуры диаграмм моноазеотропных трехкомпонентных систем, принадлежащие одному классу и типу, могут трансформироваться в структуры диаграмм биазеотропных трехкомпонентных систем, принадлежащие одному классу, но различным типам; в отличие от случаев взаимных преобразований структур диаграмм трехкомпонентных систем путем образования бинарного внутреннего тангенциального азеотропа [13]. Кроме того, структуры диаграмм биазеотропных трехкомпонентных систем, принадлежащие одному и тому же классу, типу и подтипу, могут быть образованы из структур диаграмм моноазеотропных трехкомпонентных систем, принадлежащих одному классу, но различным типам.
Взаимосвязь диаграмм парожидкостного равновесия, принадлежащих подмножествам моно- и биазеотропных трехкомпонентных систем, полученных путем образования бинарных граничных тангенциальных азеотропов, отражена на рис. 11.
ЗАКЛЮЧЕНИЕ
Полученные результаты позволяют установить закономерности появления бинарной биазеотропии в трехкомпонентных системах через стадию образования ГТА, в том числе выявить строгое соответствие между структурой диаграммы дистилляционных линий и путями возможного изменения концентрационного симплекса. Так, если взаимное преобразование диаграмм дистилляционных линий моно- и биазеотропных трехкомпонентных систем осуществляется путем образования бинарного граничного тангенциального азеотропа типа сложное односегментное седло, это приводит к появлению (исчезновению) одной из областей дистилляции; если же путем образования бинарного ГТА типа сложный односегментный узел, количество областей дистилляции остается неизменным.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 18-03-01224-а).
Список литературы
King C.J. Separation Processes. New York: Dover, 2013.
Тимофеев В.С., Серафимов Л.А., Тимошенко А.В. Принципы технологии основного органического и нефтехимического синтеза: учебное пособие для вузов. М.: Высшая школа, 2010.
Gorak A., Sorensen E. Distillation: Operation and Applications. Amsterdam: Elsevier, 2014.
Shen W.F., Benyounes H., Song J. A review of ternary azeotropic mixtures advanced separation strategies // Theor. Found. Chem. Eng. 2016. V. 50. № 1. P. 28.
Серафимов Л.А., Фролкова А.К., Тимофеев В.С. Качественные исследования технологических процессов и производств как этап их интенсификации на основе математического моделирования с помощью ЭВМ // Интенсиф. технол. процессов: матер., технол., оборуд. 2009. № 6. С. 9.
Жаров В.Т., Серафимов Л.А. Физико-химические основы дистилляции и ректификации. Л.: Химия, 1975.
Серафимов Л.А. Правило азеотропии и классификация многокомпонентных смесей. VIII. Общие закономерности тангенциальной азеотропии // Журн. физ. хим. 1971. Т. 45. № 5. С. 1140.
Серафимов Л.А. Правило азеотропии и классификация многокомпонентных смесей. IX. Тангенциальная азеотропия и общее соотношение между особыми точками разных типов // Журн. физ. хим. 1971. Т. 45. № 6. С. 1473.
Серафимов Л.А. Правило азеотропии и классификация многокомпонентных смесей. X. Двукратно тангенциальные азеотропы // Журн. физ. хим. 1971. Т. 45. № 7. С. 1620.
Серафимов Л.А. Правило азеотропии и классификация многокомпонентных смесей. XI. Тангенциальная азеотропия в трехкомпонентных смесях и цепи топологических структур // Журн. физ. хим. 1971. Т. 45. № 10. С. 2448.
Serafimov L.A. Thermodynamic and topological analysis of heterogeneous equilibrium diagrams of multicomponent mixtures // Russ. J. Phys. Chem. A. 2002. V. 76. № 8. P. 1211. [Серафимов Л.А. Термодинамико-топологический анализ диаграмм гетерогенного равновесия многокомпонентных смесей // Журн. физ. хим. 2002. Т. 76. № 8. С. 1351.]
Свентославский В.В. Азеотропия и полиазеотропия. М: Химия, 1968.
Serafimov L.A., Chelyuskina T.V., Polkovnichenko A.V., Yakushev R.A. The analysis of the mutual transformations of the structures of diagrams of ternary systems via the formation of binary internal tangential azeotropes // Theor. Found. Chem. Eng. 2018. V. 52. № 6. P. 963. [Серафимов Л.А., Челюскина Т.В., Полковниченко А.В., Якушев Р.А. Анализ взаимных преобразований структур диаграмм трехкомпонентных систем путем образования бинарных внутренних тангенциальных азеотропов // Теор. осн. хим. технол. 2018. Т. 52. № 6. С. 636.]
Serafimov L.A., Chelyuskina T.V. Principles of classifying diagrams for different types of biazeotropic ternary mixtures // Russ. J. Phys. Chem. A. 2011. V. 85. № 5. P. 767. [Серафимов Л.А, Челюскина Т.В. Принципы классификации диаграмм различных типов биазеотропных тройных смесей // Журн. физ. хим. 2011. Т. 85. № 5. С. 854.]
Serafimov L.A., Chelyuskina T.V. Basic properties of tie-line vector fields of two-phase ternary mixtures: complex singular points // Theor. Found. Chem. Eng. 2003. V. 37. № 5. P. 482. [Серафимов Л.А., Челюскина Т.В. Основные закономерности векторных полей нод двухфазных трехкомпонентных смесей. Сложные особые точки // Теор. осн. хим. технол. 2003. Т. 37. № 5. С. 516.]
Serafimov L.A., Chelyuskina T.V. Complex singular points of the tie-line vector field diagrams of ternary mixtures // Theor. Found. Chem. Eng. 2005. V. 39. № 6. P. 599. [Серафимов Л.А., Челюскина Т.В. Сложные особые точки диаграмм векторных полей нод трехкомпонентных смесей // Теор. осн. хим. технол. 2005. Т. 39. № 6. С. 634.]
Serafimov L.A., Razova O.B., Frolkova A.V., Chelyuskina T.V. Observance of the Gibbs–Konovalov law at complex singular points of two-phase multicomponent systems // Theor. Found. Chem. Eng. 2008. V. 42. № 4. P. 415. [Серафимов Л.А., Разова О.Б., Фролкова А.В., Челюскина Т.В. Соблюдение закона Гиббса–Коновалова в сложных особых точках двухфазных многокомпонентных систем // Теор. осн. хим. технол. 2008. Т. 42. № 4. С. 429.]
Баутин Н.Н., Леонтович Е.А. Методы и приемы качественного исследования динамических систем на плоскости. М.: Наука, 1990.
Якушев Р.А., Устиненкова А.Д., Челюскина Т.В. Анализ эволюции структур диаграмм равновесия жидкость–пар трехкомпонентной системы, содержащей биазеотропную бинарную составляющую // Сб. науч. тр. Международной научно-практической конференции “Вопросы технических наук: новые подходы в решении актуальных проблем”. Казань, 2017. С. 99.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии



