Теоретические основы химической технологии, 2020, T. 54, № 6, стр. 775-783
Исследование изменения состава этилбензольной шихты в реакторе производства стирола с учетом парциальных давлений реагентов
С. Л. Подвальный a, А. П. Попов b, С. Г. Тихомиров b, О. В. Карманова b, *, О. Г. Неизвестный a, Е. Н. Ковалева b
a Воронежский государственный технический университет
Воронеж, Россия
b Воронежский государственный университет инженерных технологий
Воронеж, Россия
* E-mail: karolga@mail.ru
Поступила в редакцию 29.07.2019
После доработки 28.01.2020
Принята к публикации 14.02.2020
Аннотация
Разработано математическое описание процесса дегидрирования этилбензола с учетом изменения парциальных давлений и парциальных мольных объемов компонентов реакционной смеси. В проведенных вычислительных экспериментах пароэтилбензольная смесь рассмотрена как система взаимодействующих газов, для которой выполнено исследование влияния парциальных параметров компонентов на изменение компонентного состава реакционной среды, конверсии этилбензола, селективности по целевому продукту, а также на скорость снижения величин удельных скоростей реакций. Установлено, что мольные парциальные объемы и давления веществ оказывают существенное влияние на скорость протекания бимолекулярных реакций процесса и, как следствие, на динамику образования побочных продуктов; чувствительность констант скоростей реакций к изменению рассматриваемых параметров снижается по длине реакторной ступени. Полученные математические зависимости являются связующим звеном между управляемыми параметрами (конверсия этилбензола, селективность по целевому продукту) и физическими величинами состояния контактного газа. Модель может быть использована для оценки степени закоксованности каталитического слоя в процессе эксплуатации реакционного аппарата.
ВВЕДЕНИЕ
В процессе дегидрирования этилбензола регулирование содержания стирола в реакционной смеси производится в режиме “постфактум” (т.е. после того, как выявлено изменение содержания целевого продукта в контактном газе). Основной причиной данного производственного недостатка является отсутствие достоверного прогноза динамики физико-химических параметров в пространственно-временной области реакционной среды.
В связи с этим не представляется возможным применить концепцию упреждающего программного управления технологическим процессом по заранее построенным горизонтам изменения основных производственных показателей: концентрации стирола, конверсии этилбензола и селективности по целевому продукту. Существующие автоматизированные системы управления данным технологическим процессом производят расчет управляющих воздействий в условиях неопределенности.
Одним из условий улучшения качества управления и достижения высоких показателей энергоэффективности работы реакторной установки является устранение этого фактора. Эффективным путем решения этой задачи является применение метода имитационного моделирования динамики физических процессов и химических превращений, протекающих в реакционной зоне в зависимости от изменения параметров потока многокомпонентной среды.
При реализации данного подхода необходимо выявить источники “динамического хаоса”, влияющие на состав контактного газа на выходе из ступеней реакторного блока: состав каталитического слоя, изменения физико-химических параметров этилбензольной шихты в реакционном пространстве, случайные колебания технологических параметров (расходы и температуры потоков веществ, поступающих в реакторный блок), флуктуация (случайное отклонение) начального состава этилбензольной шихты [1].
Существующие математические модели реакционного механизма процесса требуют уточнения их структуры, поскольку их использование не обеспечивает требуемую точность прогнозирования. В то же время реализация алгоритма предиктивного программного управления предполагает наличие прогнозирующей модели. Расчет управляющих воздействий выполняется с учетом детерминированных изменений технологических параметров и значений физико-химических параметров потока реагирующих веществ в каждой точке реакционного пространства и временного интервала эксплуатации технологической линии [2, 3]. Это обусловливает актуальность усовершенствования математического описания динамики изменения основных параметров технологического процесса дегидрирования этилбензола [4–6].
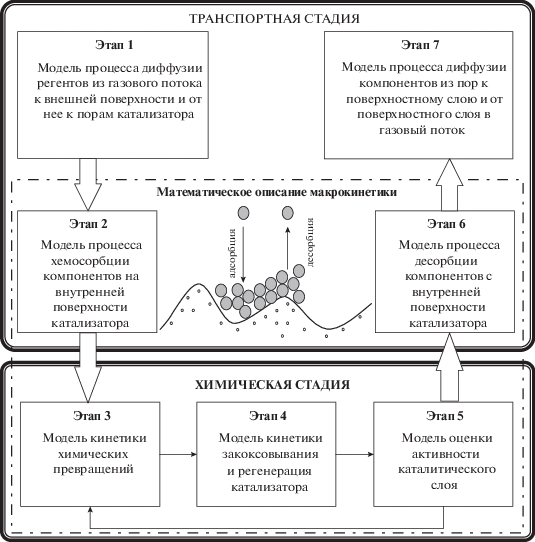
Получение стирола относится к классу гетерогенно-каталитических реакций, протекающих в газовой фазе на поверхности твердого неподвижного слоя катализатора. Как и все гетерогенные системы рассматриваемый процесс протекает в двух областях: кинетической и диффузионной. Поэтому для точного прогнозирования количества выделившегося целевого продукта необходимо провести исследование динамики каждой из указанных областей и переходной области между ними. Использование методов математического моделирования предполагает синтез математического описания процесса дегидрирования, включающий в себя модели всех его физико-химических стадий (рис. 1):
диффузии реагентов из реакционного потока к катализатору и обратно в реакционный поток;
хемосорбции и десорбции реагентов на поверхностях каталитической системы;
теплообменных процессов внутри реакционной зоны;
химических превращений, а также процессов закоксовывания и спекания каталитического слоя.
На основе результатов системного анализа исследуемого технологического процесса как объекта управления [7], а также с учетом особенностей протекания химических превращений предложена структура прогнозирующей модели дегидрирования и разработаны математические описания (модули) основных процессов, протекающих в процессе движения реакционного потока через ступени реакторного блока [8]. Интенсивность протекания гетерогенного химического процесса определяется скоростью его наиболее медленной стадии: транспортной (диффузионной) или химической (кинетической). При этом необходимо отметить, что реакция образования целевого продукта (стирола) существенно зависит от температуры, которая протекает на фоне высокой скорости газового потока, проходящего через реакторную ступень. Поэтому процесс протекает в кинетической области. Таким образом, основой математического описания процесса является модель механизма кинетики основных и побочных химических превращений.
Созданием подобных моделей и алгоритмов их реализации с последующим использованием для анализа энергетических потоков и управления различного типа реакторами производства стирола занимались многие ученые [9–11]. Анализ работ позволил выявить ряд существенных недостатков. В разработанных моделях химической кинетики константы скоростей прямых и обратных реакций являются функциями температуры, а их изменение подчиняется закону Аррениуса [12–14], при этом этилбензольная шихта и водяной пар рассматриваются как смесь химически не взаимодействующих газов [15]. Вследствие этого состав контактного газа рассчитывается без учета парциальных параметров компонентов среды [16], а итоговое содержание целевого продукта в смеси оказывается завышенным [17].
Производство стирола в настоящее время реализовано с использованием новых технологических регламентов и технических средств управления. В каждой ступени реактора вакуум-насосами создается давление, значение которого ниже атмосферного и не изменяется по всей длине реакторного пространства [18]. При постоянном давлении во всех сечениях ступеней реакторного блока процесс протекает с увеличением объема контактного газа, поглощением тепла и изменением парциальных давлений, парциальных мольных объемов каждого из реагирующих веществ по длине реакционного аппарата. Одним из наиболее важных научных результатов, полученных ранее в области инженерной химии гетерогенных процессов, является то, что для оценки степени снижения активности частиц катализатора дегидрирования этилбензола важно знать парциальные давления компонентов реакционного потока, а также величины давлений водяного пара и общего давления смеси. Наибольшее значение скорости дезактивации катализатора происходит под воздействием водяного пара с величиной давления, находящейся в интервале от 0 до 0.1 МПа [19].
Известные в настоящее время математические модели не позволяют производить расчет и оперативную оценку состояния компонентов шихты и каталитического слоя с требуемой степенью точности. Во всех приведенных работах [9–18] описываются процессы дегидрирования, протекающие в различных типах реакторных установок. В работах [9, 10, 12, 17] расчет кинетики процесса производился при постоянных значениях давлений составляющих реакционной смеси и водяного пара. Одновременно с этим считалось, что процесс дегидрирования лежит в диффузионной области и протекает с изменением давления потока по длине реактора. В более поздних статьях моделирование процесса проводилось с учетом изменения давлений только химических компонентов [11, 13] или исходя из допущения, что пароэтилбензольная смесь рассматривается как идеальный газ [15]. Известны модели, с помощью которых расчет кинетики процесса осуществляется с использованием таких параметров, как плотность катализатора [16] и изменение объема компонентов газовой смеси при диффузии в реакторе мембранного типа [11].
В результате проведенного анализа выделены кинетические аспекты дегидрирования этилбензола, требующие углубленного изучения.
Целью данной работы является решение первого этапа рассмотренной научно-технической задачи: разработка математического описания и исследование динамики изменения значений констант скоростей химических превращений и концентраций компонентов по длине реактора с учётом факторов, которые ранее не рассматривались при синтезе математических моделей. Для дегидрирования этилбензольной шихты этими факторами являются парциальные давления и мольные парциальные объемы реагентов.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
При математическом описании потенциальной энергии химических реакций наряду с температурой необходимо учитывать парциальное давление и парциальный мольный объем каждого из реагентов. При синтезе модели приняты следующие допущения:
– константы скоростей реакций являются функциями состояния контактного газа: парциальных давлений, мольных парциальных объемов соответствующих компонентов и температуры потока;
– реакция дегидрирования протекает в кинетической области;
– активность катализатора и парциальное давление водяного пара по длине реакционной зоны постоянны на фиксированном временном интервале;
– общее давление в аппарате рассматривается как сумма давлений взаимодействующих компонентов контактного газа;
– в произвольном сечении реакторной ступени величины парциальных мольных объемов реагентов принимаются как отношения общего объема смеси к количеству вещества отдельного взятого компонента при условии квазистационарности остальных физических величин реагентов на рассматриваемом участке.
Исходя из закона действующих масс, концентрации веществ рассчитываются как отношения Pj/(RT) и выполняется переход к количеству молей реагентов. Тогда кинетические уравнения математической модели [6, 19] можно представить в виде системы
(1)
$\left\{ \begin{gathered} {{n}_{j}}(l - \Delta l) = \frac{{\sum {{{C}_{j}}(l - \Delta l){{V}_{{sm}}}(l - \Delta l)P{{p}_{j}}(l - \Delta l)} }}{{{{P}_{{sm}}}}}, \hfill \\ j = \overline {A, \ldots ,G} \hfill \\ {{T}_{{sm}}}(l) = \frac{{{{Q}_{{sm}}}\left( 0 \right) - \Delta H{{n}_{A}}(l){{M}_{A}}}}{{{{c}_{{sm}}}(l)F{{m}_{{sm}}}}} \hfill \\ P{{p}_{j}}(l) = \frac{{{{n}_{j}}(l)R{{T}_{{sm}}}(l)}}{{{{V}_{{sm}}}(l) - Kr{{b}_{j}}{{n}_{j}}(l)}} - \frac{{Kr{{a}_{j}}{{n}_{j}}{{{(l)}}^{2}}}}{{{{V}_{{sm}}}{{{(l)}}^{2}}}} \hfill \\ \frac{{d{{C}_{j}}(l)}}{{dl}} = {{F}_{j}}\left( {\vec {x}(l),\vec {u},\vec {k}(l)} \right) \hfill \\ {{V}_{{sm}}}(0) = {{V}_{{sm}}}^{0},\,\,\,\,P{{p}_{j}}(0) = Pp_{j}^{0},\,\,\,\,{{T}_{{sm}}}(l) = T_{{_{{sm}}}}^{0}, \hfill \\ {{C}_{j}}\left( 0 \right) = C_{0}^{j},\,\,\,\,{{k}_{i}}\left( 0 \right) = k_{0}^{i},\,\,\,\,i = \overline {1,4} \hfill \\ \end{gathered} \right.,$Учет зависимости скоростей газофазных химических реакций от парциальных давлений веществ, вступающих во взаимодействие по гетерогенно-каталитическому механизму, обусловливает необходимость включения в состав математического описания эффективных констант скоростей значений парциальных давлений и парциальных мольных объемов реагентов. При этом сумма произведений этих величин
умноженная на 1/(RT(l)), является составляющей показателя степени экспоненты уравнения Аррениуса [20, 21].
Согласно упрощенной кинетической схеме реакций процесса, к бимолекулярной относится реакция образования толуола и метана, где в качестве реагентов выступают этилбензол и выделяющийся вместе со стиролом водород:
Полагая, что константа равновесия стадии образования водорода и стирола зависит только от температуры, а сумма давлений компонентов контактного газа равна общему давлению в аппарате, получена система дифференциальных уравнений, описывающая влияние парциальных давлений на динамику концентрационного состава шихты и на смещение химического равновесия в зависимости от линейной скорости реакционного потока:
(3)
$\left\{ {\begin{array}{*{20}{l}} \begin{gathered} \upsilon \frac{{d{{n}_{A}}(l)}}{{dl}} = {{k}_{1}}(l)\frac{{\sum {{{G}_{j}}(l){{V}_{{sm}}}(l)P{{p}_{B}}(l)} }}{{{{P}_{{sm}}}}} - \hfill \\ - \,\,\frac{{{{k}_{2}}(l)}}{{{{V}_{{sm}}}(l)}}\frac{{\sum {{{G}_{j}}{{{(l)}}^{2}}} {{V}_{{sm}}}{{{(l)}}^{2}}P{{p}_{A}}(l)P{{p}_{B}}(l)}}{{P_{{sm}}^{2}}}, \hfill \\ \end{gathered} \\ \begin{gathered} \upsilon \frac{{d{{n}_{B}}(l)}}{{dl}} = \frac{{{{k}_{2}}(l)}}{{{{V}_{{sm}}}(l)}}\frac{{\sum {{{G}_{j}}{{{(l)}}^{2}}} {{V}_{{sm}}}{{{(l)}}^{2}}P{{p}_{A}}(l)P{{p}_{B}}(l)}}{{P_{{sm}}^{2}}} - \hfill \\ - \,\,{{k}_{1}}(l)\frac{{\sum {{{G}_{j}}(l){{V}_{{sm}}}(l)P{{p}_{B}}(l)} }}{{{{P}_{{sm}}}}} - \hfill \\ - \,\,{{k}_{3}}(l)\frac{{\sum {{{G}_{j}}(l){{V}_{{sm}}}(l)P{{p}_{B}}(l)} }}{{{{P}_{{sm}}}}} - \hfill \\ - \,\,\frac{{{{k}_{4}}(l)}}{{V_{{sm}}^{{}}(l)}}\frac{{\sum {{{G}_{j}}{{{(l)}}^{2}}} {{V}_{{sm}}}{{{(l)}}^{2}}P{{p}_{A}}(l)P{{p}_{c}}(l)}}{{P_{{sm}}^{2}}}, \hfill \\ \end{gathered} \\ \begin{gathered} \upsilon \frac{{d{{n}_{C}}(l)}}{{dl}} = {{k}_{1}}(l)\frac{{\sum {{{G}_{j}}(l){{V}_{{sm}}}(l)P{{p}_{B}}(l)} }}{{{{P}_{{sm}}}}} - \frac{{{{k}_{2}}(l)}}{{{{V}_{{sm}}}(l)}} \times \hfill \\ \times \,\,\frac{{\sum {{{G}_{j}}{{{(l)}}^{2}}} {{V}_{{sm}}}{{{(l)}}^{2}}P{{p}_{A}}(l)P{{p}_{B}}(l)}}{{P_{{sm}}^{2}}} - \hfill \\ - \,\,\frac{{{{k}_{4}}(l)}}{{V_{{sm}}^{{}}(l)}}\frac{{\sum {{{G}_{j}}{{{(l)}}^{2}}} {{V}_{{sm}}}{{{(l)}}^{2}}P{{p}_{A}}(l)P{{p}_{c}}(l)}}{{P_{{sm}}^{2}}}, \hfill \\ \end{gathered} \\ {\upsilon \frac{{d{{n}_{D}}(l)}}{{dl}} = {{k}_{3}}(l)\frac{{\sum {{{G}_{j}}(l){{V}_{{sm}}}(l)P{{p}_{B}}(l)} }}{{{{P}_{{sm}}}}},} \\ {\upsilon \frac{{d{{n}_{E}}(l)}}{{dl}} = {{k}_{3}}(l)\frac{{\sum {{{G}_{j}}(l){{V}_{{sm}}}(l)P{{p}_{B}}(l)} }}{{{{P}_{{sm}}}}},} \\ {\upsilon \frac{{d{{n}_{F}}(l)}}{{dl}} = \frac{{{{k}_{4}}(l)}}{{{{V}_{{sm}}}(l)}}\frac{{\sum {{{G}_{j}}{{{(l)}}^{2}}} {{V}_{{sm}}}{{{(l)}}^{2}}P{{p}_{A}}(l)P{{p}_{C}}(l)}}{{P_{{sm}}^{2}}},} \\ {\upsilon \frac{{d{{n}_{G}}(l)}}{{dl}} = \frac{{{{k}_{4}}(l)}}{{{{V}_{{sm}}}(l)}}\frac{{\sum {{{G}_{j}}{{{(l)}}^{2}}} {{V}_{{sm}}}{{{(l)}}^{2}}P{{p}_{A}}(l)P{{p}_{C}}(l)}}{{P_{{sm}}^{2}}},} \\ {{{{\left. {{{n}_{A}}} \right|}}_{{l = 0}}} = {{{\left. {{{n}_{C}}} \right|}}_{{l = 0}}} = {{{\left. {{{n}_{E}}} \right|}}_{{l = 0}}} = {{{\left. {{{n}_{G}}} \right|}}_{{l = 0}}} = 0,} \\ {{{{\left. {{{n}_{B}}} \right|}}_{{l = 0}}} = n_{B}^{0},\,\,\,\,{{{\left. {{{n}_{D}}} \right|}}_{{l = 0}}} = n_{D}^{0},} \\ {{{{\left. {{{n}_{F}}} \right|}}_{{l = 0}}} = n_{F}^{0},} \end{array}} \right.$(4)
${{k}_{1}}(l) = k_{1}^{0}{{e}^{{ - \,\frac{{Ea + V{{p}_{B}}(l)P{{p}_{B}}(l)}}{{R{{T}_{{sm}}}(l)}}}}},$(5)
${{k}_{2}}(l) = {{{{k}_{1}}(l)} \mathord{\left/ {\vphantom {{{{k}_{1}}(l)} {kp(l)}}} \right. \kern-0em} {kp(l)}},$(7)
${{k}_{3}}(l) = k_{3}^{0}{{e}^{{ - \,\frac{{Ea\, + \,V{{p}_{B}}(l){{P}_{B}}(l)}}{{R{{T}_{{sm}}}(l)}}}}},$(8)
${{k}_{4}}(l) = k_{4}^{0}{{e}^{{ - \,\frac{{Ea\, + \,V{{p}_{B}}(l){{P}_{B}}(l)\, + \,V{{p}_{C}}(l){{P}_{C}}(l)}}{{R{{T}_{{sm}}}(l)}}}}}.$Применительно к процессам производства стирола подобного вида научных исследований не проводилось, что обусловливает оригинальность разработанной модели и вычислительных экспериментов.
ЧИСЛЕННЫЙ ЭКСПЕРИМЕНТ, РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Исследование влияния параметров состояния газофазной реакционной среды на скорости химических превращений и количественное распределение образовавшихся веществ проведено путем сравнительного анализа вычислительных экспериментов, выполненных с помощью исходной модели, приведенной в [6] (модель 1), и полученной системы дифференциальных уравнений (3) совместно с уравнениями расчета констант скоростей химических реакций (4)–(8) (модель 2).
Результаты расчета, полученные в виде значений процентных и мольных концентраций реагентов, общей конверсии этилбензола и конверсии по целевому продукту на выходе из первой реакторной ступени, отражены в табл. 1 и 2 и на рис. 2 соответственно.
Таблица 1.
Результаты расчетов по моделям 1 и 2
| Расход шихты, т/ч | Перепад температуры смеси между входом и выходом реакторной ступени (∆T) | Компонент шихты | Концентрация компонентов шихты на выходе из реакционной зоны | |||||
|---|---|---|---|---|---|---|---|---|
| Модель 1/Модель 2 | Модель 2 | Модель 1 | Отклонение | |||||
| ∆T1/∆T2, К | ωm2, мас. % | nm2, моль/л | ωm1, мас. % | nm1, моль/л | ωm1 – ωm2, мас. % |
nm1 – nm2, моль/л |
||
| 20 | 33.06/32.65 | Стирол | 34.57 | 18.44 | 35.00 | 18.67 | 0.431 | 0.230 |
| Этилбензол | 60.85 | 31.84 | 60.28 | 31.55 | –0.570 | –0.298 | ||
| Водород | 0.626 | 17.26 | 0.632 | 17.43 | 0.006 | 0.171 | ||
| Бензол | 1.166 | 0.830 | 1.180 | 0.839 | 0.013 | 0.010 | ||
| Этилен | 0.383 | 0.758 | 0.388 | 0.768 | 0.005 | 0.010 | ||
| Толуол | 2.063 | 1.244 | 2.161 | 1.303 | 0.098 | 0.059 | ||
| Метан | 0.342 | 1.184 | 0.359 | 1.243 | 0.017 | 0.059 | ||
| 26 | 28.53/28.21 | Стирол | 29.88 | 20.72 | 30.22 | 20.96 | 0.343 | 0.238 |
| Этилбензол | 66.38 | 45.16 | 65.94 | 44.86 | -0.440 | –0.299 | ||
| Водород | 0.546 | 19.56 | 0.551 | 19.75 | 0.005 | 0.187 | ||
| Бензол | 1.021 | 0.944 | 1.031 | 0.954 | 0.011 | 0.010 | ||
| Этилен | 0.331 | 0.851 | 0.334 | 0.861 | 0.004 | 0.010 | ||
| Толуол | 1.581 | 1.240 | 1.647 | 1.291 | 0.066 | 0.052 | ||
| Метан | 0.258 | 1.161 | 0.269 | 1.213 | 0.011 | 0.052 | ||
| 30 | 26.18/25.90 | Стирол | 27.44 | 21.96 | 27.74 | 22.20 | 0.299 | 0.239 |
| Этилбензол | 69.23 | 54.35 | 68.85 | 54.05 | –0.377 | –0.296 | ||
| Водород | 0.504 | 20.82 | 0.508 | 21.02 | 0.005 | 0.192 | ||
| Бензол | 0.945 | 1.008 | 0.954 | 1.018 | 0.009 | 0.010 | ||
| Этилен | 0.303 | 0.902 | 0.307 | 0.912 | 0.003 | 0.010 | ||
| Толуол | 1.356 | 1.226 | 1.408 | 1.273 | 0.052 | 0.047 | ||
| Метан | 0.219 | 1.136 | 0.228 | 1.183 | 0.009 | 0.047 | ||
Таблица 2.
Результаты расчета величины процентного отклонения значений концентраций реагентов, рассчитанных с помощью модели 2 от концентраций, полученных по модели 1
| Расход шихты, т/ч | $\delta \, = \frac{{{{\omega }_{{m1}}} - {{\omega }_{{m2}}}}}{{{{\omega }_{{m1}}}}} \times 100\% $ | ||||||
|---|---|---|---|---|---|---|---|
| Компонент | |||||||
| Стирол | Этилбензол | Водород | Бензол | Этилен | Толуол | Метан | |
| 20 | 1.23 | –0.95 | 0.98 | 1.14 | 1.24 | 4.51 | 4.73 |
| 22 | 1.20 | –0.84 | 0.97 | 1.10 | 1.21 | 4.33 | 4.56 |
| 24 | 1.17 | –0.74 | 0.96 | 1.07 | 1.17 | 4.15 | 4.40 |
| 26 | 1.14 | –0.67 | 0.94 | 1.03 | 1.14 | 3.99 | 4.25 |
| 28 | 1.11 | –0.60 | 0.93 | 1.00 | 1.11 | 3.84 | 4.11 |
| 30 | 1.08 | –0.55 | 0.91 | 0.97 | 1.08 | 3.69 | 3.98 |
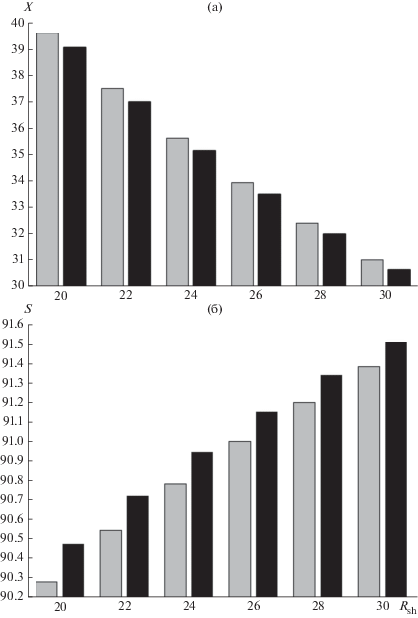
Рис. 2.
Влияние парциального давления и парциального мольного объема на общую конверсию этилбензола X (а) и на конверсию этилбензола в стирол S (б): серый цвет – модель 1, черный цвет – модель 2.
В ходе сравнительного анализа полученных результатов установлено на образование каких продуктов оказывают влияние парциальные мольные объемы и давления компонентов. Произведена оценка численных значений отклонений между результатами, полученными по моделям 1 и 2. Значения δ отражают процент отклонений концентраций веществ, рассчитанных с помощью модели 1, и представлены в табл. 2.
Анализ полученных результатов показал необходимость учета динамики свойств физических параметров пароэтилбензольной смеси при моделировании процессов, протекающих в реакционной зоне. Введение в математическую модель химической кинетики парциальных параметров обусловило снижение концентраций всех составляющих смеси при одновременном уменьшении общей конверсии этилбензола (рис. 2а). Увеличение расходов входящих в аппарат потоков реагентов и, как следствие, сокращение времени их контакта с каталитической системой приводит к снижению конверсии этилбензола и повышению селективности процесса относительно результатов, полученных по модели 1 (рис. 2б).
Одним из результатов проведенных вычислительных экспериментов является то, что концентрации основного и побочных продуктов, полученных при протекании мономолекулярных реакций, отличаются от подобных величин, рассчитанных по модели 1, в среднем на 1%. Для бимолекулярной реакции эта величина составила 4%. При варьировании величины расхода шихты отклонение количества этилбензола, вступившего в реакцию, находится в интервале 0.55–0.95%. Следовательно, учет парциальных величин газовых компонентов обусловливает увеличение выхода целевого продукта при снижении общей конверсии этилбензола, что подтверждается изменением величины конверсии этилбензола в стирол (рис. 2б).
Существенный вклад в изменение значений констант скоростей вносят элементарные химические акты, осуществляемые при взаимодействии двух и более молекул (бимолекулярные и тримолекулярные реакции), что подтверждается численными результатами моделирования процесса (табл. 1 и 2), а также исследованиями динамики изменения констант скоростей реакций (рис. 3).
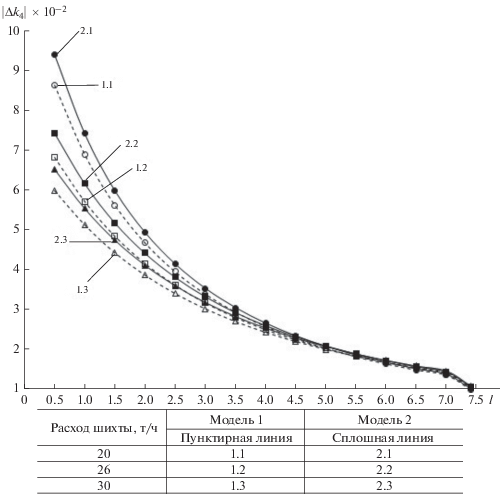
Рис. 3.
Изменение модуля величины приращения константы скорости реакции образования толуола и метана |∆k4|.
Исследование полученных траекторий приращений констант скоростей реакций дегидрирования позволило выявить следующие закономерности:
– парциальные характеристики состояния контактного газа оказывают незначительное влияние на изменение констант скоростей мономолекулярных реакций;
– по мере прохождения пароэтилбензольной смеси через реакционную ступень влияние парциальных параметров среды на динамику значений констант скоростей реакций стремится к нулю при произвольной величине нагрузки реактора по сырью; при этом необходимо отметить, что приращения констант скоростей k1 и k4 не зависят от парциальных объемов и давлений взаимодействующих веществ, начиная с участка, находящегося на расстоянии 4–4.5 м от входа в реактор (рис. 3);
– поскольку парциальные давления и объемы входят в показатели степени экспонент уравнений (4)–(8), константы скоростей и, следовательно, концентрации компонентов чувствительны к их абсолютным величинам и приращениям;
– учет основных физических характеристик веществ приводит к снижению значений скоростей химических реакций относительно данных параметров, полученных при использовании функциональных зависимостей между изменениями концентраций и температурным режимом внутри реакционного пространства;
– увеличение линейной скорости потока приводит к уменьшению общей конверсии сырья, которое сопровождается снижением количественного содержания побочных продуктов; одновременно с этим наблюдается повышение селективности по стиролу (рис. 2б).
ЗАКЛЮЧЕНИЕ
Результаты анализа проведенных вычислительных экспериментов позволили обосновать необходимость учета физико-химических параметров поступающих сред для расчета химической стадии процесса дегидрирования. Это позволило повысить точность моделирования и прогнозирования динамики скоростей основных и побочных реакций, конверсии сырья и селективности процесса. Установленные взаимосвязи служат основой для расчета управляющих (корректирующих) воздействий в случае возникновения возмущений по соотношению парциальных давлений исходных веществ и снижению активности каталитического слоя.
ОБОЗНАЧЕНИЯ
| a(l) | активность каталитической системы |
| С(l) | концентрация, моль/л |
| с(l) | удельная теплоемкость, Дж/(кг °С) |
| Ea | энергия активации, Дж/моль |
| Fmsm | массовый расход пароэтилбензольной смеси, кг/с |
| ∆H | количество энергии, затраченной на образование одного килограмма стирола, Дж/кг |
| Kraj | постоянная, зависящая от сил взаимодействия молекул компонента смеси |
| Krbj | постоянная, зависящая от величин критических температур, давлений и объема компонента смеси, кг/с |
| k1(l) | константа скорости образования стирола и водорода, с–1 |
| k2(l) | константа скорости обратной реакции, л/(моль с) |
| k3(l) | константа скорости образования бензола и этилена, с–1 |
| k4(l) | константа скорости образования толуола и метана, л/(моль с) |
| $k_{1}^{0}$, $k_{3}^{0}$, $k_{4}^{0}$ | предэкспоненциальные множители |
| $\overrightarrow k $ | вектор значений констант скоростей химических реакций |
| kp(l) | константа равновесия |
| ∆k | величина приращения константы скорости химической реакции |
| l | длина реакторной ступени, м |
| Ma | молярная масса стирола, кг/моль |
| n(l) | количество вещества, моль |
| P | давление, Па |
| Pp(l) | парциальное давление, Па |
| Q(0) | количество теплоты реакционной смеси на входе в реактор, Дж |
| R | расход этилбензольной шихты, кг/с |
| S | селективность по стиролу, % |
| T(l) | температура в реакторной ступени, К |
| ∆T | перепад температуры смеси между входом и выходом реакторной ступени, °С |
| $\vec {u}$ | вектор технологических параметров и управляющих воздействий |
| V(l) | объем смеси, л |
| Vp(l) | парциальный объем, л/моль |
| X | конверсия этилбензола, % |
| $\vec {x}$ | вектор значений физико-химических параметров потока реагентов и начальных значений концентраций веществ реакционной смеси |
| Z(l) | величина соотношения давлений водяного пара и этилбензольной шихты |
| δ | процент отклонения значений концентраций реагентов, рассчитанных с помощью модели 2 от величин концентраций, полученных по модели 1, % |
| ω | массовая доля |
ИНДЕКСЫ
Список литературы
Арапов Д.В., Тихомиров С.Г., Подвальный С.Л., Курицын В.А., Карманова О.В. Математическое моделирование промышленных процессов пиролиза бензина в трубчатых печах // Теор. осн. хим. технол. 2018. Т. 52. № 6. С. 649.
Зиятдинов Н.Н. Моделирование и оптимизация химико-технологических процессов и систем // Теор. осн. хим. технол. 2017. Т. 51. № 6. С. 613.
Островский Г.М., Зиятдинов Н.Н., Лаптева Т.В. Оптимизация технических систем. М.: КноРус, 2012.
Тихомиров С.Г., Семенов М.Е., Хаустов И.А., Битюков В.К., Хвостов А.А., Карманова О.В., Попов А.П. Контроль и прогнозирование параметров качества полимеров в процессе их деструкции в растворе // Теор. осн. хим. технол. 2018. Т. 52. № 4. С. 466.
Тихомиров С.Г., Подвальный С.Л., Хвостов А.А., Карманова О.В., Битюков В.К. Исследование и моделирование процесса деструкции полимера в массе // Теор. осн. хим. технол. 2018. Т. 52. № 1. С. 83.
Podvalny S.L., Popov A.P., Neizvestny O.G., Tikhomi-rov S.G. Software implementation of the dynamic model of the first stage of the reactor unit for styrene production in the MATLAB/SIMULINK environment // J. Phys.: Conf. Ser. 2019. V. 1203. Article number 012072. https://doi.org/10.1088/1742-6596/1203/1/012072
Попов А.П., Битюков В.К., Тихомиров С.Г., Неизвестный О.Г., Чертов Е.Д. Системный анализ реактора дегидрирования этилбензола как объекта управления // Вестн. ВГУИТ. Сер.: инф. технол., модел. упр. 2018. Т. 80. № 2 (76). С. 77.
Тихомиров С.Г., Подвальный С.Л., Попов А.П., Неизвестный О.Г. Синтез структуры прогнозирующей модели системы управления реактором дегидрирования этилбензола // Вестн. ТГТУ. Сер.: Автом. Инф. Упр. Приб. 2019. Т. 25. № 1. С. 6.
Tamsilian Y., Ebrahimi A.N., Ramazani A.S.A., Abdollahzadeh H. Modeling and sensitivity analysis of styrene monomer production process and investigation of catalyst behavior // Comput. Chem. Eng. 2012. V. 40. P. 1.
Abo-Ghander N.S., Grace J.R., Elnashaie S.S.E.H., Lim C.J. Modeling of a novel membrane reactor to integrate dehydrogenation of ethylbenzene to styrene with hydrogenation of nitrobenzene to aniline // Chem. Eng. Sci. 2008. V. 63. P. 1817.
Shelepova E.V., Vedyagin A.A., Mishakov I.V., Noskov A.S. Modeling of ethylbenzene dehydrogenation in catalytic membrane reactor with porous membrane // Catal. Sustainable Energy. 2014. V. 2. P. 1.
Abdalla B.K., Elnashaie S.S.E.H., Alkhowaite S., Elshishini S.S. Intrinsic kinetics and industrial reactors modeling for the dehydrogenation of ethylbenzene to styrene on promoted iron oxide catalysts // Appl. Catal., A. 1994. V. 113. P. 89.
Ali E., Hadj-Kali M. Energy efficiency analysis of styrene production by adiabatic ethylbenzene dehydrogenation using exergy analysis and heat integration // Pol. J. Chem. Technol. 2018. V. 20. № 1. P. 35.
Pérez-Sánchez A., Pérez Sánchez E.J., Segura Silva R.M. Simulation of the styrene production process via catalytic dehydrogenation of ethylbenzene using CHEMCAD® process simulator // Tecnura. 2017. V. 21. № 53. P. 15.
Mousavi S.M., Panahi P.N., Niaei A., Farzi A., Salari D. Modeling and Simulation of Styrene Monomer Reactor: Mathematical and Artificial Neural Network Model // Int. J. Sci. Eng. Res. 2012. V. 3. № 3. P. 1.
Gunorubon A.J. Simulation of an Isothermal Catalytic Membrane Reactor for the Dehydrogenation of ETHYLBENZENE // Chem. Process Eng. Res. 2012. V. 3. P. 1.
Assabumrungrat S., Suksomboon K., Praserthdam P., Tagawa T., Goto S. Simulation of a Palladium Membrane Reactor for Dehydrogenation of Ethylbenzene // J. Chem. Eng. Jpn. 2002. V. 35. № 3. P. 263.
Журавлева К.А., Назаров А.А. Получение стирола дегидрированием этилбензола // Вестн. Казан. технол. унив. 2012. С. 149.
Масагутов Р.М. Алюмосиликатные катализаторы и изменение их свойств при крекинге нефтепродуктов. М.: Химия, 1975.
Подвальный С.Л. Моделирование промышленных процессов полимеризации. М.: Химия, 1979.
Zagoruiko A.N., Belyi A.S., Smolikov M.D., Noskov A.S. Unsteady-State Kinetic Simulation of Oil Reforming and Coke Combustion Processes in the Fixed and Moving Catalyst beds // Catal. Today. 2014. V. 220–222. P. 168.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии