Теоретические основы химической технологии, 2020, T. 54, № 6, стр. 687-694
Динамика массообмена через поверхность раздела несмешивающихся жидкостей при резонансном воздействии ультразвука
О. М. Градов a, *, Ю. А. Заходяева a, А. А. Вошкин a
a Институт общей и неорганической химии им. Н.С. Курнакова РАН
Москва, Россия
* E-mail: lutt.plm@igic.ras.ru
Поступила в редакцию 21.07.2020
После доработки 24.07.2020
Принята к публикации 24.07.2020
Аннотация
Рассмотрены особенности резонансного поведения радиальных колебаний жидкой капли, помещенной в несмешивающуюся с ней жидкость, на основе полученного нелинейного уравнения, учитывающего вынуждающее воздействие в виде периодически меняющегося во времени акустического давления. Получены аналитические формулы для скорости массообмена в зависимости от амплитуды осцилляций акустического давления и времени ультразвуковой обработки объема экстрактора. Найдены пороговые значения амплитуды ультразвука и характерное время (инкремент) параметрической неустойчивости. Предложен метод варьирования частоты накачки для достижения максимальной эффективности экстракции в условиях применения стимулирующего воздействия ультразвука.
ВВЕДЕНИЕ
Экстракционные процессы постоянно совершенствуются на всем протяжении существования человеческого общества, поскольку тесно связаны с улучшением благосостояния людей. Это достигается в основном путем прямого использования развивающихся возможностей химии и физики в течение всего периода существования цивилизации [1]. В частности, проблема экстракции органических и неорганических веществ из растворов получает постоянное обогащение новыми аппаратурными решениями и теоретическими моделями [2–19], среди которых особый интерес представляют гибридные и совмещенные процессы [7–9, 15]. Задача извлечения и разделения металлов [15–19] занимает в этом ряду особое место и требует для своего успешного решения привлечение современных методов интенсификации. К ним можно отнести, прежде всего, использование ультразвука, воздействие которого способно оказать существенное влияние на результаты самых различных экспериментов от очистки почв от нефтепродуктов [20] до упрочнения металла [21]. Способность ультразвука интенсифицировать разнообразные физико-химические процессы опирается на его возможности изменять те или иные характеристики рассматриваемого явления и поэтому регулируемым способом влиять на конечный продукт. В частности, в работе [22] разработана методология ультразвуковой очистки почвы от неорганических загрязнений, а в [23] исследована зависимость сонохимических реакций от частоты ультразвукового воздействия на основе учета особенностей кавитационного процесса. К последним достижениям можно отнести и успешное применение ультразвукового облучения [24] для увеличения коэффициента адсорбции различных токсичных органических красителей и тяжелых металлов с помощью наночастиц, нанесенных на углеродную основу. Тем же методом последовательного отбора были выявлены также оптимальные условия использования ультразвука для осуществления непрерывной жидкостной экстракции ряда имеющих существенную практическую значимость органических веществ [25, 26]. На процессы экстракции можно повлиять в нужном направлении путем создания условий для реализации механизмов нелинейной акустики, как это показано в работах [27–32]. Но и в самом простом случае обыкновенного облучения рабочего объема экстрактора относительно слабым ультразвуковым излучением можно выявить определенные особенности, вносимые внешним воздействием, которые способны существенно изменить эффективность процесса. В настоящей работе такая важнейшая характеристика экстракции, как массообмен, реализуемая в условиях дробления исходного раствора, содержащего целевой компонент, на капли, исследуется для случая, когда внешнее ультразвуковое излучение непосредственно влияет на этот процесс, вынуждая жидкие шары совершать радиальные колебания и тем самым существенно изменяя картину извлечения целевого компонента по сравнению с традиционной схемой обработки жидкости. На основе полученного нелинейного уравнения для радиуса капли исследованы параметры вынужденных колебаний сферической поверхности при наличии резонансного воздействия ультразвука и выполнен анализ особенностей процесса массообмена через осциллирующую границу раздела сред. В результате этого выявленная специфичность зависимости концентрации экстрагируемого соединения от времени и интенсивности акустического излучения может оказаться решающим ориентиром при выборе рационального режима применения ультразвуковой интенсификации экстракционного процесса.
ПОСТАНОВКА ЗАДАЧИ И ИСХОДНЫЕ СООТНОШЕНИЯ
Получение достаточно обоснованной оценки влияния ультразвука на массообмен в условиях применения схемы дробления поступающей жидкой фракции связано с решением задачи о пульсациях капли, находящейся в другой несмешивающейся с ней жидкости, в которой давление меняется со временем t под воздействием ультразвука. В результате решения такой задачи становится возможным описание колебаний радиуса R(t) капли, с помощью которого вычислить изменение площади ее поверхности, на которой происходит массообмен.
Состояние равновесия между каплей и окружающей жидкостью, имеющих соответственно плотности ρ1(r, t) и ρ2(r, t), определяется балансом всех сил, действующих на ее сферической поверхности. С учетом вязкости, характеризуемой коэффициентами η1 и η2, соответствующее соотношение может быть записано в следующем виде [33]:
(1)
${{P}_{{\text{1}}}}{\text{(}}t{\text{)}} = {{P}_{{\text{2}}}}{\text{(}}t{\text{)}} + \frac{{2\alpha }}{{R{\text{(}}t{\text{)}}}} + 4{{\left. {\mu \frac{{\partial u}}{{\partial r}}} \right|}_{{r = R}}};\,\,\,\,\mu = {{\eta }_{1}} - {{\eta }_{2}}.$Здесь Р1(t) – внутреннее давление капли на ее поверхности, а Р2(t) – соответствующее значение со стороны окружающей жидкости, α – коэффициент поверхностного натяжения, u(r, t) – скорость перемещения жидкости по радиусу, зависящая от радиальной координаты r в системе, начало которой находится в центре капли. Это движение описывается уравнениями [33]
(2)
$\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial r}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial r}},$(3)
$\frac{{\partial \rho }}{{\partial t}} + \frac{{\text{1}}}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}\left( {{{r}^{{\text{2}}}}{{\rho }_{{}}}u} \right) = 0.$Локальное значение давления p = p(r) определяется уравнением состояния для этой области пространства, в которой находится сфера с радиусом r. Если при радиусе R0 капля находится в состоянии покоя вместе с окружающей ее жидкостью с гидростатическим давлением P0, то это условие равновесия в соответствии с (1) принимает вид
А уравнение состояния жидкости достаточно хорошо описывается формулой Тэта [34], которую в рассматриваемом случае можно записать в следующей форме
(5)
${{P}_{{\text{1}}}}{\text{(}}t{\text{)}} = {{A}_{{\text{1}}}}\left\{ {{{{\left( {\frac{{{{R}_{{\text{0}}}}}}{{R{\text{(}}t{\text{)}}}}} \right)}}^{{3\sigma }}} - 1} \right\} + {{P}_{{{\text{10}}}}}.$Здесь σ, А1 – константы, определяемая опытным путем для конденсированных сред.
Пренебрегая сжимаемостью жидкости, учет которой практически не меняет конечный результат, из (3) для скорости движения поверхности капли U(t) = dR/dt можно записать следующее выражение:
(6)
$u{\text{(}}r,t{\text{)}} = \frac{{{{R}^{{\text{2}}}}{\text{(}}t{\text{)}}U{\text{(}}t{\text{)}}}}{{{{r}^{{\text{2}}}}}}.$Вводя потенциал скорости φ(r, t) (u = ∂φ/∂r), уравнение (2) можно проинтегрировать по радиусу r в диапазоне от r до ∞ и представить в виде
(7)
$\frac{{\partial \varphi }}{{\partial t}} + \frac{{{{u}^{{\text{2}}}}}}{2} + \int\limits_r^\infty {\frac{{{\text{d}}p}}{\rho }} = 0.$Ввиду того, что для r → ∞ имеют место равенства φ = 0, u = 0 и p(r → ∞) = P∞, а плотность связана с давлением уравнением состояния, а из (6) следует, что φ = –UR2/r, то из (7) на поверхности капли получается с учетом (5) уравнение
(8)
$\begin{gathered} \frac{{\text{1}}}{r}\left\{ {{{R}^{{\text{2}}}}\frac{{dU}}{{dt}} + 2UR\frac{{dR}}{{dt}}} \right\} - {{U}^{{\text{2}}}}R\frac{{{{R}^{{\text{4}}}}}}{{{\text{2}}{{r}^{{\text{4}}}}}} + \\ + \,\,\frac{1}{{{{\rho }_{2}}}}[{{P}_{\infty }} - p{\text{(}}r,t{\text{)]}} = 0. \\ \end{gathered} $Поскольку P∞ складывается из гидростатического P0 и акустического давления Pmsinωt с амплитудой Pm и частотой ω, то с учетом (1) и очевидного соотношения P10 = P0 + 2α/R0уравнение (8) на поверхности сферы приобретает вид
(9)
$\begin{gathered} R{\text{(}}t{\text{)}}\frac{{{{d}^{{\text{2}}}}R}}{{d{{t}^{{\text{2}}}}}} + \frac{3}{2}{{\left( {\frac{{dR}}{{dt}}} \right)}^{2}} + \\ + \,\,\frac{1}{{{{\rho }_{2}}}}\left\{ {{{P}_{{\text{m}}}}{\text{sin}}\omega t + \frac{{4\mu }}{R}\frac{{dR}}{{dt}} + 2\alpha \frac{{{{R}_{{\text{0}}}} - R{\text{(}}t{\text{)}}}}{{R{\text{(}}t{\text{)}}{{R}_{{\text{0}}}}}} + \frac{{^{{^{{^{{}}}}}}}}{{_{{_{{_{{}}}}}}}}} \right. \\ \left. { + \,\,{{A}_{{\text{1}}}}\left[ {1 - {{{\left( {\frac{{{{R}_{{\text{0}}}}}}{{R{\text{(}}t{\text{)}}}}} \right)}}^{{3\sigma }}}} \right]} \right\} = 0. \\ \end{gathered} $Уравнение (9) описывает движение сферической поверхности капли жидкости, помещенной в несмешивающуюся с ней жидкую среду, которая находится под воздействием осциллирующего акустического давления. С особенностями динамики этого процесса могут быть связаны разнообразные проявления возможностей интенсификации экстракции с помощью ультразвука.
Существование у капли жидкости сферической формы собственных радиальных колебаний представляет определенный интерес для прямого использования при решении проблемы интенсификации процессов массообмена в жидких средах под ультразвуковым воздействием, хотя это и связано иногда с решением некоторых достаточно сложных вопросов. Дело в том, что применение ультразвука большой мощности приводит к целому ряду нежелательных побочных эффектов, таких как нагрев, кавитационное перемешивание, турбулизация и хаотизация потоков и т.д. Но простой ввод в жидкость ультразвуковых колебаний слабой интенсивности также не приводит к ожидаемым результатам. Вместе с тем хорошо известно [27, 34], что с помощью параметрического резонанса на собственных частотах любой колебательной системы можно сравнительно небольшим внешним усилием добиться больших амплитуд собственных колебаний. Поэтому изучение особенностей и условий реализации такого резонансного процесса могут представлять определенный интерес для успешной разработки эффективных ультразвуковых схем экстракции.
Анализ параметрического резонанса сферической капли, помещенной в несмешивающуюся с ней жидкость, которая находится под воздействием ультразвука, можно выполнить с помощью уравнения (9). Считая ультразвуковое воздействие слабым, а отклонение радиуса капли δR(t) от равновесного значения R0 небольшим, можно переписать уравнение (9) в виде разложения по малым нелинейным слагаемым:
(10)
$\begin{gathered} {{R}_{{\text{0}}}}\delta R{\kern 1pt} {\text{''}} + \frac{3}{2}{{\left( {\delta R{\kern 1pt} {\text{'}}} \right)}^{2}} + \delta R\delta R{\kern 1pt} {\text{''}} + {{\Omega }^{2}}{{R}_{{\text{0}}}}\delta R + {{P}_{{\text{S}}}}{\text{sin}}\omega t + \\ + \,\,{\text{2}}{{\gamma }_{{\text{d}}}}{{R}_{{\text{0}}}}\delta R{\kern 1pt} {\text{'}} - (\Omega _{{\,1}}^{2} - \Omega _{{\,2}}^{2})\delta {{R}^{{\text{2}}}} + \\ + \,\,\left[ {\frac{{3\sigma + 2}}{3}\Omega {\kern 1pt} _{1}^{2} - \Omega _{{\,2}}^{2}} \right]\frac{{\delta {{R}^{{\text{3}}}}}}{{{{R}_{{\text{0}}}}}} = 0. \\ \end{gathered} $Здесь штрихом обозначена производная по времени и приняты следующие обозначения:
(11)
$\begin{gathered} {{P}_{{\text{S}}}} = \frac{{{{P}_{{\text{m}}}}}}{{{\text{2}}{{\rho }_{2}}R_{{\text{0}}}^{{\text{2}}}}},\,\,\,\,{{\Omega }^{2}} = \frac{{\Omega _{{\,1}}^{2}}}{{1 + {\text{3}}\sigma }} - \Omega _{{\,2}}^{2}; \\ \Omega _{{\,1}}^{2} = \frac{{{\text{3}}\sigma (1 + {\text{3}}\sigma ){{A}_{{\text{1}}}}}}{{{{\rho }_{2}}R_{{\text{0}}}^{{\text{2}}}}},\,\,\,\Omega _{{\,2}}^{2} = \frac{{2\alpha }}{{{{\rho }_{2}}R_{{\text{0}}}^{{\text{3}}}}},\,\,\,{{\gamma }_{{\text{d}}}} = \frac{{2\mu }}{{{{\rho }_{2}}R_{{\text{0}}}^{{\text{2}}}}}. \\ \end{gathered} $Линеаризация уравнения (10) позволяет получить (в условиях, когда ультразвук отсутствует) частоту и декремент затухания собственных радиальных колебаний капли, которые оказываются равными величинам Ω и γd соответственно, представленными формулой (11).
В линейном приближении радиус капли, помещенной в несмешивающуюся с ней жидкость, которая находится под воздействием ультразвука с частотой ω = 2Ω, может быть представлен в виде
(12)
$\begin{gathered} {{R}_{{}}} = {{R}_{{\text{0}}}} + \delta {{R}_{{\text{m}}}}{\text{(}}t{\text{)sin}}\Omega t + \delta {{R}_{{\text{0}}}}{\text{sin2}}\Omega t + \ldots {\text{,}} \\ \left| {\partial {\text{ln}}{{\delta {{R}_{{\text{m}}}}} \mathord{\left/ {\vphantom {{\delta {{R}_{{\text{m}}}}} {\partial t}}} \right. \kern-0em} {\partial t}}} \right| \ll \Omega . \\ \end{gathered} $Как это уже подчеркивалось выше, наиболее интересным представляется случай, когда воздействие ультразвука на процессы массообмена проявляются при относительно малых интенсивностях его применения, исключающих создание нежелательных побочных явлений силового характера (нагрев, кавитация и пр.), т.е. когда R0$ \gg $ δR0, δRm. При этом на начальной стадии параметрической неустойчивости δR0$ \gg $ δRm, а на стадии ее насыщения, когда δRm перестает зависеть от времени и обретает постоянное значение δRS, эти амплитуды могут иметь произвольное соотношение друг к другу по величине.
Гармонический анализ уравнения (10) для второй гармоники собственной частоты позволяет получить в линейном приближении, достаточном для вычисления инкремента неустойчивости на начальной стадии ее развития слабым внешним воздействием, следующее выражение для амплитуды δR0 накачки:
(13)
$\delta {{R}_{{\text{0}}}} = \frac{{{{P}_{{\text{S}}}}}}{{3{{\Omega }^{2}}}}{{R}_{{\text{0}}}}.$На начальной стадии развития параметрического резонанса, когда возбуждаемые на частоте Ω колебания экспоненциально быстро нарастают во времени от малых начальных значений амплитуд, можно, используя известную методику [27, 34], получить из (10) следующее значение для инкремента γ неустойчивости:
(14)
$\gamma = - \gamma {}_{{\text{d}}}\,\, + \,\,\frac{{\Omega _{{\text{p}}}^{2}}}{{2\Omega }}\frac{{\delta {{R}_{0}}}}{{{{R}_{0}}}};\,\,\,\,\Omega {\kern 1pt} _{{\text{p}}}^{2}\,\, = 2\Omega {\kern 1pt} _{1}^{2}\,\, - 2\Omega _{2}^{2}\,\, - {{\Omega }^{2}}.$По мере нарастания интенсивности колебаний их инкремент уменьшается и становится равным нулю на стадии насыщения неустойчивости, когда амплитуда на частоте Ω достигает предельного значения δRS, определяемого нелинейностью исходного уравнения (10):
(15)
$\delta {{R}_{{\text{S}}}} = \sqrt {{{R}_{{\text{0}}}}\delta {{R}_{{\text{0}}}}} \frac{{{{\Omega }_{{\text{p}}}}}}{{\sqrt 3 \Omega {{{\kern 1pt} }_{{\text{m}}}}}};\,\,\,\Omega \,_{{\text{m}}}^{{\text{2}}}\,\, = \frac{{3\sigma + 2}}{3}\Omega {\kern 1pt} _{{\text{1}}}^{{\text{2}}}\,\, - \Omega {\kern 1pt} _{{\text{2}}}^{{\text{2}}}.$Пороговое значение амплитуды накачки δRth, в случае превышения которого (δR0 ≥ δRth) развивается параметрическая неустойчивость, определяется результатом выполнения требования равенства нулю инкремента (14):
(16)
$\delta {{R}_{{{\text{th}}}}} = \frac{{2\gamma {}_{{\text{d}}}{\kern 1pt} \Omega }}{{\Omega {\kern 1pt} _{{\text{p}}}^{{\text{2}}}}}{{R}_{0}}.$С учетом (13) из формулы (16) можно получить соответствующее пороговое значение для амплитуды внешнего акустического давления.
Таким образом, капля жидкости радиусом R0 и частотой Ω собственных радиальных колебаний испытывает экспоненциально быстрое нарастание их амплитуды в случае, когда она подвергается акустическому облучению на частоте 2Ω с интенсивностью, превышающей некоторое пороговое значение (16), (13). При этом отклонение частоты внешнего воздействия от резонансного значения, когда параметрическая раскачка еще возможна, пропорционально, как показывает анализ [34], величине ΩδR0/R0, что соответствует допустимой девиации ΔR радиуса капли величине δR0. Поэтому для достижения ощутимой эффективности рассматриваемого механизма ультразвуковой экстракции требуется обеспечить достаточно высокую однородность дробления исходной жидкости, т.е. идентичность капель по размеру должна иметь малые отклонения от стандарта.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Жидкость жидкостная экстракция обладает некоторыми характерными особенностями, которые можно использовать при проведении ориентировочных оценок на основе построения упрощенной модели процесса. Такой центральной особенностью является массообмен через поверхность раздела несмешивающихся жидкостей. Использование ультразвука приводит к тому, что площадь этой поверхности осциллирует во времени. Поэтому вполне естественно ожидать, что его влияние на параметры экстракции может оказаться весьма заметным. Для выполнения соответствующих расчетов следует рассмотреть жидкую каплю сферической формы, находящуюся в несмешивающейся с ней жидкости, в которой среди действующих силовых факторов присутствует осциллирующее во времени акустическое давление. Важнейшие упрощающие предположения связаны при этом с требованием пространственной однородности плотности извлекаемых соединений (далее частиц) в объеме капли и с условием мгновенности их извлечения в тот момент, когда соединение касается поверхности раздела сред. В результате этих предположений весь ход экстракции моделируется фактически дискретным процессом, когда мгновенная экстракция всех частиц из приповерхностного слоя капли толщиной L, равной их характерному размеру, обеспечивает изменение без экстрагирования радиуса капли R(t) на величину L за время Δt. Введение этой дискретности позволяет воспользоваться результатом деятельности переходных процессов, приводящих к равномерности пространственного распределения извлекаемых частиц, без детального рассмотрения их сущности. На рис. 1 представлена схема, поясняющая в рамках дискретной модели взаимосвязь между продолжительностью цикла дискретности Δt и глубиной L зоны извлечения частиц.
Рис. 1.
Взаимосвязь параметров модели дискретной экстракции частиц с характерным размером L из капли жидкости при изменении во времени ее радиуса R(t) под воздействием ультразвука. Извлекаемые частицы схематично изображены в виде случайно расположенных шариков.
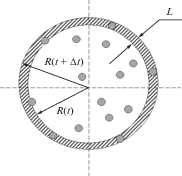
Обозначив через N число частиц в капле, которые подлежат извлечению, для их плотности n0 пространственного распределения, которое должно, по предположению, быть однородным за счет возникающих ультразвуковых потоков, можно записать очевидное определение n0 = ${{3N} \mathord{\left/ {\vphantom {{3N} {4pR_{0}^{3}}}} \right. \kern-0em} {4pR_{0}^{3}}}$. Необходимо также отметить, что в отсутствие ультразвука время Δt заполнения частицами приповерхностного слоя определяется скоростью диффузионных процессов. Поэтому обсуждаемая схема описания динамики экстракции применима и в случае, когда ультразвука нет. Но в случае быстрых (по сравнению с диффузией или другими процессами установления равновесия) осцилляций, когда именно они определяют скорость экстракции, это время легко рассчитать с помощью представления (12):
(17)
$L = \delta {{R}_{{\text{m}}}}\left| {{\text{sin}}\omega (t + \Delta t{\text{)}} - {\text{sin}}\omega t} \right|.$В формуле (17) использовано абсолютное значение прироста радиуса капли, поскольку интерес представляет только размер приповерхностного слоя, а направление движения поверхности капли может быть произвольным. Для ωΔt < 1 из (17) получается следующая оценка периода Δt дискретности процесса экстракции:
(18)
$\Delta t \cong \frac{L}{{\delta {{R}_{{\text{m}}}}\omega \left| {{\text{cos}}\omega t} \right|}}.$Из (18) видно, что величина Δt в рассматриваемой модели существенно зависит от того момента времени от начала текущего периода ультразвуковых колебаний, когда произошел акт извлечения частиц из капли. Строгий учет этой особенности ультразвуковой пульсации капли усложняет вычисления, но не приводит к существенной коррекции конечного результата. Поэтому выражение (18) можно усреднить по периоду ультразвуковых осцилляций Т = 2π/ω. В результате из (18) можно приближенно записать
Пусть dn – количество циклов экстрагирования, произошедших за промежуток времени dτ = = Δtdn. В этом случае число частиц dN, извлеченных из капли, определяется очевидной формулой
(20)
$dN = - 4\pi {{R}^{2}}(t)L{{n}_{0}}dn \equiv - 4\pi {{R}^{2}}(t)L\frac{{{{n}_{0}}}}{{\Delta t}}d\tau .$Из (20) после интегрирования получается следующее выражение для изменения во времени числа частиц в капле:
(21)
$N(\tau ) \cong {{N}_{0}}\exp \{ - 6\delta {{R}_{{\text{m}}}}{{\omega \tau } \mathord{\left/ {\vphantom {{\omega \tau } {(\pi {{R}_{0}})}}} \right. \kern-0em} {(\pi {{R}_{0}})}}\} .$Из (21) видно, что число частиц экспоненциально быстро убывает со временем от начального значения N0, и характерный период этого изменения зависит от амплитуды и частоты ультразвука. Вид этой зависимости определяется типом колебаний, который заставляет осциллировать радиус капли и устанавливается в результате решения уравнения (10). В случае параметрического резонанса, когда частота этих осцилляций равна частоте собственных колебаний Ω, их амплитуда связана с накачкой формулами (13), (15). Если параметрического резонанса нет (например, величина расстройки $\left| {\omega --2\Omega } \right|$ превышает границу диапазона, в которой резонанс возможен [34]), но ω ≈ 2Ω, то на этой частоте амплитуда осцилляций радиуса капли соотносится с внешним акустическим давлением по формуле (13). Наконец, при выполнении условий линейного резонанса, когда ω ≈ Ω, для амплитуды δRm из (10) можно получить следующее приближенное выражение:
(22)
$\frac{{\delta {{R}_{{\text{m}}}}}}{{{{R}_{{\text{0}}}}}} \approx \frac{1}{3}{{\left( {\frac{{{{P}_{{\text{S}}}}}}{{{{\omega }^{2}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}.$Сравнение результатов экстракции, полученных при одинаковой интенсивности ультразвука, но для разных частот его воздействия, можно получить с помощью формулы (21), из которой для меняющейся во времени плотности δn(τ) вещества, извлекаемого из капли (или одновременно из какого-то множества капель), вытекает следующая очевидная формула:
(23)
$\delta n(\tau ) \cong D\left[ {1 - \exp \{ - 6\delta {{R}_{{\text{m}}}}{{\omega \tau } \mathord{\left/ {\vphantom {{\omega \tau } {(\pi {{R}_{0}})}}} \right. \kern-0em} {(\pi {{R}_{0}})}}\} } \right].$Здесь D – максимальная плотность экстрагируемой субстанции, которая может быть извлечена с применением задействованных методов очистки.
Таким образом, подставляя значение амплитуды колебаний поверхности капли для каждого из трех выбранных выше диапазонов частот внешнего ультразвукового воздействия с помощью формул (13), (15) и (22) в (23), можно реально проследить динамику процесса ультразвуковой экстракции на примере поведения отдельного элемента дробления исходного раствора в экстракторе. Результаты соответствующих расчетов представлены на рис. 2.
Рис. 2.
Сравнительные результаты экстракции под воздействием ультразвука для разных типов колебаний радиуса капли: 1 – колебания на частоте Ω в условиях линейного резонанса ω = Ω; 2 – колебания на частоте Ω в условиях параметрического резонанса ω = 2Ω; 3 – колебания на частоте 2Ω в условиях отсутствия параметрического резонанса в окрестности диапазона ω ≈ 2Ω.
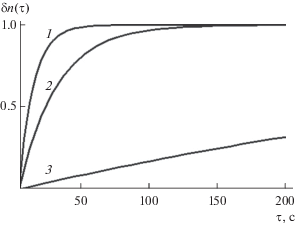
Кривые, изображающие на рис. 2 функцию δn(τ) в соответствии с выражением (23), получены для амплитуды ультразвука Рm = 0.1 Па и следующих значений параметров жидкости: α = 0.075 кг/с, μ = 0.5 × 10–3 (Н с)/м2, ρ = 103 кг/м3, Ω = 300 кГц, D = 1.
Из полученных расчетов видно, что в условиях резонанса (ω = Ω или ω = 2Ω) скорость извлечения частиц значительно превышает соответствующее значение, характеризующее экстракцию в отсутствие резонанса. Следует отметить, что кривая 3 на этом рисунке близка к описанию поведения функции δn(τ) во всем ультразвуковом диапазоне частот за исключением узких окрестностей резонансов ω = Ω и ω = 2Ω. Вследствие малой ширины областей резонансов довольно сложно обеспечить попадание в них одновременно множества капель, находящихся в рабочей зоне экстрактора, поскольку в этом случае их размеры должны были бы практически точно совпадать друг с другом. Тем не менее при наличии приемлемого разброса по величине радиусов капель можно варьированием частоты ультразвука с правильно подобранной скоростью добиться резонансной ультразвуковой экстракции от большинства из них, обеспечив нужную быстроту извлечения частиц.
Если оптимальное время обработки τ0 ультразвуком определять по количеству извлеченных частиц εN0 (0 < ε < 1), то из (21) можно записать
(24)
${{\tau }_{0}} = \frac{{\pi {{R}_{{\text{0}}}}}}{{6\delta {{R}_{{\text{m}}}}\omega }}{\text{ln}}\left( {\frac{1}{\varepsilon }} \right).$Из (24) следует, что, задавая уровень концентрации извлекаемых частиц, который требуется в конце ультразвуковой обработки, можно определить необходимое время акустического воздействия для выбранной интенсивности и частоты ультразвука. При этом оно оказывается обратно пропорциональным амплитуде акустического давления, обращаясь формально в бесконечность с уменьшением к нулю внешнего воздействия. На самом деле такое развитие событий никогда на практике не реализуется, и экстракция осуществляется за конечное время из-за диффузии и конвекции, которые были исключены из настоящего рассмотрения. Формула (24) указывает также на сокращение времени обработки с уменьшением размера капли и ростом частоты ультразвука. В условиях резонанса время τ0 задает скорость варьирования частотой ультразвука, обеспечивая пребывание частоты ω(t) в диапазоне значений, находящихся в границах области существенного увеличения амплитуды колебаний.
ЗАКЛЮЧЕНИЕ
Результаты настоящей работы позволяют сформулировать несколько заключений, обобщающих важнейшие итоги выполненных исследований.
Выполненный анализ особенностей воздействия ультразвукового излучения на отдельную каплю показывает, что механизм ультразвуковой экстракции, основу которого составляют осциллирующие потоки жидкости в исходной капле дробления, может обеспечить многократное ускорение экстракции в окрестности частот линейного ω = Ω и параметрического ω = 2Ω резонансов. Несмотря на то, что обеспечить полную идентичность по размерам всех капель в рабочем объеме экстрактора, необходимую для одновременного их вовлечения в резонансный процесс, практически невозможно, тем не менее, варьирование частотой ультразвука позволяет максимально полно использовать преимущества резонанса. К последним относятся, прежде всего, высокая скорость экстракции и малая интенсивность внешнего воздействия, когда параметры системы остаются фактически неизменными после подключения ультразвукового облучения.
Полученные выражения для времени ультразвукового облучения рабочего объема экстрактора, амплитуды колебаний поверхности капли, порогового значения интенсивности ультразвуковой накачки и других характеристик позволяют создать определенные схемы ультразвуковой обработки, которые способны значительно повысить эффективность применения ультразвука путем использования резонансного характера экстракционных процессов. Выявленные связи параметров ультразвука с показателями экстракции открывают перспективы внедрения новых методов регулируемого динамики межфазного распределения.
Резонансное использование ультразвука существенно снижает требования к мощности соответствующих установок и дает определенные преимущества по отношению к компактности конструкции, возможности оптимального размещения узлов и обеспечения легкости необходимого регулирования и корректирования параметров. Применение резонансных схем ультразвука при экстракции имеет все возможности оказаться существенно более экономичным, эффективным, удобным и перспективным способом интенсификации экстракционных процессов.
Работа выполнена в рамках государственного задания ИОНХ РАН в сфере фундаментальных научных исследований и при финансовой поддержке Российского фонда фундаментальных исследований в рамках научного проекта № 18-29-24170.
ОБОЗНАЧЕНИЯ
| А1 | константа, входящая в уравнение состояния Тэта |
| L | характерный размер частиц, извлекаемых из жидкости, м |
| N | число частиц, экстрагируемых из капли |
| P0 | гидростатическое давление в жидкости, Па |
| Р1(t) | внутреннее давление капли на ее поверхности, Па |
| Р2(t) | внешнее давление на поверхность капли, Па |
| Pm | амплитуда акустического давления, Па |
| p(r) | локальное значение давления, Па |
| R(t) | осциллирующий радиус капли жидкости, м |
| R0 | равновесный радиус капли жидкости, м |
| δR(t) | отклонение радиуса капли от равновесного значения, м |
| δR0 | амплитуды параметрической накачки, м |
| δRm | амплитуда колебаний радиуса капли, м |
| r | радиальная координата в цилиндрической системе, м |
| t | время, с |
| U(t) | скорость движения поверхности капли, м/с |
| u(r, t) | скорость перемещения жидкости по радиусу, м/с |
| α | коэффициент поверхностного натяжения, Дж/м2 |
| γ | декремент затухания собственных колебаний капли или инкремент неустойчивости, Гц |
| η1 | вязкость жидкости в капле, кг/(м с) |
| η2 | вязкость жидкости, окружающей каплю, кг/(м с) |
| ρ1 | плотность жидкости в капле, кг/м3 |
| ρ2 | плотность жидкости, окружающей каплю, кг/м3 |
| σ | константа, входящая в уравнение состояния Тэта |
| τ | суммарная продолжительность ряда циклов экстрагирования, с |
| τ0 | длительность экстрагирования заданного числа частиц из капли, с |
| φ(r, t) | потенциал скорости собственных колебаний, с–1 |
| Ω | круговая частота собственных колебаний капли жидкости, Гц |
| ω | круговая частота ультразвуковых колебаний, Гц |
ИНДЕКСЫ
Список литературы
Chemat F., Rombaut N., Sicaire A., Meullemiestre A., Fabiano-Tixier A., Abert-Vian M. Ultrasound assisted extraction of food and natural products. Mechanisms, techniques, combinations, protocols and applications. A review // Ultrason. Sonochem. 2017. V. 34. P. 540.
Chemat F., Cravotto G. Combined extraction techniques // Enhancing Extraction Processes in the Food Industry / Eds. Lebovka N., Vorobiev E., Chemat F. Cambridge: CRC, 2011. Ch. 6. P. 173.
Palma M., Barbero G.F., Pineiro Z., Liazid A., Barroso C.G., Rostagno M.A., Prado J.M., Meireles M.A.A. Extraction of natural products: principles and fundamental aspects // Natural Product Extraction: Principles and Applications / Eds. Rostagno M.A., Prado J.M. Cambridge: Royal Society of Chemistry, 2013. Ch. 2. P. 58.
Wan P.J., Wakelyn P.J. Technology and Solvents for Extracting Oilseeds and Nonpetroleum Oils. Urbana, Ill.: American Oil Chemists’ Society, 1997.
Bligh E.G., Dyer W.J. A rapid method of total lipid extraction and purification // Can. J. Biochem. Physiol. 1959. V. 37. P. 911.
Folch J., Lees M., Sloane Stanley G.H. A simple method for the isolation and purification of total lipides from animal tissues // J. Biol. Chem. 1957. V. 226. P. 497.
Kostanyan A.E., Voshkin A.A. Support-free pulsed liquid-liquid chromatography // J. Chromatogr. A. 2009. V. 1216. № 45. P. 7761.
Kostanyan A.E., Voshkin A.A., Kodin N.V. Controlled-cycle pulsed liquid-liquid chromatography. A modified version of Craig’s counter-current distribution // J. Chromatogr. A. 2011. V. 1218. № 36. P. 6135.
Kostanyan A.E., Voshkin A.A. Pulsation cyclic liquid-liquid chromatography // Theor. Found. Chem. Eng. 2009. V. 43. № 5. P. 729.
Kostanyan A.E., Voshkin A.A. Analysis of cyclic liquid chromatography // Theor. Found. Chem. Eng. 2011. V. 45. № 1. Р. 68. [Костанян А.Е., Вошкин А.А. Анализ циклического процесса жидкостной хроматографии // Теор. осн. хим. технол. 2011. Т. 45. № 1. С. 68.]
Kostanyan A.E., Voshkin A.A., Kodin N.V. Pulsed cyclic device for liquid countercurrent chromatography // Theor. Found. Chem. Eng. 2011. V. 45. № 5. P. 779.
Hewitson P., Sutherland I., Kostanyan A.E., Voshkin A.A., Ignatova S. Intermittent counter-current extraction—Equilibrium cell model, scaling and an improved bobbin design // J. Chromatogr. A. 2013. V. 1303. P. 18.
Kostanian A.E., Voshkin A.A. Analysis of new counter-current chromatography operating modes // J. Chromatogr. A. 2007. V. 1151. № 1–2. P. 126.
Voshkin A.A., Kodin N.V., Kostanyan A.E. Column miniextractors with a vibrating nozzle // Theor. Found. Chem. Eng. 2010. V. 44. № 4. P. 616.
Kostanyan A.E., Egorova N.S., Voshkin A.A., Zonov S.S. Extraction of uranyl, ytterbium, and lanthanum nitrates in a three-compartment multiphase extractor // Theor. Found. Chem. Eng. 2008. V. 42. № 5. P. 718.
Voshkin A.A., Kodin N.V., Kondakov D.F., Kostanyan A.E. Study of metal extraction in high-frequency vibration mini-columns // Russ. J. Inorg. Chem. 2010. V. 55. № 5. Р. 794. [Вошкин А.А., Кодин Н.В., Кондаков Д.Ф., Костанян А.Е. Исследование экстракции металлов в высокочастотных вибрационных миниколоннах // Журн. неорг. хим. 2010. Т. 55. № 5. С. 852.]
Mellah A., Benachour D. The solvent extraction of zinc, cadmium and chromium from phosphoric acid solutions by tri-n-butyl phosphate in kerosene diluent // Sep. Purif. Technol. 2007. V. 56. P. 220.
Daryabor M., Ahmadi A., Zilouei H. Solvent extraction of cadmium and zinc from sulphate solutions: comparison of mechanical agitation and ultrasonic irradiation // Ultrason. Sonochem. 2017. V. 34. № 1. P. 931.
Jha M.K., Gupta D., Choubey P.K., Kumar V., Jeong J., Lee J.-C. Solvent extraction of copper, zinc, cadmium and nickel from sulfate solution in mixer settler unit (MSU) // Sep. Purif. Technol. 2014. V. 122. P. 119.
Mullakaev M.S., Vexler G.B., Mullakaev R.M. Sonochemical technology for separating oil sludge and oil-contaminated soil // Pet. Sci. Technol. 2018. V. 36. № 8. P. 604.
Abramov V.O., Abramov O.V., Sommer F., Gradov O.M., Smirnov O.M. Surface hardening of metals by ultrasonically accelerated small metal balls // Ultrasonics. 1998. V. 36. № 10. P. 1013.
Newman A.P., Lorimer J.P., Mason T.J., Hunt K.R. An investigation into the ultrasonic treatment of polluted solids // Ultrason. Sonochem. 1997. V. 4. P. 153.
Entezari M.H., Kruus P. Effect of frequency on sonochemical reactions. I: Oxidation of iodide // Ultrason. Sonochem. 1994. V. 1. P. 75.
Dashamiri S., Ghaedi M., Dashtian K., Rahimi M.R., Goudarzi A., Jannesar R. Ultrasonic enhancement of the simultaneous removal of quaternary toxic organic dyes by CuO nanoparticles loaded on activated carbon: central composite design, kinetic and isotherm study // Ultrason. Sonochem. 2016. V. 31. P. 546.
Hu Y., Kwan T., Daoud W., Lin C. Continuous ultrasonic-mediated solvent extraction of lactic acid from fermentation broths // J. Cleaner Prod. 2017. V. 145. P. 142.
Dordevic T., Antov M. Ultrasound assisted extraction in aqueous two-phase system for the integrated extraction and separation of antioxidants from wheat chaff // Sep. Purif. Technol. 2017. V. 182. P. 52.
Voshkin A.A., Gradov O.M. Parametric splitting and transfer of liquid cuts for the intensification of mass exchange in a cylindrical volume // Theor. Found. Chem. Eng. 2017. V. 51. № 3. Р. 274. [Вошкин А.А., Градов О.М. Параметрическое дробление и перенос жидких фракций для интенсификации массообмена в цилиндрическом объеме // Теор. осн. хим. технол. 2017. Т. 51. № 3. С. 261.]
Gradov O.M., Voshkin A.A., Zakhodyaeva Yu.A. Analysis of the possible applications of the acoustic flow effect for the breakup and transfer of liquid substances in a cylindrical volume // Theor. Found. Chem. Eng. 2017. V. 51. № 5. P. 876.
Gradov O.M., Voshkin A.A., Zakhodyaeva Yu.A. Estimating the parameters of ultrasonically induced mass transfer and flow of liquids in the pseudomembrane method // Chem. Eng. Process. 2017. V. 118. P. 54.
Gradov O.M., Zakhodyaeva Y.A., Voshkin A.A. Breakup of immiscible liquids at the interface using high-power acoustic pulses // Chem. Eng. Process. 2018. V. 131. P. 125.
Gradov O.M., Zakhodyaeva Y.A., Zinov’eva I.V., Voshkin A.A. Some features of the ultrasonic liquid extraction of metal ions // Molecules. 2019. V. 24. № 19. P. 3549.
Flynn H.G. Physics of acoustic cavitation in liquids // Physical Acoustics. V. 1. Part B / Ed. Mason W.P. New York: Academic, 1964. P. 57.
Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1986.
Ландау Л.Д., Лифшиц Е.М. Механика. М.: Наука, 1988.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


