Теоретические основы химической технологии, 2020, T. 54, № 6, стр. 668-686
Микросмесители и микрореакторы со сталкивающимися струями: современное состояние и перспективы применения в химической технологии наноматериалов (обзор)
a Санкт-Петербургский государственный технологический институт (технический университет)
Санкт-Петербург, Россия
b Физико-технический институт им. А.Ф. Иоффе РАН
Санкт-Петербург, Россия
c Институт химии силикатов им. И.В. Гребенщикова РАН
Санкт-Петербург, Россия
* E-mail: abiev.rufat@gmail.com
Поступила в редакцию 25.05.2020
После доработки 05.06.2020
Принята к публикации 08.06.2020
Аннотация
В данном обзоре рассматриваются особенности процессов микроперемешивания, существующие конструкции, примеры применения и преимущества микросмесителей и микрореакторов со сталкивающимися струями – одного из современных средств интенсификации процессов перемешивания и проведения химических реакций с высокой селективностью. Показано, что микросмесители и микрореакторы со сталкивающимися струями являются перспективным инструментом для управляемого синтеза наноразмерных частиц, одной из аппаратных модификаций методов “мягкой” химии – либо непосредственно в самом микрореакторе (при комнатной температуре и атмосферном давлении) как при синтезе CoFe2O4, LaPO4, или с последующей термической, в том числе гидротермальной, обработкой – например, при получении BiFeO3, GdFeO3, TiO2.
ВВЕДЕНИЕ
Перемешивание существенным образом влияет на протекание сложных химических реакций. Активные и пассивные методы микроперемешивания – одно из направлений интенсификации процессов в химии и химической технологии. Микросмесители, активно разрабатываемые в последние два десятилетия [1, 2], являются не только средством тонкого смешения растворов, но и мощным инструментом для проведения химических реакций, поскольку способны обеспечить равномерность распределения реагентов в реакционной зоне, близкую к идеальной. Как было показано в недавних работах [3–6], это приводит к получению продуктов в соответствии со стехиометрией реакций, а вероятность возникновения побочных продуктов снижается практически до нуля.
Оценка эффективности микросмесителей по селективности реакций уже стало своеобразным стандартом оценки их качества [7]: чем выше качество микроперемешивания, т.е. ниже вероятность протекания побочных реакций, тем выше селективность процесса синтеза целевого продукта. В то же время, задача предсказания влияния перемешивания на селективность является комплексной, и пока что плохо поддается точной количественной оценке. При этом, как показано в работе [7], именно удельная скорость диссипации энергии, практически независимо от геометрии аппарата, является ключевым параметром, от которого зависит эффективность микрореактора.
В данной работе описаны особенности и перспективы применения микрореакторов со сталкивающимися струями (МРСС). В частности, в недавних работах показано, что МРСС является удобным средством для управляемого синтеза наночастиц в условиях методов “мягкой” химии. Синтез нанокристаллических частиц проходит либо непосредственно в самом микрореакторе (при комнатной температуре и атмосферном давлении), как, например, при формировании CoFe2O4 [3], LaPO4 [8] или с последующей термической обработкой – например, при получении BiFeO3 [5, 6], GdFeO3 [9].
МРСС известны, по крайней мере, с 1950-х годов, когда они использовались Национальным консультативным комитетом по воздухоплаванию (National Advisory Committee for Aeronautics – NACA) для образования тонкодисперсных капель топлива в камере сгорания жидкостных ракетных двигателей [10–12], т.е. изначально МРСС рассматривалось как средство для образования капель (“атомизации”) [13, 14]. Отметим, что в этом случае рассматривались свободно сталкивающиеся струи. Уже в 1990-х годах были предприняты первые попытки использования данного принципа для проведения быстропротекающих реакций, главным образом реакции осаждения, появились реакторы со свободно сталкивающимися струями – Free Impinging Jets Reactors (FIJR).
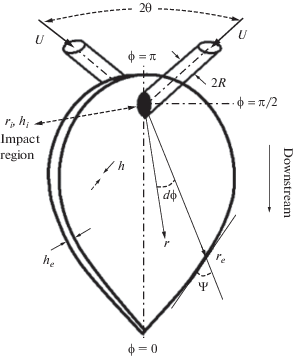
В 1960-х годах было разработано математическое описание формы жидкостной пелены, образующейся при столкновении двух струй (рис. 1) [15], которое впоследствии было подвергнуто пересмотру и уточнению [16].
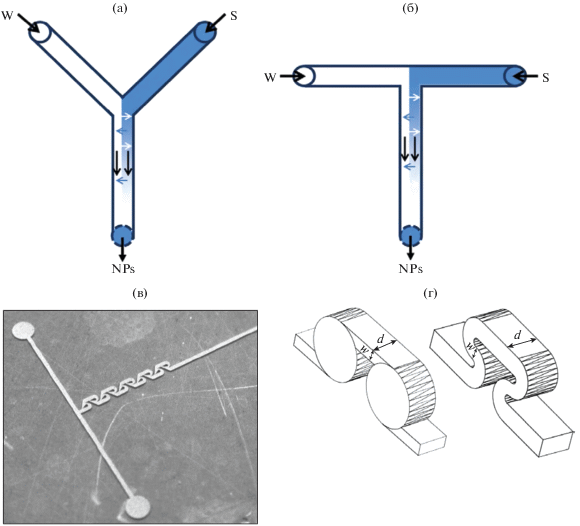
Позднее, в 1980-х годах появились работы по применению микрореакторов со струями, сталкивающимися в ограниченном пространстве (стесненные струи) – Confined Impinging Jets Reactors (CIJR, рис. 2). Такой вариант использования сталкивающихся струй нашел интерес в производстве полимеров [17–19]. Сам процесс литья полимеров при смешении в МРСС стали называть в литературе RIM (Reaction Injection Moulding) [20]. При столкновении струй в замкнутом объеме (примеры размеров: диаметр струй d = 0.5 мм, диаметр камеры смешения D = 2 мм [21], d = 1.5 мм, D = 10 мм [22]) в зоне столкновения струй образуются мощные вихри, которые распространяются по объему камеры смешения, которые совершают колебания (рис. 3). В этом направлении выполнено довольно много исследований, включая фундаментальные работы [23, 24], а также оригинальные исследования по автоколебаниям, возникающим в реакторе со стесненными струями [25, 26], в том числе с индуцированными резонансными колебаниями, когда потоки в реактор вводились со скоростями модулированными гармоническими колебаниями [27]. Средняя скорость струй составляла 3.33 м/с, а амплитуда колебаний скорости – от 0.25 до 1 от средней скорости. Показано, что частота f осцилляций струй, близкая к собственной частоте колебаний системы (ϕ = 200 Гц), приводит к ярко выраженному осцилляторному поведению в зоне столкновения струй и к образованию более регулярной структуры в системе. Наиболее быстрое смешение достигается в двух случаях: 1) противофазные колебания струй с большой амплитудой (амплитуда модуляции скорости равна средней скорости потока, f = ϕ = 200 Гц); 2) частота модуляций составляет f = ϕ/2 = 100 Гц.
Рис. 2.
Схема микрореактора со струями, сталкивающимися в ограниченном пространстве [84]. Размеры указаны в миллиметрах.
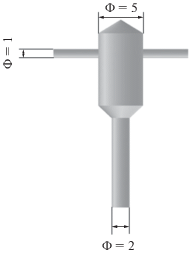
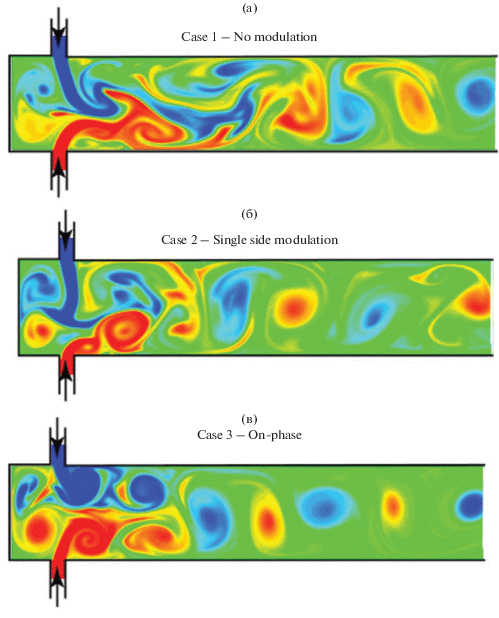
Рис. 3.
Вихри, возникающие в микрореактора со струями, сталкивающимися в ограниченном пространстве: (а) – без модуляции струй; (б) – односторонняя модуляция (A1 = 0,5, A2 = 0); (в) – с синфазной модуляцией струй (A1 = A2 = 0,5, сдвиг по фазе φ = 0) (из статьи [27]).
В данной статье мы сфокусируемся на микрореакторном синтезе со свободно сталкивающимися струями (МРСС; FIJR), поскольку такой способ взаимодействия струй представляется наиболее привлекательным с точки зрения кратковременного контакта растворов реагентов, когда увеличенная длительность перемешивания может приводить к росту кристаллов образующихся фаз. Ниже будет показано, что время микроперемешивания является фактором, определяющим селективность конкурирующих реакций. Вместе с тем для многих реакций большой интерес может представлять и применение микрореакторов со стесненными струями – CIJR (особенно там, где требуется сравнительно большое время контакта реагентов).
Целью данной работы является краткая систематизация информации о состоянии исследований МРСС, изученных и перспективных областях их применения, а также о методах исследования и критериях микроперемешивания.
МАСШТАБЫ ПЕРЕМЕШИВАНИЯ И КЛАССИФИКАЦИЯ МИКРОСМЕСИТЕЛЕЙ
Масштабы перемешивания. Принято различать три уровня (масштаба) перемешивания – макроперемешивание, мезоперемешивание и микроперемешивание [28–32].
Макроперемешивание соответствует масштабу аппарата в целом. Оно определяет условия переноса вещества крупномасштабной конвекцией по всем объему течения в реакторе, т.е. средней скоростью движения макрообъемов. Основной характеристикой макроперемешивания является кривая распределения времени пребывания. По существу, время пребывания характеризует продолжительность нахождения макрообъемов жидкости от точки ввода в аппарат до точки вывода из него. В то же время именно такое движение отвечает за перенос макрообъемов жидкости от зон без перемешивания к зонам с высокой скоростью диссипации энергии. Простой пример – циркуляционное течение в реакторе с пропеллерной или турбинной мешалкой.
Мезоперемешивание имеет место на промежуточном уровне и отвечает за крупномасштабный турбулентный перенос между вводимым в аппарат энергонесущим потоком (например, в виде струи) и окружающей его средой. Быстрая химическая реакция обычно протекает вблизи точки ввода (зона “питания”, ввода “свежего” потока), формирующей “облако” (сгусток, англ.: plume, blob) с высокой концентрацией продукта вокруг вводимого потока. Это облако является промежуточным масштабом между уровнем микроперемешивания и размером реактора. Пространственная эволюция облака может быть идентифицирована как процесс турбулентной диффузии. Другой аспект мезоперемешивания относится к инерционно-конвективному процессу дезинтеграции больших вихрей, и характеризуется почти полным отсутствием влияния молекулярной диффузии. С другой стороны, инерционно-конвективное перемешивание оказывает влияние на процессы микроперемешивания. Полное понимание и точное описание инерционно-конвективного перемешивания пока отсутствует. В качестве количественных характеристик мезоперемешивания используют кинетическую энергию турбулентности k, масштаб длины турбулентных флуктуаций L, и их сочетание, выраженное коэффициентом турбулентной диффузии Dt. Вместе с тем мезоперемешивание зависит и от конкретных условий, таких как диаметр трубы, отношение скоростей питания и средней скорости среды в аппарате.
Микроперемешивание – последний этап перемешивания в традиционных аппаратах, состоит их вязко-конвективной деформации элементов жидкости, который ускоряет распад агрегатов жидкости вплоть до диффузионного масштаба [33]. Селективность реакций в конечном счете зависит от микроперемешивания, т.е. от того, как перемешиваются реагенты на молекулярном уровне [30]. Этот механизм влечет за собой вовлечение (англ.: engulfment) и деформацию вихрей колмогоровского масштаба λk (см. ниже), и является лимитирующим процессом в уменьшении локальных градиентов концентрации. Количественными характеристиками являются время микроперемешивания, связанное со скоростью диссипации энергии ε [30] (см. ниже): чем выше ε, тем лучше микроперемешивание и выше селективность быстропротекающих реакций.
Классификация микросмесителей. Микроперемешивание – важнейший процесс в микрофлюидных аппаратах, к которым относятся микрореакторы и микросмесители. Отметим, что хорошее микросмешение – обязательный атрибут микрореакторов, поскольку в противном случае снижается селективность реакции. Согласно общепринятой классификации, принято различать два класса микросмесителей – пассивные и активные [1, 2]. В первом случае в микросмесителе используется энергия потока, переданная ему насосом или компрессором. Типичные разновидности пассивных микросмесителей [1]:
а) с разделением потока на множество параллельных ламинарных потоков (slit-type interdigital micromixer); б) по принципу разделения и рекомбинации потоков (зигзагообразные); в) хаотическое перемешивание путем формирования вихрей и поворотов (спиральные, с различными канавками, поворотами на 90° и т.п.); г) инжектирование струй в поток; д) со столкновением струй (в том числе Т- и Y-образные, рис. 4, с фокусировкой потоков, капельные); е) с закруткой потоков в плоскости или в цилиндрическом циклоне; ж) специальные случаи (в том числе основанные на эффекте Коанда).
В активных микросмесителях для интенсификации перемешивания к энергии потока добавляются различные внешние силы:
а) ультразвук; б) акустические вибрации; в) пьезоэлектрические вибрации мембраны; г) электрокинетическая неустойчивость; д) слияние капель, индуцированное электросмачиванием; е) магнитогидродинамические; ж) маленькие импеллеры; з) встроенные микроклапаны/микронасосы.
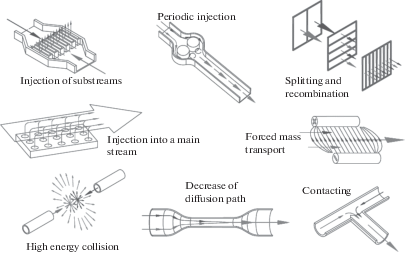
На рис. 5 представлены схемы некоторых пассивных и активных методов микроперемешивания.
Микросмесители представляют собой устройства с характерным поперечным размером элементов потока (микроканалов, струй и т.п.) порядка 1 мм и меньше. Такие аппараты часто изготавливают в виде стеклянных микрочипов, размером не более визитной карточки, и их производительность – от мл/ч до л/ч. Микроструктурированные смесители – более габаритные аппараты, содержащие структуры, состоящие из большого количества параллельных микроканалов, число которых может достигать несколько десятков тысяч. Производительность таких аппаратов достигает от 10 до 104 л/ч [1]. При достижении верхней границы они сравнимы со статическими смесителями и могут успешно применяться не только для аналитических целей, но и для решения производственных задач.
Изначально микросмесители и микроструктурированные смесители были ориентированы на создание оптимальных условий для проведения быстропротекающих реакций, которые требуют быстрого перемешивания. Они были использованы для быстрых реакций в жидкостях (например, синтез органометаллических соединений) или в газах (например, формирование оксида этилена), а также для проведения анализа “в потоке”, в том числе для биологических процессов [1]. Перемешивание в микрореакторах происходит, как правило, в ламинарном режиме, и поэтому может использоваться для вязких сред. Помимо короткого времени перемешивания и стабильности режима течения (в том числе двухфазного), микроструктурированные смесители обладают малым внутренним объемом. Это особенно ценно при работе с токсичными, взрывоопасными средами, а также когда количество реагентов ограничено из-за их высокой стоимости. Кроме того, малый поперечный размер микроканалов d позволяет легко управлять тепловым режимом в аппарате, поскольку время нагрева/охлаждения τh ∝ d2/κ, где κ – коэффициент температуропроводности.
Отметим, что в микроаппаратах преобладает ламинарный режим. Так, при диаметре микроканалов 100 мкм и скорости потока до 20 м/с для воды число Рейнольдса составит <2000. Однако в струйных микрореакторах диаметр струй может составлять 0.5–1 мм, и при скорости 10–20 м/с число Рейнольдса достигает 10000–20000, что соответствует турбулентному режиму.
Обширный обзор микросмесителей представлен в работах [1, 34].
МИКРОРЕАКТОРЫ СО СВОБОДНО СТАЛКИВАЮЩИМИСЯ СТРУЯМИ: МОДИФИКАЦИИ, ОСНОВНЫЕ ХАРАКТЕРИСТИКИ, РЕЖИМЫ ТЕЧЕНИЯ
Микрореакторы самого различного принципа действия используются в последние 20 лет для интенсификации процессов синтеза органических соединений, полимерных и неорганических материалов, в том числе металлов и их оксидов, квантовых точек, полимерных микро- и наночастиц [35]. В данной статье мы сосредоточились именно на микрореакторах для синтеза неорганических материалов, поскольку получение наноразмерных оксидных материалов в микрореакторах представляет особый интерес, как один из перспективных методов получения материалов с особыми свойствами – мульферроиков, катализаторов, в том числе фотокатализаторов, предкерамических нанопорошков и т.д. Вместе с тем в “классических” микрореакторах (где поперечный размер составляет от десятков микрон до примерно 2–3 мм – в последнем случае иногда применяют название “миллиреакторы”), осуществление золь-гель метода затруднено, поскольку микрореакторы являются проточными устройствами, а гели, по определению, не обладают достаточной текучестью [36].
Как отмечалось выше, микрореакторы со струями, сталкивающимися в ограниченном пространстве (CIJR), довольно хорошо изучены для процессов смешения полимеров. Были предприняты успешные попытки их использования и для быстропротекающих реакций, таких как осаждение [37–39], где микроперемешивание играет исключительно важную роль в синтезе наноразмерных частиц. Эти реакторы обладают явными преимуществами по сравнению с традиционными аппаратами с мешалками. Вместе с тем применение таких микрореакторов для проведения золь-гель процессов не возможно в силу тех же причин блокирования реактора образующейся гелеобразной суспензией с только что образованными наночастицами, т.е. перемешивание уже не происходит в свободном объеме, и роль стенок аппарата в торможении потока существенно возрастает.
Режимы течения в жидкостной пелене. В связи с этим микрореакторы со свободно сталкивающимися струями являются удобным инструментом для усовершенствованного золь-гель метода, когда процесс синтеза происходит в непрерывном режиме. Смешение двух плоских струй с образованием жидкостной пелены было впервые исследовано Демьяновичем и Борном в 1989 г. в ETH (Цюрих) [40, 41]. Показано, что в силу закона сохранения энергии и пренебрежимо малым взаимодействием с окружающим пелену газом скорость в ней остается практически постоянной. В 2006 г. появилась работа [42], в которой систематизированы данные о моделях формирования жидкостной пелены и описаны условия ее распада, включая капиллярную неустойчивость, неустойчивость Кельвина–Гельмгольца для угла между струями 2θ = 60°, 90° и 120°. Определяющими критериями распада пелены, по мнению авторов [42], являются числа Рейнольдса и Вебера. Ранее [11, 43] были обнаружены два основных режима разрушения пелены: 1) формирование сравнительно гладкой пелены, которая разрушается в результате суперпозиции аэродинамических волн; 2) волны возникают в зоне столкновения струй, их называют гидродинамическими ударными волнами (возникают даже в вакууме, где аэродинамических волн быть не может). В работе [43] обнаружено, что при больших значениях угла между струями 2θ и высоких скоростях струй ударные волны доминируют по всей пелене. В работе [44] при изучении лобового столкновения двух вертикальных струй (2θ = 180°) также выявлено два режима распада пелены. В первом случае пелена имеет практически идеально круглую форму, и с увеличение расходов жидкости в струях радиус пелены увеличивался, а ее поверхность оставалась гладкой. Во втором режиме радиус разрушения пелены уменьшался по мере увеличения расходов жидкости в струях, и распад наблюдался при колебаниях пелены, напоминающих движение флага на ветру; форма края пелены при этом становилась нерегулярной.
В работе [42] по результатам исследований на струях диаметром 0.4 мм выделены два основных режима формирования, роста и последующего распада пелены, по существу разновидностей аэродинамических волн. Режим I – капиллярная неустойчивость, когда существует баланс между капиллярными силами и силами инерции на краях пелены. В результате малых возмущений на краях пелены формируется цепочка мелких капелек (beads) по всему периметру пелены. Режим II – неустойчивость Кельвина–Гельмгольца, особенность которой – взаимодействие между жидкостью и окружающим ее газом, характеризуемое высокими касательными напряжениями. Распад возникает при достижении амплитудой колебаний поверхности некоторого критического значения, пелена фрагментируется, затем распадается на лигаменты (струйки), а они, в свою очередь, на капли. Эксперименты показали, что в этом режиме увеличение скорости струй приводит к уменьшению размеров пелены. Размеры лигаментов здесь меньше, чем для режима I, поскольку жидкость уже не способна собираться на нижнем кончике пелены. Размер капель, формируемых в данном режиме, меньше, а кривая распределения существенно уже, чем в режиме I.
Ли и Ашгриц [42] выделили следующие этапы роста пелены по первому механизму:
1) Подрежим R-I-A – формирование зародышевой пелены. Возникает при очень маленьких скоростях (U < 2.5–2.8 м/с). Капли на краях пелены при этом не возникают, сама “пелена” покрыта рябью и имеет крайне малые размеры. В этом подрежиме капли преимущественно образуются в результате распада струи, сформированной в нижней части пелены (рис. 6, фото 1; рис. 7, фото 1, 2).
Рис. 6.
Распад жидкостной пелены при угле между струями 2θ = 90° (из работы [42]). R I-A: фото 1: U = 2.06 м/с; R I-B: фото 2: U = 2.67 м/с; фото 3: U = 3.98 м/с; фото 4: U = 5.13 м/с; R II-A: фото 5: U = 5.5 м/с; R II-B: фото 6: U = 7.64 м/с.

Рис. 7.
Распад жидкостной пелены при угле между струями 2θ = 60° (из работы [42]). R I-A: фото 1: U = 2.55 м/с; фото 2: U = 2.79 м/с; R I-B: фото 3: U = 4.54 м/с; R I-C: фото 4: U = 5.57 м/с; R II-A: фото 5: U = 6.05 м/с; R II-B: фото 6: U = 8.75 м/с.
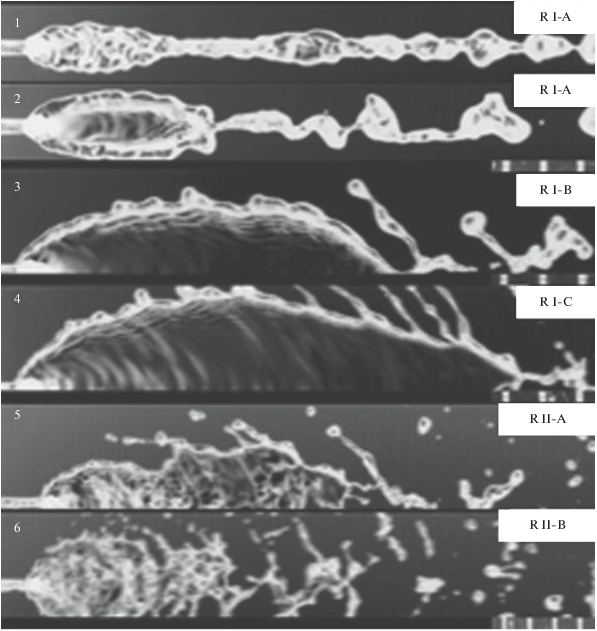
2) Подрежим R-I-B – гладкая пелена. В этом подрежиме на краях пелены в результате преобладания сил инерции над капиллярными возникает капиллярная неустойчивость, начинают формироваться мелкие капельки. Они медленно растут, продвигаясь вдоль края пелены и слетая с него. Эти капельки являются зародышами капель и лигаментов (струек), которые затем распадаются на капли. При малых скоростях струй мелкие капельки не могут вырасти до момента отрыва с нижнего кончика пелены. Они объединяются в большие лигаменты, которые затем распадаются на крупные капли (рис. 6, фото 2–4; рис. 7, фото 3).
3) Подрежим R-I-С – пелена с рябью. При дальнейшем увеличении скорости струй (по сравнению с предыдущим подрежимом) поверхность пелены становится волнистой, покрывается рябью. На фотографиях (рис. 7, фото 4) видно, что некоторые возмущения возникают из области столкновения струй. Эти возмущения распространяются по всей пелене, но ее форма остается относительно стабильной.
Этапы роста и распада пелены по второму механизму обусловлены неустойчивостью Кельвина–Гельмгольца по [42]:
1) Подрежим R-II-A – пелена с незамкнутым ободком. На рис. 6, фото 5; рис. 7, фото 5 показано, как пелена распадается вниз по потоку и потом снова вырастает в полностью выросшую пелену. Это явление происходит по той причине, что вверх по потоку пелена остается неразрушенной, но возмущенной (с рябью). В этом подрежиме распад пелены происходит в результате роста амплитуды волн, а формирование капель на краях пелены – по капиллярному механизму, как в случае R-I-B.
2) Подрежим R-II-B – турбулентная пелена (рис. 6, фото 6; рис. 7, фото 6). Распад в этом случае существенно более жесткий по сравнению с R-II-A, поскольку пелена вверх по потоку уже нестабильна, и поэтому восстановление (рост) пелены невозможно. Это происходит при очень высоких скоростях струй.
Размеры жидкостной пелены. Ключевыми гидродинамическими параметрами являются “струйные” числа Рейнольдса
и “струйные” числа Вебера
где σj – поверхностное натяжение жидкости (раствора прекурсора) в j-й струе.Показано, что с увеличением числа Вебера и высота, и ширина пелены (при фиксированном диаметре струи) линейно возрастают до тех пор, пока сохраняется замкнутый ободок на пелене. Критическое значение числа Вебера Wecr составляет 150 для 2θ = 120°, 165 для 2θ = 90°, 200 для 2θ = 60°, причем теоретические оценки хорошо подтверждаются результатами экспериментов, полученных с соплом диаметром d = 0.4 мм [42]. По достижению Wecr начинается распад ободка, и пелена укорачивается.
Чем ближе значение 2θ к 180°, тем ближе форма образующейся пелены к кругу, и ширина при этом максимальна. Длина пелены, напротив, возрастает при уменьшении 2θ, так как проекции импульсов струй на вертикальную ось складываются, и пелена вытягивается вниз.
Распределение скорости в жидкостной пелене. По простейшей теории взаимодействие между жидкостью и окружающим газом не учитывается, поэтому скорость в пелене считается постоянной и равной скорости струй. Эксперименты показали, что в целом это предположение можно считать вполне обоснованным, хотя и были выявлены некоторые отклонения от идеального распределения.
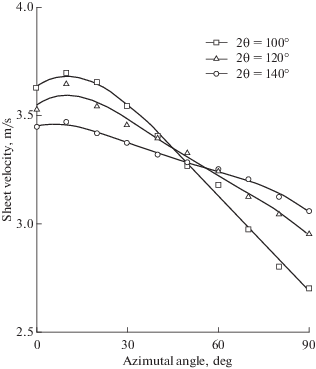
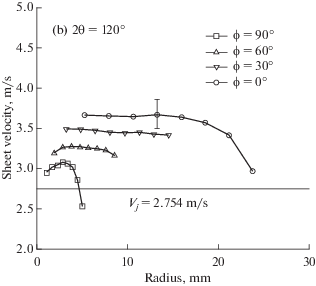
В работе [45], используя лазерную доплеровскую анемометрию, измерили неравномерность поля скоростей в жидкостной пелене. Некоторые результаты воспроизведены на рис. 8, из которого видно, что усредненная по радиусу скорость в жидкостной пелене при ϕ = 0°–10° имеет максимальное значение, которое в 1.23–1.34 раза выше скорости струи. Минимальное значение скорости соответствует значению ϕ = 180°. Этот эффект объясняется действием гравитации: в направлении движения сверху вниз гравитация способствует ускорению пелены, и наоборот.
На рис. 9 показаны зависимости локальной скорости в жидкостной пелене от радиуса r и азимутального угла ϕ из работы [45]. Из графиков видно, что при фиксированном значении ϕ скорость слабо зависит от радиуса, снижаясь на 20% только вблизи края пелены.
Ли и Ашгриц [42] оценивали скорость жидкости по скорости волн на поверхности пелены. Их исследования показали, что при Rej в интервале 1250–2500 (для 2θ = 120° и 90°) и в интервале 1250–3000 (для 2θ = 60°) скорость в жидкостной пелене превышает скорость струй, максимально на 20–30%, тогда как при Rej < 1250 и Rej > 2500 (для 2θ = 120° и 90°) скорость в пелене становится меньше скорости струй.
Распределение толщины жидкостной пелены. Толщина пелены, образующейся при столкновении струй, согласно [16], определяется следующими ключевыми значениями (см. рис. 1):
– на краях пелены
где R – радиус струи (R = d/2); ψ – угол между вектором скорости w на крае пелены и локальной касательной к контуру края пелены [42] (см. рис. 1).На границе между зоной столкновения струй и образующейся пелены толщина пелены определена в [14, 16] как функция азимутального угла φ :
(4)
${{h}_{i}} = \frac{{\beta {{{\mathbf{e}}}^{{\beta \left( {1 - \frac{\varphi }{\pi }} \right)}}}}}{{{{{\mathbf{e}}}^{\beta }} - 1}}R{\mathbf{sin}}\theta ,$Согласно закону сохранения массы, произведение толщины пелены на радиальную координату hr, есть величина постоянная, поскольку скорость в пелене считается постоянной: u = const, а расход через пелену определяется как
Отсюда следует, что для любого азимутального угла ϕ имеет место равенство hr = hiri = here = const, где индекс i соответствует зоне столкновения струй, индекс e – внешнему контуру пелены. Таким образом, с увеличением радиуса толщина пленки становится меньше.
МЕТОДЫ ИССЛЕДОВАНИЯ ЭФФЕКТИВНОСТИ МИКРОПЕРЕМЕШИВАНИЯ. ХАРАКТЕРИСТИКИ И ПОКАЗАТЕЛИ КАЧЕСТВА МИКРОПЕРЕМЕШИВАНИЯ
Интенсивность перемешивания в аппаратах со сталкивающимися струями зависит от толщины образующейся пелены, потерь давления и вязкости жидкостей [36]. Неупругий характер столкновения струй приводит к высокой скорости диссипации энергии, вызывая турбулизацию пелены, и, следовательно, способствует высококачественному перемешиванию.
Среди методов исследования эффективности микроперемешивания можно выделить следующие основные направления:
1) теоретические методы оценки макро- и микрохарактеристик перемешивания [30, 46–48];
2) инструментальные методы с использованием модельных реакций [49–55];
3) методы вычислительной гидродинамики и тепломассообмена, включая метод популяционного баланса [37, 55, 56].
В качестве дополнительного, косвенного метода исследования эффективности микроперемешивания, по нашему мнению, может быть использованы такие показатели, как размер капель микроэмульсий (при эмульгировании) или размер синтезируемых наноразмерных частиц, точнее, кристаллитов. Хотя этот способ и более затратный, но в каждом конкретном случае он позволяет определить эффективность использованного метода перемешивания на конечных характеристиках готового продукта.
1) Как известно, в турбулентном течении осуществляется передача энергии от крупномасштабных вихрей к менее крупным, образующимся за счет потери устойчивости более крупных вихрей. Этот механизм передачи энергии называют каскадным. А.Н. Колмогоров высказал гипотезу об универсальности статистического режима мелкомасштабной турбулентности и его зависимости только от скорости диссипации ε и коэффициента вязкости ν, что позволило оценить нижнюю границу линейных, скоростных и временных масштабов структур (вихрей), участвующих в процессе диссипации энергии. Среди них – колмогоровские микромасштабы длины λk и времени τk:
(6)
${{\lambda }_{k}} = {{\left( {\frac{{{{\nu }^{3}}}}{\varepsilon }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}},$(7)
${{\tau }_{k}} = {{\left( {\frac{\nu }{\varepsilon }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$Колмогоровский масштаб длины λk характеризует минимальный размер структур, в которых роль вязкости еще значительна для диссипации кинетической энергии, а τk соответствует времени диссипации в вихре минимального масштаба
Позже предложены еще два характерных масштаба времени [30]:
– время “поглощения”, характеризующее период вовлечения вихрем окружающей его жидкости:
– константа времени для вязкостно-конвективного и вязкостно-диффузионного смешения
где Sc = ν/D – число Шмидта.Время “поглощения” представляет собой характеристическое время вихрей, отражающее их динамику (а не время “жизни”). Оно представляет собой величину, обратную частоте вращения вихря [30, 33], т.е. в известной мере отражает интенсивность движения вихря.
Балдыга и Борн в 1984 г. [57] предложили выражение для расчета времени перемешивания при ламинарном режиме течения для перемежающихся слоев, учитывающее молекулярную диффузию и сдвиг слоев, в результате которого происходит растяжение слоев, и перпендикулярно к направлению течения процесс переноса ускоряется
(10)
${{\tau }_{{diff + shear}}} = \frac{1}{{2\dot {\gamma }}}{\text{arsinh}}\left( {\frac{{0.76\dot {\gamma }\delta _{0}^{2}}}{D}} \right),$Фальк и Комменже [7], учитывая высокие числа Пекле, преобразовали формулу (10) для случая микроканалов круглого сечения, получив в конечном счете выражение
(11)
${{\tau }_{{diff + shear}}} = \frac{1}{{\sqrt 2 }}{{\left( {\frac{\nu }{\varepsilon }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\ln (1.52{\text{Pe}}),$Проведенный ими анализ показал, что диаметр микроканала в интервале от 50 мкм до 1 мм практически не влияет на время перемешивания, тогда как удельная скорость диссипации энергии оказывает решающее влияние: ${{\tau }_{{diff + shear}}} \approx 0.0075{{\varepsilon }^{{ - 0.5}}}$ [7]. Сравнение формул (11) и (7) показывает, что модель Фалька и Комменже по существу является модификацией колмогоровского масштаба времени.
Для турбулентного перемешивания скорость растяжения может быть оценена как 0.5(ε/ν)1/2, а толщина ламинарных слоев – как минимальный колмогоровский масштаб длины λk, тогда время перемешивания
(12)
${{\tau }_{m}} = {{\left( {\frac{\nu }{\varepsilon }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{\text{arsinh}}\,(0.1{\text{Sc}}),$2) Метод модельных реакций – эффективный экспериментальный метод изучения микроперемешивания. Заключается он в проведении как минимум двух параллельных или последовательно-параллельных реакций, одна из которых быстрая, а другая – практически мгновенная.
С точки зрения производства высокое качество перемешивания позволяет достичь максимального выхода желаемого продукта [58]. С точки зрения научных исследований при сравнении различных типов реакторов важно иметь надежный экспериментальный инструмент количественной оценки процесса перемешивания, качества перемешивания и эффективности перемешивания. По этой причине необходимо оценивать индекс сегрегации, временные константы и энергетическую эффективность процесса перемешивания.
Когда реагенты не смешиваются достаточно быстро, одиночная реакция может замедляться (диффузионный режим реакции), что приводит к необходимости увеличения объема реактора для достижения заданной конверсии. Очевидно, что одиночная очень быстрая реакция может быть использована для визуализации процесса перемешивания. Простой пример – реакция нейтрализации с использованием фенолфталеина в качестве индикатора. В двухфазных системах жидкость–жидкость процессы перемешивания, диспергирования капель и массопереноса могут существенно затормозить скорость быстропротекающей реакции, когда исходные реагенты находятся в разных фазах [59].
Эффективная (кажущаяся) скорость быстрых сложных реакций может также лимитироваться перемешиванием. Часто желаемые химические реакции сопровождаются побочными реакциями, замедление первых приводит к образованию нежелательных продуктов. Очевидно, что хорошее перемешивание приводит к улучшению селективности синтеза. Поскольку распределение продуктов реакций (промежуточных и конечных), их селективность зависят от процессов перемешивания, они могут использоваться как индикаторы интенсивности перемешивания, а также для сравнения эффективности оборудования [54].
Существует большое число схем сложных химических реакций, распределение продуктов которых может быть применено для характеризации перемешивания [30, 58].
Все такие реакции состоят из комбинации двух типов первичных реакций:
1) конкурирующие или параллельные реакции второго порядка:
2) конкурирующие или последовательные реакции второго порядка:
К тестовым реакциям предъявляется ряд требований, исходя из того, что любое изменение в распределении продуктов должно быть однозначно связано с перемешиванием, а не с химическими явлениями. Эти требования были сформулированы в монографии [30]:
1. Сложные реакции могут использоваться как тестовые, если распределение продуктов зависит от перемешивания.
2. Реакции должны быть необратимыми, так что распределение продуктов сохраняет историю перемешивания по всей реакционной зоне.
3. Важно иметь однозначные данные обо всех реакциях, их кинетике и механизмах. Сюда входят зависимость скорости реакции от всех концентраций, ионной силы, pH, растворителя, температуры, гомогенных катализаторов, включая кислоты и основания.
4. Желательными являются реакции второго порядка с небольшим числом продуктов (желательно двумя) и без побочных реакций.
5. Константы реакций должны отличаться, поскольку это необходимо для определения различий в распределении продуктов в зависимости от условий проведения реакций. Подходящими являются реакции с отличием примерно на два порядка скорости.
6. Все реагенты и продукты должны быть растворимыми, во избежание влияния фазовых переходов на общую скорость процесса. Растворимости реагентов и всех продуктов должны быть известны.
7. Должны существовать точные количественные методы определения распределения продуктов, стандартные и достаточно доступные по стоимости.
8. Концентрация реагентов должна быть низкой, а сами они доступны на рынке реактивов, так, чтобы не требовалась их последующая очистка.
9. Реагенты и продукты должны быть строго проверены на продукт токсичности, возможности утилизации, коррозионной активности, взрыво- и пожароопасности, и должны быть сравнительно недорогими.
Если реакция протекает медленней по сравнению с перемешиванием (т.е. τr > τm), то поле концентраций можно считать равномерным во время протекания реакции, т.е. ионы каждого компонента представлены в любом микрообъеме. При такой гидродинамической обстановке перемешивание не влияет на кажущуюся скорость реакции (имеет место кинетический режим).
Если же, напротив, скорость реакции превышает скорость перемешивания (τr < τm), то среда недостаточно перемешана, и она ведет себя как гетерогенная система, каждый микрообъем которой имеет собственную кажущуюся скорость реакции.
Следовательно, для заданного времени перемешивания (например, для данного типа реактора при заданном расходе), при разных концентрациях компонентов могут быть получены разные селективности. В связи с этим, требуется придерживаться единой методологии проведения экспериментов.
В ряде работ, например, [49–54], обсуждаются реакции, удовлетворяющие вышеприведенным требованиям. Рассмотрим те из них, которые наиболее подходят для исследований интенсивности и эффективности перемешивания в микрореакторах, с точки зрения доступности инструментальных методов.
1. Йодид-иодатная методика, предложенная в 1990-х [60], подробней описана в работах [49, 50] и основана на параллельных конкурирующих реакциях Виллермо–Душмана – реакции нейтрализации (R1) и окислительно-восстановительной (R2):
(R1)
${{{\text{H}}}_{{\text{2}}}}{\text{BO}}_{3}^{ - } + {{{\text{H}}}^{ + }} \rightleftarrows {{{\text{H}}}_{{\text{3}}}}{\text{B}}{{{\text{O}}}_{3}},$(R2)
${\text{IO}}_{3}^{ - } + 5{{{\text{I}}}^{ - }} + 6{{{\text{H}}}^{ + }} \rightleftarrows 3{{{\text{I}}}_{2}} + 3{{{\text{H}}}_{{\text{2}}}}{\text{O}}.$Метод основан на измерении чувствительного к перемешиванию выхода йода, который зависит от конкуренции между нейтрализацией кислоты, и ее ролью в освобождении йода в реакции Душмана.
Реакция (R2) быстрая, имеет тот же порядок времени, что и перемешивание, но гораздо медленней реакции (R1).
Йодид-иодатная методика заключается в следующем [7, 49]:
Предварительно готовится смесь растворов йодида I– и иодата IO3– в буферном растворе ${{{{{\text{H}}}_{2}}{\text{BO}}_{3}^{--}} \mathord{\left/ {\vphantom {{{{{\text{H}}}_{2}}{\text{BO}}_{3}^{--}} {{{{\text{H}}}_{3}}{\text{B}}{{{\text{O}}}_{3}}}}} \right. \kern-0em} {{{{\text{H}}}_{3}}{\text{B}}{{{\text{O}}}_{3}}}},$ а также раствор серной кислоты, который является поставщиком протонов H+ в реакции (R1) и (R2). Концентрация кислоты должна быть фиксированной, чтобы обеспечить стехиометрический недостаток протонов по отношению к ионам бората.
В случае идеального перемешивания, кислота расходуется только первой реакцией (R1), которая протекает существенно быстрее окислительно-восстановительной реакцией (R2). Вторая реакция при этом не может протекать в силу стехиометрического недостатка серной кислоты.
В случае плохого перемешивания время распределения серной кислоты может оказаться больше характерного времени окислительно-восстановительной реакции. В результате возникает локальное пересыщение некоторых объемов реактора серной кислотой, которая, после участия в реакции (R1) с ионами бората, способна реагировать с ионами йодида и иодата, с образованием йода I2.
Таким образом, образование йода является мерой сегрегации жидкости. В этой системе йод может далее реагировать с иодидом, формируя ионы трийодида I3–:
Данные о скоростях реакций и другие подробности экспериментальной процедуры приведены в [7, 49, 50].
Концентрация трийодида может быть легко измерена при помощи UF/vis-спектрофотометрии на длине волны 353 нм и определена по закону Бугера–Ламберта–Бера:
где OD – оптическая плотность, отн. ед.; ε353 – коэффициент затухания волн в трийодиде на длине волны 353 нм (ε353 = 26047 л/(моль см)); L – длина оптического пути измерительной ячейки.В качестве показателя качества микроперемешивания используется индекс сегрегации XS [49], значения которого могут варьироваться от XS = 0 (идеальное микросмешение) до XS = 1 (полная сегрегация). В общем случае индекс сегрегации рассчитывают по формуле
где Y – селективность по определяемому веществу (в данному случае – йоду), индекс “ST” соответствует полной сегрегации.Для йодид-иодатной методики значения селективности определяют по следующим формулам:
(15)
$Y = \frac{{2({{n}_{{{{{\text{I}}}_{2}}}}} + {{n}_{{{\text{I}}_{3}^{ - }}}})}}{{{{n}_{{{\text{H}}_{0}^{ + }}}}}} = \frac{{2{{V}_{r}}([{{{\text{I}}}_{2}}] + [{\text{I}}_{3}^{ - }])}}{{{{V}_{{inj}}}[{\text{H}}_{0}^{ + }]}},$(16)
${{Y}_{{{\text{ST}}}}} = \frac{{6\,{{{[{\text{IO}}_{3}^{ - }]}}_{0}}}}{{6\,{{{[{\text{IO}}_{3}^{ - }]}}_{0}} + {{{[{{{\text{H}}}_{2}}{\text{BO}}_{3}^{ - }]}}_{0}}}},$В числителе формулы (15) – количество молей, соответствующее числу молей кислоты, потребленной в реакции (R2) (с учетом той части I2, которая преобразовалась в ${\text{I}}_{3}^{ - }$ в реакции (R3)), в знаменателе – общее число молей кислоты, инжектированной в аппарат.
В числителе формулы (16) – количество молей, соответствующее числу молей кислоты, потребленной в реакции (R2), в знаменателе – общее число молей кислоты, потребленных в реакциях (R2) и (R1).
По существу, индекс сегрегации XS отражает конверсию кислоты, инжектированной в реактор, с учетом ее участия в реакциях (R2) и (R3), выраженную через концентрацию йода и трийодида ${\text{I}}_{3}^{ - }$.
Другой показатель качества микросмешения – относительный объем идеального смешения [61]:
(17)
$\alpha = \frac{{{{V}_{{{\text{PM}}}}}}}{{{{V}_{{{\text{ST}}}}}}} = \frac{{1 - {{X}_{{\text{S}}}}}}{{{{X}_{{\text{S}}}}}},$Очевидно, что по мере приближения к идеальному микросмешению α → ∞, для полной сегрегации α = 0.
2. Каталитическая реакция гидролиза 2,2-диметоксипропана (ДМП) [24, 47]
Еще одна доступная методика основана на двух параллельных конкурирующих реакциях
(R4)
${\text{HCl}} + {\text{NaOH}}\xrightarrow{{{{k}_{1}}}}{\text{NaCl}} + {{{\text{H}}}_{{\text{2}}}}{\text{O}},$(R5)
$\begin{gathered} {{{\text{H}}}_{{\text{3}}}}{\text{CC(OC}}{{{\text{H}}}_{{\text{3}}}}{{{\text{)}}}_{{\text{2}}}}{\text{C}}{{{\text{H}}}_{3}} + {{{\text{H}}}_{{\text{2}}}}{\text{O}}\xrightarrow{{{{k}_{2}}}} \\ \to \,\,{{({\text{C}}{{{\text{H}}}_{3}})}_{2}}{\text{CO}} + 2{\text{C}}{{{\text{H}}}_{{\text{3}}}}{\text{OH}}, \\ \end{gathered} $В работе [34] в качестве показателя эффективности микросмешения предлагается использовать среднее квадратическое отклонение концентраций в зоне смешения σС. Далее это значение относят либо к средней концентрации в объеме, либо к среднему квадратическому отклонению концентраций в зоне с полной сегрегацией (где перемешивания нет) σС0. Отметим, что такой метод оценки качества микросмешения удобно использовать скорей при применении вычислительных экспериментов, поскольку точечное определение концентраций в экспериментах затруднено.
3) Методы вычислительной гидродинамики и тепломассообмена, включая метод популяционного баланса имеют существенные ограничения применительно к анализу процессов перемешивания с химической реакцией.
Для определения времени перемешивания в общем случае необходимо построение полной модели с полным описанием полей скорости и концентрации в реакторе. Эта задача крайне сложная, поскольку требует описания процессов переноса, растяжения вихрей и диффузии, соединенных с реакцией в очень тонкой структуре сетки, вплоть до масштаба Бэтчелора, имеющего порядок нескольких микрон:
(18)
${{\lambda }_{B}} = \frac{{{{\lambda }_{k}}}}{{{\text{S}}{{{\text{c}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}} = {{\left( {\frac{{\nu {{D}^{2}}}}{\varepsilon }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}.$Масштаб Бэтчелора характеризует размер “капли” скалярной величины (например, концентрации), которая диффундирует до тех пор, пока не диссипируется вихрем размером λk. Другими словами, λB – это минимальный масштаб флуктуаций концентрации, который может существовать до момента их выравнивания за счет диффузии. Отметим, что для жидкостей число Шмидта Sc $ \gg $ 1 (для водных растворов Sc ≈ 1000), поэтому масштаб Бэтчелора существенно меньше масштаба Колмогорова.
Кроме того, при расчетах часто вынужденно применяют сетки разных масштабов для определения гидродинамических характеристик и поля концентраций. Все это существенно усложняет решение задач перемешивания с химической реакцией.
Для того, чтобы обойти эти проблемы, для получения интегральных характеристик реакторов используют различные феноменологические модели [60–64]. Пример таких моделей – “взаимодействие при обмене средним” (the Interaction by Exchange with the Mean, IEM) [61, 64], согласно которой зона, обогащенная кислотой, участвует в массообмене с зоной, обогащенной боратом, с характеристическим временем, равном времени смешения. Задача этой модели – определить порядок времени микроперемешивания для практических приложений, без детального описания явлений перемешивания. Точность оценки при этом не превышает ±30%.
В ряде работ используется комбинированный эйлерово-лагранжевый подход для описания флуктуаций перемешивания [65], основанный на прямом численном моделировании уравнений гидродинамики, конвекции и диффузии. Для описания реакции осаждения в работах [56, 65] применен метод популяционного баланса (population balance method). Результаты моделирования довольно хорошо согласуются с экспериментальными данными, средний размер частиц составляет 50–60 нм.
В [65] отмечается, что в модели вовлечения (engulfment model) процесс перемешивания учитывается на масштабах от гидродинамически наиболее активных вихрей (размером порядка 12λk, см. формулу (18)) до масштаба Бэтчелора. Согласно модели вовлечения, происходит экспоненциальное расширение объема вихря, в который захватывается окружающие вихрь объемы. Показано, что модель вовлечения более точно описывает микроперемешивание, чем модель IEM [48]: с увеличением числа Дамкёлера, характеризующего отношение времени микросмешения к характерному времени реакции, индекс сегрегации в модели вовлечения стремится к единице, а в модель IEM – к значениям порядка 0.1–0.3 [48].
ПЕРСПЕКТИВЫ ПРИМЕНЕНИЯ МИКРОРЕАКТОРОВ СО СТАЛКИВАЮЩИМИСЯ СТРУЯМИ
Важным для развития технологии наноматериалов является интенсификация синтеза нанокристаллов в условиях методов “мягкой” химии, в том числе при их формировании в жидких средах. Необходимость интенсификации синтеза твёрдых фаз определяется тем, что только в случае быстропротекающих реакций можно рассчитывать на образование предельно малых нанокристаллических частиц с узким распределением по размерам [66, 67]. Интенсификация процессов в условиях методов “мягкой” химии достигается использованием структурно-подобных целевому продукту прекурсоров [68–70], использование ультразвуковой обработки реакционных сред [71–73], высокоскоростного, в частности микроволнового, нагрева реагентов [74–78], применение методов механохимии [79, 80] и др.
С учетом изложенных в предыдущих разделах фактов микрореакторы со сталкивающимися струями уверенно можно отнести к средствам интенсификации процессов микроперемешивания и, как следствие, к способам интенсификации химических реакций, в том числе реакций образования твёрдых фаз, в жидких средах. В частности, микрореакторы со свободно сталкивающимися струями были успешно использованы в ряде золь-гель процессов, модифицированных к условиям “струйной” методики, для синтеза нанокристаллических материалов:
– MgO [36]; CoFe2O4 [3, 4], LaPO4 [8]; BiFeO3 [5, 6]; GdFeO3 [9]; TiO2 [81, 82];
Микроразмерные частицы полученные в МРСС:
– NH4ClO4 [83] (средний размер 50–70 мкм).
Ряд оригинальных конструкций микросмесителей и методов определения характеристик массопереноса описан в работах [84–90]. В работе [7] проведен сопоставительный анализ параметров микроперемешивания в микросмесителях восьми различных типов (микрореактор со сталкивающимися струями в этот список не вошел), полученных разными авторами по йодид-иодатной методике.
Данные по восьми типам реакторов, построенные в координатах lg(Re) – lg(τm/d2), хорошо описывались прямой линией, причем для большинства устройств исследованный режим течения оказался ламинарным (что не удивительно для микрофлюидных устройств). Те же данные в координатах lg(ε) – lg(τm), показали, что для более 80% случаев экспериментальные точки оказались в ±30% “коридоре” значений, описываемых уравнением τm = 0.15ε–0.45, которое с точностью до коэффициентов практически совпадает с уравнениями (11) и (12). Отмечается очень высокий достижимый уровень скорости диссипации энергии в микросмесителях (существенно выше, чем в традиционных перемешивающих устройствах с турбулентным режимом течения). При этом показано, что энергетическая эффективность микросмесителей составляет 3%, что втрое выше, чем для традиционных смесителей (1%). Примечательным является тот факт, что удельная скорость диссипации энергии является единой характеристикой смесителей, независимо от их геометрии. Так, например, использование мультиламинации (multilamination, разбиение потока на множество тонких параллельных слоев) должно было бы улучшить микроперемешивание за счет уменьшения толщины слоев; однако процесс формирования микрослоев потребовал дополнительных затрат энергии, которые также необходимо учитывать в общем балансе.
Одной из очевидных задач является оптимизация геометрии микросмесителей – микрореакторов, позволяющая сократить затраты энергии, т.е. повысить эффективность перемешивания.
Учитывая высокую производительность одиночного микрореактора – до 2–4 л/мин, вполне можно рассчитывать на их использование в промышленном производстве наноразмерных частиц, причем в непрерывном режиме. Так, для получения одного грамма BiFeO3 требуется 100 мл растворов нитратов и 100 мл осадителя, т.е. в одном лабораторном микрореакторе можно получать до 20–40 г/мин (1.2–2.4 кг/ч), а это уже довольно значительная производительность. При необходимости можно установить параллельно несколько десятков реакторов; учитывая малый их объем, такое количество нетрудно разместить в помещении площадью не более 20 м2, в два-три яруса.
Для промышленной реализации технологий необходимо помнить, однако, о необходимости обеспечения непрерывности процессов промывки и термообработки синтезированных в МРСС частиц, если эти операции требуются по технологии получаемого продукта.
ЗАКЛЮЧЕНИЕ
Данный обзор позволяет составить представление о комплексном характере процессов, протекающих в микрореакторах со сталкивающимися струями.
И хотя эффективность использования энергии в микросмесителях-микрореакторах различных типов оценена в 3% [7], микроаппараты способны осуществлять перемешивание в течение нескольких миллисекунд, что существенно меньше, чем в смесителях традиционных типов.
Анализ литературы показывает, что использование микрореакторов со сталкивающимися струями является перспективным методом интенсификации процессов микроперемешивания, и в последние годы интерес к их применению для синтеза различных веществ возрастает, поскольку МРСС позволяют сконцентрировать большой удельный поток энергии в малом объеме, что приводит к сокращению времени перемешивания до долей миллисекунды.
Вместе с тем до сих пор теория гидродинамики жидкостной пелены еще далека от завершенности, и на многие вопросы еще предстоит найти ответы; в частности, нет достоверных сведений о критических условиях существования пелены. Очевидно, что с увеличением скорости струй возрастает их кинетическая энергия, а значит, и скорость диссипации энергии ε. Это означает, что уменьшается время микроперемешивания τm, и когда оно снижается до τm = 10–3 с, этого должно быть достаточно для обеспечения условий, близких к идеальному микросмешению. По данным [7], для достижения такого значения τm достаточно, чтобы ε было порядка 105 Вт/кг.
Вместе с тем по мере увеличения скорости струй возрастает риск их распада. Полученное в работе [42] значение критического числа Рейнольдса составляет Rej = 3400–3500, за которым происходит турбулизация и распад жидкостной пелены. Надо отметить, что это значение было получено для воды при комнатной температуре, для d = 0.4 мм. По полученным нами экспериментальным данным, существование жидкостной пелены возможно и при Rej > 3500. При этом возможна также корректировка критических чисел Вебера, обсуждавшихся в п. 2.2. Для уточнения этих обстоятельств необходимо проведение исследований в некотором интервале значений d и свойств жидкости.
Кроме того, необходимо ответить на вопрос об оптимальной скорости струй и оптимальном размере пелены. С одной стороны, с увеличением скорости струй пелена становится меньше из-за ускоренного распада. Это означает, что уменьшается объем зоны столкновения струй (объем зоны смешения Vm), т.е. удельная скорость диссипации энергии ε = N/Vm растет, а время перемешивания τm сокращается. С другой стороны, нельзя сбрасывать со счетов тот факт, что при увеличении скорости струй возрастает дисперсия времени пребывания микрообъемов жидкости в зоне столкновения струй: одна часть этих микрообъемов находится дольше в ядре зоны столкновения, а другая быстрее разлетается в виде брызг. В результате вполне вероятен такой сценарий: частично реакция протекает в зоне столкновения струй, где условия перемешивания близки к идеальным, и там образуются частицы требуемых размеров; другая часть растворов разлетается в виде брызг, которые налипают на стенки аппарата, и взаимодействие между реагентами происходит либо в летящих брызгах, к которым уже не подводится достаточное количество энергии, либо на стенках аппарата, где под действием гравитации смешиваются медленно стекающие струйки. В дальнейших исследованиях предполагается прояснить и этот вопрос.
Работа выполнена при поддержке Российского научного фонда, проект № 20-63-47016.
Список литературы
Hessel V., Löwe H., Schönfeld F. Micromixers—a review on passive and active mixing principles // Chem. Eng. Sci. 2005. V. 60. P. 2479.
Capretto L., Cheng W., Hill M., Zhang X. Micromixing within microfluidic devices // Top. Curr. Chem. 2011. V. 304. P. 27. https://doi.org/10.1007/128_2011_150
Abiev R.S., Almyasheva O.V., Izotova S.G., Gusarov V.V. // J. Chem. Tech. App. 2017. V. 1. № 1. P. 7.
Абиев Р.Ш., Альмяшева О.В., Гусаров В.В., Изотова С.Г. Пат. 2625981 РФ // Бюлл. изобрет. 2017. № 20.
Проскурина О.В., Ноговицин И.В., Ильина Т.С., Данилович Д.П., Абиев Р.Ш., Гусаров В.В. Формирование наночастиц BiFeO3 с использованием струйного микрореактора // Журн. общ. хим. 2018. Т. 88. № 10. С. 1699.
Proskurina O.V., Abiev R.S., Danilovich D.P., Panchuk V.V., Semenov V.G., Nevedomsky V.N., Gusarov V.V. Formation of nanocrystalline BiFeO3 during heat treatment of hydroxides co-precipitated in an impinging-jets microreactor // Chem. Eng. Process. 2019. V. 143. P. 107598 https://doi.org/10.1016/j.cep.2019.107598
Falk L., Commenge J.-M. Performance comparison of micromixers // Chem. Eng. Sci. 2010. V. 65. P. 405. https://doi.org/10.1016/j.ces.2009.05.045
Proskurina O.V., Sivtsov E.V., Enikeeva M.O., Sirotkin A.A., Abiev R.Sh., Gusarov V.V. Formation of rhabdophane-structured lanthanum orthophosphate nanoparticles in an impinging-jets microreactor and rheological properties of sols based on them // Nanosyst.: Phys., Chem., Math. 2019. V. 10. № 2. P. 206. https://doi.org/10.17586/2220-8054-2019-10-2-206-214
Албади Я., Сироткин А.А., Семенов В.Г., Абиев Р.Ш., Попков В.И. Синтез суперпарамагнитных наночастиц GdFeO3 с использованием микрореактора со свободно сталкивающимися струями // Изв. Акад. наук. Сер. хим. 2020. № 7. С. 1290. [Albadi Y., Sirotkin A.A., Semenov V.G., Abiev R.S., Popkov V.I. Synthesis of superparamagnetic GdFeO3 nanoparticles using a free impinging-jets microreactor// Russian Chemical Bulletin, International Edition, 2020, V. 69, № 7. P. 1290. DOI: 10.1007/s11172-020-2900-x].
Heidmann M.F., Humphrey J.C. Fluctuations in a Spray Formed by Two Impinging Jets (NACA Technical Note 2349). Washington, DC: National Advisory Committee for Aeronautics (NACA), 1951.
Heidmann M.F., Priem R.J., Humphrey J.C. A Study of Sprays Formed by Two Impinging Jets (NACA Technical Note 3835). Washington, DC: National Advisory Committee for Aeronautics (NACA), 1957.
Ashgriz N., Brocklehurst W., Talley D. // J. Propul. Power. 2001. V. 17. № 3. P. 736. https://doi.org/10.2514/2.5803
Ryan H.M., Anderson W.E., Pal S., Santoro R.J. Atomization Characteristics of Impinging Liquid Jets // J. Propul. Power. 1995. V. 11. № 1. P. 135.
Handbook of Atomization and Sprays / Ed. Ashgriz N. Toronto: Springer, 2011. Ch. 30. P. 685. https://doi.org/10.1007/978-1-4419-7264- 4_30
Hasson D., Peck R.E. Thickness distribution in a sheet formed by impinging jets // AIChE J. 1964. V. 10. № 5. P. 752.
Ibrahim E., Przekwas A. Impinging jets atomization // Phys. Fluids A. 1991. V. 3. P. 2981.
Lee L.J., Ottino J.M., Ranz W.E., Macosko C.W. Impingement Mixing in Reaction Injection Molding // Polym. Eng. Sci. 1980. V. 20. P. 868.
Tucker C.L., Suh N.P. Mixing for Reaction Injection Molding. I. Impingement Mixing of Liquids // Polym. Eng. Sci. 1980. V. 20. P. 875.
Nguyen L.T., Suh N.P. Processing of Polyurethane/Polyester Interpenetrating Polymer Networks by Reaction Injection Molding: Part II. Mixing at High Reynolds Numbers and Impingement Pressures // Polym. Eng. Sci. 1986. V. 26. P. 799.
Santos R.J., Teixeira A.M., Lopes J.C.B. Study of mixing and chemical reaction in RIM // Chem. Eng. Sci. 2005. V. 60. P. 2381.
Metzger L., Kind M. On the mixing in confined impinging jet mixers – Time scale analysis and scale-up using CFD coarse-graining methods // Chem. Eng. Res. Des. 2016. V. 109. P. 464.
Fonte C.P., Sultan M.A., Santos R.J., Dias M.M., Lopes J.C.B. Flow imbalance and Reynolds number impact on mixing in Confined Impinging Jets // Chem. Eng. J. 2015. V. 260. P. 316.
Macosko C.W. RIM: Fundamentals of Reaction Injection Molding. Munich: Hanser, 1989.
Johnson B.K., Prud’homme R.K. Chemical processing and micromixing in confined impinging jets // AIChE J. 2003. V. 49. P. 2264.
Johnson D.A., Wood P. Self-sustained oscillations in opposed impinging jets in an enclosure // Can. J. Chem. Eng. 2000. V. 78. P. 867.
Santos R.J., Erkoc E., Dias M.M., Teixeira A.M., Lopes J.C.B. Hydrodynamics of the Mixing Chamber in RIM: PIV Flow-Field Characterization // AIChE J. 2008. V. 54. № 5. P. 1153. https://doi.org/10.1002/aic.11472
Erkoc E., Fonte C.P., Dias M.M., Lopes J.C.B., Santos R.J. Numerical study of active mixing over a dynamic flow field in a T-jets mixer—Induction of resonance // Chem. Eng. Res. Des. 2016. V. 106. P. 74. https://doi.org/10.1016/j.cherd.2015.12.002
Bałdyga J., Bourne J.R. Transport phenomena and hydrodynamics of complex flows // Encyclopedia of Fluid Mechanics / Ed. Cheremisinoff N.P. Houston: Gulf, 1986. V. 1. P. 145.
Bałdyga J., Bourne J.R. Interactions between mixing on various scales in stirred tank reactors // Chem. Eng. Sci. 1992. V. 47. P. 1839.
Bałdyga J., Bourne J.R. Turbulent Mixing and Chemical Reactions. Chichester: Wiley, 1999.
Fournier M.C., Falk L., Villermaux J. A new parallel competing reaction system for assessing micro-mixing efficiency – Experimental approach // Chem. Eng. Sci. 1996. V. 22. P. 5053. https://doi.org/10.1016/0009-2509(96)00270-9
Ghanem A., Lemenand T., Della Valle D., Peerhossaini H. Static mixers: Mechanisms, applications, and characterization methods – A review // Chem. Eng. Res. Des. 2014. V. 92. P. 205.
Bałdyga J., Bourne J.R. Simplification of micro-mixing calculations: I. Derivation and application of a new model // Chem. Eng. J. 1989. V. 42. P. 83.
Cai G., Xue L., Zhang H., Lin J. A Review on Micromixers // Micromachines. 2017. V. 8. № 9. P. 274. https://doi.org/10.3390/mi8090274
Park J.I., Saffari A., Kumar S., Günther A., Kumacheva E. Microfluidic synthesis of polymer and inorganic particulate materials // Annu. Rev. Mater. Res. 2010. V. 40. P. 415.
Ravi Kumar D.V., Prasad B.L.V., Kulkarni A.A. Impinging Jet Micromixer for Flow Synthesis of Nanocrystalline MgO: Role of Mixing/Impingement Zone // Ind. Eng. Chem. Res. 2013. V. 52. P. 17376. https://doi.org/10.1021/ie402012x
Marchisio D.L., Rivautella L., Barresi A.A. Design and scale-up of chemical reactors for nanoparticle precipitation // AIChE J. 2006. V. 52. № 5. P. 1877.
Casanova H., Higuita L.P. Synthesis of calcium carbonate nanoparticles by reactive precipitation using a high pressure jet homogenizer // Chem. Eng. J. 2011. V. 175. P. 569.
Hacherl J.M., Paul E.L., Buettner H.M. Investigation of impinging-jet crystallization with a calcium oxalate model system // AIChE J. 2004. V. 49. № 9. P. 2352.
Demyanovich R.J., Bourne J.R. Rapid micromixing by the impingement of thin liquid sheets. 1. A photographic study of the flow pattern // Ind. Eng. Chem. Res. 1989. V. 28. № 6. P. 825.
Demyanovich R.J., Bourne J.R. Rapid micromixing by the impingement of thin liquid sheets. 2. Mixing study // Ind. Eng. Chem. Res. 1989. V. 28. № 6. P. 830.
Li R., Ashgriz N. Characteristics of liquid sheets formed by two impinging jets // Phys. Fluids. 2006. V. 18. P. 087104.
Dombrowski N., Hooper P.C. A study of the sprays formed by impinging jets in laminar and turbulent flow // J. Fluid Mech. 1964. V. 18. P. 392.
Huang J.C.P. The breakup of axisymmetric liquid sheets // J. Fluid Mech. 1970. V. 43. P. 305.
Choo Y.-J., Kang B.-S. The velocity distribution of the liquid sheet formed by two low-speed impinging jets // Phys. Fluids. 2002. V. 14. № 2. P. 622. https://doi.org/10.1063/1.1429250
Kolmogorov A.N. On the disintegration of drops in a turbulent flow // Dokl. Akad. Nauk SSSR. 1949. V. 66. P. 825.
Bałdyga J., Bourne J.R., Walker B. Non-isothermal micromixing in turbulent liquids: Theory and experiment // Can. J. Chem. Eng. 1998. V. 76. P. 641. https://doi.org/10.1002/cjce.5450760336
Bałdyga J., Bourne J.R. Comparison of the engulfment and the interaction-by-exchange-with-the–mean micromixing models // Chem. Eng. J. 1990. V. 45. P. 25. https://doi.org/10.1016/0300-9467(90)80022-5
Guichardon P., Falk L. Characterisation of micromixing efficiency by the iodide-iodate reaction system. Part I: Experimental procedure // Chem. Eng. Sci. 2000. V. 55. P. 4233. https://doi.org/10.1016/S0009-2509(00)00068-3
Guichardon P., Falk P., Villermaux J. Characterisation of mixing efficiency by the iodide/iodate reaction system. Part 2. Kinetic study // Chem. Eng. Sci. 2000. V. 55. P. 4243. https://doi.org/10.1016/S0009-2509(00)00069-5
Kölbl A., Kraut M., Schubert K. The iodide iodate method to characterize microstructured mixing devices // AIChE J. 2008. V. 54. P. 639. https://doi.org/10.1002/aic.11408
Kölbl A., Schmidt-Lehr S. The iodide iodate reaction method: The choice of the acid // Chem. Eng. Sci. 2010. V. 65. P. 1897. https://doi.org/10.1016/j.ces.2009.11.032
Commenge J.-M., Falk L. Villermaux–Dushman protocol for experimental characterization of micromixers // Chem. Eng. Process. 2011. V. 50. P. 979.
Jasińska M. Test reactions to study efficiency of mixing // Chem. Process Eng. 2015. V. 36. № 2. P. 171.
Guo T., Ruan B., Liu Z., Jamal M.A., Wen L., Chen J. Numerical and experimental investigations of liquid mixing in two-stage micro-impinging stream reactors // Chin. J. Chem. Eng. 2017. V. 25. P. 391.
Schwarzer H.-C., Schwertfirm F., Manhart M., Schmid H.-J., Peukert W. Predictive simulation of nanoparticle precipitation based on the population balance equation // Chem. Eng. Sci. 2006. V. 61. P. 167.
Bałdyga J., Bourne J.R. Mixing and fast chemical reaction – VIII. Initial deformation of material elements in isotropic, homogeneous turbulence // Chem. Eng. Sci. 1984. V. 39. P. 329. https://doi.org/10.1016/0009-2509(84)80031-7
Levenspiel O. Chemical Reaction Engineering. New York: Wiley, 1972.
Bourne J.R. Mixing and the selectivity of chemical reactions // Org. Process Res. Dev. 2003. V. 7. P. 471. https://doi.org/10.1021/op020074q
Fournier C., Falk L., Villermaux J. A new parallel competing reaction system for assessing micromixing efficiency – experimental approach // Chem. Eng. Sci. 1996. V. 22. P. 5053.
Villermaux J. Micromixing phenomena in stirred reactors // Encyclopedia of Fluid Mechanics. Houston: Gulf, 1986. Ch. 27. P. 708.
Baldyga J. A closure model for homogenous chemical reactions // Chem. Eng. Sci. 1994. V. 49. № 12. P. 1985.
Baldyga J., Bourne J.R. Simplification of micromixing in homogeneous stirred tank reactors // Chem. Eng. Res. Des. 1988. V. 66. P. 33.
Villermaux J., Falk L. A generalized mixing model for initial contacting of reactive fluids // Chem. Eng. Sci. 1994. V. 49. № 24. P. 5127.
Gradl J., Schwarzer H.-C., Schwertfirm F., Manhart M., Peukert W. Precipitation of nanoparticles in a T-mixer: Coupling the particle population dynamics with hydrodynamics through direct numerical simulation // Chem. Eng. Process. 2006. V. 45. P. 908.
Gusarov V.V. Fast solid phase chemical reactions // Russ. J. Gen. Chem. 1997. V. 67. № 12. P. 1846. [Гусаров В.В. Быстропротекающие твердофазные химические реакции // Журн. общ. хим. 1997. Т. 67. № 12. С. 1959.]
Almjasheva O.V., Lomanova N.A., Popkov V.I., Proskurina O.V., Tugova E.A., Gusarov V.V. The minimal size of oxide nanocrystals: phenomenological thermodynamic vs crystal-chemical approaches // Nanosyst.: Phys., Chem., Math. 2019. V. 10. № 4. P. 428. https://doi.org/10.17586/2220-8054-2019-10-4-428-437
Pozhidaeva O.V., Korytkova E.N., Romanov D.P., Gusarov V.V. Formation of ZrO2 Nanocrystals in Hydrothermal Media of Various Chemical Compositions // Russ. J. Gen. Chem. 2002. V. 72. № 6. P. 849. [Пожидаева О.В., Корыткова Э.Н., Романов Д.П., Гусаров В.В. Формирование нанокристаллов диоксида циркония в гидротермальных средах различного химического состава // Ж. общ. хим. 2002. Т. 72. № 6. С. 910.]https://doi.org/10.1023/a:1020409702215
Almjasheva O.V. Heat-stimulated transformation of zirconium dioxide nanocrystals produced under hydrothermal conditions // Nanosyst.: Phys., Chem., Math. 2015. V. 6. № 5. P. 697. https://doi.org/10.17586/2220-8054-2015-6-5-697-703
Popkov V.I., Almjasheva O.V., Panchuk V.V., Semenov V.G., Gusarov V.V. The role of pre-nucleus states in formation of nanocrystalline yttrium orthoferrite // Dokl. Chem. 2016. V. 471. № 2. P. 356. https://doi.org/10.1134/S0012500816120041
Mahdavi R., Ashraf Talesh S.S. The effect of ultrasonic irradiation on the structure, morphology and photocatalytic performance of ZnO nanoparticles by sol-gel method // Ultrason. Sonochem. 2017. V. 39. P. 504. https://doi.org/10.1016/j.ultsonch.2017.05.012
Baranchikov A.Y., Ivanov V.K., Tretyakov Yu.D. Sonochemical synthesis of inorganic materials // Russ. Chem. Rev. 2007. V. 76. № 2. P. 133. [Баранчиков А.Е., Иванов В.К., Третьяков Ю.Д. Сонохимический синтез неорганических материалов // Усп. хим. 2007. Т. 76. № 2. С. 147.]https://doi.org/10.1070/RC2007v076n02ABEH003644
Kuznetsova V.A., Almjasheva O.V., Gusarov V.V. Influence of microwave and ultrasonic treatment on the formation of CoFe2O4 under hydrothermal conditions // Glass Phys. Chem. 2009. V. 35. P. 205. [Кузнецова В.А., Альмяшева О.В., Гусаров В.В. Влияние микроволновой и ультразвуковой обработки на образование CoFe2O4 в гидротермальных условиях // Физ. хим. стекла. 2009. Т. 35. № 2. С. 266.]https://doi.org/10.1134/S1087659609020138
Korotkov R.F., Baranchikov A.E., Boytsova O.V., Goldt A.E., Kurzeev S.A., Ivanov V.K. Selective hydrothermal microwave synthesis of various manganese dioxide polymorphs // Russ. J. Inorg. Chem. 2016. V. 61. P. 129. https://doi.org/10.1134/S0036023616020091
Meskin P.E., Gavrilov A.I., Maksimov V.D., Ivanov V.K., Churagulov B.P. Hydrothermal/microwave and hydrothermal/ultrasonic synthesis of nanocrystalline titania, zirconia, and hafnia // Russ. J. Inorg. Chem. 2007. V. 52. № 11. P. 1648. [Мескин П.Е., Гаврилов А.И., Максимов В.Д., Иванов В.К., Чурагулов Б.Р. Гидротермально-микроволновой и гидротермально-ультразвуковой синтез нанокристаллических диоксидов титана, циркония, гафния // Ж. неорг. хим. 2007. Т. 52. № 11. С. 1755.]https://doi.org/10.1134/S0036023607110022
Honghui T., Shukun X., Jiku W. Ultrasonication-assisted hydrothermal synthesis of ultralong TiO2 nanotubes // Rare Met. Mater. Eng. 2014. V. 43. № 10. P. 2326. https://doi.org/10.1016/S1875-5372(14)60163-6
Almjasheva O.V., Gusarov V.V. Prenucleation formations in control over synthesis of CoFe2O4 nanocrystalline powders // Russ. J. Appl. Chem. 2016. V. 89. P. 851. [Альмяшева О.В., Гусаров В.В. Роль предзародышевых образований в управлении синтезом нанокристаллических порошков CoFe2O4 // Ж. прикл. хим. 2016. Т. 89. № 6. С. 689.]https://doi.org/10.1134/S107042721606001X
Ivanov V.K., Polezhaeva O.S., Gil’ D.O., Kopitsa G.P., Tret’yakov Yu.D. Hydrothermal microwave synthesis of nanocrystalline cerium dioxide // Dokl. Chem. 2009. V. 426. P. 131. [Иванов В.К., Полежаева О.С., Гиль Д.О., Копица Г.П., Третьяков Ю.Д. Гидротермально-микроволновой синтез нанокристаллического диоксида церия // Докл. Акад. наук. 2009. Т. 426. № 5. С. 632.]https://doi.org/10.1134/S0012500809060056
Boldyrev V.V. Mechanochemistry and mechanical activation of solid // Russ. Chem. Rev. 2006. V. 75. № 3. P. 177. https://doi.org/10.1070/RC2006v075n03ABEH001205
Isupov V.P., Chupakhina L.E., Mitrofanova R.P. Mechanochemical Synthesis of Double Hydroxides // J. Mater. Synth. Process. 2000. V. 8. № 3–4. P. 251. https://doi.org/10.1023/A:1011376513081
Здравков А.В., Кудряшова Ю.С., Уголков В.Л., Абиев Р.Ш. Получение фотокатализаторов на основе диоксида титана, синтезированного с использованием микрореактора со сталкивающимися струями // Физ. хим. стекла. 2020. Т. 46. № 4. с. 427. [Kudryashova Yu.S., Zdravkov A.V., Ugolkov V.L., Abiev R.Sh. Glass Physics and Chemistry. 2020. V. 46. № 4. P. 335–340. https://doi.org/10.1134/S1087659620040082].
Здравков А.В., Кудряшова Ю.С., Абиев Р.Ш. Фотокатализаторы на основе допированного неодимом диоксида титана, синтезированные в микрореакторе со сталкивающимися струями // Журн. общ. хим. 2020. Т. 90. № 9. С. 1422. https://doi.org/10.31857/S0044460X20090140.
Pal S., Madane K., Kulkarni A.A. Antisolvent based precipitation: Batch, capillary flow reactor and impinging jet reactor // Chem. Eng. J. 2019. V. 369. P. 1161.
Lince F., Marchisio D.L., Barresi A.A. A comparative study for nanoparticle production with passive mixers via solvent-displacement: Use of CFD models for optimization and design // Chem. Eng. Process. 2011. V. 50. P. 356.
Tao J., Chow S.F., Zheng Y. Application of Flash Nanoprecipitation to Fabricate Poorly Water-soluble Drug Nanoparticles // Acta Pharm. Sin. B. 2019. V. 9. № 1. P. 4. https://doi.org/10.1016/j.apsb.2018.11.001
Bayareh M., Ashani M.N., Usefian A. Active and passive micromixers: A comprehensive review // Chem. Eng. Process. 2020. V. 147. P. 107771. https://doi.org/10.1016/j.cep.2019.107771
Hong C.C., Choi J.W., Ahn C.H. A novel in-plane microfluidic mixer with modified Tesla structures // Lab Chip. 2004. V. 4. P. 109. https://doi.org/10.1039/B305892A
Mielke E., Plouffe P., Koushik N., Eyholzer M., Gottsponer M., Kockmann N., Macchi A., Roberge D.M. Local and overall heat transfer of exothermic reactions in microreactor systems // React. Chem. Eng. 2017. V. 2. P. 763. https://doi.org/10.1039/c7re00085e
Barabash V.M., Abiev R.S., Kulov N.N. Theory and Practice of Mixing: A Review // Theor Found. Chem. Eng. 2018. V. 52, № 4. P. 473. https://doi.org/10.1134/S004057951804036X [Барабаш В.М., Абиев Р.Ш., Кулов Н.Н. Обзор работ по теории и практике перемешивания // Теор. осн. хим. технол. 2018. Т. 52. № 4. С. 367. https://doi.org/10.1134/S0040357118040024]
Haase S., Bauer T., Hilpmann G., Lange M., Ayubi M.-M., Abiev R. Simultaneous Detection of Hydrodynamics, Mass Transfer and Reaction Rates in a Three-Phase Microreactor // Theor. Found. Chem. Eng. 2020. V. 54. № 1. P. 48. https://doi.org/10.1134/S0040579520010091
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии