Теоретические основы химической технологии, 2020, T. 54, № 6, стр. 758-767
Прогнозирование скорости звука в смесях природного газа с помощью уравнения состояния CP-PC-SAFT
И. В. Приходько a, *, А. А. Самаров a, А. М. Тойкка a, М. Фарзанех-Горд b
a Санкт-Петербургский государственный университет
Санкт-Петербург, Россия
b Мешхедский университет им. Фирдоуси
Мешхед, Иран
* E-mail: i.prikhodko@spbu.ru
Поступила в редакцию 16.06.2020
После доработки 23.06.2020
Принята к публикации 26.06.2020
Аннотация
В работе успешно применено уравнение состояния на основе статистической теории ассоциирующего флюида с возмущенной цепью для оценки скорости звука в смесях природного газа. Результаты прогнозирования скорости звука представлены для пяти бинарных и шести многокомпонентных систем (массив данных включает 1000 литературных экспериментальных точек), содержащих углеводороды, азот, диоксид углерода в широком интервале температур (250–415 К) и давлений (0.1–60 МПа). В расчетах не были использованы подгоночные параметры бинарного взаимодействия. Показано, что результаты моделирования скорости звука находятся в хорошем соответствии с литературными данными.
ВВЕДЕНИЕ
Скорость звука является важной термодинамической величиной, широко используемой для характеристики систем, содержащих нефтегазовые компоненты, флюиды в одно-, двух- или многофазных состояниях в широком диапазоне температур и давлений [1–5]. Измерения термодинамических свойств для флюидных смесей часто связаны с оценкой скорости звука, поскольку она помогает определить плотность, компонентный состав и, как следствие, молекулярную массу смеси [6–8]. Это термодинамическое свойство представляет особый интерес с теоретической точки зрения для тех исследователей, которые проверяют возможности термодинамических моделей, включая уравнения состояния (УС), для точной оценки скорости звука; эта величина выражается через производную второго порядка энергии Гельмгольца по объему [9]. Скорость звука (u) рассчитывается в соответствии с известным уравнением [10]
(1)
$u = \sqrt { - \frac{{{{V}^{2}}}}{{{{M}_{w}}}}\frac{{{{C}_{P}}}}{{{{C}_{V}}}}{{{\left( {\frac{{\partial P}}{{\partial V}}} \right)}}_{{T,n}}}} ,$Среди современных уравнений состояния, которые в последние годы тестируются разными исследователями для улучшения количественного описания скорости звука в чистых и смешанных флюидах различной природы, выделяются уравнения семейства SAFT (Statistical Associating Fluid Theory). Оригинальное УС на основе статистической теории ассоциирующего флюида было предложено в [11] и получило дальнейшее развитие в работах [12, 13]. Одной из успешных модификаций этой модели является PC-SAFT (Perturbed Chain-SAFT) [14]. Это УС основано на теории возмущений [15], в которой стандартная “невозмущенная” часть уравнения представляет собой цепочку из твердых сфер для описания сил отталкивания, а члены, связанные с возмущением, отражают различные взаимодействия с учетом сил притяжения. Для ассоциированных флюидов предполагается, что поверхность молекулы имеет контактные участки, которые способны специфически взаимодействовать с контактными участками других молекул, имитируя тем самым водородные связи.
В настоящее время можно говорить уже о целом семействе уравнений состояния на основе PC-SAFT; в частности, предлагаются новые версии этого УС, причем авторами делается акцент на более точную оценку скорости звука [10, 16–23], сохраняя при этом надежное описание P-V-T свойств изучаемых систем, включая плотность жидкости и давление пара на линии насыщения. Одним из удачных вариантов уравнения состояния PC-SAFT можно считать CP-PC-SAFT (Critical Point-based PC-SAFT). Это УС, разработанное в [16, 17, 20, 23], обеспечило более высокую точность описания скорости звука в различных чистых флюидах и бинарных системах в широком диапазоне условий, включая однофазные и двухфазные состояния, а также околокритическую область. Авторы преодолели некоторые недостатки оригинальной версии уравнения состояния PC-SAFT (неточная оценка скорости звука в жидкой фазе, завышенные значения критических констант чистых веществ, некорректное поведение теплоемкостей при очень высоких давлениях) и внесли незначительные улучшения в выражения для “остаточного” вклада в энергию Гельмгольца, чтобы улучшить описание термодинамических свойств чистых и смешанных флюидов. Тем не менее апробация этого УС еще недостаточна: не проводилось тщательного тестирования его способности предсказывать скорость звука в многокомпонентных системах. Недавно впервые была применена модель семейства PC-SAFT (CP-PC-SAFT) для оценки скорости звука для ряда многокомпонентных систем, содержащих нефтегазовые флюиды [24].
Целью настоящей работы является продолжение начатых исследований по применению этого уравнения состояния, чтобы получить более полную картину оценки скорости звука с помощью CP-PC-SAFT, расширение возможностей модели для прогнозирования скорости звука для бинарных систем, образованных нефтегазовыми компонентами, смесей природного газа, содержащих от пяти до десяти компонентов, применяя в расчетах предложенный в [17] стандартизированный подход “на основе критической точки”. Для выполнения поставленной цели в задачу работы входила оценка недостающих параметров модели для нескольких чистых компонентов.
ТЕОРИЯ
Согласно модели CP-PC-SAFT выражение для “остаточного” (т.е. за счет межмолекулярного взаимодействия) вклада в энергию Гельмгольца (Ares) в системе, содержащей неполярные компоненты, можно записать следующим образом (по аналогии с уравнением состояния PC-SAFT):
(2)
${{A}_{{res}}} = {{A}^{{hs}}}~ + {\text{ }}{{A}^{{chain}}} + {{A}^{{disp}}}~ = {{A}^{{hc}}} + {{A}^{{disp}}},$Приведем здесь основные уточнения в уравнении состояния CP-PC-SAFT, сделанные в [17], по сравнению с оригинальным вариантом PC-SAFT. Чтобы избежать предсказания отрицательных теплоемкостей и пересечений изотерм при очень высоких давлениях (что не имеет физического смысла и наблюдалось при использовании модели PC-SAFT), выражение для вклада твердых сфер (Ahs) было изменено. Соответствующее уточненное выражение для “остаточного” вклада в энергию Гельмгольца имеет следующий вид:
(3)
$\begin{gathered} {{A}^{{hs}}} = RT\frac{m}{{{{\xi }_{0}}}}\left( {\frac{{3{{\zeta }_{1}}{{\zeta }_{2}}}}{{1 - {{\zeta }_{3}}}}} \right) + \frac{{\zeta _{2}^{3}}}{{{{\zeta }_{3}}{{{(1 - {{\zeta }_{3}})}}^{2}}}} + \\ + \,\,\left( {\frac{{\zeta _{2}^{3}}}{{\zeta _{3}^{2}}} - {{\zeta }_{0}}} \right)\ln [1 - {{\zeta }_{3}}]\sqrt {\frac{{{{d}^{3}}({{\zeta }_{3}} - 1)}}{{{{\zeta }_{3}}{{\sigma }^{3}} - {{d}^{3}}}}} , \\ \end{gathered} $(4)
$\theta = \frac{{1 + 0.2977({k \mathord{\left/ {\vphantom {k \varepsilon }} \right. \kern-0em} \varepsilon })T}}{{1 + 0.33163({k \mathord{\left/ {\vphantom {k \varepsilon }} \right. \kern-0em} \varepsilon })T + 0.0010477{{{({k \mathord{\left/ {\vphantom {k \varepsilon }} \right. \kern-0em} \varepsilon })}}^{2}}{{T}^{2}}}}.$Этот множитель, учитывающий температурную зависимость для диаметра сегмента, был введен, для того чтобы получить правильное описание термодинамических свойств при температурном пределе и разумно предсказать кривую инверсии эффекта Джоуля–Томсона. Дополнительно:
(5)
${{\zeta }_{k}} = \frac{{\pi {{N}_{{av}}}}}{{6v}}\sum\limits_i {{{x}_{i}}} {{m}_{{ii}}}d_{{ii}}^{k},$(6)
${{A}^{{chain}}} = RT\sum\limits_{i,j} {{{x}_{i}}{{x}_{j}}} (1 - {{m}_{{ij}}})\ln \left\lfloor {{{g}_{{ij}}}{{{({{d}_{{ij}}})}}^{{hs}}}} \right\rfloor ,$(7)
$\begin{gathered} {{g}_{{ij}}}{{({{d}_{{ij}}})}^{{hs}}} = \frac{1}{{1 - {{\zeta }_{3}}}} + \frac{{3{{d}_{{ii}}}{{d}_{{jj}}}{{\zeta }_{2}}}}{{({{d}_{{ii}}} + {{d}_{{jj}}}){{{(1 - {{\zeta }_{3}})}}^{2}}}} + \\ + \,\,2{{\left( {\frac{{{{d}_{{ii}}}{{d}_{{jj}}}}}{{{{d}_{{ii}}} + {{d}_{{jj}}}}}} \right)}^{2}}\frac{{\zeta _{2}^{2}}}{{{{{(1 - {{\zeta }_{3}})}}^{3}}}}. \\ \end{gathered} $Выражение для дисперсионного вклада в энергию Гельмгольца содержит аналитические функции (I1 и I2), которые представляют интегралы радиальной функции распределения в поправках (членах) возмущения первого и второго порядков:
(8)
$\begin{gathered} {{A}^{{disp}}} = - R{{N}_{{av}}}\left( {\frac{{2\pi ({\varepsilon \mathord{\left/ {\vphantom {\varepsilon k}} \right. \kern-0em} k}){{m}^{2}}{{\sigma }^{3}}}}{v}} \right){{I}_{1}} + \\ + \,\,\frac{{\pi {{{({\varepsilon \mathord{\left/ {\vphantom {\varepsilon k}} \right. \kern-0em} k})}}^{2}}{{m}^{3}}{{\sigma }^{3}}}}{{vT(1 + {{m(8{{\zeta }_{3}} - 2\zeta _{3}^{2})} \mathord{\left/ {\vphantom {{m(8{{\zeta }_{3}} - 2\zeta _{3}^{2})} {{{{(1 - {{\zeta }_{3}})}}^{4}} + (1 - m)(20{{\zeta }_{3}} - {{27\zeta _{3}^{2} + 12\zeta _{3}^{3} - 2\zeta _{3}^{4})} \mathord{\left/ {\vphantom {{27\zeta _{3}^{2} + 12\zeta _{3}^{3} - 2\zeta _{3}^{4})} {{{{((1 - {{\zeta }_{3}})(2 - {{\zeta }_{3}}))}}^{2}}}}} \right. \kern-0em} {{{{((1 - {{\zeta }_{3}})(2 - {{\zeta }_{3}}))}}^{2}}}}}}} \right. \kern-0em} {{{{(1 - {{\zeta }_{3}})}}^{4}} + (1 - m)(20{{\zeta }_{3}} - {{27\zeta _{3}^{2} + 12\zeta _{3}^{3} - 2\zeta _{3}^{4})} \mathord{\left/ {\vphantom {{27\zeta _{3}^{2} + 12\zeta _{3}^{3} - 2\zeta _{3}^{4})} {{{{((1 - {{\zeta }_{3}})(2 - {{\zeta }_{3}}))}}^{2}}}}} \right. \kern-0em} {{{{((1 - {{\zeta }_{3}})(2 - {{\zeta }_{3}}))}}^{2}}}}}}}}{{I}_{2}}, \\ \end{gathered} $(9)
${{I}_{1}} = \sum\limits_{i = 1}^6 {\left( {{{a}_{{0i}}} + \frac{{m - 1}}{m}{{a}_{{1i}}} + \frac{{m - 1}}{m}\frac{{m - 2}}{m}{{a}_{{2i}}}} \right)\zeta _{3}^{i},} $(10)
${{I}_{2}} = \sum\limits_{i = 1}^6 {\left( {{{b}_{{0i}}} + \frac{{m - 1}}{m}{{b}_{{1i}}} + \frac{{m - 1}}{m}\frac{{m - 2}}{m}{{b}_{{2i}}}} \right)\zeta _{3}^{i}} .$В выражениях (9) и (10) a0–2i и b0–2i – универсальные параметры модели, значения которых можно найти в [17]; универсальные параметры радиальной функции распределения в члене, связанном с возмущениями первого порядка, были переоценены с использованием второго и третьего вириальных коэффициентов н-алканов. Когда УС используется для смесей, применяются правила смешения и вводятся подгоночные параметры бинарного взаимодействия kij для корректировки дисперсионной составляющей взаимодействий и/или lij, которые учитывают различия в размерах диаметров сегментов. В модели CP-PC-SAFT предложены более гибкие дополнительные правила смешения по сравнению с PC-SAFT:
(11)
$\frac{\varepsilon }{k} = \frac{{\sum\limits_i {\sum\limits_j {{{x}_{i}}{{x}_{j}}} {{m}_{{ii}}}{{m}_{{jj}}}\sigma _{{ij}}^{3}{{{({\varepsilon \mathord{\left/ {\vphantom {\varepsilon k}} \right. \kern-0em} k})}}_{{ij}}}} }}{{{{\sigma }^{3}}{{{\left( {\sum\limits_i {{{x}_{i}}} {{m}_{{ii}}}} \right)}}^{2}}}}.$(12)
$\sigma = \sqrt[3]{{\frac{{\sum\limits_i {\sum\limits_j {{{x}_{i}}{{x}_{j}}} {{m}_{{ii}}}{{m}_{{jj}}}\sigma _{{ij}}^{3}} }}{{{{{\left( {\sum\limits_i {{{x}_{i}}} {{m}_{{ii}}}} \right)}}^{2}}}}}},$(16)
$({\varepsilon \mathord{\left/ {\vphantom {\varepsilon k}} \right. \kern-0em} k}) = (1 - {{k}_{{ij}}})\sqrt {{{{({\varepsilon \mathord{\left/ {\vphantom {\varepsilon k}} \right. \kern-0em} k})}}_{{ii}}}{{{({\varepsilon \mathord{\left/ {\vphantom {\varepsilon k}} \right. \kern-0em} k})}}_{{jj}}}} .$В вышеприведенных формулах индексы i и j относятся к разным сегментам системы.
Для описания чистого неполярного вещества i в рамках модели CP-PC-SAFT требуется четыре параметра: число сегментов, образующих молекулу-цепь mi, диаметр сегмента σi, параметр энергии взаимодействия, деленный на постоянную Больцмана, для сегментов i-го типа εi/k. Кроме того требуется дополнительный параметр δvc, отвечающий за смещение критического объема (отношение между вычисленным по модели критическим объемом и его экспериментальным значением). Параметры модели CP-PC-SAFT для многих чистых компонентов уже определены [17]; список параметров расширяется и включает также полярные и ассоциирующие компоненты [16, 20, 23]. Прогностическая способность уравнения состояния CP-PC-SAFT повышается за счет значительного сокращения данных, необходимых для оценки молекулярных параметров индивидуальных веществ. Для нахождения параметров модели вместо их подгонки с использованием оптимизационной процедуры для обработки большого массива экспериментальных данных (как это делается для модели PC-SAFT), эти параметры определяются для двух реперных точек (состояний), а именно критической и тройной точек, путем реализации стандартизированной численной процедуры с использованием пакета Mathematica.
МЕТОДОЛОГИЯ РАСЧЕТОВ
Процедура расчета на основании численного решения системы четырех уравнений для нахождения параметров уравнения состояния CP-PC-SAFT подробно описана в работе [17]. Система уравнений имеет следующий вид:
(17)
${{\left. {{{{\left( {\frac{{\partial P}}{{\partial V}}} \right)}}_{{{{T}_{C}}}}} = 0} \right|}_{{{{V}_{{C,{\text{EOS}} = \delta {{v}_{C}}}}}}}},$(18)
${{\left. {{{{\left( {\frac{{{{\partial }^{2}}P}}{{\partial {{V}^{2}}}}} \right)}}_{{{{T}_{C}}}}} = 0} \right|}_{{{{V}_{{C,{\text{EOS}} = \delta {{v}_{C}}}}}}}},$(20)
$\rho _{{{\text{EOS}}}}^{L} = \left. {\rho _{{\exp }}^{L}} \right|\,\,\,\,{\text{в тройной точке}}{\text{.}}$Идея используемого подхода состоит в том, что параметры уравнения CP-PC-SAFT определяются в экспериментальных критических точках чистых компонентов (для заданных значений критических констант) и данных о плотности жидкости в тройной точке (из баз термодинамических данных, например, NIST [24]). Для решения уравнений (17)–(19) критическое давление, рассчитанное по УС (Pc, EOS), определяется путем замены температуры (T) на критическую температуру (Tc) и объема (V) на критический объем, полученный по УС (Vc, EOS, который равен Vc · δ). После этого, условия критической точки чистого компонента (уравнения (17)–(18)) могут быть получены аналитически. Хотя в уравнении (20) экспериментальное значение плотности приравнивается к рассчитанному по УС (EOS) ее значению, фактически решение сводится к равенству давлений в тройной точке (Ptp EOS = Ptp). Это связано с тем, что уравнение состояния выражается через давление как функцию температуры и плотности. В то же время, если температуры (плотности) в системе одинаковы, то и давления также должны быть равны. Система уравнений (17)–(20) может быть решена аналитически, однако эта процедура является трудоемкой и дает различные наборы решений, что требует в дальнейшем создания алгоритма для выбора окончательного решения. В отличие от этого, численная процедура дает только один набор решений; при этом необходимо задать начальные приближения для оценки параметров модели.
Большинство параметров CP-PC-SAFT для типичных нефтегазовых компонентов получено и опубликовано в [17]. В настоящей работе были оценены значения недоступных параметров для двух изоалканов – изобутана и изопентана. Значения всех используемых параметров для чистых веществ приведены в табл. 1.
Таблица 1.
Значения параметров уравнения состояния CP-PC-SAFT для чистых компонентов, используемые в настоящей работе
| Компонент | m | ε/k, К | σ, Å | δ | Литературный источник |
|---|---|---|---|---|---|
| N2 | 0.99880 | 94.351 | 3.61590 | 1.10537 | [17] |
| CO2 | 2.03351 | 163.491 | 2.81786 | 1.17358 | [17] |
| CH4 | 1.00082 | 142.508 | 3.74760 | 1.12673 | [17] |
| C2H6 | 1.56358 | 185.392 | 3.57406 | 1.16657 | [17] |
| C3H8 | 2.41440 | 184.368 | 3.39176 | 1.15188 | [17] |
| n-C4H10 | 2.48262 | 209.446 | 3.65040 | 1.15976 | [17] |
| i-C4H10 | 2.16530 | 213.128 | 3.84220 | 1.15340 | Настоящая работа |
| n-C5H12 | 3.06424 | 212.528 | 3.62421 | 1.16385 | [17] |
| i-C5H12 | 3.06420 | 212.528 | 3.62420 | 1.15640 | Настоящая работа |
| n-C6H14 | 3.51081 | 218.238 | 3.65575 | 1.16091 | [17] |
Хорошие результаты описания термодинамических свойств для различных чистых флюидов – легких углеводородов (метана, этана и пропана), длинноцепочечных алканов, углекислого газа, азота и для ряда бинарных и тройных систем, состоящих из компоненты природного газа были получены ранее [17]. Чтобы проверить предсказательную способность УС при расчете скорости звука для бинарных и многокомпонентных смесей, параметры бинарного взаимодействия (lij и kij в уравнениях (15), (16)) не подгонялись и были приняты равными нулю. Следует отметить, что и сама модель PC-SAFT позволяет прогнозировать термодинамические свойства и фазовое поведение для многокомпонентных систем, используя только параметры чистых компонентов. На текущем этапе наших исследований альтернативный подход, требующий дополнительных варьируемых параметров, не рассматривался.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
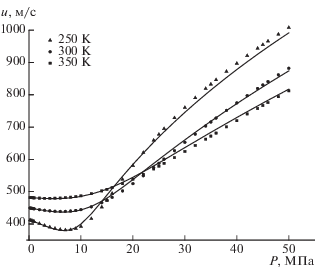
Вначале мы проверили способность CP-PC-SAFT прогнозировать скорость звука в чистом метане как основном компоненте рассматриваемых смесей природного газа. Как показано на рис. 1, не было обнаружено значительных отклонений между значениями, измеренными экспериментально [25], и значениями, предсказанными по модели. Стоит отметить, что CP-PC-SAFT конкурирует с другими моделями на основе PC-SAFT в описании скорости звука в метане [10, 17, 19, 21, 22]. Моделирование чистых компонентов является важным тестом для любого УС, однако основное практическое назначение для УС состоит в прогнозировании термодинамических свойств смесей. В связи с этим особый интерес представляют асимметричные смеси природного газа, образованные разнообразными углеводородными и неуглеводородными компонентами.
Рис. 1.
Зависимость скорости звука в метане от давления. Точки – экспериментальные значения [25], линии – результаты предсказания с помощью CP‑PC-SAFT.
Далее мы использовали CP-PC-SAFT при оценке скорости звука для бинарных и многокомпонентных смесей, образованных компонентами природного газа с различным содержанием метана. Ограниченная экспериментальная информация для скорости звука в многокомпонентных системах, используемая в нашем исследовании, не является критической для оценки прогностических возможностей модели. Было обработано не так много экспериментальных наборов данных, взятых из литературы, но их было достаточно для моделирования, чтобы отразить основные тенденции в поведении скорости звука при изменении температуры, давления и состава метана. Экспериментальные составы бинарных систем и многокомпонентных смесей синтетического/природного газа для разных месторождений и соответствующие значения скорости звука в широком диапазоне давлений для ряда температур приведены в [26–28].
Сравнение результатов, даваемых моделью CP-PC-SAFT, и экспериментальных данных оценивалось по значениям средней абсолютной ошибки в процентах (MAPE – mean absolute percentage error) и приведено в табл. 2 и 3 для бинарных и многокомпонентных систем соответственно:
(21)
$MAPE = \frac{{100\% }}{N}\sum\limits_{i = 1}^N {\left| {\frac{{u_{i}^{{{\text{расч}}}}}}{{u_{i}^{{{\text{эксп}}}}}} - 1} \right|} ,$Таблица 2.
Результаты, полученные в расчетах скорости звука для рассмотренных бинарных смесей с помощью CP-PC-SAFT
| Система | Состав, мол. д. первого компонента | Число эксперименталь-ных точек | Температура, К | Диапазон давлений, МПа | MAPE для скорости звука, % | Литературный источник |
|---|---|---|---|---|---|---|
| CH4 + C2H6 | 0.94985 | 15 14 12 20 20 |
250.00 275.00 300.00 325.00 350.00 |
0.78–9.86 0.65–10.59 0.62–10.44 0.50–10.40 0.55–10.52 |
0.75 0.35 0.28 0.23 0.26 |
[27] |
| 0.84902 | 8 9 9 9 |
250.00 275.00 300.00 350.00 |
2.52–19.96 0.52–20.08 0.51–19.75 0.55–20.05 |
2.37 1.84 1.42 0.63 |
[28] | |
| 0.68526 | 11 14 17 14 |
275.00 300.00 325.00 350.00 |
0.63–8.47 0.94–10.67 0.69–10.62 0.35–10.68 |
0.65 0.75 0.48 0.45 |
[27] | |
| 0.34524 | 7 10 15 17 15 |
250.00 275.00 300.00 325.00 350.00 |
0.25–1.42 0.54–4.21 0.50–6.45 0.70–10.37 0.48–10.57 |
0.45 0.29 0.46 1.34 0.75 |
[27] | |
| CH4 + C3H8 | 0.90016 | 7 11 14 25 14 |
250.00 275.00 300.00 325.00 350.00 |
0.48–3.05 0.58–10.22 0.55–10.45 0.48–10.41 0.62–10.25 |
0.21 0.93 0.44 0.43 0.46 |
[27] |
| CH4 + N2 | 0.95114 | 29 12 12 21 20 |
250.00 275.00 300.00 325.00 350.00 |
0.28–10.40 0.68–10.46 0.70–9.98 0.67–10.65 0.52–10.43 |
0.52 0.31 0.30 0.24 0.23 |
[27] |
| 0.71373 | 17 17 18 29 14 |
250.00 275.00 300.00 325.00 350.00 |
0.09–10.07 0.35–9.92 0.10–10.26 0.55–10.01 0.93–10.47 |
0.38 0.45 0.27 0.26 0.34 |
[27] | |
| CH4 + CO2 | 0.94979 | 19 12 12 28 9 |
250.00 275.00 300.00 325.00 350.00 |
0.58–10.52 0.45–10.50 0.49–10.60 0.60–10.38 0.69–8.01 |
0.80 0.48 0.50 0.44 0.30 |
[27] |
| 0.69944 | 16 17 17 20 15 |
250.00 275.00 300.00 325.00 350.00 |
0.63–7.48 0.56–10.40 0.69–10.38 0.58–10.45 0.63–10.37 |
0.97 1.20 1.20 0.99 1.02 |
[27] | |
| N2 + CO2 | 0.49593 | 9 9 11 19 17 |
250.00 275.00 300.00 325.00 350.00 |
0.84–3.96 2.04–10.21 1.33–10.03 0.52–10.02 1.75–10.34 |
0.30 0.64 0.69 0.63 0.86 |
[27] |
Таблица 3.
Результаты, полученные в расчетах скорости звука для рассмотренных многокомпонентных смесей с помощью CP-PC-SAFT
| Газовая смесь или месторождение | Число эксперименталь-ных точек | Температура, К | Интервал давлений, МПа | MAPE для скорости звука, % | Литературный источник |
|---|---|---|---|---|---|
| Синтетическая газовая смесь | 22 | 323.31 | 4.86–56.69 | 1.14 | [26] |
| 22 | 346.48 | 5.11–56.69 | 1.11 | ||
| 24 | 369.41 | 4.79–56.90 | 1.12 | ||
| 18 | 392.34 | 6.12–56.86 | 1.27 | ||
| 18 | 415.45 | 6.90–58.37 | 1.36 | ||
| Gulf Coast | 12 | 250.00 | 0.59–10.41 | 0.95 | [27] |
| 13 | 275.00 | 0.50–10.33 | 0.38 | ||
| 14 | 300.00 | 0.47–10.31 | 0.38 | ||
| 17 | 325.00 | 0.54–10.38 | 0.36 | ||
| 14 | 350.00 | 0.63–10.40 | 0.32 | ||
| Amarillo | 11 | 250.00 | 0.67–10.88 | 1.20 | [27] |
| 10 | 275.00 | 0.65–10.47 | 0.43 | ||
| 6 | 298.00 | 6.89–23.39 | 1.71 | ||
| 11 | 300.00 | 0.56–10.43 | 0.38 | ||
| 19 | 325.00 | 0.69–10.43 | 0.37 | ||
| 15 | 350.00 | 0.86–10.64 | 0.30 | ||
| Statoil Dry Gas | 15 | 250.00 | 0.80–9.74 | 1.52 | [27] |
| 11 | 275.00 | 0.52–10.42 | 0.65 | ||
| 18 | 300.00 | 0.53–10.30 | 0.41 | ||
| 17 | 325.00 | 0.47–10.40 | 0.42 | ||
| Statoil Statvordgass | 12 | 300.00 | 1.86–10.38 | 1.37 | [27] |
| 14 | 325.00 | 0.42–9.89 | 0.79 | ||
| 16 | 350.00 | 0.64–10.44 | 0.86 | ||
| Смесь натурального газа | 7 | 250.00 | 0.52–19.59 | 2.50 | [28] |
| 8 | 275.00 | 0.52–19.06 | 1.61 | ||
| 9 | 300.00 | 0.50–20.06 | 1.22 | ||
| 9 | 350.00 | 0.51–20.17 | 0.53 |
Результаты прогнозирования скорости звука для бинарных и многокомпонентных систем, содержащих компоненты природного газа, вместе с экспериментальными данными представлены на рис. 2.
Рис. 2.
Зависимость скорости звука от давления: (а) – точки – экспериментальные значения для бинарной системы метан (0.95) + этан (0.05) [27], линии – результаты предсказания с помощью CP-PC-SAFT; (б) – точки – экспериментальные значения для бинарной системы метан (0.95) + азот (0.05) [27], линии – результаты предсказания с помощью CP-PC-SAFT; (в) – точки – экспериментальные значения для бинарной системы метан (0.95) + диоксид углерода (0.05) [27]; линии – результаты предсказания с помощью CP-PC-SAFT; (г) – точки – экспериментальные значения для смеси природного газа месторождения Gulf Coast метан (0.95) + остальные компоненты (0.05) [27]; линии – результаты предсказания с помощью CP-PC-SAFT.
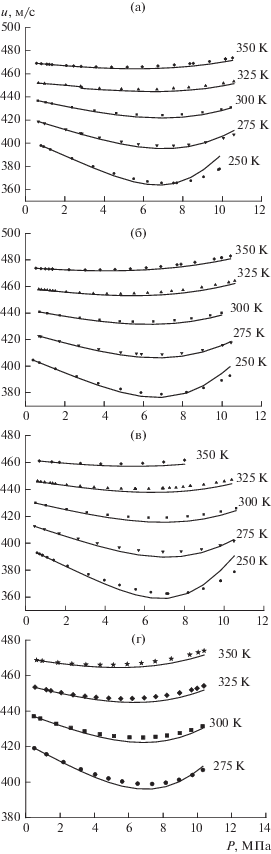
Результаты расчетов показывают, что модель правильно отражает небольшой минимум на зависимости скорости звука от давления при заданной температуре. Как видно из рис. 2, проведенные расчеты дают хорошие результаты, достаточные для разумных оценок скорости звука в исследуемых системах при рассматриваемых условиях. Несколько большее расхождение между экспериментальными и расчетными значениями скорости звука наблюдается для бинарных смесей при самых низких температурах 250 и 275 K и давлениях в диапазоне 9–10.5 МПа (рис. 2a–2в, табл. 2). При этих условиях скорость звука начинает значительно менять свое направление с увеличением давления, и предсказанная кривая идет немного круче по сравнению с экспериментальной. В этом случае подгонка параметра kij для улучшения прогнозируемых результатов не требовалась из-за, в целом, вполне надежных оценок скорости звука с помощью CP-PC-SAFT, полученных для двух- и многокомпонентных систем (рис. 2г, табл. 3), которые изучались при 250 K и более высоких температурах.
Результаты, представленные на рис. 1 и 2а–2в, демонстрируют, что в соответствии с экспериментальными данными добавление второго компонента к чистому метану приводит к уменьшению значения скорости звука для бинарной системы по сравнению с этой величиной для чистого компонента при фиксированных температуре и давлении. Рисунки 2а–2в показывают влияние на скорость звука добавки второго компонента (приблизительно 95 мол. % метана и 5 мол. % другого компонента соответственно). Принимая во внимание неполярную природу компонентов смеси (полярность, близкая к нулю), различия в величинах скорости звука в представленных бинарных подсистемах с метаном могут быть связаны с различиями в молекулярных размерах флюидов (двух компонентов). Модель правильно воспроизводит наблюдаемые зависимости.
Из табл. 3 видно, что значения MAPE для скорости звука не превышают 2.5% для изученных многокомпонентных систем, что свидетельствует о достаточно хорошей точности полученных результатов. Отметим, что ранее нами было показано [24], что помимо скорости звука CP-PC-SAFT дает довольно точные результаты в прогнозировании плотностей для многокомпонентных смесей.
Анализ вклада отдельных членов в уравнении (2) на примере неполярного флюида (н-гексана) с помощью PC-SAFT показал [10], что точная оценка производной энергии Гельмгольца по объему второго порядка дает в результате хорошую оценку величины ${{\left( {\frac{{\partial P}}{{\partial V}}} \right)}_{{T,n}}}$, что, в свою очередь, приводит к точным предсказаниям скорости звука. Поскольку эта производная определяется вкладом твердых сфер в выражении для Ahs, можно сделать вывод, что количественное описание взаимодействий, связанных с отталкиванием, возможно, улучшило бы оценку частной производной давления по объему и связанных с ней термодинамических свойств. По сути, это то, что было достигнуто в [17] с помощью CP-PC-SAFT, где был сделан ряд улучшений (уточнений) для выражения вклада Ahs. Можно резюмировать, что эта версия модели на основе PC-SAFT, по-видимому, является надежной для оценки скорости звука в смесях природного газа. На данном этапе прогнозирование скорости звука в многокомпонентных смесях представляется весьма обнадеживающим для дальнейших исследований.
ЗАКЛЮЧЕНИЕ
Было обнаружено, что результаты, полученные при расчете скорости звука в системах, состоящих из нефтегазовых компонентов, являются перспективными для дальнейшего использования уравнения состояния на основе PC-SAFT при оценке термодинамических свойств природного газа для практических целей. В настоящей работе не использовались подгоночные параметры бинарного взаимодействия, а значения MAPE для скорости звука для всех исследованных бинарных и многокомпонентных смесей составляли не более 2.5%, что связано с сильной физической основой моделей семейства PC-SAFT, включая рассмотренную версию этого УС. CP-PC-SAFT EOS можно рассматривать как подходящий инструмент для надежного прогнозирования скорости звука в различных системах с приемлемой точностью для приложений в химической инженерии.
Авторы благодарны И. Полишуку за его полезные комментарии и обсуждение.
Работа выполнена при финансовой поддержке совместного проекта Российского фонда фундаментальных исследований (РФФИ) и Национального научного фонда Ирана (INSF): контракт INSF No. 96004167 и грант РФФИ 17-58-560018.
ОБОЗНАЧЕНИЯ
| A | энергия Гельмгольца, Дж |
| a, b | универсальные константы модели CP-PC-SAFT |
| С | теплоемкость, Дж/(К моль) |
| d | расстояние между сегментами, Å |
| g | радиальная функция распределения |
| I | сокращенное выражение для интеграла в теории возмущений |
| k | постоянная Больцмана или безразмерный подгоночный параметр |
| l | безразмерный подгоночный параметр |
| Mw | молекулярная масса, г/моль |
| m | число сегментов на цепь |
| N | число экспериментальных точек |
| Nav | число Авогадро |
| P | давление, Па |
| R | газовая постоянная |
| T | температура, К |
| u | скорость звука, м/с |
| V | молярный объем, м3/моль |
| x | мольная доля |
| δ | безразмерный параметр объемного смещения в CP-PC-SAFT |
| ε | глубина парного потенциала, Дж |
| ζk | сокращенное выражение, где k = 0, 1, 2, 3, Åk– 3 |
| θ | безразмерная температура |
| π | число пи |
| ρ | молярная плотность, моль/м3 |
| σ | диаметр сегмента в CP-PC-SAFT, Å |
ИНДЕКСЫ
| 0i, 1i, 2i | номера универсальных констант в CP-PC-SAFT |
| av | Авогадро |
| c | критическое состояние |
| chain | цепь |
| disp | дисперсионный |
| EOS | уравнение состояния |
| hc | твердая цепь |
| hs | твердая сфера |
| i, j | номера компонентов или сегментов |
| L | жидкая фаза |
| n | общее число молей |
| P | изобарические условия |
| res | “остаточный” вклад |
| T | изотермические условия |
| tp | тройная точка |
| V | изохорические условия |
| w | молекулярная масса |
| расч | рассчитанное свойство |
| эксп | экспериментальное свойство |
Список литературы
Meng G., Jaworski A.J., White N.M. Composition measurements of crude oil and process water emulsions using thick-film ultrasonic transducers // Chem. Eng. Process. 2006. V. 45. P. 383.
Machefer S., Schnitzlein K. Inline concentration monitoring of binary liquid mixtures in the presence of a dispersed gas phase with a modified speed of sound immersion probe // Chem. Eng. Technol. 2007. V. 30. P. 1381.
de Medeiros J.L., de Oliveira Arinelli L., de Queiroz F. Araújo O. Speed of sound of multiphase and multi-reactive equilibrium streams: A numerical approach for natural gas applications // J. Nat. Gas Sci. Eng. 2017. V. 46. P. 222.
Nichita D.V., Khalid P., Broseta D. Calculation of isentropic compressibility and sound velocity in two-phase fluids // Fluid Phase Equilib. 2010. V. 291. P. 95.
Castier M. Thermodynamic speed of sound in multiphase systems // Fluid Phase Equilib. 2011. V. 306. P. 204.
Farzaneh-Gord M., Rahbari H.R. Numerical procedures for natural gas accurate thermodynamic properties calculation // J. Eng. Thermophys. 2012. V. 21. P. 213.
Farzaneh-Gord M., Arabkoohsar A., Koury R.N.N. Novel natural gas molecular weight calculator equation as a functional of only temperature, pressure and sound speed // J. Nat. Gas Sci. Eng. 2016. V. 30. P. 195.
Farzaneh-Gord M., Mohseni-Gharyehsafa B., Toikka A., Zvereva I. Sensitivity of natural gas flow measurement to AGA8 or GERG2008 equation of state utilization // J. Nat. Gas Sci. Eng. 2018. V. 57. P. 305.
Llovell F., Peters C.J., Vega L.F. Second-order thermodynamic derivative properties of selected mixtures by the soft-SAFT equation of state // Fluid Phase Equilib. 2006. V. 248. P. 115.
de Villiers A.J., Schwarz C.E., Burger A.J., Kontogeorgis G.M. Evaluation of the PC-SAFT, SAFT and CPA equations of state in predicting derivative properties of selected non-polar and hydrogen-bonding compounds // Fluid Phase Equilib. 2013. V. 338. P. 1.
Chapman W.G., Gubbins K.E., Jackson G., Radosz M. New Reference Equation of State for Associating Liquids // Ind. Eng. Chem. Res. 1990. V. 29. P. 1709.
Huang S.H., Radosz M. Equation of State for Small, Large, Polydisperse, and Associating Molecules // Ind. Eng. Chem. Res. 1990. V. 29. P. 2284.
Huang S.H., Radosz M. Equation of State for Small, Large, Polydisperse, and Associating Molecules: Extension to Fluid Mixtures // Ind. Eng. Chem. Res. 1991. V. 30. P. 1994.
Gross J., Sadowski G. Perturbed-chain SAFT: An equation of state based on a perturbation theory for chain molecules // Ind. Eng. Chem. Res. 2001. V. 40. P. 1244.
Barker J.A., Henderson D. Perturbation theory and equation of state for fluids: The square-well potential // J. Chem. Phys. 1967. V. 47. P. 2856.
Polishuk I., Lubarsky H., NguyenHuynh D. Predicting phase behavior in aqueous systems without fitting binary parameters II: Gases and non-aromatic hydrocarbons // AIChE J. 2017. V. 63. P. 5064.
Polishuk I. Standardized critical point-based numerical solution of statistical association fluid theory parameters: The perturbed chain-statistical association fluid theory equation of state revisited // Ind. Eng. Chem. Res. 2014. V. 53. P. 14127.
Polishuk I., Katz M., Levi Y., Lubarsky H. Implementation of PC-SAFT and SAFT + Cubic for modeling thermodynamic properties of haloalkanes. I. 11 halomethanes // Fluid Phase Equilib. 2012. V. 316. P. 66.
Burgess W.A., Tapriyal D., Gamwo I.K., Wu Y., McHugh M.A., Enick R.M. New group-contribution parameters for the calculation of PC-SAFT parameters for use at pressures to 276 MPa and temperatures to 533 K // Ind. Eng. Chem. Res. 2014. V. 53. P. 2520.
Lubarsky H., Polishuk I. Implementation of the critical point-based revised PC-SAFT for modelling thermodynamic properties of aromatic and haloaromatic compounds // J. Supercrit. Fluids. 2015. V. 97. P. 133.
Liang X., Maribo-Mogensen B., Thomsen K., Yan W., Kontogeorgis G.M. Approach to improve speed of sound calculation within PC-SAFT framework // Ind. Eng. Chem. Res. 2012. V. 51. P. 14903.
Palma A.M., Queimada A.J., Coutinho J.A.P. Using a Volume Shift in Perturbed-Chain Statistical Associating Fluid Theory to Improve the Description of Speed of Sound and Other Derivative Properties // Ind. Eng. Chem. Res. 2018. V. 57. P. 11804.
Melent’ev V.V., Postnikov E.B., Polishuk I. Experimental Determination and Modeling Thermophysical Properties of 1-Chlorononane in a Wide Range of Conditions: Is It Possible to Predict a Contribution of Chlorine Atom? // Ind. Eng. Chem. Res. 2018. V. 57. P. 5142.
Prikhod’ko I.V., Samarov A.A., Toikka A.M. On Application of PC–SAFT Model for Estimating the Speed of Sound in Synthetic and Natural Oil-and-Gas Mixtures // Russ. J. Appl. Chem. 2019. V. 92. № 2. P. 262. [Приходько И.В., Самаров А.А., Тойкка А.М. О применении модели PC-SAFT для оценки скорости звука в синтетических и природных нефтегазовых смесях // Ж. прикл. хим. 2019. Т. 92. № 2. С. 231.]
NIST Chemistry WebBook, SRD 69. Gaithersburg, Md.: National Institute of Standards and Technology (NIST), 2018. https://doi.org/https://doi.org/10.18434/T4D303
Ahmadi P., Chapoy A., Tohidi B. Density, speed of sound and derived thermodynamic properties of a synthetic natural gas // J. Nat. Gas Sci. Eng. 2017. V. 40. P. 249.
Younglove B.A., Frederick N.V, McCarty R.D. Speed of Sound Data and Related Models for Mixtures of Natural Gas Constituents (NIST Monograph 178). Washington, DC: U.S. Government Printing Office, 1993.
Costa Gomes M.F., Trusler J.P.M. The speed of sound in two methane-rich gas mixtures at temperatures between 250 K and 350 K and at pressures up to 20 MPa // J. Chem. Thermodyn. 1998. V. 30. P. 1121.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


