Теоретические основы химической технологии, 2021, T. 55, № 1, стр. 46-57

Анализ и моделирование движения частиц вблизи погруженной в кипящий слой поверхности теплообмена

О. Ю. Милованов^a, *, Р. Л. Исьемин^a, Д. В. Климов^a, В. С. Кох-Татаренко^a, О. М. Ларина^b

^a Тамбовский государственный технический университет
Тамбов, Россия

^b Объединенный институт высоких температур РАН
Москва, Россия

^* E-mail: penergy@list.ru

Поступила в редакцию 30.03.2020
После доработки 15.06.2020
Принята к публикации 18.06.2020

DOI: 10.31857/S0040357120060172

Полный текст (PDF)

Аннотация

Погружение в кипящий слой теплообменника изменяет гидродинамическую структуру слоя, которая, как показывает настоящее исследование, оказывает определяющее влияние на процесс переноса тепла. Вблизи погруженного тела с ростом скорости газа, продуваемого через слой, образуется приповерхностная зона с локальной вертикальной циркуляцией частиц и более высокой порозностью, чем в остальном объеме слоя. В настоящей работе показано, что ухудшение обмена частицами между этой зоной и остальным объемом слоя приводит к снижению интенсивности внешнего теплообмена с ростом скорости газа. Предложена модель, позволяющая рассчитать ширину приповерхностной зоны и время пребывания в ней частиц кипящего слоя.

Ключевые слова: кипящий слой, поверхность теплообмена, движение частиц, приповерхностная зона, время пребывания частиц в приповерхностной зоне

ВВЕДЕНИЕ

Время пребывания частицы вблизи погруженной в кипящий слой поверхности теплообмена необходимо определять для расчёта интенсивности внешнего теплообмена в кипящем слое с использованием всех предложенных моделей теплообмена [1–9].

В табл. 1 представлены методы определения и полученные значения времени нахождения частиц у поверхности теплообмена в предыдущих исследованиях.

Таблица 1.

Применяемые методы и результаты определения времени нахождения частиц у поверхности теплообмена

Метод определения	Время нахождения частиц у поверхности теплообмена	Источник информации
Наблюдения за колебаниями температуры в платиновой фольге	0.15–1.0 с	[5]
Наблюдения за колебаниями температуры в платиновой фольге	0.1–0.5 с	[14]
Экстраполяция от времени пребывания частиц в перемешиваемых слоях	1–1.6 с	[10]
Киносъемка меченных частиц	≈3 с	[11]
Киносъемка меченных частиц	0.02–0.36 с	[12]
Анализ киносъемки движения частиц	1.5–6.0 с	[13]
	0.04–0.08 с	[16]
	0.5–5 с	[1]
Анализ сигналов емкостных датчиков быстрого отклика	0.07–1.13 с	[15]
Обнаружение излучения частиц с помощью инфракрасной камеры	0.35–0.5 с	[18]

Обращает на себя внимание разброс значений времени пребывания частиц у поверхности теплообмена, определенного различными методами (таб. 1). С другой стороны, важность правильного определения этого параметра велика.

Это обусловлено, в частности, тем, что по-прежнему широко используемая “пакетная” модель теплообмена [4, 5] дает нереалистичную взаимосвязь между коэффициентом теплообмена и теплоемкостью твердых частиц [11, 19], а предсказанный “пакетной” моделью коэффициент теплообмена возрастает до бесконечности при уменьшении времени частиц у поверхности теплообмена [6, 11]. Чтобы преодолеть недостатки “пакетной” модели вводится дополнительное термическое сопротивление между кипящим слоем и поверхностью теплообмена (“газовая пленка”) [20–23], что порождает дополнительные неопределенности “пакетной” модели. С одной стороны, толщины “газовой пленки”, определенные в различных моделях для, по-видимому, схожих условий, сильно отличаются [24]. С другой стороны, было доказано, что существование такой “газовой пленки” противоречит физическим реалиям [1, 25].

Альтернативная “модель частиц” свободна от недостатков “пакетной” модели, так как не связана с моделированием свойств мифических “пакетов” и введением не существующего термического сопротивления в виде “газовой пленки” [10, 24].

Однако, отсутствие подробной информации в открытой литературе о движении отдельных частиц возле стенки, однако, препятствует дальнейшему развитию этой модели.

С другой стороны, экспериментально доказано, что размещение в кипящем слое теплообменных труб изменяет гидродинамическую структуру слоя. Под вертикально погруженным телом образуется прецессирующая газовая полость, которая периодически формирует газовые пузыри, поднимающиеся как вдоль погруженного тела, так и под некоторым углом к нему. В результате у погруженного тела или поверхности теплообмена образуется некоторая зона слоя, шириной равной нескольким диаметрам частиц, имеющую повышенную порозность и с локальной циркуляцией в ней частиц [26, 27]. Эту область слоя будем далее называть “приповерхностной зоной”; из-за более высокой порозности в эту зону устремляется часть газа, что приводит к снижению скорости газа в остальной части слоя [28]. Очевидно, что интенсивность обмена частицами между “приповерхностной зоной” и остальной частью слоя должен влиять на интенсивность переноса теплообмена между погруженной поверхностью и кипящим слоем.

Целью настоящей работы является исследование процесса формирования “приповерхностной зоны”, обмена частицами между этой зоной с остальным слоем, а также разработка модели для расчета времени пребывания частиц в “приповерхностной зоне”.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Проведение эксперимента. Нами исследовалось движение частиц алюмосиликатного катализатора (диаметр частиц 2.5–3.0 мм, критическая скорость псевдоожижения v_mf = 0.86 м/с) в аппарате внутренним диаметром D = 172 мм. Слой частиц алюмосиликатного катализатора псевдоожижался воздухом при комнатной температуре.

Для выяснения влияния погруженного тела на движение частиц в кипящем слое были проведены сравнительные исследования движения частиц в свободном кипящем слое и в кипящем слое, содержащем погруженное тело, которое имитировало поверхность теплообмена.

В последнем случае в аппарат по продольной оси погружался цилиндр диаметром d = 40 мм, выполненный из нержавеющей стали. Цилиндр имел скругленный нижний торец; расстояние от этого торца до воздухораспределительной решетки составляло 10 мм.

Движение частиц слоя анализировалось по результатам слежения за вводимой в слой магнитомеченной частицы, полученной при спекании ферромагнитного порошка и полипропилена. Эта магнитомеченная частица имела такие размеры и массу, как и остальные частицы слоя. После намагничивания частицы в постоянном магнитном поле магнитный момент составлял 0.39 А/м. Магнитометры, непрерывно измеряющие изменение напряжeнности магнитного поля, что позволяло в дальнейшем рассчитать координаты частицы, были установлены вне аппарата. Магнитометры снабжались блоками магниточувствительных датчиков, которые представляли собой двухстержневые дифференциальные феррозонды. Каждый измерительный канал имел следующие характеристики: диапазон измерений – ±500 × 10^–4 Эрстед; чувствительность – 0.02 В/500 × 10^–4 Эрстед; нелинейность – 5%; напряжение питания – 10 В. Выходные сигналы магнитометров регистрировались на компьютере, с помощью которого определялись в составляющие вектора перемещения частицы в кипящем слое.

Эксперименты проводились при значениях высоты неподвижного слоя равной Н₀ = 0.25D, Н₀ = = 0.5D и Н₀ = 1.0D и скоростях воздуха равных 1.5v_mf, 2.5v_mf и 3.5v_mf. Погрешность определения координат меченой частицы составляла ±10%.

Исследовалось перемещение частицы по вертикали Z(t) и по радиусу R(t), считая от центра от аппарата. Затем траектории движения частицы по вертикали и радиусу разбивались на отдельные участки через каждые 0.2 с. Это позволяло методом численного дифференцирования определить значения вектора скорости частицы v_Z и v_R.

Чтобы определить вероятность нахождения частицы в разных точках слоя весь объем слоя разбивался на ячейки размером 10 × 10 мм и подсчитывалось количество “попаданий” частицы в каждую ячейку. По этим данным строились гистограммы распределения вероятности нахождения частиц в любой точке слоя.

Для того чтобы полученные результаты по слежению за движением одной частицы можно было распространить на движение всех частиц слоя, необходимо, чтобы длительность наблюдения за отдельной частицей была в два раза больше эффективного времени корреляции, численно равного площади под кривой нормированной корреляционной функции случайного процесса R(t) или Z(t). В ходе предварительных опытов выяснилось, что эта площадь максимальна для случайного процесса R(t) при Н₀ = 1.0D и V = 1.5v_mf.

Было установлено, что время наблюдения за магнитомеченной частицы в каждом опыте должна быть не менее 78 с; фактическое время наблюдения было 100 с. При такой длительности наблюдения не имеет значения место ввода меченой частицы в слой и способ ее ввода в слой.

Анализ полученных данных. Анализ движения частиц как в свободном кипящем слое показал, что на этот процесс в свободном слое влияет перестройка профиля скорости воздуха в поперечных сечения слоя по мере удаления от воздухораспределительной решетки.

Действительно, как это было показано в работе [29], в свободном кипящем слое изначально “плоский” профиль скорости воздуха на небольшой высоте на воздухораспределительной решеткой по мере удаления от последней трансформируется в “выпуклый” профиль скорости с максимумом вблизи центра аппарата. Причем, чем выше скорость воздуха, отнесенная к сечению пустого аппарата, тем быстрее происходит эта трансформация. Это привело авторов работы [29] к утверждению, что в кипящем слое самопроизвольно формируется “очаг кипения” с локальной вертикальной циркуляцией частиц твердой фазы.

Исследование движения частиц в свободном кипящем слое подтвердило это предположение.

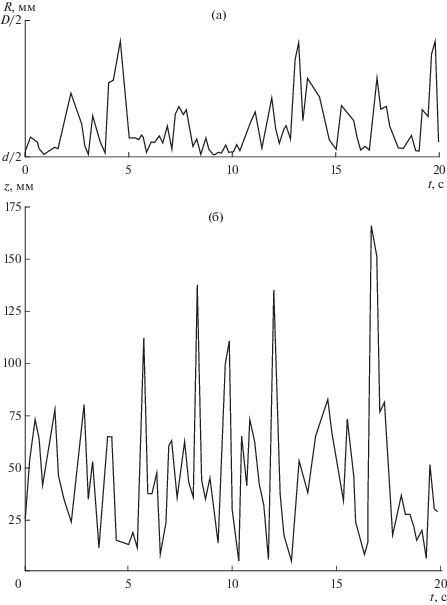
На рис. 1–3 представлены участки траектории движения меченной частицы в свободном слое в проекции на горизонтальную плоскость (а) и на вертикальную плоскость (б) при скорости воздуха v = 1.5, 2.5 и 3.5v_mf и начальной высоте слоя Н₀ = = 0.5D.

Рис. 1.

Участки проекций траектории движения частицы в свободном слое на горизонтальную (а) и вертикальную (б) плоскость (Н₀ = 0.5D и v = 1.5v_mf).

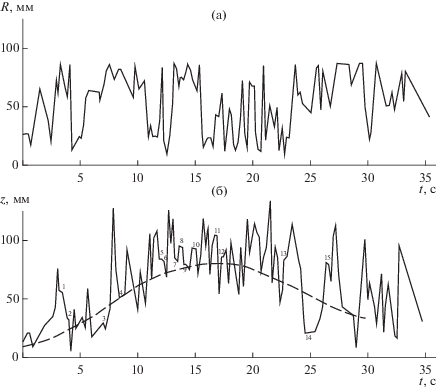
Рис. 2.

Участки проекций траектории движения частицы в свободном слое на горизонтальную (а) и вертикальную (б) плоскость (Н₀ = 0.5D и v = 2.5v_mf).

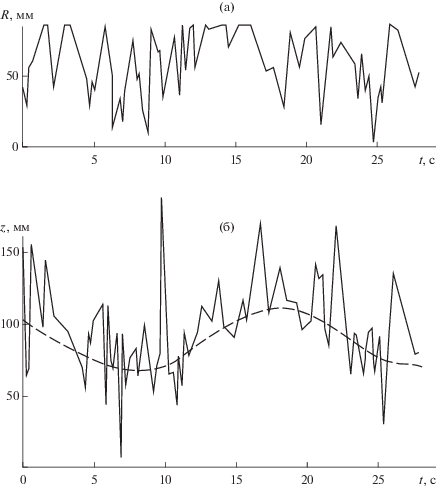
Рис. 3.

Участки проекций траектории движения частицы в свободном слое на горизонтальную (а) и вертикальную (б) плоскость (Н₀ = 0.5D и v = 3.5v_mf).

Видно, что при скорости воздуха v = 1.5v_mf частица совершает медленное циркуляционное движение по высоте слоя с периодом примерно равным 22 с. На это движение накладываются резкие флуктуации в траектории движения частиц вблизи верхней границы слоя, вызванные, очевидно, с выходом на поверхность слоя и разрушением воздушных пузырей. С ростом скорости воздуха до v = 2.5v_mf период в циркуляции частиц по вертикали сокращается до 15 с, а при скорости v = 3.5v_mf этот период уменьшается до 4.2 с.

При скорости воздуха v = 1.5v_mf нахождение частицы примерно равновероятно в любой точке радиуса аппарата.

При скорости воздуха v = 2.5v_mf повышается вероятность нахождения частиц в кольце с радиусами R = 30 и 60 мм.

При скорости воздуха v = 3.5v_mf это кольцо сужается и ограничивается радиусами R = 20 и 40 мм.

При этом с ростом скорости воздуха повышается вероятность сообщения частицам радиальной составляющей скорости близкой к нулю.

Такой характер движения частиц подтверждает, что с ростом скорости воздуха в свободном кипящем слое возникает режим очагового кипения с локальной вертикальной циркуляцией частиц в узком кольце.

Снижение начальной высоты слоя до Н₀ = = 0.25D приводит к появлению очага кипения вблизи кольца со средним радиусом 45 мм уже при скорости воздуха v = 1.5v_mf.

Увеличение начальной высоты слоя до Н₀ = 1.0D приводит к тому, что с ростом скорости воздуха режим очагового кипения вырождается и вероятность нахождения частиц в разных точках радиуса аппарата становится примерно одинаковой.

Размещение в слое вертикального цилиндра перераспределяет потоки воздуха в слое и приводит к тому, что очаговое кипение возникает близи погруженного в слой тела.

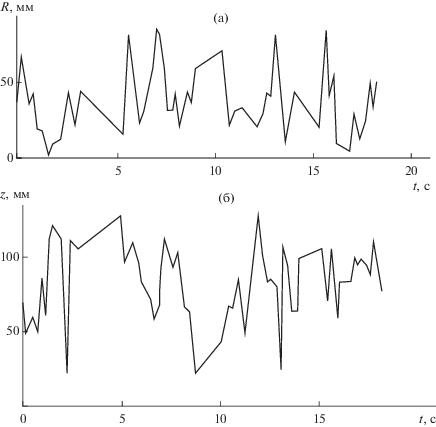
На рис. 4 представлены участка траектории частицы в слое с вертикальным цилиндром по радиусу и по вертикали при скорости v = 1.5v_mf. и начальной высоте слоя Н₀ = 0.5D.

Рис. 4.

Проекции траекторий частицы в слое с вертикальным цилиндром на горизонтальную (а) и вертикальную (б) плоскости при скорости v = 1.5v_mf и начальной высоте слоя Н₀ = 0.5D.

Как следует из рис. 4, при указанной выше скорости воздуха частица свободно перемещается по всему поперечному сечению слоя, но при этом более вероятно ее нахождение вблизи и выше границы неподвижного слоя.

Повышение скорости газа до 3.5v_mf при той же начальной высоте слоя повышает вероятность нахождения частиц в “приповерхностной зоне”, ограниченной радиусами 20 и 40 мм; в части поперечного сечения слоя с радиусом R > 50 мм вероятность нахождения частиц снижается (рис. 4). На рис. 4 видны участки траектории, когда движение частицы временно локализуется в “приповерхностной зоне”, где она совершает подъемно-опускное движение, а затем покидает “приповерхностную зону”.

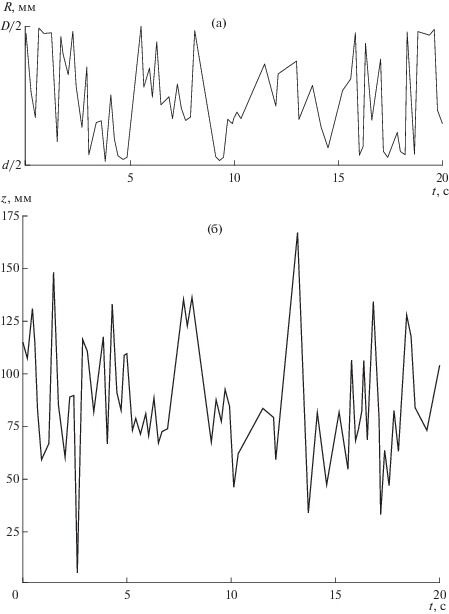
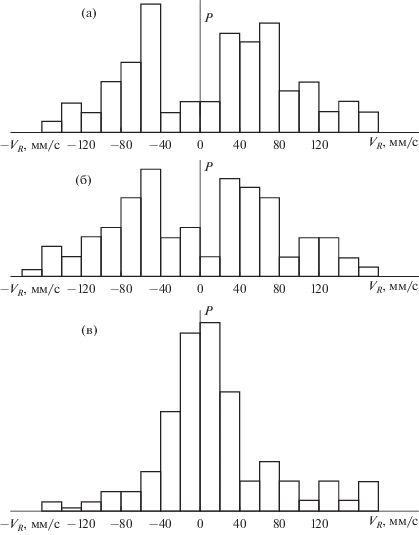
Интересно, что при скорости 3.5v_mf более вероятно, что радиальная составляющая скорости частицы v_R≈ 0 мм/с (рис. 5), тогда как при более низких значениях скорости газа частицы часто имеют скорость v_R = ±40–80 мм/с (рис. 5), причем вероятность сообщения частицам отрицательной и положительной скорости примерно одинакова.

Рис. 5.

Проекции траекторий частицы в слое с вертикальным цилиндром на горизонтальную (а) и вертикальную (б) плоскости при скорости v = 3.5v_mf и начальной высоте слоя Н₀ = 0.5D.

Описанные наблюдения позволяют предположить, что при начальной высоте слоя формирование “приповерхностной зоны” происходит при скорости воздуха 3.5v_mf. При этом в “приповерхностной зоне” наблюдается очаговое кипение находящихся там частиц, о чем свидетельствует значение v_R ≈ 0.

Уменьшение начальной высоты слоя до Н₀ = = 0.25D приводит к тому, что уже при v ≤ 2.5v_mf происходит резкое повышение вероятности нахождения частиц вблизи цилиндра в зоне шириной 10–20 мм, т.е. в этой области образуется “приповерхностная зона”.

Увеличение начальной высоты до Н₀ = 1.0D в исследованном диапазоне скоростей воздуха ярко выраженной “приповерхностной зоны” не наблюдается: вероятность нахождения частиц в области R > 50 мм при Н₀ = 1.0D и v = 3.5v_mf выше, чем при той же скорости газа, но высоте слоя Н₀ = 0.5D.

До формирования “приповерхностной зоны”, время нахождения частиц вблизи погруженного тела (на расстоянии до 20 мм от него) составляет 0.35–0.4 с, а на большем расстоянии от погруженного тела 0.3–0.38 с.

Рис. 6.

Оценка плотности распределения вероятности значений V_R в слое с вертикальным цилиндром при Н₀ = 1.0D: (а) – v = 1.5v_mf; (б) – v = 2.5v_mf; (в) – v = 3.5v_mf.

После образования “приповерхностной зоны” время нахождения в ней частиц составляет 0.36–0.5 с (эти значения близки к экспериментальным данным, полученными в работах [12, 14, 18 ]), а вне “приповерхностной зоны” 0.25–0.4 с.

Таким образом, образование “приповерхностной зоны”, ширина которой составляет 7–8 среднего диаметра частиц слоя, не оказывает значительного влияния на время нахождения частиц в этой зоне и вне ее. Но формирование “приповерхностной” зоны оказывает значительное влияние на циркуляцию частиц в радиальном направлении: до формирования “приповерхностной” зоны имеет место интенсивная циркуляция частиц в радиальном направлении, которая не наблюдается после формирования “приповерхностной зоны”.

Это должно влиять на интенсивность теплообмена между кипящим слоем и погруженным в него телом.

Данное предположение подтверждается экспериментальными данными. На рис. 7 изображены кривые изменения интенсивности теплообмена между кипящим слоем частиц алюмосиликатного катализатора диаметром 2.5–3.0 мм и вертикальным нагревателем диаметром 40 мм при скорости воздуха равной 1.5v_mf, 2.5v_mf, 3.5v_mf и 4.5v_mf [30].

Рис. 7.

Зависимость изменения коэффициента теплоотдачи от слоя частиц алюмосиликатного катализатора (средний диаметр 2, 5 мм) к вертикальному цилиндрическому нагревателю диаметром 42 мм от скорости воздуха: 1 – v = 1.5 м/с, 2 – v = 2.5 м/с, 3 – v = 3.5 м/с, 4 – v = 4.5 м/с. Воспроизводится по данным работы [30].

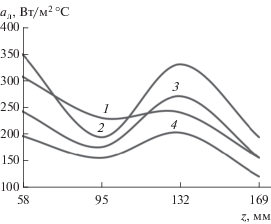
Как видно из рис. 7, интенсивность теплообмена нагревателя с кипящим слоем возрастает до тех пор, пока скорость воздуха не достигнет 3.5v_mf, т.е. до образования “приповерхностной зоны”, после чего интенсивность теплообмена снижается. Таким образом, причиной экстремальной зависимости интенсивности теплообмена между кипящем слоем и погруженной в него поверхностью является образование приповерхностной зоны и прекращение интенсивной циркуляции частиц в радиальном направлении.

Расчет времени пребывания частиц в приповерхностной зоне. В ходе выше описанных экспериментов было установлено, что в “приповерхностной зоне” наблюдается локальное фонтанирование частиц. Эти циркуляционные течения можно при известных условиях описать с помощью механики циркуляционных потоков в идеальной несжимаемой жидкости.

Предположим, что в приповерхностной зоне порозность слоя постоянна и равна ε. В этом случае векторные уравнения гидромеханики стационарного псевдоожиженного слоя имеют следующий вид [31]:

(1)

$\nabla {{{\mathbf{v}}}_{f}} = 0,$,

(2)

$\nabla {{{\text{v}}}_{s}} = 0,$

(3)

$\beta \left( \varepsilon \right)\left( {{{{\mathbf{v}}}_{f}} - {{{\mathbf{v}}}_{s}}} \right) = 0,$

(4)

$\begin{gathered} {{\rho }_{s}}\left( {1 - \varepsilon } \right)\left[ {\frac{{d{{{\mathbf{v}}}_{s}}}}{{d\tau }} + {{{\mathbf{v}}}_{s}}\nabla {{{\mathbf{v}}}_{s}}} \right] = \\ = \nabla \left( {p + {{p}_{s}}} \right) + {{\rho }_{s}}\left( {1 - \varepsilon } \right)g{\mathbf{i}}. \\ \end{gathered} $

Уравнение (4) имеет вид зависимости, описывающей движение идеальной несжимаемой жидкости плотностью ${{\rho }_{s}}\left( {1 - \varepsilon } \right)$ и давление $p + {{p}_{s}}$. Расcмотрим движение частиц в плоскости x–y. Введем функцию тока твердой фазы ψ_s:

(5)

${{v}_{{sx}}} = \frac{{d{{\psi }_{s}}}}{{dx}},\,\,\,\,{{v}_{{sy}}} = \frac{{d{{\psi }_{s}}}}{{dy}}.$

Уравнение этой функции для плоской задачи имеет следующий вид [30]:

(6)

$\frac{{{{d}^{2}}{{\psi }_{s}}}}{{d{{x}^{2}}}} + \frac{{{{d}^{2}}{{\psi }_{s}}}}{{d{{y}^{2}}}} + F{\kern 1pt} '\left( {{{\psi }_{s}}} \right) = 0,$

где

(7)

$F\left( {{{\psi }_{s}}} \right) = - \frac{{v_{{sx}}^{2} + v_{{sy}}^{2}}}{2} - \frac{{p + {{p}_{s}}}}{{{{\rho }_{s}}\left( {1 - \varepsilon } \right)}} - gx.$

Для решения уравнения (6) необходимо выбрать граничные условия.

На рис. 8 приведены реальное (геометрическое) и гипотетическое (исходя из кинематики частиц) расположения погруженного тела в псевдоожиженном слое.

Рис. 8.

Реальное (геометрическое) (a) и гипотетическое (б) расположение погруженного тела (заштриховано) в псевдоожиженном слое.

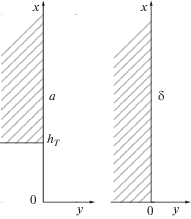
Последнее представляется с учетом распределения частиц по высоте слоя, т.е. исходя из малой вероятности нахождения частиц в прирешеточной зоне, что позволяет сделать следующий вывод:

(8)

${{\psi }_{s}} = 0\,\,\,\,{\text{при}}\,\,\,\,x = 0({{h}_{{\text{r}}}}).$

Очевидна справедливость выражения (8) при x = H.

Пусть

(9)

${{\psi }_{s}} = 0\,\,\,{\text{при}}\,\,\,\,y = 0\,\,\,\,{\text{и}}\,\,\,\,y = {{r}_{{{\text{zone}}}}}.$

С учетом условий (8) и (9) уравнение (6) имеет решение

(10)

${{\psi }_{s}} = {{A}_{n}}{{B}_{m}}\sin \left( {\frac{{n\pi x}}{H}} \right)\sin \left( {\frac{{m\pi Y}}{{{{r}_{{{\text{zone}}}}}}}} \right).$

Поскольку, как показали наши исследования, в “приповерхностной зоне” существует только один циркуляционный контур, получим

(11)

${{\psi }_{s}} = {{A}_{1}}{{B}_{1}}\sin \left( {\frac{{\pi x}}{H}} \right)\sin \left( {\frac{{\pi y}}{{{{r}_{{{\text{zone}}}}}}}} \right).$

Причем

(12)

$\psi {\kern 1pt} {}_{s}\,\, = {{A}_{1}}{{B}_{1}}\frac{\pi }{{{{r}_{{{\text{zone}}}}}}}\sin \left( {\frac{{\pi x}}{H}} \right)\cos \left( {\frac{{\pi y}}{{{{r}_{{{\text{zone}}}}}}}} \right),$

(13)

$\psi {\kern 1pt} {}_{s}\,\, = - {{A}_{1}}{{B}_{1}}\frac{\pi }{H}\cos \left( {\frac{{\pi x}}{H}} \right)\sin \left( {\frac{{\pi x}}{{{{r}_{{{\text{zone}}}}}}}} \right).$

Пусть $v_{s}^{*}$ – максимальная скорость частицы в восходящем потоке (при y = 0 и x = H/2). Тогда

(14)

${{A}_{1}}{{B}_{1}} = {{{{r}_{{{\text{zone}}}}}v_{s}^{*}} \mathord{\left/ {\vphantom {{{{r}_{{{\text{zone}}}}}v_{s}^{*}} \pi }} \right. \kern-0em} \pi },$

(15)

$v{\kern 1pt} {}_{{sx}}\,\, = v_{s}^{*}\sin \left( {\frac{{\pi x}}{H}} \right)\cos \left( {\frac{{\pi y}}{{{{r}_{{{\text{zone}}}}}}}} \right),$

(16)

$v{\kern 1pt} {}_{{sy}}\,\, = - \frac{{{{r}_{{{\text{zone}}}}}v_{s}^{*}}}{H}\cos \left( {\frac{{\pi x}}{H}} \right)\sin \left( {\frac{{\pi y}}{{{{r}_{{{\text{zone}}}}}}}} \right).$

Примем в первом приближении, что максимальная скорость частиц в восходящем потоке равна скорости всплывающих в слое газовых пузырей [32, 33]:

(17)

$v_{s}^{*} = {{U}_{{\text{b}}}},$

где

(18)

${{U}_{{\text{b}}}} = {{v}_{f}} - {{v}_{{{\text{mf}}}}}.$

Пользуясь полученными зависимостями легко рассчитать составляющие скорости частицы, циркулирующей в приповерхностной зоне. Из полученных зависимостей следует, что подъем частиц наблюдается вблизи погруженного тела, а опускание – на некотором отдалении от него. Скорость движения частиц зависит от скорости газа и увеличивается с ростом последней. Скорость частиц зависит также от геометрических характеристик слоя: высоты и радиуса “приповерхностной зоны”, который определяется высотой и диаметром слоя. Эта зависимость наиболее наглядно проявляется для радиальной составляющей скорости частицы v_sy, что, видимо, указывает на возможность снижения интенсивности движения частиц в радиальном направлении при r_zone$ \ll $ H. Как следует из выражений (15) и (16), для реальных слоев, используемых в промышленных аппаратах (r_zone < H), v_sy всегда меньше v_sx. С повышением скорости газа высота слоя H увеличивается и v_sy уменьшается по сравнению с v_sx. Это должно приводить к резкому расширению слоя в приповерхностной зоне (см. рис. 3) и повышению здесь порозности, что обусловливает снижение интенсивности внешнего теплообмена.

Для расчета среднего времени пребывания частицы у теплообменной поверхности необходимо знать наивероятнейший путь частицы около погруженного в слой тела. Предположим, что распределение значений пути, пройденных частицами вдоль поверхности теплообмена, подчиняется закону Гаусса и примем центр распределения в точке S_ср = H₀. При этом распределение заключено в пределах S > 0 и S < H. Тогда наивероятнейший путь частицы вдоль поверхности

(19)

$\begin{gathered} S = \frac{1}{{{{F}_{{\text{н}}}} - {{F}_{0}}}} \times \\ \times \,\,\left\{ {\frac{\sigma }{{\sqrt {2\pi } }}\left[ {{{e}^{{ - {{N}_{1}}}}}\, - \,{{e}^{{ - {{N}_{2}}}}}} \right]\, + \,\frac{{{{S}_{{{\text{ср}}}}}}}{{\text{2}}}\left[ {{\text{erf}}{{N}_{1}} + {\text{erf}}{{N}_{2}}} \right]} \right\}, \\ \end{gathered} $

где

(20)

${{N}_{1}} = {{{{S}_{{{\text{ср}}}}}} \mathord{\left/ {\vphantom {{{{S}_{{{\text{ср}}}}}} {\sqrt {2\sigma } }}} \right. \kern-0em} {\sqrt {2\sigma } }},\,\,\,\,{{N}_{2}} = \frac{{H - {{S}_{{{\text{av}}}}}}}{{\sqrt {2\sigma } }},$

(21)

${{F}_{{\text{н}}}} = \frac{1}{2} + \frac{1}{2}{\text{erf}}\left( {\frac{{H - {{S}_{{{\text{av}}}}}}}{{\sigma \sqrt 2 }}} \right),$

(22)

${{F}_{{\text{0}}}} = \frac{1}{2} + \frac{1}{2}{\text{erf}}\left( { - \frac{{{{S}_{{{\text{av}}}}}}}{{\sigma \sqrt 2 }}} \right),$

σ – стандартное отклонение.

Вывод зависимостей (19)–(22) сделан известными [34] методами.

Поскольку ширина “приповерхностной” зоны составляет только 7–8 диаметров частиц слоя, то можно при расчете времени нахождения частицы в этой зоне принять, что здесь частица движется вертикально.

Тогда среднее время нахождения частицы в приповерхностной зоне определится как частное от деления величины наивероятнейшего пути частицы вдоль вертикальной поверхности, определенного по зависимостям (19)–(22) на значение вертикальной составляющей скорости частицы, определяемой по выражению (15)

В табл. 2 представлены рассчитанные по полученным зависимостям и измеренные [35] значения времени пребывания частиц у теплообменной поверхности для системы воздух–стекло (d_e = 230 мкм). Для таких частиц ширина приповерхностной зоны должна составлять 1.8 мм.

Таблица 2.

Сопоставление расчетных и измеренных значений времени пребывания частиц у погруженной в псевдоожиженный слой поверхности

${{v}_{f}} = {{v}_{{{\text{mf}}}}}$, м/с	${{\bar {\tau }}_{{{\text{calc}}}}}$, с	${{\bar {\tau }}_{{{\text{meas}}}}}$, с
0.0285	2.61	0.399
0.114	0.67	0.287
0171	0.395	0.447
0.228	0.33	0.37
0.285	0.23	0.27

Как видно из табл. 2, с ростом скорости воздуха, т.е. по мере формирования “приповерхностной зоны”, значения расчётных и измеренных значений времени пребывания частиц у поверхности теплообмена сближаются и предложенный метод расчета позволяет оценить это время – важный параметр для расчета интенсивности внешнего теплообмена в псевдоожиженном слое.

ЗАКЛЮЧЕНИЕ

Высказанная гипотеза о существовании особой зоны у погруженной в псевдоожиженный слой поверхности теплообмена и о влиянии обмена частицами между этой зоной и остальным объемом слоя на интенсивность процессов внешнего теплообмена в псевдоожиженном слое нашла свое экспериментальное подтверждение.

Выявленные особенности движения частиц в указанной приповерхностной зоне позволили разработать метод расчета времени пребывания частицы у поверхности теплообмена – важный параметр для оценки интенсивности внешнего теплообмена по любой из существующих моделей теплообмена между псевдоожиженным слоем и погруженной в него поверхностью.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 19-58-04004).

ОБОЗНАЧЕНИЯ

А, B	постоянные
C	теплоемкость, Дж/(кг град)
c	константа
D, d	диаметр, м
erf	функция ошибки
F	аэродинамическая сила, Н
g	ускорение свободного падения, м/с²
H	высота неподвижного слоя, м
h	расстояние, м
i	единичный вектор
K	коэффициент теплообмена, Вт/(м² град)
m	масса, кг
p	давление, Па
R	перемещение частицы по радиусу, м
S	наивероятнейшее перемещение, м
T	температура, K
U, v	скорость, м/с;
Z	перемещение частицы по вертикали, м
$\alpha $	коэффициент теплоотдачи, Вт/(м² град)
β	некоторая функция
$\dot {\gamma }$	сила сдвига, Н/м²
$\gamma $	угол естественного откоса слоя, рад
ε	порозность слоя
λ	эффективная теплопроводность, Дж/(м² град)
π	математическая постоянная
ρ	плотность, кг/м³
σ	стандартное отклонение
τ	время, с
ψ	функция тока

ИНДЕКСЫ

0	начальное значение
а	аппарат
av	среднее значение
b	пузыри газа
calc	расчетное значение
core	ядро
e	эквивалент
meas	измеренное значение
mf	критическое значение
s	частица слоя
${\text{х}}$,$y$	координаты положения частицы
zone	приповерхностная зона
$\overrightarrow {} $	случайное значение

Список литературы

Botterill J.S.M. Fluid-bed Heat Transfer. London: Academic, 1975.
Kuipers J.A.M., Prins W., van Swaaij W.P.M. Numerical calculation of wall-to-bed heat-transfer coefficients in gas fluidized beds // AIChE J. 1992. V. 38. P. 1079.
Martin H. Heat transfer between gas-fluidized beds of solid particles and the surface of immersed heat exchanger elements // Chem. Eng. Proceed. 1984. Part I. V. 18. P. 157.
Mickley H.S., Fairbanks D.F. Mechanism of heat transfer to fluidized beds // AIChE J. 1955. V. 1. P. 374.
Mickley H.S., Fairbanks D.F., Hawthorn R.D. The relation between the transfer coefficient and thermal fluctuations in fluidized-bed heat transfer // Chem. Eng. Prog. Symp. Ser. 1961. V. 57 (32). P. 51.
Brown R.C., Overmann, S.P. The influence of particle thermal time constants on convection coefficients in bubbling fluidized beds // Powder Technol. 1998. V. 98. P. 13.
Rahel Y., Britt H. Morten Christian Melaaen Eulerian–Eulerian simulation of heat transfer between a gas–solid fluidized bed and an immersed tube-bank with horizontal tubes // Chem. Eng. Sci. 2011. V. 66. P. 1550.
Armstrong L.M., S. Gu K.H. Study of wall-to-bed heat transfer in a bubbling fluidized bed: the kinetic theory of granular flow // Int. J. Heat Mass Transfer. 2010. V. 53. № 21–22. P. 4949.
Hou Q.F., Zhou Z.Y., Yu A.B. Gas–solid flow and heat transfer in fluidized beds with tubes: Effects of material properties and tube array settings // Powder Technol. 2016. V. 296. P. 59.
Botterill J.S.M., Williams J.R. The mechanism of heat transfer to gas-fluidized beds // Trans. Inst. Chem. Eng. 1963. V. 41. P. 217.
Koppel L.B., Patel R.D., Holmes J.T. Statistical models for surface renewal in heat and mass transfer: Part 4. Wall to fluidized bed heat transfer coefficients // AIChE J. 1970. V. 16. P. 464.
Agrawal S., Ziegler E.N. On the optimum transfer coefficient at an exchange surface in a gas – fluidized bed // Chem. Eng. Sci. 1969. V. 24. P. 1235.
Gabor J.D. Wall-to-bed heat transfer in fluidized beds // AIChE J. 1972. V. 18. P. 249.
Baskakov A.P., Berg B.V., Vitt O.K. Filippovsky N.F., Kirakosyan V.A., Goldobin J.M., Maskaev V.K. Heat transfer to objects immersed in fluidized beds // Powder Technol. 1973. V. 8. P. 273.
Ozkaynak T.F., Chen J.C. Emulsion phase residence time and its use in heat transfer models in fluidized beds // AIChE J. 1980. V. 26. P. 544.
Rhodes M., Mineo H., Hirama T. Particle motion at the wall of a circulating fluidized bed // Powder Technol. 1992. V. 70. P. 207.
Molerus O., Burschka A., Dietz S. Particle migration at solid surfaces and heat transfer in bubbling fluidized beds – 1. Particle migration measurement systems // Chem. Eng. Sci. 1995. V. 50. P. 871.
Noymer P.D., Glicksman L.R. Cluster motion and particle-convective heat transfer at the wall of a circulating fluidized bed // Int. J. Heat Mass Transfer. 1998. V. 41. P. 147.
Ziegler E.N., Koppel L.B., Brazelton W.T. Effect of solid thermal properties on heat transfer to gas fluidized beds // Ind. Eng. Chem. Fundam. 1964. V. 3. P. 324.
Бородуля В.А., Теплицкий Ю.С., Ганжа В.Л., Макаревич И.И. Моделирование процессов внешнего и межфазного теплообмена в дисперсных средах // Тепломассообмен – Минский международный форум (24–27 мая 1988 г.). Секции 4, 5. Тепломассообмен в двухфазных и дисперсных системах: проблемные доклады. Минск: ИТМО им. А.В. Лыкова АН БССР, 1988. С. 122.
Антонишин Н.В., Лущиков В.В. Перенос тепла в дисперсных средах // Процессы переноса в аппаратах с дисперсными с дисперсными системами. Сборник научных трудов. Минск: ИТМО им. А.В. Лыкова АН БССР, 1986. С. 3.
Бородуля В.А., Теплицкий Ю.С., Маркевич И.И., Хасан А.Ф., Еременко Т.П. Теплообмен между псевдоожиженным слоем и поверхностью // Инж.-физ. журн. 1990. Т. 58. № 4. С. 597.
Антонишин Н.В., Лущиков В.В. Вырождение влияния дисперсной структуры слоя на теплообмен с поверхностью // Тепломассообмен – Минский международный форум (24–27 мая 1988 г.). Секции 4, 5. Тепломассообмен в двухфазных и дисперсных системах: проблемные доклады. Минск: ИТМО им. А.В. Лыкова АН БССР, 1988. С. 159.
Xavier A.M., Davidson J.F. Heat transfer in fluidized beds: Convective heat transfer in fluidized beds // Fluidization / Eds. Davidson J.F., Clift R., Harrison D. London: Academic, 1985. P. 437.
Gabor J.D. Wall-to-bed heat transfer in fluidized and packed beds // Chem. Eng. Prog. Symp. Ser. 1970. V. 66(105). P. 76.
Буевич Ю.А. // Тепломассообмен–VI. Тез. докл. Науч. конф. Проблемные доклады VI Всесоюзной конференции по тепломассообмену. Часть 2. Минск: ИТМО им. А.В. Лыкова АН БССР, 1981. С. 54.
Королев В.Н. Структурно-газодинамические условия и внешний теплообмен в псевдоожиженных средах. Автореф. дис. … докт. техн. наук. Свердловск: Институт теплофизики АН СССР, 1988.
Кондуков Н.Б., Френкель Л.И., Нагорнов С.А., Романенко Н.Я., Таров В.П. Некоторые особенности гидродинамики и внешнего теплообмена в псевдоожиженном слое // Докл. Акад. наук СССР. 1975. Т. 224. № 5. С. 1138.
Френкель Л.И., Кондуков Н.Б. Исследование профиля скоростей газа в монодисперсном псевдоожиженном слое // Хим. пром-сть. 1966. № 6. С. 418.
Нагорнов С.А. Интенсификация теплопереноса в неоднородных псевдоожиженных и виброциркуляционных средах. Дис. … докт. техн. наук. Тамбов: Всероссийский научно-исследовательский и проектно-технологический институт по использованию техники и нефтепродуктов в сельском хозяйстве, 2003.
Протодьяконов И.О., Чесноков Ю.Г. Гидромеханика псевдоожиженного слоя. Л.: Химия, 1982.
Grace J.R., Harrison D. The influence of bubble shape on the rising velocities of large bubbles // Chem. Eng. Sci. 1967. V. 22. № 10. P. 1337.
Rowe P.N., Everett D.J. Beobachtungen von blasen in fliessbetten mittels roentgenstrahlen. T l.2: der uebergang zwischen zweidimensionalen und dreidimensionalen betten // Trans. Inst. Chem. Eng. 1972. V. 50. № 1. P. 49.
Корн Г., Корн Т. Справочник по математике. М.: Наука, 1977.
Selzer V.W., Tomson W.J. Fluidized Bed Heat Transfer – The Packet Theory Revisited // AIChE Symp. Ser. 1977. V. 73. № 161. P. 29.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал