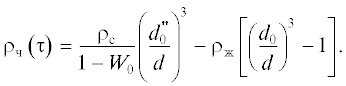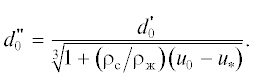Теоретические основы химической технологии, 2021, T. 55, № 1, стр. 34-45
Термогидродинамические процессы при распылительной сушке в условиях конвективно-радиационного энергоподвода
П. В. Акулич a, *, Д. С. Слижук a
a Институт тепло- и массообмена имени А.В. Лыкова НАН Беларуси
Минск, Республика Беларусь
* E-mail: akul@hmti.ac.by
Поступила в редакцию 14.09.2020
После доработки 25.09.2020
Принята к публикации 30.09.2020
Аннотация
Приведены результаты численного моделирования тепломассообмена капель при сушке жидкости в условиях конвективно-радиационного энергоподвода и встречных потоков теплоносителя. Проанализировано влияние различных параметров, в частности плотности потока инфракрасного излучения, скорости встречных потоков теплоносителя, температуры перегрева жидкости перед сушкой, на кинетику испарения капель. Показаны возможности сокращения продолжительности сушки капель за счет лучистого воздействия. Приведены результаты экспериментальных исследований влияния потока инфракрасного излучения на показатели работы распылительной сушильной установки, свидетельствующие об уменьшении удельных затрат энергии на испарение влаги, увеличении влагонапряженности, производительности и коэффициента полезного действия установки.
ВВЕДЕНИЕ
Процессы распылительной сушки жидких материалов находят широкое применение в различных отраслях промышленности, в том числе при разработке новых перспективных технологий и производстве новых материалов. Они применяются для получения высококачественных мелкодисперсных, гранулированных, быстрорастворимых, ультрадисперсных (нанодисперсных) материалов. Однако расход энергии на данные процессы достаточно высок, особенно при обезвоживании высоковлажных материалов [1–6]. Кроме того, распылительные установки имеют низкий съем влаги с единицы объема камеры, прежде всего при невысоких температурах теплоносителя. Поэтому, несмотря на многочисленные исследования в этой области, проблемам повышения их эффективности и разработки новых перспективных технологий и оборудования данного типа в настоящее время уделяется особое внимание многих исследователей [2, 3, 7–11 ]. Развитие находят различные методы, направленные на их решение, например, предварительный перегрев термостойких жидкостей; создание современных двухстадийных технологий обезвоживания (выпаривания и сушки или распылительной сушки и досушивания материала в кипящем слое); активизация гидродинамического режима на основе струйных, закрученных и сильно нестационарных потоков теплоносителя, генерируемых камерами пульсационного горения и других мероприятий. Развиваются исследования конвективно-радиационного подвода энергии в процессах распылительной сушки. В работе [12] рассматривается конвективно-радиационный способ сушки распылением, причем поток излучения создается за счет нагрева стенок камеры или расположения нагревателя по оси цилиндрической камеры. Известны [13] исследования в распылительной установке, в которой инфракрасные (ИК) излучатели расположены на боковой поверхности между жалюзями, через которые подается дополнительный поток теплоносителя. В работах [14, 15] приведены описание и некоторые исследования способа распылительной сушки, сущность которого состоит в комбинированном энерговоздействии на капли распыляемой жидкости конвекцией и инфракрасным излучением, направленным на область факела распыла.
Для оптимизации и поиска методов интенсификации и повышения эффективности процессов распылительной сушки применяются различные подходы. Моделирование часто основывается на механике сплошных сред, раздельном описании фаз с учетом тепломассообмена капель, описании структуры потоков на основе идеализации их смешения. При этом широко применяются различные программные комплексы. Однако множество факторов и взаимосвязанных физических явлений при сушке распылением усложняют как задачу, так и интерпретацию результатов. В частности, процесс сушки капель растворов и суспензий связан с образованием структуры твердой фазы или корочки на их поверхности, изменением физико-химических свойств и механизмов переноса [2, 16, 17]. Исследования в данном направлении развиваются, в частности, анализируются вопросы влияния циркуляции жидкости внутри капель на тепломассообмен особенно многокомпонентных жидкостей, закономерности испарения малых капель, влияние комбинированных энерговоздействий, в том числе конвективно-радиационного энергоподвода, сильно нестационарных термогидродинамических течений [18–22]. Наиболее исследованы процессы конвективного тепломассообмена капель. Вместе с тем необходимость развития данных теплотехнологий требуют дальнейших исследований и поиска новых методов повышения энергоэффективности.
В данной работе рассмотрены вопросы интенсификации тепломассообмена капель при сушке распылением путем комбинированного теплового воздействия конвекцией и ИК-излучением, перегрева жидкости, создания режима встречных потоков теплоносителя.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
Постановка задачи. Рассматривается одномерное движение и тепломассообмен капель раствора или суспензии, которые движутся сверху вниз под действием парогазовой смеси (влажного воздуха) и силы тяжести. На капли воздействует инфракрасное излучение, направленное спутно их движению. Объемная концентрация частиц в потоке мала. Поэтому можно пренебречь соударением и взаимодействием частиц, а также эффектами, связанными с изменением межфазной поверхности (дроблением, коагуляцией), а следовательно, ограничиться рассмотрением одиночной частицы. Скорость несущей фазы направлена вниз для прямоточного движения и встречно для вертикальных соударяющихся потоков и в зависимости от режима движения задается постоянной величиной или функцией координат и времени. Решение такой задачи позволяет исследовать влияние отдельных параметров на кинетику процесса сушки капель и в некотором приближении оценить возможность интенсификации и целесообразность их использования в новых технологиях и распылительных сушильных аппаратах с комбинированным энергоподводом.
Тепломассообмен при испарении свободной влаги. Процесс массообмена капли раствора или суспензии моделируется в две стадии. Начиная
от начального состояния капли, включая состояние перегрева, до момента образования
структуры твердой фазы, характеризующегося достижением диаметра капли некоторого значения
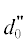 процесс удаления свободной влаги описывается в рамках механизма испарения чистой
жидкости.
процесс удаления свободной влаги описывается в рамках механизма испарения чистой
жидкости.
Уравнение массообмена для рассматриваемой стадии испарения свободной влаги
(1)
$\frac{{d\left( d \right)}}{{d\tau }} = - \frac{{2{{D}_{п}}}}{{{{\rho }_{ж}}d}}\operatorname{Sh} \left( {{{\rho }_{{п.н}}} - {{\rho }_{{п.г}}}} \right)\frac{1}{{1 - {{{{\rho }_{{п.н}}}} \mathord{\left/ {\vphantom {{{{\rho }_{{п.н}}}} {{{\rho }_{г}}}}} \right. \kern-0em} {{{\rho }_{г}}}}}}.$Множитель ${1 \mathord{\left/ {\vphantom {1 {\left( {1 - {{{{\rho }_{{п.н}}}} \mathord{\left/ {\vphantom {{{{\rho }_{{п.н}}}} {{{\rho }_{г}}}}} \right. \kern-0em} {{{\rho }_{г}}}}} \right)}}} \right. \kern-0em} {\left( {1 - {{{{\rho }_{{п.н}}}} \mathord{\left/ {\vphantom {{{{\rho }_{{п.н}}}} {{{\rho }_{г}}}}} \right. \kern-0em} {{{\rho }_{г}}}}} \right)}}$ учитывает конвективный поток пара с испаряющейся поверхности капли (поток Стефана).
Уравнение для определения температуры капли при подводе теплоты конвекцией и инфракрасным излучением на низкотемпературной стадии испарения свободной влаги можно записать
(2)
$\begin{gathered} \frac{{dT}}{{d\tau }} = \frac{6}{{{{c}_{ч}}{{\rho }_{ч}}d}}\left[ {{{\alpha }_{{конв}}}\left( {{{T}_{г}} - T} \right) + \left( {1 - {{a}_{{отр}}}} \right){{q}_{0}}} \right. \times \\ \left. { \times \,\,\exp \left( { - kcx} \right) - \frac{{{{D}_{п}}}}{d}\operatorname{Sh} \left( {{{\rho }_{{п.н}}}\left( T \right) - {{\rho }_{{п.г}}}} \right){{r}_{п}}} \right]. \\ \end{gathered} $Плотность насыщенного пара определяется из уравнения состояния ${{\rho }_{{п.н}}}(T)$ = ${{{{p}_{{п.н}}}} \mathord{\left/ {\vphantom {{{{p}_{{п.н}}}} {{{R}_{п}}T}}} \right. \kern-0em} {{{R}_{п}}T}}.$ В начальный момент времени температура капли ${{T}_{0}}$ задается и может принимать различные значения, быть меньше или больше температуры кипения жидкости. Перегретую жидкость можно получить при ее нагреве до истечения из диспергирующего устройства (сопла форсунки) в газовую среду распылительной камеры, давление в которой мало отличается от атмосферного. При истечении жидкости из сопла быстропротекающие процессы дробления и вскипания жидкости происходят одновременно и оказывают взаимное влияние. Для упрощения полагаем, что вскипание или интенсивное парообразование жидкости происходит после образования капель. Если допустить, что аккумулированная теплота в перегретой капле при ее вскипании расходуется на парообразование, сопровождающееся охлаждением, то из уравнения теплового баланса можно приближенно определить количество испарившейся жидкости из капли и ее диаметр после достижения температуры кипения $d_{0}^{'}$ = ${{d}_{0}}\sqrt[3]{{1 - {{{{c}_{р}}{{\rho }_{р}}\left( {{{T}_{0}} - {{T}_{{кип}}}} \right)} \mathord{\left/ {\vphantom {{{{c}_{р}}{{\rho }_{р}}\left( {{{T}_{0}} - {{T}_{{кип}}}} \right)} {\left( {{{r}_{п}}{{\rho }_{ж}}} \right)}}} \right. \kern-0em} {\left( {{{r}_{п}}{{\rho }_{ж}}} \right)}}}},$ где ${{d}_{0}}$ – начальный диаметр перегретой капли, м.
Распространение инфракрасного излучения в поглощающей двухфазной среде описывается на основе закона Бугера–Бера. Плотность теплового потока, подведенная к частице за счет инфракрасного излучения, приближенно определяется по выражению
В работе [23] для коэффициента ослабления излучения приводится выражение $k = 0.25F,$ где $F$ – удельная свободная поверхность частиц, м2/кг. Следует отметить, что в этом случае рассматривается поглощательная способность среды, состоящей из абсолютно черных монодисперсных сферических частиц, в зависимости от удельной поверхности частиц, их концентрации и толщины поглощающего слоя. Допускается выполнение законов геометрической оптики. Поэтому в действительности эмпирический коэффициент в показателе экспоненты зависит от множества факторов и не всегда принимает значение 0.25.
Коэффициент теплоотдачи определяется по корреляционной зависимости $\operatorname{Nu} $ = $\left[ {{{\left( {\ln \left( {1 + B} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {\ln \left( {1 + B} \right)} \right)} B}} \right. \kern-0em} B}} \right]$ × × $\left( {2 + 0.55{{{\operatorname{Re} }}^{{0.5}}}{{{\Pr }}^{{0.33}}}} \right),$ где $B$ – теплообменное число Сполдинга, $B$ = ${{{{c}_{{pп}}}\left( {{{T}_{г}} - T} \right)} \mathord{\left/ {\vphantom {{{{c}_{{pп}}}\left( {{{T}_{г}} - T} \right)} {{{r}_{п}}}}} \right. \kern-0em} {{{r}_{п}}}}.$ Значения физических параметров находятся по средней температуре в пограничном слое, приближенно равной ${{\left( {{{T}_{г}} + T} \right)} \mathord{\left/ {\vphantom {{\left( {{{T}_{г}} + T} \right)} 2}} \right. \kern-0em} 2}.$ Таким образом, учитывалось и анализировалось влияние вдува относительно холодного испаряющегося пара в поток газа на коэффициент теплоотдачи (поправка Сполдинга). Коэффициент массоотдачи определяется по корреляции Фреслинга $Sh = 2$ + $0.55{{\operatorname{Re} }^{{0.5}}}{{\operatorname{Sc} }^{{0.33}}}.$
Для условия адиабатического испарения капли, когда вся подведенная к капле теплота расходуется на ее испарение, можно записать
(4)
$\begin{gathered} \frac{{d\left( d \right)}}{{d\tau }} = - \frac{2}{{{{\rho }_{ж}}{{r}_{п}}}} \times \\ \times \,\,\left[ {{{\alpha }_{{конв}}}\left( {{{T}_{г}} - {{T}_{н}}} \right) + \left( {1 - {{a}_{{отр}}}} \right){{q}_{0}}\exp \left( { - kcx} \right)} \right]. \\ \end{gathered} $Текущая плотность капли
Тепломассоперенос в капле (частице) при испарении внутренней влаги. Вследствие испарения жидкой фазы в поверхностном слое капли раствора (суспензии) и внутри ее образуется структура твердой фазы. Учитывая данный факт, дальнейший процесс переноса влаги рассматривается в предположении углубления зоны испарения. Допускается, что начальный диаметр частицы для этого этапа можно приближенно определить по выражению
Допускается, что углубляющаяся поверхность испарения разделяет структурированную частицу с постоянным размером на две зоны. Внешняя область между поверхностью испарения и поверхностью частицы представляет собой слой практически сухого материала, через который теплота за счет теплопроводности подводится к границе испарения, а образующиеся пары переносятся к поверхности частицы. Принимается, что температура и давление на границе испарения связаны как параметры насыщенного пара уравнением Клапейрона–Клаузиуса. Вследствие относительно высокой теплопроводности влажной зоны градиентом температуры в ней пренебрегается. Распределение температуры в сухой зоне подчиняется квазистационарному состоянию. С учетом принятых допущений уравнение теплового баланса частицы при воздействии конвективного потока теплоты и инфракрасного излучения можно записать
(7)
$\begin{gathered} \left[ {a\left( {{{T}_{{пов}}} - {{T}_{{\xi }}}} \right) + {{c}_{м}}\left( {{{T}_{{\xi }}} - {{T}_{0}}} \right) + {{u}_{V}}{{r}_{п}}} \right]\frac{d}{{d\tau }}\left( {\frac{4}{3}\pi {{\xi }^{3}}} \right) = \\ = - 4\pi {{R}^{2}}[{{\alpha }_{{конв}}}\left( {{{T}_{г}} - {{T}_{{пов}}}} \right) + \\ + \,\,\left( {1 - {{a}_{{отр}}}} \right){{q}_{0}}\exp \left( { - kcx} \right)], \\ \end{gathered} $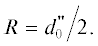
Уравнение для скорости углубления границы испарения можно привести к виду
(8)
$\frac{{d\xi }}{{d\tau }} = - \frac{{{{R}^{2}}\left( {{{T}_{г}} - {{T}_{{\xi }}}} \right)}}{{{{\xi }^{2}}\left[ {\frac{1}{\alpha } + \frac{{{{R}^{2}}}}{\lambda }\left( {\frac{1}{\xi } - \frac{1}{R}} \right)} \right]\left[ {\frac{{aR\alpha \left( {R - \xi } \right)}}{{\lambda \xi + R\alpha \left( {R - \xi } \right)}}\left( {{{T}_{г}} - {{T}_{{\xi }}}} \right) + {{c}_{м}}\left( {{{T}_{{\xi }}} - {{T}_{0}}} \right) + {{u}_{V}}{{r}_{п}}} \right]}},$Скорость испарения влаги из частицы определяется выражением
(9)
$\frac{{du}}{{d\tau }} = \frac{{3{{\xi }^{2}}{{u}_{V}}}}{{{{R}^{3}}{{\rho }_{\operatorname{c} }}}}\frac{{d\xi }}{{d\tau }}.$Влагосодержание частицы связано с координатой границы испарения соотношением u = = ${{{{\xi }^{3}}{{u}_{V}}} \mathord{\left/ {\vphantom {{{{\xi }^{3}}{{u}_{V}}} {\left( {{{R}^{3}}{{\rho }_{с}}} \right)}}} \right. \kern-0em} {\left( {{{R}^{3}}{{\rho }_{с}}} \right)}}.$
Уравнение для скорости углубления границы испарения при граничном условии третьего рода для массоотдачи можно записать
(10)
$\frac{{d\xi }}{{d\tau }} = - \frac{{\beta D{{R}^{2}}}}{{{{u}_{V}}\xi \left[ {D\xi - \beta R\left( {\xi - R} \right)} \right]}}\left( {{{p}_{{\xi }}} - {{p}_{{п.г}}}} \right),$Зависимость давления пара от температуры на границе испарения определяется уравнением Клапейрона−Клаузиуса ${{p}_{{\xi }}}$ = $p{\text{*}}exp\left( { - {{T{\text{*}}} \mathord{\left/ {\vphantom {{T{\text{*}}} {{{T}_{{\xi }}}}}} \right. \kern-0em} {{{T}_{{\xi }}}}}} \right),$ где $p{\text{*}}$ = 6.4072 × 1010 Па, $T{\text{*}}$ = 4996 К. Из этих уравнений определялась температура ${{T}_{{\xi }}}$ на границе испарения в зависимости от ее координаты $\xi $ [16]
Трансцендентное уравнение (11) представлено в виде ${{T}_{{\xi }}} = \varphi \left( {{{T}_{{\xi }}}} \right),$ которое решалось методом последовательных приближений. Достаточные условия сходимости последовательности итераций к корню уравнения следующие: в некоторой окрестности корня функция $\varphi \left( {{{T}_{{\xi }}}} \right)$ непрерывна и удовлетворяет условию “сжатия” $\left| {\varphi {\kern 1pt} '\left( {{{T}_{{\xi }}}} \right)} \right| < 1.$ Можно показать, что в исследуемой области параметров условие $\left| {\varphi {\kern 1pt} '\left( {{{T}_{{\xi }}}} \right)} \right| < 1$ выполняется.
При движении частиц в газовом потоке на них действуют силы, обусловленные градиентом давления, разностью скоростей и плотностей фаз, а также вызванные нестационарным характером движения фаз, к которым относятся: сила присоединенных масс из-за инерционных эффектов и “наследственная” сила Бассэ вследствие нестационарных эффектов в несущей фазе (нестационарности пограничного слоя вокруг частиц). Учитывая действия указанных сил на каплю, уравнение ее движения можно записать в виде
(12)
$\begin{gathered} \frac{{dw}}{{d\tau }} = \frac{{2\left( {{{\rho }_{ч}} - {{\rho }_{г}}} \right)}}{{2{{\rho }_{ч}} + {{\rho }_{г}}}}g + \frac{{3{{\rho }_{г}}}}{{2{{\rho }_{ч}} + {{\rho }_{г}}}}\frac{{dv}}{{d\tau }} + \frac{3}{2}\frac{\zeta }{d}\frac{{{{\rho }_{г}}}}{{2{{\rho }_{ч}} + {{\rho }_{г}}}} \times \\ \times \,\,\left| {{v} - w} \right|\left( {{v} - w} \right) + \frac{{18}}{{\pi d}}\frac{{\sqrt {2\pi {{\rho }_{г}}{{\mu }_{г}}\omega } }}{{2{{\rho }_{ч}} + {{\rho }_{г}}}} \times \\ \times \,\,\left[ {{v} - {v}\left( 0 \right) - w + w\left( 0 \right)} \right]. \\ \end{gathered} $Плотность частицы после образования структуры твердой фазы ${{\rho }_{ч}}\left( \tau \right) = {{\rho }_{c}}$ + $\left( {{{{{\xi }^{3}}} \mathord{\left/ {\vphantom {{{{\xi }^{3}}} {{{R}^{3}}}}} \right. \kern-0em} {{{R}^{3}}}}} \right){{u}_{V}}.$ При отсутствии пульсаций газового потока силой Бассэ пренебрегалось. Коэффициент гидродинамического сопротивления капель определяется по зависимости Р.Б. Розенбаума
(13)
$\zeta = \frac{{24}}{{\operatorname{Re} }} + 0.248\left( {1 + \sqrt {1 + \frac{{194}}{{\operatorname{Re} }}} } \right);\,\,\,\,\operatorname{Re} = \frac{{d\left| {{v} - w} \right|}}{\nu }.$Для анализа влияния плотности лучистого потока и других факторов на кинетику испарения капель при прямоточном движении фаз вертикальная составляющая скорости газа принималась постоянной величиной или аппроксимировалась степенной функцией вертикальной координаты. В области соударения потоков газа, их скорость аппроксимировалась следующим образом: ${v} = A$ при $0 \leqslant x \leqslant a;$ ${v} = - A$ при $a < x \leqslant b;$ ${{{v}}_{r}} = B$ при $0 \leqslant r \leqslant {{r}_{1}},$ ${{h}_{1}} \leqslant x \leqslant {{h}_{2}};$ ${{{v}}_{r}} = {{с{\text{*}}} \mathord{\left/ {\vphantom {{с{\text{*}}} r}} \right. \kern-0em} r}$ при $r > {{r}_{1}},$ ${{h}_{1}} \leqslant x \leqslant {{h}_{2}};$ ${{{v}}_{r}} = 0$ при $0 \leqslant x < {{h}_{1}}$ и $x > {{h}_{2}}.$
Начальные условия $\tau = 0{\text{:}}$ $x = 0,$ $\xi = R,$ $w = {{w}_{0}},$ $T = {{T}_{0}},$ $u = {{u}_{0}}$ = ${{{{W}_{0}}} \mathord{\left/ {\vphantom {{{{W}_{0}}} {\left( {1 - {{W}_{0}}} \right)}}} \right. \kern-0em} {\left( {1 - {{W}_{0}}} \right)}}.$
Обсуждение результатов. Вышеприведенная система уравнений решалась при следующих теплофизических параметрах жидкой и твердой фаз (например, суспензии жидкой керамики): ${{d}_{0}} = 0.0003$ м; ${{W}_{0}} = 0.5$ кг/кг; ${{с}_{с}} = 1080$ Дж/(кг К); ${{с}_{ж}} = 4190$ Дж/(кг К); ${{c}_{ч}} = 2635$ Дж/(кг К); $\lambda = $ = 2.0 Вт/(м К); ${{\rho }_{с}}$ = 1200 кг/м3; ${{с}_{г}} = 1026$ Дж/(кг К); ${{\lambda }_{г}} = 0.0393$ Вт/(м К); ${{p}_{{п.г}}} = 20$ кПа; ${{\rho }_{г}} = $ = 0.746 кг/м3; ${{\mu }_{п}}$ = 1.2 × 10–5 Па с; ${{r}_{п}}$ = 2250 кДж/(кг К); ${{\rho }_{р}} = 1500$ кг/м3; ${{a}_{{отр}}} = 0.1;$ $a = 0.6$ м; $b = 1.2$ м; ${{h}_{1}} = 0.5$ м; ${{h}_{2}} = 0.7$ м; $c* = 0.05;$ $B = 1;$ ${{r}_{1}} = 0.05$ м.
Для анализа влияния параметров энергетического воздействия на кинетику сушки капель получено численное решение системы уравнений движения и тепломассообмена методом Рунге–Кутты.
Для прямоточного движения фаз, капель и газа сверху вниз, получены кинетические зависимости сушки капли при различной плотности потока инфракрасного излучения, которые приведены на рис. 1.
Рис. 1.
Зависимости среднего влагосодержания (а) и температуры (б) капли при различной температуре излучателя (${{T}_{г}} = 473$ К; ${{k}_{п}} = 1 \times {{10}^{{ - 15}}}$ м2; ${v} = 1$ м/с; ${{w}_{0}} = 0$): 1 – ${{T}_{{изл}}} = 0;$ 2 – ${{T}_{{изл}}} = 873$ К; 3 – ${{T}_{{изл}}} = 1073$ К.
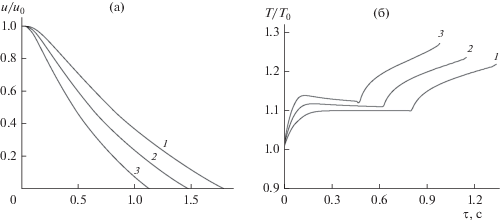
Видно, что повышение температуры излучателей, а следовательно, плотности потока ИК-излучения приводит к заметному возрастанию интенсивности испарения капель и уменьшению времени обезвоживания. При этом на температурной кривой (рис. 1б) наблюдается период прогрева капли и период постоянной температуры, соответствующей температуре мокрого термометра. Далее по мере убывания влагосодержания и углубления зоны испарения, температура капли возрастает на высокотемпературной стадии, а снижение влагосодержания несколько замедляется.
Численно исследовано влияние конвективного переноса пара (поток Стефана) с испаряющейся поверхности капли, а также вдува относительно холодного пара в поток горячего воздуха на коэффициент теплоотдачи (поправка Сполдинга). Установлено, что учет вышеуказанных эффектов приводит к незначительному замедлению скорости испарения капли, а также к снижению ее температуры, причем в большей степени на высокотемпературной стадии [17].
Далее исследовалось влияние перегрева жидкости и плотности лучистого потока на кинетику процесса сушки. При перегреве жидкости, когда начальная температура капли выше температуры кипения на кривых сушки наблюдается резкое снижение влагосодержания (рис. 2).
Рис. 2.
Кинетические зависимости сушки капли при перегреве жидкости и различном потоке инфракрасного излучения (${{T}_{0}} = 473$ К (${{t}_{{пер}}} = 100$°С); ${{T}_{г}} = 473$ К; ${{k}_{п}} = 1 \times {{10}^{{ - 15}}}$ м2; ${v} = 1$ м/с): 1 – ${{T}_{{изл}}} = 0,$ 2 – ${{T}_{{изл}}} = 973$ К, 3 – ${{T}_{{изл}}} = 1173$ К.
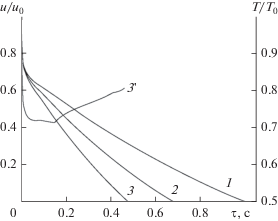
Чем больше температура перегрева жидкости, тем до более низких значений снижается влагосодержание капли на начальной стадии процесса. При этом температура капли резко падает (рис. 2, кривая 3'). Это происходит вследствие интенсивного парообразования и вскипания жидкости. Отметим, что в данной модели не учитывается дробление капли вследствие ее вскипания. После периода интенсивного парообразования и снижения влагосодержания и температуры капли наблюдается первый период сушки, характеризующийся постоянной температурой капли. Продолжительность первого периода зависит от температуры перегрева и сокращается с ее повышением. Затем на высокотемпературной стадии, сопровождающейся углублением зоны испарения, температура капли возрастает, а скорость сушки замедляется. Кинетические зависимости сушки капли при перегреве жидкости и инфракрасном воздействии свидетельствуют о значительном увеличении интенсивности испарения с повышением плотности потока ИК-излучения. В расчетах изменялась температура на поверхности излучателя. В диапазоне исследованных параметров время сушки капли сокращается в 1.5−2 раза. Следует отметить, что перегрев жидкости существенно сокращает продолжительность периода удаления свободной влаги. С увеличением плотности потока ИК-излучения температура капли на стадии испарения свободной влаги повышается, причем ее продолжительность сокращается, а затем происходит более быстрый рост температуры капли.
Отметим, что наибольшая продолжительность процесса обезвоживания имеет место при меньшей начальной температуре капли. Причем, когда начальная температура капли меньше адиабатической температуры испарения (мокрого термометра), то в периоде прогрева происходит конденсация пара из газовой фазы, приводящее к возрастанию влагосодержания капли.
Численное исследование тепломассообмена капель в период прогрева или испарительного охлаждения и удаления свободной влаги с применением модели адиабатического испарения, в которой движущей силой является разность температур, приводит к несколько большему, но незначительному снижению влагосодержания по сравнению с моделью массоотдачи.
Далее исследовано влияние встречных потоков теплоносителя и воздействия ИК-излучения на тепломассообмен капель. Получены зависимости траектории движения капли при различной скорости встречных потоков теплоносителя (горячего воздуха). На рис. 3 видно, что при движении сверху вниз капля тормозится и перемещается вверх под действием встречного нижнего потока.
Рис. 3.
Зависимость вертикальной координаты капли во встречных потоках теплоносителя ($A = 5$ м/с; ${{T}_{{изл}}} = 1073$ К; ${{T}_{0}} = 293$ К): 1 – ${{d}_{0}} = 0.0001$ м; 2 – ${{d}_{0}} = 0.0003$ м; 3 – ${{d}_{0}} = 0.0005$ м.
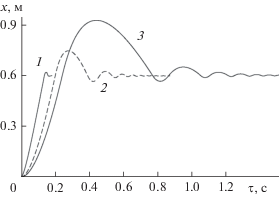
В результате капля совершает колебательное движение в зоне соударения потоков теплоносителя, но с течением времени амплитуда смещения капли затухает. С увеличением диаметра капель возрастает амплитуда и период их колебаний в зоне соударения потоков теплоносителя. Малые капли быстро отдают влагу, практически не совершая колебательного движения (кривая 1). Наблюдается лишь их торможение и некоторое смещение вверх. С уменьшением скорости встречных потоков период колебаний возрастает. При малой скорости потоков, например ${v} = \pm 1$ м/с, капля проникает во встречный поток, но не совершает колебательное движение. Создание колебательного движения капель в вертикальном направлении или их торможение приводит к увеличению времени пребывания в зоне интенсивного инфракрасного излучения, что служит одной из причин интенсификации тепломассообмена.
Получены кинетические кривые испарения капель во встречных потоках и при воздействии инфракрасного излучения, представленные на рис. 4.
Рис. 4.
Зависимости влагосодержания (а) и температуры (б) капли от времени при различной скорости встречных потоков (${{d}_{0}} = 0.0003$ м; ${{T}_{{изл}}} = 1073$ К; ${{T}_{0}} = 293$ К): 1 – $A = 1$ м/с; 2 – $A = 5$ м/с; 3 – $A = 10$ м/с.
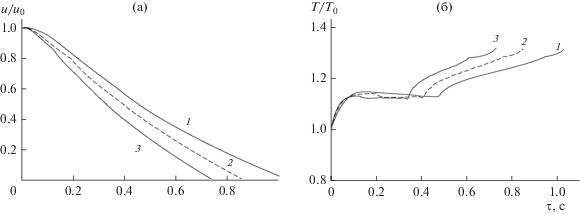
Видно, что с увеличением скорости встречных потоков скорость испарения влаги возрастает, а время обезвоживания заметно сокращается. Это связано с тем, что при увеличении скорости потоков газа частицы совершают колебательное движение, при котором возрастает относительная скорость движения фаз. В результате возрастает интенсивность тепло- и массоотдачи, приводящая к возрастанию скорости процесса сушки. Температурные кривые имеют следующие характерные периоды. Начальный период прогрева капли, на котором температура капли увеличивается от начальной температуры до температуры мокрого термометра. Период постоянной температуры, соответствующей температуре мокрого термометра. В данный период вся теплота, передаваемая от газа конвекцией и инфракрасным излучением от излучателей, расходуется на испарение влаги. Второй период, соответствующий удалению внутренней влаги в частицах с практически сформированной структурой твердой фазы. В этот период температура частиц возрастает и вследствие подвода теплоты инфракрасным излучением может быть больше температуры газа.
Конвективный теплообмен к частицам жидкого материала характеризуют зависимости числа Нуссельта от времени, приведенные на рис. 5.
Рис. 5.
Зависимость числа Нуссельта от времени (${{d}_{0}} = 0.0003$ м; ${{T}_{{изл}}} = 1073$ К; ${{T}_{0}} = 293$ К): 1 – $A = 1$ м/с; 2 – $A = 5$ м/с; 3 – $A = 10$ м/с.
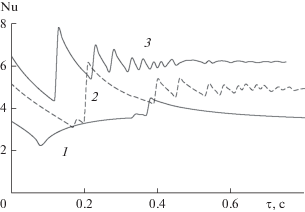
Видно, что в начальный период времени значение числа Нуссельта падает, а затем возрастает и далее имеет колебательный характер с затухающей амплитудой. Это, безусловно, вызвано гидродинамическим колебательным характером движения частиц во встречных потоках теплоносителя. Уменьшение числа Нуссельта на начальном участке обусловлено разгоном капель и уменьшением при этом относительной скорости движения фаз.
Для анализа достоверности модели было выполнено сравнение расчетных результатов с экспериментальными данными по кинетике сушки неподвижной капли раствора стрептомицина [2], свидетельствующее об удовлетворительном их соответствии [17].
Зависимости температуры на границе испарения при ее углублении подобны зависимостям средней температуры капли (частицы). На высокотемпературной стадии граница испарения перемещается вовнутрь частицы и температура на ней возрастает. Это происходит вследствие возрастания сопротивления движению пара и повышения давления пара внутри частицы. Частица с большей пористостью или проницаемостью характеризуется более высокой скоростью испарения влаги.
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ
Описание установки. Схема экспериментальной распылительной установки приведена на рис. 6. В ней реализован новый способ распылительной сушки, сущность которого состоит в комбинированном энерговоздействии на капли распыляемой жидкости конвекцией и инфракрасным излучением, направляемым на область факела с наибольшей концентрацией частиц [14, 15]. Принцип ее работы следующий. Жидкий материал из емкости 7 подают в сушильную камеру 1 диаметром 1.2 м на распылитель 5, посредством которого материал распыляется, образуя факел. Одновременно в распылительную камеру подают теплоноситель в верхней ее части через газораспределительное устройство 2 и в нижней части по оси камеры через канал 13, который снабжен завихрителем 14. Ввод нижнего теплоносителя позволяет реализовать встречное взаимодействие вертикальных потоков и тем самым активизировать гидродинамический режим в зоне факела распыла, где имеет место наибольшая концентрация частиц дисперсной фазы. В качестве теплоносителя используется воздух, который нагревается в электрических калориферах 3, 4 и 15.
Рис. 6.
Схема распылительной установки с конвективно-радиационным подводом теплоты и встречными потоками теплоносителя: 1 – сушильная камера; 2 – газораспределительное устройство; 3, 4 – электрические калориферы; 5 – распылитель; 6 – излучатели; 7 – емкость с жидким материалом; 8 – дозатор; 9 – циклон; 10 – рубашка; 11 – сборник для сухого продукта; 12 – вентилятор; 13 – канал; 14 – завихритель; 15 – электрический калорифер.
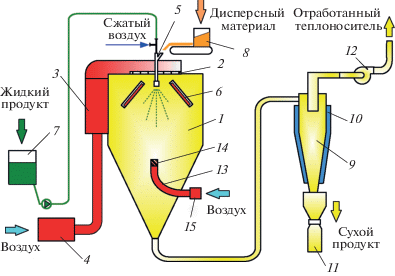
На факел жидкого материала воздействуют инфракрасным электромагнитным излучением с помощью излучателей 6. В специальном устройстве закреплено 9 инфракрасных керамических излучателей марки ИКН-101 мощностью 1 кВт, каждый из которых установлен в собственном корпусе с направляющим отражателем. Конструкция обеспечивает крепление излучателей под углами 0°, 15°, 30° и 45° к вертикальной оси. В результате в области факела жидкого материала теплота к распыленным частицам материала подводится конвективным способом от теплоносителя и инфракрасным излучением с высокой интенсивностью, вследствие наложения потоков от излучателей 6, расположенных под углом к вертикальной оси. Высушенные частицы материала вместе с отработанным теплоносителем поступают в циклон 9, в котором сепарируются и попадают в сборник 11 для сухого продукта. В установке для диспергирования жидкостей используются двух- и трехканальные пневматические форсунки 5, последние позволяют вводить в факел распыла дисперсный материал – наполнитель, который подается дозатором 8. Пневматичекая форсунка 5 расположена по оси инфракрасного устройства 6 в верхней его части. При этом факел распыла жидкости находится в зоне максимального воздействия излучателей.
Для предотвращения налипания термопластичных материалов на стенки циклона они охлаждаются водой, подаваемой в рубашку 10. Теплоноситель подается в установку вентилятором 12.
Результаты и их обсуждение. Для определения изменения потока инфракрасного излучения по объему камеры, а также соотношения радиационного и конвективного потоков были выполнены измерения приведенного коэффициента теплоотдачи и относительной плотности радиационного потока с помощью специального датчика, воспринимающего преимущественно инфракрасное излучение. Основу датчика составляет медный диск с черной матовой поверхностью диаметром 31 мм и толщиной 2 мм. В центре диска в углублении зачеканена термопара 4, по показаниям которой определяется температура диска. Для предотвращения конвективного нагрева диск помещен в металлический корпус, нижняя и боковая поверхность которого теплоизолированы. Сверху медный диск покрыт прозрачным для инфракрасного излучения стеклом (СаF2) толщиной 3 мм с воздушным зазором 2 мм. Позиционирование датчика в точках измерения осуществлялось с помощью регулируемого кронштейна. Температура датчика во времени записывалась автоматической системой измерений. Производительность установки по испаренной влаге определялась непрерывной компьютерной регистрацией массы жидкости, подаваемой в форсунку. Давление сжатого воздуха в пневматической форсунке составляло около 0.25 МПа.
Экспериментально определены значения приведенного коэффициента теплоотдачи, учитывающего теплоотдачу излучением и частично конвекцией, и относительной плотности потока излучения по оси распылительной камеры на различных расстояниях от инфракрасных излучателей. Из анализа представленных зависимостей видно, что с увеличением расхода жидкости приведенный коэффициент теплоотдачи и плотность потока инфракрасного излучения значительно снижаются (рис. 7).
Рис. 7.
Зависимости приведенного коэффициента теплоотдачи и относительной плотности потока излучения по оси камеры в точке, расположенной от сопла форсунки $x = 0.75$ м (угол расположения излучателей к вертикальной оси 30°).
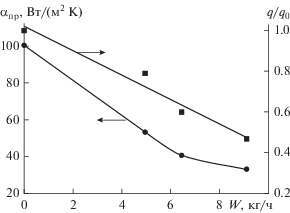
Приведенный коэффициент теплоотдачи уменьшается более чем в три раза. Это обусловлено поглощением инфракрасного излучения каплями. При этом наибольшее уменьшение этих величин наблюдается в верхней части камеры. При больших расходах жидкости интегральная плотность потока теплоты к датчику инфракрасным излучением в нижней части камеры составляет меньше, чем плотность потока теплоты конвекцией. Высокая поглощательная способность излучения двухфазным потоком важна и является положительным свойством с точки зрения эффективности работы распылительных установок.
Далее исследовано влияние комбинированного подвода теплоты на характеристики экспериментальной распылительной сушильной установки. В данных исследованиях количество дополнительной теплоты вводимой в камеру инфракрасным излучением регулировалось количеством включенных излучателей. Опыты проводились с 3, 6 и 9 включенными излучателями и без них при прочих равных условиях. Инфракрасные излучатели распологались под углом 30° относительно оси камеры. Температура теплоносителя на входе в камеру задавалась на уровне 130 ± 1°С, на выходе из камеры поддерживалась с помощью регулирования расхода испаряемой воды на уровне 70 ± 1°С. Следует отметить, что конвективный поток с подаваемым теплоносителем (нагретым воздухам) во всех опытах оставался постоянным. Расход электроэнергии потребляемой излучателями регистрировался с помощью электронного счетчика. По количеству испаренной воды в стационарном режиме работы установки определяли влагонапряженность камеры, т.е. количество воды испаряемой в единицу времени с 1 м3 камеры.
В результате экспериментально были получены зависимости удельного расхода теплоты, влагонапряженности объема камеры, производительности по испаренной влаге и КПД установки для двух режимов работы: прямоточного движения фаз сверху вниз (рис. 8, кривая 1) и режима встречных вертикальных потоков теплоносителя (кривая 2).
Рис. 8.
Зависимости удельного расхода теплоты на испарение влаги (а), влагонапряженности камеры (б), производительности по испаренной влаге (в) и КПД установки (г) от теплового потока, вводимого в распылительную камеру инфракрасными излучателями: 1 – прямоточное движение фаз (без встречных потоков), 2 – со встречными потоками теплоносителя.
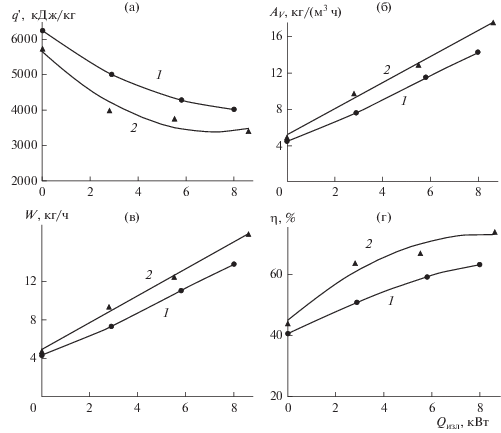
Из рис. 8а видно, что с увеличением потока инфракрасного излучения удельный расход теплоты на испарение воды заметно снижается. При этом темп падения замедляется с ростом вводимого теплового потока. В значительной степени возрастает влагонапряженность камеры (рис. 8б) и производительность установки по испаренной влаге (рис. 8в). КПД установки также возрастает, о чем свидетельствуют зависимости, приведенные на рис. 8г. Они также свидетельствуют о некотором улучшении параметров установки в режиме встречных потоков теплоносителя. Наблюдаемый эффект повышения эффективности работы установки обусловлен как интенсификацией тепломассообмена за счет теплового воздействия на капли распыляемой жидкости конвекцией и инфракрасным излучением, так и уменьшением потерь теплоты с отработанным теплоносителем.
Экспериментальные исследования влияния угла наклона излучателей к вертикали показали, что изменение угла наклона излучателей с 30° до 45° незначительно влияет на характеристики установки.
Ранее показано, что с увеличением температуры воздуха снижение удельных затрат теплоты на процесс испарения становится меньше. Однако возрастает влагонапряженность камеры и производительность по испаренной влаге. КПД установки возрастает, но его рост замедляется. Поэтому дополнительный ввод теплоты наиболее эффективен при низких температурах теплоносителя.
ЗАКЛЮЧЕНИЕ
Полученные данные теоретических и экспериментальных исследований конвективно-радиационного подвода теплоты и режима встречных вертикальных потоков теплоносителя при распылительной сушке свидетельствуют о возможности интенсификации процесса испарения жидкости и повышения эффективности работы распылительных установок. Эти результаты могут быть использованы при совершенствовании процессов, технологий и оборудования данного типа.
Вместе с тем следует отметить, что эффективность работы распылительных сушильных установок и их технико-экономические показатели зависят от множества факторов, которые следует учитывать при выборе энергосберегающих мероприятий.
ОБОЗНАЧЕНИЯ
| ${{A}_{V}}$ | влагонапряженность объема камеры, кг/(м3 ч) |
| ${{a}_{{отр}}}$ | коэффициент отражения |
| $c$ | концентрация частиц в газе, кг/м3 |
| ${{c}_{ж}},$${{c}_{с}},$${{c}_{р}}$ | удельная теплоемкость жидкости (воды), сухой частицы, раствора (суспензии), Дж/(кг К) |
| ${{c}_{{pп}}}$ | удельная изобарная теплоемкость пара, Дж/(кг К) |
| ${{D}_{п}}$ | коэффициент диффузии пара, м2/с |
| $d,$${{d}_{0}}$ | текущий и начальный диаметр капли, ${{d}_{0}} = 2{{R}_{0}},$ м |
| $g$ | ускорение свободного падения, м/с2 |
| $k$ | коэффициент ослабления излучения |
| ${{k}_{п}}$ | коэффициент проницаемости, м2 |
| ${{p}_{{пов}}},$${{p}_{{\xi }}},$${{p}_{{п.г}}}$ | соответственно парциальное давление пара на поверхности частицы, границе испарения, газе (влажном воздухе), Па |
| ${{q}_{0}}$ | начальная плотность потока инфракрасного излучения при $x = 0,$ Вт/м2 |
| $q{\kern 1pt} '$ | удельный расход теплоты на процесс сушки, кДж/кг влаги |
| $R$ | радиус частицы, м |
| ${{R}_{п}}$ | газовая постоянная пара, Дж/(кг К) |
| $r$ | радиальная координата, м |
| ${{r}_{п}}$ | удельная теплота парообразования, Дж/кг |
| $T,$${{T}_{{изл}}},$${{T}_{{кип}}},$${{T}_{{пов}}},$${{T}_{0}},$${{T}_{{\xi }}},$${{T}_{г}}$ | соответственно текущая температура капли (частицы), инфракрасного излучателя, кипения жидкости, поверхности частицы, начальная температура капли, температура на границе испарения и газа, К |
| ${{t}_{{пер}}}$ | температура перегрева жидкости, °С |
| ${{u}_{0}}$ | начальное влагосодержание капли, кг/кг |
| ${{u}_{V}}$ | начальное объемное влагосодержание частицы, кг/м3 |
| ${{u}_{ * }}$ | влагосодержание капли, соответствующее образованию структуры твердой фазы (частицы) и началу углубления зоны испарения, ${{u}_{ * }} = {{{{u}_{V}}} \mathord{\left/ {\vphantom {{{{u}_{V}}} {{{\rho }_{c}}}}} \right. \kern-0em} {{{\rho }_{c}}}},$ кг/кг |
| ${v},$$w$ | соответственно скорость газа и частицы, м/с |
| ${{v}_{r}}$ | радиальная скорость газа, м/с |
| $W$ | производительность установки по испаренной влаге, кг/ч |
| ${{W}_{0}}$ | начальная влажность капли (раствора), кг влаги/кг раствора |
| $x$ | вертикальная координата, отсчитываемая от сопла форсунки, м |
| ${{\alpha }_{{изл}}},$${{\alpha }_{{конв}}}$ | коэффициенты теплоотдачи излучением и конвекцией, Вт/(м2 К) |
| $\beta $ | коэффициент массоотдачи, кг/(м2 с Па) |
| $\zeta $ | коэффициент гидродинамического сопротивления |
| $\lambda $ | эффективный коэффициент теплопроводности сухой зоны частицы, Вт/(м К) |
| $\mu $ | динамический коэффициент вязкости, Па с |
| $\nu $ | кинематический коэффициент вязкости, м2/с |
| $\xi $ | текущая координата границы испарения, м |
| ${{\rho }_{г}},$${{\rho }_{р}},$${{\rho }_{ж}},$${{\rho }_{{п.н}}},$${{\rho }_{{п.г}}},$${{\rho }_{с}},$${{\rho }_{ч}}$ | соответственно плотность газа (влажного воздуха), раствора (суспензии), жидкости (воды), насыщенного пара, пара в газе (влажном воздухе), сухого материала частицы, частицы (капли), кг/м3 |
| $\tau $ | время, с |
| $\omega $ | частота колебаний скорости газа, Гц |
| В | число Сполдинга |
| Nu | число Нуссельта |
| Pr | число Прандтля |
| Re | число Рейнольдса |
| Sc | число Шмидта |
| Sh | число Шервуда |
ИНДЕКСЫ
| 0 | параметры начального состояния |
| г | газ (влажный воздух) |
| ж | жидкость (влага, вода) |
| изл | инфракрасное излучение |
| кип | кипение |
| конв | конвекция |
| н | насыщенное состояние |
| п | пар |
| п.н | пар насыщенный |
| пов | поверхность частицы |
| р | раствор (суспензия) |
| с | сухой материал |
| ч | частица (капля) |
| ξ | граница испарения |
| – | знак осреднения |
Список литературы
Тутова Э.Г., Куц П.С. Сушка продуктов микробиологического производства. М.: Агропромиздат, 1987.
Долинский А.А., Малецкая К.Д. Распылительная сушка: в 2-х томах. Т. 1. Теплофизические основы. Методы интенсификации и энергосбережения. Киев: Академпериодика, 2011.
Handbook of Industrial Drying / Ed. Mujumdar A.S. Boca Raton, Fla.: CRC, 2014.
Лыков М.В. Сушка в химической промышленности. М.: Химия, 1970.
Kudra T., Mujumdar A.S. Advanced Drying Technologies. N.Y.: Marcel Dekker, 2002.
Акулич П.В., Драгун В.Л., Куц П.С. Технологии и техника сушки и термообработки материалов. Минск: Белорусская наука, 2006.
Акулич П.В. Расчеты сушильных и теплообменных установок. Минск: Беларуская навука, 2010.
Акулич П.В., Акулич А.В. Конвективные сушильные установки: методы и примеры расчета. Минск: Вышэйшая школа, 2019.
Modern Drying Technology. V. 5. Process Intensification / Ed. Tsotsas E., Mujumdar A.S. Weinheim: Wiley-VCH, 2014.
Wu Z., Yue L., Li Z. et al. Pulse Combustion Spray Drying of Egg White: Energy Efficiency and Product Quality // Food Bioprocess Technol. 2015. № 8. P. 148.
Gulyaev Yu.V., Belgorodskii V.S., Kosheleva M.K. Review of Papers Presented at the “Second International Kosygin Readings: Energy- and Resource-Efficient Environmentally Safe Technologies and Equipment,” an International Scientific and Technical Symposium Celebrating the 100th Anniversary of the Kosygin State University of Russia // Theor. Found. Chem. Eng. 2020. V. 54. № 3. P. 522. [Гуляев Ю.В., Белгородский В.С., Кошелева М.К. Обзор материалов симпозиума “Вторые международные Косыгинские чтения “Энергоресурсоэффективные экологически безопасные технологии и оборудование”, приуроченные к 100-летию РГУ имени А.Н. Косыгина // Теор. осн. хим. технол. 2020. Т. 54. № 3. С. 392.]
Wisniewski R. Spray Drying Technology Review // Proc. 45th International Conference on Environmental Systems. Bellevue, Washington, 2015. P. 1.
Феклунова Ю.С. Разработка и научное обоснование способа распылительной сушки пюре из тыквы при конвективно-радиационном энергоподводе. Автореф. дис. … канд. техн. наук. Астрахань: Астраханский государственный технический университет, 2015.
Акулич П.В. Способ сушки жидких материалов. Патент 18467 Республики Беларусь // Офиц. бюлл. 2013. № 2. С. 23.
Акулич П.В., Бородуля В.А., Слижук Д.С. Методы повышения эффективности процессов распылительной сушки // Энергоэффективность. 2018. № 4. С. 28.
Акулич П.В. Тепломассообмен капли раствора при комбинированном энергетическом воздействии и углублении зоны испарения // Инж.-физ. журн. 2016. Т. 89. № 3. С. 527.
Акулич П.В. Моделирование тепломассообмена капель при сушке перегретой жидкости в условиях комбинированного энерговоздействия // Инж.-физ. журн. 2019. Т. 92. № 2. С. 404.
Prakash S., Sirignano W.A. Theory of convective droplet vaporization with unsteady heat transfer in the circulating liquid phase // Int. J. Heat Mass Transfer. 1980. V. 23. P. 253.
Козырев А.В., Ситников А.Г. Испарение сферической капли в газе среднего давления // Усп. физ. наук. 2001. Т. 171. № 7. С. 765.
Терехов В.И., Терехов В.В., Шимкин Н.Е., Би К.Ч. Экспериментальное и численное исследования нестационарного испарения капель жидкости // Инж.-физ. журн. 2010. Т. 83. № 5. С. 829.
Varghese S., Gangamma S. Evaporation of Water Droplets by Radiation: Effect of Absorbing Inclusions // Aerosol Air Qual. Res. 2007. V. 7. № 1. P. 95.
Mezhericher M., Levy A., Borde I. The Influence of Thermal Radiation on Drying of Single Droplet/Wet Particle // Drying Technol. 2008. V. 26. № 1. P. 78.
Блох А.Г. Основы теплообмена излучением. М.: Госэнергоиздат, 1962.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии