Теоретические основы химической технологии, 2021, T. 55, № 1, стр. 58-66
Сравнение способов управления теплообменным аппаратом
Л. Г. Тугашова a, *, А. В. Затонский b
a Альметьевский государственный нефтяной институт
Альметьевск, Россия
b Пермский национальный исследовательский политехнический университет,
Березниковский филиал
Березники, Россия
* E-mail: tugashova@yandex.ru
Поступила в редакцию 16.12.2019
После доработки 14.02.2020
Принята к публикации 14.02.2020
Аннотация
Актуальность работы обусловлена необходимостью поддержания заданной температуры на выходе теплообменного аппарата в условиях переменного расхода и состава сырья. Выполнен обзор методов усовершенствования управления теплообменными аппаратами. Выполнен выбор параметров объекта управления и определены его особенности. Получена динамическая модель подогревателя с паровым пространством (кожухотрубного испарителя), применяемого для нагрева бензиновой фракции на выходе отбензинивающей колонны установки стабилизации нефти. Определены доля отгона и фракционный состав бензиновой фракции, являющийся возмущающим фактором. Математическая модель кожухотрубного испарителя представлена как объект с сосредоточенными параметрами в виде теплового баланса в дифференциальной форме с учетом транспортного запаздывания. Определен коэффициент теплоотдачи со стороны бензиновой фракции для пузырькового режима кипения и со стороны отбензиненной нефти для турбулентного режима. В Simulink реализована одноконтурная система автоматического регулирования (САР) и САР с участием полученной модели. В первом случае модель объекта представлена в пространстве состояний в канонической форме. Промежуточные сигналы (с матричных усилителей обратных связей) используются как управляющие воздействия. Во втором случае построена комбинированная система регулирования температуры на выходе теплообменника. Выходной сигнал модели поступает в качестве текущего параметра на регулятор 2, который формирует управляющий сигнал, компенсирующий возмущение. Заданием регулятору 2 служит выходной сигнал регулятора 1, который корректирует работу по выходной температуре объекта. Приведено сравнение способов регулирования с применением типовых регуляторов и с участием разработанной модели объекта. Показано, что показатели переходного процесса при применении моделей в управлении выше.
ВВЕДЕНИЕ
Объекты теплоэнергетики и нефтепереработки имеют ряд особенностей: взаимосвязанность технологических параметров, наличие нелинейностей, транспортного запаздывания, функционирование в условиях воздействия контролируемых и неконтролируемых возмущений. Перечисленные факторы затрудняют управление такими объектами. Выход технологических параметров за регламентные значения может привести к аварийным ситуациям, перерасходу электроэнергии, снижению качества выпускаемой продукции и т.д.
Значительную часть аппаратов теплоэнергетических и нефтеперерабатывающих установок составляют теплообменники. Они различаются по назначению, принципу действия, конструктивному исполнению. Наиболее распространенными среди них являются кожухотрубные, пластинчатые, теплообменники типа «труба в трубе», аппараты воздушного охлаждения, испарители.
В основном, на установках применяется управление по типовому проектному решению с одноконтурными и каскадными системами автоматического управления (САУ). Виды САУ теплообменниками и другими объектами теплоэнергетики и нефтепереработки приведены, например, в работах [1, 2]. Управление с помощью пропорционально-интегрально-дифференцирующих (ПИД)-регуляторов не обеспечивает требуемого качества переходных процессов в условиях воздействия возмущений и транспортного запаздывания [3].
В работе приведено сравнение систем управления теплообменниками с типовыми регуляторами и с применением моделей в условиях воздействия возмущений при наличии транспортного запаздывания.
ОБЗОР ЛИТЕРАТУРНЫХ ИСТОЧНИКОВ
Приведем краткий обзор существующих методов совершенствования управления теплообменными аппаратами. Авторами предлагаются следующие методы, улучшающие качество управления при воздействии возмущений. В статье [4] предложена адаптивная система регулирования температуры углеводородного конденсата на выходе из кожухотрубного теплообменника, состоящая из ПИ-регулятора и корректирующего устройства динамических свойств системы (запаса устойчивости по амплитуде). В работе [5] предложена САУ тепловой нагрузки барабанного котла с компенсатором расхода доменного газа. Системы с компенсаторами отличаются сложностью реализации, возмущений может быть несколько.
В ряде работ предложено управление на базе регуляторов с внутренней моделью IMC (Internal Model Control). В статье [6] показана разработка математической модели кожухотрубного теплообменника и системы управления температурой нагреваемой жидкости с IMC-моделью. В [7] предложено применение каскадной САУ теплоэнергетическими объектами на базе IMC-модели для компенсации возмущений. В [8] для этих же целей используется усовершенствованная IMC-модель – 2DOF (Two-Degree-Of-Freedom). Сложностью при применении таких систем является получение обращенной модели объекта. В Skogestad IMC-модели [9] параметром настройки метода является число, связанное с желаемым временем переходного процесса. Объект задается звеном первого или второго порядка.
В работе [10] предложен принцип управления тепловым объектом по модели, когда объект представляется в виде системы в пространстве состояний, и промежуточные сигналы (с матричных усилителей обратных связей) используются как управляющие воздействия. В работе [11] предложена комбинированная система регулирования температуры на выходе теплообменника, в которой расход греющего агента дополнительно корректируют по давлению в аппарате и расходу нагреваемой среды.
Кроме этого, следует отметить, что важной задачей при управлении является учет транспортного запаздывания. Транспортное запаздывание может определяться по взаимной корреляционной функции [12], с использованием EM-алгоритма [13], по контролируемым технологическим параметрам и др. При управлении технологическими процессами с транспортным запаздыванием применяется предиктор Смита, его модификации [14, 15], предиктивный ПИ-регулятор, регулятор Ресвика и др. В работе [16] показаны результаты управления с помощью ШИМ-регулирования температуры теплового объекта с распределенными параметрами с большим транспортным запаздыванием с предсказанием.
ВЫБОР ПАРАМЕТРОВ УПРАВЛЕНИЯ
Объектом исследования выбран подогреватель с паровым пространством (испаритель), предназначенный для подвода тепла в отпарную колонну установки стабилизации нефти малого нефтеперерабатывающего завода (НПЗ). Целью является повышение качества регулирования температуры на выходе из теплообменного аппарата в условиях воздействия возмущений и транспортного запаздывания.
В связи с поставленной целью необходимо решить следующие задачи.
1. Определить основные параметры объекта с разделением на группы.
2. Разработать математическую модель объекта управления с учетом взаимосвязанности параметров и реализовать полученную модель с помощью программного обеспечения (Matlab/Simulink).
3. Составить модель САУ температурой на выходе теплообменного аппарата, применить методы настройки параметров типовых регуляторов и методы управления по модели. Затем сравнить эффективность применения различных методов при внесении возмущений и наличии транспортного запаздывания.
Кратко опишем технологический процесс (рис. 1).
Рис. 1.
Схема автоматизации объекта управления: 1 – бензиновая фракция из отбензинивающей колонны; 2 – бензиновая фракция из отпарной колонны; 3 – отбензиненная нефть из отбензинивающей колонны; 4 – отбензиненная нефть из испарителя; 5 – бензиновая фракция из испарителя; 6 – паровая бензиновая фракция из испарителя; 7 – легкие углеводороды из отпарной колонны.
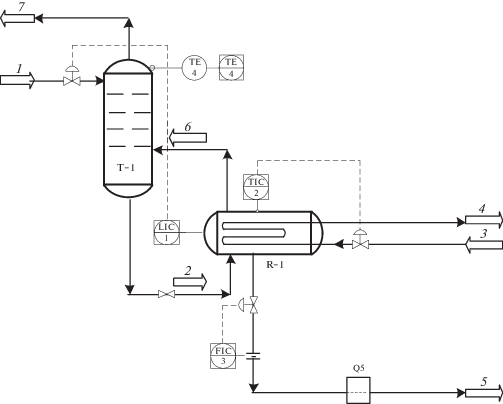
Вывод бензиновой фракции 1 с температурой начала кипения (НК)-85°С производится с тарелок отбензинивающей колонны и поступает в верхнюю часть отпарной колонны T-1 для дополнительной отгонки легких фракций. Отбор бензиновой фракции НК-85°С производится по уровню в подогревателе R-1, который поддерживается регулятором уровня LIC-1. Контроль уровня в испарителе осуществляется с выводом показаний на системное управление.
Из куба Т-1 бензиновая фракция (поток 2) самотеком поступает в подогреватель R-1, где осуществляется её нагрев до температуры в пределах 85–95°С за счет отбензиненной нефти (поток 3) с температурой в пределах 200–210°С, поступающей от насоса в змеевик испарителя R-1. Температура в испарителе регулируется клапаном TIC-2, установленным на линии отбензиненной нефти после насоса в испаритель, и контролируется прибором с выводом показаний на системное управление. Паровая фаза (поток 6) возвращается под первую тарелку отпарной колонны Т-1, а жидкая фаза (поток 5) направляется по технологической линии в трубчатую печь. Отбор проб бензиновой фракции для анализа фракционного состава осуществляется на линии 5 (Q5).
Показателем эффективности работы испарителя является температура паровой фазы бензиновой фракции НК-85°С на выходе из теплообменного аппарата. Задача управления состоит в поддержании температуры на выходе испарителя на заданном значении.
Все параметры объекта управления можно разделить на следующие взаимосвязанные группы:
− управляющее воздействие: F3 – расход отбензиненной нефти, кг/с;
− вектор возмущающих воздействий: F2 – расход бензиновой фракции на входе испарителя, кг/с; x – состав бензиновой фракции;
− векторы промежуточных параметров: Ttr – температура трубок в испарителе, °С; T4 – температура отбензиненной нефти на выходе испарителя, °С;
− векторы выходных (управляемых) параметров: T6 – температура паров бензиновой фракции на выходе испарителя, °С.
РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ КОЖУХОТРУБНОГО ИСПАРИТЕЛЯ
Обзор литературы показал, что, в основном, математические модели теплообменников получены для схем теплообмена, когда горячий поток охлаждается, а холодный нагревается (кожухотрубные аппараты), горячий поток конденсируется, холодный нагревается (конденсаторы, паро-жидкостные теплообменники), горячий поток конденсируется, холодный кипит (вертикальные термосифонные испарители, горизонтальные с паровым пространством), в которых теплоносителем является водяной пар. Особенностью объекта исследования является то, что горячий поток не меняет агрегатного состояния, то есть горячий поток (отбензиненная нефть) охлаждается, а холодный (бензиновая фракция) кипит.
Запишем уравнение теплового баланса для этого случая:
(1)
$Q = {{F}_{3}}{{с}_{3}}({{T}_{3}} - {{T}_{4}}) = e{{F}_{2}}{{r}_{6}} + (1 - e){{F}_{2}}{{с}_{3}}({{T}_{5}} - {{T}_{2}}){\text{.}}$Расход жидкой фазы бензиновой фракции F5, уходящей из испарителя, определяем, исходя из того, что содержание бензиновой фракции в нефти на действующей технологической установке составляет 5.24%. Следовательно, если на установку поступает сырье (нефть) в количестве 11.77 кг/с, то расход нефтепродукта составит F5 = 0.6123 кг/с. Тогда расход бензиновой фракции, поступающей в испаритель F2, можно найти с учетом массовой доли отгона (доли образовавшихся паров из исходной смеси) e и по известному расходу жидкой фазы из испарителя F5: F2 = F5/(1 – e). Доля отгона e позволяет определить расход паровой и жидкой фаз. Расход паровой фазы составляет F6 = eF2.
Для определения значения e при заданных давлении и температуре бензиновой фракции используется уравнение Трегубова [17]:
(2a)
$\sum\limits_{j = 1}^{NC} {\frac{{{{x}_{{{\text{ml}},j}}}({{k}_{j}} - 1)}}{{1 + {{e}_{{{\text{ml}}}}}({{k}_{j}} - 1)}}} = {\text{0}}{\text{.}}$На исследуемой установке отбор проб бензиновой фракции осуществляется на линии после испарителя R-1 (рис. 1). Следовательно, считаем, что известен состав бензиновой фракции на выходе. В выражении (2а) также неизвестными величинами являются xml,j. Для их нахождения по известному составу жидкой фазы бензиновой фракции на выходе используем следующее выражение:
(2б)
$x_{{{\text{ml}},j}}^{{{\text{out}}}} = \frac{{{{x}_{{{\text{ml}},j}}}}}{{1 + {{e}_{{{\text{ml}}}}}({{k}_{j}} - 1)}}.$Бензиновая фракция НК-85°С разбивается на 4 узкие фракции по температурам кипения (NC = 4). Затем определяем массовый выход узких фракций на нефть, используя аппроксимацию истинных температур кипения (ИТК) нефти, полученную авторами в работе [18]. Также для определения точек ИТК бензиновой фракции могут применяться виртуальные датчики – анализаторы качества нефтепродуктов, представляющие собой математическую зависимость показателей качества (точек ИТК) от технологических параметров.
Затем переходим к массовым долям узких фракций в бензиновой фракции:
Задаем температуру в испарителе: T = 92°С. Определяем молярные массы, плотности узких фракций. Следующий шаг – переходим к молярным долям ${\mathbf{x}}_{{{\text{ml}}}}^{{{\text{out}}}}$, определяем давление насыщенных паров, константы фазового равновесия kj [17, 19]. Система уравнений (2а)–(2б) решалась с использованием функции Matlab fsolve [20]. В результате получены значения мольной доли отгона eml и мольных долей узких фракций в сырье xml,j:
Найденное из системы уравнений (2а), (2б) значение eml переводится в массовую долю отгона: e = 0.71. Тогда расход бензиновой фракции, поступающей в испаритель, составит 0.6123/(1 – 0.4603) = 2.1113 кг/с. Поступившая жидкость частично испаряется: расход паровой фазы в испарителе 1.1345 × 0.4603 = 1.4998 кг/с. Жидкая фаза (F5 = 0.6123 кг/с) нагревается от температуры на входе в аппарат до температуры 92°С. Бензиновая фракция в испаритель поступает из отпарной колонны, следовательно, определить температуру на входе (T2) можно из изотермы жидкой фазы, поступающей из отпарной колонны:
Откуда находим значение температуры T2 = = 89°С.
Тепловую нагрузку Q определим из уравнения теплового баланса испарителя (1). Решая уравнение (1), находим значение Q = 180.6381 кВт. Затем определяем удельную нагрузку: q = Q/S. Рассчитанное значение q = 16.4216 кВт/м2, что меньше критического значения удельной теплововй нагрузки, следовательно, принимаем пузырьковый режим кипения в испарителе.
Для способа управления по модели необходимо разработать динамическую модель объекта. При получении системы уравнений динамической математической модели кожухотрубного испарителя принимаем следующие допущения: при постоянном давлении температура жидкой и паровой фаз одинакова; плотности, теплоемкости, коэффициенты теплоотдачи не изменяются во времени.
Уровень жидкой фазы в испарителе H поддерживается постоянным:
Количество теплоты, вошедшее в испаритель с жидкой бензиновой фракцией и полученное через стенки трубок от отбензиненной нефти, тратится на испарение и нагрев жидкости в аппарате и отводится уходящей жидкой и паровой фазой. Количество теплоты, поступившее с отбензиненной нефтью, идет на изменение температуры стенок трубок и отводится с уходящей нефтью.
Составим математическую модель кожухотрубного испарителя как объекта с сосредоточенными параметрами в виде теплового баланса в дифференциальной форме:
(2)
$\begin{gathered} {{{\rho }}_{{{\text{tr}}}}}{{V}_{{{\text{tr}}}}}{{c}_{{{\text{tr}}}}}\frac{{d(\Delta {{T}_{{{\text{tr}}}}})}}{{dt}} = \\ = {{{\alpha }}_{{{\text{vn}}}}}{{S}_{{{\text{vn}}}}}(\Delta {{T}_{{\text{4}}}} - \Delta {{T}_{{{\text{tr}}}}}) - {{{\alpha }}_{{\text{n}}}}{{S}_{{\text{n}}}}(\Delta {{T}_{{{\text{tr}}}}} - \Delta {{T}_{{\text{6}}}}); \\ \end{gathered} $Коэффициенты теплоотдачи, удельные теплоемкости, поверхность теплообмена в системе уравнений (2) определяем по известным формулам [21, 22].
При нахождении коэффициента теплоотдачи со стороны отбензиненной нефти для турбулентного режима (число Рейнольдса >104) ведем расчет по следующей формуле:
(3)
${{\alpha }_{{{\text{vn}}}}} = 0.021\frac{{\lambda }}{{{{d}_{{{\text{vn}}}}}}}{{\operatorname{Re} }^{{0.9}}}{{\Pr }^{{0.43}}}{{\left( {\frac{{\Pr }}{{{{{\Pr }}_{{{\text{tr}}}}}}}} \right)}^{{0.25}}}.$По формуле (3) находим αvn = 1.8474 кВт/(м2 °С).
Для пузырькового режима кипения коэффициент теплоотдачи со стороны бензиновой фракции определяем по следующей зависимости [23]:
(4)
$\begin{gathered} {{\alpha }_{{\text{n}}}} = b{{\left( {\frac{{{{{\lambda }}^{2}}}}{{{\nu \sigma }{{T}_{k}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{{q}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}, \\ b = 0.075 + 0.75{{\left( {\frac{{{{{\rho }}_{V}}}}{{{{{\rho }}_{L}} - {{{\rho }}_{V}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}. \\ \end{gathered} $По найденным значениям q = 16.4216 кВт/м2, ν = 0.5941 × 106 м2/с, σ = 0.0141 Н/м и другим определяем αn = 1.2243 кВт/(м2 °С).
Система уравнений (2) записана без учета транспортного запаздывания. Приведем математические выражения для транспортного запаздывания τ. Определим τ через контролируемые параметры технологического процесса, которые можно измерить или вычислить.
Запаздывание можно определить, зная среднюю скорость движения потока ʋ и расстояние L или через расход F, плотность ρ и объем трубопровода V [24]:
Преобразуем систему уравнений (2) с учетом транспортного запаздывания (6) к следующему виду:
(7)
$\begin{gathered} \frac{{d{{T}_{6}}(t)}}{{dt}} = - a(1){{T}_{6}}(t) + a(2){{T}_{{{\text{tr}}}}}(t) + a(3){{F}_{2}}(t); \\ \frac{{d{{T}_{{{\text{tr}}}}}(t)}}{{dt}} = - a(4){{T}_{{{\text{tr}}}}}(t) + a(5){{T}_{6}}(t) + a(6){{T}_{4}}(t); \\ {{\rho }_{{4.0}}}{{V}_{{4.0}}}{{c}_{{4.0}}}\frac{{d{{T}_{4}}(t)}}{{dt}} = \\ = \,\, - a(7){{T}_{4}}(t) + a(8){{T}_{{{\text{tr}}}}}(t) + a(9){{F}_{3}}(t - \tau ). \\ \end{gathered} $Здесь τ – запаздывание, обусловленное временем прохождения расстояния от исполнительного механизма на линии подачи отбензиненной нефти до испарителя;
Запишем систему уравнений (7) в следующем виде:
(8)
$\begin{gathered} \frac{{dX}}{{dt}} = AX(t) + {{B}_{0}}u(t - \tau ) + {{B}_{1}}f(t); \\ y(t) = CX(t). \\ \end{gathered} $Состав бензиновой фракции является возмущающим фактором. Изменение состава бензиновой фракции соответствует изменению доли отгона e и температуры на входе T2 (уравнения (2а)–(2в)), которые учитываются коэффициентами модели.
С учетом вычисленных коэффициентов a(1)–a(9) получены следующие матрицы системы (8):
Для определения транспортного запаздывания τ по формуле (6) использовались значения технологических параметров и характеристик трубопровода из технологического регламента на действующую установку.
СРАВНЕНИЕ КАЧЕСТВА РЕГУЛИРОВАНИЯ
Математическая модель испарителя (8) реализована в программе Matlab в виде m-файла. Для удобства исследования представим полученную модель в Simulink с помощью библиотечного блока S-function, использующего m-файл.
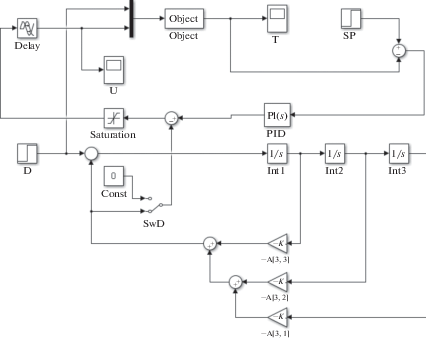
Реализуем в Simulink системы автоматического регулирования (САР) следующих видов: одноконтурную и с участием полученной модели. Разместим блоки источников входных сигналов D (возмущение), SP (задание), запаздывание Delay, мультиплексор, модель объекта Object, регулятор PID, блок ограничителя выходного сигнала регулятора Saturation, дисплеи для наблюдения полученных результатов T, U (рис. 2).
С помощью ключа SwD выполняется подключение модели. При подаче сигнала SwD = 0 (блок Const) получим одноконтурную САР температуры на выходе испарителя. Параметры ПИ-регулятора в этом случае определяем с помощью инструмента Matlab pidtune.
Для улучшения качества регулирования дополним схему моделью, для чего преобразуем САР следующим образом.
Представим модель объекта (7) в пространстве состояний в канонической форме. Для такого перехода запишем модель объекта в следующем виде:
(9)
$\begin{gathered} W(p) = \frac{{{{b}_{2}}p + {{b}_{1}}p + {{b}_{0}}}}{{{{a}_{3}}{{p}^{3}} + {{a}_{2}}{{p}^{2}} + {{a}_{1}}p + {{a}_{0}}}} + \\ + \,\,\frac{{{{b}_{{0u}}}}}{{{{a}_{3}}{{p}^{3}} + {{a}_{2}}{{p}^{2}} + {{a}_{1}}p + {{a}_{0}}}}. \\ \end{gathered} $Здесь первое слагаемое является передаточной функцией по каналу возмущения, а второе – передаточной функцией по каналу управления.
По передаточной функции по каналу возмущения определим матрицы A, B, C, D в пространстве состояний в канонической форме. Для этого применяем следующие преобразования:
(10)
$\begin{gathered} A = \left[ {\begin{array}{*{20}{c}} 0&1&0 \\ 0&0&1 \\ { - \frac{{{{a}_{0}}}}{{{{a}_{3}}}}}&{ - \frac{{{{a}_{1}}}}{{{{a}_{3}}}}}&{ - \frac{{{{a}_{2}}}}{{{{a}_{3}}}}} \end{array}} \right];\,\,\,\,B\,\,{\text{ = }}\left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 1 \end{array}} \right]; \\ C = \left[ {\begin{array}{*{20}{c}} {\frac{{{{b}_{{\text{0}}}}}}{{{{a}_{{\text{3}}}}}}}&{\frac{{{{b}_{{\text{1}}}}}}{{{{a}_{{\text{3}}}}}}}&{\frac{{{{b}_{{\text{2}}}}}}{{{{a}_{{\text{3}}}}}}} \end{array}} \right];\,\,\,\,D = 0. \\ \end{gathered} $С помощью блоков усилителей и интеграторов Int построим схему согласно каноническому представлению (10) (рис. 2). Матрицы C, D не используются и на рис. 2 не приведены. Сигналы с матричных усилителей обратных связей модели (–A(3,3), –A(3,2), –A(3,1)) будем использовать в качестве управляющих воздействий. При подключении модели с помощью SwD промежуточные сигналы суммируются с выходным сигналом ПИ-регулятора.
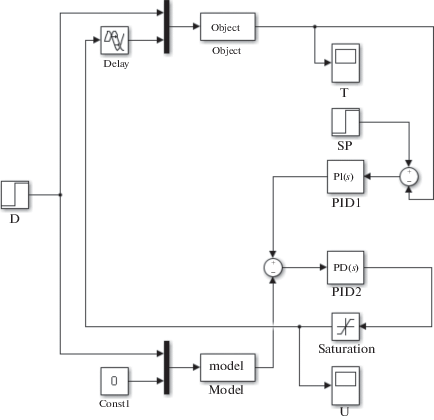
Следующим способом управления с участием модели является комбинированная система, приведенная на рис. 3.
В блок Model поступают сигналы возмущающего и управляющего воздействия. В этом же блоке учитывается изменение фракционного состава бензиновой фракции (изменением параметров модели). Выходной сигнал блока поступает в качестве текущего параметра на П-регулятор PID2. П-регулятор PID2 формирует управляющий сигнал, компенсирующий возмущение. Заданием регулятору служит выходной сигнал регулятора PID1, который корректирует работу по выходной температуре объекта.
Сравним качество регулирования трех САР (рис. 4). Зададим изменение расхода сырья в виде ступенчатого воздействия (момент времени 600 с), в блоках T, U получим графики переходных процессов температуры на выходе испарителя для каждой САР. Сплошная линия 1 соответствует САР с типовым регулятором, штриховая линия 2 – САР с промежуточными сигналами модели, штрих-пунктирная линия 3 – комбинированная САР с моделью.
Рис. 4.
Графики переходных процессов: (а) – изменение расхода отбензиненной нефти; (б) – изменение температуры бензиновой фракции на выходе испарителя; 1 – САР с типовым регулятором, 2 – САР с промежуточными сигналами модели; 3 – комбинированная САР с моделью.
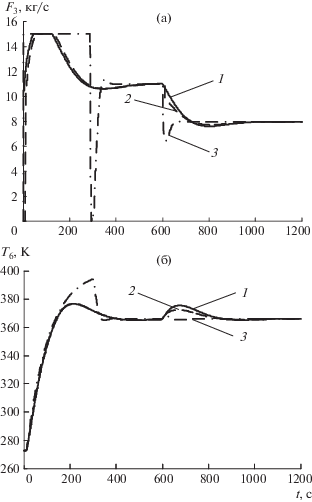
Как видим из рис. 4, качество регулирования с применением моделей лучше как по времени переходного процесса, так и величине перерегулирования.
ЗАКЛЮЧЕНИЕ
Разработана динамическая модель испарителя установки стабилизации нефти малой нефтеперерабатывающей установки с учетом транспортного запаздывания. Модель представлена системой дифференциальных уравнений теплового баланса с последующим преобразованием в модель в пространстве состояний.
Реализованы три вида САР температуры на выходе теплообменного аппарата. Получено, что при управлении с участием модели при воздействии возмущений и наличии транспортного запаздывания показатели переходных процессов (время переходного процесса, перерегулирование) лучше. Результаты моделирования САР показали возможность использования в управлении моделей для поддержания температуры на выходе теплообменного аппарата на заданном значении.
Результаты исследований могут применяться на действующих технологических установках при управлении теплообменными аппаратами в условиях изменения расхода и состава поступающего сырья. Применение модели возможно без изменения существующей структуры системы управления в виде дополнительного модуля.
ОБОЗНАЧЕНИЯ
| A, B0, B1, C | матрицы системы |
| a(1)–a(9) | коэффициенты матрицы состояния |
| с | удельная теплоемкость, Дж/(кг °С) |
| d | диаметр труб, м |
| e | мольная доля отгона |
| F | расход, кг/с |
| f | возмущающее воздействие |
| k | константа фазового равновесия |
| L | расстояние |
| Q | тепловая нагрузка, Дж/с |
| q | удельная тепловая нагрузка, Вт/м2 |
| r | удельная теплота испарения, Дж/кг |
| S | поверхность теплообмена, м2 |
| s | площадь сечения, м2 |
| T | температура, K |
| u | управляющее воздействие |
| V | объем, м3 |
| X | переменные состояния |
| x | мольные доли компонентов в сырье |
| y | регулируемый параметр |
| α | коэффициент теплоотдачи, Вт/(м2 °С) |
| Δ | отклонение |
| λ | коэффициент теплопроводности, Вт/(м °С) |
| ν | коэффициент кинематической вязкости жидкой фазы при температуре кипения, м2/с |
| ρ | плотность, кг/м3 |
| σ | поверхностное натяжение на границе раздела между жидкой и паровой фазой, Н/м |
| τ | транспортное запаздывание, обусловленное временем прохождения расстояния от исполнительного механизма на линии подачи отбензиненной нефти до испарителя |
| v | средняя скорость движения потока |
| Prtr | число Прандля при температуре стенки трубок |
| Re | число Рейнольдса |
ИНДЕКСЫ
| 0 | номинальное значение |
| 1–6 | номера потоков, обозначенные на рис. 1 |
| к | кипение |
| j = 1, NC | число узких фракций |
| L | жидкая фаза |
| ml | мольный |
| n | наружный |
| out | выход |
| tr | трубки |
| V | паровая фаза |
| vn | внутренний |
Список литературы
Дудников Е.Г., Казаков А.В., Софиева Ю.Н., Софиев А.Э., Цирлин А.М. Автоматическое управление в химической промышленности. М.: Химия, 1987.
Демченко В.А. Автоматизация и моделирование технологических процессов АЭС и ТЭС. Одесса: Астропринт, 2001.
Тугашова Л.Г. Исследование возможности управления процессом ректификации нефти с применением типовых регуляторов // Вестн. ЮУрГУ. Сер. Компьют. технол., упр., радиоэлектрон. 2016. Т. 16. № 3. С. 120.
Скороспешкин М.В., Цапко Г.П., Скороспешкин В.Н. Адаптивная система регулирования температуры кожухотрубного теплообменника // Изв. Томск. политех. унив. 2010. Т. 316. № 5. С. 151.
Исматходжаева С.К., Кузищин В.Ф. Повышение эффективности тепловой нагрузки паровых котлов при сжигании топлива нескольких видов // Теплоэнергетика. 2017. № 5. С. 82.
Sahoo A., Radhakrishnan T.K., Sankar Rao C. Modeling and control of a real time shell and tube heat exchanger // Resour.-Effic. Technol. 2017. V. 3. № 1. P. 124.
Степанец А.В. Регулирующий адаптивный комплекс на основе каскадной системы с моделью объекта управления // Вост.-Евр. ж. передовых технол. 2012. № 2/10 (56). С. 14.
Pan S., Anwar Md N. A PID controller design in 2DOF-IMC structure for integrating processes with dead-time // 5th International Symposium on Advanced Control of Industrial Processes (ADCONP), Hiroshima, 2014.
Skogestad S. Probably the best simple PID tuning rules in the world // J. Process Control. 2001. V. 1. P. 3.
Бильфельд Н.В. Управление технологическими объектами по модели // Нов. унив. Сер.: Тех. науки. 2016. № 3 (49). С. 22.
Редин В.Н., Туровский Ю.Е., Коваленко В.С., Ханин И.М. Способ автоматического управления теплообменным аппаратом. А. с. 572639 СССР // Бюлл. изобрет. 1977. № 34.
Штейнберг Ш.Е. Идентификация в системах управления. М.: Энергоатомиздат, 1987.
Гончаров А.А., Тугашова Л.Г., Жуков И.В. Определение транспортного запаздывания при получении виртуального анализатора для процесса ректификации нефти // Нефтеперераб. нефтехим. 2018. № 8. С. 10.
Huang H.P., Chen C.L., Chao Y.C., Chen P.L. Modified smith predictor with an approximate inverse of dead time // AIChE J. 1990. V. 36. № 7. P. 1025.
Кузищин В.Ф., Мерзликина Е.И., Хоанг В.В. ПИД-регулятор с предиктором и алгоритмом автоматической настройки: исследование эффективности для тепловых объектов // Теплоэнергетика. 2017. № 9. С. 80.
Евсеенко О.Н. Обзор существующих типов регуляторов температуры тепловых объектов // Вестн. НТУ “ХПИ”. 2016. № 15 (1187). С. 16.
Гайле А.А., Пекаревский Б.В. Расчет ректификационных колонн. СПб.: СПбГТИ(ТУ), 2007.
Затонский А.В., Тугашова Л.Г. Моделирование статического режима процесса ректификации с идентификацией состава и свойств нефти // Изв. высш. учебн. завед. Нефть газ. 2015. № 6. С. 109.
Тугашова Л.Г. Разработка Matlab-модели аппарата воздушного охлаждения процесса атмосферной перегонки нефти // Вестн. науки образ. Сев.-Запада Росс. 2015. Т. 1. № 3. С. 7.
Затонский А.В., Тугашова Л.Г. Моделирование объектов управления в MatLab: учебное пособие. СПб.: Лань, 2019.
Технология переработки нефти. В 2-х частях. Часть первая. Первичная переработка нефти / Под ред. Глаголевой О.Ф., Капустина В.М. М.: Химия, КолосС, 2006.
Филиппов В.В. Теплообмен в химической технологии. Теория. Основы проектирования: учебное пособие. Самара: Самар. гос. техн. ун-т, 2014.
Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курсу процессов и аппаратов химической технологии. М.: Химия, 2005.
Чермак И., Петерка В., Заворка И. Динамика регулируемых систем в теплоэнергетике и химии. М.: Мир, 1972.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии