Теоретические основы химической технологии, 2021, T. 55, № 1, стр. 16-33
Влияние гидродинамических условий в микрореакторе со сталкивающимися струями на формирование наночастиц на основе сложных оксидов
Р. Ш. Абиев a, b, c, *, О. В. Проскурина a, c, М. О. Еникеева a, c, В. В. Гусаров c
a Санкт-Петербургский государственный технологический институт (технический университет)
Санкт-Петербург, Россия
b Институт химии силикатов им. И.В. Гребенщикова РАН
Санкт-Петербург, Россия
c Физико-технический институт им. А.Ф. Иоффе РАН
Санкт-Петербург, Россия
* E-mail: abiev.rufat@gmail.com
Поступила в редакцию 02.07.2020
После доработки 28.08.2020
Принята к публикации 28.08.2020
Аннотация
Изучено влияние гидродинамической обстановки (главным образом – условий смешения растворов реагентов) на состав и размеры наночастиц, формирующихся в микрореакторе со сталкивающимися струями (МРСС) при столкновении струй реагентов – водных растворов нитрата лантана и дигидроортофосфата аммония. В МРСС создаются уникальные условия, обеспечивающие кратковременный контакт струй растворов, движущихся с большой скоростью (порядка 10–20 м/с). Рассчитаны характеристики турбулентности в МРСС. Показано, что скорость диссипации кинетической энергии турбулентности в зоне столкновения струй может достигать 107–109 Вт/кг, что сопоставимо с уровнем диссипации энергии в ультразвуковых ваннах и на несколько порядков выше, чем практически в любых других типах реакторов. Определено влияние области, имеющей размер минимального масштаба турбулентности Колмогорова, т.е. самоорганизующегося “нанореактора”, на размер формируемых частиц при осаждении частиц сложного состава. Сравнение результатов расчета с экспериментальными данными показало, что в ряде случаев объем “нанореактора” с учетом концентрации растворов определяет массу и размер образующихся частиц. Дано объяснение эффекту различного влияния скорости столкновения струй на размер формирующихся при микрореакторном смешении реагентов наночастиц в зависимости от особенностей механизмов химических реакций в условиях “мягкой” химии.
ВВЕДЕНИЕ
Одним из перспективных направлений развития химических технологий является разработка высокоэффективной микромасштабной аппаратуры – одной из разновидностей микрофлюидных устройств [1–3]. Микроаппараты для проведения тонкого синтеза – микрореакторы – уже прекрасно зарекомендовали себя в процессах получения различных органических соединений, включая активные фармацевтические ингредиенты [4, 5]. Интенсификации процессов в микрореакторах посвящены недавно вышедшие работы [6–10].
Среди современных методов синтеза наноразмерных оксидных материалов привлекательными являются методы “мягкой” химии, в том числе с применением средств, интенсифицирующих фазообразование [11–13].
Микрореакторы различных типов используются для синтеза наноразмерных частиц большого числа неорганических соединений, в том числе, например, таких как оксид магния, ферриты кобальта и висмута, сульфаты бария, свинца, цинка, никеля, меди, карбонат бария, фосфаты лантана, церия, железа, свинца и др. [14–18].
Микроаппараты, используемые для синтеза наноразмерных частиц, можно разделить на две группы по геометрическим и гидродинамическим признакам: первая – микроаппараты с течением жидких (одно- или двухфазных) сред в микроканалах, оборудованные микросмесителями различной геометрии; вторая – микроаппараты со сталкивающимися струями.
В первой группе микрореакторов подгруппу 1А образуют аппараты с перемешиванием растворов реагентов (как правило, в воде) в замкнутом микрообъеме с Т-образными микросмесителями [19], Y-образными [20] (или других), где происходит интенсивное смешивание водных растворов.
Подгруппу 1Б в первой группе микрореакторов образуют аппараты с применением двухфазного сегментированного потока в микроканалах [21] (тейлоровское течение), когда реагенты вводятся внутрь вытянутых капель дисперсной среды, движущихся в виде непрерывной цепочки в микроканале и сохраняющих свою идентичность вплоть до выхода из него. Эти аппараты использовались для синтеза квантовых точек, суперпарамагнитных оксидов железа и других соединений [22, 23].
Вторую группу микрореакторов – микрореакторы со сталкивающимися струями (МРСС) – логично разделить на две подгруппы: 2А – с затопленными струями и 2Б – со свободно сталкивающимися струями. В первом случае струи подаются в объем жидкости, во втором – в газ (чаще всего – воздух), формируя при столкновении пелену (пленку) жидкости.
МРСС подгруппы 2А исследованы для синтеза высокомолекулярных соединений, в том числе, для смешения высокомолекулярных спиртов с отвердителями в производстве полимеров [14, 24].
Хотя МРСС подгруппы 2Б пока изучены недостаточно, существующие публикации демонстрируют их перспективность, как средство синтеза наноразмерных частиц [14, 17, 18, 25, 26] и органических соединений [14, 21].
Принципиальной особенностью МРСС со свободно сталкивающимися струями является крайне высокий уровень скорости диссипации энергии, достигающий 107–109 Вт/кг [25, 27], что сопоставимо с уровнем энергонапряженности в ультразвуковых ваннах (УЗВ). При этом в МРСС вся диссипируемая энергия сосредоточена в малом объеме (порядка 150 нанолитров), формируемом при столкновении струй, тогда как в УЗВ механическая энергия акустических колебаний быстро затухает по нормали к излучателю, а в объеме обрабатываемой жидкости энергия диссипируется преимущественно в пучностях стоячих волн. Эти особенности МРСС способствуют тому, что в объеме жидкостной пелены (рис. 1), формирующейся в результате столкновения струй, происходит быстрое и эффективное микросмешение растворов контактирующих реагентов и, как следствие, быстрый процесс образования наноразмерных частиц.
Основы математического описания процесса формирования пелены, заложенные в работах [28, 29], были развиты в [30–32]. Выполненное в [32] численное моделирование позволило воспроизвести процесс образования пелены, формирование ободка вокруг нее, образование волн в пелене и последующий ее распад на капли.
Глобальная задача комплексных исследований, проводимых совместно специалистами по химико-технологическому оборудованию и специалистами по физикохимии наноструктурированных материалов, заключается в определении условий, способствующих получению наноразмерных частиц заданного состава и структуры при использовании микрореакторного смешения реагентов с последующей сепарацией образовавшегося продукта от жидкой фазы и с проведением при необходимости дальнейших технологических операций, в частности, термообработки. На готовый продукт, очевидно, влияет каждая из стадий процесса; по этой причине необходимо выявить адекватные показатели и исследовать роль каждой из стадий. Следует отметить сложность и многообразие факторов, влияющих на образование наночастиц, начиная от гидродинамической обстановки при микроперемешивании растворов, условий нуклеации, агрегации частиц и роста кристаллитов, включая влияние концентрации реагентов, pH растворов, температуры и скорости изменения температуры, длительности процесса, химического состава среды и других условий фазообразования. Для каждой стадии процесса синтеза необходимо выделить наиболее значимые факторы и изучить их влияние на характеристики промежуточных продуктов и, в конечном счете, на свойства целевого продукта.
Целью данной работы является изучение влияния гидродинамической обстановки (главным образом – условий микросмешения реагентов) в зоне столкновения струй (в жидкостной пелене) в микрореакторе со сталкивающимися струями на состав и размеры образующихся наночастиц, в частности, наночастиц ортофосфата лантана.
МИКРОРЕАКТОР СО СТАЛКИВАЮЩИМИСЯ СТРУЯМИ: ОСНОВЫ РАСЧЕТА ГИДРОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК
Математическая модель процесса образования жидкостной пелены и перемешивания в ней. В работах [30, 31] рассматривается модель столкновения двух струй, представленная на рис. 2. Отметим, что в [33] рассматривается аналогичный случай, отличающийся тем, что пелена образуется при натекании на плоскую твердую поверхность струи круглого сечения площадью А со скоростью U. При высокой скорости струи (точнее, при больших числах Фруда Fr = U2/gdjet, где g – ускорение силы тяжести, м/с2; djet – диаметр струи, м), влиянием гравитации по отношению к направлению струи можно пренебречь. Тогда жидкость будет растекаться по площадке (считаем, что ее размеры значительно превышают djet), образуя плоскую пелену. В области пелены линии тока прямолинейны и, следовательно, давление в ней всюду равно атмосферному, как и в самой струе до соударения с плоской поверхностью. Тогда из теоремы Бернулли следует первый важный вывод о том, что для невязкой и несжимаемой жидкости (эйлерова жидкость) радиальная компонента скорости в пелене всюду равна скорости струи U. Движущей силой этого радиального течения является избыточное давление в непосредственной близости точки столкновения струи с поверхностью, где происходит полное торможение струи (U = 0), а избыточное давление, согласно теореме Бернулли, равно ρU2/2. До тех пор, пока пленка сохраняет целостность, в ней соблюдается условие неразрывности – постоянство расхода при любом радиусе:
где h(r) – толщина пелены. Это означает, что площадь сечения пелены на радиусе r равна площади А поперечного сечения исходной струи.Рис. 2.
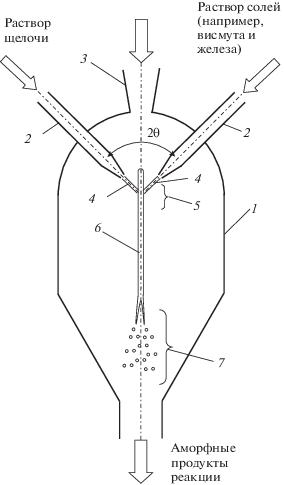
Принцип действия микрореактора со сталкивающимися струями (на примере синтеза ортоферрита висмута): 1 – корпус микрореактора; 2 – сопла; 3 – воздушник; 4 – струи; 5 – зона столкновения струй; 6 – пелена жидкости; 7 – зона распада пелены на брызги и капли.
Из (1) следует вторая важная зависимость – для зависимости толщины пелены от радиуса справедливо выражение
По мере расширения пелены ее толщина становится настолько малой, что любые флуктуации способны привести к ее распаду на капли под действием сил поверхностного натяжения (рис. 3). При превышении критического числа Вебера (Wej > Wecr ≈ 150–200) распадается жидкостный ободок вокруг пелены, а при струйном числе Рейнольдса выше 3500 происходит турбулизация пелены и ее распад [31].
Рис. 3.
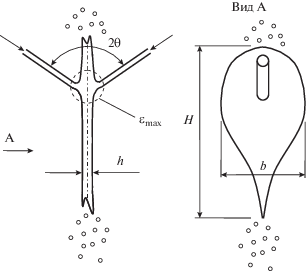
Схема формирования и основные размеры жидкостной пелены в МРСС: 2θ – угол между струями; H – условная высота пелены; b – условная ширина пелены; h – толщина жидкостной пелены.
Интересно отметить, что этот теоретический вывод, полученный для невязкой жидкости, подтвержден в экспериментальных исследованиях для сталкивающихся струй, с точностью до коэффициентов. Так, в работе [34] экспериментально, с использованием лазерной доплеровской анемометрии выявлено, что радиальная скорость (а остальные компоненты скорости равны нулю) в пелене действительно довольно слабо зависит от радиальной координаты, а азимутальный угол влияет на скорость в пелене немного более существенно. Максимальная скорость направлена вниз, минимальная – вверх от точки столкновения; этот эффект, очевидно, обусловлен влиянием гравитации. Там же показано, что угол 2θ между струями (рис. 1) радикальным образом влияет на форму пелены и на распределение радиальной скорости в ней: чем ближе угол 2θ к 180°, тем меньше различие в скорости между верхней и нижней половинами пелены. Так, при 2θ = 140° скорость по направлению вниз составила 3.5 м/с, а скорость по направлению вверх – 3.15 м/с, а при 2θ = 100° аналогичные скорости были равны 3.7 и 2.9 м/с соответственно.
Авторы работ [30, 31] считают, что удельная мощность потерь в реакторе может быть использована для оценки времени смешения. Удельную скорость диссипации энергии для микрореактора со сталкивающимися струями можно оценить, используя соотношение
где ε – удельная массовая скорость диссипации механической энергии (Вт/кг); Р – скорость диссипации механической энергии (Вт), предполагается определяющейся кинетической энергией двух сталкивающихся струй; ρ – плотность жидкости (кг/м3), V – объем жидкости, в котором рассеивается энергия (м3).В точке столкновения двух струй требуется равный импульс двух струй, чтобы сохранить вертикальную и центрированную пленку между ними. Скорость общей диссипации энергии рассчитывается по формуле [30]
где mj – массовый расход j-й струи (кг/с); wj – скорость j-й струи (м/с). Тот же результат легко получить, используя понятие удельной кинетической энергии струй (динамического напора, в Па):Значение Р равно сумме произведений динамических напоров на объемный расход жидкости Q1, Q2 в каждой струе:
где справа приведено соотношение для часто используемого случая равных расходов Q = Q1 = Q2. В результате найдем выражение, совпадающее с (4):(7)
$P = \frac{1}{2}\left( {{{m}_{1}}w_{1}^{2} + {{m}_{2}}w_{2}^{2}} \right) = \frac{1}{2}\left( {{{\rho }_{1}}{{Q}_{1}}w_{1}^{2} + {{\rho }_{2}}{{Q}_{2}}w_{2}^{2}} \right).$Для оценки объема жидкости в зоне столкновения струй воспользуемся представлениями о геометрии пленки, образующейся при столкновении струй, полученными в работах [29, 31, 35].
Ключевыми гидродинамическими параметрами являются струйные числа Рейнольдса
и струйные числа Вебера
где σj – поверхностное натяжение жидкости (раствора прекурсора) в j-й струе; dj – диаметр j-й струи (м).Толщина пелены, образующейся при столкновении струй, согласно результатам [29], определяется следующими ключевыми значениями (рис. 1).
На краях пелены
где R – радиус струи (R = d/2); ψ – угол между вектором скорости w на краю пелены и локальной касательной к контуру края пелены [30, 31, 35] (см. рис. 1).Поскольку диаметры струй dj в проведенных нами экспериментах отличались незначительно (550 и 650 мкм), в качестве расчетного значения радиуса было принято среднее арифметическое значение R = (d1 + d2)/4 = 300 мкм, по средним значениям рассчитывался и критерий Вебера: We = (We1 + We2)/2.
На границе между зоной столкновения струй и образующейся пелены толщина пелены определена в [29, 35] как функция азимутального угла φ:
(11)
${{h}_{i}} = \frac{{\beta {{\operatorname{e} }^{{{\beta }\left( {1 - \frac{{\varphi }}{{\pi }}} \right)}}}}}{{{{\operatorname{e} }^{{\beta }}} - 1}}R\sin \theta ,$Значение коэффициента затухания в [29] предлагается находить как корень трансцендентного уравнения
(12)
$\cos \theta \left[ {1 + {{{\left( {\frac{\pi }{\beta }} \right)}}^{2}}} \right] = \frac{{{{\operatorname{e} }^{{\beta }}} + 1}}{{{{\operatorname{e} }^{{\beta }}} - 1}}.$В качестве объема V, в котором диссипируется энергия струй (см. формулу (3)), следует принять ту часть жидкостной пелены, в которой давление выше атмосферного, т.е. зону, ограниченную радиусом столкновения струй. Для расчета объема зоны столкновения струй Vi запишем уравнение (13), которое связывает указанный объем со средней толщиной пелены hi.av (на практике интегрирование удобно заменять суммированием по J сегментам):
где ri – радиус зоны столкновения струй, которую в работах [29, 35] предлагается приближенно считать имеющей круглую форму радиусомПредполагая, что кинетическая энергия сталкивающихся струй преимущественно диссипируется в объеме Vi зоны их столкновения, найдем удельную скорость диссипации энергии:
(15)
$\varepsilon = \frac{P}{{{{\rho }_{{{\text{av}}}}}{{V}_{i}}}} = \frac{{P\left( {{{Q}_{1}} + {{Q}_{2}}} \right)}}{{\left( {{{\rho }_{1}}{{Q}_{1}} + {{\rho }_{2}}{{Q}_{2}}} \right){{V}_{i}}}},$Для примера приведем результаты расчета по указанным выше формулам случая формирования гидроксидного прекурсора для синтеза нанокристаллов феррита висмута BiFeO3, полученного в [25, 26] с использованием МРСС в установке, описанной в [36]. В указанных работах реагенты в виде растворов подавали в МРСС (рис. 1, 4) через сопла с диаметрами d1 = 550 мкм, d2 = 650 мкм при помощи перистальтических насосов Heidolph 5201 с пятироликовой головкой SP Quick. Один из исходных растворов – водный раствор эквимолярной смеси нитратов висмута и железа, второй реагент – 4 M водный раствор KOH. Внутренний диаметр МРСС составлял 48 мм, высота его цилиндрической части 80 мм, угол при вершине конического дна 90°. Исходные растворы подавали с фиксированным расходом 250 мл/мин в виде тонких струй со скоростями w1 = 17.5 м/с и w2 = = 12.6 м/с в вертикальной плоскости при 2θ ≈ 85°, при температуре 20°С и атмосферном давлении в аппарате. Плотность и вязкость первого раствора была близка к свойствам воды при соответствующей температуре (ввиду малых значений концентраций): ρ1 = 998 кг/м3, динамическая вязкость μ1 = 1.004 × 10–3 Па с. Для раствора KOH плотность и вязкость были взяты из [37]: ρ2 = 1216 кг/м3, μ2 = 1.81 × 10–3 Па с.
Рис. 4.
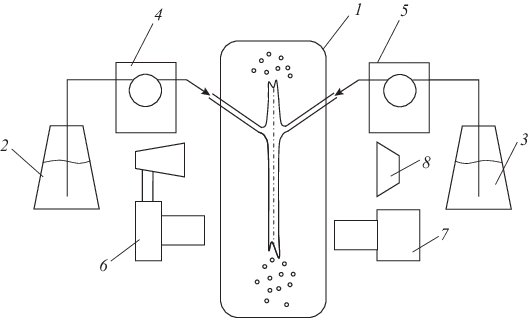
Схема установки для исследования гидродинамики и процессов синтеза наноразмерных частиц в МРСС: 1 – аппарат; 2, 3 – колбы с исходными растворами; 4, 5 – перистальтические насосы Heidolph PD 5201; 6 – фотокамера Canon 20D с макрообъективом 60D и вспышкой Speedlight 580 EX; 7 – видеокамера Evercam 2000-8-М; 8 – светодиодный источник света MultiLed LT white 15°.
Числа Рейнольдса при этом составили Re1 = = 9588, Re2 = 5483, что соответствует турбулентному режиму обеих струй. Числа Вебера We1 = 2313, We2 = = 1707 много больше единицы, характеризуют преобладание инерционных сил над капиллярными в обеих струях.
Для рассматриваемых условий были получены следующие значения величин: We = 2010; β = 5.15; ri = 444 мкм; hi.av = 218 мкм; Vi = 0.135 мкл; P = = 1.04 Вт, ε = 6.96 × 106 Вт/кг.
Следует иметь в виду, что P ∝ Q3, и при увеличении расходов всего в 1.128–2.431 раз несложно достичь значений ε ∼ 107–108 Вт/кг (1.1283 × 6.96 × × 106 = 107; 2.4313 × 6.96 × 106 = 108), которые многократно превышают уровень скорости диссипации энергии в традиционно используемых в промышленной практике аппаратах, и сопоставимы только с уровнем ε для ультразвуковых излучателей.
Как было показано в [25, 26], достижение указанных уровней удельной скорости диссипации энергии позволило в отличие от традиционно используемых методов смешения реагентов получить нанокристаллический феррит висмута BiFeO3 без примесей других фаз, реализующихся в системе Bi2O3–Fe2O3. При этом размер частиц гидроксидного предшественника нанокристаллов BiFeO3 был сопоставим с размером частицы, которая может сформироваться в вихре масштаба Колмогорова, образующегося при диссипации энергии столкновения струй в микрореакторе. Т.е. такой вихрь можно рассматривать как самоорганизующийся нанореактор при синтезе наночастиц BiFeO3.
Временные и частотные характеристики смешения реагентов в пелене. Одной из основных временных характеристик турбулентных потоков является колмогоровский микромасштаб времени τk:
(17)
${{\tau }_{k}} = {{\left( {\frac{\nu }{\varepsilon }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$Наряду с масштабом времени Колмогорова (и на его основе) в [38] предложены еще два характерных масштаба времени:
– время “поглощения”, характеризующее период вовлечения вихрем окружающей его жидкости:
– константа времени для вязкостно-конвективного и вязкостно-диффузионного смешения
где Sc = ν/D – число Шмидта.Время “поглощения” – характеристическое время вихрей, отражающее их динамику (а не время “жизни”). Оно представляет собой величину, обратную частоте вращения вихря [38], т.е. в известной мере отражает интенсивность движения вихря.
Экспериментальные исследования процесса образования жидкостной пелены и перемешивания в ней. Для описания гидродинамических характеристик жидкостной пелены разработано несколько моделей, описанных выше [28, 29]. В рамках данной работы проведены экспериментальные исследования для определения наиболее адекватной модели, описывающей геометрию жидкостной пелены – ее форму и толщину.
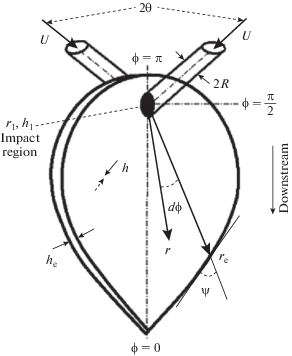
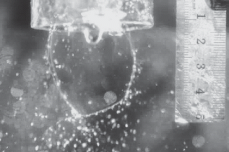
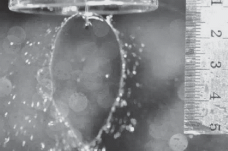
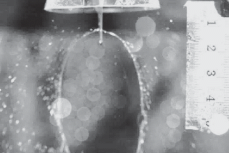
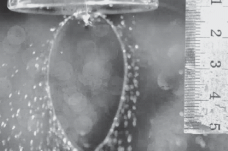
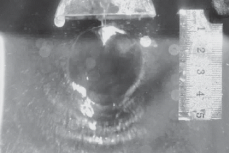
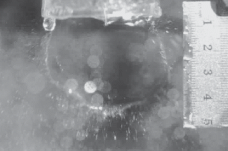
Для этого была изготовлена экспериментальная установка, схема которой показана на рис. 4. Аппарат МРСС 1 был выполнен в нескольких вариантах: для проведения синтеза – цельный (см. рис. 2), для выполнения фото- и видеосъемки – без нижней части, чтобы исключить влияние каких-либо искажений изображения при съемке. Пример фотографии сталкивающихся струй и жидкостной пелены в процессе синтеза представлен на рис 5. В табл. 2 приведены фотографии жидкостной пелены, полученные в МРСС при различных расходах через сопла (Q1 = Q2 = 100, 150, 200 и 280 мл/мин) и значениях углов 2θ между струями (2θ = 82°, 100°, 140°), а также результаты моделирования формы пелены по двум моделям, описанным выше [28, 29].
Рис. 5.
Фотография сталкивающихся струй и жидкостной пелены, образующейся в МРСС, при угле между струями 71°. Плоскость пелены лежит под углом 45° к плоскости фотоснимка.
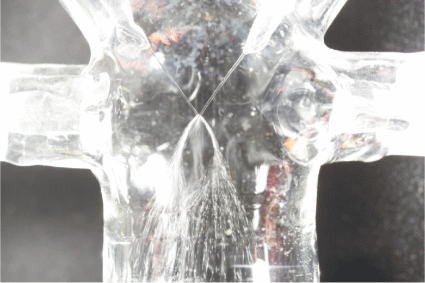
Экспериментальное исследование процесса синтеза наночастиц ортофосфата лантана. Для установления связи между гидродинамическими условиями, создаваемыми в МРСС, с получением продукта, был выбран процесс, при котором конечный продукт образуется вследствие микрореакторного смешения реагентов, т.е. без последующей термообработки, например, гидроксидного прекурсора, как это было при синтезе BiFeO3 [25, 26]. Подходящей в этом плане реакцией является образование ортофосфата лантана.
Синтез LaPO4 · nH2O проводился в следующих условиях. В качестве реагентов использовали водные растворы нитрата лантана (ХЧ) и дигидроортофосфата аммония NH4H2PO4 (Ч). Водные растворы La(NO3)3 и NH4H2PO4 готовили таких концентраций, чтобы в результате взаимодействия содержание LaPO4 в образовавшейся суспензии составляло C1 = 7.5 или C2 = 30 мг/см3.
Для синтеза частиц ортофосфата лантана был использован струйный микрореактор, описанный в [18, 26, 27] и схематически изображенный на рис. 1. В струйный микрореактор через два сопла диаметром 440 и 460 мкм подавались исходные растворы. Растворы нитрата лантана и фосфата аммония подавались в виде тонких струй с фиксированными расходами 100, 130 или 200 мл/мин, сталкивающихся со скоростями до 23 м/с в вертикальной плоскости под углом около 72°, при температуре 22°С и атмосферном давлении. Взаимное расположение сопел и расход были заданы таким образом, чтобы при столкновении струй образовалась жидкостная пелена (при расходе 200 мл/мин средняя толщина пелены вблизи зоны столкновения струй 170 мкм, толщина по внешнему контуру ~1 мкм), в которой происходил контакт и смешение растворов исходных компонентов (рис. 2–5). Объем зоны столкновения струй при расходе 200 мл/мин составляет 78 нл. Контакт реагентов в струйном микрореакторе осуществлялось в течение 12–24 мс (расчет по времени пребывания в объеме зоны столкновения струй, меньшие значения соответствуют большим расходам).
В результате смешения реагентов формировалась дисперсная система, содержащая ортофосфат лантана, которая превращалась в устойчивый золь. Полученные образцы исследовали методами рентгеновской дифракции, сканирующей электронной микроскопии (СЭМ), элементного рентгеноспектрального микроанализa, просвечивающей электронной микроскопии (ПЭМ), электронной микродифракции.
Съемка рентгеновских дифрактограмм полученных золей осуществлялась на дифрактометре Rigaku SmartLab 3 (CuKα-излучение) в диапазоне углов 10°–65° с шагом 0.01° и скоростью 3°/мин. Фазовый анализ образцов определялся по базе данных ICSD PDF-2. Размер кристаллитов определяли с помощью программного пакета SmartLab Studio II от Rigaku. Данные были получены для рефлексов (200) и (003), в наибольшей степени характеризующих неизометричность нанокристалла. Распределение кристаллитов по размерам определяли для отдельно расположенного пика (101) по методу фундаментальных параметров в приближении логнормальной модели распределения с помощью программного пакета SmartLab Studio II. Размеры кристаллитов для пика (101) также рассчитывались по формуле Шеррера.
Морфологию и размеры частиц, образующихся после промывки и сушки золей, а также их элементный состав определяли с использованием сканирующего электронного микроскопа Tescan Vega 3 SBH с приставкой для энергодисперсионной рентгеновской спектроскопии Oxford Instruments. Образцы перед анализом были диспергированы в этиловом спирте в течение 15 мин в УЗВ.
Исследования методом ПЭМ с определением электронной микродифракции образцов выполнены с использованием микроскопа JEOL JEM-2100F при ускоряющем напряжении 200 кВ. Перед анализом образцы подвергали диспергированию в этиловом спирте в течение 15 мин в УЗВ.
РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТОВ И ИХ ОБСУЖДЕНИЕ
Проведенные экспериментальные исследования и моделирование жидкостной пелены позволили сформулировать следующие результаты.
Для характерных значений коэффициента диффузии молекул в воде при комнатной температуре D = 10–9 м2/с и кинематической вязкости ν = 10–6 м2/с число Шмидта Sc = 1000, т.е., как следует из (18) и (19),
(20)
$\frac{{{{\tau }_{{VCVD}}}}}{{{{\tau }_{E}}}} = \frac{{0.5\ln \left( {{\text{Sc}}} \right)}}{{12.7}} = 0.272.$(21)
${{\lambda }_{k}} = \frac{{{{\nu }^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}}}{{{{\varepsilon }^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}}}.$В табл. 1 приведены значения характеристических времен τk, τE, τVCVD, найденные по формулам (17)–(19), а также λk для интервала значений удельной скорости диссипации энергии ε – от 101 до 109 Вт/кг, для расчетов использованы свойства воды при комнатной температуре [37].
Таблица 1.
Зависимость значений τk, τE, τVCVD, λk от удельной скорости диссипации энергии ε
| Параметр | Свободная конвекция | Аппараты с мешалками | Умеренная интенсивность перемешивания | Микрореакторы со сталкивающимися струями | |||||
|---|---|---|---|---|---|---|---|---|---|
| ε, W/kg | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 |
| τk, μs | 316 | 100 | 31.6 | 10 | 3.16 | 1 | 0.316 | 0.1 | 0.032 |
| τE, μs | 4016 | 1270 | 401.6 | 127 | 40.2 | 12.7 | 4.02 | 1.27 | 0.402 |
| τVCVD, μs | 1092 | 345.4 | 109.2 | 34.5 | 10.9 | 3.4 | 1.09 | 0.345 | 0.109 |
| λk, μm | 17.8 | 10 | 5.62 | 3.16 | 1.78 | 1 | 0.562 | 0.316 | 0.178 |
Из данных, представленных в табл. 1, видно, что с ростом ε уменьшаются все зависящие от ε значения – τk, τE, τVCVD и λk. Отметим, что в традиционных аппаратах с мешалками, с ε = 10–1–102 Вт/кг [39, 40], характерное время микроперемешивания τE имеет порядок более 1270 мкс, а частота вращения микровихрей (f = 1/τE) не превышает 0.8 кГц и λk имеет масштаб более 10 мкм. В результате медленного перемешивания резко возрастает риск избытка одного из реагентов в микрообъеме аппарата, что может приводить к образованию побочных продуктов, не отвечающих заданной стехиометрии.
Для сравнения характерные значения для МРСС: ε = 107–109 Вт/кг, которым соответствует характерное время микроперемешивания τE порядок 0.4–4.0 мкс, а частота вращения микровихрей (f = 1/τE) порядка 250–2500 кГц, при этом колмогоровский масштаб λk ≈ 180–560 нм. Такие значения времени τE определяют очень высокую равномерность распределения компонентов в реакционной среде при микроперемешивании [41–43]. Это, в свою очередь, позволит обеспечить заданную стехиометрию реагентов в зоне реакции, что необходимо для получения целевого продукта без примесей сосуществующих с ним фаз.
Как легко убедиться по данным, приведенным в табл. 2, наиболее точно форма пелены описывается моделью [29]. Чем ближе угол 2θ к 180°, тем сильнее форма пелены приближается к круглой. Это легко объяснить преобладанием сил инерции над гравитацией (высокими значениями числа Фруда, которое при w = 20 м/с, dс = 0.5 мм составляет Fr = 80 000). При уменьшении угла 2θ пелена вытягивается в вертикальном направлении, вниз от точки столкновения струй, что объясняется сложением импульса двух струй по вертикальной координате.
На рис. 6. представлены зависимости толщины по внешнему краю пелены he от азимутального угла φ для исследованных расходов жидкости (рис. 6а) и углов между струями (рис. 6б).
Рис. 6.
Влияние скорости струй (расходы жидкости) (а) и угла между струями 2θ (б) на толщину пелены he (м) в МРСС (толщина по краю пелены). Азимутальный угол φ (рад) отсчитывается снизу (см. рис 1); 1–4: 2θ = 82°; 5–7: Q1 = Q2 = = 100 мл/мин; 1 – 100 мл/мин; 2 – 130 мл/мин; 3 – 150 мл/мин; 4 – 200 мл/мин; 5 – 82°; 6 – 100°; 7 – 140°. Данные по скорости струй и скорости диссипации энергии приведены в табл. 3.
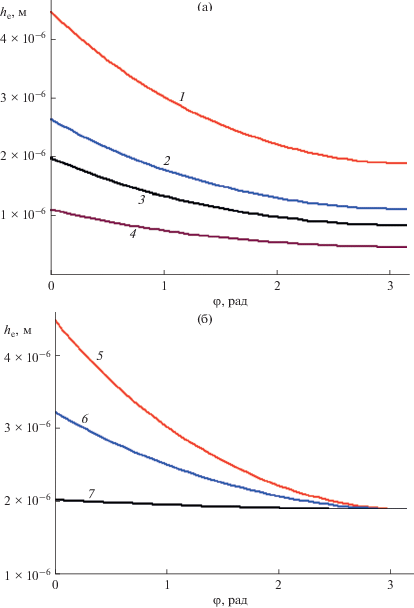
Таблица 3.
Скорости струй (U1, U2) и удельная скорость диссипации энергии ε для пелены, представленной в табл. 2. Диаметры сопел: d1 = 0.514 мм, d2 = 0.471 мм, жидкость – вода при комнатной температуре
| Параметр | 2θ, град | Q1 = Q2 = = 100 мл/мин | Q1 = Q2 = = 130 мл/мин |
Q1 = Q2 = = 150 мл/мин |
Q1 = Q2 = = 200 мл/мин |
|---|---|---|---|---|---|
| U1, м/с | 82 | 8.032 | 10.442 | 12.048 | 16.064 |
| U2, м/с | 9.566 | 12.435 | 14.349 | 19.131 | |
| ε, Вт/кг | 1.687 × 106 | 3.707 × 106 | 5.694 × 106 | 1.350 × 107 | |
| U1, м/с | 100 | 8.032 | 10.442 | 12.048 | 16.064 |
| U2, м/с | 9.566 | 12.435 | 14.349 | 19.131 | |
| ε, Вт/кг | 2.005 × 106 | 4.405 × 106 | 6.767 × 106 | 1.604 × 107 | |
| U1, м/с | 140 | 8.032 | 10.442 | 12.048 | 16.064 |
| U2, м/с | 9.566 | 12.435 | 14.349 | 19.131 | |
| ε, Вт/кг | 2.516 × 106 | 5.528 × 106 | 8.493 × 106 | 2.013 × 107 |
Как следует из полученных зависимостей, толщина пелены на ее краю имеет порядок 1–4 мкм, причем она уменьшается от нижней точки к верхней. Чем ближе угол 2θ к 180°, и чем больше расход (скорость струй), тем слабее это изменение. При этом роль угла между струями выражена более значимо. Так, для 2θ = 140° при расходе 100 мл/мин разница между максимальной и минимальной толщиной равна 6% (1.886 и 2.021 мкм), а для 2θ = 82° толщина в верхней части составляет 42% от толщины в нижней части (0.471 и 1.118 мкм соответственно).
Важно отметить, что с увеличением расходов уменьшается толщина пелены. Это, очевидно, будет приводить к ее распаду на капли. С точки зрения перемешивания такой сценарий, по-видимому, не очень благоприятен, поскольку внутри отдельных капель, отделившихся от источника энергии (струи, пелены) перемешивание будет не столь интенсивным. С другой стороны, если в каждой микрокапле находится необходимое по стехиометрии соотношение реагентов, в ней может образоваться продукт заданного состава. Ответ на вопрос о преимуществах или недостатках раннего распада пелены на капли с точки зрения синтеза неорганических соединений в растворах требует дальнейшего изучения.
Был проведен анализ образцов ортофосфата лантана, полученных после микрореакторного смешения при различных расходах и при разных концентрациях растворов реагентов. Данные по скорости струй исходных растворов и скорости диссипации энергии при синтезе LaPO4 при его содержании в реакционной среде C1 = 7.5 мг/см3 приведены в табл. 4. Те же данные в случае синтеза LaPO4 при содержании C2 = 30 мг/см3 (с использованием плотности и вязкости раствора LaPO4 из [44]) приведены в табл. 5. Увеличение значений концентрации исходных растворов реагентов с 0.064 до 0.26 моль/л, отвечающих содержанию LaPO4 в реакционной среде C1 = = 7.5 мг/см3 и C2 = 30 мг/см3 соответственно, не приводит к существенному изменению удельной скорости диссипации энергии.
Таблица 4.
Скорости струй (U1, U2) и удельная скорость диссипации энергии ε для пелены, использованной при синтезе LaPO4. Диаметры сопел: d1 = 0.440 мм, d2 = 0.460 мм. Свойства разбавленных растворов La(NO3)3 и NH4H2PO4 (0.064 моль/л) принимались равными свойствам воды при 20°С
| Параметр | 2θ, град | Q1 = Q2 = 100 мл/мин | Q1 = Q2 = 130 мл/мин | Q1 = Q2 = 150 мл/мин | Q1 = Q2 = 200 мл/мин |
|---|---|---|---|---|---|
| U1, м/с | 72 | 10.961 | 14.249 | 16.442 | 21.922 |
| U2, м/с | 10.029 | 13.037 | 15.043 | 20.057 | |
| ε, Вт/кг | 2.767 × 106 | 6.079 × 106 | 9.338 × 106 | 2.213 × 107 |
Таблица 5.
Скорости струй (U1, U2) и удельная скорость диссипации энергии ε для пелены, использованной при синтезе LaPO4. Диаметры сопел: d1 = 0.440 мм, d2 = 0.460 мм. Свойства La(NO3)3 при 20°С, 0.26 моль/л [44]: ρ1 = = 1052 кг/м3, μ1 = 1.073 мПа с. Свойства NH4H2PO4 при 20°С, 0.26 моль/л: ρ2 = 1015 кг/м3, μ2 = 1.00 мПа с
| Параметр | 2θ, град | Q1 = Q2 = 100 мл/мин | Q1 = Q2 = 130 мл/мин | Q1 = Q2 = 150 мл/мин | Q1 = Q2 = 200 мл/мин |
|---|---|---|---|---|---|
| U1, м/с | 72 | 10.961 | 14.249 | 16.442 | 21.922 |
| U2, м/с | 10.029 | 13.037 | 15.043 | 20.057 | |
| ε, Вт/кг | 2.771 × 106 | 6.088 × 106 | 9.353 × 106 | 2.217 × 107 |
Атомное отношение P : La в образцах по данным EDX равно (49 ± 2) : (51 ± 1), что в пределах погрешности метода отвечает заданному при синтезе отношению, соответствующему стехиометрии LaPO4.
Данные рентгеновской дифракции образцов приведены на рис. 7а. Дифрактограммы всех образцов соответствуют фазе рабдофана (PDF 00-046-1439). Примесных кристаллических фаз не наблюдается. Средний размер кристаллитов вдоль разных кристаллографических направлений для всех образцов меняется от ~3 до ~7 нм. Значительные различия в ширине линий рентгеновских дифрактограмм показывают, что нанокристаллы LaPO4 имеют неизометрическую форму и вытянуты вдоль оси, перпендикулярной кристаллографической плоскости (100). Например, средневзвешенные размеры кристаллитов, определенные с помощью программного пакета SmartLab Studio II, составляют d = 3.2 нм (200), d = 13.6 нм (003) для образца 3 и d = 3.4 нм (200), d = 19.2 нм (003) для образца 4 (в скобках указаны рефлексы, по которым определялись размеры кристаллитов) (рис. 7). Следует отметить, что несмотря на заметное различие в размерах кристаллитов по разным направлениям, они по всем направлениям могут рассматриваться как нанокристаллические объекты.
Рис. 7.
(а) – рентгеновские дифрактограммы образцов LaPO4, полученных в различных условиях микрореакторного смешения реагентов. (б) – распределение кристаллитов LaPO4 по размеру, определенное по рефлексу (101): 1 – ε = = 2.8 МВт/кг, С1 = 7.5 мг/см3; 2 – ε = 6.1 МВт/кг, С1 = 7.5 мг/см3; 3 – ε = 22 МВт/кг, С1 = 7.5 мг/см3; 4 – ε = 22 МВт/кг, С2 = 30 мг/см3. (в) – зависимость размеров кристаллитов LaPO4 от удельной скорости диссипации энергии. Размеры кристаллитов рассчитаны по формуле Шеррера (кружочки и линия 1 при С1 = 7.5 мг/см3 и С2 = 30 мг/см3) для рефлекса (101); определены как средневзвешенное значение по данным распределения на рис. 7б (квадратики и линия 2 при С1 = 7.5 мг/см3 и С2 = 30 мг/см3). (г) – зависимость средневзвешенных значений размеров кристаллитов LaPO4, определенных для рефлексов (003) и (200), и их отношение от удельной скорости диссипации энергии для С1 = 7.5 мг/см3. Светлыми значками отмечены точки для концентрации С2 = 30 мг/см3.
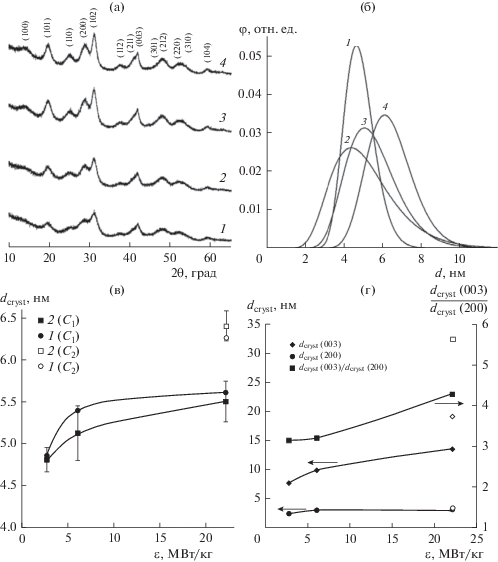
Распределение кристаллитов по размеру, определенное по рефлексу (101) (рис. 7б) показывает, что с увеличением расхода выше 100 мл/мин и, следовательно, удельных скоростей диссипации энергии больше 2.8 МВт/кг размеры кристаллитов имеют более широкое распределение.
Увеличение расхода от 100 до 200 мл/мин и, следовательно, удельной скорости диссипации энергии от 2.8 до 22 МВт/кг (при одинаковой концентрации растворов реагентов) приводит к увеличению размера кристаллитов LaPO4, определенных по рефлексу (101), примерно на 12–20% (рис. 7в).
Увеличение содержания LaPO4 в реакционной среде от 7.5 до 30 мг/см3 при удельной скорости диссипации энергии около 22 МВт/кг приводит к увеличению средних размеров кристаллитов примерно на 8–10% (рис. 7в).
На рис. 8а приведена в качестве примера микрофотография СЭМ образца 3 ортофосфата лантана (см. рис. 7). Образец LaPO4 представлен частицами в форме стержней. Распределение стержней по длине и толщине хорошо описывается логнормальными зависимостями. Среднее значение длины стержней по полученным данным составляет Lpart = 0.68 мкм (среднее квадратичное отклонение ΔLpart = 0.25 мкм). Среднее значение толщины стержней – hpart = 19.6 нм (среднее квадратичное отклонение Δhpart = 7.4 нм). На рис. 8б представлена микрофотография ПЭМ того же образца после его ультразвукового диспергирования. Частицы представлены тонкими стержнями. Данные электронной микродифракции показывают, что частицы являются поликристаллическими (дифракционные кольца вместо четко определенных пятен). Построенная по данным ПЭМ гистограмма распределения наностержней по толщине показывает, что средневзвешенное значение толщины частиц составляет hpart = 5.4 нм (средневзвешенное квадратичное отклонение Δhpart = 0.7 нм). Следует отметить близкое соответствие значений средних размеров нанокристаллов (рис. 7г) и средних значений размеров толщины наночастиц ортофосфата лантана после ультразвукового диспергирования образца (рис. 8б). Это позволяет предположить, что частицы ортофосфата лантана после их диспергирования представлены монокристаллическими стержнеобразными наночастицами, или по крайней мере сростками нанокристаллов вдоль оси стержня. За последнее предположение говорит и сопоставление длины этих частиц с максимальными размерами кристаллитов, определенными по данным рентгеновской дифракции, которые оказываются значительно меньших размеров. Эти стержнеобразные нанокристаллические частицы агрегируют в дисперсной системе с образованием сростков как по толщине, так и по длине стержней (рис. 8а). На рис. 8б можно заметить (выделено овалом) фрагмент такого агрегата.
Сложное иерархическое строение нанокристаллических стержнеобразных частиц, образующихся в процессе микрореакторного смешения показывает, что их формирование протекает в несколько стадий. На первой стадии при контакте растворов реагентов образуются нанокристаллические кластеры вытянутые вдоль оси [100] со средними размерами по толщине около 3 нм, которые, по-видимому, близки к минимально возможным размером кристаллитов LaPO4 со структурой рабдофана [45], и со средними размерами порядка 10 нм по перпендикулярному направлению. Наблюдающееся увеличение средних размеров кристаллитов с увеличением удельной скорости диссипации энергии (рис. 7г) объясняется увеличением скорости формирования нанокристаллических кластеров LaPO4 на данном этапе процесса за счет контактного фактора, связанного с улучшением смешения реагентов. Аналогичным образом влияет и повышение концентрации реагентов, которое так же приводит к увеличению вероятности контакта химически взаимодействующих компонентов. Образовавшиеся нанокристаллические кластеры на следующем этапе синтеза, по-видимому, ориентированно срастаются, формируя устойчиво существующие нанокристаллы, как, например, описано в [46–48]. Формирование нанокристаллических частиц путем ориентированного срастания нанокристаллических кластеров анизотропной формы может протекать, в частности, при их движении по линиям тока в дисперсионной среде. Следующий этап формирования стержнеобразных нанокристаллических частиц с логнормальным распределением по их длине и толщине состоит в агрегировании нанокристаллических стержней в пучки за счет сил вандерваальсовского взаимодействия. Данная стадия формирования наностержней является, по всей видимости, самой длительной по времени и происходит в дисперсной системе уже вне области микрореакторного смешения. Подтверждением этого является тот факт, что формирование устойчивого золя стержнеобразных наночастиц толщиной около 10–30 нм и длиной до ~1 мкм наблюдается только после выдержки дисперсной системы в течение 30–60 мин после окончания синтеза LaPO4 в условиях микрореакторного смешения.
Следует отметить, что описанный процесс формирования нанокристаллических стержнеобразных частиц ортофосфата лантана в условиях микрореакторного смешения кардинальным образом отличается от случая использования микрореакторного смешения для синтеза нанокристаллов BiFeO3. В последнем случае гидроксидные прекурсоры и сами кристаллы феррита висмута принимали минимальные значения с увеличением удельной скорости диссипации энергии при столкновении струй раствора смеси солей реагентов и раствора щелочи, что определялось быстрым образованием частиц смешанных оксигидроксидов висмута и железа в вихре масштаба Колмогорова [25, 26], блокирующих возможность дальнейшего взаимодействия растворов реагентов, которое бы приводило к росту частиц.
ЗАКЛЮЧЕНИЕ
Проведены экспериментальные исследования процесса синтеза наноразмерных частиц оксидных материалов в микрореакторе со свободно сталкивающимися струями, а также теоретический анализ гидродинамических характеристик микроперемешивания в образующейся при столкновении струй жидкостной пелене и моделирование жидкостной пелены. Показано, что наиболее точно форму пелены описывает модель, предложенная в [29].
Теоретический анализ показал, что для МРСС характерны значения удельной скорости диссипации энергии порядка ε = 107–109 Вт/кг, которым соответствует характерное время микроперемешивания τE порядок 0.4–4.0 мкс, а частота вращения микровихрей (f = 1/τE) порядка 250–2500 кГц, при этом колмогоровский масштаб λk = = 180–560 нм. Таким образом, пространственные и временные масштабы турбулентности в жидкостной пелене достаточно малы, что, с одной стороны, обеспечивает возможность завершения быстропротекающей реакции осаждения твердофазных продуктов из раствора, с другой – препятствует росту кристаллов.
Показано, что при синтезе ортофосфата лантана наблюдается увеличение размеров кристаллов LaPO4 с увеличением концентрации исходных реагентов в растворе и с увеличением их расхода. Этот эффект связан с увеличением вероятности контакта реагентов при смешении их растворов.
Рассмотрение образующихся в микрореакторе со свободно сталкивающимися струями микровихрей минимального колмогоровского масштаба λk в качестве самоорганизующихся нанореакторов позволило выявить зависимость минимальных размеров образующихся наночастиц от гидродинамических условий их синтеза.
Таким образом, МРСС является средством, позволяющим в непрерывном режиме синтезировать сложные неорганические соединения в виде нанокристаллических порошкообразных материалов с определенной морфологией и регулируемыми значениями размерных параметров.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 18-29-12119).
ОБОЗНАЧЕНИЯ
| A | площадь поперечного сечения струи (для эйлеровой жидкости равна площади сечения пелены на радиусе r), м2 |
| a | показатель степень в уравнении Ауэрбаха |
| b | условная ширина жидкостной пелены, м |
| D | коэффициент диффузии, м2/с |
| d | размер кристаллита, нм |
| dj | диаметр j-й струи, м |
| djet | диаметр струи, м |
| E | удельная кинетическая энергия струй (динамический напор), Па |
| f | частота вращения микровихрей, Гц |
| g | ускорение свободного падения, м/с2 |
| h | толщина жидкостной пелены, м |
| hpart | толщина частицы, нм |
| Lpart | длина частицы, мкм |
| M | молекулярная масса диффундирующих ионов, кг/моль |
| mj | массовый расход j-й струи, кг/с |
| Р | скорость диссипации механической энергии, Вт |
| Qj | объемный расход жидкости в j-й струе, м3/с |
| R | радиус струи (R = d/2), м |
| r, φ | полярные координаты |
| ri | радиус зоны столкновения струй, м |
| t | время, с |
| V | объем жидкости, в котором рассеивается энергия, м3 |
| U | скорости струи, м/с |
| w | вектор скорости на краю пелены, м/с |
| wj | скорость j-й струи, м/с |
| β | коэффициент затухания в формуле (11) |
| ε | удельная скорость диссипации кинетической энергии турбулентности, Вт/кг |
| λk | колмогоровский микромасштаб, м |
| μ | динамическая вязкость жидкости, Па с |
| ν | кинематическая вязкость жидкости, м2/с |
| ρ | плотность жидкости, кг/м3 |
| τE | время “поглощения”, c |
| τk | колмогоровский микромасштаб времени, с |
| τVCVD | константа времени для вязкостно-конвективного и вязкостно-диффузионного смешения, с |
| ψ | угол между вектором w и локальной касательной к контуру края пелены, рад |
| Fr | число Фруда |
| Re | число Рейнольдса |
| Sc = ν/D | число Шмидта |
| We | число Вебера |
ИНДЕКСЫ
СОКРАЩЕНИЯ
Список литературы
Hessel V., Löwe H., Müller A., Kolb G. Chemical Micro Process Engineering: Processing and Plants. Weinheim: Wiley-VCH, 2005.
Capretto L., Cheng W., Hill M., Zhang X. Micromixing within microfluidic devices // Top. Curr. Chem. 2011. V. 304. P. 27. https://doi.org/10.1007/128_2011_150
Su Y., Song Y., Xiang L. Continuous-Flow Microreactors for Polymer Synthesis: Engineering Principles and Applications // Top. Curr. Chem. 2018. V. 376. P. 44. https://doi.org/10.1007/s41061-018-0224-1
Popova E.A., Abiev R.Sh., Lappalainen L.A., Svetlov S.D., Andreeva T.V., Trifonov R.E., Ostrovskii V.A. Synthesis of 5-phenyltetrazole and its N-methyl derivatives in a microreactor // Chem. Biochem. Eng. Q. 2014. V. 28. № 2. P. 241.
Abiev R.Sh., Pavlyukova Y.N., Nesterova O.M., Svetlov S.D., Ostrovskii V.A. Mass Transfer Intensification of 2-Methyl-5-Nitrotetrazole synthesis in Two-phase Liquid-Liquid Taylor Flow in Microreactor // Chem. Eng. Res. Des. 2019. V. 144. P. 444.
Wörner M. A Correlation for the Characteristic Velocity Ratio to Predict Hydrodynamics of Capillary Gas–Liquid Taylor Flow // Theor. Found. Chem. Eng. 2020. V. 54. P. 3.
Mei M., Felis F., Hébrard G., Dietrich N., Loubière K. Hydrodynamics of Gas–Liquid Slug Flows in a Long In-Plane Spiral Shaped Milli-Reactor // Theor. Found. Chem. Eng. 2020. V. 54. P. 25.
Abiev R.Sh. Miniaturization as One of the Paths to Process Intensification in Chemical Engineering // Theor. Found. Chem. Eng. 2020. V. 54. P. 1.
Haase S., Bauer T., Hilpmann G., Lange M., Ayubi M.-M., Abiev R. Simultaneous Detection of Hydrodynamics, Mass Transfer and Reaction Rates in a Three-Phase Microreactor // Theor. Found. Chem. Eng. 2020. V. 54. P. 48.
Kumar R., Yadav V., Abiev R.Sh. Concurrent Removal of Heat Transfer and Mass Flow Rate Nonuniformities in Parallel Channels of Microchannel Heat Sink // Theor. Found. Chem. Eng. 2020. V. 54. P. 77.
Meskin P.E., Gavrilov A.I., Maksimov V.D., Ivanov V.K., Churagulov B.P. Hydrothermal/microwave and hydrothermal/ultrasonic synthesis of nanocrystalline titania, zirconia, and hafnia // Russ. J. Inorg. Chem. 2007. V. 52. № 11. P. 1648. [Мескин П.Е., Гаврилов А.И., Максимов В.Д., Иванов В.К., Чурагулов Б.Р. Гидротермально-микроволновой и гидротермально-ультразвуковой синтез нанокристаллических диоксидов титана, циркония, гафния // Ж. неорг. хим. 2007. Т. 52. № 11. С. 1755.]https://doi.org/10.1134/S0036023607110022
Proskurina O.V., Tomkovich M.V., Bachina A.K., Sokolov V.V., Danilovich D.P., Panchuk V.V., Semenov V.G., Gusarov V.V. Formation of Nanocrystalline BiFeO3 under Hydrothermal Conditions // Russ. J. Gen. Chem. 2017. V. 87. № 11. P. 2507. [Проскурина О.В., Панчук В.В., Данилович Д.П., Бачина А.К., Томкович М.В., Семенов В.Г., Соколов В.В., Гусаров В.В. Формирование нанокристаллического BiFeO3 в гидротермальных условиях // Журн. общ. хим. 2017. Т. 87. № 11. С. 1761.]
Chen C., Cheng J., Yu S., Che L., Meng Z. Hydrothermal synthesis of perovskite bismuth ferrite crystallites // J. Cryst. Growth. 2006. V. 291. P. 135.
Zhu Z. Flash Nanoprecipitation: Prediction and Enhancement of Particle Stability via Drug Structure // Mol. Pharm. 2014. V. 11. 776.
Margulis K., Magdassi S., Lee H.S., Macosko C.W. Formation of curcumin nanoparticles by flash nanoprecipitation from emulsions // J. Colloid Interface Sci. 2014 V. 434. P. 65.
Han J., Zhu Z., Qian H., Wohl A.R., Beaman C.J., Hoye T.R., Macosko C.W. A Simple Confined Impingement Jets Mixer for Flash Nanoprecipitation // J. Pharm. Sci. 2012. V. 101. № 10. P. 4018.
Ravi Kumar D.V., Prasad B.L.V., Kulkarni A.A. Impinging Jet Micromixer for Flow Synthesis of Nanocrystalline MgO: Role of Mixing/Impingement Zone // Ind. Eng. Chem. Res. 2013. V. 52. P. 17376.
Abiev R.S., Almyasheva O.V., Izotova S.G., Gusarov V.V. Synthesis of cobalt ferrite nanoparticles by means of confined impinging-jets reactors // J. Chem. Tech. App. 2017. V. 1. № 1. P. 7.
Kawase M., Miura K. Fine particle synthesis by continuous precipitation using a tubular reactor // Adv. Powder Technol. 2007. V. 18. № 6. P. 725.
Che D., Zhu X., Liu P., Duan Y., Wang H., Zhang Q., Li Y. A facile aqueous strategy for the synthesis of high-brightness LaPO4:Eu nanocrystals via controlling the nucleation and growth process // J. Lumin. 2014. V. 153. P. 369.
Nightingale A.M., deMello J.C. Segmented Flow Reactors for Nanocrystal Synthesis // Adv. Mater. 2013. V. 25. P. 1813.
Nightingale A.M., Krishnadasan S.H., Berhanu D., Niu X., Drury C., McIntyre R., Valsami-Jones E., deMello J.C. A stable droplet reactor for high temperature nanocrystal synthesis // Lab Chip. 2011. V. 11. P. 1221.
Doh I., Erdem E.Y., Pisano A.P. Trapping and Collection of Uniform Size Droplets for Nanoparticle Synthesis // Appl. Phys. Lett. 2012. V. 100. P. 074106.
Salvador H.M.M. Fully Resolved Dynamics of Mixing in Confined Impinging Jets Reactors. Master Dissertation. Univ. de Porto, 2015.
Proskurina O.V., Nogovitsin I.V., Il’ina T.S., Danilovich D.P., Abiev R.Sh., Gusarov V.V. Formation of BiFeO3 Nanoparticles Using Impinging Jets Microreactor // Russ. J. Gen. Chem. 2018. V. 88. № 10. P. 2139. [Проскурина О.В., Ноговицин И.В., Ильина Т.С., Данилович Д.П., Абиев Р.Ш., Гусаров В.В. Формирование наночастиц BiFeO3 с использованием струйного микрореактора // Журн. общ. хим. 2018. Т. 88. № 10. С. 1699.]
Proskurina O.V., Abiev R.S., Danilovich D.P., Panchuk V.V., Semenov V.G., Nevedomsky V.N., Gusarov V.V. Formation of nanocrystalline BiFeO3 during heat treatment of hydroxides co-precipitated in an impinging-jets microreactor // Chem. Eng. Process. 2019. V. 143. P. 107598.
Proskurina O.V., Sivtsov E.V., Enikeeva M.O., Sirotkin A.A., Abiev R.Sh., Gusarov V.V. Formation of rhabdophane-structured lanthanum orthophosphate nanoparticles in an impinging-jets microreactor and rheological properties of sols based on them // Nanosyst.: Phys., Chem., Math. 2019. V. 10. № 2. P. 206. https://doi.org/10.17586/2220-8054-2019-10-2-206-214
Hasson D., Peck R.E. Thickness distribution in a sheet formed by impinging jets // AIChE J. 1964. V. 10. № 5. P. 752.
Ibrahim E., Przekwas A. Impinging jets atomization // Phys. Fluids A. 1991. V. 3. P. 2981.
Ashgriz N. Impinging Jet Atomization // Handbook of Atomization and Sprays: Theory and Applications / Ed. Ashgriz N. N.Y.: Springer, 2011. P. 685.
Li R., Ashgriz N. Characteristics of liquid sheets formed by two impinging jets // Phys. Fluids. 2006. V. 18. P. 087104.
Chen X., Ma D., Yang V., Popinet S. High-fidelity simulations of impinging jet atomization // Atomization Sprays. 2013. V. 23. № 14. P. 1079.
Faber T.E. Fluid Dynamics for Physicists. Cambridge: Cambridge Univ. Press, 1997. [Фабер Т.Е. Гидроаэродинамика. М.: Постмаркет, 2001.]
Choo Y.-J., Kang B.-S. The velocity distribution of the liquid sheet formed by two low-speed impinging jets // Phys. Fluids. 2002. V. 14. № 2. P. 622.
Ashgriz N., Brocklehurst W., Talley D. Mixing Mechanisms in a Pair of Impinging Jets // J. Propul. Power. 2001. V. 17. № 3. P. 736.
Абиев Р.Ш., Альмяшева О.В., Гусаров В.В., Изотова С.Г. Способ получения нанопорошков феррита кобальта и микрореактор для его реализации. Пат. 2625981 РФ. 2017.
Perry’s Chemical Engineers’ Handbook / Eds. Green D.W., Perry R.H. N.Y.: McGraw-Hill, 2007.
Baldyga J., Bourne J.R. Turbulent Mixing and Chemical Reactions. N.Y.: Wiley, 1999.
Atiemo-Obeng V.A., Calabrese R.V. Rotor–stator mixing devices // Handbook of Industrial Mixing: Science and Practice / Eds. Paul E.L., Atiemo-Obeng V.A., Kresta S.M. Hoboken, N.J.: Wiley, 2004. Ch. 8. P. 479.
Davies J.T. A physical interpretation of drop sizes in homogenizers and agitated tanks, including the dispersion of viscous oils // Chem. Eng. Sci. 1987. V. 42. P. 1671.
Guichardon P., Falk L. Characterisation of micromixing efficiency by the iodide-iodate reaction system. Part I: Experimental procedure // Chem. Eng. Sci. 2000. V. 55. P. 4233.
Commenge J.-M., Falk L. Villermaux–Dushman protocol for experimental characterization of micromixers // Chem. Eng. Process. 2011. V. 50. P. 979.
Jasińska M. Test reactions to study efficiency of mixing // Chem. Process Eng. 2015. V. 36. № 2. P. 171.
Qadeer R., Khalid N. Influence of concentration and temperature on viscosity of nitrate solutions of some trivalent lanthanides // J. Chem. Eng. Data. 2004. V. 49. P. 892.
Almyasheva O.V., Lomanova N.A., Popkov V.I., Proskurina O.V., Tugova E.A., Gusarov V.V. The minimal size of oxide nanocrystals: Phenomenological thermodynamic vs crystal-chemical approaches // Nanosyst.: Phys., Chem., Math. 2019. V. 10. № 4. P. 428.
Almjasheva O.V., Gusarov V.V. Metastable clusters and aggregative nucleation mechanism // Nanosyst.: Phys., Chem., Math. 2014. V. 5. № 3. P. 405.
Almjasheva O.V. Formation and structural transformations of nanoparticles in the TiO2–H2O system // Nanosyst.: Phys., Chem., Math. 2016. V. 7. № 6. P. 1031.
Ivanov V.K., Fedorov P.P., Baranchikov A.E., Osiko V.V. Oriented attachment of particles: 100 years of investigations of non-classical crystal growth // Russ. Chem. Rev. 2014. V. 83. № 12. P. 1204. [Иванов В.К., Федоров П.П., Баранчиков А.Е., Осико В.В. Ориентированное сращивание частиц: 100 лет исследований неклассического механизма роста кристаллов // Усп. хим. 2014. Т. 83. № 12. С. 1204.]
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии