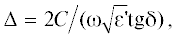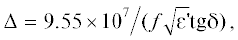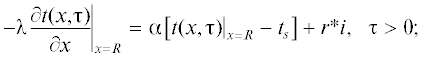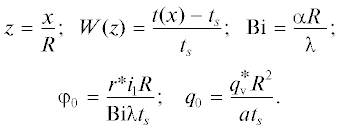Теоретические основы химической технологии, 2021, T. 55, № 2, стр. 195-203

Тепломассоперенос при сушке пластины в непрерывно действующем электромагнитном поле высокой и сверхвысокой частоты

С. П. Рудобашта^a, *, Э. М. Карташов^b, Г. А. Зуева^c

^a Российский государственный аграрный университет – МСХА им. К.А. Тимирязева
Москва, Россия

^b Российский технологический университет – МИРЭА (Институт тонких химических технологий им. М.В. Ломоносова)
Москва, Россия

^c Ивановский государственный химико-технологический университет,
Иваново, Россия

^* E-mail: rudobashta@mail.ru

Поступила в редакцию 25.09.2020
После доработки 16.11.2020
Принята к публикации 20.11.2020

DOI: 10.31857/S0040357121020093

Полный текст (PDF)

Аннотация

Рассмотрено поглощение электромагнитной энергии пластиной в высокочастотном и сверхвысокочастотном диапазонах. Сформулированы и аналитически решены линейные (постоянство параметров процесса) задачи нагрева пластины при этих видах энергоподвода в условиях конвективной сушки и с учетом ее конвективного тепло- и массообмена с внешней газовой средой – как в общем случае, так и при сушке в первом периоде. В первом случае интенсивность сушки описана на основе аналитического решения задачи массопроводности (диффузии влаги) при условии, что фазовые превращения происходят у поверхности тела. Применительно к процессу сушки в первом периоде принято, что вся подводимая к телу теплота расходуется на испарение влаги и поэтому нагрев тела не происходит и что парциальное давление пара у поверхности пластины равно давлению насыщенного пара при температуре поверхности пластины. При этом зависимость давления насыщенного пара от температуры описана уравнением Антуана. Решения задач нагрева получены применительно к локальной и средней по объему пластины температуре. На их основе проведено численное моделирование процесса нагрева тела и его влияния на кинетику сушки, показывающее работоспособность полученных уравнений. Для учета изменения параметров процесса в его ходе предложено использовать зональный кусочно-ступенчатый метод расчета.

Ключевые слова: сушка, электромагнитный нагрев, токи высокой и сверхвысокой частоты, конвективный тепломассообмен, аналитическое решение

ВВЕДЕНИЕ

В последние годы большое внимание в исследованиях уделяется процессу электромагнитной сушки различных материалов, особенно пищевых, в электромагнитном поле (ЭМП) токов высокой и сверхвысокой частоты (ТВЧ- и СВЧ-сушка). Этот процесс достаточно широко применяется в промышленности [1–4]. При этом для термолабильных материалов для сохранения их качества электромагнитный энергоподвод осуществляется, как правило, в прерывистом режиме [5–11], который позволяет не перегревать материал. Электромагнитную сушку часто комбинируют с конвективной сушкой [1–4, 10, 12]. Математические модели, описывающие прерывистый процесс конвективной, электромагнитной и комбинированной сушки, приведены в [5, 8, 11–15]. Они используют как численные [5, 6, 11–13], так и аналитические [8, 14, 15] решения задач. В [8, 14, 15] полученные решения были использованы для компьютерного анализа процесса осциллирующей электромагнитной сушки семян овощных культур с целью поиска необходимого технологического режима процесса.

Осциллирующий подвод электромагнитной энергии, как отмечено выше, необходим при сушке термолабильных материалов. Однако на практике высушивается достаточно большое количество материалов, которые таковыми не являются. Для расчета и анализа тепломассопереноса при их сушке необходимы математические модели, описывающие их непрерывный электромагнитный нагрев с учетом стока теплоты на испарение влаги. В [18] приведены математические модели для “чистого” (без массообмена) нагрева тела в форме пластины при постоянном внутреннем источнике теплоты.

Целью данной работы является разработка аналитических математических моделей, описывающих процесс непрерывного электромагнитного нагрева влажного тела в форме пластины в поле токов высокой и сверхвысокой частоты, учитывающей сток теплоты на испарение влаги и конвективный теплообмен поверхности тела с внешней газовой средой, в процессе которого может происходить либо дополнительный нагрев тела (при температуре внешней среды выше температуры поверхности тела), либо его охлаждение, когда температура поверхности тела ниже температуры внешней среды. В сочетании с представленным в работе математическим описанием массообмена эти модели позволят рассчитывать кинетику сушки.

АНАЛИЗ ВНУТРЕННИХ ИСТОЧНИКОВ ТЕПЛОТЫ ПРИ ТВЧ- И СВЧ-СУШКЕ

За глубину проникновения ЭМП в материал принимают глубину Δ, на которой напряженность поля уменьшается в e раз, где e – основание натуральных логарифмов. Величина Δ (м) определяется формулой [1]

(1)

где С – скорость света, равная 3 × 10⁸ м/с; ω – круговая (угловая) частота, рад/с; ${{\varepsilon }}{\kern 1pt} {\text{'}}$ – относительная диэлектрическая проницаемость материала;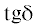

– тангенс угла диэлектрических потерь.

Поскольку ω = 2πf, то формулу (1) можно представить также в виде

(2)

где f – частота электромагнитного поля, Гц.

Из уравнения (2) видно, что глубина проникновения ЭМП в материал обратно пропорциональна частоте поля f.

При ТВЧ-сушке f = 10–25 МГц, при СВЧ-сушке обычно используется разрешенная частота f = = 2450 МГц. Анализ глубины проникновения ЭМП в высушиваемый материал на основе уравнения (2) при частотах f, характерных для ТВЧ- и СВЧ-диапазонов, показывает, что она достаточно велика (масштаб сантиметров), а коэффициент затухания лучистого потока, поступающего в тело, соответственно мал. Поэтому при сушке дисперсных материалов в аппарате, в котором происходит облучение материала по всей поверхности частиц, можно принять, что при ТВЧ- и СВЧ сушке в силу большой глубины проникновения ЭМП во все частицы внутренний объемный источник теплоты ${{q}_{{\text{v}}}}$ (Вт/м³) в каждой частице постоянен: ${{q}_{{\text{v}}}} = {\text{const}}{\text{.}}$

Величину внутреннего объемного источника теплоты q_V можно определить из теплового баланса сушильного аппарата, содержащего этот источник

(3)

${{N}_{{{\text{em}}}}}{{\eta }_{t}}_{~} = {{q}_{{\text{V}}}}V~ = {{q}_{{\text{V}}}}{{V}_{{rab}}}\left( {1--\varepsilon } \right),$

откуда получаем

(4)

${{q}_{{{\text{V\;}}}}} = {{{{N}_{{em}}}{{\eta }_{t}}} \mathord{\left/ {\vphantom {{{{N}_{{em}}}{{\eta }_{t}}} {({{V}_{{rab}}}(1--\varepsilon ))}}} \right. \kern-0em} {({{V}_{{rab}}}(1--\varepsilon ))}},$

где N_em – действующий внутри сушильного аппарата источник электромагнитной энергии, Вт; η_t – термический кпд этого источника; V_rab – рабочий объем аппарата, м³; (1 – ε) – доля рабочего объема, занятого материалом, м³/м³.

ПОСТАНОВКА ЗАДАЧ НАГРЕВА МАТЕРИАЛА ПРИ СУШКЕ В ПОЛЕ ТВЧ- И СВЧ

С учетом вышеизложенного сформулируем задачу нагрева влажного тела в форме неограниченной пластины при ее сушке в поле токов высокой и сверхвысокой частоты, приняв следующие условия и допущения:

– объемный источник теплоты в теле постоянен: q_v = const;

– у поверхностей пластины имеет место конвективный тепло- и массообмен с внешней газовой средой в соответствии с граничными условиями теплообмена [18] и массообмена [19] 3-го рода;

– температура внешней среды постоянна;

– в момент начала процесса температура в пластине распределена равномерно;

– все теплофизические характеристики процесса постоянны;

– пластина равномерно облучается с обеих сторон;

– испарение влаги происходит у поверхностей пластины (внутренние фазовые стоки теплоты отсутствуют);

– термодиффузия (термовлагопроводность) пренебрежимо мала;

– усадка пластины отсутствует.

С учетом изложенного сформулируем линейную задачу электромагнитного нагрева пластины, поместив начало координат в ее центральную плоскость, в виде

(5)

$\frac{{\partial t}}{{\partial {{\tau }}}} = a\frac{{{{\partial }^{2}}t}}{{\partial {{x}^{2}}}} + q_{{\text{v}}}^{*},\,\,\,\,0 < x < R,\,\,\,\,\tau > 0;$

(6)

$t{{\left. {(x,{{\tau }})} \right|}_{{{{\tau }} = 0}}} = {{t}_{n}},\,\,\,\,0 \leqslant x \leqslant R;$

(7)

(8)

${{\left. {\frac{{\partial t}}{{\partial x}}} \right|}_{{x = 0}}} = 0,\,\,\,\,{{\tau }} \geqslant 0,$

где a, $q_{{\text{V}}}^{*} = \frac{{{{q}_{{\text{V}}}}}}{{c\rho }},$ λ, r*, α, R, t_n, t_s = const.

Когда температура пластины больше температуры внешней среды (за счет электромагнитного энергоподвода), то левая часть уравнения (7) больше нуля и, поскольку ${{\left. {t(x,{{\tau }})} \right|}_{{x = R}}} - {{t}_{s}}$ > 0, то имеет место теплоотдача с поверхности пластины во внешнюю более холодную среду, кроме того, отводимая от пластины теплота расходуется на испарение влаги: $r{\text{*}}i({{\tau )}}{\text{.}}$ При ${{\left. {t(x,{{\tau }})} \right|}_{{x = R}}} - {{t}_{s}}$ < 0 (температура внешней среды больше температуры пластины) теплота из этой среды подводится к пластине, расходуется на испарение влаги, а оставшаяся часть идет на нагрев пластины. Таким образом, уравнение (7) учитывает как теплопотери в окружающую холодную среду, так и комбинированный нагрев пластины за счет электромагнитного энергоподвода и подвода теплоты конвекцией от внешней горячей среды. В обоих случаях учитывается сток теплоты на испарение влаги.

Интенсивность сушки i изменяется в ходе процесса, ее можно представить в зависимости от скорости сушки $\left| {\frac{{d\bar {u}}}{{d{{\tau }}}}} \right|$ в виде [19]: $i = \left| {\frac{{d\bar {u}}}{{d{{\tau }}}}} \right|{{R}_{{\text{V}}}}{{{{\rho }}}_{{\text{0}}}},$ где ${{R}_{{\text{V}}}}$ – отношение объема тела к его поверхности (для пластины R_V = R). Воспользуемся аналитическим решением линейной задачи массопроводности для среднеобъемного влагосодержания в пластине при граничном условии массообмена 3-го рода [19]

$\bar {E} = \frac{{\bar {u} - u_{r}^{*}}}{{{{u}_{n}} - u_{r}^{*}}} = \sum\limits_{k = 1}^\infty {\frac{{2{\text{Bi}}_{m}^{2}}}{{{{\mu }}_{k}^{2}\left( {{\text{Bi}}_{m}^{2} + {{\mu }}_{k}^{2} + {\text{B}}{{{\text{i}}}_{m}}} \right)}}} \exp \left( { - {{\mu }}_{k}^{2}{\text{F}}{{{\text{o}}}_{m}}} \right),$

из которого найдем $\left| {\frac{{d\bar {u}}}{{d{{\tau }}}}} \right|$ и далее i(Fo), имея ввиду, что ${\text{F}}{{{\text{o}}}_{m}} = {\text{LuFo,}}$ в виде

(9)

$i({\text{Fo}}) = \left[ {\frac{{{{{{\rho }}}_{{\text{0}}}}a}}{R}{\text{Lu}}\sum\limits_{k = 1}^\infty {{{B}_{k}}{{\mu }}_{k}^{2}\exp ( - {{\mu }}_{k}^{2}{\text{LuFo}})} } \right]\left( {{{{\bar {u}}}_{n}} - u_{r}^{*}} \right),$

где

(10)

${{B}_{k}} = \frac{{2{\text{Bi}}_{m}^{2}}}{{{{\mu }}_{k}^{2}\left( {{\text{Bi}}_{m}^{2} + {{\mu }}_{k}^{2} + {\text{B}}{{{\text{i}}}_{m}}} \right)}},$

${{{{\mu }}}_{k}}$ – корни характеристического уравнения

(11)

${\text{ctg}}{{{{\mu }}}_{k}} = \frac{{{{{{\mu }}}_{k}}}}{{{\text{B}}{{{\text{i}}}_{m}}}}.$

Найдем решение задачи (5)–(8), перейдем к безразмерным величинам:

(12)

$\begin{gathered} z = \frac{х}{R};\,\,\,\,{\text{Fo}} = \frac{{a{{\tau }}}}{{{{R}^{2}}}};\,\,\,\,{\text{Bi}} = \frac{{\alpha R}}{{{\lambda }}}; \\ \varphi ({\text{Fo}}) = 1 - \frac{{r{\text{*}}i({\text{Fo}})R}}{{{\text{Bi}}\lambda ({{t}_{s}} - {{t}_{n}})}} = 1 - \frac{{r{\text{*}}i({\text{Fo}})}}{{{{\alpha }}({{t}_{s}} - {{t}_{n}})}}; \\ W(z,{\text{Fo}}) = \frac{{t(x,{{\tau }}) - {{t}_{n}}}}{{({{t}_{s}} - {{t}_{n}})}};\,\,\,\,{{q}_{0}} = \frac{{q_{{\text{v}}}^{*}{{R}^{2}}}}{{a({{t}_{s}} - {{t}_{n}})}}. \\ \end{gathered} $

Тогда задача (5)–(8) примет следующий вид:

(13)

$\frac{{\partial W}}{{\partial {\text{Fo}}}} = \frac{{{{\partial }^{2}}W}}{{\partial {{{\text{z}}}^{{\text{2}}}}}} + {{q}_{0}},\,\,\,\,0 < z < {\text{1}},\,\,\,\,{\text{Fo}} > 0;$

(14)

${{\left. W \right|}_{{{\text{Fo}} = 0}}} = 0,\,\,\,\,0 \leqslant z \leqslant 1;$

(15)

${{\left. {\frac{{\partial W}}{{\partial z}}} \right|}_{{z = 0}}} = 0,\,\,\,\,{\text{Fo}} > 0;$

(16)

${{\left. {\frac{{\partial W}}{{\partial z}}} \right|}_{{z = 1}}} = - {\text{Bi}}\left[ {{{{\left. W \right|}}_{{z = 1}}} - \varphi ({\text{Fo}})} \right],\,\,\,\,{\text{Fo}} > 0.$

Задачу (13)–(16) решаем методом интегральных преобразований по таблицам Карташова [20, 21]. Запишем три формулы:

интегральное преобразование

(17)

$\bar {W}({{{{\mu }}}_{n}},{\text{Fo)}} = \int\limits_0^1 {W(z,{\text{Fo}})} \cos {{{{\mu }}}_{n}}z{\text{d}}z;$

формула отображения

(18)

$W(z,{\text{Fo}}) = 2\sum\limits_{n = 1}^\infty {\frac{{\left( {{{\mu }}_{n}^{2} + {\text{B}}{{{\text{i}}}^{2}}} \right)}}{{{{\mu }}_{n}^{2} + {\text{B}}{{{\text{i}}}^{2}} + {\text{Bi}}}}} \bar {W}({{{{\mu }}}_{n}},{\text{Fo);}}$

изображение оператора $\frac{{{{\partial }^{2}}W}}{{\partial {{z}^{2}}}}{\text{:}}$

(19)

$\begin{gathered} \int\limits_0^1 {\frac{{{{\partial }^{2}}W}}{{\partial {{z}^{2}}}}} \cos {{\mu }_{n}}z{\text{d}}z = \left( {\frac{{\partial W}}{{\partial z}}{\text{Bi}}W} \right)\cos {{\mu }_{n}} - {{\left. {\frac{{\partial W}}{{\partial z}}} \right|}_{{z = o}}} - \\ - \,\,\mu _{n}^{2}\bar {W}({{\mu }_{n}},{\text{Fo),}} \\ \end{gathered} $

где ${{\mu }_{n}}$ > 0 – корни уравнения ${\text{ctg}}{{\mu }_{n}} = \frac{{{{\mu }_{n}}}}{{{\text{Bi}}}}.$

При нахождении решения с помощью (17)–(19) учли, что

$\int\limits_0^1 {{\text{cos}}{{\mu }_{n}}} z{\text{d}}z = \frac{1}{{{{\mu }_{n}}}}{\text{sin}}{{\mu }_{n}};\,\,\,\,2{\text{cos}}{{\mu }_{n}}{\text{sin}}{{\mu }_{n}} = {\text{sin2}}{{\mu }_{n}}.$

Решение для локальной температуры в безразмерных переменных имеет вид

(20)

$\begin{gathered} W(z,{\text{Fo}}) = 2{\text{Bi}}\sum\limits_{n = 1}^\infty {\frac{{\left( {{{\mu }}_{n}^{2} + {\text{B}}{{{\text{i}}}^{2}}} \right){\text{cos}}{{{{\mu }}}_{n}}{\text{cos}}{{{{\mu }}}_{n}}z}}{{{{\mu }}_{n}^{2} + {\text{B}}{{{\text{i}}}^{2}} + {\text{Bi}}}}} \times \\ \times \,\,\int\limits_{\text{0}}^{{\text{Fo}}} {\varphi (\xi )} \exp \left( { - {{\mu }}_{n}^{2}{\text{(Fo}} - \xi {\text{)}}} \right){\text{d}}\zeta + \\ + \,\,2{{q}_{0}}\sum\limits_{n = 1}^\infty {\frac{{\left( {{{\mu }}_{n}^{2} + {\text{B}}{{{\text{i}}}^{2}}} \right)\sin {{{{\mu }}}_{n}}{\text{cos}}{{{{\mu }}}_{n}}z}}{{{{\mu }}_{n}^{3}\left( {{{\mu }}_{n}^{2} + {\text{B}}{{{\text{i}}}^{2}} + {\text{Bi}}} \right)}}} \left( {1 - \exp \left( { - {{\mu }}_{n}^{2}{\text{Fo}}} \right)} \right){\text{.}} \\ \end{gathered} $

Найдем решение для среднеобъемной температуры $\bar {W}({\text{Fo)}} = \int\limits_0^1 {W(z,{\text{Fo}})} z{\text{d}}z$

(21)

$\begin{gathered} \bar {W}({\text{Fo)}} = {\text{Bi}}\sum\limits_{n = 1}^\infty {\frac{{\left( {{{\mu }}_{n}^{2} + {\text{B}}{{{\text{i}}}^{2}}} \right)\sin 2{{{{\mu }}}_{n}}}}{{{{{{\mu }}}_{n}}\left( {{{\mu }}_{n}^{2} + {\text{B}}{{{\text{i}}}^{2}} + {\text{Bi}}} \right)}}} \int\limits_{\text{0}}^{{\text{Fo}}} {\varphi ({{\xi }})} \times \\ \times \,\,\exp \left( { - {{\mu }}_{n}^{2}{\text{(Fo}} - \xi {\text{)}}} \right){\text{d}}\zeta + \\ + \,\,{{q}_{0}}\sum\limits_{n = 1}^\infty {\frac{{\left( {{{\mu }}_{n}^{2} + {\text{B}}{{{\text{i}}}^{2}}} \right){{{\sin }}^{2}}{{{{\mu }}}_{n}}}}{{{{\mu }}_{n}^{4}\left( {{{\mu }}_{n}^{2} + {\text{B}}{{{\text{i}}}^{2}} + {\text{Bi}}} \right)}}} \left( {1 - \exp \left( { - {{\mu }}_{n}^{2}{\text{Fo}}} \right)} \right){\text{.}} \\ \end{gathered} $

Если $\varphi ({\text{Fo}}) = {{\varphi }_{0}}$ = const, то в выражении (21) интеграл может быть найден. Он равен

(22)

$\int\limits_{\text{0}}^{{\text{Fo}}} {\varphi (\xi )} \exp \left( { - \mu _{n}^{2}{\text{(Fo}} - \xi {\text{)}}} \right){\text{d}}\zeta = \frac{{{{\varphi }_{0}}}}{{\mu _{n}^{2}}}\left( {1 - \exp \left( {\mu _{n}^{2}{\text{Fo}}} \right)} \right){\text{.}}$

Условию φ₀ = const соответствует постоянная интенсивность сушки: i = const (первый период сушки).

Для этого случая можно получить также независимое (более простое) решение задачи электромагнитного нагрева пластины в процессе сушки, если принять, что в периоде постоянной скорости сушки вся подводимая теплота расходуется на испарение влаги и поэтому нет изменения температуры пластины во времени. Сформулируем для этого случая задачу в виде

(23)

$a\frac{{{{d}^{2}}t}}{{d{{x}^{2}}}} + q_{{\text{v}}}^{*} = 0,\,\,\,\,0 < x < R,$

(24)

${{\left. { - {{\lambda }}\frac{{dt(x)}}{{dx}}} \right|}_{{x = R}}} = {{\alpha }}\left[ {{{{\left. {t(x)} \right|}}_{{x = R}}} - {{t}_{s}}} \right] + r{\text{*}}{{i}_{1}},\,\,\,\,x = R,$

(25)

${{\left. {\frac{{dt}}{{dx}}} \right|}_{{x = 0}}} = 0,\,\,\,\,x = 0,$

где a, $q_{{\text{v}}}^{*},$ r*, λ, α, i₁, R, t_s = const.

Получим решение задачи (23)–(25). Перейдем к безразмерным величинам:

(26)

Задача (23)–(25) примет следующий вид:

(27)

$\frac{{{{{\text{d}}}^{2}}W}}{{{\text{d}}{{z}^{{\text{2}}}}}} + {{q}_{0}} = 0,\,\,\,\,0 < z < {\text{1}};$

(28)

${{\left. {\frac{{{\text{d}}W}}{{{\text{d}}z}}} \right|}_{{z = 0}}} = 0;$

(29)

${{\left. {\frac{{{\text{d}}W}}{{{\text{d}}z}}} \right|}_{{z = 1}}} = - {\text{Bi}}\left[ {{{{\left. {W(z)} \right|}}_{{z = 1}}} - {{\varphi }_{0}}} \right].$

Решение задачи (27)–(29) находим по таблицам Карташова [20, 21]. В безразмерных величинах оно имеет вид

(30)

$\begin{gathered} W(z) = 2{{q}_{0}}\sum\limits_{n = 1}^\infty {\frac{{\left( {\mu _{n}^{2} + {\text{B}}{{{\text{i}}}^{2}}} \right)\sin {{\mu }_{n}}{\text{cos}}{{\mu }_{n}}z}}{{\mu _{n}^{3}\left( {\mu _{n}^{2} + {\text{B}}{{{\text{i}}}^{2}} + {\text{Bi}}} \right)}}} - \\ - \,\,2{\text{Bi}}{{\varphi }_{{\text{0}}}}\sum\limits_{n = 1}^\infty {\frac{{\left( {\mu _{n}^{2} + {\text{B}}{{{\text{i}}}^{2}}} \right)\cos {{\mu }_{n}}{\text{cos}}{{\mu }_{n}}z}}{{\mu _{n}^{2}\left( {\mu _{n}^{2} + {\text{B}}{{{\text{i}}}^{2}} + {\text{Bi}}} \right)}}} {\text{,}} \\ \end{gathered} $

где μ_n > 0 – корни уравнения: ctgμ_n = μ_n/Bi.

Средняя по толщине температура $\bar {W}$ = = $\int\limits_0^1 {W(z)} z{\text{d}}z$ равна

(31)

$\begin{gathered} \bar {W} = 2{{q}_{0}}\sum\limits_{n = 1}^\infty {\frac{{\left( {{{\mu }}_{n}^{2} + {\text{B}}{{{\text{i}}}^{2}}} \right){{{\sin }}^{2}}{{{{\mu }}}_{n}}}}{{{{\mu }}_{n}^{4}\left( {{{\mu }}_{n}^{2} + {\text{B}}{{{\text{i}}}^{2}} + {\text{Bi}}} \right)}}} - \\ - \,\,{\text{Bi}}{{\varphi }_{{\text{0}}}}\sum\limits_{n = 1}^\infty {\frac{{\left( {{{\mu }}_{n}^{2} + {\text{B}}{{{\text{i}}}^{2}}} \right)\sin 2{{{{\mu }}}_{n}}}}{{{{\mu }}_{n}^{3}\left( {{{\mu }}_{n}^{2} + {\text{B}}{{{\text{i}}}^{2}} + {\text{Bi}}} \right)}}} . \\ \end{gathered} $

ЧИСЛЕННЫЙ АНАЛИЗ ПРОЦЕССА

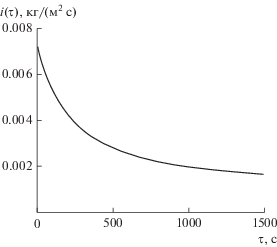
Полученные решения были использованы для численного анализа влияния параметров процесса на кинетику сушки и кинетику электромагнитного нагрева пластины в условиях сушки. Примем: t_s = 20°С; t_n = 18°С; λ = 0.5 Вт/(м К); с = 1250 Дж/(кг К); ρ = 2000 кг/м³; N_em = 75 × 10³ Вт; η_t = 0.9; V_rab = 0.4 × 0.4 × 1 = 0.16 м³; ε = 0.5; r* = = 2400 × 10³ Дж/кг; R = 0.040 м; примем далее α = 10 Вт/(м² К); k = 0.5 × 10^–7 м²/с, что соответствует порядку коэффициента массопроводности капиллярно-пористых материалов с макрокапиллярами [19]. Приведенным выше данным соответствуют следующие параметры задачи: q_V = 8.44 × 10⁵ Вт/м³; $q_{{\text{V}}}^{ * }$ = 0.3375°С/с; q₀ = 1350; a = 2 × 10^–7 м²/с; Bi = 0.8; φ(Fo) = 1 – r*i(Fo)/(α(t_s – ‒ t_n))=1–1.2 × 10⁵i(Fo). Примем далее, что $u_{r}^{*}$ = 0, а ${{\bar {u}}_{n}}$ = 0.25. При принятых толщине пластины 2R = = 0.08 м и величине коэффициента массопроводности k = 0.5 × 10^–7 м²/с задача массообмена будет чисто внутренней, поэтому анализ будем проводить при Bi_m = 100. Рассчитанная по уравнению (9) интенсивность сушки i(τ) при выбранных параметрах процесса показана на рис. 1. Как видно из графика, она в ходе процесса планомерно снижается.

Рис. 1.

Зависимость i(τ) согласно уравнению (9) (k = 0.5 × 10^–7 м²/с; ${{\bar {u}}_{n}}$ = 0.25; $u_{r}^{*}$ = 0; R = 0.040 м; Bi_m = 100).

Примем приведенные выше значения a и k, которым соответствует число Lu = 0.25 и рассмотрим чисто электромагнитный нагрев (температура t_s = 20°С). На основе приведенных выше данных по уравнению (21) с использованием уравнения (9) были рассчитаны функции $\bar {W} = f({\text{Fo)}}$ при значениях числа Bi_m = 100, которые далее были пересчитаны в функции $\bar {t} = f({{\tau )}}{\text{.}}$ Результаты расчетов показаны на рис. 2.

Рис. 2.

Зависимость $\bar {t} = f({{\tau ):}}$ 1 – при i = 0 (отсутствие сушки), 2 – при $i \ne 0$ (сушка при Bi_m = 100).

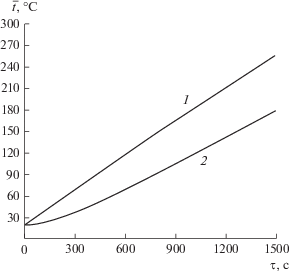
Как видно из графиков, в отсутствие испарения (i = 0) нагрев материала, как и следовало ожидать, происходит более быстро, наличие испарения замедляет процесс нагрева.

Проанализируем далее влияние мощности электромагнитного источника на кинетику нагрева пластины при тех же условиях ее сушки. Результаты этого анализа показаны на рис. 3.

Рис. 3.

Зависимость $\bar {t} = f({{\tau )}}$ при N_em, равном: 1 – 40 кВт; 2 – 50; 3 – 60; 4 – 75 кВт (t_s = 20°С; t_n = 18°С; λ = 0.5 Вт/(м К); с = 1250 Дж/(кг °C); ρ = 2000 кг/м³; η_t = 0.9; V_rab = 0.16 м³; ε = 0.5; r* = 2400 × 10³ Дж/кг; R = 0.040 м; Bi = 0.8; Lu = 0.25; Bi_m = 100).

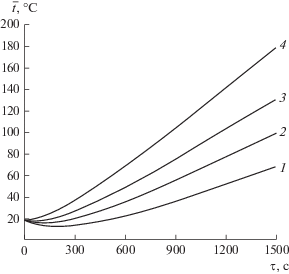
Как показывает рисунок, с увеличением мощности N_em темп нагрева высушиваемого тела закономерно увеличивается. При мощностях электромагнитного источника N_em = 40 и 50 кВт (кривые 1 и 2 на графиках) наблюдается сначала понижение температуры материала во времени, а затем ее рост. Это объясняется влиянием испарительного охлаждения: мощность электромагнитного источника в этих случаях мала и ее вначале не хватает на испарение влаги, поэтому для испарения влаги частично используется теплота, аккумулированная в материале, что понижает его температуру. По мере сушки интенсивность сушки снижается (рис. 1), поэтому подводимая с помощью электромагнитного источника теплота идет уже не только на испарение влаги, но и на нагрев материала, в результате чего его температура растет. При мощностях 60 и 50 кВт подводимой с помощью электромагнитного источника теплоты достаточно для испарения влаги, в результате чего его температура растет сразу после начала процесса. Проведение такого рода расчетов по представленной модели позволяет подобрать необходимую мощность электромагнитного источника.

Если известно, что сушка пластины протекает в первом периоде (высоковлажные материалы), то интенсивность сушки можно рассчитать, используя уравнение (30). При обычной конвективной сушке расчет интенсивности сушки в первом периоде проводят по уравнению массоотдачи

(32)

${{i}_{1}} = {{\beta }_{с}}\left( {{{C}_{{s.p}}}--{{C}_{s}}} \right) = {{\beta }_{p}}\left( {{{p}_{p}}--{{p}_{s}}} \right),$

где β_с, β_p – коэффициенты массоотдачи, отнесенные соответственно к разности концентраций пара в воздухе (кг/(м² с (кг/м³)) и к разности парциальных давлений пара (кг/(м² с Па); C_s.p, C_s – концентрация пара соответственно у поверхности тела и в ядре потока внешней фазы (в среде), кг/м³; p_p, p_s – давление пара соответственно у поверхности испарения и в ядре потока внешней фазы (в среде), Па. Отметим, что расчет интенсивности массоотдачи с использованием коэффициента β_p характерен для работ немецкой научной школы [22].

Концентрацию пара у поверхности материала при конвективной сушке материала в первом периоде находят обычно по температуре мокрого термометра t_m.t с помощью H,d-диаграммы влажного воздуха. Но при электромагнитной или комбинированной “электромагнитно-конвективной” сушке температура поверхности материала в первом периоде не равна температуре мокрого термометра, поэтому для нахождения интенсивности сушки i₁ в этом случае необходимо найти температуру поверхности тела, а по ней определить давление насыщенного пара у поверхности материала (считая, что p_p = р_nas._p) – например, с помощью уравнения Антуана, имеющего вид [23]

(33)

${{р}_{{nas}}} = {\text{ }}{{10}^{5}}\exp {{\left( {A--{B \mathord{\left/ {\vphantom {B {\left( {T--C} \right)}}} \right. \kern-0em} {\left( {T--C} \right)}}} \right)} \mathord{\left/ {\vphantom {{\left( {A--{B \mathord{\left/ {\vphantom {B {\left( {T--C} \right)}}} \right. \kern-0em} {\left( {T--C} \right)}}} \right)} {760}}} \right. \kern-0em} {760}},$

где р_nas – давление насыщенного пара, Па; А, В, С – константы, для воды равные: А = 18.3036; В = = 3816.44; С = 46.13; Т = t + 273, K.

В этих расчетах сначала по соответствующему критериальному уравнению определяют коэффициент массоотдачи β_с, который затем пересчитывают в коэффициент массоотдачи β_p по соотношению [22, 24]: ${{{{\beta }}}_{p}} = {{{{{{\beta }}}_{с}}} \mathord{\left/ {\vphantom {{{{{{\beta }}}_{с}}} {({{R}_{{par}}}{{T}_{{sr}}})}}} \right. \kern-0em} {({{R}_{{par}}}{{T}_{{sr}}})}},$ где ${{T}_{{sr}}} = \frac{{{{T}_{p}} + {{T}_{s}}}}{2}$ – средняя температура пограничного слоя, К [24]. Расчет интенсивности сушки по уравнению (32) ведут в следующей последовательности: 1) задают произвольно температуру поверхности тела t_p; 2) по этой температуре по уравнению Антуана рассчитывают давление насыщенного пара р_nas; 3) по критериальному уравнению определяют коэффициент β_с, который затем пересчитывают в коэффициент β_p; 4) по уравнению (32) рассчитывают интенсивность сушки; 5) по уравнению (30) определяют температуру поверхности тела t_p и сопоставляют ее с предварительно заданной; 6) при несовпадении рассчитанной температуры t_p с предварительно принятой по рассчитанной температуре t_p по уравнению Антуана определяют новое значение р_nas и повторяют расчет (вторая итерация). Итерации повторяют до нужного совпадения предыдущего и последующего значений t_p; 7) получив необходимое совпадение значений t_p, по уравнению (32) находят окончательно интенсивность сушки.

В качестве примера рассчитаем распределение температуры по толщине пластины и интенсивность сушки i₁ при следующих параметрах процесса: N_em = 0.5 кВт; V_rab = 0.16 м³; ε = 0.5; λ = = 0.5 Вт/(м К); с = 1250 Дж/(кг К); ρ = 2000 кг/м³; η_t = 0.9; r* = 2400 × 10³ Дж/кг; R = 0.040 м; α = = 10 Вт/(м² К). Указанным параметрам соответствует значение числа Bi = 0.8. Коэффициент массоотдачи β_с пересчитаем из коэффициента теплоотдачи, используя соотношение [22]:

(34)

$\frac{{{\alpha }}}{{{{{{\beta }}}_{с}}}} = {{\rho }}{{c}_{p}}\frac{{P - {{p}_{{par.sr}}}}}{P},\,\,{{{\text{Дж}}} \mathord{\left/ {\vphantom {{{\text{Дж}}} {\left( {{{{\text{м}}}^{{\text{3}}}}\,{\text{К}}} \right)}}} \right. \kern-0em} {\left( {{{{\text{м}}}^{{\text{3}}}}\,{\text{К}}} \right)}},$

где p_{par. sr} – среднее парциальное давление пара в пограничном слое, Па; ρc_p – объемная изобарная теплоемкость влажного воздуха (Дж/(м³ К), которую находили как теплоемкость газовой смеси, состоящей из двух компонентов – сухого воздуха (условный газ) и водяного пара – по правилу: объемная теплоемкость газовой смеси равна сумме произведений объемных теплоемкостей компонентов на их объемные доли, которые для газовой смеси равны мольным долям. Для сухого воздуха в расчетном температурном интервале приняли ρ_vс_p.v = = 1300 Дж/(м³ К), для водяного пара ρ_parс_p.par = = 1550 Дж/(м³ К) [25]. Тогда теплоемкость влажного воздуха равна

(35)

$\rho {{с}_{p}} = {{\rho }_{{\text{v}}}}{{c}_{{p.{\text{v}}}}}\left( {1--{{y}_{{sr}}}} \right) + {{r}_{{par}}}{{c}_{{p.{\text{ }}par}}}{{y}_{{sr}}},$

где y_sr – средняя мольная доля пара в пограничном слое, равная согласно закону Дальтона y_sr = = p_{par. sr}/P, причем p_{par. sr} = (p_{par. p} + p_{par. s})/2.

Примем влагосодержание воздуха, поступающего в сушилку, d_s = 0.008 кг/(кг сух. воздуха), ему при атмосферном давлении $P = 0.98 \times {{10}^{5}}$ Па соответствует парциальное давление пара p_s = = $\frac{{P{{d}_{s}}}}{{0.622 + {{d}_{s}}}}$ = 1244 Па. Примем далее для 1-го варианта расчета t_s = 20°С; для 2-го варианта t_s = 100°С. Для рассматриваемого процесса: q_V = 0.5625 × × 10⁴ Вт/м³; a = 2 × 10^–7 м²/с; $q_{{\text{V}}}^{*} = 2.25 \times {{10}^{{ - 3}}}$ К/с; φ₀ = 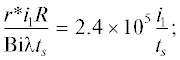${{q}_{0}} = \frac{{q_{{\text{V}}}^{*}{{R}^{{\text{2}}}}}}{{а{{t}_{s}}}} = \frac{{18}}{{{{t}_{s}}}}.$ Результаты расчета при этих параметрах приведены на рис. 4 и в табл. 1.

Рис. 4.

Распределение температуры по толщине пластины при ее сушке в первом периоде (t_s = 100°С; N_em = 0.5 кВт; λ = 0.5 Вт/(м К); с = 1250 Дж/(кг К); ρ = = 2000 кг/м³; η_t = 0.9; V_rab = 0.16 м³; d_s = 0.008 кг/(кг сух. воздуха)).

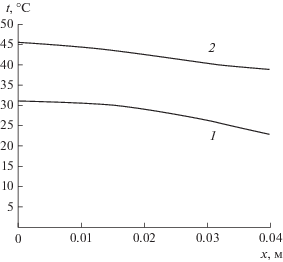
Таблица 1.

Влияние электромагнитного энергоподвода на интенсивность сушки

t_s, °С	q_V = 0		q_V = 5.625 кВт/(м³ материала)
t_s, °С	t_m.t, °С	i₁, г/(м² ч)	t_p, °С	i_1.dop, г/(м² ч)	i_1.dop/i₁
20	14	61.9	22.9	303	4.9
100	34.5	945.4	38.7	1296	1.4

Как видно из рис. 4, при данных параметрах в пластине устанавливается достаточно пологий профиль температуры с ее понижением у поверхности к температуре t_p, которая обеспечивает постоянство скорости сушки. Температура поверхности пластины выше температуры мокрого термометра, которая при d_s = 0.008 кг/(кг сух. воздуха) и t_s = 20°С равна t_{m. t} = 14°C, а при t_s = 100°С равна t_{m. t} = 34.5°C. В случае же электромагнитного энергоподвода и t_s = 20°С температура t_p = 22.9°С, а при t_s = 100°С температура t_p = 38.7°С. Таким образом, дополнительный электромагнитный энергоподвод удельной объемной мощностью q_V = 5.625 кВт/(м³ материала) приводит к повышению температуры поверхности материала соответственно на 8.9 и 4.2°С.

Таблица 1 показывает влияние электромагнитного энергоподвода на интенсивность сушки.

Как видно из табл. 1, электромагнитный энергоподвод в рассматриваемом случае интенсифицирует процесс сушки при t_s = 20°С в 4.9 раза, а при t_s = 100°С – в 1.4 раза. Эти примеры показывают, что предложенная методика позволяет рассчитать интенсивность сушки в первом периоде как при чисто электромагнитном, так и при комбинированном “электромагнитно-конвективном” энергоподводе и численным методом определять эффект интенсификации процесса.

Приведенные математические модели получены при условии постоянства параметров процесса, однако, ряд из них изменяется в ходе процесса (коэффициенты λ, ρ, c, а зависят от влагосодержания и температуры материала, теплота парообразования r* – от температуры). Для учета их изменения может быть использован зональный кусочно-ступенчатый метод расчета [19].

ЗАКЛЮЧЕНИЕ

Развиты аналитические математические модели, описывающие нагрев пластины при ее сушке с действующим внутри непрерывным постоянным электромагнитном источником энергии в условиях конвективного тепло- и массообмена пластины с внешней газовой средой. На основе полученных решений выполнен численный анализ процессов тепло- и массообмена, показывающий их работоспособность как в условиях “чистого” электромагнитного, так и комбинированного “электромагнитно-конвективного” энергоподвода. Применительно к первому периоду сушки получено отдельное решение задачи, позволяющее рассчитывать интенсивность сушки, а также локальные и среднеобъемную температуры пластины. Для учета изменения параметров процесса в его ходе предложено использовать зональный кусочно-ступенчатый метод.

ОБОЗНАЧЕНИЯ

a	коэффициент температуропроводности пластины, м²/с
С	скорость света, м/с
C_s	концентрация пара в сушильном агенте, кг/(м³)
c	теплоемкость пластины, Дж/(кг К)
d	влагосодержание воздуха, обдувающего высушиваемый материал, кг/(кг сух. воздуха)
$\bar {E} = \frac{{\bar {u}({{\tau )}} - {{u}_{r}}}}{{{{u}_{n}} - {{u}_{r}}}}$	среднеобъемное относительное влагосодержание пластины;
f	частота электромагнитного поля, Гц
i	интенсивность сушки пластины, кг/(м² с)
k	коэффициент массопроводности (коэффициент диффузии влаги в пластине), м²/с
N_em	мощность электромагнитного источника, Вт
${{q}_{0}}$	плотность потока лучистой энергии, падающего на поверхность пластины, Вт/м²
${{q}_{{\text{v}}}} = \frac{{{{N}_{e}}\eta }}{{V(1 - {{\varepsilon )}}}}$	внутренний объемный источник теплоты в пластине, Вт/м³
$q_{{\text{v}}}^{*} = \frac{{{{q}_{{\text{v}}}}}}{{c{{\rho }}}}$	внутренний объемный источник теплоты в пластине, отнесенный к ее объемной теплоемкости, °С/с
P	общее давление, Па
R	половина толщины пластины, м
$R_{{par}}^{*}$	газовая постоянная водяного пара, равная 462 Дж/(кг К)
R_V	отношение объема пластины к ее поверхности, м
$r{\text{*}}$	теплота парообразования, включая теплоту десорбции влаги, Дж/кг
T	температура, К
t	локальная температура в пластине, °С
$\bar {t}$	среднеобъемная температура пластины, °С
$u,\bar {u}$	локальное и среднее по объему пластины влагосодержание соответственно, кг/(кг сух. материала)
V	внутренний объем аппарата, м³
x	декартова координата, м
α	коэффициент теплоотдачи, Вт/(м² К)
β_с	коэффициент массоотдачи, отнесенный к разности концентраций C_s, м/с
β_p	коэффициент массоотдачи, отнесенный к разности парциальных давлений пара, кг/(м² с Па)
ε	доля свободного объема аппарата, м³/м³
$\lambda $	коэффициент теплопроводности пластины, Вт/(м К)
ρ	плотность материала пластины, кг/м³
τ	время, с
ω	круговая (угловая) частота электромагнитного поля, рад/с
${\text{Bi}} = {{{{\alpha }}R} \mathord{\left/ {\vphantom {{{{\alpha }}R} {{\lambda }}}} \right. \kern-0em} {{\lambda }}}$	тепловое число Био
Bi_m	модифицированное массообменное число Био
$Fo = {{a\tau } \mathord{\left/ {\vphantom {{a\tau } {{{R}^{2}}}}} \right. \kern-0em} {{{R}^{2}}}}$	тепловое число Фурье
$F{{o}_{m}} = {{k\tau } \mathord{\left/ {\vphantom {{k\tau } {{{R}^{2}}}}} \right. \kern-0em} {{{R}^{2}}}}$	массообменное число Фурье
Lu = k/a	число Лыкова

ИНДЕКСЫ

0	абсолютно сухой материал
1	первый период сушки
dop	с дополнительным электромагнитным энергоподводом
em	электромагнитный
m	массообменный
m. t	мокрый термометр
n	начальный
p	поверхность пластины
par	пар
r	равновесный
s	сушильный агент
sr	среднее значение
t	термический
v	воздух

Список литературы

Рогов И.А., Некрутман С.В. Сверхвысокочастотный нагрев пищевых продуктов: учебное пособие. М.: Агропромиздат, 1986.
Kudra T., Strumillo Cz. Thermal Processing of Bio-Materials. Amsterdam: Gordon and Breach Science, 1998.
Акулич П.В., Драгун В.Л., Куц П.С. Технологии и техника сушки и термообработки материалов. Минск: Белорусская наука, 2006.
Ratti C., Mujumdar A.S. Handbook of Industrial Drying. Boca Raton, Fla.: CRC, 2007.
Bon J., Kudra T. Enthalpy-Driven Optimization of Intermittent Drying // Drying Technol. 2007. V. 25. № 4. P. 523.
Vaquiro H.A., Clemente G., Garcia-Perez J.V., Mulet A., Bonb J. Enthalpy-driven optimization of intermittent drying of Mangifera indica L. // Chem. Eng. Res. Des. 2009. V. 87. P. 885.
Рудобашта С.П., Григорьев И.В. Импульсная инфракрасная сушка семян // Пром. теплотех. 2011. Т. 33. № 8. С. 85.
Рудобашта С.П., Карташов Э.М., Зуев Н.А. Тепломассоперенос при сушке в осциллирующем электромагнитном поле // Теор. осн. хим. технол. 2011. Т. 45. № 6. С. 641.
Zhao D., An K., Ding S., Liu L., Xu Z., Wang Z. Two-stage intermittent microwave coupled with hot-air drying of carrot slices: Drying kinetics and physical quality // Food Bioprocess Technol. 2014. V. 7. № 8. P. 2308.
Kumar C., Joardder M.U.H., Farrell T.W., Millar G.J., Karim M.A. Mathematical model for intermittent microwave convective drying of food materials // Drying Technol. 2016. V. 34. № 8. P. 962.
Гринчик Н.Н., Акулич П.В., Адамович А.Л., Куц П.С., Кундас С.П. Моделирование неизотермического тепло- и влагопереноса в капиллярно-пористых средах при периодическом микроволновом нагреве // Инж.-физ. журн. 2007. Т. 80. № 1. С. 3.
Акулич П.В. Тепломассообмен капли раствора при комбинированном энергетическом воздействии и углублении зоны испарения // Инж.-физ. журн. 2016. Т. 89. № 3. С. 527.
Акулич П.В., Темрук А.В., Акулич А.В. Моделирование и эксперименталь ное исследование тепло- и влагопереноса при СВЧ-конвективной сушке растительных материалов // Инж.-физ. журн. 2012. Т. 85. № 5. С. 951.
Rudobashta S.P., Zueva G.A. Heat and mass transfer when drying a spherical particle in an oscillating electromagnetic field // Theor. Found. Chem. Eng. 2016. V. 50. № 5. P. 718.
Rudobashta S.P., Zueva G.A., Kartashov E.M. Heat and mass transfer in the drying of a cylindrical body in an oscillating electromagnetic field // J. Eng. Phys. Thermophys. 2018. V. 91. № 1. P. 227.
Rudobashta S., Zueva G., Zuev N. Mathematical Modeling and Numerical Simulation of Oscillating Infrared Seeds Drying Process // Drying Technol. 2014. V. 32. № 11. P. 1352.
Rudobashta S., Zueva G. Drying of seeds through oscillating infrared heating // Drying Technol. 2016. V. 34. № 5. P. 505.
Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1968.
Рудобашта С.П. Массоперенос в системах с твердой фазой. М.: Химия, 1980.
Рудобашта С.П., Карташов Э.М. Химическая технология: диффузионные процессы. Часть 2. М.: Юрайт, 2015.
Карташов Э.М. Оригиналы операционных изображений для обобщенных задач нестационарной теплопроводности // Тонкие хим. технол. 2019. Т. 14. № 4. С. 77.
Krischer O. Die wissenchaftlichen Grundlagen der Trocknung Technick. Heidelberg: Springer-Verlag, 1957.
Рид Р., Праусниц Дж., Шервуд Т. Свойства газов и жидкостей. Л.: Химия, 1982.
Лыков А.В. Теория сушки. М.: Госэнергоиздат, 1950.
Рабинович О.М. Сборник по технической термодинамике. М.: Машиностроение, 1969.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал