Теоретические основы химической технологии, 2021, T. 55, № 3, стр. 359-366
Процесс α-релаксации и температурно-частотная неупругость композита поливиниловый спирт–хитозан
В. А. Ломовской a, *, Н. А. Абатурова a, Н. Ю. Ломовская a, Т. Б. Галушко a
a Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
Москва, Россия
* E-mail: lomovskoy@phyche.ac.ru
Поступила в редакцию 27.07.2020
После доработки 27.10.2020
Принята к публикации 20.11.2020
Аннотация
По спектрам внутреннего трения и температурным зависимостям частоты свободных затухающих крутильных колебаний, возбуждаемых в композитной системе хитозан–поливиниловый спирт при соотношении компонентов 1 : 1, проведен расчет физико-механических и физико-химических характеристик процесса α-релаксации и дан теоретический анализ использования функции Кольрауша для описания релаксационной микронеоднородности структурно-кинетических элементов, подвижность которых и определяет возникновение этого диссипативного процесса.
ВВЕДЕНИЕ
Системам хитозан–поливиниловый спирт посвящен целый ряд физико-химических исследований [1–6].
Отдельно следует упомянуть труды некоторых авторов, всесторонне изучавших влияние молекулярной массы и степени дезацетилирования хитозана и поливинилового спирта [7] на свойства смесевых пленок и кинетику сорбции воды такими композитами [8]. Также исследовали гидрогели, содержащие хитозан и поливиниловый спирт с точки зрения использования их в медицине [9, 10].
Композиты из хитозана (ХЗ) и поливинилового спирта (ПВС) изучаются как с целью улучшения физико-механических свойств пленок хитозана, так и с целью придания пленкам ПВС уникальных свойств хитозана.
Композиты создаются различными способами: например из сухих компонентов путем воздействия давления и сдвиговых напряжений [11], поливом на подложку смесей компонентов в общем растворителе [12, 13]. При формировании хитозановых волкон (нановолокон) ввиду высокой жесткости заряженных цепей ХЗ для снижения вязкости формовочных растворов применяется введение гибкоцепного полимера ПВС [14, 15].
Как было отмечено в работе [16], композитная система (ПВС–ХЗ), в которой соотношение компонентов может варьироваться в интервале от 0 до 100%, является перспективной системой для получения материала биомедицинского назначения. При этом одним из условий использования этих материалов является возможность их получения с различной степенью жесткости, т.е. с определенными температурными областями проявления неупругой реакции на внешнее деформирующее воздействие как статического, так и динамического режимов.
Целью настоящей работы является проведение теоретического анализа влияния соотношения компонентов в системе ПВС–ХЗ на температурно-частотную область неупругости, определяемую процессом α-релаксации. Требовалось представить вид функции релаксации, определяющей релаксационную микронеоднородность процесса в этой области неупругости для отработки химической технологии получения композита с заданными свойствами. Для достижения цели решались следующие задачи.
1. Получение спектров внутреннего трения $\lambda = f(T)$ композитной системы ПВС–ХЗ (в соотношении 1 : 1), а также исходных компонентов, и
температурных зависимостей частоты $\nu = f(Т)$ свободных затухающих крутильных колебаний, возбуждаемых в исследуемой системе;
$\lambda = f(T)$ композитной системы ПВС–ХЗ (в соотношении 1 : 1), а также исходных компонентов, и
температурных зависимостей частоты $\nu = f(Т)$ свободных затухающих крутильных колебаний, возбуждаемых в исследуемой системе;
2. Определение физико-механических и физико-химических характеристик $\alpha $-релаксации в данной композитной системе;
3. Определение функции релаксации, описывающей $\alpha $-процесс и ее связи с температурной зависимостью частоты $\nu = f(Т)$ изучаемого процесса;
4. Теоретический анализ возможности использования определенной функции релаксации в динамических режимах внешнего деформирующего воздействия для расчета непрерывных спектров времен процесса $\alpha $-релаксации.
ОБРАЗЦЫ И МЕТОДИКИ
Для получения композитной системы ПВС–ХЗ использовали хитозан производства ЗАО “Биопрогресс”, полученный щелочным дезацетилированием крабового хитина (степень дезацетилирования 78%, ММ 12 × 104 Да) и поливиниловый спирт марки “MOWIOL Kurary Specialinies Europe” (степень гидролиза 88%, ММ 68 × 103 Да). Молекулярную массу ПВС определяли вискозиметрически. Отдельно готовились растворы каждого из компонентов, входящих в состав композита. ПВС растворяли в дистиллированной воде при нагревании, ХЗ растворяли в 2% водном растворе уксусной кислоты. Приготовленные растворы смешивались в определенном соотношении и тщательно перемешивались. Готовую смесь разливали на подложки и высушивали до полного отделения от подложки, с последующим досушиванием в термошкафу и в эксикаторе над хлористым кальцием. Спектры внутреннего трения λ = f(T) и температурные зависимости частоты ν = f(T) изучали на горизонтальном крутильном маятнике в режиме свободно затухающих крутильных колебаний в диапазоне температур от ‒150 до 250°С с шагом нагрева в 1°С, (подробное описание дано в работе [17]). Суть метода и принцип работы прибора изложены в [18].
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
На рис. 1 представлены полученные спектры $\lambda = f(T)$ и температурные зависимости частоты $\nu = f(Т)$ для композита и для чистых исходных компонентов. Видно, что наиболее интенсивные диссипативные процессы наблюдаются в области температур стеклования Tα max.
Рис. 1.
Спектры внутреннего трения λ = f(T) (а) и температурные зависимости частоты ν = f(T) (б) для ПВС (1), композита (2) и хитозана (3).
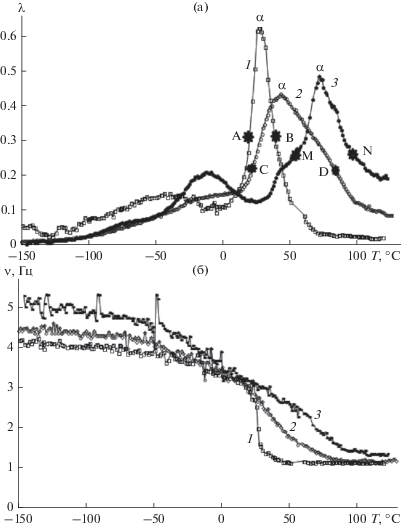
Интенсивность диссипативных потерь в максимуме пика α-релаксации, т.е. λα max = f(x), различна у исследуемых образцов и имеет минимум у композита (рис. 2а).
Рис. 2.
Изменение величины диссипативных потерь α-релаксации (а) и ширина пика диссипативных потерь на уровне λαmax/2 (б) для ПВС, хитозана и композита.
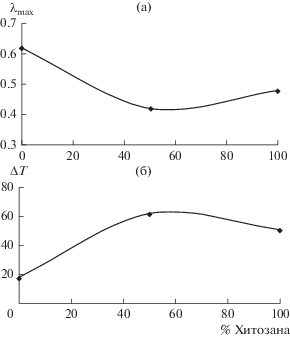
Кроме того, изменяется и температурный интервал $\Delta {{T}_{{{\alpha }}}}$ в исследуемых системах. Температурный интервал ΔТα рассматривается по секущей линии на уровне: $\frac{{\lambda \alpha \max }}{2}:$ точки А–В, С–D, М–N (рис. 1а, кривые 1–3; рис. 2б.; табл. 1).
Таблица 1.
Физико-химические характеристики изучаемых релаксационных процессов
| Состав пленки | ναmax, Гц | ταmax, с | Uαmax, кДж/моль | Тαmax, К | Δτ, с | λαmax | ΔTτ, °С |
|---|---|---|---|---|---|---|---|
| ПВС | 2.0 | 8.0 × 10–2 | 58.7 | 301 | 0.117 | 0.62 | 18 |
| ПВС–ХЗ | 2.1 | 7.6 × 10–2 | 61.5 | 316 | 0.306 | 0.42 | 62 |
| ХЗ | 3.0 | 5.3 × 10–2 | 66.0 | 344 | 0.194 | 0.48 | 51 |
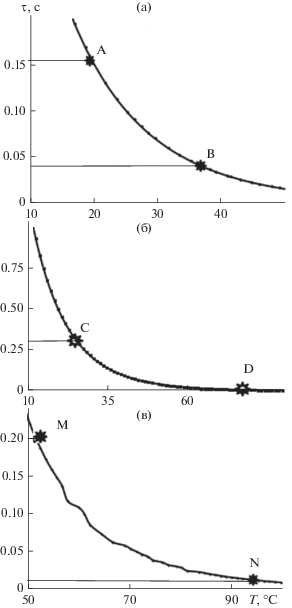
Температурная зависимость частоты $\nu = f(Т)$ колебательного процесса, возбуждаемого в исследуемой системе (рис. 1б) в области проявления на спектре α-релаксации, характеризуется аномалией различной интенсивности и различного температурного интервала. Эта аномалия описывается в виде дефекта модуля $\Delta G,$ определяемого диапазоном изменения квадратов частот $\nu _{i}^{2}$ [16]. По методике расчета физико-химических характеристик релаксационных процессов, проявляемых в виде пика диссипативных потерь на спектре $\lambda = f(T)$ [16], были рассчитаны изменения этих характеристик для исследуемых образцов (табл. 1, рис. 3).
Рис. 3.
Температурная зависимость времени релаксации α-диссипативного процесса τα для ПВС (а), композита (б) и хитозана (в). Точки А–B, C–D и M–N соответствуют температурам, отмеченным на рис. 1.
Для качественного анализа изменения непрерывного спектра времен релаксации H(τ) следует принять во внимание, что любой диссипативный процесс релаксационной природы является локальным (по температурному проявлению в режиме свободных затухающих крутильных колебаний) процессом неупругости, что и вызывает появление положительного дефекта модуля сдвига ΔG [19].
Учитывая связь частоты колебательного процесса, возбужденного в исследуемом образце, и модуля сдвига (упругости) исследуемой системы, образующей данный образец, можно использовать температурную зависимость $\nu = f(Т)$ в интервале наблюдения дефекта модуля ΔG, как определенного вида функцию релаксации φ(t – ti) ≡ φ(θ) [20] в интегральном уравнении теории неупругости – уравнении Больцмана–Вольтерра:
(1)
${{\sigma }_{{ij}}}\left( t \right) = {{\gamma }_{0}}G - G\int\limits_0^t {\varphi \left( {t - {{t}_{0}}} \right)} \gamma \left( {{{t}_{0}}} \right)d\theta ,$Уравнение Больцмана–Вольтерра (1) показывает связь между изменением модуля и временем, однако для использования этого уравнения при описании H(τ) требуется решение трех теоретических проблем:
– установить аналитическую зависимость между модулем (дефектом модуля) и температурой;
– определить аналитический вид функции релаксации φ(θ) и ее связь с температурой и дефектом модуля ΔG;
– определить границы использования выбранной функции релаксации в режиме динамических внешних деформирующих воздействий.
ОПРЕДЕЛЕНИЕ АНАЛИТИЧЕСКОЙ ЗАВИСИМОСТИ МЕЖДУ МОДУЛЕМ (ДЕФЕКТОМ МОДУЛЯ) И ТЕМПЕРАТУРОЙ
Экспериментальные исследования процесса структурного стеклования, имеющего релаксационный механизм диссипативных потерь в аморфных стеклообразных системах различной химической природы [21–23], показали, что непрерывный спектр времен релаксации H(τ) этого процесса в статическом режиме внешнего воздействия, выводящего систему из состояния термодинамического и механического равновесия, может быть описан дробно-экспоненциальной функцией Кольрауша:
(2)
$\varphi \left( t \right) = \exp \left[ { - {{{\left( {\frac{t}{\tau }} \right)}}^{b}}} \right],$Для исследования функции (2) для релаксационных явлений, наблюдаемых в исследуемых системах в виде отклика на динамические внешние воздействия в широком температурно-частотном диапазоне, необходимо установить связь между функцией релаксации φ(t), полученной в статическом режиме с функцией релаксации φ(θ), полученной в динамическом режиме.
Функция релаксации Кольрауша (2) представляет собой обычную максвелловскую экспоненту, у которой параметр дробности b = 1.
Учитывая температурную зависимость времени релаксации в виде
и соотношения
функция релаксации φ(t) (соотношение (2)) может быть представлена для описания релаксационного процесса в динамических режимах в следующем виде:
(6)
$\varphi \left( \theta \right) = \exp \left[ { - \frac{\theta }{{2\pi {{\tau }_{0}}\exp \left( {\frac{{{{U}_{{{\alpha }}}}}}{{R{{T}_{i}}}}} \right)}}} \right],$Таким образом, φ(θ) зависит как от температуры исследования Т, так и от времени (периода) наблюдения или частоты ν. Эта зависимость является экспоненциальной.
Итак, установлено, что зависимость дефекта модуля от температуры и частоты свободных затухающих колебаний, т.е. ΔG = f(T; ν), где ν также есть функция температуры ν = f(T), является экспоненциальной в приближении максвелловской экспоненты (b = 1).
Однако, как видно из экспериментальных зависимостей ν = f(T) (рис. 1б), температурный интервал изменения модуля сдвига для α-релаксации, т.е. ΔG = f(T), различен для исследуемых систем.
Из этого следует, что описать зависимость ν = = f(T), а следовательно, и G = f(T) одной простой экспонентой Максвелла не удастся.
Поэтому необходимо использовать дробно-экспоненциальную функцию Кольрауша, в которой показатель степени b характеризует “протяженность” эксперимента.
В работах [16, 24, 25] был проведен теоретический анализ использования функции Максвелла в динамических режимах внешнего деформирующего воздействия.
В данной работе требуется провести аналогичный анализ использования дробно-экспоненциальной функции Кольрауша (соотношение (2)), при этом данная функция должна удовлетворять следующим условиям:
(7)
$\begin{gathered} 1.\,\,\mathop {\lim }\limits_{t = 0} \varphi \left( t \right) = 1, \hfill \\ 2.\,\,\mathop {\lim }\limits_{t \to 0} \varphi \left( t \right) = \mathop {\lim }\limits_{p \to \infty } p\bar {\varphi }\left( p \right), \hfill \\ 3.\,\,\mathop {\lim }\limits_{t \to \infty } \varphi \left( t \right) = 0 = {\text{const,}} \hfill \\ {\text{4}}{\text{.}}\,\,\mathop {\lim }\limits_{t \to \infty } \varphi \left( t \right) = \mathop {\lim }\limits_{p \to 0} p\bar {\varphi }\left( p \right). \hfill \\ \end{gathered} $Преобразование Лапласа для функции Кольрауша имеет следующий вид:
(8)
$\begin{gathered} \bar {\varphi }\left( p \right) = \Lambda \left[ {\varphi \left( t \right)} \right] = \int\limits_0^\infty {\exp \left[ { - {{{\left( {\frac{t}{\tau }} \right)}}^{b}}} \right]} \exp \left( { - pt} \right)dt = \\ = \int\limits_0^\infty {\exp \left\{ { - \left[ {\exp {{{\left( {\frac{t}{\tau }} \right)}}^{b}} + pt} \right]} \right\}dt} , \\ \end{gathered} $Использование степенного ряда, сходимого по всей числовой оси t в виде
(9)
$\begin{gathered} {{e}^{{{{{\left( { - \frac{t}{{{\tau }}}} \right)}}^{b}}}}} = 1 - {{\left( {\frac{t}{\tau }} \right)}^{b}} + \frac{1}{{2!}}{{\left( {\frac{t}{\tau }} \right)}^{{2b}}} - \frac{1}{{3!}}{{\left( {\frac{t}{\tau }} \right)}^{{3b}}} + .... + \\ + \,\,\frac{1}{{n!}}{{\left( {\frac{t}{\tau }} \right)}^{{nb}}} + .... = \sum\limits_{n = 0}^\infty {\frac{{{{{\left( { - 1} \right)}}^{n}}}}{{n!}}} {{\left( {\frac{t}{\tau }} \right)}^{{nb}}} \\ \end{gathered} $позволяет представить соотношение (8) в виде
(10)
$\begin{gathered} \bar {\varphi }\left( p \right) = \Lambda \left[ {{{e}^{{ - {{{\left( {\frac{t}{{{\tau }}}} \right)}}^{b}}}}}} \right] = \sum\limits_{n = 0}^\infty {\frac{{{{{\left( { - 1} \right)}}^{n}}}}{{n!{{\tau }^{{nb}}}}}} \Lambda \left[ {{{t}^{{nb}}}} \right] = \\ = \sum\limits_{n = 0}^\infty {\frac{{{{{\left( { - 1} \right)}}^{n}}}}{{n!{{\tau }^{{nb}}}}}} \frac{{{\text{Г}}\left( {nb + 1} \right)}}{{{{p}^{{nb + 1}}}}} = \sum\limits_{n = 0}^\infty {\frac{{{{{\left( { - 1} \right)}}^{n}}}}{{n!}}} \frac{{\tau {\text{Г}}\left( {nb + 1} \right)}}{{{{{\left( {p\tau } \right)}}^{{nb + 1}}}}} = \\ = \tau \sum\limits_{n = 0}^\infty {{{{\left( { - 1} \right)}}^{n}}} \frac{{{\text{Г}}\left( {nb + 1} \right)}}{{n!}}\frac{1}{{{{{\left( {pt} \right)}}^{{nb + 1}}}}}. \\ \end{gathered} $При разложении в ряд соотношение (10) будет сходиться во всей комплексной области, кроме начала координат. Но так как каждый член ряда имеет смысл лишь в правой полуплоскости, т.е. Rep > 0, то этот ряд нужно рассматривать также при всех значениях Rep > 0.
Таким образом, функция Кольрауша может быть использована для описания процессов локальной неупругости, определяемых по спектрам внутреннего трения λ = f(T) и температурными зависимостями частоты свободно затухающего колебательного процесса ν = f(T), возбуждаемого в исследуемом образце.
Для определения зависимости функции релаксации φ(t) от температуры, т.е. φ(t) = f(T), и от частоты ν колебательного процесса, возбуждаемого в исследуемой системе, т.е. φ(t) = f(ν), необходимо установить следующие функциональные связи:
– зависимость времени релаксации τα от температуры, т.е. τα = f(T);
– зависимость дефекта модуля ΔG температуры, т.е. ΔG = f(T);
– возможность описания температурной зависимости ΔG = f(T) экспоненциальной функцией релаксации, т.е. выявить корреляционные связи $\Delta G = f(T) \equiv \varphi (T).$
Расчет зависимости τα = f(T) для системы ПВС, композит ПВС–ХЗ, ХЗ представлен на рис. 3.
Температурный интервал изменения τ (ΔТ) для исследуемых объектов различен (табл. 1). Минимальный интервал характерен для системы ПВС (рис. 3а), а максимальный – для системы ПВС–ХЗ (рис. 3б). Интервал ΔТ для системы ХЗ представлен на рис. 3в.
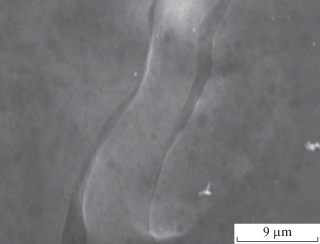
В композитной системе обе структурно-кинетические подсистемы неупруго реагируют на внешнее деформирующее воздействие, что и приводит к значительному расширению по температуре локальной области неупругости. Следует отметить, что эти подсистемы не образуют совместных связанных кинетическими связями структурных подсистем. На рис. 4 четко видны поверхности раздела для этих подсистем.
При температурах T < T = 43°C основными релаксирующими элементами являются сегменты ПВС, а при Т > 43°С – элементы ХЗ, т.е. структурный комплекс представляет собой систему проникновения двух невзаимодействующих структурных подсистем (компонентов) в объеме композита. Плавное изменение соотношения, рассмотренное в работе [16], приводит к взаимному обратимому переходу подсистем на матрицу и наполнитель.
Как было показано ранее [16, 26], температурная зависимость модуля сдвига G = f(T) описывается экспериментальной зависимостью частоты ν = f(T) с последующим расчетом величины и знака дефекта модуля ΔG, и соответственно определения температурной зависимости дефекта модуля, т.е. ΔG = f(T).
Кроме того, в той же работе [16] было показано, что зависимость ΔG = f(T) коррелирует с температурной зависимостью – экспоненциальной функцией релаксации, где в качестве времени наблюдения (статический режим) используется период колебательного процесса, возбуждаемого в исследуемой системе (динамический режим), т.е.
где θ – период колебания.Теоретическое исследование зависимости lnτ = = $f\left( {\frac{1}{T}} \right)$ для рассматриваемых систем (рис. 5) показывает их несовпадение, хотя энергия активации этого процесса изменяется незначительно (табл. 1).
Рис. 5.
Логарифмическая зависимость времен релаксации от обратной температуры для ПВС (1), композита (2) и ХЗ (3).
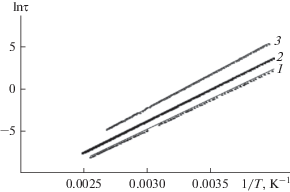
В этом случае причиной или одной из основных причин этого несовпадения является различное численное значение параметра дробности b в функции Кольрауша (0 < b ≤ 1).
Именно численное значение этого параметра характеризует степень релаксационной микронеоднородности реагирующей неупруго подсистемы или совокупности подсистем в композите ПВС–ХЗ.
ЗАКЛЮЧЕНИЕ
В настоящей работе установлено, что температурное положение Tαmax, интенсивность λαmax и энергия активации Uα диссипативного процесса α-релаксации различны для ПВС, ХЗ и композитного материала ПВС–ХЗ, причем значения указанных величин для системы ПВС–ХЗ свидетельствуют об улучшении механических свойств образцов ХЗ. Очевидно влияние введения ПВС в хитозан на свойства композитного материала.
Показано, что в качестве ядра релаксации при описании α-процесса в рамках наследственной теории неупругости Больцмана–Вольтерра может быть использована дробно-экспоненциальная функция Кольрауша. Параметр дробности этой функции может характеризовать степень релаксационной микронеоднородности структурно-кинетических элементов, подвижность которых и определяет возникновение наблюдаемого диссипативного процесса.
Работа выполнена в рамках государственного задания Института физической химии и электрохимии им. А.Н. Фрумкина РАН.
ОБОЗНАЧЕНИЯ
| b | параметр дробности в функции Кольрауша |
| ΔG | дефект модуля сдвига |
| Н(τ) | непрерывный спектр времен релаксации |
| T | температура, °C |
| t | текущее время, с |
| t0 | время приложения внешнего деформирующего воздействия, с |
| Uα | энергия активации, Дж |
| γ | деформация (угол закручивания образца) |
| θ = t – t0 | время наблюдения процесса релаксации, период колебания, с |
| Λ | оператор Лапласа |
| λ | логарифмический декремент |
| ν | частота затухания колебательного процесса, Гц |
| σij | касательные напряжения, возникающие в образце при кручении, Па |
| τ | дискретное время релаксации системы для постоянной температуры, c |
| φ(t) | функция релаксации в статическом режиме |
| φ(θ) | функция релаксации в динамическом режиме |
| $\bar {\varphi }$ | преобразование Лапласа |
| ω | угловая частота (ω = 2 πν), c–1 |
Список литературы
Хитозан / Под ред. Скрябиной К.Г., Михайлова С.Н., Варламова В.П. М.: Центр “Биоинженерия” РАН, 2013.
Grebennikov S.F., Vnuchkin A.V., Sashina E.S. Тhermodynamic features of mixing of chitosan with polyvinyl alcohol and polyethylene oxide // Russ. J. Appl. Chem. 2010. V. 83. № 7. P. 1189. [Гребенников С.Ф., Внучкин А.В., Сашина Е.С. Термодинамика смешения хитозана с поливиниловым спиртом и полиэтиленоксидом // Журн. прикл. хим. 2010. Т. 83. № 7. С. 1085.
Внучкин А.В. Физико-химическое исследование совместимости хитозана с поливиниловым спиртом и полиэтиленоксидом в растворах и пленках. Автореф. дис. … канд. хим. наук. СПб., 2009.
Чалых А.Е., Петрова Т.Ф., Матвеев В.В., Герасимов В.К., Хасбиуллин Р.Р. Фазовые равновесия и фазовая структура смеси хитозан–поливиниловый спирт // Сборник тр. XXV Всероссийской конференции “Структура и динамика молекулярных систем” и 16-й школы молодых ученых / Под ред. Щербиной А.А. 2018. С. 384.
Внучкин А.В., Сашина Е.С., Добровольская И.П., Попрядухин П.В. Свойства растворов смесей хитозана и поливинилового спирта и волокон на их основе // Вестн. С.-Петерб. гос. унив. технол. дизайна. Естеств. техн. науки. 2010. № 1. С. 3.
Sashina E.S., Vnuchkin A.V., Novoselov N.P. A study of the thermodynamics of chitosan interaction with polyvinyl alcohol and polyethylene oxide by differential scanning calorimetry // Russ. J. Appl. Chem. 2006. V. 79. № 10. P. 1643. [Сашина Е.С., Внучкин А.В., Новоселов Н.П. Термодинамические параметры взаимодействия хитозана с поливиниловым спиртом и полиэтиленоксидом по данным дифференциальной сканирующей калориметрии // Журн. прикл. хим. 2006. Т. 79. № 10. С. 1664.]
Lewandowska K. Miscibility and thermal stability of poly(vinyl alcohol)/chitosan mixtures // Thermochim. Acta. 2009. V. 493. P. 42.
Mucha M. Ludvwiczak S., Kawinska M. Kinetics of water sorption by chitosan and its blends with poly(vinyl alcohol) // Carbohydr. Polym. 2005. V. 62. P. 42.
Kim S.J., Park S.J., Kim S.I. Swelling behavior of interpenetrating polymer network hydrogels composed of poly(vinyl alcohol) and chitosan // React. Funct. Polym. 2003. V. 55. P. 53.
Wang T., Turhan M., Gunasekaran S. Selected properties of pH-sensitive, biodegradable chitosan–poly(vinyl alcohol) hydrogel // Polym. Int. 2004. V. 53. P. 911.
Ozerin A.N., Perov N.S., Zelenetskii A.N., Akopova T.A., Ozerina L.A., Kechek’yan A.S., Surin N.M., Vladimirov L.V., Yulovskaya V.D. Hybrid Nanocomposites Based on Graft Copolymer of Chitosan with Poly(vinyl alcohol) and Titanium Oxide // Nanotechnol. Russ. 2009. V. 4. № 5–6. P. 331. [Озерин А.Н., Перов Н.С., Зеленецкий А.Н., Акопова Т.А., Озерина Л.А., Кечекьян А.С., Сурин Н.М., Владимиров Л.В., Юловская В.Д. Гибридные нанокомпозиты на основе привитого сополимера хитозана с поливиниловым спиртом и оксида титана // Росс. нанотехнол. 2009. Т. 4. № 5–6. С. 76.]
Kulish E.I., Kolesov S.V. A study of structure formation in chitosan-polyvinyl alcohol blends by turbidity spectroscopy // Russ. J. Appl. Chem. 2005. V. 78. № 9. P. 1486. [Кулиш Е.И., Колесов С.В. Исследование структурообразования в смесях хитозан–поливиниловый спирт // Журн. прикл. хим. 2005. Т. 78. № 9. С. 1511.]
Mukhina V.R., Pastukhov N.V., Semchikov Yu.D., Smirnova L.A., Kir’yanov K.V., Zhernenkov N.N. Properties of solutions and films of chitosan blends with poly(vinyl alcohol) // Polym. Sci., Ser. A. 2001. V. 43. № 10. P. 1034. [Мухина В.Р., Пастухова Н.В., Семчиков Ю.Д., Смирнова Л.А., Кирьянов К.В., Жерненков Н.Н. Свойства растворов и пленок смесей хитозана с поливиниловым спиртом // Высокомол. соедин. Сер. А. 2001. Т. 43. № 10. С. 1797.]
Сонина А.Н., Симаненкова О.М., Вихорева Г.А., Гальбрайх Л.С. Свойства формовочных растворов хитозана, ПВС и их смесей и переработка их методом электроформования // Композ. нанострукт. 2012. № 2. С. 44.
Дресвянина Е.Н., Добровольская И.П., Внучкин А.В., Попрядухин П.В. Получение и свойства волокон из хитозана // Изв. высш. учебн. завед. Технол. легк. пром-сти. 2011. Т. 11. № 1. С. 48.
Lomovskoy V.A., Abaturova, N.A., Lomovskaya N.Y., Galushko T.B. Effect of the Ratio of Components in a Polyvinyl Alcohol-Chitosan Composite on the Temperature Range of its Inelasticity // Mech. Compos. Mater. 2020. V. 56. № 1. P. 27. [Ломовской В.А., Абатурова Н.А., Ломовская Н.Ю., Галушко Т.Б. Влияние соотношения компонентов в композите поливиниловый спирт-хитозан на температурные области неупругости // Мех. композ. матер. 2020. Т. 56. № 1. С. 1.]
Lomovskoy V.A., Abaturova N.A., Lomovskaya N.Y., Khlebnikova O.A., Galushko T.B. Areas of local inelasticity and relaxation phenomena in poly(vinyl formal) // Polym. Sci., Ser. A. 2018. V. 60. № 3. P. 284. [Ломовской В.А., Абатурова Н.А., Ломовская Н.Ю., Хлебникова О.А., Галушко Т.Б. Области локальной неупругости и релаксационные явления в поливинилформале // Высокомол. соедин. Сер. А. 2018. Т. 60. № 3. С. 201.]
Ломовской В.А. Устройство для исследования локальных диссипативных процессов в твердых материалах различной химической природы // Научн. приборостр. 2019. Т. 29. № 1. С. 33.
Lomovskoy V.A., Abaturova N.A., Lomovskaya N.Yu., Galushko T.B., Zolotarevskii V.I. Local Dissipative Processes in Chitosan-Poly(vinyl alcohol) Composite System // Polym. Sci., Ser. A. 2019. V. 61. № 4. P. 491. [Ломовской В.А., Абатурова Н.А., Ломовская Н.Ю., Галушко Т.Б., Золотаревский В.И. Локальные диссипативные процессы в композитной системе хитозан–поливиниловый спирт // Высокомол. соедин. Сер. А. 2019. Т. 61. № 4. С. 346.]
Aslamazova T.R., Kotenev V.A., Lomovskaya N.Yu., Lomovskoy V.A., Tsivadze A.Yu. Theoretical Analysis of Relaxation Processes in Acrylate Latex Polymers // Theor. Found. Chem. Eng. 2020. V. 54. № 1. P. 13. [Асламазова Т.Р., Котенев В.А., Ломовская Н.Ю., Ломовской В.А., Цивадзе А.Ю. Теоретический анализ релаксационных процессов в акрилатных латексных полимерах // Теор. осн. хим. технол. 2020. Т. 54. № 1. С. 10.]
Bartenev G.M., Lomovskoi V.A. Continuous spectrum of alpha-relaxation times in vitreous B2O3 // Neorg. Mater. 1991. V. 27. № 12. P. 2635.
Бартенев Г.М., Ломовской В.А., Карандашева Н.Ю. Спектры времен релаксации в полиметилметакрилате // Высокомол. соедин. Сер. Б. 1993. Т. 35. № 9. С. 45.
Мазурин О.В. Стеклование и стабилизация неорганических стекол. Л.: Наука, 1978.
Ломовской В.А., Мазурина С.А. Анализ и применение дробно-экспоненциальной функции для описания процессов релаксации в кристаллических областях полиэтилена // Сб. тр. XXIV Междунар. симп. “Динамические и технологические проблемы механики конструкций и сплошных сред” им. А.Г. Горшкова. ТРП, 2018. Т. 2. С. 37.
Белашова И.С., Горшков А.А., Ломовской В.А. Теоретический анализ различных функций релаксации локальных диссипативных процессов, наблюдаемых на спектрах внутреннего трения // Сб. тр. XII Международной конференции по прикладной математике и механике в аэрокосмической отрасли – NPNJ’2018. М.: МАИ, 2018. С. 340.
Lomovskoy V.A., Abaturova N.A., Lomovskaya N.Yu., Galushko T.B. Relaxation Phenomena in Films of Chitosan of Various Chemical Forms // Polym. Sci., Ser. A. 2019. V. 61. № 1. P. 46. [Ломовской В.А., Абатурова Н.А., Ломовская Н.Ю., Галушко Т.Б. Релаксационные явления в пленочных материалах из хитозана различных химических форм // Высокомол. соедин. Сер. А. 2019. Т. 61. № 1. С. 52.]
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии