Теоретические основы химической технологии, 2021, T. 55, № 3, стр. 347-358
Синтез теплообменных систем, интегрированных с технологическим процессом
А. М. Цирлин a, *, Л. Г. Гагарина b, А. И. Балунов c
a Институт программных систем им. А.К. Айламазяна РАН
Переславль-Залесский, Россия
b Национальный исследовательский университет “МИЭТ”
Зеленоград, Россия
c Ярославский государственный технический университет
Ярославль, Россия
* E-mail: tsirlin@sarc.botik.ru
Поступила в редакцию 25.09.2020
После доработки 27.01.2021
Принята к публикации 27.01.2021
Аннотация
Предложен алгоритм синтеза систем, интегрированных с технологическим процессом, когда фиксированы температуры и теплоемкости всех или части потоков и нужно построить систему регенерации тепла с минимальным суммарным коэффициентом теплопередачи (поверхностью контакта). Алгоритм основан на построении двухпоточного расчетного теплообменника, термодинамически эквивалентного многопоточной системе. Показано, что предложенный алгоритм справедлив для любой формы кинетики теплообмена, которую можно представить как произведение коэффициента теплопередачи на множитель, зависящий от температур контактирующих потоков.
ВВЕДЕНИЕ
Многие технологические процессы в химической, пищевой, металлургической промышленности характеризуются значительными потоками выделяемой и потребляемой энергии, которую можно использовать как в самом процессе для нагрева или охлаждения поступающих потоков, так и для других целей. Для утилизации этой энергии применяют системы теплообмена, интегрированные с технологическим процессом [1–4] и др.
При синтезе таких систем первоначально рассчитывают суммарные тепловые нагрузки для холодных и для горячих потоков с фиксированными температурами на входе и выходе и теплоемкостями. Как правило, эти нагрузки не совпадают. Тогда в систему вводят дополнительные потоки, у которых расходы (теплоемкости потоков) и температуры на выходе можно выбирать. Если применение дополнительных потоков не обеспечивает нужной тепловой нагрузки, в систему вводят дополнительные подогреватели (охладители), использующие электрическую энергию или энергию горения.
Мы будем предполагать, что в системе без нагревателей (исходных потоков и утилит) такие параметры как начальные и конечные температуры, фазовые состояния и теплоемкости фиксированы для всех или для большинства потоков. Выбору подлежат оставшиеся свободные параметры и структура контактов, т.е. структура и параметры системы двухпоточных теплообменников, которая при некоторых ограничениях с максимальной эффективностью реализует утилизацию теплоты. Для каждого такого теплообменника нужно выбрать температуры, теплоемкости и гидродинамический режим контактирующих потоков, коэффициент теплопередачи, косвенно связанный с размерами аппарата.
В качестве показателя эффективности используют технико-экономические и технологические критерии. В первом случае критерий учитывает стоимость создания и эксплуатации системы теплообмена [3, 4], во втором – такие показатели как потери энергии от необратимости теплообмена при ограничении на суммарный коэффициент теплопередачи [5, 6]. Потери работоспособной энергии используются и при эксергетической оценке термодинамических систем (см. [7, 8] и др.).
Технико-экономические критерии в значительной мере субъективны, так как они зависят от цен на производство и монтаж системы, от принятого соотношения между затратами на ее изготовление и на эксплуатацию. Главное же, использование такого рода критериев предопределяет численные процедуры синтеза и не позволяет получить аналитические условия оптимальности искомой системы.
Потери эксергии пропорциональны производству энтропии в системе и температуре окружающей среды. При эксергетическом анализе теплообменных систем рассчитывают производство энтропии в системе через известные теплоемкости потоков и их температуры на входе и на выходе системы, но не ставят задачу синтеза системы: каким условиям должна удовлетворять система теплообмена, чтобы производство энтропии в ней при тех или иных ограничениях было минимально возможным?
В работах [9, 10] получены условия минимальной диссипации теплообмена и реализующая их “идеальная система теплообмена” – система, у которой при заданных поверхности контакта между горячими и холодными потоками (общем коэффициенте теплопередачи $\bar {K}$) и тепловой нагрузкой $\bar {Q}$ производство энтропии минимально $\sigma {\text{*}}.$ Наряду с суммарным коэффициентом теплопередачи и суммарным тепловым потоком предполагались известными вид кинетики теплообмена и характеристики горячих или холодных потоков: их теплоемкости, равные произведению расхода на удельную теплоемкость ${{W}_{i}} = {{g}_{i}}{{C}_{i}},$ а также температуры на входе в систему $T_{i}^{{{\text{in}}}}.$ Входные температуры и теплоемкости остальных потоков подлежали выбору. Все результаты в этой работе получены для случая, когда тепловой поток пропорционален разности температур теплоносителей $q({{T}_{ + }},{{T}_{ - }})$ = $k({{T}_{ + }} - {{T}_{ - }}).$ Такую кинетику часто называют Ньютоновской. Изменение фазового состояния потоков в [10] не рассматривалось. Синтез систем по условию минимума диссипации приводит к системе, в которой при заданных ограничениях поток, параметры которого подлежат выбору, имеет минимально возможную эксергию.
Для систем, интегрированных с технологическим процессом, такой подход не применим, так как параметры и холодных и горячих потоков в значительной мере фиксированы, нужно организовать утилизацию тепла в системе, имеющей минимальные размеры. Ниже будет использован технологический критерий эффективности в форме требования минимума суммарного коэффициента теплопередачи $\bar {K}$ при заданных ограничениях на параметры потоков.
При пинч-анализе [1, 2] строят зависимость температур потоков от тепловой нагрузки, находят значение нагрузки, для которой эти температуры наиболее близки (пинч-состояние) и дают рекомендации по увеличению разности температур в этом состоянии. Этот подход основан на интуиции и опыте проектирования. Приведенные ниже количественные построения, показывают, что суммарный коэффициент теплопередачи системы действительно в значительной мере определяется пинч-состоянием, но связь этого коэффициента с профилями температур и количественная постановка задачи, приведенные ниже, позволяют дать точную формулировку и построить алгоритм задачи синтеза, причем для широкого класса уравнений кинетики.
Коэффициент теплопередачи, в свою очередь, коррелирован с размерами аппаратов и стоимостью системы, что позволяет во многих случаях заменить технико-экономический критерий критерием минимизации суммарного коэффициента теплопередачи.
– Первоначально остановимся на теплообменной системе с двумя потоками, в которой теплоемкости потоков могут быть переменными.
– Затем покажем, как многопоточная система может быть приведена к эквивалентной ей двухпоточной и запишем условия эквивалентности.
– Найдем минимально возможный коэффициент теплопередачи для двухпоточной системы и, воспользовавшись условиями эквивалентности, синтезируем многопоточную систему с тем же суммарным коэффициентом теплопередачи.
Полученное значение для минимального $\bar {K}$ позволяет:
• выяснить, как влияют на возможности системы те или иные из заданных факторов (температуры и теплоемкости потоков, тепловая нагрузка и пр.);
• оценить эффективность реальной теплообменной системы путем сравнения фактического значения коэффициента теплопередачи с минимально возможным;
• построить границу реализуемости системы: если в процессе проектирования требования к теплообменной системе таковы, что значение коэффициента теплопередачи в ней должно быть меньше, чем найденное минимально-возможное, то система физически не реализуема, как не реализуема тепловая машина, КПД которой превышает КПД Карно;
• проследить, как изменятся возможности системы при введении дополнительных нагревателей.
В ряде случаев те или иные ограничения делают выполнение условий минимума $\bar {K}$ невозможным, но полученные условия дают ориентир, к которому надо стремиться.
Мы ограничимся зависимостью теплового потока от температур теплоносителей вида
(1)
$\begin{gathered} q({{T}_{ + }},{{T}_{ - }}) = kz({{T}_{ + }},{{T}_{ - }}),\,\,\,\,{{T}_{ + }} > {{T}_{ - }},\,\,\,\,z > 0, \\ \frac{{\partial z}}{{\partial {{T}_{ + }}}} > 0,\,\,\,\,\frac{{\partial z}}{{\partial {{T}_{ - }}}} < 0. \\ \end{gathered} $Эта форма включает многие известные законы теплопереноса, например, Ньютона, Фурье, лучистого теплообмена:
(2)
$\begin{gathered} q = ({{T}_{ + }},{{T}_{ - }}) = k({{T}_{ + }} - {{T}_{ - }}),\,\,\,\,q = ({{T}_{ + }},{{T}_{ - }}) = \\ = k\left( {{1 \mathord{\left/ {\vphantom {1 {{{T}_{ - }}}}} \right. \kern-0em} {{{T}_{ - }}}} - {1 \mathord{\left/ {\vphantom {1 {{{T}_{ + }}}}} \right. \kern-0em} {{{T}_{ + }}}}} \right),\,\,\,\,q = ({{T}_{ + }},{{T}_{ - }}) = k\left( {T_{ + }^{4} - T_{ - }^{4}} \right) \\ \end{gathered} $и др., но не включает, например, кинетику вида $q = ({{T}_{ + }},{{T}_{ - }})$ = ${{k}_{1}}{{z}_{1}}({{T}_{ + }},{{T}_{ - }})$ + ${{k}_{2}}{{z}_{2}}({{T}_{ + }},{{T}_{ - }}).$ Важно, что для любой формы кинетики, имеющий вид (1), коэффициент k пропорционален поверхности контакта.
Обозначим через F – поверхность контакта и будем предполагать, что поверхности контакта F соответствует интегральный коэффициент теплопередачи K(F), а коэффициент $k(F) = \frac{{dK}}{{dF}} > 0$ пропорционален удельному коэффициенту теплопередачи. Размерность k равна размерности потока теплоты, деленной на размерность температурного множителя и, следовательно, зависит от кинетики теплообмена.
ДВУХПОТОЧНЫЕ СИСТЕМЫ ТЕПЛООБМЕНА
Остановимся на стационарных двухпоточных системах и будем наряду с поверхностью контакта F, изменяющейся от нуля до $\bar {F},$ рассматривать промежуточную тепловую нагрузку Q, изменяющуюся от нуля до полной тепловой нагрузки $\bar {Q}.$
Промежуточной тепловой нагрузкой назовем поток теплоты, полученный холодным теплоносителем до достижения им промежуточной температуры ${{T}_{ - }} > T_{ - }^{{{\text{in}}}}.$ Этот же поток теплоты в режиме противотока отдает горячий теплоноситель при снижении его температуры от ${{T}_{ + }},$ соответствующей контакту с ${{T}_{ - }},$ до конечной температуры $T_{ + }^{{{\text{out}}}}.$ Ниже для краткости будем называть Q тепловой нагрузкой, а $\bar {Q}$ – полной тепловой нагрузкой.
Связь между поверхностью контакта и тепловой нагрузкой имеет форму:
Знаки dQ и dF одинаковы.
Постановка задачи о минимуме коэффициента теплопередачи при заданной полной тепловой нагрузке примет следующий вид:
(4)
$\bar {K} = \int\limits_0^{\bar {F}} {k(F)dF} \to {{\min } \mathord{\left/ {\vphantom {{\min } {\int\limits_0^{\bar {F}} {k(F)z({{T}_{ + }},{{T}_{ - }})dF} }}} \right. \kern-0em} {\int\limits_0^{\bar {F}} {k(F)z({{T}_{ + }},{{T}_{ - }})dF} }} = \bar {Q},$(5)
$\frac{{d{{T}_{ + }}}}{{dF}} = - \frac{{kz({{T}_{ + }},{{T}_{ - }})}}{{{{W}_{ + }}(F)}},\,\,\,\,\frac{{d{{T}_{ - }}}}{{dF}} = \frac{{kz({{T}_{ + }},{{T}_{ - }})}}{{{{W}_{ - }}(F)}}.$Здесь ${{W}_{ + }}(F),$ ${{W}_{ - }}(F)$ – теплоемкости потоков, которые подлежат выбору.
Если режим контактирования противоточный, то знак минус в первом равенстве следует заменить на плюс и наклон кривых ${{T}_{ + }}(F),$ ${{T}_{ - }}(F)$ окажется положительным. Ниже предполагается, что режим противоточный, т.е.:
Преобразуем поставленную задачу, перейдя в качестве аргумента от поверхности контакта F к тепловой нагрузке Q, что существенно упростит решение. Возможность такого перехода связана с тем, что в силу положительности потока теплообмена эти две переменные монотонно зависят друг от друга.
Выразим из равенства (3) dF через dQ и, подставив в условия задачи, получим
(8)
$\begin{gathered} \frac{{d{{T}_{ + }}}}{{dQ}} = \frac{1}{{{{W}_{ + }}(Q)}},\,\,\,\,\frac{{d{{T}_{ - }}}}{{dQ}} = \frac{1}{{{{W}_{ - }}(Q)}}, \\ W_{ + }^{{\max }}(Q) \leqslant {{W}_{ + }}(Q) \leqslant W_{ + }^{{\min }}(Q), \\ W_{ - }^{{\max }}(Q) \leqslant {{W}_{ - }}(Q) \leqslant W_{ - }^{{\min }}(Q). \\ \end{gathered} $Ограничение на полную тепловую нагрузку в (4) при таком переходе учтено выбором верхнего предела интегрирования в преобразованной задаче. Отметим, что условия (8) не зависят от кинетики теплообмена, а связаны лишь с изменениями теплоемкостей. Форма кинетики входит только в критерий оптимальности.
Условия оптимальности задачи (7), (8) вытекают из принципа максимума Понтрягина [11]. Функция Гамильтона для невырожденного решения примет форму
Принцип максимума утверждает, что существуют такие функции ${{\psi }_{ + }}(Q),$ ${{\psi }_{ - }}(Q),$ удовлетворяющие уравнениям
(9)
$\frac{{d{{\psi }_{j}}}}{{dQ}} = - \frac{{\partial H}}{{\partial {{T}_{j}}}} = \frac{1}{{{{z}^{2}}}}\frac{{\partial z}}{{\partial {{T}_{j}}}},\,\,\,\,j = + , - ,$что функция Гамильтона на оптимальном решении максимальна по ${{W}_{ + }}(Q)$ и по ${{W}_{ - }}(Q).$
В силу свойств (1) температурного множителя $\frac{{d{{\psi }_{ + }}}}{{dQ}} > 0,$ $\frac{{d{{\psi }_{ - }}}}{{dQ}} < 0,$ значит, первая из этих функций монотонно растет и может изменить знак лишь один раз с минуса на плюс, а вторая монотонно уменьшается и может изменить знак только с плюса на минус. Так что водяной эквивалент горячего потока, если решение переключательное, доставляет максимум если он принимает минимальное значение при малых и максимальное при больших значениях тепловой нагрузки. Для холодного потока, наоборот, водяной эквивалент, если оптимальное решение переключательное, при малых значениях тепловой нагрузки должен быть на верхней, а при больших на нижней границе своих допустимых значений. При этом переключение того и другого единственно.
Пусть температуры горячего потока на входе $T_{ + }^{{{\text{in}}}}$ и на выходе $T_{ + }^{{{\text{out}}}}$ фиксированы, $T_{ + }^{{{\text{in}}}} > T_{ + }^{{{\text{out}}}}.$ В предположении противотока первая температура соответствует полной тепловой нагрузке, а вторая – нулевому ее значению. Из принципа максимума следует, что оптимальное изменение температуры горячего потока должно лежать на верхней границе множества ее значений. Она определяется решением уравнений
(10)
$\frac{{d{{T}_{ + }}}}{{dQ}} = \frac{1}{{W_{ + }^{{\min }}(Q)}},\,\,\,\,{{T}_{ + }}(0) = T_{ + }^{{{\text{out}}}},\,\,\,\,Q \leqslant {{Q}_{{ + r}}},$(11)
$\frac{{d{{T}_{ + }}}}{{dQ}} = \frac{1}{{W_{ + }^{{\max }}(Q)}},\,\,\,\,Q \geqslant {{Q}_{{ + r}}},\,\,\,\,{{T}_{ + }}(\overline Q ) = T_{ + }^{{{\text{in}}}}.$Здесь точка переключения ${{Q}_{{ + r}}}$ соответствует пересечению участков границы, соответствующих минимальному и максимальному значению теплоемкостей.
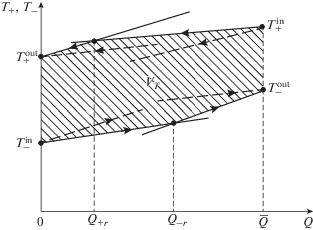
Аналогично для холодного потока из точек, соответствующих температурам на входе и выходе, строят нижнюю границу значений ${{T}_{ - }}(Q)$, состоящую из начального участка, где теплоемкость соответствует своему максимальному значению, и конечного участка, на котором теплоемкость потока минимальна. Пересечение этих границ определяет точку переключения ${{Q}_{{ - r}}}$ (см. рис. 1). Пунктиром показаны профили температур при обратном выборе порядка изменения теплоемкостей.
Таким образом, для любой формы зависимости теплового потока от контактирующих температур, имеющей вид (1), оптимальное решение задачи о минимуме коэффициента теплопередачи для двухпоточного теплообменника одинаково. На этом решении температура горячего потока лежит на своей верхней границе, а температура холодного на своей нижней границе. Форма этих границ зависит от температур потоков на входе и на выходе теплообменника и ограничений, наложенных на значения их теплоемкостей. Так как теплоемкость потока равна произведению его расхода на удельную теплоемкость, то управляющей переменной может являться расход, если его можно изменять в заданных пределах. Если температура потока на выходе не фиксирована, то при построении решения для холодного потока ее нужно выбирать минимальной, а для горячего – максимальной.
Множество, лежащее между верхней границей температуры горячего и нижней границей температуры холодного потоков, будем называть температурным множеством и обозначать через ${{V}_{T}}.$ Температурное множество на рис. 1 заштриховано.
Теплоемкости могут зависеть от тепловой нагрузки или от температуры соответствующего потока. Если эта зависимость однозначна, то граница определена только одной из температур: температурой потока на входе или его температурой на выходе. Вторая граничная температура (для определенности соответствующая $\overline Q $) определена решением уравнения
(12)
$\begin{gathered} \frac{{d{{T}_{j}}}}{{dQ}} = \frac{1}{{{{W}_{j}}({{T}_{j}})}},\,\,\,\,{{T}_{j}}(0) = T_{j}^{{{\nu }}},\,\,\,\,j = - \,\,{\text{для}}\,\,\nu = {\text{in}}, \\ j = + \,\,{\text{для}}\,\,\nu = {\text{out}}. \\ \end{gathered} $Примером может служить поток, поступающий в систему в форме жидкости, а покидающий ее в форме перегретого пара, у которого теплоемкость зависит от температуры и при температуре кипения сколь угодно велика.
Значение $\bar {K}$ определено температурным множителем $z({{T}_{ + }},{{T}_{ - }}).$ Его рассчитывают после подстановки граничных значений температурного множества ${{V}_{T}}$ в интеграл (7).
МНОГОПОТОЧНЫЕ СИСТЕМЫ ТЕПЛООБМЕНА
Постановка задачи. Пусть в систему поступает m горячих и n холодных потоков. Каждый поток характеризуется несколькими параметрами: температурой на входе, температурой на выходе, теплоемкостью. Некоторые из этих параметров фиксированы, некоторые свободны, или могут изменяться в определенных пределах. Нужно выбрать эти свободные параметры и структуру системы так, чтобы система имела минимальный суммарный коэффициент теплопередачи $\bar {K}$ при дополнительных условиях, наложенных на систему в целом, например, при заданной суммарной тепловой нагрузке. Задача предполагает оптимальный выбор контактирующих потоков (структура системы, состоящей из двухпоточных теплообменников), их температур и теплоемкостей, распределение между двухпоточными ячейками найденного минимального коэффициента теплопередачи. Гидродинамический режим в каждой ячейке априори примем противоточным.
Последовательность решения:
– По характеристикам потоков синтезируем “эквивалентный” двухпоточный теплообменник, который имеет тот же коэффициент теплопередачи $\bar {K},$ что и многопоточная система.
– Для этого “эквивалентного” теплообменника строим температурное множество и решаем задачу о минимуме коэффициента теплопередачи.
– Создаем систему двухпоточных теплообменников таким образом, чтобы были выполнены “условия эквивалентности”, а значит, эта система имела минимальный суммарный коэффициент теплопередачи.
Остановимся подробнее на каждом из этих этапов.
Эквивалентность двух- и многопоточной систем. Для того, чтобы применить результаты, полученные для двухпоточного теплообменника, к многопоточным системам, введем понятия эквивалентного горячего и холодного потоков и покажем, как через характеристики этих потоков выразить коэффициент теплопередачи, и текущую тепловую нагрузку многопоточной системы.
Отметим, что фактически переход к эквивалентному двухпоточному теплообмену используют и в пинч-анализе [1, 2], на основе интуитивных соображений, без какого либо обоснования, без постановки задачи синтеза и без использования связи (7) между K и температурным множителем.
Введем понятие эквивалентного потока: Эквивалентным холодным (горячим) потоком назовем поток, теплоемкость которого при каждой его температуре равна сумме теплоемкостей холодных (горячих) потоков, имеющих ту же температуру. Каждый поток изменяет свою температуру в определенном диапазоне. В том же диапазоне его теплоемкость входит в теплоемкость эквивалентного потока.
Температура ${{T}_{ + }}(Q)$ эквивалентного горячего потока на входе в двухпоточную систему равна самой высокой из входных температур горячих потоков, температура эквивалентного горячего потока на выходе из системы равна самой низкой из выходных температур горячих потоков:
(13)
$\begin{gathered} {{T}_{ + }}(\overline Q ) = \mathop {\max }\limits_{i + } T_{{i + }}^{{{\text{in}}}}, \\ {{T}_{ + }}(0) = \mathop {\min }\limits_{i + } T_{{i + }}^{{{\text{out}}}},\,\,\,\,i + = 1, \ldots ,m. \\ \end{gathered} $Аналогично для эквивалентного холодного потока:
(14)
$\begin{gathered} {{T}_{ - }}(\overline Q ) = \mathop {\max }\limits_{i - } T_{{i - }}^{{{\text{out}}}}, \\ {{T}_{ - }}(0) = \mathop {\min }\limits_{i - } T_{{i - }}^{{{\text{in}}}},\,\,\,\,i - = 1, \ldots ,n. \\ \end{gathered} $Теплоемкости эквивалентных потоков
изменяются с изменением температуры или тепловой нагрузки как из-за изменения теплоемкости каждого из составляющих их потоков так и из-за изменения состава содержащихся в них при этой температуре потоков. Состав потоков изменяется потому, что каждый из составляющих потоков имеет различные температуры на входе и на выходе из системы.
Если хотя бы один составляющий поток изменяет свое фазовое состояние, то при температуре кипения (конденсации) теплоемкость эквивалентного потока сколь угодно велика, а значит зависимость его температуры от текущей тепловой нагрузки имеет горизонтальный участок, протяженность которого равна произведению расхода на теплоту парообразования ${{g}_{i}}{{r}_{i}}.$
Все свободные, подлежащие оптимальному выбору, параметры потоков подлежат выбору и в эквивалентной системе.
Определение: Две теплообменные системы эквивалентны, если у них температуры потоков на входе и на выходе связаны условиями (13), (14), одинаковы полные тепловые нагрузки $\bar {Q}$ и суммарные коэффициенты теплопроводности $\bar {K}.$
– Далее будем считать фиксированными входные температуры у тех потоков (холодных или горячих), число которых меньше (для определенности пусть это будут холодные потоки).
– Запишем условия, при которых двухпоточная система эквивалентна системе, состоящей из двухпоточных теплообменников, в каждый из которых поступает один холодный поток.
– Решим задачу о минимальном коэффициенте теплопередачи для двухпоточной системы, построив границы ее температурного множества ${{V}_{T}}.$
– Выберем параметры многопоточной системы (тепловые нагрузки, коэффициенты теплопередачи, теплоемкости управляемых потоков) так, чтобы она была эквивалентна двухпоточной системе с минимальным $\bar {K}.$
Изменение температуры эквивалентного холодного потока. Температура эквивалентного холодного потока ${{T}_{ - }}(Q)$ отвечает условиям
(15)
$\frac{{d{{T}_{ - }}}}{{dQ}} = \frac{1}{{{{W}_{ - }}(Q)}} = \frac{1}{{\sum\limits_{i - } {{{W}_{{i - }}}({{T}_{{i - }}})} }}.$В этом выражении теплоемкости холодных потоков ${{W}_{{i - }}}({{T}_{{i - }}})$ = $\frac{1}{{{{d{{T}_{{i - }}}} \mathord{\left/ {\vphantom {{d{{T}_{{i - }}}} {d{{Q}_{{i - }}}}}} \right. \kern-0em} {d{{Q}_{{i - }}}}}}}$ равны нулю при ${{T}_{{i - }}} < T_{{i - }}^{{{\text{in}}}}$ и при ${{T}_{{i - }}} > T_{{i - }}^{{{\text{out}}}}.$
Зависимость ${{T}_{ - }}(Q)$ представляет собой непрерывную кусочно-линейную на участках постоянства теплоемкости функцию. В каждой из точек излома температура ${{T}_{ - }}(Q)$ либо равна температуре кипения одного из потоков, либо температуре на входе или на выходе из системы одного из холодных потоков. В последнем случае абсциссы точек излома обозначим как $Q_{{i - }}^{{{\text{in}}}}$ и $Q_{{i - }}^{{{\text{out}}}}.$
Докажем Утверждение: Для любого закона изменения температуры горячего потока ${{T}_{ + }}(Q) > {{T}_{ - }}(Q)$ расчетная двухпоточная система эквивалентна многопоточной, состоящей из N теплообменников, в каждом из которых i– холодный поток контактирует с i+ горячим, при условиях:
– Температуры контактирующих потоков ${{T}_{{i + }}}(Q),$ ${{T}_{{i - }}}(Q)$ в каждом i-ом теплообменнике совпадают с температурами эквивалентных потоков на интервале контакта $Q_{i}^{{{\text{in}}}} \leqslant Q \leqslant Q_{i}^{{{\text{out}}}}.$ Это означает, что температуры потоков на входе в теплообменник должны быть равны температурам эквивалентных потоков ${{T}_{ + }}\left( {Q_{i}^{{{\text{out}}}}} \right),$ ${{T}_{ - }}\left( {Q_{i}^{{{\text{in}}}}} \right),$ а теплоемкости потоков на всем интервале контакта должны относиться друг к другу так же, как теплоемкости эквивалентных потоков:
(16)
$\frac{{{{W}_{{i + }}}}}{{{{W}_{{i - }}}}} = \frac{{d{{T}_{{i - }}}}}{{d{{T}_{{i + }}}}} = \frac{{{{W}_{ + }}}}{{{{W}_{ - }}}}.$– Каждый теплообменник является противоточным с полной тепловой нагрузкой:
(17)
${{\bar {Q}}_{i}} = \int\limits_{T_{{i - }}^{{{\text{in}}}}}^{T_{{i - }}^{{{\text{out}}}}} {{{W}_{{i - }}}({{T}_{{i - }}})d{{T}_{{i - }}}} + {{g}_{{i - }}}{{r}_{{i - }}}.$Доказательство: Полная тепловая нагрузка в предположении, что давление в системе мало изменяется, равна
(18)
$\bar {Q} = \int\limits_{T_{{i - }}^{{{\text{in}}}}}^{T_{{i - }}^{{{\text{out}}}}} {\sum\limits_{i - } {{{W}_{{i - }}}({{T}_{{i - }}})d{{T}_{{i - }}}} } + \sum\limits_{i - } {{{g}_{{i - }}}{{r}_{{i - }}}} = \sum\limits_{i - } {{{{\bar {Q}}}_{{i - }}}} ,$Температурные профили в теплообменниках и в эквивалентной системе, а значит и зависящие от них температурные множители одинаковы (${{z}_{{i - }}}({{T}_{{i + }}},{{T}_{{i - }}})$ = $z({{T}_{ + }},{{T}_{ - }})$), так что коэффициент теплопередачи в соответствии с (7) равен
(19)
$\begin{gathered} \bar {K} = \int\limits_0^{\bar {Q}} {\frac{{dQ}}{{z({{T}_{ + }},{{T}_{ - }})}}} = \int\limits_0^{\bar {Q}} {\frac{{\sum\limits_{i - } {d{{Q}_{{i - }}}} }}{{z({{T}_{ + }},{{T}_{ - }})}}} = \sum\limits_{i - } {\int\limits_{Q_{{i - }}^{{{\text{in}}}}}^{Q_{{i - }}^{{{\text{out}}}}} {\frac{{d{{Q}_{{i - }}}}}{{{{z}_{{i - }}}({{T}_{{i + }}},{{T}_{{i - }}})}}} } = \\ = \sum\limits_{i - } {{{{\bar {K}}}_{{i - }}}} . \\ \end{gathered} $Здесь $d{{Q}_{{i - }}}$ = $dQ\frac{{{{W}_{{i - }}}}}{{{{W}_{ - }}}}.$
Таким образом, утверждение о термодинамической эквивалентности доказано.
Следствие: Если найдены профили температур эквивалентных потоков, для которых коэффициент теплопередачи в двухпоточной системе минимален, а в многопоточной системе выполнены условия эквивалентности (16), (18), то суммарный коэффициент теплопередачи и в этой системе минимален.
Постановка и результаты решения рассмотренной выше задачи о минимуме необратимости двухпоточной системы в полной мере относятся к системе с эквивалентными потоками и определяют минимальное значение коэффициента теплопроводности в эквивалентной многопоточной системе, если теплообмен в каждом из двухпоточных теплообменников организован так, что отношение теплоемкостей потоков в нем равно отношению теплоемкостей эквивалентных потоков, а температуры потоков на его входе равны температурам эквивалентных потоков, полученным в результате решения задачи (7).
СИНТЕЗ СИСТЕМЫ ДВУХПОТОЧНЫХ ТЕПЛООБМЕННИКОВ
Решение задачи о построении границ температурного множества для случая двухпоточной системы, эквивалентной многопоточной, имеет некоторые особенности, на которых остановимся подробнее.
Распределение теплоемкостей и расчет температур на выходе для эквивалентных потоков. При решении задачи (7) было указано, что если температуры потоков на выходе не фиксированы то для построения границ температурного множества ${{V}_{T}}$ следует выбирать свободные параметры так, чтобы эти температуры оказались минимальными для холодного и максимальными для горячего потоков.
В эквивалентной системе при заданных суммарной теплоемкости и тепловой нагрузке потоков можно эти теплоемкости (расходы) перераспределять между составляющими их потоками и тем самым влиять на температуры эквивалентных потоков на выходе. Так как суммарная теплоемкость фиксирована, то при таком распределении увеличению выходной температуры одного из составляющих потоков сопутствует уменьшение температуры другого. В силу условий (13), (14) минимум температуры эквивалентного холодного потока соответствует минимуму максимальной по i– выходной температуры. Требование минимума максимального значения выполнено, когда температуры на выходе одинаковы.
То же относится к температурам горячих потоков. Если их можно изменять, перераспределяя расходы, а значит, теплоемкости и тепловые нагрузки, то это распределение должны быть таким, чтобы минимальная по i+ температура $T_{{i + }}^{{{\text{out}}}}$ была максимальна, т.е. одинакова для тех потоков, у которых она не фиксирована.
Конкретизируем эти условия на примере горячих потоков (для холодных процедура совершенно аналогична).
Упорядочим горячие потоки по величине их температуры на входе, так что $T_{{i + }}^{{{\text{in}}}} > T_{{(i + 1) + }}^{{{\text{in}}}}.$ При этом поток, изменяющий свое фазовое состояние, представим как три расчетных потока: охлаждающийся перегретый пар, конденсирующийся насыщенный пар и жидкость, охлаждающаяся от температуры кипения до температуры на выходе. При таком разбиении входной температурой жидкости и выходной температурой пара является температура конденсации потока.
Температура эквивалентного горячего потока на выходе из системы равна минимальной из выходных температур горячих потоков. Максимум этого минимального значения достигается тогда, когда тепловая на грузка между потоками распределена так, что их температура на выходе $T_{ + }^{{{\text{out}}}}$ одинакова для тех горячих потоков, для которых она не фиксирована.
В предположении постоянства давления запишем условие теплового баланса для горячих потоков:
(20)
$\begin{gathered} \sum\limits_{i + } {{{W}_{{i + }}}\left( {T_{{i + }}^{{{\text{in}}}} - T_{{i + }}^{{{\text{out}}}}} \right)} + \sum\limits_j {{{g}_{{j + }}}{{r}_{j}}sign\left( {{{T}_{{bj}}} - T_{ + }^{{{\text{out}}}}} \right)} = \\ = {{{\bar {Q}}}_{ + }}\left( {T_{ + }^{{{\text{out}}}}} \right) = \bar {Q}. \\ \end{gathered} $В этом уравнении для $T_{ + }^{{{\text{out}}}}$ первое слагаемое в левой части – разность энтальпий на входе и на выходе из системы для потоков, не изменяющих свое фазовое состояние, второе слагаемое – разность энтальпий конденсирующихся потоков. Функция sign равна единице при $\left( {{{T}_{{bj}}} - T_{ + }^{{{\text{out}}}}} \right) > 0$ и равна нулю в остальных случаях. В первом слагаемом для потоков, выходные температуры которых не фиксированы, вместо $T_{{i + }}^{{}}$ стоит $T_{ + }^{{{\text{out}}}}.$
В простейшем случае, когда конденсирующиеся потоки отсутствуют, а температуры всех горячих потоков свободны, уравнение (20) легко решается:
(21)
$T_{ + }^{{{\text{out}}}} = \frac{{\sum\limits_{i + = 1}^m {{{W}_{{i + }}}T_{{i + }}^{{{\text{in}}}}} - \bar {Q}}}{{\sum\limits_{i + = 1}^m {{{W}_{{i + }}}} }}.$Левая часть уравнения (20) ${{\bar {Q}}_{ + }}\left( {T_{ + }^{{{\text{out}}}}} \right)$ представляет собой теплоотдачу горячих потоков. С ростом температуры $T_{ + }^{{{\text{out}}}}$ эта теплоотдача монотонно уменьшается, испытывая скачки при температурах конденсации, так что решение этого уравнения единственно. Если решению соответствует температура конденсации, то при этой температуре левая часть уравнения (20) пересекает линию $\bar {Q}$ с полной или частичной конденсацией потока насыщенного пара.
С уменьшением полной тепловой нагрузки системы $\bar {Q}$ температура эквивалентного горячего потока возрастает, а минимальное значение коэффициента теплопередачи уменьшается.
Определение состава потоков, участвующих в теплообмене. Набор используемых в системе горячих потоков подлежит выбору. В этот набор включают потоки, температура которых на входе в систему превышает значение $T_{ + }^{{{\text{out}}}},$ найденное в результате решения уравнения (20).
Если полученное значение $T_{ + }^{{{\text{out}}}}$ больше, чем минимальная температура холодного потока на входе в систему ${{T}_{ - }}(0),$ то система может быть синтезирована, в противном случае в ее состав требуется ввести дополнительные горячие потоки или подогреватели.
Тепловые нагрузки каждого i+ горячего потока выбирают по формуле
где ${{H}_{{i + }}}$ – энтальпия на входе и на выходе горячего потока, зависящая от того, меняется ли его температура при охлаждении либо он полностью или частично конденсируется (см. (20)).Построение границ температурного множества. Как только состав потоков и распределение теплоемкостей (расходов) их составляющих найдено, определена и зависимость теплоемкости каждой составляющей эквивалентного потока, а значит и их суммы, от тепловой нагрузки. Построение верхней границы начинается с температуры ${{T}_{ + }}(\bar {Q}) = T_{{i + }}^{{{\text{in}}}}$ самого горячего потока. По мере уменьшения температуры эквивалентного потока с уменьшением Q к первому потоку присоединяют второй, третий…горячие потоки с их теплоемкостями. Решение уравнения
(23)
$\frac{{d{{T}_{ + }}}}{{dX}} = - \frac{1}{{{{W}_{ + }}(X)}},\,\,\,\,{\text{где}}\,\,\,\,X = \bar {Q} - Q,$является верхней границей ${{V}_{T}}.$
Аналогично для холодного эквивалентного потока решение уравнения
(24)
$\frac{{d{{T}_{ - }}}}{{dX}} = - \frac{1}{{{{W}_{ - }}(Q)}},\,\,\,\,{\text{где}}\,\,\,\,{{T}_{ - }}(0) = T_{{i - }}^{{{\text{in}}}},$Построенные границы температурного множества позволяют для каждой температуры потока ${{T}_{ - }}(Q)$ и теплоемкости ${{W}_{ - }}(Q)$ найти соответствующую ей температуру ${{T}_{ + }}(0)$ и теплоемкость ${{W}_{ + }}(Q)$ эквивалентного горячего потока, а также вычислить суммарный минимальный коэффициент теплопередачи многопоточной системы после подстановки этих температур в (19).
ПАРАМЕТРЫ ДВУХПОТОЧНЫХ ТЕПЛООБМЕННИКОВ
Реализация многопоточной системы, соответствующей расчетной двухпоточной, предполагает синтез структуры двухпоточных теплообменников, выбор для каждого из них тепловой нагрузки ${{\bar {Q}}_{i}},$ температур и теплоемкостей контактирующих потоков, а также коэффициента теплопередачи так, чтобы эквивалентные потоки для этой системы имели те же характеристики, что и для расчетной двухпоточной. Для краткости каждый двухпоточный теплообменник будем называть ячейкой.
По условию эквивалентности (16) теплоемкость горячего потока, определяющая его расход, для каждого значения тепловой нагрузки Q равна
Если холодный поток испаряется при температуре ${{T}_{{ib - }}} = {{T}_{ - }},$ то теплоемкость контактирующего с ним в двухпоточной ячейке горячего потока на участке испарения равна ${{W}_{ + }}(Q),$ так как дробь в выражении (25) равна единице. Совершенно аналогично, на участке, когда горячий поток конденсируется, теплоемкость контактирующего с ним холодного потока равна ${{W}_{ - }}(Q).$
Коэффициент теплопередачи i-го теплообменника ${{\bar {K}}_{{i - }}}$ вычисляют по формуле (19) как
(26)
${{\bar {K}}_{{i - }}} = \int\limits_{Q_{{i - }}^{{{\text{in}}}}}^{Q_{{i - }}^{{{\text{out}}}}} {\frac{{{{W}_{{i - }}}dQ}}{{{{W}_{ - }}z({{T}_{ + }},{{T}_{ - }})}}} .$Последовательность синтеза
1. Задают исходные параметры системы указав температуры потоков на входе и на выходе (некоторые из последних могут быть свободны), фазовое состояние, теплоемкости. Если поток испаряется, то указаны его температура кипения, расход и теплота парообразования и он может рассматриваться как три потока.
2. Рассчитывают суммарную тепловую нагрузку системы $\bar {Q}$ и находят распределение тепловых нагрузок и теплоемкостей потоков по условию равенства не фиксированных выходных температур. Находят значения температур на выходе.
3. Строят верхнюю и нижнюю границы ${{V}_{T}}$ и рассчитывают минимальный суммарный коэффициент теплопередачи по формуле (19). Интеграл в (19) вычисляют на интервалах, для которых теплоемкости эквивалентных потоков постоянны – интервалах однородности.
Для ньютоновской кинетики и ν-го интервала, на котором теплоемкости обоих потоков постоянны, прирост коэффициента теплопередачи равен
(27)
$\begin{gathered} \Delta {{K}_{{{\nu }}}} = \int\limits_{{{Q}_{b}}}^{{{Q}_{e}}} {\frac{{dQ}}{{{{T}_{ + }}({{Q}_{b}}) - {{T}_{ - }}({{Q}_{b}}) + (Q - {{Q}_{b}})({1 \mathord{\left/ {\vphantom {1 {{{W}_{{{{\nu }} + }}}}}} \right. \kern-0em} {{{W}_{{{{\nu }} + }}}}} - {1 \mathord{\left/ {\vphantom {1 {{{W}_{{{{\nu }} - }}}}}} \right. \kern-0em} {{{W}_{{{{\nu }} - }}}}})}}} = \\ = {{{\bar {W}}}_{{{\nu }}}}\ln \frac{{\Delta {{T}_{{{\nu }}}} + {{({{Q}_{e}} - {{Q}_{b}})} \mathord{\left/ {\vphantom {{({{Q}_{e}} - {{Q}_{b}})} {{{{\bar {W}}}_{{{\nu }}}}}}} \right. \kern-0em} {{{{\bar {W}}}_{{{\nu }}}}}}}}{{\Delta {{T}_{{{\nu }}}}}}, \\ \Delta {{K}_{{{\nu }}}} = \frac{{{{Q}_{e}} - {{Q}_{b}}}}{{\Delta {{T}_{{{\nu }}}}}}\,\,\,{\text{при}}\,\,\,\,{{W}_{{{{\nu }} - }}} = {{W}_{{{{\nu }} + }}}. \\ \end{gathered} $4. Для того, чтобы система двухпоточных ячеек была эквивалентна расчетной двухпоточной, в каждой ячейке отношение теплоемкостей потоков должно быть таким же, как отношение теплоемкостей эквивалентных потоков; гидродинамика ячейки соответствовала противотоку, а температуры потоков на входе в ячейку были равны температурам эквивалентных потоков, для соответствующих значений тепловой нагрузки.
Температуру горячего потока на входе в каждую ячейку выбирают равной температуре эквивалентного горячего потока, соответствующей $T_{{i - }}^{{{\text{out}}}},$ а его теплоемкость (расход) выбирают так, чтобы отношение теплоемкостей горячего и холодного потоков в ячейке было равно отношению теплоемкостей эквивалентных потоков для ${{T}_{ - }}(Q) = T_{{i - }}^{{{\text{out}}}}.$
5. Для каждого потока, например, холодного известны его теплоемкость ${{W}_{{i - }}},$ температуры на входе и на выходе из теплообменника, а значит и тепловая нагрузка соответствующей ячейки
Если теплоемкость эквивалентного горячего потока ${{T}_{ + }}(Q)$ на интервале контакта увеличивается за счет включения в него дополнительных потоков, то и в ячейку вводится дополнительно горячий поток с таким расходом, чтобы отношение теплоемкостей стало равно их отношению для эквивалентных потоков.
6. Если два холодных потока кипят при одной и той же температуре, то горячий поток так распределяют между ячейками с кипением, чтобы его температуры на выходе из ячеек были одинаковы, т.е. распределяют общую теплоемкость эквивалентного потока пропорционально тепловой нагрузке каждой из ячеек. Аналогично для конденсации двух горячих потоков при одинаковой температуре.
Сложность синтезируемой системы можно охарактеризовать числом N простых двухпоточных теплообменников, в каждом из которых теплоемкости контактирующих потоков постоянны. Каждый i-ый поток входит в состав эквивалентного потока в начальной точке Qi некоторого ν-го интервала однородности, а покидает систему в конечной точке (ν + ki)-го интервала. Общее число двухпоточных ячеек
(28)
$\begin{gathered} N = \min \left( {\sum\limits_{i - = 1}^{{{n}_{ - }}} {({{k}_{{i - }}} + 1)} } \right){\text{;}}\,\,\,\,\sum\limits_{i + = 1}^{{{n}_{ + }}} {({{k}_{{i + }}} + 1)} , \\ {{k}_{{i - }}},{{k}_{{i + }}} = 0,1, \ldots ,M - 1. \\ \end{gathered} $Оно растет с увеличением общего числа M интервалов однородности.
Пример. Рассмотрим систему теплообмена, с тремя холодными и двумя горячими потоками. Для холодных потоков фиксированны следующие параметры:
– первый поступает в виде жидкости с температурой $T_{{1 - }}^{{{\text{in}}}}$ = 300 K и теплоемкостью $W_{{1 - }}^{l}$ = = 4.2 КВт/К, нагревается до температуры кипения ${{T}_{b}}$ = 373 K, r = 225.8 КВт/К, а затем перегревается и покидает систему в форме парового потока с теплоемкостью $W_{{1 - }}^{{{\nu }}}$ = 2 КВт/К и температурой $T_{{1 - }}^{{{\text{out}}}}$ = 423 К.
– второй и третий потоки поступают в систему и покидают ее в виде жидкости с параметрами:
Параметры двух горячих потоков:
– перегретый пар с температурой $T_{{1 + }}^{{{\text{in}}}}$ = 500 K, расходом 1 моль/c, теплотой конденсации r+ = = 1000 КВт/моль, теплоемкостью ${{W}_{s}}$ = 2.5 КВт/К.
– поток жидкости с температурой $T_{{2 + }}^{{{\text{in}}}}$ = 500 K и теплоемкостью ${{W}_{l}}$ = 20 кВт/К.
Следуя изложенному выше алгоритму, синтезируем теплообменную систему с минимальным суммарным коэффициентом теплопередачи.
1. Полная тепловая нагрузка системы $\bar {Q}$ = = 1113.4 кВт определена холодными потоками и рассчитана как
Зависимость температуры эквивалентного потока от тепловой нагрузки ${{T}_{ - }}(Q)$ представляет собой кусочно-линейную непрерывную функцию, наклон которой на каждом участке равен ${1 \mathord{\left/ {\vphantom {1 {\sum\limits_i {{{W}_{i}}} }}} \right. \kern-0em} {\sum\limits_i {{{W}_{i}}} }},$ где сумма берется по всем потокам, входящим в эквивалентный на этом участке. Получим
(29)
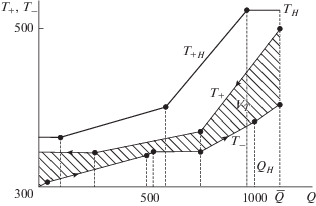
$\begin{gathered} {{T}_{ - }}(Q) = 300 + {Q \mathord{\left/ {\vphantom {Q {4.2}}} \right. \kern-0em} {4.2}}\,\,\,{\text{при}}\,\,\,0 \leqslant Q \leqslant 42; \\ 310 + {{(Q - 42)} \mathord{\left/ {\vphantom {{(Q - 42)} {9.2}}} \right. \kern-0em} {9.2}}\,\,\,{\text{при}}\,\,\,42 \leqslant Q \leqslant 502; \\ 360 + {{(Q - 502)} \mathord{\left/ {\vphantom {{(Q - 502)} {4.2}}} \right. \kern-0em} {4.2}}\,\,\,{\text{при}}\,\,\,502 \leqslant Q \leqslant 555; \\ {\text{373}}\,\,\,{\text{при}}\,\,\,555 \leqslant Q \leqslant 782; \\ 373 + {{(Q - 782)} \mathord{\left/ {\vphantom {{(Q - 782)} 5}} \right. \kern-0em} 5}\,\,\,{\text{при}}\,\,\,782 \leqslant Q \leqslant 1032; \\ 423 + {{(Q - 1032)} \mathord{\left/ {\vphantom {{(Q - 1032)} {3\,\,\,{\text{при}}\,\,\,}}} \right. \kern-0em} {3\,\,\,{\text{при}}\,\,\,}}1032 \leqslant Q \leqslant 1113.4. \\ \end{gathered} $Эти границы показаны на рис. 2.
2. Верхняя граница ${{V}_{T}}$ рассчитана аналогично. Здесь температуры горячих потоков на выходе свободны, а, следовательно, тепловая нагрузка между ними должна быть распределена так, чтобы они оказались одинаковы.
Предположим, что теплоотдача двух потоков с самой высокой температурой на входе без конденсации обеспечит нужную тепловую нагрузку. Найдем по формуле (21)
Эта температура ниже температуры конденсации, так что сделанное предположение неверно. Поэтому нужно принять $T_{ + }^{{{\text{out}}}} = 373\,\,{\text{К}}$ и по уравнению (20) подсчитать долю x насыщенного пара, которую нужно сконденсировать. Получим $x = 0.256.$
3. Температура $T_{ + }^{0}(Q)$ эквивалентного горячего потока равна
Ее график показан на рис. 2. Поток конденсата использовать в теплообменной системе нецелесообразно.
4. Найдем границы интервалов однородности ${{Q}_{1}},$ ${{Q}_{2}}$, …, ${{Q}_{7}}$ графиков эквивалентных температур. На каждой из этих границ меняется теплоемкость одного из потоков (см. табл. 1). В этой же таблице приведены для каждого интервала однородности теплоемкости потоков, разница температур потоков для начальной точки интервала и рассчитанные по формуле (27) приросты коэффициента теплопроводности $\Delta {{K}_{{{\nu }}}}.$ Минимально-возможное его значение ${{K}_{{\min }}} = \sum\limits_{{\nu }} {\Delta {{K}_{{{\nu }}}}} $ = $47.8\,\,{\text{КВт/К}}{\text{.}}$
Таблица 1.
Границы интервалов однородности для температур эквивалентных потоков
| ν | Qbν…Qlν | Wν– | Wν+ | ΔTbν | ΔKν | $\frac{{{{W}_{{1\nu - }}}}}{{{{W}_{{\nu - }}}}}$ | $\frac{{{{W}_{{2\nu - }}}}}{{{{W}_{{\nu - }}}}}$ |
|---|---|---|---|---|---|---|---|
| 1 | 0…42 | 4.2 | ∞ | 75 | 0.62 | 1.0 | 0 |
| 2 | 42…256 | 9.2 | ∞ | 63 | 9.3 | 4.2/9.2 | 5/9.2 |
| 3 | 256…502 | 9.2 | 22.5 | 40 | 14.4 | 4.2/9.2 | 5/9.2 |
| 4 | 502…555 | 4.2 | 22.5 | 24 | 2.3 | 1.0 | 0 |
| 5 | 555…863 | ∞ | 22.5 | 13.4 | 15.8 | 1.0 | 0 |
| 6 | 863…1032 | 5.0 | 2.5 | 27 | 4.1 | 3/5 | 0 |
| 7 | 1032…1113 | 3.0 | 2.5 | 60.8 | 1.3 | 0 | 0 |
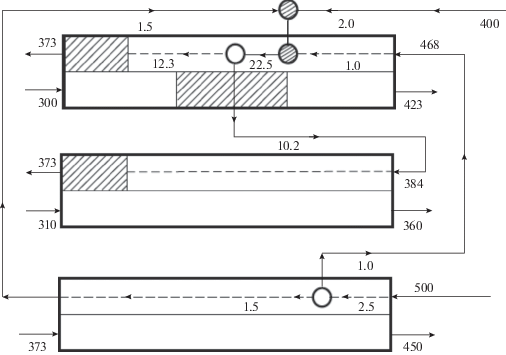
5. На рис. 3 изображена структура синтезированной системы, на входе и на выходе потоков обозначены их температуры. Заштрихованные кружки соответствуют объединению, а светлые – разделению горячих потоков.
6. Для того чтобы найти теплоемкости горячих потоков и прирост коэффициента теплопроводности в j-м теплообменнике для v-го интервала однородности $\Delta {{K}_{{j{{\nu }}}}},$ нужно теплоемкость эквивалентного горячего по тока и величину $\Delta {{K}_{{{\nu }}}},$ умножить на отношение теплоемкости холодного потока, контактирующего с ним ${{W}_{{j{{\nu }} - }}},$ к теплоемкости эквивалентного $W(Q)$ на этом интервале.
Таким образом, получены значения теплоемкостей потоков и коэффициентов теплопроводности каждого из двухпоточных теплообменников K1 = 32 кВт/К, K2 = 12.9 кВт/К, K3 = 2.9 кВт/К. Теплоемкости потоков проставлены на рис. 3 под стрелками, изображающими их направление.
Если ограничения на температуры потоков не являются жесткими, то систему можно упростить, уменьшив число интервалов однородности, за счет некоторого увеличения ${{K}_{{\min }}}.$ Из профилей температур, показанных на рис. 2, видно, что уменьшив на 10 К входную и увеличив на 13 К выходную температуру второго из холодных потоков, можно уменьшить число интервалов однородности с семи до пяти без существенного увеличения коэффициента теплопередачи.
Системы с дополнительными подогревателями. В ряде случаев может оказаться, что температура эквивалентного горячего потока на выходе системы, рассчитанная по условию (20), будет меньше входной температуры эквивалентного холодного потока. Это означает, что система теплообмена, использующая имеющиеся в распоряжении проектировщика горячие потоки, не может быть реализована.
В иных случаях рассчитанное по приведенному выше алгоритму минимальное значение K может оказаться слишком большим, а система слишком дорогой. В этих случаях в систему вводят дополнительные подогреватели, газовые, электрические и др. Стоимость таких нагревателей гораздо ниже стоимости системы теплообмена, но эксплуатационные расходы значительны. Остановимся на выборе рационального значения дополнительной тепловой нагрузки QH, подводимой в систему дополнительным подогревателем. При этом температура подогревателя TH известна. Она, как правило, выше температур горячих потоков и остается постоянной при изменении тепловой нагрузки.
На рис. 2 показаны температуры эквивалентных потоков. Верхняя кривая соответствует эквивалентной температуре горячего потока ${{T}_{{ + {\text{Н}}}}}(Q)$ в системе с добавочным нагревателем. При этом на участке от Q = 0 до $Q = {{\bar {Q}}_{ - }}$ QH эта температура ${{T}_{{ + {\text{Н}}}}}(Q)$ = = ${{T}_{ + }}(Q + {{Q}_{{\text{Н}}}}).$ А при большей тепловой нагрузке она равна TH.
Для выбора рационального значения QH нужно знать зависимость минимальной стоимости $C{\text{*}}(\bar {Q})$ теплообменной системы, полученную в результате решения задачи о минимуме коэффициента теплопередачи K, от полной тепловой нагрузки. В системе с подогревателем нужно в эту зависимость вместо $\bar {Q}$ подставить $\bar {Q} - {{Q}_{{\text{Н}}}}.$
В экономике, для сопоставления эксплуатационных расходов и капитальных вложений используют текущую ставку по кредитам s, соответствующую доле от стоимости оборудования, которую нужно возвращать банку в единицу времени.
Будем предполагать, что расходы на дополнительный подогрев в ту же единицу времени равны cQH. Постановка задачи о выборе QH примет форму
Из условий стационарности этого выражения по QH получим уравнение ${{dC{\text{*}}} \mathord{\left/ {\vphantom {{dC{\text{*}}} {d{{Q}_{{\text{Н}}}}}}} \right. \kern-0em} {d{{Q}_{{\text{Н}}}}}} = {c \mathord{\left/ {\vphantom {c s}} \right. \kern-0em} s},$ определяющее целесообразность использования и тепловую нагрузку добавочных нагревателей.
ЗАКЛЮЧЕНИЕ
Для систем, интегрированных с технологическим процессом, предложен алгоритм вычисления нижней границы для коэффициента теплопроводности теплообменной системы с заданной полной тепловой нагрузкой и параметрами контактирующих потоков. Показано, что оптимальное решение в отличие от минимального значения коэффициента одинаково для различных форм кинетики теплообмена.
Доказано, что многопоточная теплообменная система может быть приведена к эквивалентной ей расчетной двухпоточной и предложен алгоритм расчета оптимальных профилей температур эквивалентных потоков, образующих верхнюю и нижнюю границы температурного множества.
Как следствие получен алгоритм построения структуры и расчета параметров системы, состоящей из двухпоточных теплообменников, которая при заданной полной тепловой нагрузке имеет минимальный суммарный коэффициент теплопроводности.
ОБОЗНАЧЕНИЯ
| C | удельная теплоемкость, Дж/(моль К) |
| F | поверхность контакта, м2 |
| $\bar {F}$ | полная поверхность контакта, м2 |
| g | расход потока, моль/с |
| K | интегральный коэффициент теплопередачи |
| Q | тепловая нагрузка, Вт |
| $\bar {Q}$ | полная тепловая нагрузка, Вт |
| r | удельная теплота парообразования/конденсации, Дж/моль |
| T | температура, К |
| W | теплоемкость потока, Вт/К |
| z | температурный множитель |
| σ | производство энтропии, Вт/К |
ИНДЕКСЫ
Список литературы
Linnhoff B. Pinch analysis–A state-of-the-art overview: Techno-economic analysis // Chem. Eng. Res. Des. 1993. V. 71. № 5. P. 503.
Linnhoff B., Vredeveld D.R. Pinch Technology // Chem. Eng. Prog. 1984. V. 88. № 7. P. 33.
Ziyatdinov N.N., Ostrovskii G.M., Emel’yanov I.I. Designing a Heat Exchange System upon the Reconstruction and Synthesis of Optimal Systems of Distillation Columns // Theor. Found. Chem. Eng. 2016. V. 50. № 2. P. 178. [Зиятдинов Н.Н., Островский Г.М., Емельянов И.И. Построение системы теплообмена при реконструкции и синтезе оптимальных систем ректификационных колонн // Теор. осн. хим. технол. 2016. Т. 50. № 2. С. 184.]
Ziyatdinov N.N., Emel’yanov I.I., Tuen Le Quard. Method for the synthesis of optimum multistage heat exchange systems // Theor. Found. Chem. Eng. 2018. V. 52. № 6. P. 943. [Зиятдинов Н.Н., Емельянов И.И. Построение системы теплообмена при реконструкции и синтезе оптимальных систем ректификационных колонн // Теор. осн. хим. технол. 2018. Т. 52. № 6. С. 184.]
Berry R.S., Kasakov V.A., Sieniutycz S., Szwast Z., Tsirlin A.M. Thermodynamic Optimization of Finite Time Processes. Chichester: Wiley, 1999.
Tsirlin A.M., Akhremenkov An.A. On the possibility of improving the thermodynamic characteristics of multiflow heat transfer systems // J. Eng. Phys. Thermophys. 2019. V. 92. № 4. P. 844.
Brodjanskiy V.M., Fratsher V., Mikhalek K. Exergy methods and its applications. Moscow: Energoatomizdat, 1988.
Bosnjakovic F. Technical Thermodynamics. N.Y.: Holt R&W, 1965.
Tsirlin A.M. Optimal comtrol of the irreversible processes of heat and mass transfer // Izv. Akad. Nauk SSSR. Tekh. Kibern. 1991. V. 2. P. 171.
Tsirlin A.M. Ideal heat exchange system // J. Eng. Phys. Thermophys. 2017. V. 90. № 5. P. 1035.
Понтрягин Л.С. Оптимальные процессы регулирования // УМН. 1959. 14. № 1. С. 3.
Поляк Б.Т. Введение в оптимизацию. М.: Наука, 1983.
Andresen B., Gordon J. M. Optimal heating and cooling strategies for heat exchanger design // J. Appl. Phys. 1992. V. 71. № 1. P. 76.
Tsirlin A.M., Mironova V.A., Amelkin S.A., Kazakov V.A. Finite-time thermodynamics Conditions of minimal dissipation for thermodynamics process with given rat // Phys. Rev. E. 1998. V. 58. № 1. P. 215.
Prigogine I. Thermodynamics of Irreversible Processes. N.Y.: Interscience, 1961.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии