Теоретические основы химической технологии, 2021, T. 55, № 3, стр. 291-298

Теоретическая оценка области существования технологических решений биотехнологического процесса получения молочной кислоты

Л. В. Равичев^a, Ю. Л. Гордеева^b, *, Н. В. Меньшутина^a, Е. Л. Гордеева^a, О. А. Кишкинова^b

^a Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия

^b Московская государственная академия ветеринарной медицины и биотехнологии им. К.И. Скрябина
Москва, Россия

^* E-mail: l.s.gordeev@yandex.ru

Поступила в редакцию 02.11.2020
После доработки 16.11.2020
Принята к публикации 20.11.2020

DOI: 10.31857/S0040357121030180

Полный текст (PDF)

Аннотация

Приведены результаты теоретического анализа с оценкой технологических показателей, обеспечивающих возможность реального осуществления непрерывного биотехнологического процесса получения молочной кислоты. Анализ выполнен с использованием математического моделирования, включающего учет образования продукта, биомассы, побочного продукта. В качестве сырьевых источников рассмотрены основной субстрат, потребляемый микроорганизмами, и компонент, образующий основной субстрат в процессе синтеза. В анализе решены две задачи – определение области значений входных показателей, обеспечивающих реальное осуществление технологии для заданного значения продуктивности по целевому продукту (молочной кислоте), и оценка множественности входных показателей при заданном значении одного из них. Приведены аналитические соотношения расчета показателей множественности для точек, ограничивающих область реального осуществления процесса. Приведены примеры численных вычислений, реализующих теоретические выводы. Результаты численных расчетов показали значительные возможности пользователя в выборе исходных показателей процесса для реализации технологии при одинаковом значении продуктивности.

Ключевые слова: биотехнология, молочная кислота, особые точки, множественность показателей

ВВЕДЕНИЕ

Молочная кислота CH₃CHOHCOOH является продуктом ферментативного метаболизма, генерируемая определенными микроорганизмами. Молочная кислота может существовать в виде двух оптических изомеров, отличающихся пространственным расположением водородных атомов и спиртовых гидроксилов: D(–) молочная кислота не усваивается организмом; L(+) молочная кислота полностью усваивается организмом [1, 2]. Настоящий анализ относится к L(+) молочной кислоте, получаемой непрерывной ферментацией.

Молочная кислота рассматривается как наиболее полезный продукт для пищевой, косметической, фармацевтической, текстильной и химической промышленности. Значение молочной кислоты выросло в связи с возможностью ее использования как мономера для получения биоразлагаемых полимеров.

В работе [1] приведен достаточно подробный анализ проблемы получения молочной кислоты, в том числе с учетом pH среды, температуры и др. Наиболее важным является представление перечня штаммов микроорганизмов, продуцирующих молочную кислоту с указанием видов субстратов, используемых соответствующими штаммами (всего 61 штамм). Здесь же представлен перечень способов ферментации, которые использовались в ряде публикаций. Число способов содержит около 50 позиций, некоторые из которых повторяются для различных видов штаммов. Основной вывод здесь заключается в том, что наиболее часто в технологии используются процессы периодической и непрерывной ферментации, реже с рециркуляцией клеток. Таким образом, в виде технологических аппаратов чаще всего применяются реакторы с перемешиванием, реже аппараты со стационарным слоем, с псевдоожиженным слоем, с волокнистой насадкой и др.

В обзоре [2] показано, что исследования по математическому моделированию биотехнологических процессов ориентировано на периодическую ферментацию в аппаратах с перемешиванием.

Основополагающим при моделировании процесса синтеза молочной кислоты является кинетика еe образования. Разнообразие штаммов, производящих молочную кислоту, формирует собственную кинетику. Приемлемые кинетические соотношения (естественно, разные) приведены в обзорной публикации [3]. В большинстве исследований кинетика учитывает эффекты ингибирования биомассой, продуктом, субстратом и т.п.

Исследования по математическому моделированию направлены на оценку эффективности той или иной технологии. В работе [4] математическая модель содержит только три уравнения: баланса по биомассе, субстрату и продукту. В уравнениях семь констант, требующих экспериментальной оценки. Приведем численные значения констант в публикации: µ_max = 0.48 ч^–1; P_max = 50 г/л; K_m = 1.2 г/л; K_i = = 22 г/л; Y_X/S = 0.4 г/г; α = 2.2 г/г; β = 0.2 ч^–1.

Отметим, что в данной публикации в качестве субстрата учитывается только компонент, непосредственно потребляемый микроорганизмами (основной субстрат).

Более сложная математическая модель изучалась в публикации [5], где в технологии предполагается использовать основной субстрат и компонент, воспроизводящий основной субстрат в процессе синтеза. Например, основным субстратом являлась глюкоза, а компонентом, воспроизводящим основной субстрат, мальтоза.

Математическая модель включает четыре уравнения, т.е. добавлено уравнение баланса по мальтозе. В системе дополнительно появляется константа k_M, определяющая скорость дегидратации мальтозы. Численное значение k_M в публикации равно 0.035 ч^–1 при µ_max = 0.28 ч^–1.

В работе [6] изучалась математическая модель, в которой учитывался только основной субстрат, однако штамм микроорганизмов в качестве продукта метаболизма кроме молочной кислоты еще воспроизводил побочный продукт – бактериоцин. При этом бактериоцин рассматривался как ценный продукт. Моделировалась периодическая ферментация для штаммов Lactococcus lactis и Pediococcus acidilactici. В математическую модель введено уравнение образования побочного продукта.

В настоящем исследовании приведена обобщенная математическая модель, учитывающая как образование побочного продукта, так и использование компонента сырья, воспроизводящего основной субстрат.

Математическая модель включает уравнения баланса по биомассе, баланса по продукту; баланса по побочному продукту, баланса по основному субстрату, баланса по компоненту, воспроизводящему основной субстрат в процессе синтеза.

Модель включает кинетическое соотношение общего характера, учитывающее ингибирование биомассой, продуктом и субстратом.

Уравнения математической модели имеют следующий вид:

(1)

$ - DX + \mu X = 0,$

(2)

$\left( {\alpha \mu + \beta } \right)X - DP = 0,$

(3)

$\left( {{{\alpha }_{B}}\mu + {{\beta }_{B}}} \right)X - DB = 0,$

(4)

$D\left( {{{S}_{0}} - S} \right) - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\mu X + {{k}_{M}}M = 0,$

(5)

$D\left( {{{M}_{0}} - M} \right) - {{k}_{M}}M = 0,$

(6)

$\mu = {{\mu }_{{\max }}}{{\left( {1 - \frac{X}{{{{X}_{{\max }}}}}} \right)}^{{{{n}_{1}}}}}{{\left( {1 - \frac{P}{{{{P}_{{\max }}}}}} \right)}^{{{{n}_{2}}}}}\frac{S}{{{{K}_{m}} + S + {{{{S}^{2}}} \mathord{\left/ {\vphantom {{{{S}^{2}}} {{{K}_{i}}}}} \right. \kern-0em} {{{K}_{i}}}}}}.$

В приложении приведены соотношения (П.1)–(П.5), полученные преобразованием системы (1)–(6).

Входными показателями процесса получения молочной кислоты являются величина протока D, ч^–1 (D = V/ν, где V – объем заполнения ферментера, л; ν – объемная скорость, л/ч); концентрация основного субстрата S₀, г/л (основной субстрат, непосредственно потребляемый микроорганизмами); концентрация компонента, воспроизводящего основной субстрат в процессе синтеза, M₀, г/л.

Определяющим показателем процесса является величина продуктивности по целевому продукту Q_P, г/(л ч), Q_P = PD, где P, г/л – концентрация продукта (молочной кислоты) на выходе из ферментера.

Теоретический анализ [2, 3, 7] показал, что для каждого значения концентрации входного компонента существует множество значений двух других для одного и того же Q_P.

Отсюда возникают две задачи. Первая – определить область значений входных показателей, обеспечивающих реальное осуществление технологии для заданного Q_P; вторая – получить оценки входных показателей компонентов множеств при заданном значении одного из них, т.е. если задано D необходимо получить множество {S₀, M₀}; если задано S₀ – получить {D, M₀}; если задано M₀ – получить {D, S₀}.

Решение этих задач реализуется посредством математического моделирования процесса. В настоящем сообщении используется математическая модель достаточно общего характера (обобщенная математическая модель), сформированная на базе ряда исследований [4–6].

ФОРМИРОВАНИЕ ОБЛАСТИ ЗНАЧЕНИЙ ВХОДНЫХ ПОКАЗАТЕЛЕЙ ПРОЦЕССА (ПЕРВАЯ ЗАДАЧА)

В формировании области ключевым элементом является величина протока D, ч^–1, так как эта величина, практически является независимой, в то время как S₀ и M₀ связаны соотношением (П.2).

Однако величина D является ограниченной в любом непрерывном процессе. Ограничением является значение D_пред, при которой имеет место вымывание поступающих компонентов, “не успевших” вступить в процесс синтеза. В этом случае в (П.1) имеем A(D) = 1.0; S = S₀. Откуда для D_пред получаем

(7)

${{D}_{{{\text{пред}}}}} = {{\mu }_{{\max }}}\frac{{{{K}_{i}}{{S}_{0}}}}{{{{K}_{m}}{{K}_{i}} + {{S}_{0}}{{K}_{i}} + S_{0}^{2}}}.$

Используя условие maxD_пред по S₀, получаем

(8)

${{S}_{{\text{0}}}} = {{\left( {{{K}_{m}}{{K}_{i}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$

Максимальное значение D_пред, используя (7) и (8):

(9)

$\max {{D}_{{{\text{пред}}}}} = \frac{{{{\mu }_{{\max }}}}}{{2{{{\left( {\frac{{{{K}_{m}}}}{{{{K}_{i}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + 1}}.$

Таким образом, максимальное значение D_пред определяется только величинами кинетических констант.

Для дальнейшего анализа область значений входных показателей представлена в двух вариантах.

В первом – область сформирована в виде зависимости S₀ от D; во втором – M₀ от D.

Формирование областей значений входных показателей реализуется вычислением значений D, обеспечивающих существование решения уравнений (П.3) и (П.4).

Вычисляется D^opt для максимального значения Q_P по уравнению

(10)

${{\left( {\frac{{{{K}_{i}}}}{2}} \right)}^{2}}{{\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right]}^{2}} - {{K}_{m}}{{K}_{i}} = 0,$

где A(D) по (П.1).

Получаем значения D^opt и maxQ_P(D^opt). Вычисляется S₀(D^opt) по решению (П.3) и (П.4) при D^opt и maxQ_P(D^opt), т.е. S₀(D^opt) получаем по формуле

(11)

$\begin{gathered} {{S}_{0}}\left( {{{D}^{{{\text{opt}}}}}} \right) = S_{{\text{1}}}^{'}\left( {{{D}^{{{\text{opt}}}}}} \right) = S_{{\text{2}}}^{'}\left( {{{D}^{{{\text{opt}}}}}} \right) = \\ = \frac{{\max {{Q}_{P}}}}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}\left( {\alpha {{D}^{{{\text{opt}}}}} + \beta } \right)}} + {{\left( {{{K}_{m}}{{K}_{i}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}. \\ \end{gathered} $

Получили координату оптимальной точки:

(12)

$\left[ {{{D}^{{{\text{opt}}}}},{{S}_{0}}\left( {{{D}^{{{\text{opt}}}}}} \right)} \right]\,\,\,{\text{для}}\,\,\,{\text{первого}}\,\,\,{\text{варианта}};$

(13)

$\left[ {{{D}^{{{\text{opt}}}}},{{M}_{0}}\left( {{{D}^{{{\text{opt}}}}}} \right)} \right]\,\,\,{\text{для}}\,\,\,{\text{второго}}\,\,\,{\text{варианта}},$

где

(14)

${{M}_{0}}\left( {{{D}^{{{\text{opt}}}}}} \right) = \frac{{{{D}^{{{\text{opt}}}}} + {{k}_{M}}}}{{{{k}_{M}}}}{{S}_{0}}\left( {{{D}^{{{\text{opt}}}}}} \right).$

Определяются границы по D для обоих вариантов формирования областей при условии

(15)

${{Q}_{P}} < \max {{Q}_{P}}.$

Для этого также решается уравнение (10), в котором используют A(D) по (П.1) при Q_P по (15).

Получено два значения D₁ и D₂. Значения одинаковы для обоих вариантов.

Вычисляются координаты S₀(D₁), S₀(D₂) и M₀(D₁), M₀(D₂). Отметим, что D₂ > D₁:

(16)

$\begin{gathered} {{S}_{0}}\left( {{{D}_{1}}} \right) = \frac{{{{Q}_{P}}}}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}\left( {\alpha {{D}_{1}} + \beta } \right)}} + {{\left( {{{K}_{m}}{{K}_{i}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}; \\ {{S}_{0}}\left( {{{D}_{2}}} \right) = \frac{{{{Q}_{P}}}}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}\left( {\alpha {{D}_{2}} + \beta } \right)}} + {{\left( {{{K}_{m}}{{K}_{i}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ \end{gathered} $

(17)

$\begin{gathered} {{M}_{0}}\left( {{{D}_{1}}} \right) = \frac{{{{D}_{1}} + {{k}_{M}}}}{{{{k}_{M}}}}{{S}_{0}}\left( {{{D}_{1}}} \right); \\ {{M}_{0}}\left( {{{D}_{2}}} \right) = \frac{{{{D}_{2}} + {{k}_{M}}}}{{{{k}_{M}}}}{{S}_{0}}\left( {{{D}_{2}}} \right). \\ \end{gathered} $

Учитывая D₂ > D₁, получаем S₀(D₁) > S₀(D₂) и M₀(D₂) > M₀(D₁).

Координаты двух ограничивающих точек:

для первого варианта

(18)

$\left[ {{{D}_{1}},{{S}_{0}}\left( {{{D}_{1}}} \right)} \right]\,\,\,\,{\text{и}}\,\,\,\,\left[ {{{D}_{2}},{{S}_{0}}\left( {{{D}_{2}}} \right)} \right]$

для второго варианта

(19)

$\left[ {{{D}_{1}},{{M}_{0}}\left( {{{D}_{1}}} \right)} \right]\,\,\,{\text{и}}\,\,\,\left[ {{{D}_{2}},{{M}_{0}}\left( {{{D}_{2}}} \right)} \right].$

Далее вычисляются ограничивающие значения D₃ и D₄.

Для двух вариантов эти значения разные.

Для первого варианта обозначим D₃ и D₄ как $D_{3}^{1}$ и $D_{4}^{1}.$

(20)

$\begin{gathered} D_{3}^{1}\,\,{\text{по}}\,\,{\text{условию}}\,\,\max S_{{\text{1}}}^{'}\left( D \right), \\ {\text{где}}\,\,S_{{\text{1}}}^{'}\left( D \right)\,\,{\text{по}}\,\,\left( {{\text{П}}{\text{.3}}} \right). \\ \end{gathered} $

(21)

$\begin{gathered} D_{4}^{1}\,\,{\text{по}}\,\,{\text{условию}}\,\,\min S_{{\text{2}}}^{'}\left( D \right), \\ {\text{где}}\,\,S_{{\text{2}}}^{'}\left( D \right)\,\,{\text{по}}\,\,\left( {{\text{П}}{\text{.4}}} \right). \\ \end{gathered} $

По $D_{3}^{1}$ и $D_{4}^{1}$ вычисляются ${{S}_{0}}\left( {D_{3}^{1}} \right)$ и ${{S}_{0}}\left( {D_{4}^{1}} \right){\text{:}}$ ${{S}_{0}}\left( {D_{3}^{1}} \right) = S_{{\text{1}}}^{'}\left( {D_{3}^{1}} \right);$ ${{S}_{0}}\left( {D_{4}^{1}} \right) = S_{{\text{2}}}^{'}\left( {D_{4}^{1}} \right).$

Для первого варианта определены координаты еще двух ограничивающих точек:

(22)

$\left[ {D_{3}^{1},{{S}_{0}}\left( {D_{3}^{1}} \right)} \right]\,\,\,{\text{и}}\,\,\,\left[ {D_{4}^{1},{{S}_{0}}\left( {D_{4}^{1}} \right)} \right].$

Таким образом, область значений S₀ для первого варианта полностью определена.

D₃ и D₄ для второго варианта обозначим $D_{3}^{2}$ и $D_{4}^{2}.$ $D_{3}^{2}$ вычисляется по условию

(23)

$\begin{gathered} D_{3}^{2}\,\,{\text{есть}}\,\,\max \frac{{D + {{k}_{M}}}}{{{{k}_{M}}}}S_{{\text{1}}}^{'}\left( D \right), \\ {\text{где}}\,\,S_{{\text{1}}}^{'}\left( D \right)\,\,{\text{по}}\,\,\left( {{\text{П}}{\text{.3}}} \right); \\ \end{gathered} $

(24)

$\begin{gathered} D_{4}^{2}\,\,{\text{есть}}\,\,\min \frac{{D + {{k}_{M}}}}{{{{k}_{M}}}}S_{{\text{2}}}^{'}\left( D \right), \\ {\text{где}}\,\,S_{{\text{2}}}^{'}\left( D \right)\,\,{\text{по}}\,\,\left( {{\text{П}}{\text{.4}}} \right). \\ \end{gathered} $

По $D_{3}^{2}$ и $D_{4}^{2}$ вычисляются

$\begin{gathered} {{M}_{0}}\left( {D_{3}^{2}} \right) = \frac{{D_{3}^{2} + {{k}_{M}}}}{{{{k}_{M}}}}S_{{\text{1}}}^{'}\left( {D_{3}^{2}} \right); \\ {{M}_{0}}\left( {D_{4}^{2}} \right) = \frac{{D_{4}^{2} + {{k}_{M}}}}{{{{k}_{M}}}}S_{{\text{1}}}^{'}\left( {D_{4}^{2}} \right). \\ \end{gathered} $

Для второго варианта также определены координаты еще двух ограничивающих точек:

(25)

$\left[ {D_{3}^{2},{{M}_{0}}\left( {D_{3}^{2}} \right)} \right]\,\,{\text{и}}\,\,\left[ {D_{4}^{2},{{M}_{0}}\left( {D_{4}^{2}} \right)} \right].$

Таким образом, область значений M₀ для второго варианта полностью определена.

Точки с координатами для первой области (по S₀) и второй (по M₀) назовем “особыми” точками. Номера особых точек для первого варианта обозначим 1, 2, 3, 4, 5; для второго 1′, 2′, 3′, 4′, 5′:

(26)

$\begin{gathered} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{первый}}\,\,{\text{вариант}}\,\,\,\,\,\,\,\,\,\,\,{\text{второй}}\,\,{\text{вариант}} \hfill \\ {\text{особая точка }}1\,\,\left[ {{{D}_{1}},{{S}_{0}}\left( {{{D}_{1}}} \right)} \right]\,\,\,\,\,\,\,\,\,\,\,\,1'\,\,\left[ {{{D}_{1}},{{M}_{0}}\left( {{{D}_{1}}} \right)} \right] \hfill \\ \end{gathered} $

(27)

${\text{особая точка }}2\,\,\,\left[ {{{D}_{2}},{{S}_{0}}\left( {{{D}_{2}}} \right)} \right]\,\,\,\,\,\,\,\,\,2{\kern 1pt} '\,\,\,\left[ {{{D}_{2}},{{M}_{0}}\left( {{{D}_{2}}} \right)} \right]$

(28)

${\text{особая точка }}3\,\,\,\left[ {D_{3}^{1},{{S}_{0}}\left( {D_{3}^{1}} \right)} \right]\,\,\,\,\,\,\,\,3'\,\,\left[ {D_{3}^{2},{{M}_{0}}\left( {D_{3}^{2}} \right)} \right]$

(29)

${\text{особая точка }}4\,\,\left[ {D_{4}^{1},{{S}_{0}}\left( {D_{4}^{1}} \right)} \right]\,\,\,\,\,\,\,\,\,4'\,\,\left[ {D_{4}^{2},{{M}_{0}}\left( {D_{4}^{2}} \right)} \right]$

(30)

${\text{особая точка }}5\,\,\left[ {{{D}^{{{\text{opt}}}}},{{S}_{0}}\left( {{{D}^{{{\text{opt}}}}}} \right)} \right]\,\,\,5'\,\,\left[ {{{D}^{{{\text{opt}}}}},{{M}_{0}}\left( {{{D}^{{{\text{opt}}}}}} \right)} \right]$

Точки 5 и 5′ есть точки экстремума.

ОЦЕНКИ КОМПОНЕНТОВ МНОЖЕС В ВХОДНЫХ ПОКАЗАТЕЛЕЙ (ВТОРАЯ ЗАДАЧА)

Для каждой из особых точек первого и второго варианта сформированы формулы вычисления компонентов множеств S₀ и M₀. Значение величины протока для каждой особой точки является фиксированным.

В табл. 1 представлены соотношения, формирующие множества S₀ и M₀ для точки экстремума и особых точек первого варианта.

Таблица 1.

Соотношения для вычисления компонент множеств для S₀ и M₀ для точки оптимального условия и особых точек

Обозначения
Оптимальная точка
${{D}^{{{\text{opt}}}}}$, ч^–1; ${{S}_{{{\text{opt}}}}} = {{S}_{0}}\left( {{{D}^{{{\text{opt}}}}}} \right)$, г/л

$S_{0}^{i} = {{S}_{{{\text{opt}}}}}\frac{{{{n}_{0}} - i}}{{{{n}_{0}}}}$ (31)
$M_{0}^{i} = \frac{i}{{{{n}_{0}}}} \cdot \frac{{{{D}^{{{\text{opt}}}}} + {{k}_{M}}}}{{{{k}_{M}}}}{{S}_{{{\text{opt}}}}}$ (32)

k = 1.0. Особая точка 1:
$D{}_{1}$; ${{S}_{1}} = {{S}_{0}}\left( {{{D}_{1}}} \right)$
k = 2.0. Особая точка 2:
$D{}_{2}$; ${{S}_{2}} = {{S}_{0}}\left( {{{D}_{2}}} \right)$
k = 3.0. Особая точка 3:
${{D}_{3}} = D_{3}^{1}$; ${{S}_{3}} = {{S}_{0}}\left( {D_{3}^{1}} \right)$
k = 4.0. Особая точка 4:
${{D}_{4}} = D_{4}^{1}$; ${{S}_{4}} = {{S}_{0}}\left( {D_{4}^{1}} \right)$

$S_{0}^{i} = {{S}_{k}}\frac{{{{n}_{k}} - i}}{{{{n}_{k}}}}$ (33)
$M_{0}^{i} = \frac{i}{{{{n}_{k}}}} \cdot \frac{{{{D}_{k}} + {{k}_{M}}}}{{{{k}_{M}}}}{{S}_{k}}$ (34)
Значения ${{n}_{0}}$ и ${{n}_{k}}$ задает пользователь;
$i = 0 - {{n}_{0}}$; $i = 0 - {{n}_{k}}$

Условия вычисления $S_{0}^{i}$ определяются следующими неравенствами:

для оптимальной точки

$0 \leqslant S_{0}^{i} \leqslant {{S}_{{{\text{opt}}}}};$

для особых точек 1–4

$0 \leqslant S_{0}^{i} \leqslant {{S}_{k}}.$

Пользователь имеет возможность выбрать или задать значение $S_{0}^{i},$ отвечающее условиям точки оптимума или какой-либо из особых точек.

Формула вычисления $M_{0}^{i}$ в табл. 1 получена для каждого принятого или заданного значения $S_{0}^{i}{\text{:}}$

$\begin{gathered} M_{0}^{i} = \frac{{{{D}^{{{\text{opt}}}}} + {{k}_{M}}}}{{{{k}_{M}}}}\left[ {{{S}_{{{\text{opt}}}}} - S_{0}^{i}} \right]-- \\ {\text{для}}\,\,{\text{оптимальной}}\,\,{\text{точки}}, \\ \end{gathered} $

$\begin{gathered} M_{0}^{i} = \frac{{{{D}_{k}} + {{k}_{M}}}}{{{{k}_{M}}}}\left[ {{{S}_{k}} - S_{0}^{i}} \right]--~ \\ {\text{для}}\,\,{\text{особых}}\,\,{\text{точек}}\,\,{\text{1}}{\kern 1pt} --{\kern 1pt} {\text{4}}, \\ \end{gathered} $

где ${{S}_{{{\text{opt}}}}}$ и ${{S}_{k}}$ – значения исходных данных.

В табл. 2 представлены соотношения, формирующие множества M₀ и S₀ для точки экстремума и особых точек второго варианта.

Таблица 2.

Соотношения для вычисления компонент множеств для M₀ и S₀ для точки оптимального условия и особых точек

Обозначения
Оптимальная точка
${{D}^{{{\text{opt}}}}}$, ч^–1; ${{M}_{{{\text{opt}}}}} = {{M}_{{\text{0}}}}\left( {{{D}^{{{\text{opt}}}}}} \right)$, г/л

$M_{0}^{i} = {{M}_{{{\text{opt}}}}}\frac{{{{n}_{0}} - i}}{{{{n}_{0}}}}$ (39)
$S_{0}^{i} = \frac{i}{{{{n}_{0}}}} \cdot \frac{{{{k}_{M}}}}{{{{D}^{{{\text{opt}}}}} + {{k}_{M}}}}{{M}_{{{\text{opt}}}}}$ (40)

k = 1.0. Особая точка 1′:
$D{}_{1}$; ${{M}_{1}} = {{M}_{0}}\left( {{{D}_{1}}} \right)$
k = 2.0. Особая точка 2′:
$D{}_{2}$; ${{M}_{2}} = {{M}_{0}}\left( {{{D}_{2}}} \right)$
k = 3.0. Особая точка 3′:
${{D}_{3}} = D_{3}^{2}$; ${{M}_{3}} = {{M}_{0}}\left( {D_{3}^{2}} \right)$
k = 4.0. Особая точка 4′:
${{D}_{4}} = D_{4}^{2}$; ${{M}_{4}} = {{M}_{0}}\left( {D_{4}^{2}} \right)$

$M_{0}^{i} = {{M}_{k}}\frac{{{{n}_{k}} - i}}{{{{n}_{k}}}}$ (41)
$S_{0}^{i} = \frac{i}{{{{n}_{k}}}} \cdot \frac{{{{k}_{M}}}}{{{{D}_{k}} + {{k}_{M}}}}{{M}_{k}}$ (42)

Условия вычисления $M_{0}^{i}$ определяются следующими неравенствами:

для точки экстремума

(43)

$0 \leqslant M_{0}^{i} \leqslant {{M}_{{{\text{opt}}}}};$

для особых точек

(44)

$0 \leqslant M_{0}^{i} \leqslant {{M}_{k}}.$

Пользователь имеет возможность выбрать или задать значение $M_{0}^{i},$ отвечающее условиям точки оптимума или какой-либо из особых точек.

Формула вычисления $S_{0}^{i}$ в табл. 2 получена для каждого принятого или заданного значения $M_{0}^{i}.$

ЧИСЛЕННЫЙ РАСЧЕТ

Численный расчет выполняется с использованием констант для уравнений (1)–(6), приведенных в табл. 3 [1–3].

Таблица 3.

Численные значения констант для базового варианта

K_m, г/л	K_i, г/л	µ_max, ч^–1	X_max, г/л	P_max, г/л	n₁	n₂	Y_X/S, г/г	k_M, ч^–1	α, г/г	β, ч^–1	α_B, г/г	β_B, ч^–1
1.2	164	0.48	30	98.0	0.5	0.5	0.4	0.035	2.2	0.02	1.1	0.01

Используя теоретические соотношения, получены следующие координаты особых точек для обоих вариантов:

1: S₀ = 77.6 г/л; ${{D}_{1}} = 0.09818$ ч^–1; 2: S₀ = 35.35 г/л; ${{D}_{2}} = 0.3107$ ч^–1; 3: ${{S}_{0}} = 143.28$ г/л; ${{D}_{3}} = 0.138$ ч^–1; 4: ${{S}_{0}} = 29.0$ г/л; ${{D}_{4}} = 0.28$ ч^–1; 5: ${{S}_{{\text{0}}}} = 57.4$ г/л; ${{D}_{5}} = 0.205$ ч^–1.

1′: ${{M}_{0}} = 295.28$ г/л; ${{D}_{1}} = 0.09818$ ч^–1; 2′: ${{M}_{0}} = 349.16$ г/л; ${{D}_{2}} = 0.3107$ ч^–1; 3′: M₀ = 773.1 г/л; ${{D}_{3}} = 0.18$ ч^–1; 4′: ${{M}_{0}} = 234.96$ г/л; ${{D}_{4}} = 0.18$ ч^–1; 5′: ${{M}_{0}} = 393.6$ г/л; ${{D}_{5}} = 0.205$ ч^–1.

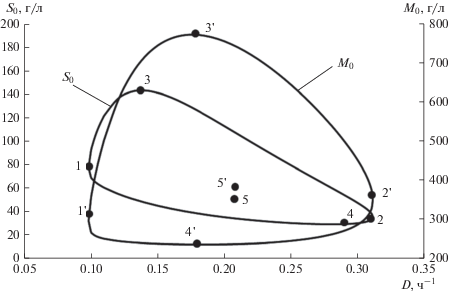
На рис. 1 показаны портреты областей для обоих вариантов, построенные с использованием численных значений констант (табл. 3) для продуктивности Q_P = 6 г/(л ч).

Рис. 1.

Портреты для S₀ и M₀: 1–5 и 1′–5′ положения особых точек.

Портреты построены по уравнениям (П.3) и (П.4) с использованием (П.2). Для портрета S₀ в (П.2) M₀ = 0. Для портрета M₀ в (П.2) S₀ = 0.

Полученные координаты особых точек отвечают следующим условиям: для первого варианта при M₀ = 0, для второго – при S₀ = 0.

Ниже приведем численные значения обеспечения положения особых точек величинами $S_{0}^{i}$ и $M_{0}^{i},$ т.е. примеры формирования множеств $\left\{ {S_{0}^{i},M_{0}^{i}} \right\}$ для каждой из особых точек, используя соотношения табл. 1 и 2 .

Для вычисления элементов множеств для особых точек обоих вариантов использовано условие Q_P = 6 г/(л ч) < maxQ_P.

Значение n₀ и n_k для всех особых точек (табл. 1 и 2 ) принято равным четырем (n₀ = 4, n_k = 4), значение i в расчетах по условию i = 0 – n₀ и i = 0 – n_k было одинаковым 0.0; 1.0; 2.0; 3.0; 4.0.

Вычисляются элементы множеств для особых точек с использованием вышеприведенных исходных данных.

В табл. 4 результаты вычислений $S_{0}^{i}$ и $M_{0}^{i}$ по исходным данным, приведенным выше (первый вариант).

Таблица 4.

Результаты расчета элементов множеств S₀ (г/л) и M₀ (г/л)

№ п/п	i	0	1	2	3	4
1	Особая точка 1	$S_{0}^{0} = 77.6$ $M_{0}^{0} = 0.0$	$S_{0}^{1} = 58.2$ $M_{0}^{1} = 73.82$	$S_{0}^{2} = 38.8$ $M_{0}^{2} = 147.64$	$S_{0}^{3} = 19.4$ $M_{0}^{3} = 231.46$	$S_{0}^{4} = 0.0$ $M_{0}^{4} = 295.28$
2	Особая точка 2	$S_{0}^{0} = 35.35$$M_{0}^{0} = 0.0$	$S_{0}^{1} = 26.51$ $M_{0}^{1} = 87.29$	$S_{0}^{2} = 17.67$ $M_{0}^{2} = 174.58$	$S_{0}^{3} = 8.83$ $M_{0}^{3} = 261.87$	$S_{0}^{4} = 0.0$ $M_{0}^{4} = 349.16$
3	Особая точка 3	$S_{0}^{0} = 143.28$$M_{0}^{0} = 0.0$	$S_{0}^{1} = 107.46$$M_{0}^{1} = 177.05$	$S_{0}^{2} = 71.64$$M_{0}^{2} = 354.11$	$S_{0}^{3} = 35.82$ $M_{0}^{3} = 531.16$	$S_{0}^{4} = 0.0$ $M_{0}^{4} = 708.06$
4	Особая точка 4	$S_{0}^{0} = 29.0$ $M_{0}^{0} = 0.0$	$S_{0}^{1} = 21.75$ $M_{0}^{1} = 65.25$	$S_{0}^{2} = 14.5$ $M_{0}^{2} = 13.05$	$S_{0}^{3} = 7.25$ $M_{0}^{3} = 195.75$	$S_{0}^{4} = 0.0$ $M_{0}^{4} = 261.0$
5	Особая точка 5	$S_{0}^{0} = 57.4$ $M_{0}^{0} = 0.0$	$S_{0}^{1} = 43.05$$M_{0}^{1} = 98.4$	$S_{0}^{2} = 28.7$ $M_{0}^{2} = 196.8$	$S_{0}^{3} = 14.35$$M_{0}^{3} = 295.7$	$S_{0}^{4} = 0.0$$M_{0}^{4} = 393.6$

В табл. 5 результаты вычислений $M_{0}^{i}$ и $S_{0}^{i}$ по исходным данным, приведенным выше (второй вариант).

Таблица 5.

Результаты расчета элементов множеств M₀ (г/л) и S₀ (г/л)

№ п/п	i	0	1	2	3	4
1	Особая точка 1′	$M_{0}^{0} = 295.28$$S_{0}^{0} = 0.0$	$M_{0}^{1} = 221.46$$S_{0}^{1} = 19.4$	$M_{0}^{2} = 147.64$$S_{0}^{2} = 38.8$	$M_{0}^{3} = 73.82$$S_{0}^{3} = 58.2$	$M_{0}^{4} = 0.0$$S_{0}^{4} = 77.6$
2	Особая точка 2′	$M_{0}^{0} = 349.16$$S_{0}^{0} = 0.0$	$M_{0}^{1} = 251.87$$S_{0}^{1} = 8.83$	$M_{0}^{2} = 174.58$$S_{0}^{2} = 17.67$	$M_{0}^{3} = 87.29$$S_{0}^{3} = 26.51$	$M_{0}^{4} = 0.0$$S_{0}^{4} = 35.35$
3	Особая точка 3′	$M_{0}^{0} = 773.1$$S_{0}^{0} = 0.0$	$M_{0}^{1} = 579.81$$S_{0}^{1} = 31.46$	$M_{0}^{2} = 386.54$$S_{0}^{2} = 62.93$	$M_{0}^{3} = 193.27$$S_{0}^{3} = 94.39$	$M_{0}^{4} = 0.0$$S_{0}^{4} = 125.85$
4	Особая точка 4′	$M_{0}^{0} = 234.96$$S_{0}^{0} = 0.0$	$M_{0}^{1} = 176.22$$S_{0}^{1} = 9.56$	$M_{0}^{2} = 117.48$$S_{0}^{2} = 19.125$	$M_{0}^{3} = 39.79$$S_{0}^{3} = 28.69$	$M_{0}^{4} = 0.0$$S_{0}^{4} = 38.25$
5	Особая точка 5′	$M_{0}^{0} = 393.6$$S_{0}^{0} = 0.0$	$M_{0}^{1} = 295.2$$S_{0}^{1} = 14.35$	$M_{0}^{2} = 196.8$$S_{0}^{2} = 28.7$	$M_{0}^{3} = 98.4$$S_{0}^{3} = 43.05$	$M_{0}^{4} = 0.0$$S_{0}^{4} = 57.4$

ЗАКЛЮЧЕНИЕ

Полученные координаты особых точек для обоих вариантов и теоретические соотношения для вычисления множеств технологических показателей для каждой из особых точек дают возможность более широкого использования сырьевых ресурсов (особенно в условиях их ограничения) для реального формирования технологического процесса получения молочной кислоты.

Исследование выполнено при финансовой поддержке РХТУ им. Д.И. Менделеева.

ПРИЛОЖЕНИЕ

(П.1)

$A\left( D \right) = {{\left( {1 - \frac{{{{Q}_{P}}}}{{{{X}_{{\max }}}\left( {\alpha D + \beta } \right)}}} \right)}^{{{{n}_{1}}}}}{{\left( {1 - \frac{{{{Q}_{P}}}}{{{{P}_{{\max }}}D}}} \right)}^{{{{n}_{2}}}}},$

(П.2)

$S{\kern 1pt} ' = {{S}_{0}} + \frac{{{{k}_{M}}{{M}_{0}}}}{{D + {{k}_{M}}}},$

(П.3)

$\begin{gathered} S_{{\text{1}}}^{'} = \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{{{{Q}_{P}}}}{{\left( {\alpha D + \beta } \right)}} + \frac{{{{K}_{i}}}}{2}\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right] + \\ + \,\,\sqrt {{{{\left( {\frac{{{{K}_{i}}}}{2}} \right)}}^{2}}{{{\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right]}}^{2}} - {{K}_{m}}{{K}_{i}}} , \\ \end{gathered} $

(П.4)

$\begin{gathered} S_{{\text{2}}}^{'} = \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{{{{Q}_{P}}}}{{\left( {\alpha D + \beta } \right)}} + \frac{{{{K}_{i}}}}{2}\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right] - \\ - \,\,\sqrt {{{{\left( {\frac{{{{K}_{i}}}}{2}} \right)}}^{2}}{{{\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right]}}^{2}} - {{K}_{m}}{{K}_{i}}} , \\ \end{gathered} $

(П.5)

${{\left( {\frac{{{{K}_{i}}}}{2}} \right)}^{2}}{{\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right]}^{2}} - {{K}_{m}}K = 0.$

ОБОЗНАЧЕНИЯ

B	концентрация суммарного количества побочных продуктов, г/л
D	величина протока, ч^–1
K_i	константа ингибирования, г/л
K_m	константа насыщения субстрата, г/л
k_M	константа, определяющая количество воспроизведенного субстрата, ч^–1
M	концентрация сырья, дополнительно воспроизводящего субстрат, г/л
P	концентрация продукта, г/л
Q_P	продуктивность, г/(л ч)
S	концентрация субстрата, г/л
X	концентрация биомассы, г/л
Y_X/S	стехиометрический коэффициент, г/г
α, α_B, β, β_B	константы
µ	удельная скорость роста микроорганизмов, ч^–1

ИНДЕКСЫ

0	начальное значение
max	максимальное значение
opt	оптимальное значение

Список литературы

Hofvendahl K., Hahn-Hägerdal B. Factors affecting the fermentative lactic acid production from renewable resources // Enzyme Microb. Technol. 2000. V. 26. P. 87.
Gordeeva Yu.L., Rudakovskaya E.G., Gordeeva E.L., Borodkin A.G. Mathematical modeling of biotechnological process of lactic acid production by batch fermentation: A review // Theor. Found. Chem. Eng. 2017. V. 51. № 3. P. 282. [Гордеева Ю.Л., Рудаковская Е.Г., Гордеева Е.Л., Бородкин А.Г. Математическое моделирование биотехнологического процесса периодической ферментации получения молочной кислоты. Обзор // Теор. осн. хим. технол. 2017. Т. 51. № 3. С. 270.]
Gordeev L.S., Koznov A.V., Skichko A.S., Gordeeva, Yu.L. Unstructured mathematical models of lactic acid biosynthesis kinetics: A review // Theor. Found. Chem. Eng. 2017. V. 51. № 2. P. 175. [Гордеев Л.С., Кознов А.В., Скичко А.С., Гордеева Ю.Л. Неструктурированные математические модели кинетики биосинтеза молочной кислоты. Обзор // Теор. осн. хим. технол. 2017. Т. 51. № 2. С. 8.]
Гордеева Ю.Л., Меньшутина Н.В., Гордеева Е.Л., Комиссаров Ю.А. Алгоритм обеспечения реальных условий множественности в процессах микробиологического синтеза при заданной величине протока // Вестн. Астрах. гос. тех. унив. Сер.: Упр., вычисл. тех. инф. 2016. № 2. С. 60.
Gonzalez K., Tebbani S., Lopes F., Thorigné A., Givry S., Dumur D., Pareau D. Modeling the continuous lactic acid production process from wheat flour // Appl. Microbiol. Biotechnol. 2016. V. 100. № 1. P. 147.
Vázquez J.A., Murado M.A. Unstructured mathematical model for biomass, lactic acid and bacteriocin production by lactic acid bacteria in batch fermentation // J. Chem. Technol. Biotechnol. 2008. V. 83. № 1. P. 91.
Bouguettoucha A., Balannec B., Amrane A. Unstructured models for lactic acid fermentation – A Review // Food Technol. Biotechnol. 2011. V. 49. № 1. P. 3.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал