Теоретические основы химической технологии, 2021, T. 55, № 3, стр. 339-346
Математическое моделирование тепло- и массопереноса при сушке гранул носителя для никелевого катализатора
М. К. Кошелева a, *, В. П. Мешалкин b, О. Р. Дорняк c
a Российский государственный университет им. А.Н. Косыгина (Технологии. Дизайн. Искусство)
Москва, Россия
b Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия
c Воронежский государственный лесотехнический университет им. Г.Ф. Морозова
Воронеж, Россия
* E-mail: oxtpaxt@yandex.ru
Поступила в редакцию 21.12.2020
После доработки 11.01.2021
Принята к публикации 14.01.2021
Аннотация
Представлены результаты исследования процесса конвективной сушки цилиндрических гранул носителя для никелевого катализатора методами математического моделирования. Сформулирована математическая модель интенсивного тепло- и массопереноса в грануле, которая позволяет выбирать рациональные режимы конвективной сушки. Особенностью математической модели является аналитический расчет локальных коэффициентов массопереноса жидкости с учетом сорбционных свойств материала, коэффициента проницаемости, локальных значений влажности и температуры. Сравнение результатов математического моделирования тепло- и массопереноса в грануле и данных лабораторного эксперимента показало их удовлетворительное совпадение.
ВВЕДЕНИЕ
Технологическая схема производства никелевого катализатора включает процессы, связанные с получением носителя, характеристики которого имеют важное значение для его активности [1]. Активность никелевых катализаторов в отношении реакции гидрирования зависит от площади поверхности, покрытой никелем [2].
В качестве сырья для носителя наибольшее применение имеют оксиды алюминия и магния, шамот, портландцемент, природные глины. Гранулы носителя для никелевого катализатора получают из влажной пасты методом экструзии [1]. При высушивании гранул формируется капиллярно-пористая система с высокой удельной поверхностью. В последующих технологических операциях развитая поверхность носителя адсорбирует необходимые активные вещества. Выбор режимов подготовительных операций, в том числе, операции сушки имеет важное значение. Конвективная сушка гранул носителя – интенсивный высокотемпературный процесс, при осуществлении которого возможно нарушение целостности гранул. Разрушение гранул обусловлено высоким уровнем интенсивности внутренних напряжений вследствие формирования высоких градиентов влагосодержания в высушиваемом материале [3].
Цель работы – изучение развития нестационарных полей влагосодержания, температуры, давления парогазовой фазы от параметров сушильного агента для определения наиболее эффективных технологических режимов конвективной сушки выбранного носителя. Прогнозирование результата термообработки влажных гранул носителя, которое дает возможность оценки надежности химико-технологического процесса, выполнено с использованием методов и принципов математического моделирования [4, 5].
Математическое моделирование процесса конвективной сушки капиллярно-пористых материалов проводилось многими исследователями на основе различных подходов. В публикациях [6–11] используются уравнения для усредненных по объему значений температуры и концентрации влаги, которые анализируются с помощью численных [6–9] или аналитических методов [10, 11].
Авторы [12–14] в своих исследованиях опираются на диффузионно-фильтрационную модель А.В. Лыкова [3], которая позволяет изучать взаимосвязанный тепломассоперенос в капиллярно-пористой среде. Зависимыми переменными модели наиболее часто являются усредненные по объему материала температура, влагосодержание (в виде жидкой и паровой фаз), а также реже – общее давление. В [15, 16] разработаны математические модели сушки проблемы сушки исследуются на основе уравнений двухфазной фильтрации и уравнений изотерм сорбции.
В работах [17–19] проанализированы результаты моделирования процессов сушки на основе более общего подхода, в основу которого положено представление о ненасыщенных капиллярно-пористых материалах как трехфазных систем [20, 21]. Сложность описания теплофизических явлений в данном случае связана, в том числе, с необходимостью изучения процессов переноса в каждой фазе в отдельности с учетом эффектов взаимодействия фаз, не все из которых исследованы в настоящее время в полной мере. В данной работе используется математическая модель интенсивного тепло- и массопереноса [22–24], полученная как частный случай многофазной модели, которая является некоторым обобщением модели тепло- и влагопереноса А.В. Лыкова [3].
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Математическая модель тепло- и массопереноса в цилиндрической грануле носителя построена при следующих предположениях. Температура всех фаз капиллярно-пористого тела одинакова (однотемпературное приближение). Фазовые переходы происходят по равновесной схеме. Конвективным переносом тепла можно пренебречь. Давление, температура и относительная влажность воздуха в сушильной камере имеют постоянные значения. Все теплофизические характеристики не зависят от угловой координаты. Для изучения процессов переноса достаточно рассмотреть задачу в осесимметричном приближении, т.е. влагосодержание u, температура T, давление парогазовой смеси p и концентрация пара χ являются функциями времени, радиальной и осевой координат – u = u(t, r, z), T = T(t, r, z), p = p(t, r, z), χ = χ(t, r, z). Математическая модель включает:
– уравнение переноса жидкой фазы
(1)
$\begin{gathered} \frac{{\partial u}}{{\partial t}} = \frac{1}{r}\frac{\partial }{{\partial r}}\left[ {r{{a}_{m}}(u,T)\frac{{\partial u}}{{\partial r}}} \right] + \frac{\partial }{{\partial z}}\left[ {{{a}_{m}}(u,T)\frac{{\partial u}}{{\partial z}}} \right] - \frac{{{{s}_{{12}}}j}}{{{{\alpha }_{3}}\rho _{3}^{^\circ }}}, \\ {{a}_{m}} = \frac{{{{K}_{{23}}}}}{{{{\mu }_{2}}}} \cdot \frac{{RTu}}{{{\bar {v}}}} \cdot \frac{1}{\varphi }\frac{{\partial \varphi }}{{\partial u}}, \\ \end{gathered} $– уравнение теплопроводности
(2)
$\begin{gathered} c\rho \frac{{\partial T}}{{\partial t}} = \frac{1}{r}\frac{\partial }{{\partial r}}\left[ {r\lambda (u,T)\frac{{\partial T}}{{\partial r}}} \right] + \frac{\partial }{{\partial z}}\left[ {\lambda (u,T)\frac{{\partial T}}{{\partial z}}} \right] + \\ + \,\,L{\kern 1pt} '\varepsilon \rho \frac{{\partial u}}{{\partial t}},\,\,\,\,\varepsilon = \frac{{{{c}_{{v1}}}}}{{L{\kern 1pt} '}}\frac{1}{{1 + u}}(T - {{T}_{{sat}}}({{p}_{{1v}}})), \\ \lambda = {{\alpha }_{1}}{{\lambda }_{1}} + {{\alpha }_{2}}{{\lambda }_{2}} + {{\alpha }_{3}}{{\lambda }_{3}}, \\ c\rho = {{c}_{{p1}}}\rho _{1}^{^\circ }{{\alpha }_{1}} + {{c}_{{p2}}}\rho _{2}^{^\circ }{{\alpha }_{2}} + {{c}_{{p3}}}\rho _{3}^{^\circ }{{\alpha }_{3}}; \\ \end{gathered} $– уравнение давления парогазовой смеси [24]
(3)
$\begin{gathered} \frac{{\partial {{p}_{1}}}}{{\partial t}} = {{p}_{1}}\frac{{{{K}_{{13}}}}}{{{{\mu }_{1}}}}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{p}_{1}}}}{{\partial r}}} \right) + \frac{{{{\partial }^{2}}{{p}_{1}}}}{{\partial {{z}^{2}}}}} \right] + \frac{{{{p}_{1}}}}{T}\frac{{\partial T}}{{\partial t}} + \\ + \,\,\frac{{{{p}_{1}}}}{{{{B}_{1}}}}\frac{{\partial {{B}_{1}}}}{{\partial t}} - \frac{{{{p}_{1}}}}{{{{\alpha }_{1}}}}\frac{{\partial {{\alpha }_{1}}}}{{\partial t}} + \frac{{{{s}_{{12}}}j{{T}_{1}}{{B}_{1}}}}{{{{\alpha }_{1}}}}, \\ \end{gathered} $– уравнение для концентрации газовой компоненты в паровоздушной смеси
(4)
$\begin{gathered} \frac{{\partial \left( {\rho _{1}^{^\circ }{{\alpha }_{1}}(1 - \chi )} \right)}}{{\partial t}} + \frac{1}{r}\frac{\partial }{{\partial r}}\left[ {r\left( {\rho _{1}^{^\circ }{{\alpha }_{1}}(1 - \chi )\left( {{v}_{1}^{r} + w_{{1g}}^{r}} \right)} \right)} \right] + \\ + \,\,\frac{{\partial (\rho _{1}^{^\circ }{{\alpha }_{1}}(1 - \chi )(v_{1}^{z} + w_{{1g}}^{z}))}}{{\partial z}} = 0; \\ \chi = \frac{{\rho _{{1v}}^{^\circ }}}{{\rho _{1}^{^\circ }}},\,\,\,\,1 - \chi = \frac{{\rho _{{1g}}^{^\circ }}}{{\rho _{1}^{o}}}. \\ \end{gathered} $Уравнения переноса (1)–(4) дополняются:
– уравнением политермы сорбции, полученной путем обработки экспериментальных данных вида
– уравнениями состояния для паровой и газовой компонент
(6)
$\begin{gathered} {{p}_{1}} = \rho _{1}^{^\circ }T{{B}_{1}},\,\,\,\,{{p}_{{1g}}} = \rho _{{1g}}^{^\circ }T{{B}_{{1g}}},\,\,\,\,{{p}_{{1v}}} = \rho _{{1v}}^{^\circ }T{{B}_{{1v}}}, \\ \rho _{1}^{^\circ } = \rho _{{1g}}^{^\circ } + \rho _{{1v}}^{^\circ },\,\,\,\,{{B}_{1}} = \chi {{B}_{{1v}}} + (1 - \chi ){{B}_{{1g}}}, \\ \end{gathered} $– законом диффузии Фика
(7)
$w_{{1g}}^{r} = \frac{{\rho _{1}^{^\circ }}}{{\rho _{{1g}}^{^\circ }}}D\frac{{\partial \chi }}{{\partial r}},\,\,\,\,w_{{1g}}^{z} = \frac{{\rho _{1}^{^\circ }}}{{\rho _{{1g}}^{^\circ }}}D\frac{{\partial \chi }}{{\partial z}},$– законом фильтрации Дарси
(8)
${v}_{1}^{r} = - \frac{{{{K}_{{13}}}}}{{{{\mu }_{1}}}}\frac{{\partial {{p}_{1}}}}{{\partial r}},\,\,\,\,{v}_{1}^{z} = - \frac{{{{K}_{{13}}}}}{{{{\mu }_{1}}}}\frac{{\partial {{p}_{1}}}}{{\partial z}},$– законом Дальтона для вычисления интенсивности фазовых переходов
– формулой Антуана для определения давления насыщенного пара при данной температуре
(10)
${{p}_{{sat}}} = \exp ({{{{A}_{s}} - {{B}_{s}}} \mathord{\left/ {\vphantom {{{{A}_{s}} - {{B}_{s}}} {(T + {{C}_{s}})}}} \right. \kern-0em} {(T + {{C}_{s}})}}),$а также начальными и граничными условиями
(11)
$\begin{gathered} T(0,r,z) = {{T}_{0}}(r,z),\,\,\,\,u(0,r,z) = {{u}_{0}}(r,z), \\ {{p}_{1}}(0,r,z) = {{p}_{{10}}}(r,z),\,\,\,\,\chi (0,r,z) = {{\chi }_{0}}(r,z), \\ \end{gathered} $(12)
$\begin{gathered} {{\left. { - \lambda \frac{{\partial T}}{{\partial n}}} \right|}_{\Gamma }} = {{\alpha }^{Г}}\left( {{{{\left. T \right|}}_{\Gamma }} - {{T}_{m}}} \right),\,\,\,\,{{\left. u \right|}_{\Gamma }} = {{u}_{{eq}}}, \\ {{\left. \chi \right|}_{\Gamma }} = {{\chi }_{m}},\,\,\,\,{{\left. {{{p}_{1}}} \right|}_{\Gamma }} = {{p}_{{atm}}}. \\ \end{gathered} $Отметим, что важной особенностью модели является применение оригинальных расчетных формул для вычисления изменяющихся со временем локальных коэффициентов диффузии жидкости am и значений критерия фазового перехода ε в (1) и (2).
Нестационарная нелинейная математическая модель (1)–(12) исследована численно с использованием метода контрольного объема и итерационного алгоритма [25]. Тестирование программного комплекса проведено на основе ряда точных решений для линейных уравнений параболического типа с дополнительными источниковыми членами. Корректность расчетов подтверждена также исследованием сходимости конечно-разностного аналога задачи с использованием сгущающихся сеток.
РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ
Численные расчеты проведены для гранул, содержащих каолин, окись магния, нитрат и карбонат никеля с плотностью ρ0 = 1250 кг/м3. Плотность вещества, образующего пористый скелет $\rho _{3}^{^\circ }$ = = 1920 кг/м3. Объем пор носителя в грамме материала составляет 0.28 см3/г. Радиус основания цилиндрической гранулы R варьировался в диапазоне 0.005 до 0.01 м, а высота L – 0.002–0.04 м.
Расчеты выполнены при следующих значениях теплофизических параметров.
Водяной пар и воздух: R = 8.3144 Дж/(моль К); B1v = 461.9 Дж/(кг K); B1g = 284 Дж/(кг K); μ1 = = 10–6 Па с; λ1 = 0.0248 Вт/(м K); сp 1v = 2.034 × × 103 Дж/(кг K); сp 1g = 9.05 × 102 Дж/(кг K); сv 1v = = 1.58 × 103 Дж/(кг K); сv 1g = 7.07 × 102 Дж/(кг K); patm = 1.013 × 105 Па; D = 2.16 × 10‑5 м2/c.
Вода: $\rho _{2}^{^\circ }$ = 103 кг/м3; μ2 = 10–3 Па с; $V_{2}^{'}$ = 18 × × 10–6 м3/моль; λ2 = 0.648 Вт/(м K), сp2 = 4.2 × × 103 Дж/(кг K); L' = 2.25 × 106 м3/моль; κ2 = = 3.375 × 10–7.
Твердая фаза материала носителя никелевого катализатора: λ3 = 1.75 Вт/(м K), сp3 = 865 Дж/(кг K); Κ13 = 10–10 м2; Κ23 = 10–19 м2; s12 = 7.5 × 107 м–1.
Коэффициент теплоотдачи от образца к сушильному агенту вычислялся по критерию Нуссельта для вынужденной конвекции согласно эмпирической формуле А.В. Нестеренко в зависимости от чисел Рейнольдса и Прандтля [3]. Среднее значение αГ = 3.1 × 102 Вт/(м2 K). Число Био Bi3 = λ3αГ/R для образца с радиусом R = 0.005 м равно ~2.2.
Для описания сорбционных возможностей материала носителя принято уравнение Л.Б. Цимерманиса, полученное в [26] на основе термодинамического анализа. Для типичных капиллярно-пористых тел это уравнение имеет следующий вид:
(17)
$u = {{u}_{{mg}}}{{\varphi }^{{{{a}_{0}}{{k}^{{{\varphi }}}}}}},\,\,\,\,{{u}_{{mg}}} = {{u}_{{SO}}} - {{\alpha }_{{ST}}}(T - 273),$На основе опытных изотерм сорбции для материала носителя с использованием метода наименьших квадратов определены постоянные уравнения политермы сорбции (17): а0 = 1.111; k = 5.021; us0 = 0.3; αST = 1.17 × 10–4.
Принято, что конвективная сушка происходит при постоянном внешнем давлении, равном атмосферному. Температура сушильного агента и его относительное влагосодержание варьировались в интервалах: Tm = 353–423 K, φm = 0.015–0.85. Скорость потока равна 7 м/с. Начальные значения влагосодержания и температуры образцов: u0 = 0.46, T0 = 298 К.
Для верификации математической модели использованы данные лабораторного эксперимента [27], полученные при конвективной сушке гранул с влагоизолированными боковыми поверхностями. Предварительно материал подвергался термической обработке в термостате до достижения им практически однородного распределения температуры со значением равным температуре сушильного агента. Рисунок 1 показывает удовлетворительное совпадение результатов расчета кинетики сушки гранул носителя никелевого катализатора с экспериментальными временными зависимостями для величины усредненного влагосодержания при различных режимах сушки.
Рис. 1.
Зависимость среднего влагосодержания от времени при сушке гранул носителя никелевого катализатора с изолированными боковыми поверхностями при R = 0.005 м, R/L = 0.125 для различных режимов: 1 – Tm = 353 K и φm = 0.45; 2 – 373 K и 0.05; 3 – 393 K и 0.025; 4 – 423 K и 0.015. Кривые – расчет, точки – эксперимент.
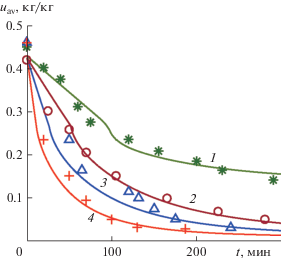
Результаты моделирования, представленные далее, относятся к обычному способу сушки гранул, когда влагоизолирующее покрытие отсутствует. Рисунок 2а иллюстрирует влияние геометрических характеристик частиц на интенсивность процесса сушки. Для рассматриваемого размерного ряда с увеличением отношения радиуса частицы к ее длине при постоянном радиусе процессы тепло- и массопереноса в грануле становятся более интенсивными. Длительность процесса сушки для гранулы с R/L = 2.5 примерно в 6 раз меньше, чем для частиц с R/L = 0.125.
Рис. 2.
Изменение со временем среднего влагосодержания (a) и числа Кирпичева (б) при сушке гранул различной длины с радиусом R = 0.005 м для режима Tm = 423 K, φm = 0.015: 1 – R/L = 0.125, 2 – 1.0, 3 – 2.5.
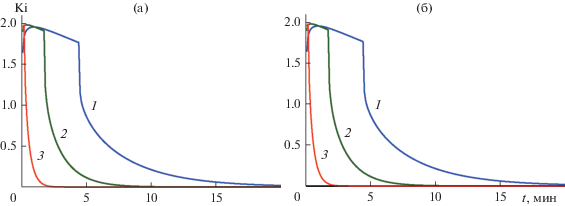
Для оценки качества процесса сушки можно использовать число Кирпичева Ki. Это число равно удвоенному значению разности величин влагосодержания в центре гранулы и на ее поверхности, отнесенной к начальному влагосодержанию [3]. В расчетах принято
Значение ${{\left. u \right|}_{{Г - 0}}}$ отнесено к частице материала гранулы вблизи ее поверхности.
Обычно для выявления критического значения Ki, при котором происходит растрескивание образца, используется натурный эксперимент. Предлагаемая математическая модель позволяет прогнозировать динамику изменения числа Ki, что создает предпосылки проектирования безопасных технологических режимов сушки гранул носителя. Характер расчетных кривых на рис. 2б указывает на возможность повреждения гранулы в начальном периоде сушки (при выбранных параметрах сушильного агента). Для гранул всех выбранных размеров имеет место резкий рост числа Кирпичева практически до максимума.
Уменьшение величины Ki возможно за счет регулирования режимных параметров сушки. Как видно из зависимостей на рис. 3, повышение относительной влажности сушильного агента приводит к снижению числа Ki (рис. 3б), при этом одновременно снижается и скорость обезвоживания (рис. 3а).
Рис. 3.
Изменение со временем среднего влагосодержания (a) и числа Кирпичева (б) в процессе сушке гранул с радиусом R = 0.005 м, R/L = 0.125 для различных режимов при Tm = 393 K: 1 – φm = 0.015, 2 – 0.25, 3 – 0.45, 4 – 0.65, 5 – 0.85.
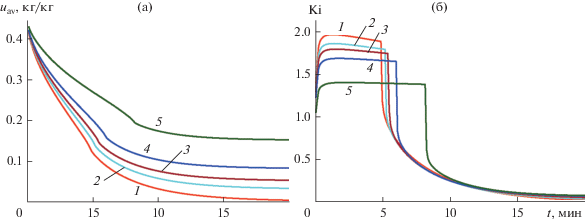
На рис. 4 представлены распределения влагосодержания u и локального коэффициента массопроводности am для достаточно “жесткого” режима сушки гранул. Соответствующая кривая сушки приведена на рис. 3а (кривая 1).
Рис. 4.
Распределение в плоскости r–z значений влагосодержания (a, а'), локальных коэффициентов диффузии жидкой фазы (б, б') и интенсивности парообразования (в, в') в моменты времени t = 3.4 мин (a–в) и 10 мин (a'–в') при сушке гранул с радиусом R = 0.005 м, R/L = 0.125 при Tm = 393 К, φm = 0.015.
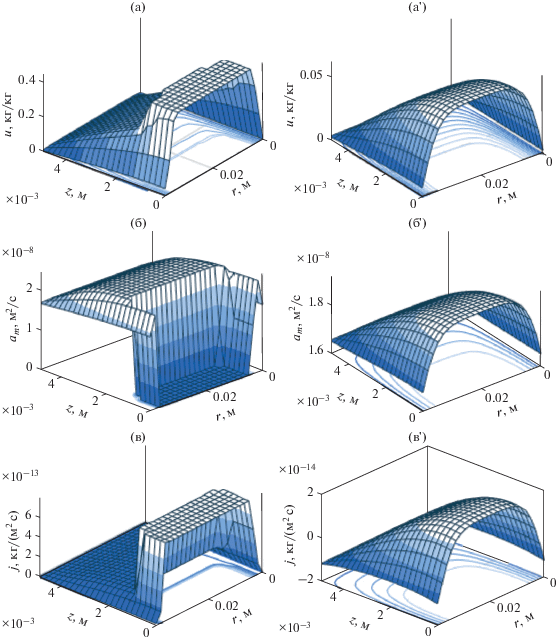
В момент времени t = 3.4 мин, относящийся к началу процесса сушки, часть объема пористой системы еще занята свободной водой (рис. 4а). В этой области осуществляется перенос влаги только в виде пара, жидкофазный перенос отсутствует, здесь коэффициент влагопроводности am = 0 (рис. 4б). В приграничных зонах величина u ниже максимального гигроскопического влагосодержания. Здесь обезвоживание происходит как за счет градиента расклинивающего давления, так и вследствие фазового перехода жидкость–пар. Интенсивность производства пара наиболее высока в водонасыщенной центральной зоне гранулы (рис. 4в), где выше давление насыщенного пара (к этому моменту времени температурное поле практически однородно).
В момент времени t = 10 мин (завершающий этап сушки) в центральной зоне гранулы уже отсутствует область, где величина u превышает максимальную гигроскопическую влажность (рис. 4а'). Массоперенос происходит здесь как за счет испарения жидкой фазы, так и за счет переноса связанной воды в граничных слоях. Интенсивность жидкофазного переноса выше в центральных областях (рис. 4б'), где, в частности, выше значения концентрации связанной воды. Интенсивность парообразования к концу процесса снижается практически на порядок (рис. 4в').
ЗАКЛЮЧЕНИЕ
В работе представлена математическая модель процессов тепло- и массопереноса при конвективной сушке пористых гранул из глиняного сырья. Аналитические формулы для коэффициентов массопроводности жидкой фазы и коэффициента фазовых переходов позволяют рассчитывать их локальные значения в любой момент времени.
Сравнение расчетных и экспериментальных данных позволяет сделать вывод о возможности практического использования модели для выбора энергоэффективных режимов обезвоживания гранул носителя никелевого катализатора. Модель может быть адаптирована к другим капиллярно-пористым материалам и видам сушки.
ОБОЗНАЧЕНИЯ
| As, Bs, Cs | коэффициенты в формуле Антуана |
| am | коэффициент массопроводности, м2/с |
| a0 | коэффициент уравнения политермы сорбции |
| B | индивидуальная газовая постоянная, Дж/(кг К) |
| с | теплоемкость, Дж/(кг К) |
| D | коэффициент бинарной диффузии, м2/с |
| j | поток массы пара, обусловленный фазовыми переходами, отнесенный к единице времени и единице площади, кг/(м2 с) |
| Κj3 | коэффициент проницаемости j-й фазы при полном насыщении пористой системы, м2 |
| k | коэффициент уравнения политермы сорбции |
| L | длина гранулы, м |
| L' | скрытая теплота парообразования, Дж/кг |
| p | давление, Па |
| R | радиус гранулы, м |
| r | радиальная координата, м |
| T | температура, К |
| t | время, с |
| u | влагосодержание, кг/кг |
| uS0 | максимальное гигроскопическое содержание при T = 273 K, кг/кг |
| ${v}$ | скорость, м/с |
| ${\bar {v}}$ | молярный объем жидкости, м3/моль |
| sij | удельная поверхность раздела фаз i и j, м–1 |
| $w$ | диффузионная скорость, м/с |
| z | осевая координата, м |
| α | объемное содержание фазы |
| αГ | коэффициент теплоотдачи на внешней границе гранулы, Вт/(м2 K) |
| αST | коэффициент уравнения политермы сорбции |
| ε | критерий фазовых переходов |
| κ2 | коэффициент в формуле Дальтона |
| λ | коэффициент теплопроводности, Вт/(м К) |
| μ | вязкость, Па ⋅ с |
| ρ | плотность, кг/м3 |
| j | относительная влажности воздуха |
| χ | концентрация пара |
| Ki | число Кирпичева |
ИНДЕКСЫ
| 0 | начальное состояние |
| 1, 2, 3 | газообразная, жидкая и твердая фазы |
| atm | атмосферный |
| av | средний |
| eq | равновесное значение |
| g | газовая компонента |
| m | среда сушильного агента |
| r | радиальная компонента вектора |
| sat | состояние насыщения |
| v | пар |
| z | осевая компонента вектора |
| Г | внешние границы гранулы |
| ° | истинное значение физической величины |
Список литературы
Мухленов И.П., Добкина Е.И., Дерюжкина В.И., Сороко В.Е. Технология катализаторов. Л.: Химия, 1979.
Надиров Н.К., Слуцкин Р.Л. Каталитическое гидрирование и гидрогенолиз углеводов. М.: Химия, 1976.
Лыков А.В. Явления переноса в капиллярно-пористых телах. М.: Гос. изд. науч.-техн. лит., 1954.
Кафаров В.В., Перов В.Л., Мешалкин В.П. Принципы математического моделирования химико-технологических систем (введение в системотехнику химических производств). М.: Химия, 1974.
Gulyaev Y.V., Belgorodskii V.S., Kosheleva M.K. State-of-the-art review of papers presented at the symposium “Modern energy and resource-saving technologies MERST 2017” held within the international scientific and technical forum "First International Kosygin Readings "Current topics in engineering sciences” // Theor. Found. Chem. Eng. 2018. V. 52. № 3. P. 412. [Гуляев Ю.В., Белгородский В.С., Кошелева М.К. Аналитический обзор материалов симпозиума “Современные энерго- и ресурсосберегающие технологии” Международного научно-технического форума “Первые международные Косыгинские чтения” Современные задачи инженерных наук” // Теор. осн. хим. технол. 2018. Т. 52. № 3. С. 361.]
Alnak D.E., Karabulut K. Computational Analysis of Heat and Mass Transfer of Impinging Jet onto Different Foods during the Drying Process at Low Reynolds Numbers. // J. Eng. Phys. Thermophys. 2019. V. 28. P. 255. https://doi.org/https://doi.org/10.1134/S1810232819020073
Chandramohan V.P., Talukdar P. Three-dimensional numerical modeling of simultaneous heat and moisture transfer in a moist object subjected to convective drying // Int. J. Heat Mass Transfer. 2010. V. 53. P. 4638. https://doi.org/10.1016/j.ijheatmasstransfer.2010.06.029
Kaya A., Aydın O., Dincer I. Numerical modeling of heat and mass transfer during forced convection drying of rectangular moist objects // Int. J. Heat Mass Transfer. 2006. V. 49. № 17–18. P. 3094. https://doi.org/10.1016/j.ijheatmasstransfer.2006.01.043
Hussain M.M., Dincer I. Two-dimensional heat and moisture transfer analysis of a cylindrical moist object subjected to drying: A finite-difference approach // Int. J. Heat Mass Transfer. 2003. V. 46. № 21. P. 4033. https://doi.org/10.1016/s0017-9310(03)00229-1
Absalan, G., Kianmehr M., Arabhosseini A. Effective moisture diffusivity and mathematical modeling of drying compost pellet // Agric. Eng. Int. 2016. V. 18. P. 156.
Bobkov V.I., Fedulov A.S., Dli M.I., Meshalkin V.P. Studying the chemical and energy engineering process of the strengthening calcination of phosphorite pellets containing free carbon // Theor. Found. Chem. Eng. 2018. V. 52. № 4. P. 525. [Бобков В.И., Федулов А.С., Дли М.И., Мешалкин В.П. Исследование химико-энерготехнологического процесса упрочняющего обжига фосфоритовых окатышей, содержащих свободный углерод // Теор. осн. хим. технол. 2018. Т. 52. № 4. С. 423.]
Lamnatou C., Papanicolaou E., Belessiotis V., Kyriakis N. Finite-volume modelling of heat and mass transfer during convective drying of porous bodies – Non-conjugate and conjugate formulations involving the aerodynamic effects // Renewable Energy. 2010. V. 35. № 7. P. 1391. https://doi.org/10.1016/j.renene.2009.11.008
Rudobashta S.P., Kosheleva M.K., Kartashov É.M. Nonstationary mass transfer near the surface of a cylindrical body // J. Eng. Phys. Thermophys. 2015. V. 88. № 6. P. 1320. [Рудобашта С.П., Кошелева М.К., Карташов Э.М. Нестационарная массоотдача у поверхности цилиндрического тела // Инж.-физ. журн. 2015. Т. 88. № 6. С. 1276.]
Akulich P.V., Temruk A.V., Akulich A.V. Modeling and experimental investigation of the heat and moisture transfer in the process of microwave-convective drying of vegetable materials // J. Eng. Phys. Thermophys. 2012. V. 85. № 5. P. 1034. [Акулич П.В., Темрук А.В., Акулич А.В. Моделирование и экспериментальное исследование тепло- и влагопереноса при свч-конвективной сушке растительных материалов // Инж.-физ. журн. 2012. Т. 85. № 5. С. 951.]
Bobkov V.I., Borisov V.V., Dli M.I., Meshalkin V.P. Multicomponent fuzzy model for evaluating the energy efficiency of chemical and power engineering processes of drying of the multilayer mass of phosphorite pellets // Theor. Found. Chem. Eng. 2018. V. 52. № 5. P. 786. [Бобков В.И., Борисов В.В., Дли М.И., Мешалкин В.П. Многокомпонентная нечеткая модель оценки энергоэффективности химико-энерготехнологических процессов сушки многослойной массы фосфоритовых окатышей // Теор. осн. хим. технол. 2018. Т. 52. № 5. С. 504.]
Grinchik N.N., Akulich P.V., Kuts P.S., Adamovich A.L., Kundas S.P. Modeling of nonisothermal heat and moisture transfer in capillary-porous media in periodic microwave heating // J. Eng. Phys. Thermophys. 2007. V. 80. № 1. P. 1. [Гринчик Н.Н., Акулич П.В., Адамович А.Л., Куц П.С., Кундас С.П. Моделирование неизотермического тепло- и влагопереноса в капиллярно-пористых средах при периодическом микроволновом нагреве // Инж.-физ. журн. 2007. Т. 80. № 1. С. 3.]
Дорняк О.Р., Усачев А.М., Шмитько Е.И., Аль Сарраджи С.Х.М. Математическое моделирование тепло- и массопереноса при адсорбционно-контактной сушке керамических материалов (математическая модель) // Политемат. сетевой электрон. научн. журн. Кубан. гос. аграр. унив. 2013. № 89. С. 655.
Дорняк О.Р., Шульман З.П. Математическое моделирование процесса вакуумной сушки древесины // Вестн. Воронеж. гос. тех. унив. 2006. Т. 2. № 6. С. 113.
Ljung A.L., Staffan Lundström T., Daniel Marjavaara B., Tano K. Convective drying of an individual iron ore pellet – Analysis with CFD // Int. J. Heat Mass Transfer. 2011. V. 54. № 17–18. P. 3882. https://doi.org/10.1016/j.ijheatmasstransfer.2011.04.040
Whitaker S. Simultaneous Heat, Mass, and Momentum Transfer in Porous Media: A Theory of Drying // Adv. Heat Transfer. 1977. V. 13. P. 119.
Нигматулин Р. И. Динамика многофазных сред. Часть I. М.: Наука, 1987.
Дорняк О.Р., Аль Сарраджи С.Х.М., Усачев А.М., Шмитько Е.И. Математическое моделирование тепло- и массопереноса при адсорбционно-контактной сушке керамических материалов (вычислительный эксперимент) // Политемат. сетевой электрон. научн. журн. Кубан. гос. аграр. унив. 2013. № 89. С. 836.
Kosheleva M.K., Dornyak O.R., Maklusova M.S. Modeling of kinetics of drying process of polycaproamide granules considering its sorption properties // Proc. 21st International Drying Symposium (IDS-2018). 2018. P. 387. https://doi.org/10.4995/ids2018.2018.7553
Дорняк О.Р. Уравнение общего давления в математической модели диффузионно-фильтрационного влаготеплопереноса в коллоидных капиллярно-пористых телах // Вестн. Воронеж. гос. тех. унив. 2011. Т. 7. № 12-1. С. 68.
Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. М.: Энергоатомиздат, 1984.
Цимерманис Л.Х.Б. Сорбция, структурообразование, массоперенос (термодинамика влажного тела). М.: Алекс, 2006.
Kosheleva M.K., Rudobashta S.P., Apalkova M.S. Research and selection of drying operating parameters of intermediate product for nickel catalysts // Trans. TSTU. 2015. V. 21. № 2. P. 305. [Кошелева М.К., Рудобашта С.П., Апалькова М.С. Исследование и выбор режимных параметров процесса сушки промежуточного продукта получения никелевого катализатора // Вестн. Тамбов. гос. тех. унив. 2015. Т. 21. № 2. С. 305.]
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


