Теоретические основы химической технологии, 2021, T. 55, № 4, стр. 462-470
Нечетко-логический алгоритм экологического зонирования лесных массивов в регионах химических предприятий на основе иерархической системы нечетких интегральных индексов
О. Б. Бутусов a, b, *, В. П. Мешалкин a, c, Р. Р. Кантюков a, d, Я. П. Баранова a
a Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия
b Московский международный университет
Москва, Россия
c Институт общей и неорганической химии им. Н.С. Курнакова РАН
Москва, Россия
d НИИ природных газов и газовых технологий – Газпром ВНИИГАЗ
Москва, Россия
* E-mail: butusov-1@mail.ru
Поступила в редакцию 23.03.2021
После доработки 24.03.2021
Принята к публикации 25.03.2021
Аннотация
Предложена иерархическая система нечетких интегральных индексов, рассчитываемых с использованием естественных ярусов лесного массива. В каждом из отдельных ярусов вычисляется собственный интегральный индекс (ИИ), который далее используется для вычисления обобщенного интегрального индекса (ОИИ) верхнего уровня. Для вычисления нечетких ИИ нижнего уровня можно использовать взвешенные средние с экспертными оценками весовых коэффициентов. Для вычисления нечеткого ОИИ предложено использовать нечеткий метод главных компонент (МГК), обобщенный на использование нечетких показателей. Сущность предложенного алгоритма состоит в использовании симметричных треугольных нечетких чисел и в том, что МГК применяется только для центров нечетких треугольных чисел, а нечеткости при расчете главных компонент учитываются только в линейных комбинациях нечеткостей исходных показателей. Приведен пример использования предложенного нечетко-логического алгоритма и нечеткого метода главных компонент для экологического зонирования лесных массивов в регионе химических предприятий.
ВВЕДЕНИЕ
Как показано в работах [1–3], оценки состояния лесных массивов, постоянно находящихся под воздействием химических загрязнений от выбросов химических предприятий можно осуществлять с помощью зависимостей доза–эффект. Сущность метода заключается в том, что первоначально определяются распределения концентраций химических загрязнений, выбрасываемых химическими предприятиями (ХП), по территории лесных массивов (ЛМ), а затем полученные распределения пересчитываются с помощью зависимостей доза–эффект в интегральные показатели экологического состояния ЛМ. Кроме постоянно действующих источников химического загрязнения, таких как заводские трубы ХП, необходимо учитывать экологические риски от возможных техногенных аварий на ХП, при которых возникают лесные пожары, наносящие существенный ущерб ЛМ.
В работе [4] обосновано использование для моделирования зависимостей доза–эффект скалярных функций скалярного аргумента следующего вида:
где ${{I}_{E}} = \sum\limits_{i = 1}^m {{{a}_{i}}{{e}_{i}}} ,$ $\sum\limits_{i = 1}^m {{{a}_{i}}} = 1$ – суммарный интегральный индекс нормализованных показателей эффекта; ${{I}_{D}} = \sum\limits_{j = 1}^n {{{b}_{j}}{{d}_{j}}} ,$ $\sum\limits_{j = 1}^n {{{b}_{j}}} = 1$ – суммарный интегральный индекс нормализованных показателей дозы; f(x) – скалярная функция зависимости доза–эффект; ai, bi – весовые коэффициенты; ${{e}_{i}} = \frac{{{{E}_{i}}}}{{{{E}_{{i,\max }}}}},$ ${{d}_{j}} = \frac{{{{D}_{j}}}}{{{{D}_{{j,\max }}}}}$ – нормализованные показатели эффекта и дозы; ${{E}_{i}},{{D}_{j}}$ – ненормализованные показатели эффекта и дозы.Функция “доза–эффект"-зависимости (ДЭЗ) может быть представлена таблично, графически и аналитически, а также с помощью искусственных нейронных сетей (ИНС).
НЕЧЕТКИЕ ИНТЕГРАЛЬНЫЕ ИНДЕКСЫ И НЕЧЕТКИЕ “ДОЗА–ЭФФЕКТ” ЗАВИСИМОСТИ
В отличие от четкой теории ДЭЗ [1–4], в данной работе развиты методы многоатрибутного нечеткого оценивания, которая получила название нечеткой ДЭЗ. В работе [5] обосновано применение для расчета средневзвешенных значений треугольных нечетких чисел. Представим нечеткий i-й показатель эффекта и нечеткий j-й показатель дозы в виде треугольных нечетких чисел: ${{\tilde {e}}_{i}} = \left( {e_{i}^{{\left( 1 \right)}},e_{i}^{{\left( 0 \right)}},e_{i}^{{\left( 2 \right)}}} \right),$ ${{\tilde {d}}_{i}} = \left( {d_{i}^{{\left( 1 \right)}},d_{i}^{{\left( 0 \right)}},d_{i}^{{\left( 2 \right)}}} \right),$ тогда интегральные индексы, как средневзвешенные значения можно вычислить по следующим формулам:
(2)
${{\tilde {I}}_{E}} = \left( {\sum\limits_{i = 1}^m {{{a}_{i}}e_{i}^{{\left( 1 \right)}}} ,\,\,\sum\limits_{i = 1}^m {{{a}_{i}}e_{i}^{{\left( 0 \right)}}} ,\,\,\sum\limits_{i = 1}^m {{{a}_{i}}e_{i}^{{\left( 2 \right)}}} } \right),$(3)
${{\tilde {I}}_{D}} = \left( {\sum\limits_{j = 1}^n {{{b}_{j}}d_{j}^{{\left( 1 \right)}}} ,\,\,\sum\limits_{j = 1}^n {{{b}_{j}}d_{j}^{{\left( 0 \right)}}} ,\,\,\sum\limits_{j = 1}^n {{{b}_{j}}d_{j}^{{\left( 2 \right)}}} } \right).$Принимая гипотезу об одинаковых весовых коэффициентах, формулы (2) и (3) можно упростить
(4)
${{\tilde {I}}_{E}} = \frac{1}{m}\left( {\sum\limits_{i = 1}^m {e_{i}^{{\left( 1 \right)}}} ,\,\,\sum\limits_{i = 1}^m {e_{i}^{{\left( 0 \right)}}} ,\,\,\sum\limits_{i = 1}^m {e_{i}^{{\left( 2 \right)}}} } \right),$(5)
${{\tilde {I}}_{D}} = \frac{1}{n}\left( {\sum\limits_{j = 1}^n {d_{j}^{{\left( 1 \right)}}} ,\,\,\sum\limits_{j = 1}^n {d_{j}^{{\left( 0 \right)}}} ,\,\,\sum\limits_{j = 1}^n {d_{j}^{{\left( 2 \right)}}} } \right).$В приближении симметричных треугольных нечетких чисел формулы (4) и (5) можно упростить
(6)
${{\tilde {I}}_{E}} = \left( {\sum\limits_{i = 1}^m {{{a}_{i}}e_{i}^{{\left( 1 \right)}}} ,\,\,\sum\limits_{i = 1}^m {{{a}_{i}}e_{i}^{{\left( 2 \right)}}} } \right),$(7)
${{\tilde {I}}_{D}} = \left( {\sum\limits_{j = 1}^n {{{b}_{j}}d_{j}^{{\left( 1 \right)}}} ,\,\,\sum\limits_{j = 1}^n {{{b}_{j}}d_{j}^{{\left( 2 \right)}}} } \right).$В приближении одинаковых весовых коэффициентов
(8)
${{\tilde {I}}_{E}} = \frac{1}{m}\left( {\sum\limits_{i = 1}^m {e_{i}^{{\left( 1 \right)}}} ,\,\,\sum\limits_{i = 1}^m {e_{i}^{{\left( 2 \right)}}} } \right),$(9)
${{\tilde {I}}_{D}} = \frac{1}{n}\left( {\sum\limits_{j = 1}^n {d_{j}^{{\left( 1 \right)}}} ,\,\,\sum\limits_{j = 1}^n {d_{j}^{{\left( 2 \right)}}} } \right).$Вместо (8) и (9) можно использовать симметричные треугольные нечеткие числа в виде центральной точки и размеров нечеткого числа
(10)
${{\tilde {I}}_{E}} = \left( {\sum\limits_{i = 1}^m {{{a}_{i}}e_{i}^{{\left( 0 \right)}}} ,\,\,\sum\limits_{i = 1}^m {{{a}_{i}}\left| {\Delta {{e}_{i}}} \right|} } \right) = \left( {I_{E}^{{\left( 0 \right)}},\left| {\Delta {{I}_{E}}} \right|} \right),$(11)
${{\tilde {I}}_{D}} = \left( {\sum\limits_{j = 1}^n {{{b}_{j}}d_{j}^{{\left( 0 \right)}}} ,\,\,\sum\limits_{j = 1}^n {{{b}_{j}}\left| {\Delta {{d}_{j}}} \right|} } \right) = \left( {I_{D}^{{\left( 0 \right)}},\left| {\Delta {{I}_{D}}} \right|} \right),$Из формул (10), (11) следует, что нечеткая ДЭЗ может быть представлена в следующем виде:
(12)
$\left( {I_{E}^{{(0)}},\left| {\Delta {{I}_{E}}} \right|} \right) = f\left( {I_{D}^{{(0)}},\left| {\Delta {{I}_{D}}} \right|} \right).$Формулы (10), (11) и (12) показывают, что размеры симметричных треугольных нечетких чисел можно оценить с помощью средних квадратических отклонений.
Рассмотрим оценку экологического состояния ЛМ (оценка эффекта) с помощью следующих трех важных показателей: общее проективное покрытие (ОПП), жизненное состояние древостоя (ЖСД), которое оценивается группами экспертов в баллах и видовое разнообразие травяно-кустарничкового яруса (ВР). Для оценки уровней химического загрязнения (оценка дозы) будем использовать концентрацию SO2 и результат химтрансформации ${\text{S}}{{{\text{O}}}_{2}} \to {\text{SO}}_{4}^{{2----}}$ [6]. При этом интегральный индекс эффекта и интегральный индекс дозы можно представить в следующем виде:
Для решения задачи определения нечеткой ДЭЗ измеряют показатели, входящие в уравнения (13) и (14). Показатель ОПП измеряется по шкале с помощью люксметра. Чем больше освещенность, тем меньше проективное покрытие на данном конкретном участке ЛМ. Измерения ОПП выполняются в различных точках исследуемого участка ЛМ, по результатам которых вычисляется среднее арифметическое $\overline {{\text{ОПП}}} \left( x \right)$ и среднее квадратичное отклонение ${{\sigma }_{{{\text{ОПП}}}}}\left( x \right),$ где x – вектор координат участка.
Показатель ЖСД оцениваются разными экспертами. В результате вычисляются среднее арифметическое $\overline {{\text{ЖСД}}} \left( x \right)$ и среднее квадратичное отклонение ${{\sigma }_{{{\text{ЖСД}}}}}\left( x \right).$
Показатель ВР оценивается на нескольких экспериментальных площадках. Далее вычисляются среднее арифметическое $\overline {{\text{ВР}}} \left( x \right)$ и среднее квадратичное отклонение ${{\sigma }_{{{\text{ВР}}}}}\left( x \right).$
Укрупненная блок-схема алгоритма экологического зонирования ЛМ представлена на рис. 1.
Рис. 1.
Блок-схема алгоритма оценки состояния лесных массивов и экологического зонирования ЛМ в промышленном регионе.
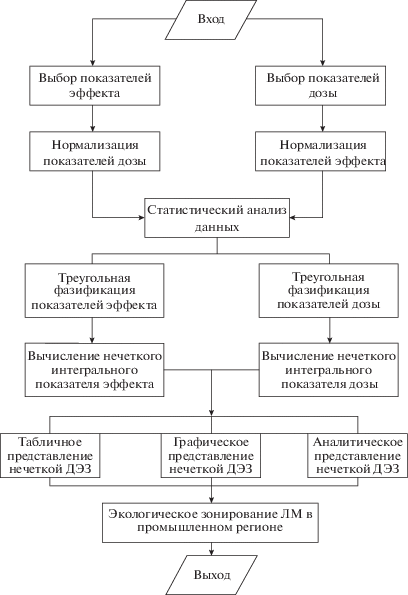
Алгоритм начинается с выбора показателей, которые далее объединяются с помощью метода взвешенного среднего в интегральные индексы. Экологическое зонирование ЛМ выполняется с использованием найденной нечеткой ДЭЗ.
Поясним работу алгоритма на примере экологических показателей, использованных в уравнениях (13), (14). Вместо средневзвешенных рассмотрим средние арифметические. При этом формулы (13) и (14) примут следующий вид:
(16)
${{I}_{D}} = \frac{1}{2}\left( {{\text{S}}{{{\text{O}}}_{2}} + {\text{SO}}_{4}^{{2--}}} \right).$Численные значения нормализованных показателей в разных точках выбранного участка ЛМ представлены в табл. 1.
Таблица 1.
Нормализованные показатели “дозы” и “эффекта”
| № | ОПП | ЖСД | ВР | SO2 | ${\text{SO}}_{4}^{ - }$ |
|---|---|---|---|---|---|
| 1 | 0.43 | 0.26 | 0.54 | 0.34 | 0.58 |
| 2 | 0.00 | 0.57 | 0.45 | 0.41 | 0.70 |
| 3 | 0.33 | 0.73 | 0.40 | 0.66 | 0.47 |
| 4 | 0.51 | 0.34 | 0.46 | 0.40 | 0.44 |
| 5 | 0.26 | 0.21 | 0.29 | 0.64 | 0.34 |
| 6 | 0.42 | 0.20 | 0.29 | 0.57 | 0.53 |
| 7 | 0.18 | 0.25 | 0.50 | 0.54 | 0.20 |
| 8 | 0.33 | 0.46 | 0.52 | 0.70 | 0.33 |
| 9 | 0.18 | 0.27 | 0.21 | 0.93 | 0.29 |
| 10 | 0.53 | 0.71 | 0.00 | 0.79 | 0.53 |
| 11 | 0.39 | 0.23 | 0.00 | 0.18 | 0.80 |
| 12 | 0.58 | 0.16 | 0.00 | 0.61 | 0.93 |
| 13 | 0.29 | 0.41 | 0.10 | 0.25 | 0.15 |
| 14 | 0.29 | 0.35 | 0.39 | 0.10 | 0.57 |
| 15 | 0.36 | 0.39 | 0.14 | 0.26 | 0.37 |
| 16 | 0.59 | 0.00 | 0.28 | 0.06 | 0.28 |
| 17 | 0.00 | 0.27 | 0.37 | 0.27 | 0.52 |
| 18 | 0.00 | 0.00 | 0.02 | 0.77 | 0.41 |
| 19 | 0.55 | 0.34 | 0.13 | 0.40 | 0.51 |
| 20 | 0.68 | 0.45 | 0.15 | 1.00 | 0.65 |
Данные табл. 1 были использованы для вычисления нечетких треугольных чисел отдельных показателей:
Нечеткие интегральные индексы можно рассчитать с помощью приведенных выше нечетких частных показателей по формулам (15) и (16):
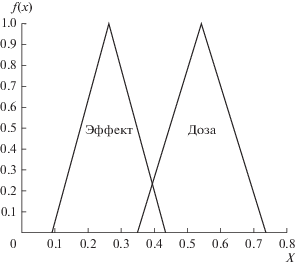
Нечеткие треугольные интегральные индексы можно представить с помощью треугольных функций принадлежности (см. рис. 2).
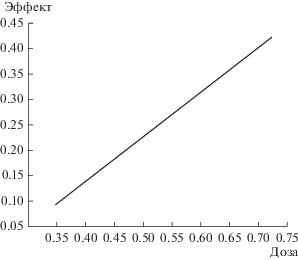
График ДЭЗ представлен на рис. 3.
Как следует из рис. 3, ДЭЗ является линейной и проходит через начало координат. Эта функция преобразовывает интервал нечеткости “дозы” в интервал нечеткости “эффекта”. В данном случае интервал нечеткости “дозы” [0.35; 075] преобразовывается в интервал нечеткости “эффекта” [0.1; 0.4].
Аналитическое представление ДЭЗ имеет следующий вид (линейная функция, проходящая через начало координат):
где d – величина “дозы”, e – величина “эффекта”, k – угловой коэффициент (в данном примере k = 0.57).Табличное представление ДЭЗ получается с помощью формулы (17). Полученные результаты могут быть использованы в качестве основы для расчета более сложных нечетких ДЭЗ.
ВЫЧИСЛЕНИЕ НЕЧЕТКИХ ДЭЗ С ПОМОЩЬЮ НЕЧЕТКОГО МЕТОДА ГЛАВНЫХ КОМПОНЕНТ
Как отмечено выше, экологическая информация имеет нечеткий характер, что обусловлено наличием большого количества качественных показателей и лингвистических переменных, необходимых для ее описания. Для получения интегральных индексов первого уровня достаточно разделить экологические показатели на отдельные группы. При этом в качестве критерия разграничения экологических показателей ЛМ можно использовать естественные ярусы лесного массива, например, ярус древостоя, травяно-кустарничковый ярус (ТКЯ), ярус подстилки, ярус почвы и пр. В каждом из отдельных ярусов вычисляют собственный интегральный индекс, который далее используют для вычисления обобщенного интегрального индекса (ОИИ) верхнего уровня. Для вычисления ИИ первого уровня можно использовать взвешенные средние с экспертными оценками весовых коэффициентов, или в простейшем случае средние арифметические. При этом необходимо учитывать нечеткий характер экологических данных.
Для вычисления нечеткого ОИИ предложено использовать нечеткий метод главных компонент (МГК) [7, 8], обобщенный на использование нечетких показателей. МГК позволяет построить иерархическую последовательность интегральных индексов (главных компонент) в виде линейных комбинаций исходных показателей [9]. Полученные в результате интегральные индексы могут быть использованы для выявления закономерностей в статистических данных. В [10] отмечается, что при использовании треугольных нечетких чисел (ТНЧ) арифметические операции усреднения также приводят к ТНЧ.
Рассмотрим применение нечеткого МГК для симметричных треугольных нечетких чисел (СТНЧ). В этом приближении каждое СТНЧ может быть представлено в виде совокупности центров и размеров полуширины СТНЧ: ${{e}_{i}} = \left( {{{a}_{i}};\Delta {{a}_{i}}} \right),$ где ${{a}_{i}},\Delta {{a}_{i}}$ – центр и полуширина i-го СТНЧ.
В работе [5] показано, что при расчете среднего взвешенного ТНЧ можно использовать следующую формулу:
(18)
$\begin{gathered} \bar {A} = \left( {{{{\bar {A}}}^{{(1)}}};{{{\bar {A}}}^{{(m)}}};{{{\bar {A}}}^{{(2)}}}} \right) = \\ = \,\,\left( {\sum\limits_{i = 1}^n {{{w}_{i}}a_{i}^{{(1)}}} ;\,\,\sum\limits_{i = 1}^n {{{w}_{i}}a_{i}^{{(m)}}} ;\,\,\sum\limits_{i = 1}^n {{{w}_{i}}a_{i}^{{(2)}}} } \right), \\ \end{gathered} $Для СТНЧ формула (18) принимает вид
(19)
$\bar {A} = \left( {{{{\bar {A}}}^{{(1)}}};{{{\bar {A}}}^{{(2)}}}} \right) = \left( {\sum\limits_{i = 1}^n {{{w}_{i}}a_{i}^{{(1)}}} ;\,\,\sum\limits_{i = 1}^n {{{w}_{i}}a_{i}^{{(2)}}} } \right).$Из (19) следует, что ${{\bar {A}}^{{(m)}}} = \frac{1}{2}\left( {{{{\bar {A}}}^{{(1)}}} + {{{\bar {A}}}^{{(2)}}}} \right),$ $\Delta \bar {A}$ = = ${{\bar {A}}^{{(m)}}} - {{\bar {A}}^{{(1)}}}$ = ${{\bar {A}}^{{(2)}}} - {{\bar {A}}^{{(m)}}},$ где $\Delta \bar {A}$ = ${{\bar {A}}^{{(m)}}} - {{\bar {A}}^{{(1)}}}$ = = $\frac{1}{2}\left( {{{{\bar {A}}}^{{(1)}}} + {{{\bar {A}}}^{{(2)}}}} \right)$ – ${{\bar {A}}^{{(1)}}}$ = $\frac{1}{2}\left( {{{{\bar {A}}}^{{(2)}}} - {{{\bar {A}}}^{{(1)}}}} \right).$ Таким образом, формула (19) эквивалентна следующей формуле:
(20)
$\bar {A} = \left( {{{{\bar {A}}}^{{(m)}}};\Delta \bar {A}} \right) = \left( {\sum\limits_{i = 1}^n {{{w}_{i}}A_{i}^{{(m)}}} ;\,\,\sum\limits_{i = 1}^n {{{w}_{i}}\Delta {{A}_{i}}} } \right).$При этом для экологических показателей необходимо соблюдение следующих дополнительных условий $a_{i}^{{(1)}} = a_{i}^{{(m)}} - \Delta {{a}_{i}} \geqslant 0;$ $a_{i}^{{(2)}} = a_{i}^{{(m)}} + \Delta {{a}_{i}} \leqslant 1.$
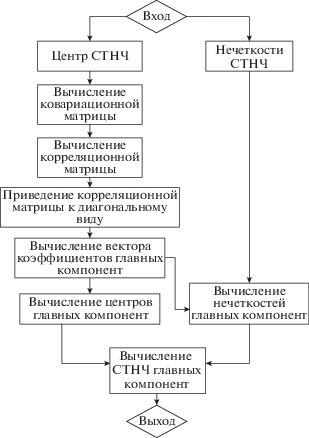
Сущность предложенного алгоритма заключается в том, что МГК применяется только для центров СНТЧ, а нечеткости учитываются только в линейных комбинациях при расчете главных компонент. Укрупненная блок-схема алгоритма представлена на рис. 4.
МГК предназначен для преобразования интегральных индексов нижних уровней в единственную главную компоненту – обобщенный интегральный индекс (ОИИ). При этом коррелированные между собой компоненты преобразовываются с помощью линейных комбинаций в новые и некоррелированные переменные. На первом этапе построения главных компонент определяется линейная комбинация исходных переменных с максимальной дисперсией. На следующей итерации определяется новая линейная комбинация переменных ортогональная предыдущему вектору и т.д.
Технология построения главных компонент основана на диагонализации ковариационной или корреляционной квадратной матрицы размером m x m, где для задачи вычисления ОИИ m – число ИИ нижнего уровня. Ковариационная и корреляционная матрицы являются симметрическими матрицами и поэтому могут быть представлены в виде следующего разложения:
где P' – транспонированная матрица.Обозначим ковариационную матрицу буквой S:
(22)
$S = \left( {\begin{array}{*{20}{c}} {s_{1}^{2}}&{s_{{12}}^{2}}& \ldots &{s_{{1m}}^{2}} \\ {s_{{21}}^{2}}&{s_{2}^{2}}& \ldots &{s_{{2m}}^{2}} \\ \ldots & \ldots & \ldots & \ldots \\ {s_{{m1}}^{2}}&{s_{{m2}}^{2}}& \ldots &{s_{m}^{2}} \end{array}} \right),$(23)
$s_{{jk}}^{2} = \frac{{n\sum\limits_{i = 1}^n {{{I}_{{jk}}}{{I}_{{ki}}} - } \sum\limits_{i = 1}^n {{{I}_{{ji}}}} \sum\limits_{i = 1}^n {{{I}_{{ik}}}} }}{{n(n - 1)}},$После нахождения ковариационной матрицы корреляционную матрицу можно рассчитать по формуле
где D – диагональная матрица стандартных отклонений следующего вида:(25)
$D = \left( {\begin{array}{*{20}{c}} {{{s}_{1}}}&0& \ldots &0 \\ 0&{{{s}_{2}}}& \ldots &0 \\ \ldots & \ldots & \ldots & \ldots \\ 0&0& \ldots &{{{s}_{m}}} \end{array}} \right).$Корреляционная матрица R также является симметричной и приводится к диагональному виду с помощью преобразования
где U и V – ортогональные матрицы, столбцы которых являются собственными векторами матрицы R; K – диагональная матрица упорядоченных по величине собственных значений матрицы R(27)
$K = \left( {\begin{array}{*{20}{c}} {{{k}_{1}}}&0& \ldots &0 \\ 0&{{{k}_{2}}}& \ldots &0 \\ \ldots & \ldots & \ldots & \ldots \\ 0&0& \ldots &{{{k}_{m}}} \end{array}} \right).$Так как столбцы матрицы U являются собственными векторами матрицы R, то для расчет главных компонент необходимо умножить строки транспонированной матрицы U' на вектор-столбец исходных переменных (в данном случае вектор-столбец интегральных индексов нижнего уровня)
где $I = \left( {{{I}_{1}},{{I}_{2}}, \ldots ,{{I}_{m}}} \right){\kern 1pt} '$ – вектор-столбец исходных компонент.В случае использования ковариационной матрицы переменные необходимо предварительно центрировать, а для корреляционной матрицы – нормализовать. При этом формулы для вычисления главных компонент имеют следующий вид:
$\bar {I} = \left( {{{{\bar {I}}}_{1}},{{{\bar {I}}}_{2}}, \ldots ,{{{\bar {I}}}_{m}}} \right){\kern 1pt} '$ – вектор-столбец средних значений исходных переменных, ${{\bar {I}}_{k}} = \frac{1}{n}\sum\limits_{j = 1}^n {{{I}_{j}}} $ – среднее значение k-го ИИ нижнего уровня, U' – матрица, строки которой содержат коэффициенты главных компонент, z – вектор-столбец, элементы которого являются нормализованные и центрированные главные компоненты
(30)
$z = \left( {\begin{array}{*{20}{c}} {{{u}_{{11}}}{\kern 1pt} \frac{{({{I}_{1}} - {{{\bar {I}}}_{1}})}}{{{{s}_{1}}}} + {{u}_{{21}}}{\kern 1pt} \frac{{({{I}_{2}} - {{{\bar {I}}}_{2}})}}{{{{s}_{2}}}} + \cdots + {{u}_{{m1}}}{\kern 1pt} \frac{{({{I}_{m}} - {{{\bar {I}}}_{m}})}}{{{{s}_{m}}}}} \\ {{{u}_{{12}}}{\kern 1pt} \frac{{({{I}_{1}} - {{{\bar {I}}}_{1}})}}{{{{s}_{1}}}} + {{u}_{{22}}}{\kern 1pt} \frac{{({{I}_{2}} - {{{\bar {I}}}_{2}})}}{{{{s}_{2}}}} + \cdots + {{u}_{{m2}}}{\kern 1pt} \frac{{({{I}_{m}} - {{{\bar {I}}}_{m}})}}{{{{s}_{m}}}}} \\ { \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots } \\ {{{u}_{{1m}}}{\kern 1pt} \frac{{({{I}_{1}} - {{{\bar {I}}}_{1}})}}{{{{s}_{1}}}} + {{u}_{{m2}}}{\kern 1pt} \frac{{({{I}_{2}} - {{{\bar {I}}}_{2}})}}{{{{s}_{2}}}} + \cdots + {{u}_{{mm}}}{\kern 1pt} \frac{{({{I}_{m}} - {{{\bar {I}}}_{m}})}}{{{{s}_{m}}}}} \end{array}} \right).$Окончательный результат в виде СТНЧ вычисляется по следующим формулам:
(31)
${{z}_{m}} = U{\kern 1pt} '(1,:) \cdot {{I}_{m}},\,\,\,\,\Delta z = U{\kern 1pt} '(1,:) \cdot \Delta I.$Применение МГК является наиболее эффективным для вычисления ОИИ при использовании только одной первой главной компоненты. Тогда именно эту единственную компоненту лучше всего использовать в качестве ОИИ.
Рассмотрим пример использования предложенного алгоритма на конкретных результатах измерения показателей ЛМ. В табл. 2 и 3 представлены нормализованные на интервал [0, 1] результаты измерений экологических данных с помощью СТНЧ. Для удобства центры представлены отдельно в табл. 2, а размеры полуширины в табл. 3.
Таблица 2.
Центры нормализованных нечетких экологических показателей
| Н/п | e1 | e2 | e3 | e4 | e5 | e6 | e7 | e8 | I1 | I2 | I3 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.773 | 0.606 | 0.380 | 0.1 | 0.2 | 0.295 | 0.583 | 0.125 | 0.586 | 0.198 | 0.354 |
| 2 | 0.1 | 0.15 | 0.2 | 0.007 | 0.1 | 0.2 | 0.3 | 0.167 | 0.150 | 0.102 | 0.233 |
| 3 | 0.695 | 0.328 | 0.239 | 0.361 | 0.847 | 0.409 | 0.375 | 0.292 | 0.421 | 0.539 | 0.333 |
| 4 | 0.8 | 0.850 | 0.9 | 0.359 | 0.736 | 0.75 | 0.9 | 0.958 | 0.850 | 0.615 | 0.929 |
| 5 | 0.200 | 0.144 | 0.014 | 0 | 0.019 | 0.136 | 0.333 | 0.000 | 0.120 | 0.052 | 0.167 |
| 6 | 0.523 | 0.467 | 0.127 | 0.183 | 0.542 | 0.364 | 0.042 | 0.000 | 0.372 | 0.363 | 0.021 |
| 7 | 0.373 | 0.417 | 0.099 | 0.246 | 0.493 | 0.364 | 0.958 | 0.625 | 0.296 | 0.367 | 0.792 |
| 8 | 0.129 | 0.1 | 0.042 | 0.013 | 0.039 | 0.136 | 0.167 | 0.125 | 0.090 | 0.063 | 0.146 |
| 9 | 0.312 | 0.222 | 0.254 | 0.110 | 0.331 | 0.318 | 0.083 | 0.125 | 0.263 | 0.253 | 0.104 |
| 10 | 0.848 | 0.467 | 0.521 | 0.444 | 0.600 | 0.545 | 0.667 | 0.95 | 0.612 | 0.530 | 0.808 |
| 11 | 0.395 | 0.217 | 0.056 | 0.013 | 0.109 | 0.227 | 0.292 | 0.042 | 0.223 | 0.116 | 0.167 |
| 12 | 0.788 | 0.483 | 0.324 | 0.269 | 0.641 | 0.318 | 0.083 | 0.2 | 0.532 | 0.409 | 0.142 |
Таблица 3.
Размеры полуширины нормализованных нечетких экологических показателей
| Н/п | ∆e1 | ∆e2 | ∆e3 | ∆e4 | ∆e5 | ∆e6 | ∆e7 | ∆e8 | ∆I1 | ∆I2 | ∆I3 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.030 | 0.128 | 0.038 | 0.023 | 0.020 | 0.004 | 0.058 | 0.019 | 0.065 | 0.016 | 0.039 |
| 2 | 0.015 | 0.068 | 0.082 | 0.002 | 0.006 | 0.098 | 0.142 | 0.007 | 0.055 | 0.036 | 0.075 |
| 3 | 0.266 | 0.144 | 0.067 | 0.152 | 0.372 | 0.123 | 0.007 | 0.126 | 0.159 | 0.216 | 0.066 |
| 4 | 0.273 | 0.378 | 0.252 | 0.103 | 0.326 | 0.107 | 0.256 | 0.206 | 0.301 | 0.179 | 0.231 |
| 5 | 0.081 | 0.000 | 0.001 | 0.000 | 0.008 | 0.034 | 0.141 | 0.000 | 0.027 | 0.014 | 0.070 |
| 6 | 0.195 | 0.158 | 0.028 | 0.043 | 0.200 | 0.082 | 0.016 | 0.000 | 0.127 | 0.109 | 0.008 |
| 7 | 0.025 | 0.069 | 0.013 | 0.108 | 0.010 | 0.122 | 0.326 | 0.219 | 0.036 | 0.080 | 0.273 |
| 8 | 0.049 | 0.049 | 0.004 | 0.002 | 0.010 | 0.027 | 0.002 | 0.041 | 0.034 | 0.013 | 0.022 |
| 9 | 0.049 | 0.019 | 0.060 | 0.026 | 0.033 | 0.095 | 0.013 | 0.029 | 0.043 | 0.051 | 0.021 |
| 10 | 0.241 | 0.009 | 0.069 | 0.073 | 0.172 | 0.128 | 0.296 | 0.240 | 0.106 | 0.124 | 0.268 |
| 11 | 0.182 | 0.071 | 0.002 | 0.001 | 0.031 | 0.098 | 0.049 | 0.020 | 0.085 | 0.043 | 0.034 |
| 12 | 0.020 | 0.132 | 0.029 | 0.098 | 0.195 | 0.127 | 0.008 | 0.054 | 0.060 | 0.140 | 0.031 |
Таблица интегральных индексов нижнего уровня представлена в табл. 4 и 5.
Таблица 4.
Центры интегральных индексов первого уровня
| I1 | I2 | I3 |
|---|---|---|
| 0.586 | 0.198 | 0.354 |
| 0.150 | 0.102 | 0.233 |
| 0.421 | 0.539 | 0.333 |
| 0.850 | 0.615 | 0.929 |
| 0.120 | 0.052 | 0.167 |
| 0.372 | 0.363 | 0.021 |
| 0.296 | 0.367 | 0.792 |
| 0.090 | 0.063 | 0.146 |
| 0.263 | 0.253 | 0.104 |
| 0.612 | 0.530 | 0.808 |
| 0.223 | 0.116 | 0.167 |
| 0.532 | 0.409 | 0.142 |
Таблица 5.
Нечеткости интегральных индексов первого уровня
| I1 | I2 | I3 |
|---|---|---|
| 0.057 | 0.078 | 0.138 |
| 0.027 | 0.023 | 0.087 |
| 0.072 | 0.099 | 0.036 |
| 0.128 | 0.157 | 0.136 |
| 0.022 | 0.019 | 0.077 |
| 0.077 | 0.065 | 0.010 |
| 0.104 | 0.109 | 0.195 |
| 0.019 | 0.013 | 0.054 |
| 0.052 | 0.017 | 0.016 |
| 0.100 | 0.047 | 0.228 |
| 0.039 | 0.020 | 0.009 |
| 0.178 | 0.113 | 0.013 |
Ковариационная матрица, построенная по табл. 4, представлена в табл. 6, а корреляционная матрица в табл. 7. Матрица коэффициентов главных компонент представлена в табл. 8.
Таблица 6.
Ковариационная матрица центров интегральных индексов первого уровня
| I1 | I2 | I3 | |
|---|---|---|---|
| I1 | 0.054 | 0.038 | 0.046 |
| I2 | 0.038 | 0.039 | 0.039 |
| I3 | 0.046 | 0.039 | 0.098 |
Таблица 7.
Корреляционная матрица центров интегральных индексов первого уровня
| I1 | I2 | I3 | |
|---|---|---|---|
| I1 | 1.000 | 0.818 | 0.632 |
| I2 | 0.818 | 1.000 | 0.633 |
| I3 | 0.632 | 0.633 | 1.000 |
Таблица 8.
Матрица коэффициентов главных компонент
| G1 | G2 | G3 | |
|---|---|---|---|
| I1 | 0.512 | –0.594 | –0.621 |
| I2 | 0.430 | –0.448 | 0.784 |
| I3 | 0.744 | 0.668 | –0.026 |
Процент вариабельности главных компонент D (%) равен 79.608, 16.076 и 4.315, из чего следует, что вариабельность первой главной компоненты на много больше вариабельности остальных двух главных компонент, что позволяет использовать G1 в качестве ОИИ. Результаты расчета ОИИ представлены в табл. 9.
Таблица 9.
Центры и нечеткости ОИИ: Im – центры; Id – нечеткости
| №/п | Im | Id |
|---|---|---|
| 1 | 0.649 | 0.165 |
| 2 | 0.294 | 0.089 |
| 3 | 0.695 | 0.106 |
| 4 | 1.391 | 0.234 |
| 5 | 0.207 | 0.077 |
| 6 | 0.362 | 0.075 |
| 7 | 0.898 | 0.246 |
| 8 | 0.182 | 0.056 |
| 9 | 0.321 | 0.046 |
| 10 | 1.142 | 0.240 |
| 11 | 0.288 | 0.035 |
| 12 | 0.554 | 0.150 |
Как следует из табл. 9, ОИИ достигает максимальных значений на площадях 4, 7 и 10, а минимальных значений на площадях 2, 5 и 8. При этом размеры нечеткостей характеризуют пределы точности полученных результатов. Важно отметить, что ОИИ количественно описывает суммарное антропогенное воздействие на ЛМ всей техногенной инфраструктуры ХП с учетом как химических загрязнений, так и других видов антропогенного воздействия, например рекреационную нагрузку или выпасы сельскохозяйственных животных. Также ОИИ учитывает влияние на ЛМ не антропогенных факторов, например, структуру и состав почвенных горизонтов или гидрологию поверхности.
ЗАКЛЮЧЕНИЕ
По результатам проведенных исследований и расчетов вытекают следующие выводы:
– нечеткий характер экологических данных необходимо учитывать при проведении расчетов показателей воздействия химических загрязнений ХП на лесные массивы, а также при моделировании процессов распространения химических загрязнений по территории ЛМ в регионах химических предприятий;
– применение нечеткого метода главных компонент позволяет получать количественные характеристики воздействия ХП на ОС, а также выделять участки ЛМ с максимальными и минимальными потерями биологических показателей;
– разработанный алгоритм нечеткого метода главных компонент может быть использован в других инженерно-технических и научных областях, например, в материаловедении при проектировании свойств композитных материалов.
ОБОЗНАЧЕНИЯ
| ${{a}_{i}},\Delta {{a}_{i}}$ | центр и полуширина i-го симметричного нечеткого треугольного числа |
| ${{a}_{i}},{{b}_{j}}$ | безразмерные весовые коэффициенты |
| D | диагональная матрица стандартных отклонений |
| di | нормализованный показатель дозы, безразмерный |
| ${{E}_{i}},{{D}_{j}}$ | ненормализованные показатели эффекта и дозы, отн. ед. |
| ei | безразмерный нормализованный показатель эффекта |
| f(x) | скалярная функция “доза–эффект”-зависимости |
| $I = \left( {{{I}_{1}},{{I}_{2}}, \ldots ,{{I}_{m}}} \right){\kern 1pt} '$ | вектор-столбец исходных компонент |
| $\bar {I} = \left( {{{{\bar {I}}}_{1}},{{{\bar {I}}}_{2}}, \ldots ,{{{\bar {I}}}_{m}}} \right){\kern 1pt} '$ | вектор-столбец средних значений исходных переменных |
| IE | безразмерный суммарный интегральный индекс нормализованных показателей эффекта |
| ID | безразмерный суммарный интегральный индекс нормализованных показателей дозы |
| K | диагональная матрица упорядоченных по величине собственных значений матрицы R |
| m | число компонент |
| P' | транспонированная матрица |
| R | корреляционная матрица |
| S | ковариационная матрица |
| $s_{j}^{2}$ | дисперсия j-й нормализованной компоненты |
| $s_{{jk}}^{2}$ | коэффициенты ковариации нормализованных компонент j и k |
| U, V | ортогональные матрицы, столбцы которых являются собственными векторами матрицы R |
| wi | безразмерные весовые коэффициенты |
| z | вектор-столбец, элементы которого являются нормализованные и центрированные главные компоненты (безразмерный) |
| ОПП | общее проективное покрытие, % |
| ЖСД | жизненное состояние древостоя, баллы |
| ВР | видовое разнообразие травяно-кустарничкового яруса |
| SO2 | безразмерная нормализованная концентрация диоксида серы |
| ${\text{SO}}_{4}^{{2 - }}$ | безразмерная нормализованная концентрация ионов ${\text{SO}}_{4}^{{2 - }}.$ |
Список литературы
Мешалкин В.П., Бутусов О.Б., Смотрич С.А., Сельский Б.Е. Информационная система для экологического зонирования воздушного бассейна в условиях городской застройки // Хим. пром-сть. 1997. № 4. С. 263.
Мешалкин В.П., Бутусов О.Б., Сельский Б.Е. Метод определения интегрального индекса химических загрязнений окружающей среды от газовых выбросов химических и нефтехимических предприятий для экологического зонирования // Хим. пром-сть. 1998. № 1. С. 44.
Бутусов О.Б., Кантюков Р.А., Мешалкин В.П., Кантюков Р.Р. Компьютерное моделирование воздействия газопроводов на окружающую среду. СПб.: Недра, 2014.
Бутусов О.Б., Леонтьев Л.И., Мешалкин В.П. Комплексная оценка воздействия металлургического комбината на лесные массивы // Все матер. 2009. № 5. С. 38.
Bojadziev G., Bojadziev M. Fuzzy Logic for Business, Finance, and Management. Singapore: World Scientific, 2007.
Литвин В.А. Многокритериальная автоматизированная региональная система моделирования эффективных атмосферных стратегий. М.: Гидрометеоиздат, 1988.
Jolliffe I.T. Principle Component Analysis. N.Y.: Springer-Verlag, 2002.
Vidal R., Ma Y., Sastry S.S. Generalized Principal Component Analysis. N.Y.: Springer-Verlag, 2016.
Jensen R., Shen Q. Computational Intelligence and Feature Selection: Rough and Fuzzy Approaches. N.Y.: Wiley, 2008.
Buckley J.J. Simulating Fuzzy Systems. Berlin: Springer, 2005.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии