Теоретические основы химической технологии, 2021, T. 55, № 4, стр. 471-477
Методика расчета нормативных показателей безотказности элементов восстанавливаемых газоаналитических систем мониторинга химических загрязнений окружающей среды по экспериментально-справочным данным
В. П. Мешалкин a, В. И. Бобков b, *, И. В. Якименко b, О. А. Канищев c, А. И. Шинкевич d
a Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия
b Национальный исследовательский университет “МЭИ” в г. Смоленске
Смоленск, Россия
c СПО “Аналитприбор”
Смоленск, Россия
d Казанский национальный исследовательский технологический университет
Казань, Россия
* E-mail: vovabobkoff@mail.ru
Поступила в редакцию 15.02.2021
После доработки 22.03.2021
Принята к публикации 23.03.2021
Аннотация
Разработана методика расчета нормативных показателей безотказности элементов восстанавливаемых газоаналитических систем мониторинга химических загрязнений окружающей среды по экспериментально-справочным данным, отличающиеся одновременным использованием различных результатов обработки экспериментальной информации, полученных стандартным методом, интервальным методом и методом Каплана–Майера, что позволяет проводить испытания на надежность малых (экономически эффективных) выборок изделий, в условиях их возможного выбывания из-под наблюдений по причинам не связанных с отказом. Разработанная методика позволяет снизить стоимость проведения опытно-конструкторских работ, уменьшить степень неопределенности при разработке стратегии технического обслуживания и ремонта не только для рассматриваемых специализированных газоаналитических систем, но и решать задачи оптимального управления эксплуатационной надежностью широкого класса восстанавливаемых сложных химико-технических систем на этапе их проектирования.
ВВЕДЕНИЕ
Газоаналитические системы мониторинга (ГАСМ) опасных химических загрязнений окружающей среды (ОС) – это сложные контрольно-измерительные системы, состоящие из устройств пробоотбора и пробоподготовки, газоаналитических преобразователей и универсальных аналитических приборов, функционирование которых осуществляется с использованием специального программно-информационного обеспечения [1, 2].
ГАСМ предназначены для измерений одного или нескольких компонентов газовой смеси в технологических потоках химико-технологических систем (ХТС), оценки эффективности процессов сжигания топлива, для экологического контроля и обеспечения требований высокой надежности и безопасности при эксплуатации ХТС [3, 4].
Важнейшим организационным способом обеспечения надежности ХТС является изменение режимов эксплуатации на основе стратегии технического обслуживания и ремонта (ТОиР) [5, 6]. Оптимизация стратегии ТОиР практически осуществляется методами математического моделирования [7, 8]. Для верификации математической модели управления эксплуатационной надежностью требуются экспериментально обоснованные данные по безотказности элементов ГАСМ [9, 10].
МЕТОДЫ СИСТЕМНОГО ПОДХОДА ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНОЙ ИНФОРМАЦИИ О ПОКАЗАТЕЛЯХ НАДЕЖНОСТИ ГАЗОАНАЛИТИЧЕСКИХ СИСТЕМ МОНИТОРИНГА ОКРУЖАЮЩЕЙ СРЕДЫ С УЧЕТОМ ПОКАЗАТЕЛЯ ВЫЖИВАЕМОСТИ
Первичным материалом для определения количественных характеристик безотказной работы элементов ГАСМ являются результаты спланированных испытаний на надежность [11, 12]. На основании полученных экспериментальных данных можно построить эмпирическую функцию распределения отказов и проверить статистическую гипотезу о предполагаемом ее теоретическом распределении, используя критерии согласия, например, критерий Пирсона, Колмогорова–Смирнова и др.
В реальных условиях обоснование эмпирической функции распределения и вычисление на его основе вероятностных показателей безотказной работы трудновыполнимо по причине больших ресурсных затрат [13, 14]. Поэтому на практике более рациональным действием является применение методов статистического анализа экспериментальных данных, которые позволяют вычислить показатели безотказной работы на основе анализа выборок малого объема, методы анализа которых объединены под общим названием “Анализ выживаемости” [15, 16].
Особенность методов анализа выживаемости состоит в том, что они предназначены для анализа цензурированных первичных данных. Цензурированные данные дают возможность описывать поведение исследуемого объекта с учетом того, что наблюдение в точности до наступления отказа не всегда возможно [17].
Методы анализа выживаемости позволяют использовать все имеющиеся экспериментальные данные, как цензурированные, так и нецензурированные.
Основными экспериментальными характеристиками, которые вычисляются методами анализа выживаемости, являются функция выживаемости $S\left( t \right)$ и функция интенсивности рисков $h\left( t \right)$ [18–20]. Для статистической совокупности функция $S\left( t \right)$ определяет вероятность изделия оставаться в исправном состоянии более времени t с момента начала наблюдения, а $h\left( t \right)$ определяет моментный потенциал на единицу времени для возникновения отказа, который может произойти, при условии, что изделие будет работоспособным до времени t.
Практический метод описания функции выживаемости, заключающийся в построении таблицы безотказной работы испытываемых изделий, состоит из трех этапов (метод таблиц времени безотказной работы):
Этап 1. Разбиение периода наблюдений на интервалы.
Этап 2. Определение средних значений (по интервалу наблюдений) интенсивности отказов
Этап 3. Определение средней (по периоду наблюдений) интенсивности отказов.
Рассмотрим сущность основных операций на каждом этапе метода. На этапе 1 период наблюдений $T$ разбивается на равные по ширине интервалы $\Delta t,$ по формуле Стерджесса. На этапе 2 определяется эмпирическая функция мгновенного риска ${{\hat {h}}_{i}}$ ${{\hat {H}}_{i}},$ которая в этом методе служит оценкой средней интенсивность отказов $\overline {{{\lambda }_{i}}} $ на интервале времени $\Delta t$ [18–20]:
(1)
$\overline {{{\lambda }_{i}}} {\text{\;}} = d_{i}^{{\text{0}}}{{\left[ {0,5\left( {x_{i}^{0} - x_{{i + 1}}^{0}} \right)\Delta t} \right]}^{{ - 1}}},$Второй метод – моментный метод (метод Каплана–Майера) состоящий из трех этапов.
Этап 1. Вычисление эмпирической вероятности $p({{t}_{i}})$ “пережить” этот момент.
Этап 2. Вычисляют эмпирическую оценку функции выживаемости $\hat {S}\left( {{{t}_{i}}} \right).$
Этап 3. Вычисление средней интенсивности отказов.
Рассмотрим сущность основных операций на каждом этапе методики. На этапе 1 регистрируют моменты времени ${{t}_{i}},$ в которые произошел отказ хотя бы одного изделия из выборочной совокупности и вычисляют эмпирическую вероятность $p({{t}_{i}})$ “пережить” этот момент по формуле [18–20]:
(2)
$p\left( {{{t}_{i}}} \right) = n\left( {{{t}_{i}}} \right){{({v}\left( {{{t}_{i}}} \right))}^{{ - 1}}},$(3)
$\hat {S}\left( {{{t}_{i}}} \right) = \prod\limits_{i = 1}^j {p\left( {{{t}_{i}}} \right)} = \prod\limits_{i = 1}^j {\left[ {1 - \frac{{d\left( {{{t}_{i}}} \right)}}{{{v}\left( {{{t}_{i}}} \right)}}} \right]} .$На этапе 4 предполагая, что вероятность безотказной работы изделий распределена по экспоненциальному закону, вычисляют среднюю интенсивность отказов $\bar {\lambda }$ по формуле [18–20]
МЕТОДИКА ПРИМЕНЕНИЯ НОРМАТИВНЫХ МЕТОДОВ ОЦЕНКИ ПОКАЗАТЕЛЕЙ БЕЗОТКАЗНОСТИ ЭЛЕМЕНТОВ ГАЗОАНАЛИТИЧЕСКИХ СИСТЕМ МОНИТОРИНГА ОКРУЖАЮЩЕЙ СРЕДЫ
Методика применения нормативных методов оценки показателей безотказности элементов ГАСМ состоит из четырех этапов.
Этап 1. Планирование испытаний.
Этап 2. Проведение испытаний и сбор экспериментальных данных по надежности.
Этап 3. Анализ экспериментальных данных, определение наработки изделий до отказа и цензурирования.
Рассмотрим сущность основных операций на каждом этапе методики. На этапе 1 проводят планирование испытаний по ГОСТ 27.410, либо устанавливают количество испытываемых изделий и продолжительность испытаний с учетом экономических ограничений. Результатом планирования является программа испытаний, в которой указываются методы, в т. ч. ускоренные методы испытаний, критерии отказа и прекращения испытаний. На этапе 2 регистрируется информация об отказах, наработки $\left( {T{{F}_{i}}} \right)$ до отказа $i{\text{ - го}}$ изделия и наработка $({{\tau }_{j}})$ до цензурирования. На этапе 3 определяется интенсивность отказов составных блоков:
а) при количестве отказов $r$ больше 5 вычисляют точечную оценку интенсивности отказов $\hat {\lambda }$ по формуле [21]:
(5)
$\hat {\lambda } = rN{{\left[ {\left( {\sum\limits_{i = 1}^r {T{{F}_{i}}} + \sum\limits_{j = 1}^с {{{\tau }_{j}}} } \right)\left( {N - 1} \right)} \right]}^{{ - 1}}}.$При числе отказов меньшем 5, вычисляют оценку верхней доверительной границы интенсивности отказов $\left( {\bar {\bar {\lambda }}} \right)~$ по формуле [21]:
где $\chi _{q}^{2}\left( {2N} \right)$ – квантиль ХИ квадрат распределения с числом степеней свободы $2N$ при доверительной вероятности $q,$ а при отсутствии отказов вычисляют оценку верхней границы интенсивности отказов $\left( {\bar {\bar {\lambda }}} \right)$ по формуле [21](7)
$\bar {\bar {\lambda }} = - ~{\text{ln}}\left( {1 - q} \right){{\left( {\sum\limits_{j = 1}^с {{{\tau }_{j}}} } \right)}^{{ - 1}}}.$Разработка расчета нормативных показателей безотказности элементов восстанавливаемых газоаналитических систем мониторинга химических загрязнений окружающей среды по экспериментально-справочным данным.
Методика состоит из пяти этапов.
Этап 1. Общий анализ функционирования элементов ГАСМ как объектов исследования надежности.
Этап 2. Определение интенсивности отказов составных блоков элементов ГАСМ на основе справочной информации по надежности электрорадиоизделий (ЭРИ).
2.1 Выделение групп ЭРИ с единым набором коэффициентов математической модели надежности (ММН).
2.2 Составление карт режимов работы ЭРИ. Определение значений коэффициентов ММН.
2.3 Вычисление интенсивности отказов ЭРИ в соответствии с ММН.
2.4 Определение интенсивности отказов составных блоков элементов ГАСМ.
Этап 3. Получение и обработка экспериментальных данных по безотказности составных блоков элементов ГАСМ.
Этап 4. Определение нормативных показателей безотказности элементов ГАСМ по экспериментально-справочным данным.
4.1 Определение вероятности безотказной работы элементов ГАСМ.
4.2 Определение интенсивности отказов элементов ГАСМ путем аппроксимации
4.3 Определение коэффициента готовности ГАСМ с использованием различных методов обработки экспериментальных данных.
4.4 Определение достаточности экспериментальных данных путем оценки влияния методов обработки экспериментальных данных на результаты определения коэффициента готовности ГАСМ.
Рассмотрим сущность основных операций на каждом этапе методики. На этапе 1 результатом общего анализа функционирования элементов ГАСМ как объектов исследования надежности является их декомпозиция на составные блоки и составление структурной блок-схемы надежности, при этом выделяются блоки, состоящие из электрорадиоэлементов, и блоки, для которых необходимо провести экспериментальные исследования для определения интенсивности отказов. Составные блоки должны быть статистически независимыми и максимально большими, не содержащими структурного резервирования и сами должны быть представимы последовательной блок-схемой надежности.
На шаге 2.1, в зависимости от условий эксплуатации, ЭРИ в каждом блоке разделяются по группам (резисторы, конденсаторы и т.д.), для которой устанавливается единообразный набор коэффициентов принятой математической модели надежности (ММН) [17]:
(8)
$\lambda = \sum\limits_{k = 1}^l {{{\lambda }_{k}}} \prod\limits_{j = 1}^{{{m}_{k}}} {{{K}_{{kj}}}} ,$На шаге 2.2 составляется карта режимов – таблица, в которой каждому ЭРИ, на основании анализа условий эксплуатации определяются коэффициенты ${{K}_{{kj}}}$ ММН. На шаге 2.3 для ЭРИ вычисляется интенсивность отказов в соответствии с ММН по формуле (1). На шаге 2.4 вычисляется интенсивность отказов составных блоков как сумма интенсивностей отказов ЭРИ.
На этапе 3 проводят планирование и проведение испытаний с последующей обработкой экспериментальных данных по формулам (1), …, (7).
На шаге 4.1 вычисляется вероятность безотказной работы элементов ГАСМ за определенный период времени с использованием теории надежности невосстанавливаемых технических систем на основании структурной блок-схемы надежности элементов и результатов определения интенсивности отказов составных блоков с использованием экспериментально-справочных данных [16]. На шаге 4.2 вероятность безотказной работы аппроксимируется экспоненциальной функцией, например, по методу наименьших квадратов или графически. На шаге 4.3 вычисляется комплексный показатель надежности ГАСМ – коэффициент готовности (${{F}_{a}}$) с использованием компьютерной полумарковской модели процесса управления эксплуатационной надежностью ГАСМ и результатов определения интенсивности отказов, полученных с использованием различных методов обработки экспериментальных данных. На шаге 4.4 значения коэффициента готовности (${{F}_{a}}$), вычисленные с использованием различных методов обработки экспериментальных данных, сопоставляются между собой. Если разностью коэффициентов готовности можно пренебречь, делается вывод о достаточности экспериментальной информации по надежности составляющих блоков, в противном случае испытания на надежность проводятся с увеличенным количеством изделий.
РЕЗУЛЬТАТЫ ВЫЧИСЛИТЕЛЬНЫХ ЭКСПЕРИМЕНТОВ НА ПОЛУМАРКОВСКОЙ МОДЕЛИ ПРОЦЕССА УПРАВЛЕНИЯ ЭКСПЛУАТАЦИОННОЙ НАДЕЖНОСТЬЮ ГАСМ С ИСПОЛЬЗОВАНИЕМ РАЗЛИЧНЫХ МЕТОДОВ ОБРАБОТКИ ДАННЫХ
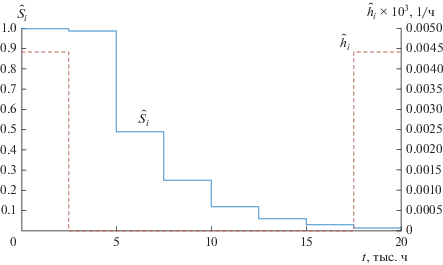
Для определения количественных характеристик безотказной работы элементов ГАСМ были проведены испытания на надежность составных частей ГАСМ: электрохимические датчики (ЭХД), инфракрасные излучатели, электромеханические клапаны и побудители расхода. Испытания были начаты в 2015 году и окончены в марте 2020 г. Исходные данные для проведения вычислительных экспериментов по определению коэффициента готовности ГАСМ приведены в табл. 1.
Таблица 1.
Исходные данные для проведения вычислительных экспериментов по определению коэффициента готовности ГАСМ
| Наименование испытываемого изделия | ЭХД | Клапан | Побудитель расхода | Излучатель |
|---|---|---|---|---|
| Количество испытываемых изделий | 93 шт. | 16 шт. | 11 шт. | 10 шт. |
| План испытаний по РД 50-690-89 | NUZ | NUZ | NUZ | NUZ |
| Количество отказавших изделий | 1 | 2 | 0 | 0 |
| Количество изделий, выбывших из-под наблюдения | 2 | 3 | 1 | 0 |
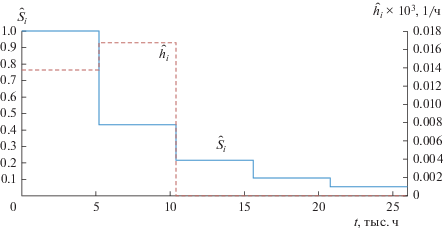
Пример результатов вычислений функции выживаемости ${{\hat {S}}_{i}}$ и мгновенного риска ${{\hat {h}}_{i}}$ по экспериментальным данным для ЭХД и клапанов приведены на рис. 1 и 2.
Рис. 2.
Функции выживаемости ${{\hat {S}}_{i}}$ и мгновенного риска ${{\hat {h}}_{i}}$ для клапанов.
Результаты вычислительных экспериментов по определению коэффициента готовности ГАСМ, полученные с использованием компьютерной полумарковской модели процесса управления эксплуатационной надежностью ГАСМ и результатов определения интенсивности отказов, полученных с использованием различных методов обработки экспериментальных данных приведены в табл. 2.
Таблица 2.
Результаты вычислительных экспериментов по определению коэффициента готовности ГАСМ
| Параметр | Интенсивность отказов составных частей ГАСМ, 1/ч | Fa | ||||
|---|---|---|---|---|---|---|
| АМД-01 | АМД-02 | Клапан | БУК | БУС | ||
| РД 50-690-89 | 2.2 × 10–5 | 2.2 × 10–5 | 3.0 × 10–9 | 4.9 × 10–7 | 3.5 × 10–7 | 0.9997 |
| Интервальный метод | 1.4 × 10–5 | 1.4 × 10–5 | 2.5 × 10–9 | 4.9 × 10–7 | 3.5 × 10–7 | 0.99975 |
| Метод Каплана–Майера | 1.4 × 10–5 | 1.4 × 10–5 | 3.5 × 10–9 | 4.9 × 10–7 | 3.5 × 10–7 | 0.99975 |
ЗАКЛЮЧЕНИЕ
Разработана методика расчета нормативных показателей безотказности элементов ГАСМ, позволяющая определять значения коэффициента готовности с использованием малых (экономически эффективных) выборок изделий, в условиях их возможного выбывания из-под наблюдений по причинам не связанных с отказом. Используя системный подход к анализу экспериментальных данных, обосновано, что продолжительность определительных испытаний на надежность и количество испытываемых составных частей могут быть приняты достаточными на основании оценки влияния экспериментальных данных по надежности на вычисленное значение коэффициента готовности ГАСМ. Приведены результаты практического применения разработанной методики для определения показателей безотказности составных частей и коэффициента готовности ГАСМ.
Исследование выполнено при финансовой поддержке РФФИ (проект № 18-29-24094 МК) и по государственному заданию (проект № FSWF-2020-0019).
ОБОЗНАЧЕНИЯ
| c | количество изделий изъятых из испытаний по причинам, не связанных с отказом, шт. |
| $d$ | количество отказавших изделий, шт. |
| ${{F}_{a}}$ | коэффициент готовности |
| $h~~$ | функция интенсивности рисков, ч–1 |
| $K$ | коэффициент, учитывающий влияние различных факторов в ММН |
| $l$ | количество независимых учитываемых потоков отказов в ММН |
| $m$ | количество факторов, учитываемых в отдельном потоке отказов в ММН |
| n | количество интервалов наблюдения |
| $N$ | количество испытываемых изделий, шт. |
| $p$ | эмпирическая вероятность изделия “пережить” определенный момент времени |
| $~r$ | количество отказов, шт. |
| ${\text{S}}~$ | функция выживаемости |
| t | время, ч |
| $TF$ | время наработки до отказа, ч |
| ${v}$ | количество наблюдаемых изделий на определенный момент, шт. |
| $x$ | nti количество исправных изделий, шт. |
| $\Delta t$ | продолжительность интервала разбиения периода наблюдений, ч |
| $\chi _{q}^{2}$ | квантиль ХИ квадрат распределения с числом степеней свободы $2N$ при доверительной вероятности $q;$ |
| $\lambda $ | интенсивность отказов, ч–1 |
| $\tau $ | наработка до цензурирования, ч |
ИНДЕКСЫ
| i | номер изделия отказавшего при испытаниях, номер интервала наблюдений |
| $j$ | номер фактора в $k{\text{ - м}}$ потоке отказов, номер изделия изъятого из испытаний |
| k | номер потока отказов |
| $q$ | доверительная вероятность |
| $0$ | количество изделий в начале интервала наблюдения |
| $\hat {й}$ | эмпирическая оценка физической величины |
| $\bar {\lambda }$ | среднее значение физической величины |
| $\bar {\bar {\lambda }}$ | оценка верхней границы значения физической величины |
Список литературы
Guuhn G., Fiehtner G., Mohr J., Kafarov V.V., Meshalkin V.P. Eine Method zum Entwurf einer Speziellen Mehrproduktanlage. Leuna-Merseburg: Wissenschaftliche Zeitschrift TH, 1987. B. 29.
Gruhn G., Kafarov V.V., Meshalkin V.P., Neumann W. Zuverlaessigkeit von Chemieanlagen. Leipzig: VEB, Deutscher Verlag fur Grundstoffindustrie, 1979.
Yang D.-Y., Tsao C.-L. Reliability and availability analysis of standby systems with working vacations and retrial of failed components // Reliab. Eng. Syst. Saf. 2019. V. 182. P. 46.
Hashe V.T., Mamatlepa M.T. Application of Reliability Engineering in a Chemical Plant to Improve Productivity // 10th International Conference on Engineering, Project, and Production Management. Lecture Notes in Mechanical Engineering. Singapore: Springer, 2020. P. 547.
Emelyanov A., Shil’nikova O., Emelyanova N. Modelling of developing information management system and supporting of its working ability // Prikl. Inf. 2015. V. 10. P. 93.
Берман А.Ф., Николайчук О.А., Юрин А.Ю., Павлов А.И. Принципы информационной технологии решения междисциплинарных задач обеспечения техногенной безопасности на основе самоорганизации // Инф. мат. технол. науке упр. 2019. Т. 2. № 14. С. 5.
Берман А.Ф., Николайчук О.А., Павлов А.И., Юрин А.Ю. Обеспечение надежности и безопасности химических и нефтехимических производств методами искусственного интеллекта // Прикл. инф. 2016. Т. 11. № 5(65). С. 63.
Egorov A., Savitskaya T., Nikitin S. The information system of reliability analysis of equipment and chemicaltechnological systems using web technologies // Prikl. Inf. 2016. V. 11. № 4(64). P. 30.
Burlyaeva E., Razlivinskaya S., Tregubov A. Development and application of the generalized functional model of one-stage chemical manufacturing // Prikl. Inf. 2016. V. 11. № 1(61). P. 64.
Vidhya Gnair, Manoharan M. Reliability analysis of a multistate system with common cause failures using Markov Regenerative Process // Reliab.: Theor. Appl. 2018. V. 13. № 3(50). P. 82.
Берман А.Ф. Искусственная самоорганизация и эвристический подход для обоснования Свойств Надежности, Живучести и Безопасности СТС // Пробл. безоп. чрезв. ситуац. 2020. № 4. С. 5.
Bogomolov B.B., Zubarev A.M., Meshalkin V.P., Men’shikov V.V., Boldyrev V.S. Intelligent logical information algorithm for choosing energy- and resource-efficient chemical technologies // Theor. Found. Chem. Eng. 2019. V. 53. № 5. P. 709. [Богомолов Б.Б., Болдырев В.С., Зубарев А.М., Мешалкин В.П., Меньшиков В.В. Интеллектуальный логико-информационный алгоритм выбора энергоресурсоэффективной химической технологии // Теорет. основы хим. технологии. 2019. Т. 53. № 5. С. 483.]
Berman A.F., Nikolaychuk O.A. Self-organizing technology for substantiating the properties of strength reliability of complex mechanical systems // IOP Conf. Ser.: Mater. Sci. Eng. 2020. V. 919. № 5.
Meshalkin V.P., Panina E.A., Bykov R.S. Principles of developing an interactive system for the semantic processing of scientific and technical texts on chemical technology of reagents and ultrapure substances // Theor. Found. Chem. Eng. 2015. V. 49. № 4. P. 422. [Мешалкин В.П., Панина Е.А., Быков Р.С. Принципы разработки интерактивной системы смысловой обработки научно-технических текстов по химической технологии реактивов и особо чистых веществ // Теорет. основы хим. технологии. 2015. Т. 49. № 4. С. 442.]
Lapteva T.V., Ziyatdinov N.N., Emel’yanov I.I. Chemical process design taking into account joint chance constraints // Theor. Found. Chem. Eng. 2020. V. 54. № 1. P. 145. [Лаптева Т.В., Зиятдинов Н.Н., Емельянов И.И. Проектирование химико-технологических систем при учете объединенных мягких ограничений // Теорет. основы хим. технологии. 2020. Т. 54. № 1. С. 17.]
Надежность технических систем. Справочник / Под общ. ред. Ушакова И.А. М.: Радио и связь, 1985.
Прытков С.Ф., Горбачева В.М., Борисов A.A. и др. Надежность ЭРИ. Справочник. М.: 22 ЦНИИИ МО РФ, 2006.
Miller R.G.Jr. Survival Analysis. N.Y.: Wiley-Interscience, 1998.
Karim M.R., Islam M.A. Reliability and Survival Analysis. Singapore: Springer, 2019.
Elsheikh A., Yacout S., Ouali M.S., Shaban Y. Failure time prediction using adaptive logical analysis of survival curves and multiple machining signals // J. Intell. Manuf. 2020. V. 3. № 2. P. 403.
Методические указания. Надежность в технике. Методы оценки показателей надежности по экспериментальным данным. РД 50-690-89. М.: Издательство стандартов, 1990.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии