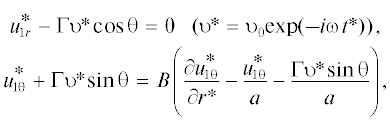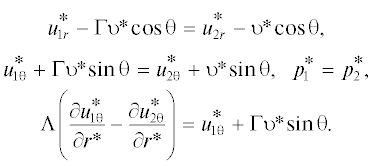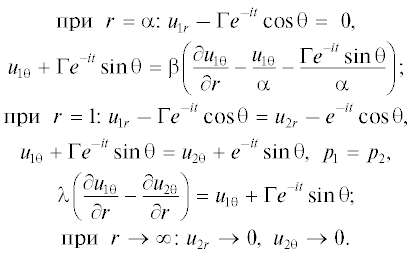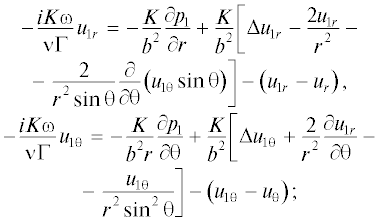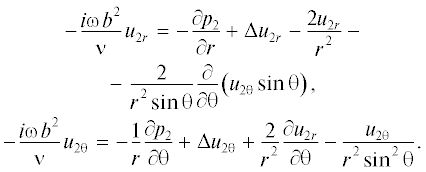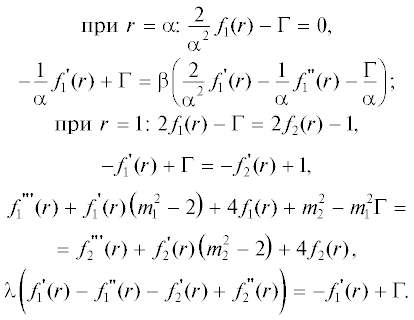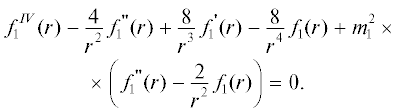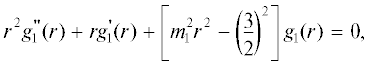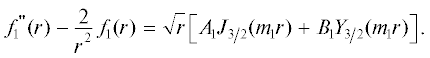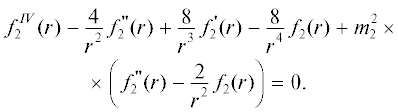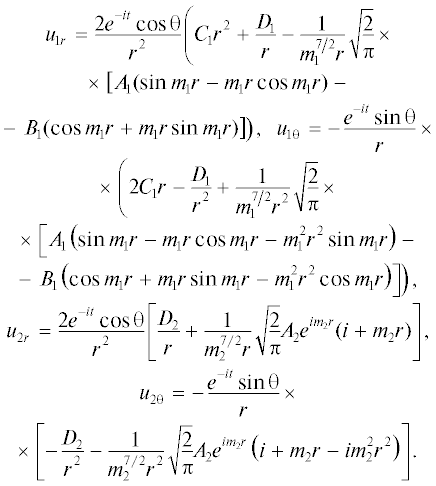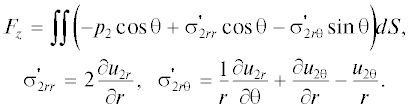Теоретические основы химической технологии, 2021, T. 55, № 5, стр. 652-660

Поступательно-колебательные движения пористой сферической оболочки с твердым непроницаемым ядром в вязкой жидкости

О. А. Базаркина^a, *, Н. Г. Тактаров^a, **

^a Мордовский государственный педагогический университет им. М.Е. Евсевьева
Саранск, Россия

^* E-mail: o.a.bazarkina@mail.ru
^** E-mail: n.g.taktarov@mail.ru

Поступила в редакцию 18.01.2021
После доработки 16.03.2021
Принята к публикации 23.03.2021

DOI: 10.31857/S0040357121040023

Аннотация

Получены аналитические решения нестационарного уравнения Бринкмана, описывающего течение жидкости внутри погруженной в нее пористой сферической оболочки с твердым непроницаемым ядром, совершающей поступательно-колебательные движения, и уравнения Навье–Стокса в приближении Стокса – вне оболочки. Определены поля скоростей фильтрации в пористой среде и скоростей свободной жидкости вне пористой оболочки. Определена сила, действующая на контрольную сферическую поверхность вокруг пористой оболочки. Приведен анализ полученных решений. Рассмотрены различные частные случаи, в том числе случай равномерного движения пористой оболочки в вязкой жидкости.

Ключевые слова: пористая сферическая оболочка, твердое непроницаемое ядро, поступательно-колебательное движение, вязкая жидкость, уравнение Бринкмана, уравнение Навье–Стокса

ВВЕДЕНИЕ

Как известно, уравнения гидродинамики в общем виде не могут быть решены точно. В связи с этим представляет большой интерес поиск и исследование важнейших из тех случаев, когда уравнения движения жидкости имеют точные аналитические решения. Некоторые из таких точных решений уравнений гидродинамики получены и подробно исследованы в [1–4].

Аналогично обстоит дело и с уравнениями движения вязких жидкостей через пористые среды: эти уравнения в общем виде также не могут быть решены точно.

Теория движения жидкостей через пористые среды интенсивно развивается в последнее время в связи с разнообразными приложениями в моделировании технологических процессов, а также при изучении природных явлений. Многие технологические процессы в химической промышленности и инженерной практике тесно связаны с движением жидкостей через пористые среды. Движение жидкостей внутри и вне пористых тел определяется уравнениями гидродинамики. Гидродинамические закономерности определяют характер протекания процессов тепло- и массообмена с учетом химических реакций в масштабных промышленных аппаратах. Многочисленные приложения стимулируют исследование течений жидкости внутри и вне пористых тел, ограниченных различными поверхностями, простейшими среди которых являются плоскость, сферическая и цилиндрическая поверхности. Для них при специальных предположениях можно найти аналитические решения соответствующих краевых задач.

В [5] приведен обзор практических приложений гидродинамики при малых числах Рейнольдса для изучения природных явлений и технологических процессов.

В [6, 7] приведены решения задач о движении сплошных (непроницаемых) твердых тел в вязкой жидкости. В частности, в [6] рассмотрены внутренние поперечные волны, возникающие при движении сплошного твердого шара, погруженного в жидкость и совершающего вращательные и поступательные колебания. В [8] при использовании модели фильтрации Бринкмана решена задача об обтекании вязкой жидкостью пористого шара, находящегося в другой пористой среде. В [9, 10] с использованием уравнения фильтрации Дарси решены задачи об обтекании пористой сферической оболочки, ограниченной двумя концентрическими сферическими поверхностями. В [11] при использовании нестационарного уравнения Бринкмана определено движение вязкой жидкости, вызванное вращательным колебательным движением погруженного в нее пористого шара.

В [12] решена задача о поступательно-колебательном движении пористого шара в вязкой жидкости в рамках модели фильтрации Бринкмана.

В [13] определены течения вязкой жидкости, вызванные вращательными колебаниями погруженной в нее пористой сферической оболочки. В приближении Стокса получены аналитические решения нестационарного уравнения Бринкмана в области внутри пористой оболочки и уравнения Навье–Стокса – вне оболочки. Определен момент сил терния, действующих на контрольную сферическую поверхность вокруг пористого тела.

В [14] решена задача о колебательных течениях вязкой жидкости, контактирующей с плоским слоем пористой среды.

В [15–19] приведен вывод уравнений движения жидкости в пористой среде и анализ границ применимости этих уравнений. В [16, 20, 21] приведен вывод и анализ граничных условий на плоской неподвижной поверхности раздела пористой среды и свободной жидкости. В настоящей работе эти граничные условия обобщаются на случай подвижной сферической поверхности раздела пористой среды и жидкости.

Целью работы является исследование влияния поступательного колебательного движения пористой сферической оболочки с твердым непроницаемым ядром в вязкой жидкости на течение жидкости внутри и вне этой оболочки.

ПОСТАНОВКА ЗАДАЧИ, УРАВНЕНИЯ И ГРАНИЧНЫЕ УСЛОВИЯ

Рассматриваются течения вязкой жидкости при колебательном поступательном движении погруженной в нее пористой сферической оболочки с внутренним и внешним радиусами равными а и b соответственно (a < b). Радиус твердого непроницаемого ядра, неизменно связанного с пористой оболочкой, равен а. Пористая среда предполагается недеформируемой, однородной и изотропной. Предполагается, что пористая среда имеет достаточно большую пористость Γ, близкую к единице, и высокую проницаемость K. При таких условиях скорость жидкости в пористой матрице может заметно отличаться от скорости матрицы.

Скорость оболочки вместе с ядром запишем как гармоническую функцию от времени t* вида υ* = υ₀ exp(–iωt*), где υ₀ – действительный вектор, ω – частота колебаний. Знаком “*” будем обозначать размерные переменные (но не параметры), чтобы отличать их от безразмерных, обозначаемых теми же символами. Поскольку все рассматриваемые в данной работе математические операции – линейные, взятие действительных частей от соответствующих комплексных выражений можно проделать в окончательных результатах. Величины, относящиеся к областям, занятым пористой оболочкой и свободной жидкостью вне оболочки, обозначаются индексами 1 и 2 соответственно.

Движение жидкости, неподвижной на бесконечности, рассматривается в неподвижной системе координат Ох*у*z*, начало О которой в данный момент времени совпадает с геометрическим центром сферической оболочки. Ось z* и вектор υ₀ = υ₀е (υ₀ > 0, |e| = 1) параллельны.

Уравнения нестационарного движения жидкости в областях 1 и 2 запишем в приближении Стокса в виде [6, 15–18]

(1)

$\begin{gathered} \frac{\rho }{\Gamma }\frac{{\partial {\mathbf{u}}_{1}^{*}}}{{\partial t{\text{*}}}} = - \nabla {\text{*}}p_{1}^{*} + \eta {\kern 1pt} '\Delta {\text{*}}{\mathbf{u}}_{1}^{*} - \frac{\eta }{K}\left( {{\mathbf{u}}_{1}^{*} - {\mathbf{u}}{\text{*}}} \right),\,\,\,\,\nabla {\text{*}}{\mathbf{u}}_{1}^{*} = 0, \\ \rho \frac{{\partial {\mathbf{u}}_{2}^{*}}}{{\partial t{\text{*}}}} = - \nabla {\text{*}}p_{2}^{*} + \eta \Delta {\text{*}}{\mathbf{u}}_{2}^{*},\,\,\,\,\nabla {\text{*}}{\mathbf{u}}_{2}^{*} = 0. \\ \end{gathered} $

Здесь ${\mathbf{u}}_{1}^{*}$ – скорость фильтрации, Г – пористость, $p_{1}^{*}$ – давление в пористой среде, ρ – плотность жидкости, η' – величина с размерностью вязкости, η – вязкость свободной (вне пористого тела) жидкости, K – коэффициент проницаемости пористой среды, u* = Гυ*, ${\mathbf{u}}_{2}^{*}$ и $p_{2}^{*}$ – скорость и давление свободной жидкости. Предполагая, что пористость близка к единице, примем далее η' = η [15, 18].

В связи с симметрией задачи ее решение удобнее рассматривать в сферической системе координат r*, θ, φ, полярная ось которой совмещена с осью z*, от которой отсчитывается угол θ. Вследствие предполагаемой осевой симметрии от угла φ величины не зависят.

Граничные условия [16, 20, 21]:

на поверхности твердого ядра, при r* = а:

(2)

на внешней поверхности сферической оболочки, при r* = b:

(3)

Условия на бесконечности при r* → ∞: $u_{{2r}}^{*} = 0,$ 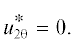К этим граничным условиям следует добавить условия конечности величин всюду в областях их определения.

Первое граничное условие (2) выражает условие непротекания жидкости на подвижной твердой поверхности ядра. Второе – это условие скольжения жидкости в пористой среде вдоль твердой поверхности ядра [5]. Величина В носит название коэффициента трения скольжения. При В = 0 скольжение жидкости отсутствует. При В → ∞ имеем случай отсутствия касательных напряжений (пузырек газа вместо твердого ядра).

Первые два условия (3) выражают условия непрерывности скорости на поверхности раздела пористой среды и свободной жидкости. Третье условие выражает непрерывность давления на поверхности раздела. Постоянная Λ в четвертом условии (3) определяется равенством $\Lambda = {{\sqrt K } \mathord{\left/ {\vphantom {{\sqrt K } \tau }} \right. \kern-0em} \tau },$ где τ – безразмерный параметр, зависящий от свойств пористой матрицы [16, 21]. При Λ = 0 (что равносильно K = 0, т.е. пористая среда непроницаема для жидкости) четвертое условие (3) принимает вид 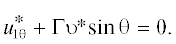При Λ → ∞ (τ → 0) четвертое условие принимает вид, формально аналогичный условию непрерывности касательных напряжений на поверхности раздела двух вязких жидкостей с одинаковой вязкостью.

РЕШЕНИЕ ЗАДАЧИ

Введем безразмерные переменные: ${\mathbf{r}} = {{{\mathbf{r}}{\text{*}}} \mathord{\left/ {\vphantom {{{\mathbf{r}}{\text{*}}} b}} \right. \kern-0em} b},$ t = = ωt*, ${\mathbf{u}} = {{{\mathbf{u}}{\text{*}}} \mathord{\left/ {\vphantom {{{\mathbf{u}}{\text{*}}} {{{\upsilon }_{0}}}}} \right. \kern-0em} {{{\upsilon }_{0}}}}$ = ${\mathbf{e}}\Gamma \exp ( - it),$ ${{{\mathbf{u}}}_{j}} = {{{\mathbf{u}}_{j}^{*}} \mathord{\left/ {\vphantom {{{\mathbf{u}}_{j}^{*}} {{{\upsilon }_{0}}}}} \right. \kern-0em} {{{\upsilon }_{0}}}},$ p_j = = $p_{j}^{*}\left( {{b \mathord{\left/ {\vphantom {b {\eta {{\upsilon }_{0}}}}} \right. \kern-0em} {\eta {{\upsilon }_{0}}}}} \right)$ (j = 1, 2).

Уравнения движения жидкости (1) в безразмерном видe

(4)

$\begin{gathered} \frac{{K\omega }}{{\nu \Gamma }}\frac{{\partial {{{\mathbf{u}}}_{1}}}}{{\partial t}} = - \frac{K}{{{{b}^{2}}}}\left( {\nabla {{p}_{1}} - \Delta {{{\mathbf{u}}}_{1}}} \right) - \left( {{{{\mathbf{u}}}_{1}} - {\mathbf{u}}} \right), \\ \nabla {{{\mathbf{u}}}_{{\text{1}}}} = 0,\,\,\,\,(\alpha < r < {\text{1}}); \\ \frac{{\omega {{b}^{2}}}}{\nu }\frac{{\partial {{{\mathbf{u}}}_{2}}}}{{\partial t}} = - \nabla {{p}_{2}} + \Delta {{{\mathbf{u}}}_{2}},\,\,\,\,\nabla {{{\mathbf{u}}}_{{\text{2}}}} = 0,\,\,\,\,(r > {\text{1}}). \\ \end{gathered} $

Здесь $\alpha = {a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b}$ (α < 1), $\nu = {\eta \mathord{\left/ {\vphantom {\eta \rho }} \right. \kern-0em} \rho }.$

Безразмерные граничные условия:

(5)

Здесь $\beta = {B \mathord{\left/ {\vphantom {B b}} \right. \kern-0em} b},$ $\lambda = {\Lambda \mathord{\left/ {\vphantom {\Lambda b}} \right. \kern-0em} b}.$ К этим граничным условиям следует добавить также условия конечности всех величин всюду в областях их определения. В связи с осевой симметрией принимаем u_1φ ≡ 0, u_2φ ≡ 0.

Скорости жидкости будем искать в виде, пропорциональном e^–it, поэтому: ${{\partial {{{\mathbf{u}}}_{j}}} \mathord{\left/ {\vphantom {{\partial {{{\mathbf{u}}}_{j}}} {\partial t}}} \right. \kern-0em} {\partial t}} = - i{{{\mathbf{u}}}_{j}}$ (j = 1, 2).

Из уравнений непрерывности следует, что компоненты скоростей жидкости u₁ и u₂ можно выразить через функции тока ψ₁ и ψ₂ для осесимметричного течения, к которому, в частности, относится обтекание пористой сферической оболочки с твердым непроницаемым ядром. Выражения компонент скорости через функции тока в сферических координатах имеют вид [6]

(6)

$\begin{gathered} {{u}_{{jr}}} = \frac{1}{{{{r}^{2}}\sin \theta }}\frac{{\partial {{\psi }_{j}}}}{{\partial \theta }},\,\,\,\,{{u}_{{j{{\theta }}}}} = - \frac{1}{{r\sin \theta }}\frac{{\partial {{\psi }_{j}}}}{{\partial r}}, \\ {{u}_{{j{{\varphi }}}}} \equiv 0\,\,\,\,(j = {\text{1}},{\text{2}}). \\ \end{gathered} $

Безразмерные уравнения движения (4) в сферической системе координат имеют следующий вид:

в области 1 (α < r < 1):

(7)

в области 2 (r > 1):

(8)

Здесь $\Delta f = \frac{1}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}\left( {{{r}^{2}}\frac{{\partial f}}{{\partial r}}} \right)$ + $\frac{1}{{{{r}^{2}}\sin \theta }}\frac{\partial }{{\partial \theta }}\left( {\sin \theta \frac{{\partial f}}{{\partial \theta }}} \right).$

Исключая давления р₁ и р₂ из уравнений (7) и (8) соответственно и используя (6), находим дифференциальные уравнения для определения функций тока ψ₁ и ψ₂:

(9)

$\left[ {{{E}^{2}}\left( {{{E}^{2}} + m_{j}^{2}} \right)} \right]{{\psi }_{j}} = 0\,\,\,\,(j = {\text{1}},{\text{2}}).$

Здесь $m_{1}^{2} = \frac{2}{\Gamma }\left[ {i{{{\left( {\frac{b}{{{{\delta }_{2}}}}} \right)}}^{2}} - {{{\left( {\frac{b}{{{{\delta }_{1}}}}} \right)}}^{2}}} \right],$ $m_{2}^{2} = 2i{{\left( {\frac{b}{{{{\delta }_{2}}}}} \right)}^{2}},$ δ₁ = = $\sqrt {\frac{{2K}}{\Gamma }} ,$ ${{\delta }_{2}}\, = \sqrt {\frac{{2\nu }}{\omega }} ,$ ${{m}_{1}}\, = \frac{b}{{\sqrt \Gamma }}\left( {\frac{1}{\delta } + \frac{{i\delta }}{{\delta _{2}^{2}}}} \right),$ $\frac{1}{{{{\delta }^{2}}}} = - \frac{1}{{\delta _{1}^{2}}}$ + + $\sqrt {\frac{1}{{\delta _{1}^{4}}} + \frac{1}{{\delta _{2}^{4}}}} ,$ ${{m}_{2}} = \frac{b}{{{{\delta }_{2}}}}\left( {1 + i} \right),$

${{E}^{2}} = \frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}} + \frac{{\sin \theta }}{{{{r}^{2}}}}\frac{\partial }{{\partial \theta }}\left( {\frac{1}{{\sin \theta }}\frac{\partial }{{\partial \theta }}} \right)$ – дифференциальный оператор [5].

Для удовлетворения граничных условий (5) функции тока будем искать в виде: ψ_j(r, θ, t) = = e^–itf_j(r)sin²θ (j = 1, 2).

Подставляя в уравнения (9) выражения для ψ₁ и ψ₂, получим обыкновенные дифференциальные уравнения для определения функций f₁(r) и f₂(r).

Граничные условия к этим дифференциальным уравнениям имеют следующий вид:

(10)

Сюда добавляется также условие конечности решений в областях их определения.

Уравнение для f₁(r) имеет вид

(11)

С помощью подстановки 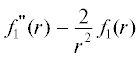= $\sqrt r {{g}_{1}}(r)$ обыкновенное дифференциальное уравнение четвертого порядка (11) сводится к дифференциальному уравнению второго порядка:

(12)

общее решение которого имеет следующий вид:

${{g}_{1}}(r) = {{А}_{1}}{{J}_{{3/2}}}({{m}_{1}}r) + {{B}_{1}}{{Y}_{{3/2}}}({{m}_{1}}r).$

Здесь ${{J}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}$ – функция Бесселя первого рода, ${{Y}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}$ – функция Бесселя второго рода [22]; A₁, B₁ – неопределeнные коэффициенты.

Таким образом, получаем линейное неоднородное дифференциальное уравнение второго порядка для определения функции f₁(r):

(13)

Общее решение уравнения (13):

${{f}_{1}}(r) = {{C}_{1}}{{r}^{2}} + \frac{{{{D}_{1}}}}{r} - \frac{{\sqrt r }}{{m_{1}^{2}}}\left[ {{{А}_{1}}{{J}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}({{m}_{1}}r) + {{B}_{1}}{{Y}_{{3/2}}}({{m}_{1}}r)} \right],$

где С₁ и D₁ – неопределенные коэффициенты.

Согласно [22] функции Бесселя ${{J}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}$ и ${{Y}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}$ могут быть записаны в виде

(14)

$\begin{gathered} {{J}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}(x) = \sqrt {\frac{{2x}}{\pi }} \left( {\frac{{\sin x}}{{{{x}^{2}}}} - \frac{{\cos x}}{x}} \right), \\ {{Y}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} = \sqrt {\frac{{2x}}{\pi }} \left( { - \frac{{\cos x}}{{{{x}^{2}}}} - \frac{{\sin x}}{x}} \right). \\ \end{gathered} $

С учетом равенств (14) общее решение уравнения (13) примет следующий вид:

(15)

$\begin{gathered} {{f}_{1}}(r) = {{C}_{1}}{{r}^{2}} + \frac{{{{D}_{1}}}}{r} - \frac{1}{{m_{1}^{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0em} 2}}}r}}\sqrt {\frac{2}{\pi }} \times \\ \times \,\,[{{А}_{1}}(\sin {{m}_{1}}r - {{m}_{1}}r\cos {{m}_{1}}r) - \\ - \,\,{{B}_{1}}(\cos {{m}_{1}}r + {{m}_{1}}r\sin {{m}_{1}}r)]. \\ \end{gathered} $

Уравнение для f₂(r) имеет вид

(16)

Аналогично общее решение уравнения (16):

${{f}_{2}}(r) = {{C}_{2}}{{r}^{2}} + \frac{{{{D}_{2}}}}{r} - \frac{{\sqrt r }}{{m_{2}^{2}}}\left[ {{{А}_{2}}{{J}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}({{m}_{2}}r) + {{B}_{2}}{{Y}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}({{m}_{2}}r)} \right].$

Здесь A₂, B₂, С₂, D₂ – неопределенные коэффициенты.

Решение уравнения (16), конечное при r → ∞ и с учетом равенств (14):

(17)

${{f}_{2}}(r) = \frac{{{{D}_{2}}}}{r} + \frac{1}{{m_{2}^{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0em} 2}}}r}}\sqrt {\frac{2}{\pi }} {{A}_{2}}{{e}^{{i{{m}_{2}}r}}}(i + {{m}_{2}}r).$

Подставляя выражения (15) и (17) в граничные условия (10), получим систему шести алгебраических уравнений для определения коэффициентов A₁, B₁, С₁, D₁, A₂, D₂. Ввиду громоздкости этих коэффициентов в настоящей статье мы их не приводим.

Компоненты скорости фильтрации и скорости свободной жидкости вне пористой среды имеют следующий вид:

В частном случае при α $ \to $ 0 из полученных результатов получается решение задачи о течении вязкой жидкости, вызванного поступательно-колебательным движением пористого шара [12]. Из этого решения, в свою очередь, следует (при K → 0, λ → 0) решение задачи о течении вязкой жидкости, вызванном поступательно-колебательным движением твердого непроницаемого шара [6, §24].

Движение жидкости является нестационарным. В связи с этим поля скоростей фильтрации и скоростей свободной жидкости во внутренней и внешней областях пористой сферической оболочки с твёрдым непроницаемым ядром непрерывно изменяются со временем. На рис. 1 показаны профили скоростей фильтрации и свободной жидкости в областях 1 и 2 в момент времени t = 0.

Рис. 1.

Зависимость Re u_r (штриховые линии) и Re u_θ (сплошные линии) от r: t = 0, α = 0.3, β = 0, λ = 1, Г = 0.95, b/δ₁ = 10, b/δ₂ = 10, θ = π/8 (1), π/4 (2) и 3π/8 (3).

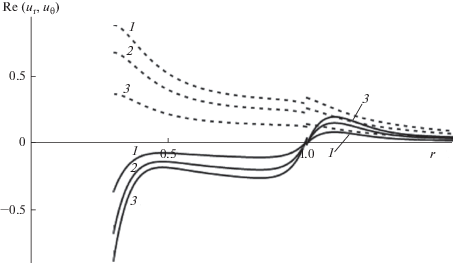
На рис. 1 приведены графики зависимости Re u_jr и Re u_jθ (j = 1, 2) от r для трех значений угла θ (π/8, π/4, 3π/8) при α = 0.3, β = 0, λ = 1, Г = 0.95, b/δ₁ = 10, b/δ₂ = 10.

Из рис. 1 видно, что Re u_jr > 0 (j = 1, 2). Величины Re u_1r и Re u_2r в областях 1 и 2 монотонно убывают. Величины Re u_1θ < 0 и Re u_2θ > 0 и немонотонны в областях внутри и вне пористой сферической оболочки. С увеличением значений угла θ скорости Re u_jr (j = 1, 2) и Re u_1θ уменьшаются при каждом заданном значении r; скорости Re u_2θ при этом возрастают.

На рис. 2, 3 приведены картины линий тока в момент времени t = 0. Линии тока во внутренней и внешней областях пористой сферической оболочки с твердым непроницаемым ядром представляют собой семейство кривых: ψ₁ = const и ψ₂ = const.

Рис. 2.

Линии тока: t = 0, α = 0.3, β = 0, λ = 1, Г = 0.95, b/δ₁ = 10, b/δ₂ = 10, const = 0.001 (1), 0.01 (2), 0.03 (3), 0.05 (4), 0.07 (5), 0.1 (6), 0.13 (7), 0.15 (8).

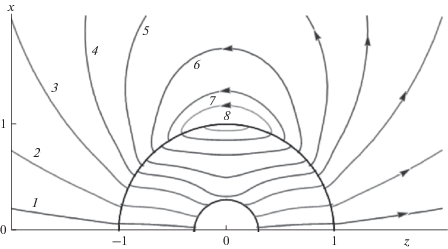
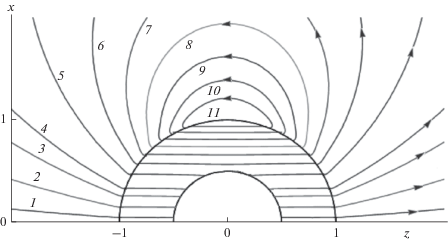
Рис. 3.

Линии тока: t = 0, α = 0.5, β = 0, λ = 1, Г = 0.95, b/δ₁ = 50, b/δ₂ = 20, const = 0.001 (1), 0.01 (2), 0.03 (3), 0.05 (4), 0.1 (5), 0.15 (6), 0.2 (7), 0.25 (8), 0.3 (9), 0.35 (10), 0.4 (11).

Уравнения линий тока в областях 1 и 2 (при t = 0):

$\begin{gathered} \operatorname{Re} {{\psi }_{j}}(r,\theta ) = \operatorname{Re} {{f}_{j}}(r){{\sin }^{2}}\theta = {\text{const}} \\ (j = {\text{1}},{\text{2}};\,\,0 < \theta < \pi ). \\ \end{gathered} $

На рис. 2 приведены линии тока, построенные при α = 0.3, β = 0, λ = 1, Г = 0.95, b/δ₁ = 10, b/δ₂ = 10, const = 0.001, 0.01, 0.03, 0.05, 0.07, 0.1, 0.13, 0.15 (1–8)

На рис. 3 линии тока построены при α = 0.5, β = 0, λ = 1, Г = 0.95, b/δ₁ = 50, b/δ₂ = 20, const = = 0.001, 0.01, 0.03, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4 (1–11).

Наличие разрывов графиков на границе пористой среды и свободной жидкости связано с тем, что скорость фильтрации не является скоростью частиц жидкости. При Г → 1 эти разрывы исчезают.

СИЛА, ДЕЙСТВУЮЩАЯ НА КОНТРОЛЬНУЮ ПОВЕРХНОСТЬ

Безразмерная сила, действующая со стороны свободной жидкости на контрольную сферическую поверхность, охватывающую внешнюю поверхность пористой оболочки с твердым непроницаемым ядром, совершающей поступательно-колебательное движение в вязкой жидкости, определяется равенством:

Здесь dS = 2π sinθ dθ – элемент площади, интегрирование проводится по всей поверхности сферы r = 1 ($0 \leqslant \theta \leqslant \pi $), $\sigma _{{2rr}}^{'}$ и $\sigma _{{2r{{\theta }}}}^{'}$ – безразмерные тензоры вязких напряжений во внешней области. Величина F_z представляет собой силу, действующую на пористую оболочку с содержащейся в ней жидкостью.

Выражение для F_z принимает вид

${{F}_{z}} = \frac{{8\pi }}{3}{{e}^{{ - it}}}\left[ {\frac{{m_{2}^{2}{{D}_{2}}}}{2} - \sqrt {\frac{2}{\pi }} \frac{{{{A}_{2}}{{e}^{{i{{m}_{2}}}}}(i + {{m}_{2}})}}{{m_{2}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}} \right]$

или

(18)

$\begin{gathered} {{F}_{z}} = \frac{{2\pi {{e}^{{ - it}}}}}{3} \times \\ \times \,\,\left[ {\frac{{{{Q}_{1}} + {{Q}_{2}}{{m}_{1}}\cos ({{m}_{1}} - \alpha {{m}_{1}}) + {{Q}_{3}}\sin ({{m}_{1}} - \alpha {{m}_{1}})}}{{{{Q}_{4}} + {{Q}_{5}}{{m}_{1}}\cos ({{m}_{1}} - \alpha {{m}_{1}}) + {{Q}_{6}}\sin ({{m}_{1}} - \alpha {{m}_{1}})}}} \right], \\ \end{gathered} $

где

$\begin{gathered} {{Q}_{1}} = 6\alpha {{m}_{1}}m_{2}^{2}\left( {2 - 2i{{m}_{2}} - 2m_{2}^{2} + \lambda \left( { - 5m_{1}^{2} + 5im_{1}^{2}{{m}_{2}} + } \right.} \right. \\ \left. {\left. { + \,\,2m_{2}^{2} - 2im_{2}^{3}} \right)} \right),\,\,\,\,{{Q}_{2}} = {{Q}_{7}} + 3{{\alpha }^{2}}{{Q}_{8}} - 2m_{1}^{2}m_{2}^{2} + \\ + \,\,3\alpha m_{2}^{2} + 27{{\alpha }^{2}} - 27i{{\alpha }^{2}}{{m}_{2}} - {{\alpha }^{3}}m_{1}^{2}m_{2}^{2} + \\ + \,\,\lambda \left( {{{Q}_{9}} + {{Q}_{{10}}} + {{Q}_{{11}}} + 3i{{\alpha }^{2}}m_{1}^{2}m_{2}^{3} + 6i{{\alpha }^{2}}m_{2}^{5}} \right), \\ {{Q}_{3}} = - {{Q}_{7}} + 3\alpha {{Q}_{8}} + m_{1}^{4}({{\alpha }^{3}} + 2)\left( {9 - 9i{{m}_{2}} - m_{2}^{2}} \right) + \\ + \,\,2m_{1}^{2}m_{2}^{3}(1 - {{\alpha }^{3}})(i + {{m}_{2}}) + 3\alpha m_{1}^{2}\left( { - 9 + 9i{{m}_{2}} - \alpha m_{2}^{2}} \right) + \\ + \,\,\lambda \left( { - {{Q}_{9}} - i{{m}_{2}}{{Q}_{{10}}} + m_{1}^{2}{{Q}_{{11}}} + 3{{\alpha }^{2}}m_{1}^{4}m_{2}^{2} + 6{{\alpha }^{2}}m_{1}^{2}m_{2}^{4}} \right), \\ {{Q}_{4}} = 6\alpha {{m}_{1}}\left( { - 1 + i{{m}_{2}} + m_{2}^{2} + \lambda \left( {m_{1}^{2} - im_{1}^{2}{{m}_{2}} - m_{2}^{2} + im_{2}^{3}} \right)} \right), \\ {{Q}_{5}} = {{Q}_{{12}}} - 2m_{1}^{2} + 3\alpha - 3i{{\alpha }^{2}}{{m}_{2}} - 3{{\alpha }^{2}}m_{2}^{2} - {{\alpha }^{3}}m_{1}^{2} + \\ + \,\,\lambda \left( {{{Q}_{{13}}} + {{Q}_{{14}}} + 3i{{\alpha }^{2}}m_{1}^{2}{{m}_{2}} - 3i{{\alpha }^{2}}m_{2}^{3} + {{\alpha }^{3}}m_{1}^{4} - {{\alpha }^{3}}m_{1}^{2}m_{2}^{2}} \right), \\ \end{gathered} $

$\begin{gathered} {{Q}_{6}} = - {{Q}_{{12}}} + 3m_{1}^{2} - 2m_{1}^{4} - im_{1}^{2}{{m}_{2}} - m_{1}^{2}m_{2}^{2} + 3\alpha m_{1}^{2} - \\ - \,\,3i\alpha {{m}_{2}} - 3\alpha m_{2}^{2} - {{\alpha }^{3}}m_{1}^{4} + i{{\alpha }^{3}}m_{1}^{2}{{m}_{2}} + {{\alpha }^{3}}m_{1}^{2}m_{2}^{2} + \\ + \,\,\lambda ( - {{Q}_{{13}}} - i{{m}_{2}}{{Q}_{{14}}} + 3{{\alpha }^{2}}m_{1}^{4} - 3{{\alpha }^{2}}m_{1}^{2}m_{2}^{2} - \\ - \,\,i{{\alpha }^{3}}m_{1}^{4}{{m}_{2}} + i{{\alpha }^{3}}m_{1}^{2}m_{2}^{3}),\,\,\,\,{{Q}_{7}} = 18m_{1}^{2} - 18im_{1}^{2}{{m}_{2}} - \\ - \,\,6m_{2}^{2} + 6im_{2}^{3} + 6m_{2}^{4} - 27\alpha + 27i\alpha {{m}_{2}} - 27{{\alpha }^{2}}m_{1}^{2} + \\ + \,\,27i{{\alpha }^{2}}m_{1}^{2}{{m}_{2}} + 9{{\alpha }^{3}}m_{1}^{2} - 9i{{\alpha }^{3}}m_{1}^{2}{{m}_{2}}, \\ {{Q}_{8}} = m_{2}^{2}( - 3 + m_{1}^{2} + 2i{{m}_{2}} + 2m_{2}^{2}), \\ {{Q}_{9}} = - 18m_{1}^{4} + 18im_{1}^{4}{{m}_{2}} + 24m_{1}^{2}m_{2}^{2} - 24im_{1}^{2}m_{2}^{3} - \\ - \,\,6m_{2}^{4} + 6im_{2}^{5} + 27\alpha m_{1}^{2} - 27i\alpha m_{1}^{2}{{m}_{2}} - 27\alpha m_{2}^{2} + \\ + \,\,27i\alpha m_{2}^{3} - 9{{\alpha }^{3}}m_{1}^{4} + 9i{{\alpha }^{3}}m_{1}^{4}{{m}_{2}} + 9{{\alpha }^{3}}m_{1}^{2}m_{2}^{2} - 9i{{\alpha }^{3}}m_{1}^{2}m_{2}^{3}, \\ \end{gathered} $

$\begin{gathered} {{Q}_{{10}}} = 2m_{1}^{4}m_{2}^{2} - 2m_{1}^{2}m_{2}^{4} - 3\alpha m_{1}^{2}m_{2}^{2} - 6\alpha m_{2}^{4} + \\ + \,\,\alpha m_{1}^{4}m_{2}^{2} + 2{{\alpha }^{3}}m_{1}^{2}m_{2}^{4},\,\,\,\,{{Q}_{{11}}} = - 27{{\alpha }^{2}}m_{1}^{2} + \\ + \,\,27i{{\alpha }^{2}}m_{1}^{2}{{m}_{2}} + 27{{\alpha }^{2}}m_{2}^{2} - 27i{{\alpha }^{2}}m_{2}^{3}, \\ {{Q}_{{12}}} = 3 - 3i{{m}_{2}} - 3m_{2}^{2} + 3\alpha m_{1}^{2}, \\ {{Q}_{{13}}} = - 3m_{1}^{2} + 3im_{1}^{2}{{m}_{2}} + 3m_{2}^{2} - 3im_{2}^{3}, \\ {{Q}_{{14}}} = 2m_{1}^{4} + m_{1}^{2}m_{2}^{2} - 3\alpha m_{1}^{2} + 3\alpha m_{2}^{2}. \\ \end{gathered} $

Коэффициенты Q₁, …, Q₁₄ определены при β = 0.

Размерная сила равна $F_{z}^{*} = \eta {{\upsilon }_{0}}b{{F}_{z}}.$

Перейдя в выражении (18) для F_z к пределу λ → 0 (K → 0), α → 0, m₁ → ∞ (m₂ – любое), получим силу, действующую на сплошной твердый шар (без пор), совершающий поступательно-колебательное движение в вязкой жидкости:

${{F}_{z}} = \frac{{2\pi }}{3}{{e}^{{ - it}}}\left( {m_{2}^{2} + 9i{{m}_{2}} - 9} \right).$

В размерном виде это выражение совпадает с приведенным в [6, §24].

При m₂ = 0 (ω = 0) формула (18) (без множителя e^–it) дает выражение для силы, действующей на контрольную поверхность пористой сферической оболочки с твердым непроницаемым ядром, движущейся равномерно и прямолинейно:

(19)

${{F}_{z}} = - 6\pi \,\left[ {\frac{{{{T}_{1}}{{m}_{1}}\cos ({{m}_{1}} - \alpha {{m}_{1}}) - {{T}_{2}}\sin ({{m}_{1}} - \alpha {{m}_{1}})}}{{6\alpha {{m}_{1}}\left( { - 1 + \lambda m_{1}^{2}} \right) + {{T}_{3}}{{m}_{1}}\cos ({{m}_{1}} - \alpha {{m}_{1}}) + {{T}_{4}}\sin ({{m}_{1}} - \alpha {{m}_{1}})}}} \right],$

где

$\begin{gathered} {{T}_{1}} = {{T}_{5}} - 3{{\alpha }^{2}} + \lambda \left( {{{T}_{6}} + 3{{\alpha }^{2}}m_{1}^{2}} \right),\,\,\,\,{{T}_{2}} = {{T}_{5}} + 2m_{1}^{4} - \,\,3\alpha m_{1}^{2} + {{\alpha }^{3}}m_{1}^{4} + \lambda \left( {{{T}_{6}} - 3{{\alpha }^{2}}m_{1}^{4}} \right), \\ {{T}_{3}} = 3 - 2m_{1}^{2} + 3\alpha + 3{{\alpha }^{2}}m_{1}^{2} - {{\alpha }^{3}}m_{1}^{2} + \,\,\lambda \left( { - 3m_{1}^{2} + 2m_{1}^{4} - 3\alpha m_{1}^{2} + {{\alpha }^{3}}m_{1}^{4}} \right), \\ {{T}_{4}} = - 3 + 3m_{1}^{2} - 2m_{1}^{4} + 3\alpha m_{1}^{2} - 3{{\alpha }^{2}}m_{1}^{2} - {{\alpha }^{3}}m_{1}^{4} + \,\,\lambda \left( {3m_{1}^{2} + 3{{\alpha }^{2}}m_{1}^{4}} \right),\,\,\,\,{{T}_{5}} = - 2m_{1}^{2} + 3\alpha + \\ + \,\,3{{\alpha }^{2}}m_{1}^{2} - {{\alpha }^{3}}m_{1}^{2},\,\,\,\,{{T}_{6}} = 2m_{1}^{4} - 3\alpha m_{1}^{2} + {{\alpha }^{3}}m_{1}^{4}. \\ \end{gathered} $

При α = 0 выражение (19) принимает вид безразмерной силы, действующей на пористый шар, движущийся равномерно и прямолинейно в вязкой жидкости:

${{F}_{z}} = - 12\pi \,\left[ {\frac{{m_{1}^{3}\left( { - 1 + \lambda m_{1}^{2}} \right)\cos {{m}_{1}} + m_{1}^{2}\left( {1 - m_{1}^{2} - \lambda m_{1}^{2}} \right)\sin {{m}_{1}}}}{{{{m}_{1}}\left( {3 - 2m_{1}^{2} + 2\lambda m_{1}^{4} - 3\lambda m_{1}^{2}} \right)\cos {{m}_{1}} + \left( {3m_{1}^{2} - 3 - 2m_{1}^{4} + 3\lambda m_{1}^{2}} \right)\sin {{m}_{1}}}}} \right].$

ЗАКЛЮЧЕНИЕ

Исследовано влияние поступательно-колебательного движения пористой сферической оболочки с твердым непроницаемым ядром, погруженной в вязкую жидкость, на движение этой жидкости внутри и вне пористого тела. В неподвижной сферической системе координат найдены аналитические решения нестационарного уравнения Бринкмана, описывающего движение жидкости в пористой среде, и уравнения Навье–Стокса, описывающего движение жидкости вне пористой среды. Приведен анализ решений полученных уравнений. Определены поля скоростей фильтрации и свободной жидкости внутри и вне пористого тела. Построены графики профилей скорости фильтрации и свободной жидкости, а также линии тока при разных значениях параметров. Определена сила, действующая на контрольную сферическую поверхность, охватывающую внешнюю поверхность пористой оболочки с твердым непроницаемым ядром, совершающую поступательно-колебательное движение.

ОБОЗНАЧЕНИЯ

a, b	радиусы пористой оболочки, м
K	проницаемость, м²
р*	давление, Па
r*, θ, φ	сферические координаты
t*	время, с
u*	скорость жидкости, м/с
$u_{{1r}}^{},$$u_{{2r}}^{},$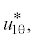	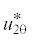компоненты скоростей
х, y, z*	декартовы координаты, м
Г	пористость
$\eta $	вязкость, кг/(м с)
η'	величина с размерностью вязкости
Λ	параметр с размерностью длины
ρ	плотность жидкости, кг/м³
υ*	скорость оболочки, м/с
υ₀	амплитуда скорости оболочки, м/с
ω	частота колебаний, с^–1

ИНДЕКСЫ

*	размерные величины
1	величины, относящиеся к пористой среде
2	величины, относящиеся к свободной жидкости
r, θ	компоненты векторов и тензоров в сферических координатах
j	номер области (внутри и вне оболочки – 1 и 2 соответственно)

Список литературы

Кутепов А.М., Полянин А.Д., Запрянов З.Д., Вязьмин А.В., Казенин Д.А. Химическая гидродинамика. Справочное пособие. М.: Квантум, 1996.
Полянин А.Д., Аристов С.Н. Новый метод построения точных решений трехмерных уравнений Навье–Стокса и Эйлера // Теор. осн. хим. технол. 2011. Т. 45. № 6. С. 696. [Polyanin A.D., Aristov S.N. A new method for constructing exact solutions to three-dimensional Navier–Stokes and Euler equations // Theor. Found. Chem. Eng. 2011. V. 45. № 6. P. 885.]
Полянин А.Д., Вязьмин А.В. Декомпозиция и точные решения трехмерных нестационарных линеаризованных уравнений вязкой жидкости // Теор. осн. хим. технол. 2013. Т. 47. № 2. С. 158. [Polyanin A.D., Vyazmin A.V. Decomposition and exact solutions of three-dimensional nonstationary linearized equations for a viscous fluid // Theor. Found. Chem. Eng. 2013. V. 47. № 2. P. 114.]
Просвиряков Е.Ю., Спевак Л.Ф. Пространственные неоднородные слоистые течения вязкой несжимаемой жидкости // Теор. осн. хим. технол. 2018. Т. 52. № 5. С. 483. [Prosviryakov E.Y., Spevak L.F. Layered three-dimensional nonuniform viscous incompressible flows // Theor. Found. Chem. Eng. 2018. V. 52. № 5. P. 765.]
Happel J., Brenner H. Low Reynolds Number Hydrodynamics. Englewood Cliffs, N.J.: Prentice-Hall, 1965. [Хаппель Дж., Бреннер Г. Гидродинамика при малых числах Рейнольдса. М.: Мир, 1976.]
Landau L.D., Lifshitz E.M. Theoretical Physics. V. 6. Fluid Mechanics. N.Y.: Pergamon Press, 2013. [Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 6. Гидродинамика. М.: Физматлит, 2006.]
Batchelor G.K. An Introduction to Fluid Dynamics. Cambridge: Cambridge University Press, 2000. [Бэтчелор Дж. Введение в динамику жидкости. М.: Мир, 1973.]
Grosan T., Postelnicu A., Pop I. Brinkman flow of a viscous fluid through a spherical porous medium embedded in another porous medium // Transp. Porous Media. 2010. V. 81. P. 89.
Jones I.P. Low Reynolds number flow past a porous spherical shell // Math. Proc. Cambridge Philos. Soc. 1973. V. 73. № 1. P. 231.
Rajvanshi S.C., Wasu S. Slow extensional flow past a non-homogeneous porous spherical shell // Int. J. Appl. Mech. Eng. 2013. V. 18. № 2. P. 491.
Taktarov N.G. Viscous fluid flow induced by rotational-oscillatory motion of a porous sphere // Fluid Dyn. 2016. V. 51. № 5. Р. 703. [Тактаров Н.Г. Движение вязкой жидкости, вызванное вращательно-колебательным движением пористого шара // Изв. Акад. наук. Мех. жидк. газа. 2016. № 5. С. 133.]
Taktarov N.G., Khramova N.A. Viscous fluid flows induced by translational-oscillatory motion of a submerged porous sphere // Fluid Dyn. 2018. V. 53. № 6. Р. 843. [Тактаров Н.Г., Храмова Н.А. Течения вязкой жидкости при поступательно-колебательном движении погруженного пористого шара // Изв. Акад. наук. Мех. жидк. газа. 2018. № 6. С. 123.]
Bazarkina O.A., Taktarov N.G. Rotational oscillations of a porous spherical shell in viscous fluid // Fluid Dyn. 2020. V. 55. № 6. Р. 98. [Базаркина О.А., Тактаров Н.Г. Вращательные колебания пористой сферической оболочки в вязкой жидкости // Изв. Акад. наук. Мех. жидк. газа. 2020. № 6. С. 98.]
Kormilitsin A.A., Taktarov N.G. Oscillatory motion of a viscous fluid in contact with a flat layer of a porous medium // Fluid Dyn. 2018. V. 53. № 1. Р. 139. [Кормилицин А.А., Тактаров Н.Г. Колебательные движения вязкой жидкости, контактирующей с плоским слоем пористой среды // Изв. Акад. наук. Мех. жидк. газа. 2018. № 1. С. 139.]
Brinkman H.C. A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles // Appl. Sci. Res. 1947. V. 1. № 1. P. 27.
Ochoa-Tapia J.A., Whitaker S. Momentum transfer at the boundary between a porous medium and a homogeneous fluid. – I. Theoretical development // Int. J. Heat Mass Transfer. 1995. V. 38. № 14. P. 2635.
Whitaker S. The Forchheimer equation: a theoretical development // Transp. Porous Media. 1996. V. 25. № 1. P. 27.
Auriault J.-L. On the domain of validity of Brinkmah’s equation // Transp. Porous Media. 2009. V. 79. № 2. P. 215.
Durlofsky L., Brady J.F. Analysis of the Brinkman equation as a model for flow in porous media // Phys. Fluids. 1987. V. 30. № 11. P. 3329.
Le Bars M., Worster M.G. Interfacial conditions between a pure fluid and a porous medium: implications for binary alloy solidification // J. Fluid Mech. 2006. V. 550. P. 149.
Tilton N., Cortelezzi L. Linear stability analysis of pressure-driven flows in channels with porous walls // J. Fluid Mech. 2008. V. 604. P. 411.
Abramowitz M., Stegun. I.A. Handbook of Mathematical Functions. Washington, DC: U. S. Government Printing Office, 1964. [Абрамовиц М., Стиган И.А. Справочник по специальным функциям. М.: Наука, 1979.]

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал