Теоретические основы химической технологии, 2021, T. 55, № 5, стр. 618-631
Эффект теплового и концентрационного расширения при синтезе титаната бария в прямоточном реакторе
А. А. Марков *
Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: markov.ipm@yandex.ru
Поступила в редакцию 28.08.2020
После доработки 17.04.2021
Принята к публикации 27.04.2021
Аннотация
Развивается двухтемпературная модель для анализа эффектов теплового и концентрационного расширения при синтезе сложных оксидов методом горения углерода. Определяющая система уравнений включает уравнения Навье–Стокса для газовой фазы и уравнения термоупругости на основе соотношений Дюамеля–Неймана. Излагаются результаты исследования воздействия теплового и концентрационного расширения на переменную пористость в процессе синтеза микронных порошков титаната бария с рассмотрением тепловой и массовой дисперсии. Приведена безразмерная форма определяющих уравнений с параметрами подобия. Безразмерные уравнения применены к численному моделированию воздействия тепловой и массовой дисперсии при переменной пористости на синтез микронных частиц титаната бария в прямоточном реакторе. Сопоставлены результаты расчетов при различных коэффициентах расширения, включающие воздействие дисперсии, коэффициента извилистости пор, диаметра частиц, локальных величин чисел Пекле. Предлагаемая модель позволяет анализировать и оценивать влияние теплового и концентрационного расширения на скорость и однородность распределения в реакторе реагентов и продукта синтеза.
ВВЕДЕНИЕ
Моделированию синтеза сложных оксидов методом горения углерода (CCSO) [1] посвящены работы [2, 3], в которых размеры пор предполагались заданными априори. В работах [4–8] предложены модели усреднения микроуравнений на основе взаимопроникающих континуумов. При таком подходе утраченная детальная информация о микромасштабах, таких как конфигурация межфазных границ и т.п., присутствует в виде коэффициентов тепло- и массопереноса. Отмечается, что в усредненных уравнениях наряду с молекулярной диффузией тепла и вещества важную роль играет дисперсионный механизм тепло- и массопереноса и пористость реагентов и продуктов синтеза в реакторе. Причиной концентрационной и тепловой дисперсии являются флуктуации массового и теплового потока, тогда как диффузия массы и тепла вызвана случайным молекулярным движением. Различные модели тепловой дисперсии изложены в работах [4–11]. Следует заметить, что потоки тепла, вещества реагентов и продуктов через пористую среду существенно зависят от структуры пористой среды и особенностей межфазного взаимодействия. Размеры пор, как правило, неравномерно распределены в реакторе синтеза и меняются во времени. Это обстоятельство обусловливает важность моделирования изменения пористости смеси реагентов и продуктов в процессе синтеза мелкодисперсных порошков методом горения. Математические модели синтеза и спекания порошковых смесей основаны на совместном описании тепловых и химических процессов объемных изменений в условиях неоднородного нагрева. Химические превращения происходят с изменением объема и сопровождаются появлением механических напряжений и деформаций дополнительно к напряжениям и деформациям вследствие высоких градиентов температуры.
В работе [12] проведены теоретические и экспериментальные исследования формирования структуры и физико-механических свойств материала при спекании с целью получения минимальной пористости. Рассмотрены математические модели спекания порошковых смесей и синтеза в твердой фазе, основанные на совместном описании тепловых и кинетических процессов спекания в условиях нагрева, с учетом взаимовлияния процессов объемных изменений в процессе спекания. Вводятся наряду с тепловым расширением коэффициенты концентрационного расширения ${{\alpha }_{j}}$, определяемые на основе термодинамики неравновесных процессов в химически активных гетерогенных системах [13] по формулам ${{\alpha }_{j}} = \frac{1}{\upsilon }\left( {\frac{{\partial \upsilon }}{{\partial {{Y}_{j}}}}} \right)$, где $\upsilon $ – удельный объем, ${{Y}_{j}}$ – концентрация компонента в газовой или твердой фазе. Процессы спекания частиц ${\text{CoF}}{{{\text{e}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{4}}}}$ и ${\text{BaTi}}{{{\text{O}}}_{{\text{3}}}}$ изучены экспериментально в работе [14]. Был применен метод CCSO для быстрого и энергоэффективного производства композита из феррита кобальта и титаната бария с образованием матричной структуры янусоподобных частиц (названных в честь древнеримского бога с двумя лицами).
Целью данного исследования является обобщение модели [2] для расчета эффектов переменной пористости при синтезе мелкодисперсных частиц сложных оксидов в прямоточном реакторе при горении углерода. На основе двухфазной модели с учетом тепловой и массовой дисперсии [10, 11] исследуется влияние объемных изменений при синтезе мелкодисперсных порошков титаната бария методом CCSO. Прекурсором синтеза ${\text{BaTi}}{{{\text{O}}}_{{\text{3}}}}$ служит ${\text{BaC}}{{{\text{O}}}_{{\text{3}}}}$ [15]. Формулируются осредненные по пространству потоки массы компонент ${\text{C,}}\,\,{\text{BaC}}{{{\text{O}}}_{{\text{3}}}}{\text{,}}$ ${\text{BaO,}}\,{\text{Ti}}{{{\text{O}}}_{{\text{2}}}}{\text{,}}$ $\,{\text{BaTi}}{{{\text{O}}}_{{\text{3}}}}{\text{,}}\,{\text{B}}{{{\text{a}}}_{{\text{2}}}}{\text{Ti}}{{{\text{O}}}_{{\text{4}}}}$, зависящие от температуры газовой и твердой фазы при заданном межфазовом теплообмене, переменном коэффициенте пористости. Основной целью предлагаемого моделирования является оценка концентрационного расширения твердой фазы, теплопроводность которой существенно превосходит теплопроводность газовой фазы. Данное исследование опирается на результаты [12]. Изучение кинетики синтеза титаната бария рассмотрено в [15–17]. В связи с требованиями промышленного производства керамики на основе ${\text{BaTi}}{{{\text{O}}}_{{\text{3}}}}$ возникает необходимость сбалансировать потребление энергии, время синтеза и качество конечного продукта, такого как форма и распределение частиц. В данной работе представлены результаты моделирования титаната бария в прямоточном реакторе на основе макроуравнений сохранения, записанных в безразмерных переменных. Представлены уравнения тепловой и массовой дисперсии. Проведено моделирование синтеза титаната бария методом CCSO в осесимметричном реакторе. Полученные результаты показывают существенное влияние объемных изменений в твердой фазе. Предлагаемая модель позволяет анализировать воздействие теплового и концентрационного расширения на распределение пористости частиц в реакторе на скорость синтеза и распределение продукта в зоне синтеза. Тепловая и массовая дисперсия интенсифицирует свободный теплообмен с внешней средой. В данной работе представлены результаты моделирования при размерах частиц реагентов и продуктов, превышающих микрон. Отметим, что при микронных размерах синтезируемых частиц характерные величины чисел Кнудсена малы и эффекты скольжения и скачков температуры [18] пренебрежимо малы. Однако для субмикронных размеров частиц и пор становится существенным влияние слоев Кнудсена в газе около поверхности пор и необходим учет эффектов скольжения [2, 18–20].
ОПИСАНИЕ МОДЕЛИ
Кинетическая схема синтеза титаната бария. Рассмотрим схему синтеза ${\text{BaTi}}{{{\text{O}}}_{{\text{3}}}}$ с прекурсором ${\text{BaC}}{{{\text{O}}}_{{\text{3}}}}$ [15–17]:
(1)
$\begin{gathered} {{{\text{O}}}_{{\text{2}}}}\,{\text{ + }}\,{\text{C}}\xrightarrow[{{{Q}_{{\text{1}}}}}]{{{{k}_{{\text{1}}}}}}{\text{C}}{{{\text{O}}}_{{\text{2}}}},\,\,\,\,{\text{BaC}}{{{\text{O}}}_{{\text{3}}}}\xrightarrow[{{{Q}_{{\text{2}}}}}]{{{{k}_{{\text{2}}}}}}{\text{C}}{{{\text{O}}}_{{\text{2}}}} + {\text{BaO}}, \\ {\text{Ti}}{{{\text{O}}}_{{\text{2}}}} + {\text{BaO}}\xrightarrow[{{{Q}_{{\text{2}}}}}]{{{{k}_{{\text{2}}}}}}{\text{BaTi}}{{{\text{O}}}_{{\text{3}}}}, \\ {\text{BaO}} + {\text{BaTi}}{{{\text{O}}}_{{\text{3}}}}\xrightarrow[{{{Q}_{{\text{3}}}}}]{{{{k}_{{\text{3}}}}}}{\text{B}}{{{\text{a}}}_{{\text{2}}}}{\text{Ti}}{{{\text{O}}}_{{\text{4}}}}, \\ {\text{Ti}}{{{\text{O}}}_{{\text{2}}}} + {\text{B}}{{{\text{a}}}_{{\text{2}}}}{\text{Ti}}{{{\text{O}}}_{{\text{4}}}}\xrightarrow[{{{Q}_{{\text{3}}}}}]{{{{k}_{{\text{3}}}}}}{\text{2BaTi}}{{{\text{O}}}_{{\text{3}}}}. \\ \end{gathered} $Компонентами газа и твердой фазы являются ${{{\text{O}}}_{{\text{2}}}}{\text{,}}\,{\text{C}}{{{\text{O}}}_{{\text{2}}}}$ и ${\text{C,}}\,{\text{BaO,}}\,{\text{BaC}}{{{\text{O}}}_{{\text{3}}}}{\text{,}}\,{\text{Ti}}{{{\text{O}}}_{{\text{2}}}}{\text{,}}$${\text{BaTi}}{{{\text{O}}}_{{\text{3}}}}{\text{,}}\,{\text{B}}{{{\text{a}}}_{{\text{2}}}}{\text{Ti}}{{{\text{O}}}_{{\text{4}}}}$ соответственно. В реакции ${\text{Ti}}{{{\text{O}}}_{{\text{2}}}}{\text{ + BaO}}$ синтез продукта ${\text{BaTi}}{{{\text{O}}}_{{\text{3}}}}$контролируется диффузией ионов бария через слой титаната бария [16].
В реакциях (1) для компонент твердой фазы реагенты не смешиваются на молекулярном уровне, диффундируют и движутся в пределах твердой фазы, ${{Q}_{{\text{1}}}}$ – тепловой эффект горения углерода. Реакции с тепловым эффектом ${{Q}_{{\text{2}}}},\,{{Q}_{3}}$ предполагаются эндотермическими.
Коэффициенты расширения. Используем для компонент тензора напряжений обобщенные соотношения Дюамеля–Неймана линейной теории термоупругости [21], ${{\sigma }_{{ij}}} = 2{{\mu }_{{S1}}}{{\varepsilon }_{{ij}}}$ + ${{\delta }_{{ij}}}\left( {{{\mu }_{{S2}}}\sum\limits_k {{{\varepsilon }_{{kk}}}} - K\omega } \right)$ и соотношение между инвариантами $\sum\limits_k {{{\sigma }_{{kk}}}} $ = = $\left( {2{{\mu }_{{S1}}} + 3{{\mu }_{{S2}}}} \right)$$\sum\limits_k {{{\varepsilon }_{{kk}}}} - 3K\omega $, следующее из соотношений Дюамеля–Неймана, где ${{\sigma }_{{ij}}}$ – компоненты тензора напряжений и ${{\varepsilon }_{{ij}}}$ – компоненты тензора деформаций, зависящие от коэффициентов расширения, ${{\mu }_{{S1}}},\,{{\mu }_{{S2}}}$ – коэффициенты Ламе, $K$ – изотермический модуль всестороннего сжатия. Предполагаем, что давление газа на поверхность поры уравновешивается нормальным напряжением твердой границы, т.е. $\sum\limits_k {{{\sigma }_{{kk}}}} = 3p$, тогда $\sum\limits_k {{{\varepsilon }_{{kk}}}} $ = $\left( {K\omega + p} \right)\mu _{S}^{{ - 1}}$, где ${{\mu }_{S}} = {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}{{\mu }_{{S1}}} + {{\mu }_{{S2}}}$. При отсутствии воздействий внешних сил ${{\sigma }_{{ii}}} = 0$ и, следовательно, $\sum\limits_k {{{\varepsilon }_{{kk}}}} = K\omega \mu _{S}^{{ - 1}}$. Величина ω = = ωT + ωg + ωS – суммарный коэффициент объемного расширения, в котором ${{\omega }_{T}}$ – коэффициент температурного расширения, ${{\omega }_{T}} = 3{{\alpha }_{T}}\left( { - \frac{{{{T}_{g}}}}{{T_{g}^{0}}} + 1} \right)$, ${{\omega }_{g}},\,{{\omega }_{S}}$ – коэффициенты концентрационного расширения компонентов газовой и твердой фазы. Величины ${{\omega }_{g}},\,{{\omega }_{S}}$ оцениваются через молярные объемы, занимаемые компонентами [12], νlg = = $\frac{{{{M}_{{lg}}}}}{{{{\rho }_{{lg}}}}},\,\,{{\nu }_{{jS}}} = \frac{{{{M}_{{jS}}}}}{{{{\rho }_{{jS}}}}}$ , и молярные концентрации компонентов ${{\bar {\alpha }}_{{il}}} = \frac{1}{3}\frac{{{{\nu }_{{lg}}}}}{{\sum\limits_{l = 1}^2 {{{\nu }_{{lg}}}} + \sum\limits_{j = 1}^6 {{{\nu }_{{jS}}}} }},$ $l = 1,2$, ${{\bar {\alpha }}_{{iS}}}$ = $\frac{1}{3}\frac{{{{\nu }_{{iS}}}}}{{\sum\limits_{l = 1}^2 {{{\nu }_{{\lg }}}} + \sum\limits_{j = 1}^4 {{{\nu }_{{jS}}}} }},$ $i = 1,...,6$ с использованием соотношений ${{\omega }_{g}} = 3\left[ {\sum\limits_{j = 1}^2 {{{\alpha }_{{jg}}}\left( { - {{B}_{{jg}}} + B_{{jg}}^{0}} \right)} } \right]$ и ${{\omega }_{S}}$ = = $3\left[ {\sum\limits_{j = 1}^6 {{{\alpha }_{{jS}}}\left( { - {{B}_{{jS}}} + B_{{jS}}^{0}} \right)} } \right]$, в которых ${{B}_{{lg}}} = \frac{{{{Y}_{{lg}}}}}{{{{Y}_{{g,tot}}}}}$, ${{B}_{{jS}}} = \frac{{{{Y}_{{jS}}}}}{{{{Y}_{{S,tot}}}}}$, ${{Y}_{{lg}}} = \frac{{{{\rho }_{{lg}}}}}{{{{M}_{{lg}}}}},$ ${{Y}_{{g{\text{,}}tot}}} = \sum\limits_{l = 1}^3 {{{Y}_{{lg}}}} $ и ${{Y}_{{jS}}} = \frac{{{{\rho }_{{jS}}}}}{{{{M}_{{jS}}}}},$ ${{Y}_{{S,tot}}} = \sum\limits_{j = 1}^6 {{{Y}_{{jS}}}} $, индекс “ноль” относится к величинам в начальный момент времени.
Переменная пористость смеси реагентов и продукта синтеза титаната бария находится с учетом эффектов теплового и концентрационного расширения компонент газовой и твердой фазы по формуле
(2)
$\chi (t,x,r) = \frac{{\chi (0,x,r)\left( {1 + {{\omega }_{g}}(t,x,r)} \right)}}{{\chi (0,x,r)\left( {1 + {{\omega }_{g}}(t,x,r)} \right) + \left( {1 - \chi (0,x,r)} \right)\left( {1 + E(t,x,r)} \right)}},$УРАВНЕНИЯ В БЕЗРАЗМЕРНЫХ ПЕРЕМЕННЫХ
Далее переходим к безразмерным переменным, отмеченным тильдой, характерные величины имеют индекс “ноль”:
(4)
$\begin{gathered} {{{\tilde {\rho }}}_{g}} = {{{{\rho }_{g}}} \mathord{\left/ {\vphantom {{{{\rho }_{g}}} {{{\rho }_{0}}}}} \right. \kern-0em} {{{\rho }_{0}}}},\,\,\,\,{{{\tilde {\rho }}}_{{jg}}} = {{{{\rho }_{{jg}}}} \mathord{\left/ {\vphantom {{{{\rho }_{{jg}}}} {{{\rho }_{0}}}}} \right. \kern-0em} {{{\rho }_{0}}}},\,\,\,\,j = 1,2,3, \\ {{{\tilde {c}}}_{{pg}}} = {{{{C}_{{pg}}}} \mathord{\left/ {\vphantom {{{{C}_{{pg}}}} {{{c}_{p}}}}} \right. \kern-0em} {{{c}_{p}}}},\,\,\,\,\tilde {D} = {D \mathord{\left/ {\vphantom {D {{{D}_{0}}}}} \right. \kern-0em} {{{D}_{0}}}},\,\,\,\,{{{\tilde {\rho }}}_{{lS}}} = {{{{\rho }_{{lS}}}} \mathord{\left/ {\vphantom {{{{\rho }_{{lS}}}} {{{\rho }_{C}}}}} \right. \kern-0em} {{{\rho }_{C}}}}, \\ l = 1,...,6,\,\,\,\,{{{\tilde {\kappa }}}_{0}} = {{{{\kappa }_{0}}{{t}_{0}}A} \mathord{\left/ {\vphantom {{{{\kappa }_{0}}{{t}_{0}}A} {\left( {{{c}_{p}}{{\rho }_{0}}V} \right)}}} \right. \kern-0em} {\left( {{{c}_{p}}{{\rho }_{0}}V} \right)}},\,\,\,{{{\tilde {D}}}_{m}} = {{{{D}_{m}}} \mathord{\left/ {\vphantom {{{{D}_{m}}} {{{D}_{0}}}}} \right. \kern-0em} {{{D}_{0}}}}, \\ {{\zeta }_{P}} = {{{{\rho }_{0}}} \mathord{\left/ {\vphantom {{{{\rho }_{0}}} {{{\rho }_{{0С}}}}}} \right. \kern-0em} {{{\rho }_{{0С}}}}},\,\,\,\,{{{\tilde {\lambda }}}_{g}} = {{{{\lambda }_{{air}}}} \mathord{\left/ {\vphantom {{{{\lambda }_{{air}}}} {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}},\,\,\,{{{\tilde {\lambda }}}_{S}} = {{{{\lambda }_{S}}} \mathord{\left/ {\vphantom {{{{\lambda }_{S}}} {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}}, \\ {{{\tilde {c}}}_{S}} = {{{{C}_{S}}} \mathord{\left/ {\vphantom {{{{C}_{S}}} {{{c}_{p}}}}} \right. \kern-0em} {{{c}_{p}}}},\,\,\,\,{\text{M}}{{{\text{a}}}^{{ - 2}}} = \frac{{{{\gamma }_{{air}}}{{p}_{0}}}}{{{{\rho }_{0}}u_{0}^{2}}},\,\,\,\,{\text{Re}} = \frac{{l_{0}^{2}}}{{{{t}_{0}}{{\nu }_{{air}}}}}, \\ \operatorname{R} _{S}^{{}} = {{p}_{0}}{{\left( {{{\zeta }_{p}}{{\mu }_{{S0}}}} \right)}^{{ - 1}}}{\text{P}}{{{\text{e}}}_{{\text{T}}}} = \frac{{l_{0}^{2}{{\rho }_{0}}{{c}_{p}}}}{{{{t}_{0}}{{\lambda }_{0}}}},\,\,\,\,{\text{P}}{{{\text{e}}}_{{\text{1}}}} = \frac{{l_{0}^{2}}}{{{{t}_{0}}{{D}_{0}}}}, \\ \tilde {Q} = \frac{{Q{{t}_{0}}k}}{{{{\rho }_{0}}{{C}_{{pg}}}{{T}_{0}}}},\,\,\,\,{{p}_{0}} = \frac{{R{{\rho }_{0}}{{T}_{0}}}}{{{{M}_{0}}}},\,\,\,\,\tilde {K} = {K \mathord{\left/ {\vphantom {K {{{\mu }_{{S0}}}}}} \right. \kern-0em} {{{\mu }_{{S0}}}}}, \\ {{{\tilde {\mu }}}_{{solid}}} = {{{{\mu }_{{solid}}}} \mathord{\left/ {\vphantom {{{{\mu }_{{solid}}}} {{{\mu }_{{S0}}}}}} \right. \kern-0em} {{{\mu }_{{S0}}}}},\,\,\,\,{{{\tilde {\mu }}}_{{sj}}} = {{{{\mu }_{{sj}}}} \mathord{\left/ {\vphantom {{{{\mu }_{{sj}}}} {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}},\,\,\,\,j = 1,2, \\ \end{gathered} $Базовые уравнения. Ниже приведены основные уравнения, используемые в работе.
Уравнения сохранения суммарной массы газовой и твердой фаз:
Уравнения сохранения массы компонент O2, CO2, N2:
(5)
$\begin{gathered} \frac{{\partial \chi {{\rho }_{g}}{{C}_{1}}}}{{\partial t}} + \nabla \left( {\chi {{\rho }_{g}}{{C}_{1}}{\mathbf{u}}} \right) = \\ = \nabla \left( {\frac{\chi }{{{\text{P}}{{{\text{e}}}_{1}}}}{{\rho }_{g}}{{{\text{D}}}_{{{\text{mg}}}}}\nabla {{C}_{1}}} \right) - \frac{{{{M}_{{1g}}}}}{{{{M}_{S}}}}J_{{S \to g}}^{{}}, \\ \frac{{\partial \chi {{\rho }_{g}}{{C}_{3}}}}{{\partial t}} + \nabla \left( {\chi {{\rho }_{g}}{{C}_{3}}{\mathbf{u}}} \right) = \nabla \left( {\frac{\chi }{{{\text{P}}{{{\text{e}}}_{1}}}}{{\rho }_{g}}{{{\text{D}}}_{{{\text{mg}}}}}\nabla {{C}_{3}}} \right), \\ {{C}_{2}} = 1 - {{C}_{1}} - {{C}_{3}}. \\ \end{gathered} $Компоненты тензора массовой дисперсии имеют следующий вид [7–11]:
Здесь ${{b}_{0}},\,{{b}_{1}}$ – постоянные, $\xi $ – коэффициент извилистости пор [8].
Уравнения сохранения массы компонент твердой фазы, включая диффузию оксида бария ${\text{BaO}}$, зависящую от концентрации титаната бария ${\text{BaTi}}{{{\text{O}}}_{{\text{3}}}}$ согласно кинетике синтеза (1):
(6)
$\begin{gathered} \frac{{\partial {{\rho }_{{1S}}}}}{{\partial t}} = - {{J}_{{1S}}},\,\,\,\,\frac{{\partial {{\rho }_{{2S}}}}}{{\partial t}} = - {{J}_{{2S}}},\,\,\,\,\frac{{\partial {{\rho }_{{3S}}}}}{{\partial t}} = \frac{{{{M}_{{3S}}}}}{{{{M}_{{2S}}}}}{{J}_{{2S}}} - \\ - \,\,\frac{{{{M}_{{3S}}}}}{{{{M}_{{4S}}}}}\left( {{{J}_{{3S}}} + {{J}_{{4S}}}} \right)J_{{3S}}^{{}} + D{{s}_{0}}\exp \left( { - {{\beta }_{D}}{{\rho }_{{5S}}}} \right), \\ \frac{{\partial {{\rho }_{{4S}}}}}{{\partial t}} = - J_{{3S}}^{{}} - J_{{5S}}^{{}},\,\,\,\,\frac{{\partial {{\rho }_{{5S}}}}}{{\partial t}} = \frac{{{{M}_{{5S}}}}}{{{{M}_{{4S}}}}}\left( {{{J}_{{3S}}} - {{J}_{{4S}}} + 2{{J}_{{5S}}}} \right), \\ \frac{{\partial {{\rho }_{{6S}}}}}{{\partial t}} = \frac{{{{M}_{{5S}}}}}{{{{M}_{{4S}}}}}\left( {{{J}_{{4S}}} - {{J}_{{5S}}}} \right). \\ \end{gathered} $Здесь $D{{s}_{0}}$ – коэффициент диффузии мигрирующей компоненты ${\text{BaO}}$, ${{\beta }_{D}}$ – параметр, характеризующий зависимость диффузии от плотности титаната бария. Массовые потоки для компонент твердой фазы ${\text{C,}}\,{\text{BaO,}}\,{\text{BaC}}{{{\text{O}}}_{{\text{3}}}}{\text{,}}\,{\text{Ti}}{{{\text{O}}}_{{\text{2}}}}{\text{,}}$${\text{BaTi}}{{{\text{O}}}_{{\text{3}}}}{\text{,}}\,{\text{B}}{{{\text{a}}}_{{\text{2}}}}{\text{Ti}}{{{\text{O}}}_{{\text{4}}}}$ приводятся в [10, 11].
Уравнение движения газа в порах [2, 10]:
(7)
$\begin{gathered} \frac{{\partial \chi {{\rho }_{g}}{\mathbf{u}}}}{{\partial t}} + \nabla \left( {\chi {{\rho }_{g}}{\mathbf{uu}}} \right) + {\text{M}}{{{\text{a}}}^{{ - 2}}}\nabla p = {{\operatorname{Re} }^{{ - 1}}}\nabla \cdot {\mathbf{\tau }} + {{S}_{V}}, \\ {\mathbf{\tau }} = \mu \left[ {\nabla {\mathbf{u}} + {{{\left( {\nabla {\mathbf{u}}} \right)}}^{T}} - \frac{2}{3}\left( {\nabla \cdot {\mathbf{u}}} \right){\mathbf{I}}} \right], \\ \end{gathered} $${{u}_{j}}$ – компоненты скорости в декартовой системе координат, $p = {{\rho }_{g}}\left( {1 + \beta {{T}_{g}}} \right)$ – давление газовой фазы.
Уравнение движения твердой фазы запишем в простейшем случае, пренебрегая влиянием работы механических напряжений на поле температуры [12]:
(8)
$\begin{gathered} \frac{{\partial \left( {1 - \chi } \right){{{{\rho }}}_{S}}{{V}_{{solid}}}}}{{\partial t}} + \\ + \,\,\nabla \left( {\left( {1 - \chi } \right){{{{\rho }}}_{S}}{{V}_{{solid}}}{{V}_{{solid}}}} \right) = \operatorname{R} _{S}^{{ - 1}}\nabla \cdot {{\sigma ,}} \\ {{\sigma }_{{ij}}} = 2{{\mu }_{{S1}}}{{\varepsilon }_{{ij}}} + {{\delta }_{{ij}}}\left( {{{\mu }_{a}}K\omega \mu _{S}^{{ - 1}} - K\omega } \right), \\ \end{gathered} $Уравнение баланса тепла в газовой фазе, включающее тепловую дисперсию [11]:
(9)
$\begin{gathered} {{\rho }_{g}}{{c}_{{pg}}}\chi \left( {\frac{{\partial {{T}_{g}}}}{{\partial t}} + {\mathbf{u}} \cdot \nabla {{T}_{g}}} \right) + {{c}_{g}}{{T}_{g}}{{J}_{{S \to g}}} = \\ = \nabla \cdot \left( {\chi \frac{{{{{\text{D}}}_{{{\text{Tg}}}}}}}{{P{{e}_{{Tg}}}}}\nabla {{T}_{g}}} \right) - \kappa \left( {{{T}_{g}} - {{T}_{S}}} \right) + {{Q}_{r}}, \\ {{Q}_{r}} = Q{{J}_{{S \to g}}}. \\ \end{gathered} $В правой части уравнения (9) $Q_{r}^{{}}$ – тепловой поток химического превращения. Тензор тепловой дисперсии [6, 10] учитывает продольную и поперечную дисперсию: ${{{\text{D}}}_{{{\text{Tg}}}}} = \left( {\begin{array}{*{20}{c}} {{{\lambda }_{{1g}}}}&0 \\ 0&{{{\lambda }_{{2g}}}} \end{array}} \right)$, где ${{\lambda }_{{1g}}} = {{\lambda }_{g}}\left( {\xi + {{\varphi }_{1}}\left( {{\text{P}}{{{\text{e}}}_{{1t}}}} \right)} \right),$ ${{\lambda }_{{2g}}} = {{\lambda }_{g}}\left( {\xi + {{\varphi }_{2}}\left( {{\text{P}}{{{\text{e}}}_{{2t}}}} \right)} \right)$.
Уравнение баланса тепла в твердой фазе:
(10)
$\begin{gathered} {{\rho }_{S}}{{c}_{S}}\left( {1 - \chi } \right)\left( {\frac{{\partial {{T}_{S}}}}{{\partial t}} + {{{\text{V}}}_{{solid}}} \cdot \nabla {{T}_{S}}} \right) - {{c}_{S}}{{T}_{S}}{{J}_{{S \to g}}} = \\ = \nabla \cdot \left( {\left( {1 - \chi } \right)\frac{{{{\lambda }_{S}}}}{{{\text{P}}{{{\text{e}}}_{{Ts}}}}}\nabla {{T}_{S}}} \right) + \kappa \left( {{{T}_{g}} - {{T}_{S}}} \right) + {{Q}_{r}}. \\ \end{gathered} $Коэффициент теплообмена между газовой и твердой фазами в (9), (10) описывается с помощью формулы Левека [2, 22], $\kappa = {{\kappa }_{0}}\left( {1 + {\text{Re}}_{{loc}}^{{0.3}}{\text{Pe}}_{{Tloc}}^{{0.3}}} \right)$, где ${\text{R}}{{{\text{e}}}_{{loc}}} = \operatorname{Re} \left| {\mathbf{u}} \right|{{\rho }_{g}}$, ${\text{P}}{{{\text{e}}}_{{Tloc}}} = {\text{P}}{{{\text{e}}}_{T}}\left| {\mathbf{u}} \right|{{\rho }_{g}}$ – локальные числа Рейнольдса и Пекле [2].
Граничные и начальные условия. Ставятся следующие соотношения в осесимметричном реакторе (рис. 1), состоящем из внешней зоны 1: $0 < x < L$, $1 - d < r < 1$, в которую поступает поток смеси кислорода и азота, а также пористой зоны 2: $0 < x < L$, $0 < r < 1 - d$, которая является двухфазной средой реагентов, продуктов газа и мелкодисперсных частиц реагентов и продуктов синтеза, ∂/∂n обозначает производную по нормали.
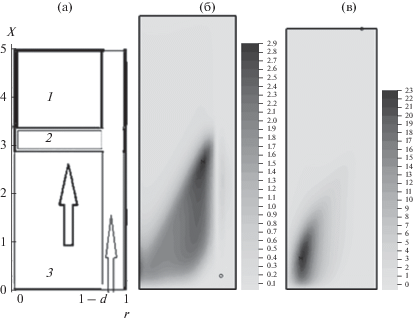
Рис. 1.
Схема реактора синтеза. Показаны холодная область (1), фронт горения (2) и горячая область (3), фронт горения движется снизу вверх, кислород поступает снизу (рис. 1а). Температура газовой фазы ${{T}_{g}}(t,{{x}_{j}},r)$ (рис. 1б) и твердой фазы ${{T}_{S}}(t,{{x}_{j}},r)$ (рис. 1в) в момент времени $t = 0.3$ при коэффициенте расширения ${{K}_{\alpha }} = 1$.
Граничные условия на входе $x = 0\,$в зоны реактора:
Граничные условия на выходе $x = L$ из зон реактора:
Граничные условия на наружной стенке реактора $r = 1$:
Граничные условия на оси симметрии реактора:
Граничное условие на внутренней границе $r = 1 - d$:
Начальные условия $t = 0$:
РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ
Численное моделирование синтеза титаната бария в реакторе с порами микронного размера проведено при следующих безразмерных параметрах [10, 11]: $L = 3,$ $d = 0.2$, ${{Q}_{f}} = 10{\kern 1pt} - {\kern 1pt} 500$, ${{t}_{{init}}} = 0.25{\kern 1pt} - {\kern 1pt} 0.5$, ${\text{Ma}} = 0.2$,${{\alpha }_{j}} = 0,\,\,{{\varsigma }_{j}} = 50$, $\beta \approx 0.075{\kern 1pt} - {\kern 1pt} 0.1$, ${{Q}_{1}} = 60,$ ${{Q}_{2}} = - 6$, ${{\chi }_{0}} = 0.05{\kern 1pt} --{\kern 1pt} 0.6$, ${{\operatorname{R} }_{S}} = {{10}^{{ - 3}}}$, ${{k}_{1}} = 0.0023,$ ${{k}_{2}} = 0.5,$ ${{k}_{3}} = 0.01$, $D{{s}_{0}} = 0.1,$ ${{\beta }_{D}} = 0.092,$ ${\text{Re}} = 0.24{\text{,}}$ ${\text{P}}{{{\text{e}}}_{{Tg}}} = 0.2,$ ${\text{P}}{{{\text{e}}}_{{Ts}}} = 0.6$, ${{\kappa }_{0}} = 1200$, ${{\zeta }_{p}} = 3.6 \times {{10}^{{ - 4}}}$, $K = 56.4$.
Здесь ${{t}_{{init}}}$ – продолжительность инициации горения. Инициация горения производится тепловым потоком ${{q}_{f}}(t)$, ${{q}_{f}}(t) = {{Q}_{f}},$ $0 \leqslant t \leqslant {{t}_{{init}}};$ ${{q}_{f}}(t) = 0,$ $t \geqslant {{t}_{{init}}}$. Задавался поток кислорода ${{O}_{{2\,f}}} = 100$, поступающий с входного сечения пористого образца углерода (рис. 1а).
Расчеты тепловой дисперсии проведены при диаметре частиц ${{d}_{p}} = 3 \times {{10}^{{ - 4}}}\,\,{\text{м}}$ для начальной пористости ${{\chi }_{0}} = 0.2$ и $0.6$ при следующих начальных условиях: ${{T}^{0}} = 0$, $\rho _{{1g}}^{0} = 0.27{{\chi }_{0}}$, $\rho _{{2g}}^{0} = 0$, $\rho _{{3g}}^{0} = 0.73{{\chi }_{0}},$ $\rho _{{1S}}^{0} = \left( {1 - {{\chi }_{0}}} \right)$, $\rho _{{2S}}^{0}{\kern 1pt} = 16.47{\kern 1pt} \left( {1 - {{\chi }_{0}}} \right),$ $\rho _{{3S}}^{0}$ = = 0, $\rho _{{4S}}^{0} = 5.7\left( {1 - {{\chi }_{0}}} \right),$ $\rho _{{5S}}^{0} = 0$, $\rho _{{6S}}^{0} = 0.08\left( {1 - {{\chi }_{0}}} \right),$ где числовые множители при ${{\chi }_{0}}$ и $\left( {1 - {{\chi }_{0}}} \right)$ равны отношению молярной массы соответствующих компонент к молярной массе углерода. Горение инициировалось потоком тепла на входе в реактор ${{Q}_{f}} = 500,$ ${{t}_{{init}}} = 0.5$.
В работе анализируются процессы синтеза титаната бария в осесимметричном реакторе (рис. 1). В начальный момент времени заданы следующие коэффициенты расширения:
$t = 0:\,\,{{\bar {\alpha }}_{{lS}}} = \alpha _{{lS}}^{0}$, $l = 1,...,6$, $\alpha _{{1S}}^{0} = 0.018$, $\alpha _{{2S}}^{0}$ = = ${{0.653} \mathord{\left/ {\vphantom {{0.653} {{{K}_{\alpha }}}}} \right. \kern-0em} {{{K}_{\alpha }}}}$, $\alpha _{{3S}}^{0} = {{2.915} \mathord{\left/ {\vphantom {{2.915} {{{K}_{\alpha }}}}} \right. \kern-0em} {{{K}_{\alpha }}}}$, $\alpha _{{4S}}^{0} = {{0.295} \mathord{\left/ {\vphantom {{0.295} {{{K}_{\alpha }}}}} \right. \kern-0em} {{{K}_{\alpha }}}}$, $\alpha _{{5S}}^{0}$ = = $2 \times {{10}^{{ - 3}}}$, $\alpha _{{6S}}^{0} = 4 \times {{10}^{{ - 3}}}$, где $\alpha _{{lS}}^{0}$ – начальные коэффициенты концентрационного расширения, ${{K}_{\alpha }}$ – параметр, характеризующий величину начальных коэффициентов расширения.
Расчеты при нулевых начальных величинах концентрационного расширения газовых компонент $\alpha _{{1g}}^{0} = \alpha _{{2g}}^{0} = \alpha _{{3g}}^{0} = 0$ для начальной пористости ${{\chi }_{0}} = 0.6$, ${{K}_{\alpha }} = 1,3,6$, представлены на рис. 1– 8, результаты при $\alpha _{{1g}}^{0} = 6.6 \times {{10}^{{ - 4}}}$, $\alpha _{{2g}}^{0} = 0.012$, $\alpha _{{3g}}^{0} = 7.1 \times {{10}^{{ - 5}}}$ для начальной пористости ${{\chi }_{0}} = 0.2$, ${{K}_{\alpha }} = 1$, приведены на рис. 9, 10. Коэффициент температурного расширения ${{\alpha }_{T}} = \alpha _{T}^{0} = 5 \times {{10}^{{ - 5}}}$ предполагался постоянным. Результаты расчетов осесимметричной нестационарной модели горения пористого углерода в осесимметричном реакторе на рис. 1 демонстрируют движение волны горения при заданном теплообмене между газом и твердой фазой ${{\kappa }_{0}}$. Как видно из рис. 1б и 1в, температура газовой и твердой фаз существенно различна. В силу большей температуропроводности компонент твердой фазы происходит более быстрый рост ${{T}_{S}}$ в сравнении с ${{T}_{g}}$. Молекулярная диффузия и тепловая дисперсия приводят к расширению области нагрева в газе в большей степени, чем в твердой фазе. Влияние ${{K}_{\alpha }} = 1$ на температуру газа (рис. 1б) и твердой фазы (рис. 1в) указывает на существенную неравномерность распределения температуры в зоне реактора. На начальных временах работы реактора максимальная величина температуры достигается вблизи границы газа с пористой зоной реактора $0 < x < L,$ $r = 1 - d$, однако на больших временах максимум температуры газа и твердой фазы смещается к оси симметрии (рис. 1a).
Рис. 2.
Плотность титаната бария ${{\rho }_{{5s}}}\left( {t,x,r} \right)$ в момент времени $t = 0.5$ для ${{K}_{\alpha }}$ = 6 (а), 3 (б) и 1 (в).
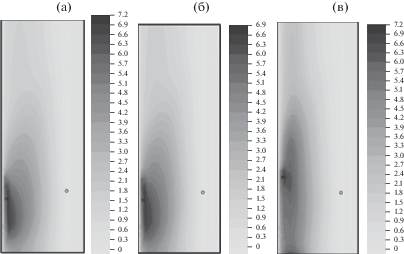
Рис. 3.
Плотность оксида бария ${{\rho }_{{3s}}}\left( {t,x,r} \right)$ в момент времени $t = 0.5$ для ${{K}_{\alpha }}$ = 6 (а), 3 (б) и 1 (в).
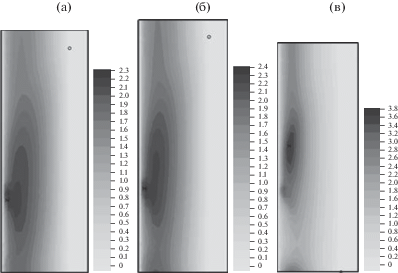
Рис. 4.
Плотность оксида титана ${{\rho }_{{2s}}}\left( {t,x,r} \right)$ в момент времени $t = 0.5$ для ${{K}_{\alpha }}$= 6 (а), 3 (б) и 1 (в).
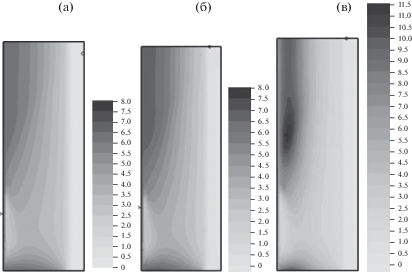
Рис. 5.
Распределение пористости $\chi (t,x,r)$в момент времени $t = 0.5$ для ${{K}_{\alpha }}$ = 6 (а), 3 (б) и 1 (в).

Рис. 6.
Динамика температуры газа ${{T}_{g}}(t,{{x}_{j}},0.5)$ (а) и температуры твердой фазы ${{T}_{S}}(t,{{x}_{j}},0.5)$ (б) для ${{x}_{1}} = 0,$ ${{x}_{2}} = 0.15,$ ${{x}_{3}} = 0.375,$ ${{x}_{4}} = 0.75$. Сплошные кривые и точки относятся соответственно к параметрам концентрационного расширения ${{K}_{\alpha }} = 1$ и 6. Пары кривых (1, 5), (2, 6), (3, 7) и (4, 8) относятся к изменению температуры со временем в точках с координатами (0,0.5), (0.15,0.5), (0.375,0.5) и (0.75,0.5) соответственно.
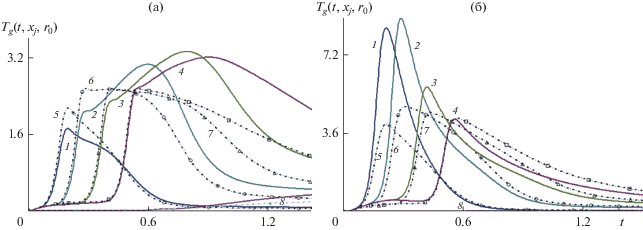
Рис. 7.
Динамика пористости $\chi (t,{{x}_{j}},0.25)\,$ (а) и $\chi (t,{{x}_{j}},0.5)$ (б) в контрольных точках $({{x}_{j}},0.25)$ и $({{x}_{j}},0.5)$. Сплошные кривые и точки относятся соответственно к параметрам ${{K}_{\alpha }} = 1$ и 6. Пары кривых (1, 4), (2, 5) и (3, 6) иллюстрируют изменение пористости со временем в точках с координатами (0,0.5), (0.15,0.5) и (0.75,0.5) соответственно.
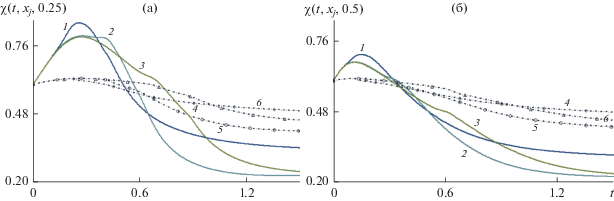
Рис. 8.
Динамика плотности оксида бария ${{\rho }_{{3s}}}(t,x,{{r}_{0}})$ (а) и титаната бария ${{\rho }_{{5s}}}(t,{{x}_{j}},{{r}_{0}})$ (б) в контрольных точках с координатами $({{x}_{j}},{{r}_{0}})$. Сплошные кривые и точки относятся соответственно к параметрам концентрационного расширения ${{K}_{\alpha }} = 1$ и 6. Пары кривых (1, 4), (2, 5) и (3, 6) показывают изменение плотности реагента и продукта со временем в точках с координатами (0,0.5), (0.15,0.5) и (0.75,0.5) соответственно.
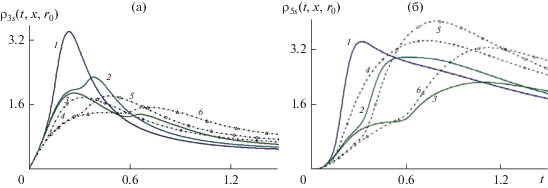
Рис. 9.
Распределение пористости от времени для ${{K}_{\alpha }} = 1$: (а) – динамика пористости $\chi (t,{{x}_{j}},0.25)$ (сплошные кривые) и $\chi (t,{{x}_{j}},0.5),\,j = 1,2,\,3$ (точки); (б) – динамика пористости$\chi \left( {t,x,0.4} \right)$(сплошные кривые) и динамика плотности ${{\rho }_{{5s}}}\left( {t,x,0.4} \right) \times 0.25$ титаната бария (точки). Кривые 1–3 относятся к ${{x}_{1}} = 0,$ ${{x}_{2}} = 0.1,$ ${{x}_{3}} = 0.625$соответственно.
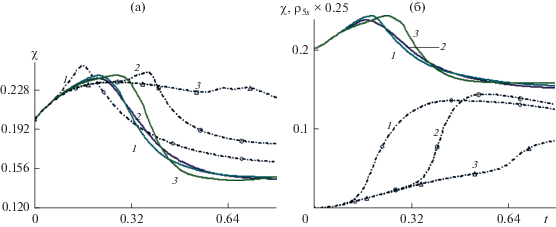
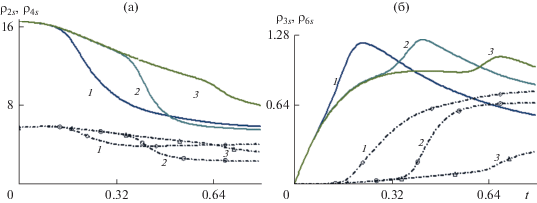
Рис. 10.
Динамика плотности реагентов для ${{K}_{\alpha }} = 1$: (а) – ${{\rho }_{{2s}}}\left( {t,x,0.4} \right)$ (сплошные кривые), ${{\rho }_{{4s}}}\left( {t,x,0.4} \right)\,$(точки); (б) – ${{\rho }_{{3s}}}\left( {t,x,0.4} \right)$ (сплошные кривые), ${{\rho }_{{6s}}}\left( {t,x,0.4} \right)$ (точки). Кривые 1–3 относятся к ${{x}_{1}} = 0,$ ${{x}_{2}} = 0.1,$ ${{x}_{3}} = 0.625$ соответственно.
Влияние переменной пористости на синтез титаната бария иллюстрируется на рис. 2–5. На рис. 2 сравниваются распределения плотности титаната бария в момент времени $t = 0.5$ для ${{K}_{\alpha }}$ = 6, 3 и 1 (рис. 2a, 2б и 2в соответственно). Можно отметить увеличение зоны равномерного распределения плотности ${\text{BaTi}}{{{\text{O}}}_{{\text{3}}}}$ при ${{K}_{\alpha }} = 1$. На большом отрезке времени моделирования плотность ${\text{BaTi}}{{{\text{O}}}_{{\text{3}}}}$ примерно на 30% больше при малом расширении ${{K}_{\alpha }} = 6$ в сравнении с ${{K}_{\alpha }} = 1$. Это можно объяснить увеличением удельного объема $1 - \chi $ твердой фазы при соответствующем уменьшении удельного объема $\chi $ газовой фазы. На рис. 3 сравниваются распределения плотности оксида бария в момент времени $t = 0.5$ для ${{K}_{\alpha }}$= 6, 3 и 1 (рис. 3a, 3б и 3в соответственно). На рис. 4 сопоставляются распределения плотности оксида титана в момент времени $t = 0.5$ для ${{K}_{\alpha }}$ = 6, 3 и 1 (рис. 4a, 4б и 4в соответственно). Изменение пористости $\chi (t,x,r)$ показано в момент времени $t = 0.5$ на рис. 5 для ${{K}_{\alpha }}$ = 6, 3 и 1 (рис. 5a, 5б и 5в соответственно). Область с наибольшей пористостью расположена вблизи оси симметрии. Минимальные величины пористости равны 0.49, 0.47 и 0.36 соответственно для коэффициентов расширения ${{K}_{\alpha }}$ = 6, 3 и 1.
Влияние параметра ${{K}_{\alpha }}$ = 6, 3 и 1 на распределение плотности продукта ${{\rho }_{{5s}}}\left( {t,x,r} \right)$, плотности реагентов синтеза ${{\rho }_{{2s}}}\left( {t,x,r} \right),$ ${{\rho }_{{3s}}}\left( {t,x,r} \right),$ $\,{{\rho }_{{4s}}}\left( {t,x,r} \right)$ (рис. 2–4) и пористости $\chi (t,x,r)$ (рис. 5) указывает на существенную неравномерность распределения указанных величин поперек пористой зоны реактора. Наиболее интенсивно химические реакции протекают в наиболее прогретой области, которая мигрирует со временем от границы пористой зоны $0 < x < L,$ $r = 1 - d$ вдоль оси реактора к области, расположенной вблизи оси симметрии $0 < x < L,\,\,r = 0$. Неравномерность распределения реагентов влияет на распределение плотности титаната бария на больших временах синтеза. Динамика синтеза представлена на рис. 6–8 при различных коэффициентах концентрационного расширения. С ростом объемного расширения температура газа и твердой фазы повышается (рис. 6). Сопоставляя рис. 1б и 1в, а также рис. 6a и 6б, можно отметить более высокую температуру твердых частиц в сравнении с температурой газовой смеси ввиду больших величин коэффициента температуропроводности в твердой фазе.
Пары кривых (1, 5), (2, 6), (3, 7) и (4, 8) на рис. 6 относятся к изменению температуры со временем в точках с координатами (0, 0.5), (0.15, 0.5), (0.375,0.5) и (0.75,0.5) соответственно. Сравнение динамики температуры газа ${{T}_{g}}(t,{{x}_{j}},0.5)$ (рис. 6a) и температуры твердой фазы ${{T}_{S}}(t,{{x}_{j}},0.5)$ (рис. 6б) в контрольных точках сечения реактора $0 < x < L,\,\,r = 0.5$ указывает на увеличение температуры газа и твердой фазы с увеличением коэффициентов концентрационного расширения и объясняется уменьшением удельного объема газа и соответствующим увеличением удельного объема твердой фазы при уменьшении пористости. Это заключение демонстрируется сплошными кривыми и точками на рис. 6a и 6б. Сплошные кривые и точки относятся соответственно к параметрам концентрационного расширения ${{K}_{\alpha }} = 1$ и 6.
Из зависимостей от времени пористости в контрольных точках с координатами (0, 0.5), (0.15, 0.5), (0.75, 0.5), (1.5, 0.5), (2.25, 0.5), (3, 0.5) на рис. 7 можно видеть динамику уменьшения пористости с ростом концентрационного расширения. Расчеты показали, что в среднем по поперечному сечению при ${{K}_{\alpha }} = 6$ пористость уменьшается от начальной величины 0.6 до 0.46, в то время как при ${{K}_{\alpha }} = 1$ пористость уменьшается от 0.6 до 0.23. Данные на рис. 7a и 7б иллюстрируют неравномерность изменения пористости в зависимости от радиальной координаты. Приведена динамика пористости $\chi (t,{{x}_{j}},0.25)$ и $\chi (t,{{x}_{j}},0.5)$ в контрольных точках $({{x}_{j}},0.25)$ и $({{x}_{j}},0.5)$. Пары кривых (1, 4), (2, 5) и (3, 6) иллюстрируют изменение пористости от времени в точках с координатами (0,0.5), (0.15,0.5) и (0.75,0.5) соответственно. Сплошные кривые и точки относятся соответственно к параметрам ${{K}_{\alpha }} = 1$ и 6.
Данные на рис. 8 иллюстрируют влияние концентрационного расширения на динамику распределение плотности реагента синтеза ${{\tilde {\rho }}_{{3S}}}(t,{{x}_{j}},{{r}_{0}})$ (рис. 8a) и плотности продукта ${{\tilde {\rho }}_{{5S}}}(t,{{x}_{j}},{{r}_{0}})$ (рис. 8б). Сплошные кривые и точки относятся соответственно к параметрам концентрационного расширения ${{K}_{\alpha }} = 1$ и 6. Можно отметить уменьшение плотности реагента и продукта на больших временах (близких к времени выхода на стационарный режим работы реактора) с уменьшением пористости. Этот вывод можно объяснить увеличением удельного объема твердой фазы с уменьшением пористости, ср. пары кривых (1, 4), (2, 5) и (3, 6), показывающие изменение плотности реагента и продукта со временем в точках с координатами (0,0.5), (0.15, 0.5) и (0.75, 0.5) соответственно.
На рис. 9 и 10 иллюстрируется динамика пористости и плотности титаната бария при начальной величине ${{\chi }_{0}} = 0.2$ для ${{K}_{\alpha }} = 1$. На рис. 9a приведено распределение пористости от времени: $\chi (t,{{x}_{j}},0.25)$ – сплошные кривые и $\chi (t,{{x}_{j}},0.5),$ j = 1, 2, 3 – точки. На рис. 9б показана динамика пористости $\chi \left( {t,x,0.4} \right)$ – сплошные кривые и динамика плотности ${{\rho }_{{5s}}}\left( {t,x,0.4} \right) \times 0.25$ титаната бария – точки. Кривые 1, 2 и 3 относятся к ${{x}_{1}} = 0,$ ${{x}_{2}} = 0.1,$ ${{x}_{3}} = 0.625$ соответственно. Отметим неравномерность изменения пористости в сечениях $r = 0.25$ и 0.5 (сплошные кривые и точки на рис. 9a) и волновой процесс изменения пористости и плотности титаната бария (рис. 9б), что указывает на существенную температурную неравновесность в работе реактора.
На рис. 10 приведена динамика реагентов для ${{K}_{\alpha }} = 1$, показана плотность реагентов ${{\rho }_{{2s}}}\left( {t,x,0.4} \right)$, ${{\rho }_{{4s}}}\left( {t,x,0.4} \right)\,$ (рис. 10a) и ${{\rho }_{{3s}}}\left( {t,x,0.4} \right)$, ${{\rho }_{{6s}}}\left( {t,x,0.4} \right)$ (рис. 10б). Линии 1–3 иллюстрируют динамику плотности реагентов при ${{x}_{1}} = 0,$ ${{x}_{2}} = 0.1,$ ${{x}_{3}} = 0.625$ соответственно. Можно видеть скорость расходования реагентов ${\text{BaC}}{{{\text{O}}}_{{\text{3}}}}$ и ${\text{Ti}}{{{\text{O}}}_{{\text{2}}}}$ согласно кинетике (1) при заданных начальных величинах концентраций этих компонентов (сплошные кривые и точки на рис. 10a). На рис. 10б показана динамика промежуточных реагентов: ${\text{BaO}}$ и ${\text{B}}{{{\text{a}}}_{{\text{2}}}}{\text{Ti}}{{{\text{O}}}_{{\text{4}}}}$. Можно отметить немонотонность изменения во времени плотности ${{\rho }_{{3s}}}\left( {t,x,0.4} \right)$, обусловленную образованием и последующим расходом промежуточных реагентов, а также диффузией оксида бария, которая зависит от концентрации титаната бария.
Заметим, что моделирование проводилось при большой величине коэффициента межфазового обмена ${{\kappa }_{0}} = 1200$. В наших расчетах при постоянной пористости [10] температуры газа и твердой фазы отличались незначительно при том же межфазовом теплообмене. Результаты данной работы позволяют утверждать существенное влияние переменной пористости на межфазовый теплообмен и динамику синтеза в рассматриваемом проточном реакторе.
ЗАКЛЮЧЕНИЕ
Проведено исследование роли объемных изменений в кинетических закономерностях процесса синтеза титаната бария в осесимметричном реакторе с протоком [2] с применением двухтемпературной модели при тепловой и массовой дисперсии [10, 11]. Коэффициенты концентрационного расширения находятся в процессе распространения фронта горения в пористой зоне реактора в зависимости от кинетики синтеза титаната бария при заданных начальных величинах плотности реагентов в газовой и твердой фазе. Оценка объемных деформаций, возникающих вследствие изменения температуры и концентраций смеси реагентов и продуктов синтеза титаната бария методом CCSO, позволяет утверждать, что изменение температуры в процессе горения углерода существенно зависит от начального фазового состава и влияет на изменение массы продукта синтеза и времени протекания процесса. Проведенное моделирование синтеза показывает рост температуры обеих фаз с уменьшением пористости. Пористость неравномерно распределена в реакторе. Получены зависимости коэффициента пористости, температур и плотностей компонент синтеза от начальных коэффициентов теплового и концентрационного расширения.
Работа выполнена по теме государственного задания № АААА-А20-120011690135-5.
ОБОЗНАЧЕНИЯ
| $A$ | площадь, м2 |
| ${{B}_{{lg}}} = \frac{{{{Y}_{{lg}}}}}{{{{Y}_{{g,tot}}}}}$ | мольные доли газовых компонент |
| ${{B}_{{jS}}} = \frac{{{{Y}_{{jS}}}}}{{{{Y}_{{S,tot}}}}}$ | мольные доли компонент твердой фазы |
| ${{b}_{0}},{{b}_{1}}$ | безразмерные константы зависимости тензоров дисперсии от локального числа Пекле |
| ${{C}_{j}}\,$ | массовые доли газовых компонент, j = 1, 2, 3 |
| ${{c}_{p}}$ | характерная теплоемкость газовой фазы при постоянном давлении, ${{c}_{p}} = \,{{C}_{{p,air}}}$, ${\text{Дж}}\,\,{\text{к}}{{{\text{г}}}^{{ - 1}}}\,{{{\text{K}}}^{{ - 1}}}$ |
| ${{\tilde {c}}_{S}},\,{{\tilde {c}}_{{pg}}}$, ${{\tilde {c}}_{S}} = {{{{C}_{S}}} \mathord{\left/ {\vphantom {{{{C}_{S}}} {{{c}_{p}}}}} \right. \kern-0em} {{{c}_{p}}}}$${{\tilde {c}}_{{pg}}} = {{{{C}_{{pg}}}} \mathord{\left/ {\vphantom {{{{C}_{{pg}}}} {{{c}_{p}}}}} \right. \kern-0em} {{{c}_{p}}}}$ | безразмерные теплоемкости твердой и газовой фазы |
| ${{D}_{0}}$ | характерная величина коэффициента диффузии, равная 2 × 10–5${{{\text{м}}}^{2}}\,{{{\text{с}}}^{{ - 1}}}$ |
| $\tilde {D}$ | безразмерный коэффициент диффузии, $\tilde {D} = {D \mathord{\left/ {\vphantom {D {{{D}_{0}}}}} \right. \kern-0em} {{{D}_{0}}}}$ |
| ${{D}_{L}}$, ${{D}_{{Tr}}}$ | компоненты продольной и поперечной дисперсии массы, ${{{\text{м}}}^{2}}\,\,{{{\text{с}}}^{{ - 1}}}$ |
| ${{D}_{{mg}}}$ | дисперсионный тензор диффузии массы, ${{{\text{м}}}^{2}}\,\,{{{\text{с}}}^{{ - 1}}}$ |
| ${{D}_{{Tg}}}$ | дисперсионный тензор диффузии тепла, ${\text{Вт}}\,\,{{{\text{м}}}^{{ - 1}}}\,\,{{{\text{K}}}^{{ - 1}}}$ |
| ${{d}_{p}}$ | диаметр частиц, ${\text{м}}$ |
| ${\mathbf{I}}$ | единичный тензор |
| $J_{{iS}}^{{}},i = 1,...5$ | массовые потоки синтеза ${\text{BaTi}}{{{\text{O}}}_{{\text{3}}}}$, ${\text{кг}}\,\,{{{\text{м}}}^{{ - 2}}}\,\,{{{\text{с}}}^{{ - 1}}}$ |
| $K$ | изотермический модуль всестороннего сжатия, Па |
| $\,{{K}_{\alpha }}$ | параметр масштабирования коэффициентов концентрационного расширения |
| $k$ | частотный фактор в формуле Аррениуса, c–1 |
| ${{l}_{0}}$ | характерный размер, м |
| ${{M}_{0}}$ | характерная молярная масса, ${\text{кг}}\,\,{\text{мо}}{{{\text{л}}}^{{ - 1}}}$ |
| ${{M}_{{1g}}},\,{{M}_{{2g}}},\,{{M}_{{3g}}}$ | молярные массы газовых компонент, ${\text{кг}}\,\,{\text{мо}}{{{\text{л}}}^{{ - 1}}}$ |
| ${{M}_{{iS}}},\,i = 1,...5\,$ | молярные массы компонент синтеза ${\text{BaTi}}{{{\text{O}}}_{{\text{3}}}}$, ${\text{кг}}\,\,{\text{мо}}{{{\text{л}}}^{{ - 1}}}$ |
| ${{p}_{0}}$ | характерное давление, Па |
| ${{p}_{g}}$ | давление газа, Па |
| $Q$ | тепловой эффект химической реакции, ${\text{Дж}}\,\,{\text{к}}{{{\text{г}}}^{{ - 1}}}$ |
| ${{Q}_{r}}$ | теплота химической реакции, ${\text{Вт}}\,\,{{{\text{м}}}^{{ - 2}}}$ |
| ${{{\mathbf{S}}}_{{\mathbf{V}}}}$ | слагаемое распределенного сопротивления газа в порах, ${\text{Па}}\,\,{{{\text{м}}}^{{ - 1}}}$ |
| T0 | характерная температура, равная 1000 К |
| ${{T}_{g}},\,{{T}_{S}}$ | температура газа и твердой фазы, K |
| ${{\tilde {T}}_{g}}$,${{\tilde {T}}_{S}}$ | безразмерная температура ${{T}_{g}} = {{T}_{0}}\left( {1 + \beta {{{\tilde {T}}}_{g}}} \right),$${{T}_{S}} = {{T}_{0}}\left( {1 + \beta {{{\tilde {T}}}_{S}}} \right)$ |
| $t$ | время, с |
| ${{t}_{0}}$ | характерное время, с |
| $\tilde {t}$ | безразмерное время, $\tilde {t} = {t \mathord{\left/ {\vphantom {t {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}}$ |
| $V$ | удельный объем, м3/кг |
| ${{V}_{{i,solid}}}$ | компоненты скорости твердой фазы, ${\text{м}}\,\,{{{\text{с}}}^{{ - 1}}}$ |
| ${{Y}_{{lg}}} = \frac{{{{\rho }_{{lg}}}}}{{{{M}_{{lg}}}}}$ | молярные плотности компонент газовой фазы, ${\text{мол}}\,\,{{{\text{м}}}^{{ - 3}}}$ |
| ${{Y}_{{jS}}} = \frac{{{{\rho }_{{jS}}}}}{{{{M}_{{jS}}}}}$ | молярные плотности компонент твердой фазы, ${\text{мол}}\,\,{{{\text{м}}}^{{ - 3}}}$ |
| ${{Y}_{{g,tot}}} = \sum\limits_{l = 1}^3 {{{Y}_{{lg}}}} $ | суммарная молярная плотность газовой фазы, ${\text{мол}}\,\,{{{\text{м}}}^{{ - 3}}}$ |
| ${{Y}_{{S,tot}}} = \sum\limits_{j = 1}^6 {{{Y}_{{jS}}}} $ | суммарная молярная плотность твердой фазы, ${\text{мол}}\,\,{{{\text{м}}}^{{ - 3}}}$ |
| ${{\alpha }_{g}}$ | коэффициент температуропроводности газа, ${{{\text{м}}}^{2}}\,{{{\text{с}}}^{{ - 1}}}$ |
| ${{\alpha }_{j}}$, $j = 1,2,3$ | коэффициенты в формуле распределенного сопротивления пористости ${{\eta }_{j}} = {{\alpha }_{j}}\left| {\text{u}} \right| + {{\varsigma }_{j}}$, ${\text{Па}}\,{{{\text{м}}}^{{ - 2}}}\,{\text{с}}$ |
| ${{\bar {\alpha }}_{{ig}}}$, ${{\bar {\alpha }}_{{iS}}}$ | безразмерные коэффициенты концентрационного расширения |
| $\beta $ | безразмерный параметр энергии активации горения, $\beta = {{R{{T}_{0}}} \mathord{\left/ {\vphantom {{R{{T}_{0}}} E}} \right. \kern-0em} E}$ |
| $E = \sum\limits_k {{{\varepsilon }_{{kk}}}} $ | первый инвариант тензора деформаций Коши |
| ${{\varepsilon }_{{ij}}}$ | тензор деформаций |
| ${{\varsigma }_{j}}$ | компоненты распределенного сопротивления пористости,${{\eta }_{j}} = {{\alpha }_{j}}\left| {\text{u}} \right| + {{\varsigma }_{j}}$, j = 1, 2, 3, ${\text{Па}}\,{{{\text{м}}}^{{ - 1}}}$ |
| $\,{{\eta }_{j}}$ | распределенное сопротивление пористости, ηj = = ${{\alpha }_{j}}\left| {\text{u}} \right| + {{\varsigma }_{j}}$, j = 1, 2, 3, Па м–1 |
| $\kappa $ | коэффициент теплообмена, ${\text{Вт}}\,{{{\text{K}}}^{{ - 1}}}\,{{{\text{м}}}^{{ - 2}}}$ |
| $\tilde {\kappa } = {{\kappa {{t}_{0}}A} \mathord{\left/ {\vphantom {{\kappa {{t}_{0}}A} {\left( {{{c}_{p}}{{\rho }_{0}}V} \right)}}} \right. \kern-0em} {\left( {{{c}_{p}}{{\rho }_{0}}V} \right)}}$ | безразмерный коэффициент межфазового теплообмена |
| ${{\kappa }_{0}}\,$ | размерный коэффициент в формуле Левека, ${\text{Вт}}\,{{{\text{K}}}^{{ - 1}}}\,{{{\text{м}}}^{{ - 2}}}$ |
| ${{\lambda }_{0}}\,$ | характерная величина коэффициента теплопроводности, ${{\lambda }_{0}} = {{\lambda }_{{air}}} = 0.06$${\text{Вт}}\,\,{{{\text{м}}}^{{ - 1}}}\,{{{\text{K}}}^{{ - 1}}}$ |
| $\,{{\tilde {\lambda }}_{g}}$, ${{\tilde {\lambda }}_{S}}$ | безразмерные коэффициенты теплопроводности газовой и твердой фаз, ${{\tilde {\lambda }}_{g}} = {{{{\lambda }_{{air}}}} \mathord{\left/ {\vphantom {{{{\lambda }_{{air}}}} {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}},\,\,\,{{\tilde {\lambda }}_{S}} = {{{{\lambda }_{S}}} \mathord{\left/ {\vphantom {{{{\lambda }_{S}}} {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}}$ |
| $\mu $ | коэффициент динамической вязкости газа, ${\text{кг}}\,\,{{{\text{м}}}^{{ - 1}}}\,\,{{{\text{с}}}^{{ - 1}}}$ |
| μS1, μS2 | коэффициенты Ламе твердой фазы, ${\text{Па}}$ |
| ${{\nu }_{{lg}}} = \frac{{{{M}_{{lg}}}}}{{{{\rho }_{{lg}}}}}$ | молярный объем компонента газовой фазы, м3/моль |
| ${{\nu }_{{jS}}} = \frac{{{{M}_{{jS}}}}}{{{{\rho }_{{jS}}}}}$ | молярный объем компонента твердой фазы, м3/моль |
| ${{\rho }_{{1g}}},\,{{\rho }_{{2g}}},\,{{\rho }_{{3g}}}$ | массовые плотности компонент ${{{\text{O}}}_{{\text{2}}}}{\text{,}}\,{{{\text{N}}}_{{\text{2}}}}{\text{,}}\,{\text{C}}{{{\text{O}}}_{{\text{2}}}}$ газовой фазы, ${\text{кг}}\,{{{\text{м}}}^{{ - 3}}}$ |
| ${{\rho }_{g}} = {{\rho }_{{1g}}} + {{\rho }_{{2g}}} + {{\rho }_{{3g}}}$ | суммарная плотность компонент газовой фазы, ${\text{кг}}\,{{{\text{м}}}^{{ - 3}}}$ |
| ${{\rho }_{{1S}}},\,{{\rho }_{{2S}}},\,{{\rho }_{{3S}}},\,{{\rho }_{{4S}}},\,\,{{\rho }_{{5S}}},\,{{\rho }_{{6S}}}$ | массовые плотности компонент C, BaCO3, BaO, TiO2, BaTiO3, Ba2TiO4 твердой фазы, ${\text{кг}}\,{{{\text{м}}}^{{ - 3}}}$ |
| ${{\rho }_{S}} = \sum\limits_{j = 1}^6 {{{\rho }_{{jS}}}} $ | суммарная плотность компонент твердой фазы, ${\text{кг}}\,{{{\text{м}}}^{{ - 3}}}$ |
| ${{\rho }_{{tot}}} = {{\rho }_{g}} + {{\rho }_{S}}$ | суммарная массовая плотность, ${\text{кг}}\,{{{\text{м}}}^{{ - 3}}}$ |
| ${{\sigma }_{{ij}}}$ | тензор напряжений в твердой фазе, ${\text{Па}}$ |
| $\,\chi $ | коэффициент пористости |
| ${{\chi }_{0}}$ | начальная пористость |
| $\omega = {{\omega }_{T}} + {{\omega }_{g}} + {{\omega }_{S}}$ | безразмерный суммарный коэффициент объемного расширения |
| ${{\omega }_{T}}$ | вклад в расширение изменения температуры |
| ${{\omega }_{g}},\,{{\omega }_{S}}$ | эффект концентрационного расширения компонентов газовой и твердой фазы |
| ${\text{Ma}}$ | число Маха |
| ${\text{P}}{{{\text{e}}}_{{\text{1}}}}$ | диффузионное число Пекле |
| ${\text{P}}{{{\text{e}}}_{{{\text{Tg}}}}}{\text{,P}}{{{\text{e}}}_{{{\text{Ts}}}}}$ | тепловые числа Пекле для газовой и твердой фазы |
| ${\text{P}}{{{\text{e}}}_{{Tloc}}}$ | локальное число Пекле |
| ${\text{P}}{{{\text{e}}}_{{{\text{1t}}}}}{\text{,}}\,{\text{P}}{{{\text{e}}}_{{{\text{2t}}}}}$ | локальные числа Пекле для продольной и поперечной дисперсии тепла |
| $\operatorname{Re} $ | число Рейнольдса |
| ${\text{R}}{{{\text{e}}}_{{loc}}}\,$ | локальное число Рейнольдса |
| $\operatorname{R} _{S}^{{}} = {{p}_{0}}{{\left( {{{\zeta }_{p}}{{\mu }_{{S0}}}} \right)}^{{ - 1}}}$ | аналог числа Рейнольдса для твердой фазы |
ИНДЕКСЫ
Список литературы
Martirosyan K.S., Luss D. Carbon combustion synthesis of complex oxides: Process demonstration and features // AIChE J. 2005. V. 51. № 10. P. 2801.
Марков А.А., Обосян М.А., Мартиросян К.С. Исследование синтеза ферритов за волной горения с применением моделей скольжения и скачков температуры и концентраций компонент газовой фазы на поверхности пор твердой фазы // Физ.-хим. кинет. газов. дин. 2015. Т. 16. № 1. С. 1.
Markov A.A., Filimonov I.A., Martirosyan K.S. Modeling of submicron complex oxides synthesis // Theor. Found. Chem. Eng. 2017. V. 51. № 1. P. 27. [Марков А.А., Филимонов И.А., Мартиросян К.С. Моделирование синтеза сложных оксидов субмикронной дисперсности // Теор. осн. хим. технол. 2017. Т. 51. № 1. С. 31.]
Fatehi M., Kaviany M. Role of gas-phase reaction and gas-solid thermal nonequilibrium in reverse combustion // Int. J. Heat Mass Transfer. 1997. V. 40. № 11. P. 2607.
Oliveira A.A.M., Kaviany M. Nonequilibrium in the transport of heat and reactants in combustion in porous media // Prog. Energy Combust. Sci. 2001. V. 27. P. 523.
Pereira F.M., Oliveira A.A.M., Fachini F.F. Theoretical analysis of ultra- lean premixed flames in porous inert media // J. Fluid Mech. 2010. V. 657. P. 285.
Fatehi M., Kaviany M. Role of gas-phase reaction and gas-solid thermal nonequilibrium in reverse combustion // Int. J. Heat Mass Transfer. 1997. V. 40. № 11. P. 2607.
Delgado J.M.P.Q. Longitudinal and transverse dispersion in porous media // Chem. Eng. Res. Des. 2007. V. 85. P. 1245.
Quintard M., Whitaker S. Theoretical Analysis of Transport in Porous Media // Handbook of Heat Transfer in Porous Media / Eds. Hadim H., Vafai K. New York: Marcel Dekker, 2000. Ch. 1. P. 1.
Markov A.A. On Thermal and Mass Dispersion Effect on Barium Titanate Synthesis via CCSO // Phys.-Chem. Kinet. Gas Dyn. 2019. V. 20. № 4. P. 1.
Марков А.А. О влиянии тепловой и массовой дисперсии на синтез микронных частиц титаната бария // Вестн. Пермск. нац. исслед. политех. унив. Хим. технол. биотехнол. 2020. № 2. С. 160. https://doi.org/10.15593/2224-9400/2020.2.12
Сорокова С.Н., Князева А.Г. Связанная модель спекания порошков системы Ti–TiAI3 // Изв. Томск. политех. унив. 2009. Т. 314. № 2. С. 96.
Князева А.Г. Введение в термодинамику необратимых процессов. Томск: Иван Федоров, 2014.
De Leo C.T., Dannangoda G.C., Hobosyan M.A., Held J.T., Samghabadi F.S., Khodadadi M., Litvinov D., Mkhoyan K.A., Martirosyan. K.S. Carbon combustion synthesis of Janus-like particles of magnetoelectric cobalt ferrite and barium titanate // Ceram. Int. 2021. V. 47. № 4. P. 5415.
Martirosyan K.S., Luss D. Carbon combustion synthesis of complex oxides: Process demonstration and features // AIChE J. 2005. V. 51. № 10. P. 2801.
Brzozowski E., Sanchez J., Castro M.S. BaCO3–TiO2 Solid State Reaction: A Kinetic Study // J. Mater. Synth. Process. 2002. V. 10. № 1. P. 1.
Beauger A., Mutin J.C., Niepce J.C. Synthesis reaction of metatitanate BaTiO3. Part 1 Effect of the gaseous atmosphere upon the thermal evolution of the system BaCO3–TiO2 // J. Mater. Sci. 1983. V. 18. P. 3041.
Markov A.A. Jump-slip simulation technique for combustion in submicron tubes and submicron pores // Comput. Fluids. 2014. V. 99. P. 83.
Markov A.A., Hobosyan M.A., Martirosyan K.S. Ferrite Synthesis Simulation via Carbon Combustion using Slip, Temperature, and Concentration Gas Species Jump at Pore Surface // Phys.-Chem. Kinet. Gas Dyn. 2015. V. 16. № 1. P. 1.
Markov A.A., Hobosyan M.A., Martirosyan K.S. Simulation of heat and mass transfer in pores as applied to synthesis of magnesium–zinc and nickel–zinc ferrite nanoparticles // Nanomech. Sci. Technol.: Int. J. 2015. V. 6. № 3. P. 209.
Боли Б., Уэйнер Дж. Теория температурных напряжений. М.: Мир, 1964.
Франк-Каменецкий Д.А. Диффузия и теплопередача в химической кинетике. М.: Наука, 1987.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


