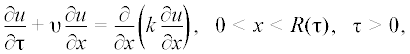Теоретические основы химической технологии, 2021, T. 55, № 5, стр. 612-617

Расчет кинетики сушки пластины с учетом ее усадки

С. П. Рудобашта^a, *, О. Р. Дорняк^b, В. М. Дмитриев^c

^a Российский государственный аграрный университет – МСХА им. К.А. Тимирязева
Москва, Россия

^b Воронежский государственный лесотехнический университет им. Г.Ф. Морозова
Воронеж, Россия

^c Тамбовский государственный технический университет
Тамбов, Россия

^* E-mail: rudobashta@mail.ru

Поступила в редакцию 18.01.2021
После доработки 18.02.2021
Принята к публикации 23.03.2021

DOI: 10.31857/S004035712104014X

Полный текст (PDF)

Аннотация

Представлена математическая модель процессов тепло- и массопереноса при конвективной сушке коллоидного капиллярно-пористого материала с учетом явления усадки. Модель сформулирована в области с подвижной границей. Уравнение массопроводности включает конвективный член для описания дополнительного внутреннего массопереноса матрицей материала. Сформулированная нелинейная задача тепломассопереноса решена численным методом с использованием полученных в настоящей работе данных по коэффициенту массопроводности и известных литературных данных по другим теплофизическим характеристикам. Верификация одномерной модели проведена на основе экспериментальных кривых сушки для яблочных дисков, вырезанных из цельного плода. Показано, что деформация образца при его обезвоживании существенно влияет на кинетику процесса сушки коллоидного капиллярно-пористого материала.

Ключевые слова: сушка, математическое моделирование, деформации усадки

ВВЕДЕНИЕ

В [1] описан универсальный зональный метод кинетического расчета массообменных аппаратов различного типа для систем с твердой фазой (сушка, адсорбция, экстрагирование), примеры реализации которого для сушилок приведены в [2]. Указанный метод и расчет сушилок на его основе приведены в [2] для капиллярно-пористых и непористых материалов, которые не имеют усадки в процессе сушки. Однако в промышленности высушивается большое количество капиллярно-пористых коллоидных материалов, подверженных в процессе сушки значительной усадке (например, такие материалы растительного происхождения, как фрукты и овощи [3]). Применение теоретических методов кинетического расчета сушилок для материалов, дающих значительную усадку в процессе сушки, требует учета этого эффекта.

Кинетика сушки капиллярно-пористых коллоидных материалов, подверженных усадке, рассмотрена в [4, 5]. Математические модели, представленные в этих работах, носят частный характер, они не в достаточной степени соотнесены с опытными данными. Так, математическая модель в [5] предполагает, что уменьшение объема материала при сушке равно объему удаленной при сушке воды, что справедливо только для некоторых частных случаев. В [6] методом электронной микроскопии изучено изменение структуры диска яблока, происходящее при его сушке, которое проанализировано с позиций воздействия капиллярных сил на структуру материала.

Целью данной работы является количественное описание кинетики сушки пластины, подверженной усадке в процессе сушки, с учетом как изменения ее толщины в ходе процесса, так и дополнительного внутреннего массопереноса матрицей материала. Проверка работоспособности представленной математической модели проведена на примере яблочного диска, вырезанного из цельного яблока.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Принято, что высушиваемое тело имеет форму неограниченной пластины толщиной l = 2R, высушиваемой одинаково с обеих поверхностей. Перенос влаги в пластине в данном случае происходит только вдоль координаты x, перпендикулярной плоскости пластины. Начало координат поместим в ее центральную плоскость. При сушке пластины усадка проявляется не только в том, что сокращается толщина пластины, но и в том, что появляется внутренний конвективный перенос влаги в результате движения матрицы материала.

Уравнение массопроводности (диффузии влаги)

(1)

$i({{\tau }}) = - k{{{{\rho }}}_{{\text{0}}}}\frac{{\partial u}}{{\partial x}}$

формулируется применительно к неподвижному сечению материала, в случае усадки – это сечение перемещается вместе с матрицей материала вдоль координаты x с некоторой скоростью υ, зависящей от координаты. Поэтому в неподвижной системе координат перенос влаги в пластине через плоскость с координатой x следует выразить уравнением

(2)

$i{\text{(}}\tau {\text{)}} = - k{{\rho }_{0}}\frac{{\partial u}}{{\partial x}} + {{\upsilon }}{{\rho }_{0}}u.$

Скорость υ перемещения сечения пластины с координатой “x” переменна; постулируем, что она линейно зависит от относительной координаты x/R и представим ее в виде

(3)

${{\upsilon }} = \frac{{dR}}{{d\tau }}\frac{x}{R} = {{{{\upsilon }}}_{R}}\frac{x}{R},$

где R = l/2 – половина толщины пластины, м. Величина ${{\upsilon }_{R}} = \frac{{dR}}{{d\tau }} < 0$ в (3) выражает скорость усадки половины толщины высушиваемой пластины у ее поверхности, а сомножитель x/R – корректирует эту скорость на сечение с координатой x. Согласно (3) максимальную скорость перемещения имеет поверхность пластины, а скорость перемещения центральной плоскости пластины, высушиваемой симметрично с обеих сторон, равна нулю.

Уравнению (2) соответствует нелинейное дифференциальное уравнение конвективной диффузии (конвективной массопроводности)

(4)

где υ – скорость перемещения сечения пластины с координатой x.

Запишем к нему краевые условия:

– начальное условие

(5)

${{\left. {u(x,\tau )} \right|}_{{\tau = 0}}} = {{u}_{{\text{n}}}} = const\,\,\,\,0 \leqslant x \leqslant R(\tau );$

– граничное условие у поверхности тела при постоянных параметрах внешней среды (полагаем, что задача массообмена является чисто внутренней)

(6)

$u(R,\tau ) = {{u}_{r}} = {\text{const}};$

– условие симметрии в центральной плоскости пластины

(7)

$\frac{{\partial u}}{{\partial x}} = 0,\,\,\,\,x = 0,\,\,\,\,\tau > 0.$

Среднеобъемное влагосодержание пластины равно

(8)

$\bar {u}({{\tau )}} = \frac{1}{R}\int\limits_0^{R({{\tau }})} {u(x,{{\tau }})dx} .$

При исследовании процессов конвективной сушки материала важным параметром является температура материала.

Запишем нелинейное дифференциальное уравнение теплопроводности для пластины, полагая, что испарение влаги происходит у поверхности пластины:

(9)

$c(u)\rho \frac{{\partial {\text{t}}}}{{\partial \tau }} = \frac{\partial }{{\partial x}}\left( {\lambda \frac{{\partial t}}{{\partial x}}} \right),\,\,\,\,\tau > 0,\,\,\,\,0 < x < R(t).$

Начальное условие теплообмена

(10)

${{\left. {t(x,\tau )} \right|}_{{\tau = 0}}} = {{t}_{n}} = const,\,\,\,\,0 < x < R(t).$

Граничное условие конвективного теплообмена 3-го рода у поверхности пластины имеет следующий вид:

(11)

${{\lambda }}\frac{{\partial t}}{{\partial x}} = \alpha ({{t}_{s}} - t(R,\tau )) - r{\text{*}}i(\tau ),\,\,\,\,\tau > 0,\,\,\,\,x = R(t),$

где $i(\tau ) = {{\left. {\left[ {k(u){{\rho }_{0}}\frac{{\partial u}}{{\partial x}}} \right]} \right|}_{{x = R}}}$ – интенсивность сушки в момент времени τ, кг/(м² с).

Условие симметрии в центральной плоскости пластины записано следующим образом:

(12)

$\frac{{\partial t}}{{\partial x}} = 0,\,\,\,\,\tau > 0,\,\,\,\,x = 0.$

Для расчета процесса по представленной модели необходимы данные для следующих параметров: k, υ_R, с, ρ, ρ₀, λ, α.

Экспериментально было получено следующее уравнение, описывающее линейную усадку яблочного диска (яблоко сорта “Гала”) по его толщине в процессе сушки:

(13)

$\delta l = {{l(\bar {u})} \mathord{\left/ {\vphantom {{l(\bar {u})} {{{l}_{n}}}}} \right. \kern-0em} {{{l}_{n}}}} = 0.448 + 0.092\bar {u}{\text{,}}$

где $\delta l = {{l(\bar {u})} \mathord{\left/ {\vphantom {{l(\bar {u})} {l({{{\bar {u}}}_{{\text{n}}}})}}} \right. \kern-0em} {l({{{\bar {u}}}_{{\text{n}}}})}}$ – относительная линейная усадка яблочного диска по толщине; $\bar {u}$ – среднее по объему диска влагосодержание материала в долях, кг/(кг сух. м-ла).

Максимальное (начальное) влагосодержание в опытах было равно ${{\bar {u}}_{{\text{n}}}} = 6$ кг/(кг сух. м-ла), поэтому в момент начала сушки согласно (13) имеем l_n = 5 мм, а при $\bar {u} = 0{\text{:}}$ ${{l}_{{\bar {u} = 0}}} = {{l}_{0}} = 2.24\,\,мм,$ т.е. максимальная усадка диска составляет 55.2%.

Уравнение (13) можно представить также в следующем виде:

(14)

$l = {{l}_{0}}(1 + {{\varepsilon }_{l}}u) = 2.24(1 + 0.205u),$

где ε_l = 0.205 – линейный коэффициент усадки, 1/м; l₀ = 2.24 мм – толщина абсолютно сухого диска, имевшего начальную толщину l_n = 5 мм; u – влагосодержание диска в долях, кг/(кг сух. м-ла).

Значения теплофизических характеристик яблок согласно [7] равны λ = 0.48 Вт/(м К), ρ = 660–860 кг/м³, с = 1340 + 28.6 × 10²w Дж/(кг К), где w – влажность, %. Среднее значение теплоты парообразования на температурном интервале 20–60°С: r* = 2.4 × 10⁶ Дж/кг. Согласно нашим измерениям плотность абсолютно сухих яблок исследованного сорта ρ₀ = 1120 кг/м³.

Среднеобъемная температура пластины

(15)

$\bar {t} = \frac{1}{R}\int\limits_0^R {t(x,\tau )} dx.$

Сформулированная нелинейная сопряженная математическая модель сушки пластины включает уравнение массопроводности (4), уравнение теплопроводности (9), начальные условия (5), (10), граничные условия (6)–(7), (11)–(12). Динамика усадки материала определяется уравнением (13), а изменение скорости υ по координате x – уравнением (3). Аналитическое решение приведенной выше нелинейной взаимосвязанной задачи массо- и теплопроводности отсутствует. В [8] для целей качественного анализа рассматриваемого процесса получено приближенное аналитическое решение задачи (4)–(8) при условии, что k = const, R = const, ${{u}_{R}} = {\text{const}}$ и ${{\upsilon }} = {\text{const}}{\text{.}}$ По полученному в [8] аналитическому решению можно судить о степени влияния конвективной составляющей на кинетику процесса. Для точных расчетов необходимо решение рассматриваемой нелинейной задачи, которое приведено ниже.

РЕЗУЛЬТАТЫ РАСЧЕТОВ СУШКИ ПЛАСТИНЫ ИЗ ЯБЛОКА С УЧЕТОМ ЕГО УСАДКИ

Решение математической модели с подвижной границей может быть выполнено с использованием численных методов. В данной работе решение задачи получено с использованием программного пакета COMSOL Multiphysics 5.3a. Создание расчетной модели осуществлено с помощью инструментария General form PDE, который предназначен для решения уравнений в частных производных произвольного вида.

Верификация математической модели проведена на основе опытных кривых сушки яблочных дисков толщиной l = 5 мм и диаметром d = 65 мм. При получении опытных кривых сушки образцы в экспериментальной сушильной установке подвергались продольному обдуву рециркулирующим по замкнутому контуру потоком воздуха со скоростью υ_s = 10 м/с при значениях температуры 30, 40, 50 и 60°С. Опытным путем было установлено, что дальнейшее увеличение скорости воздуха не приводит к увеличению скорости сушки. Это свидетельствует о том, при скорости воздуха 10 м/с имеет место внутридиффузионный кинетический режим сушки, для которого справедливо граничное условие (6). Рециркулировавший в рабочей камере воздух непрерывно осушался с помощью силикагеля,

Для определения концентрационной зависимости коэффициента массопроводности, как правило, применяют зональный метод [2], основанный на использовании решения линейного дифференциального уравнения массопроводности для тела, не подверженного усадке, при постоянном граничном условии (6). Однако поскольку в данном случае имеет место значительная усадка яблочного диска при сушке, то данный метод был применен только для заключительного этапа сушки. В результате получены значения коэффициента массопроводности k₀ при $\bar {u} \to {{u}_{r}}$ для различных значений температуры сушильного агента (табл. 1).

Таблица 1.

Значения теплофизических параметров в расчетах

t_s, °C	30	40	50	60
k₀× 10¹⁰, м²/с	0.7	1.2	1.7	2.1
ν_s× 10⁶ м²/с [11]	16.58	17.57	18.58	19.60
λ_s× 10², Вт/(м К) [11]	2.65	2.72	2.79	2.86
а_s× 10⁶, м²/с [11]	23.4	24.8	26.3	27.6
Re	19 602	18 497	17 492	16 582
Gu	0.063	0.083	0.099	0.114
Nu	110.9	112.3	112.0	111.1
α, Вт/(м² К)	90.4	94.0	96.1	97.8
Bi	4.71	4.90	5.00	5.09

Равновесное влагосодержание u_r может быть найдено из опытов. В работе [9] для яблок, нарезанных на дольки, получены изотермы десорбции при значениях температуры t_s = 25 и 35°C. Авторами [9] установлено снижение значения u_r с ростом температуры сушильного агента t_s, которое особенно заметно в диапазоне изменения его относительной влажности φ_s от 35 до 75%. В данной работе значения равновесного влагосодержания материала для исследуемого диапазона значений температуры воздуха в камере получены путем экстраполяции опытных зависимостей для скорости сушки ${{d\bar {u}} \mathord{\left/ {\vphantom {{d\bar {u}} {d\tau }}} \right. \kern-0em} {d\tau }}$ от среднего влагосодержания $\bar {u}$ на область предельно малых значений скорости сушки.

Коэффициент массопроводности капиллярно-пористых коллоидных материалов растительного происхождения является функцией влагосодержания материала, имеющей вид [2]

(16)

$k = {{k}_{0}}\exp (a{\text{*}}u),$

где k₀ – коэффициент массопроводности при $\bar {u} \to {{u}_{r}};$ a* – константа, определяющая зависимость коэффициента массопроводности от влагосодержания материала. Практические наблюдения показывают, что функция (16) является возрастающей, т.е. a* > 0 [2]. Значение величины a* найдено методом параметрической идентификации. Установлено, что этот параметр не зависит от температуры сушильного агента и равен a* = 0.45.

Необходимый для расчета теплообмена коэффициент теплоотдачи α рассчитывали по уравнению Нестеренко [10]

(17)

${\text{Nu}} = 0.51{{\Pr }^{{0.33}}}{{\operatorname{Re} }^{{0.61}}}{\text{G}}{{{\text{u}}}^{{{\text{0}}{\text{.175}}}}},$

где Re = 3150–22000. При этом длину обтекания принимали равной l' = 0.5d = 0.0325 м. При расчетах коэффициента теплоотдачи α по уравнению (17) использованы значения теплофизических характеристик воздуха [11].

Расчетные параметры представлены в табл. 1. Значения критерия Bi, приведенные в табл. 1, показывают, что задача теплообмена является смешанной: на нагрев тела в процессе сушки оказывают влияние как внутреннее, так и внешнее термические сопротивления.

Рис. 1–4 иллюстрируют процессы тепло- и массопереноса при сушке образца яблока в форме пластины с учетом его усадки.

Рис. 1.

Кривые сушки пластины из яблока (2R = 5 мм) при t_s = 30 (1), 40 (2), 50 (3) и 60 (4) °C. Точки – эксперимент, линии – расчет.

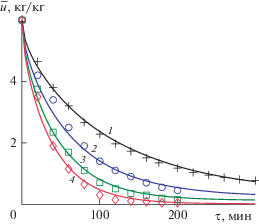
Рис. 2.

Профили влагосодержания поперек пластины из яблока (2R = 5 мм; t_s = 50°C) для различных моментов процесса сушки τ = 50 (1), 75 (2), 100 (3), 125 (4), 150 (5), 175 (6) и 300 (7) мин.

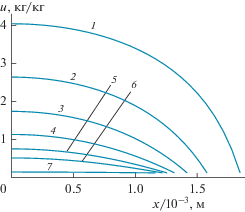
Рис. 3.

Зависимости от времени средней по сечению пластины из яблока температуры (2R = 5 мм) при t_s = = 30 (1), 40 (2) и 50 (3) °C.

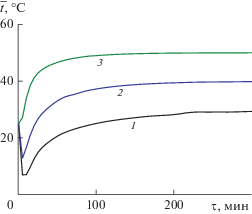
Рис. 4.

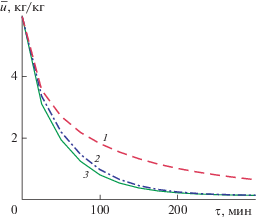
Кривые сушки пластины из яблока при t_s = = 50°C, рассчитанные без усадки и учета конвективного переноса влаги (1), с усадкой, но без учета конвективного переноса влаги (2), с усадкой и учетом конвективного члена (3).

Из графиков на рис. 1 видно, что расчетные и экспериментальные кривые сушки имеют удовлетворительное совпадение при различных температурах сушильного агента. Зависимости, представленные на рис. 1, качественно согласуются с экспериментальными результатами работы [12], полученными для образца другой формы и для других режимов сушки яблок.

Рисунок 2 иллюстрирует развитие во времени профилей влагосодержания в пластине из яблока с учетом уменьшения толщины образца вследствие усадки материала.

Расчетные значения температуры, усредненной по изменяющейся толщине образца, представлены на рис. 3. Следует отметить, что при невысоких значениях температуры сушильного агента (кривая 1) имеет место понижение средней температуры материала ниже начальной при τ < 100 мин. Это происходит по причине преобладания в этом режиме сушки величины интенсивности поглощения тепла за счет испарения над тепловым потоком, обусловленным конвективным переносом, на внешней границе пластины. Особенности изменения средней температуры материала подобного типа получены при расчетах с использованием и других моделей, в частности в [12].

Как показывают расчеты, роль процесса усадки, учитываемого в предложенной математической модели конвективной сушки, весьма существенна (кривые 1, 3 на рис. 4). При этом для процесса обезвоживания формальный вклад конвективного члена уравнения влагопроводности (4) мал по сравнению с тем эффектом, который дает усадка материала (кривые 2, 3 на рис. 4).

ЗАКЛЮЧЕНИЕ

Сформулирована одномерная нелинейная математическая модель тепло- и влагопроводности материалов, которые подвержены существенным объемным деформациям при обезвоживании. Влияние деформаций усадки на кинетику процесса сушки в модели определено двумя факторами: дополнительным потоком влаги, с одной стороны, и подвижными границами высушиваемого объекта, с другой стороны. Математическая модель может быть обобщена для двумерных и трехмерных задач сушки коллоидных капиллярно-пористых материалов.

На примере яблочных пластин показано удовлетворительное совпадение экспериментальных и расчетных кривых сушки. Выявлено существенное влияние деформаций усадки материала (яблока) на кинетику сушильного процесса.

Предложенная математическая модель может быть использована для проведения инженерных расчетов кинетики сушки пластин из капиллярно-пористого коллоидного материала с учетом деформаций усадки.

ОБОЗНАЧЕНИЯ

a	коэффициент температуропроводности, м²/с
с	массовая теплоемкость материала пластины, Дж/(кг К)
d	диаметр яблочного диска, м
i	интенсивность сушки, кг/(м² с)
k	коэффициент массопроводности, м²/с
l = 2R	толщина пластины, м
l'	длина потока в критериальном уравнении теплоотдачи, м
R	половина толщины пластины
r*	теплота парообразования, Дж/кг
T	температура, К
t	температура, °С
u, $\bar {u}$	локальное и среднее по объему пластины влагосодержание материала, кг/(кг сух. м-ла)
υ_s	скорость сушильного агента (воздуха), м/с
w	влажность яблок, кг/(кг влажн. м-ла) или %
α	коэффициент теплоотдачи, Вт/(м² К)
ε_l	линейный коэффициент усадки, 1/м
λ	коэффициент теплопроводности пластины, Вт/(м К)
ν_s	кинематическая вязкость воздуха, м²/с
ρ	плотность влажного материала, кг/м³
ρ₀	плотность абсолютно сухого материала, кг/м³
υ_R	скорость усадки (скорость перемещения сечения пластины с координатой R), м/с
${\text{Bi}} = \frac{{\alpha R}}{\lambda }$	тепловое число Био
$Gu = \frac{{{{Т}_{s}} - {{Т}_{{m.t}}}}}{{{{Т}_{s}}}}$	число Гухмана
${\text{Nu}} = \frac{{{{\alpha }}l{\kern 1pt} {\text{'}}}}{{{{\lambda }_{s}}}}$	число Нуссельта
$\Pr = \frac{{{{{v}}_{s}}}}{{{{a}_{s}}}}$	число Прандтля
${\text{Re}} = \frac{{{{\upsilon }_{s}}l{\kern 1pt} {\text{'}}}}{{{{{v}}_{s}}}}$	число Рейнольдса

ИНДЕКСЫ

m	массообмен
m.t	мокрый термометр
n	начальный
R	при координате R
r	равновесный
s	внешняя среда (воздух)

Список литературы

Rudobashta S.P., Planovskii A.N., Ochnev É.N. Zonal method of calculation of continuous mass exchange apparatuses for systems with a solid phase // Teor. Osn. Khim. Tekhnol. 1974. V. 8. № 1. P. 22. [Рудобашта С.П., Плановский А.Н., Очнев Э.Н. Зональный метод расчета непрерывно действующих массообменных аппаратов для систем с твердой фазой // Теор. осн. хим. технол. 1974. Т. 8. № 1. С. 22.]
Рудобашта С.П. Массоперенос в системах с твердой фазой. М.: Химия, 1980.
Лыков А.В. Теория сушки. М.: Энергия, 1968.
Honarvar B., Mowla D. Theoretical and experimental drying of a cylindrical sample by applying hot air and infrared radiation in an inert medium fluidized bed // Braz. J. Chem. Eng. 2012. V. 29. № 2. P. 231.
Martínez-Vera C., Vizcarra-Mendoza M. Fluidized bed drying simulation considering solid shrinkage // Proc. 6th Nordic Drying Conference (Electronic Edition). Copenhagen, 2013.
Segura L.A., Badillo G.M, Alves-Filho O. Changes in the microstructure of apples (granny smith) during drying and their relationship with the water transport mechanisms // Proc. 6th Nordic Drying Conference (Electronic Edition). Copenhagen, 2013.
Теплофизические характеристики пищевых продуктов и материалов. Справочное пособие / Под ред. Гинзбурга А.С. М.: Пищевая промышленность, 1975.
Rudobashta S.P., Kartashov É.M., Zueva G.A. Mathematical modeling of the process of convective drying of materials taking into account their shrinkage // J. Eng. Phys. Thermophys. 2020. V. 93. № 6. P. 1394. [Рудобашта С.П., Карташов Э.М., Зуева Г.А. Математическое моделирование процесса конвективной сушки материалов с учетом их усадки // Инж.-физ. журн. 2020. Т. 93. № 6. С. 1446.]https://doi.org/10.1007/s10891-020-02244-y
Рудобашта С.П., Царьков Д.В. Гигроскопические свойства нарезанных яблок // Сб. тр. всероссийской с международным участием конференции “Импортозамещающие технологии и оборудование для глубокой комплексной переработки сельскохозяйственного сырья”. Тамбов, 2019. С. 281.
Нестеренко А.В. Основы термодинамических расчетов вентиляции и кондиционирования воздуха. М.: Высшая школа, 1971.
Теоретические основы теплотехники. Теплотехнический эксперимент. Справочник. Книга 2 / Под общ. ред. Григорьева В.А. и Зорина В.М. М.: Энергоатомиздат, 1988.
Pakowski Z., Adamski A. The Comparison of Two Models of Convective Drying of Shrinking Materials Using Apple Tissue as an Example // Drying Technol. 2007. V. 25. № 7–8. P. 1139.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал