1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 56, № 3, 2022

Теоретические основы химической технологии, 2022, T. 56, № 3, стр. 326-336

Анализ процессов экстракционного разделения в каскаде смесительно-отстойных экстракторов в режиме рециркуляционной жидкостно-жидкостной хроматографии

А. Е. Костанян a, *, Ю. А Клычевских a, Н. А. Милевский a, Т. С. Сафонов a, А. А. Вошкин a

a Институт общей и неорганической химии им. Н.С. Курнакова РАН
Москва, Россия

* E-mail: kost@igic.ras.ru

Поступила в редакцию 29.01.2022
После доработки 06.02.2022
Принята к публикации 15.02.2022

Полный текст (PDF)

Аннотация

Ранее для повышения эффективности экстракционного разделения жидких смесей был предложен метод серийного импульсного ввода раствора смеси компонентов в каскад смесительно-отстойных экстракторов, работающих в режиме элюентной хроматографии. Настоящая работа посвящена дальнейшему развитию этого метода применительно к процессам разделения в каскаде смесительно-отстойных экстракторов, работающих в режиме рециркуляционной хроматографии. Разработана математическая модель и проведен анализ периодических и непрерывных процессов экстракционного разделения для условий, когда разделяемая смесь компонентов загружается в каскад смесительно-отстойных экстракторов в виде серии последовательных, разделенных короткими интервалами времени, импульсных вводов. Проведены эксперименты на каскаде смесительно-отстойных экстракторов, подтверждающие достоверность разработанной модели. На ряде примеров показано, что при серийном методе загрузки раствора компонентов в замкнутый контур экстракторов существенно повышается эффективность и производительность процессов разделения.

Ключевые слова: выделение концентрированных фракций целевых компонентов из растворов, жидкостная экстракция, рециркуляционная жидкость-жидкостная хроматография, каскад смесительно-отстойных экстракторов

ВВЕДЕНИЕ

Ранее [1] был проведен анализ процессов экстракционного разделения в каскаде смесительно-отстойных экстракторов в режиме элюентной жидкостно-жидкостной хроматографии при загрузке раствора компонентов в виде серии последовательных, разделенных короткими интервалами времени, импульсных впрысков: получены аналитические зависимости для моделирования периодических и непрерывных процессов разделения и на ряде примеров показано, что при использовании серийного метода загрузки раствора компонентов существенно (более, чем на порядок) повышается концентрация компонентов в разделенных фракциях и производительность процесса разделения. В работе [2] был проведен анализ периодических процессов экстракционного разделения в замкнутом каскаде смесительно-отстойных экстракторов, работающем в режиме рециркуляционной хроматографии, при длительной одноразовой загрузке раствора компонентов.

Настоящая работа посвящена дальнейшему развитию технологии серийной загрузки раствора компонентов применительно к процессам разделения методами рециркуляционной жидкостно-жидкостной хроматографии.

Благодаря сочетанию характеристик жидкостной экстракции и распределительной хроматографии жидкостно-жидкостная хроматография предлагает множество методов (схем и режимов проведения процессов разделения), которые позволяют значительно повысить эффективность разделения по сравнению с широко распространенным методом обычной элюентной хроматографии [3–27]. Для промышленных процессов разделения одним из наиболее перспективных представляется метод рециркуляционной жидкостно-жидкостной хроматографии [4, 5, 7, 8, 18]. В этом методе разделение компонентов проводится в замкнутом циркуляционном контуре, включающем хроматографическую колонку и систему рецикла (насос, соединительные трубки, клапана, детектор и другие контрольно-измерительные приборы), путем подачи выходящего из колонки элюента после ввода пробы в колонку на ее вход. В рециркуляционной хроматографии достигается существенное увеличение эффективности процесса разделения, за счет многократного прохода разделяемой смеси через колонку. При этом используется гораздо меньше реагентов, чем в традиционных методах хроматографии: подвижная фаза не выводится из колонки до тех пор, пока не будет достигнуто требуемое качество разделения. Метод рецикла, как и другие методы жидкостно-жидкостной хроматографии, используется главным образом в препаративных целях для разделения веществ растительного происхождения. Теория различных вариантов рециркуляционной жидкостно-жидкостной хроматографии разработана в работах [7, 8, 18 ]. Задачей настоящей работы является разработка и анализ математической модели экстракционных процессов разделения в каскаде смесительно-отстойных экстракторов в режиме рециркуляционной хроматографии для условий серийного импульсного вводов раствора компонентов в каскад.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЭКСТРАКЦИОННЫХ ПРОЦЕССОВ РАЗДЕЛЕНИЯ В КАСКАДЕ СМЕСИТЕЛЬНО-ОТСТОЙНЫХ ЭКСТРАКТОРОВ В РЕЖИМЕ РЕЦИРКУЛЯЦИОННОЙ ХРОМАТОГРАФИИ ПРИ СЕРИЙНОМ ИМПУЛЬСНОМ ВВОДЕ РАСТВОРА РАЗДЕЛЯЕМОЙ СМЕСИ

Как отмечалось раннее [1], для работы экстракционной установки в режиме хроматографии в каждой ступени каскада необходимо организовать полную рециркуляцию органической фазы между отстойником и смесителем. Таким образом органическая фаза удерживается в каскаде (в терминах хроматографии – является неподвижной), а водная фаза (подвижная фаза) проходит через все ступени каскада. При этом выбирается такая скорость рециркуляции органической фазы в ступенях каскада, чтобы доля объема, занимаемая в смесителе этой фазой (S), была в пределах 0.5 ≤ S ≤ 0.8, что обеспечивает диспергирование водной фазы в органической и способствует уменьшению уноса и повышению эффективности хроматографических процессов разделения в каскаде. Процесс разделения в режиме рециркуляционной хроматографии проводится следующим образом: после завершения серии импульсных вводов раствора компонентов в первую ступень каскада экстракторов выходящий из последней ступени каскада поток водной фазы возвращается в первую ступень и циркулирует в системе до достижения требуемой степени разделения компонентов или очистки целевого компонента. Затем контур размыкается, в установку с расходом, равным объемной скорости циркуляции в контуре подается свежая водная фаза, и из последней ступени выводятся фракции разделенных компонентов. При проведении непрерывных процессов разделения, описанные выше операции загрузки раствора компонентов и вывода фракций компонентов, повторяются через определенные равные интервалы времени.

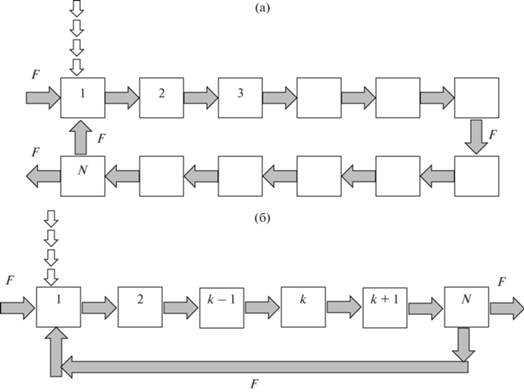
Рассмотрим два варианта аппаратурного оформления периодических и непрерывных процессов разделения в замкнутом каскаде экстракторов: без специального трубопровода рецикла (однородный контур, рис. 1а); с длинным трубопроводом рецикла, соединяющим последнюю ступень с первой ступенью (неоднородный контур, рис. 1в). Как и в предыдущей работе [1] допускаем, что эффективность разделения в каждом аппарате соответствует одной теоретической ступени.

Рис. 1.

Схемы процессов экстракционного разделения в однородном (а) и неоднородном (б) контуре.

Процессы разделения в каскаде без специального трубопровода рецикла. В рассматриваемом случае первая и последняя ступени каскада соединены между собой таким же образом, как и промежуточные ступени (рис. 1а). Такой циркуляционный контур можно назвать однородным [2] или идеальным [8].

Периодические процессы разделения. На основании подходов, изложенных в работах [7, 8, 18], получена следующая зависимость, описывающая профиль выходной концентрации компонента с коэффициентом распределения KD в однородном контуре после серийной загрузки раствора компонентов:

(1)
$X(t) = \frac{{a\sqrt N }}{{\sqrt {2\pi } }}\sum\limits_{j = 1}^m {\sum\limits_{i = 1}^n {\frac{{{{e}^{{ - \frac{{N{{{[i + a(j - 1){{t}_{{in}}} - at]}}^{2}}}}{{2i}}}}}}}{{\sqrt i }}} } ,$
(2)
$a = \frac{1}{{1 - S + S{{K}_{D}}}},$
где $X = {x \mathord{\left/ {\vphantom {x {\bar {x}}}} \right. \kern-0em} {\bar {x}}}$ – безразмерная концентрация компонента KD; $\bar {x}$ = Q/Vс – средняя концентрация компонента KD в каскаде после одного импульсного ввода раствора компонентов; Vс – общий объем каскада, состоящего из N экстракционных ступеней; Q – количество компонента KD в одной порции загруженного раствора компонентов; KD = = y/x = constant – коэффициент распределения: x – концентрация в водной фазе, y – концентрация в органической фазе; $t = \frac{{\tau F}}{{{{V}_{c}}}}$ – безразмерное время; tin= τinF/Vc – безразмерный интервал времени между импульсными вводами раствора компонентов; F – объемная скорость подачи в каскад и циркуляции через каскад водной фазы; τ – время; m – номер (количество) импульсных вводов раствора компонентов; n – номер (количество) цикла циркуляции в контуре компонента KD; S – доля объема, занимаемая в ступенях органической (непроточной) фазой.

Уравнение (1) описывает изменение концентрации компонента KD в последней ступени (N) каскада в течение всего времени его циркуляции от первого до последнего цикла n при загрузке, состоящей из m импульсных вводов раствора компонентов в первую ступень каскада в момент времени τ = 0. Для условий одного импульсного ввода раствора компонентов (j = 1) уравнение (1) упрощается и приводится к виду:

(3)
$X(t) = \frac{{a\sqrt N }}{{\sqrt {2\pi } }}\sum\limits_{i = 1}^n {\frac{{{{e}^{{ - \frac{{N{{{[i - at]}}^{2}}}}{{2i}}}}}}}{{\sqrt i }}} .$

Непрерывные процессы разделения. Если после первой серийной загрузки раствора компонентов через интервал времени τins (tins= τinsF/Vc) следует вторая серийная загрузка, выходной профиль концентрации для второй загрузки можно описать уравнением (4):

(4)
${{X}_{s}}(t) = \frac{{a\sqrt N }}{{\sqrt {2\pi } }}\sum\limits_{j = 1}^m {\sum\limits_{i = 1}^n {\frac{{{{e}^{{ - \frac{{N{{{[i + a(j - 1){{t}_{{in}}} + a{{t}_{{ins}}} - at]}}^{2}}}}{{2i}}}}}}}{{\sqrt i }}} } .$

Результирующий выходной профиль концентрации после двух последовательных серийных загрузок описывается уравнением (5):

(5)
${{X}_{c}}\left( t \right) = X\left( t \right) + {{X}_{s}}\left( t \right)~,$
где X(t) определяется уравнением (1).

С помощью уравнений (1), (4) и (5) можно моделировать непрерывные процессы разделения в замкнутом однородном контуре смесительно-отстойных экстракторов в условиях серийного импульсного ввода раствора компонентов.

Процессы разделения в каскаде с трубопроводом рецикла. Как упоминалось выше, в такой схеме процесса (неоднородный контур) последняя ступень каскада экстракторов соединяется длинным трубопроводом с первой ступенью (Рис. 1в). Математическая модель процессов разделения дополняется двумя новыми параметрами, учитывающие влияние системы рецикла: b = Vес/Vс – отношение объемов системы рецикла Vес и колонки Vс; Nec – число ячеек полного перемешивания, количественно характеризующее степень продольного перемешивания (размывание хроматографических пиков) в системе рецикла. Как и в случае однородного контура, рассмотрим периодические и непрерывные процессы экстракционного разделения в каскаде экстракторов.

Периодические процессы разделения. Уравнение, аналогичное зависимости (1), описывающее профиль выходной концентрации после одной серийной загрузки раствора компонентов получено в виде:

(6)
$X\left( t \right) = \frac{{aN\sqrt {{{N}_{{ec}}}} }}{{\sqrt {2\pi } }}\sum\limits_{j = 1}^m {\sum\limits_{i = 1}^n {\frac{{{{e}^{{ - \frac{{N{{N}_{{ec}}}{{{\left[ {i + ab\left( {i - 1} \right) + a\left( {j - 1} \right){{t}_{{{\text{in}}}}} - at} \right]}}^{2}}}}{{2i{{N}_{{ec}}} + 2N\left( {i - 1} \right){{{\left( {ab} \right)}}^{2}}}}}}}}}{{\sqrt {iN{{N}_{{ec}}} + \left( {i - 1} \right){{{\left( {abN} \right)}}^{2}}} }}} } .~$

Для условий одного импульсного ввода раствора компонентов (j = 1) уравнение (6) приводится к виду:

(7)
$X\left( t \right) = \frac{{aN\sqrt {{{N}_{{ec}}}} }}{{\sqrt {2\pi } }}\mathop \sum \limits_{i = 1}^n \frac{{{{e}^{{ - \frac{{N{{N}_{{ec}}}{{{\left[ {i + ab\left( {i - 1} \right) - at} \right]}}^{2}}}}{{2i{{N}_{{ec}}} + 2N\left( {i - 1} \right){{{\left( {ab} \right)}}^{2}}}}}}}}}{{\sqrt {iN{{N}_{{ec}}} + \left( {i - 1} \right){{{\left( {abN} \right)}}^{2}}} }}~.$

Непрерывные процессы разделения. Уравнение, аналогичное зависимости (4) для выходного профиля концентрации второй загрузки, имеет вид:

(8)
$\begin{gathered} {{X}_{s}}\left( t \right) = \frac{{aN\sqrt {{{N}_{{ec}}}} }}{{\sqrt {2\pi } }} \times \\ \times \,\,\,\mathop \sum \limits_{j = 1}^m \mathop \sum \limits_{i = 1}^n \frac{{{{e}^{{ - \frac{{N{{N}_{{ec}}}{{{\left[ {i + ab\left( {i - 1} \right) + a\left( {j - 1} \right){{t}_{{in}}} + a{{t}_{{ins}}} - at} \right]}}^{2}}}}{{2i{{N}_{{ec}}} + 2N\left( {i - 1} \right){{{\left( {ab} \right)}}^{2}}}}}}}}}{{\sqrt {iN{{N}_{{ec}}} + \left( {i - 1} \right){{{\left( {abN} \right)}}^{2}}} }}. \\ \end{gathered} $

Как и в случае однородного контура, результирующий выходной профиль концентрации после двух последовательных серийных загрузок описывается уравнением (5), в котором члены X(t) и Xs(t) определяются уравнениями (7) и (8).

АНАЛИЗ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

Для упрощения математической модели рассматриваемых процессов разделения в неоднородном контуре можно допустить, что циркулирующий через трубопровод, соединяющий последнюю ступень с первой ступенью каскада, поток водной фазы движется в режиме идеального вытеснения, т.е. форма пиков при прохождении их через систему рецикла не изменяется. Переходя в уравнениях (6)–(8) к пределу Nec → ∞, получим соответствующие зависимости для упрощенной модели:

(9)
$X\left( t \right) = \frac{{aN}}{{\sqrt {2\pi } }}\mathop \sum \limits_{j = 1}^m \mathop \sum \limits_{i = 1}^n \frac{{{{e}^{{ - \frac{{N{{{\left[ {i + ab\left( {i - 1} \right) + a\left( {j - 1} \right){{t}_{{in}}} - at} \right]}}^{2}}}}{{2i}}}}}}}{{\sqrt {iN} }},$
(10)
$X(t) = \frac{{a\sqrt N }}{{\sqrt {2\pi } }}\sum\limits_{i = 1}^n {\frac{{{{e}^{{ - \frac{{N{{{[i + ab(i - 1) - at]}}^{2}}}}{{2i}}}}}}}{{\sqrt i }}} ,$
(11)
${{X}_{s}}\left( t \right) = \frac{{aN}}{{\sqrt {2\pi } }}\mathop \sum \limits_{j = 1}^m \mathop \sum \limits_{i = 1}^n \frac{{{{e}^{{ - \frac{{N{{{\left[ {i + ab\left( {i - 1} \right) + a\left( {j - 1} \right){{t}_{{in}}} + a{{t}_{{ins}}} - at} \right]}}^{2}}}}{{2i}}}}}}}{{\sqrt {iN} }}.$

Рис. 2, где сопоставлены профили концентраций двух компонентов KD1 = 0.5 и KD2 = 1.5, рассчитанные по уравнениям (6) и (9), иллюстрирует влияние параметров системы рецикла на форму хроматографических пиков. Можно сделать вывод, что при использовании длинного трубопровода рецикла расчеты процессов разделения можно проводить на основе упрощенной модели.

Рис. 2.

Профили концентраций компонентов KD1 = 0.5 и KD2 = 1.5, рассчитанные по уравнениям (6) – сплошная линия и (9) – точки. Параметры процесса: N = 100; n = 4; m = 10; S = 0.5; tin = 0.01.

На рис. 3–6 приведены примеры моделирования периодических (рис. 3–5) и непрерывных (рис. 6) процессов разделения при однократной (m = 1) и серийной загрузке бинарных смесей в каскад смесительно-отстойных экстракторов. Профили концентраций компонентов рассчитывались по приведенным выше зависимостям. Из сравнения процессов разделения в однородном (рис. 3) и неоднородном (рис. 4, 5) контуре следует, что схема со специальным (длинным) трубопроводом рецикла более эффективна. Она обеспечивает более качественное разделение и позволяет разделить компоненты в каскаде с вдвое меньшим числом ступеней. Результаты моделирования, представленные на рис. 3–5, иллюстрируют сложный характер влияния параметра S (доли объема аппаратов, занятой непроточной органической фазой) на процесс разделения в замкнутом контуре: с увеличением S улучшается разделение компонентов в отдельных циклах, но одновременно происходит сближение и наложение концентрационных профилей соседних циклов. Как показано на рис. 4, 5, подбором параметров S, b (длины трубопровода рецикла) и n (количества циклов рециркуляции) можно определить оптимальные условия проведения процесса разделения.

Рис. 3.

Моделирование периодического процесса разделения в однородном контуре при однократной (m = 1) и серийной (m = 10) загрузке бинарной смеси KD1 = 0.3, KD2 = 0.6 в каскад смесительно-отстойных экстракторов. Параметры процесса: N = 100; n= 3; Nec = 100; tin = 0.01.

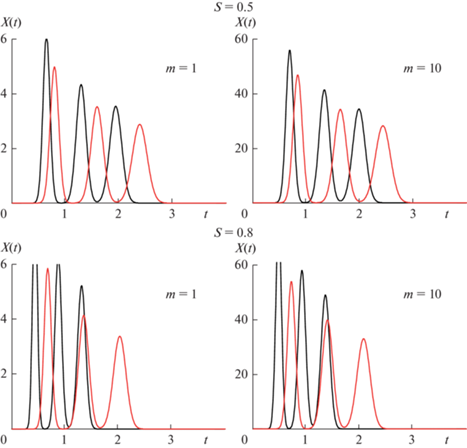
Рис. 4.

Моделирование периодического процесса разделения в неоднородном контуре при однократной (m = 1) и серийной (m = 10) загрузке бинарной смеси KD1 = 0.3, KD2 = 0.6 в каскад смесительно-отстойных экстракторов. Nec = = 100; tin = 0.01.

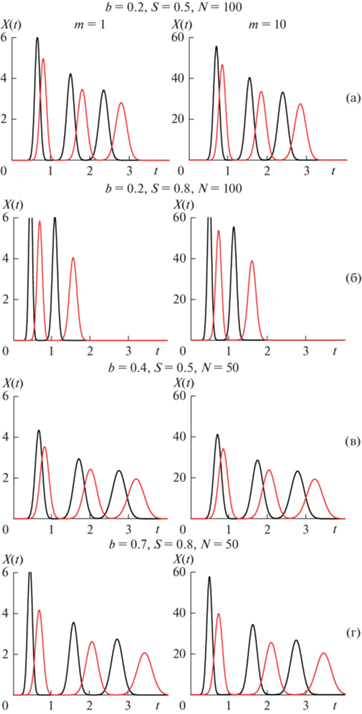
Рис. 5.

Моделирование периодического процесса разделения бинарной смеси KD1 = 0.6, KD2 = 1.2 в неоднородном контуре при однократной (m = 1) и серийной (m = 10) загрузке раствора компонентов. Nec = 100; n = 2; tin = 0.01.

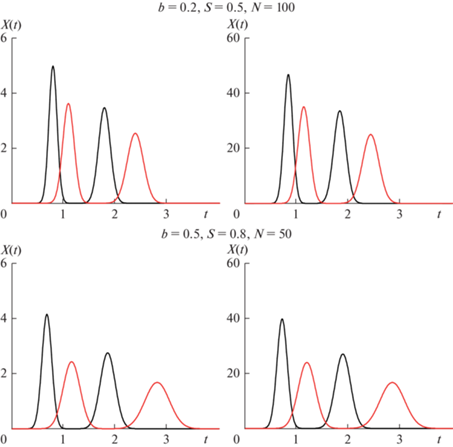
Рис. 6.

Моделирование непрерывных вариантов процессов разделения, представленных на рис. 4a, б, в. Выходные концентрационные профили после двух последовательных серийных загрузок раствора разделяемых компонентов рассчитаны по уравнениям (5), (7) и (8).

На рис. 6 приведены результаты моделирования непрерывных вариантов процессов разделения, представленных на рис. 4a, 4б, 4в. Выходные концентрационные профили после двух последовательных серийных загрузок раствора разделяемых компонентов рассчитаны по уравнениям (5), (7) и (8). Численные исследования по этим уравнениям позволяют выбрать для непрерывного режима оптимальный интервал между последовательными серийными загрузками, обеспечивающий четкое разделение выводимых фракций компонентов и высокую производительность процесса экстракционного разделения в каскаде экстракторов.

Из рис. 3–5 следует весьма важный для промышленной реализации рассмотренного метода экстракционного разделения вывод: Применение серийной загрузки раствора компонентов позволяет многократно повысить концентрации в разделенных фракциях компонентов и производительность процесса разделения. Кроме того, работа каскада экстракторов в режиме рециркуляционной хроматографии по сравнению с элюентным режимом существенно повышает эффективность процессов экстракционного разделения.

Для подтверждения достоверности разработанной математической-модели на каскаде смесительно-отстойных экстракторов были проведены эксперименты без специального трубопровода рецикла и с его использованием. Опыты проводили следующим образом: после установления стабильного гидродинамического режима в смеситель первой по ходу движения потока водной фазы ступени каскада экстракторов в момент времени τ = 0 дозатором вводили нерастворимый в органической фазе индикатор (KD = 0) одним импульсным вводом. После прохождения индикатором необходимого числа циклов, контур размыкался и в установку подавалась свежая водная фаза с расходом, равным объемной скорости циркуляции в контуре, и из последней ступени проводился отбор проб. Отбор проб производился через равные промежутки времени, изменение концентрации трассера в потоке водной фазы фиксировалось методом спектрофотометрического анализа.

На рис. 7 представлены выходные расчетный и экспериментальный концентрационные профили, полученные при использовании данного варианта аппаратурного оформления.

Рис. 7.

Выходные расчетный и экспериментальный концентрационные профили (N = 12, S = 0.63, n = 2), полученные при проведении процесса без специального трубопровода рецикла.

Расчетная кривая, приведенная на рис. 7 рассчитывалась по уравнению (3). Расчетное время выхода пиковой концентрации составило 7033 с, экспериментальное 7074 с.

На рис. 8 представлены выходные расчетный и экспериментальный концентрационные профили, полученные при проведении процесса с трубопроводом рецикла.

Рис. 8.

Выходные расчетный и экспериментальный концентрационные профили (N = 12, S = 0.62, n = 2, b = 0.033), полученные при проведении процесса с трубопроводом рецикла.

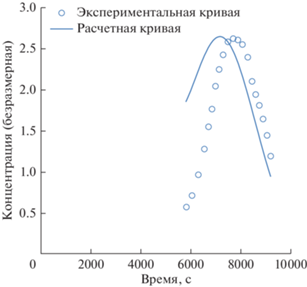
Расчетная кривая, приведенная на рис. 8 рассчитывалась по уравнению (10). Расчетное время выхода пиковой концентрации составило 7356 с, экспериментальное 7700 с.

Результаты эксперимента согласуются с расчетными результатами, полученными с использованием предложенных выше математических моделей, что подтверждает их достоверность.

ЗАКЛЮЧЕНИЕ

Проведен теоретический анализ экстракционных процессов разделения в замкнутом каскаде смесительно-отстойных экстракторов, работающих в режиме рециркуляционной хроматографии, при использовании серийного импульсного ввода раствора разделяемой смеси компонентов в каскад. Разработана математическая модель и проведен анализ периодических и непрерывных процессов экстракционного разделения в однородном (без специального трубопровода рециркуляции) и неоднородном (с трубопроводом рециркуляции) контуре, состоящем из каскада смесительно-отстойных экстракторов. Проведены эксперименты на каскаде смесительно-отстойных экстракторов в однородном и неоднородном контурах, подтверждающие достоверность разработанной модели. На ряде примеров показано, что эффективность и производительность процессов разделения существенно повышается, когда разделяемая смесь компонентов загружается в каскад в виде серии последовательных, разделенных короткими интервалами времени, импульсных вводов. Кроме того указанный метод загрузки раствора компонентов позволяет получать высококонцентрированные фракции разделенных компонентов. По сравнению с элюентным режимом работы каскада режим рециркуляционной хроматографии является экономически более выгодным: такой режим существенно повышает эффективность процессов экстракционного разделения, что позволяет значительно сократить число аппаратов в каскаде.

Исследование выполнено при финансовой поддержке РФФИ и Национального научного фонда Болгарии № 20-53-18007. Работа выполнена при финансовой поддержке Минобрнауки России в рамках государственного задания ИОНХ РАН.

Список литературы

  1. Kostanyan A.E., Milevsky N.A., Voshkin A.A. Analysis of the Processes of Extraction–Chromatographic Separation in a Cascade of Mixing–Settling Extractors. Theor Found Chem Eng 55, 862–869 (2021). https://doi.org/10.1134/S0040579521050249

  2. Kostanyan A.E., Ivanov V.K., Voshkin A.A. Theoretical Analysis of Periodic Processes of Extraction-Chromatographic Separation in a Closed Cascade of Apparatuses. Dokl Chem 499, 171–175 (2021). https://doi.org/10.1134/S0012500821080012

  3. Guilois-Dubois S., Guyot S., Poupard P. Preparative isolation of apple flavan-3-ols monomers and oligomers using pH-zone-refining centrifugal partition chromatography combined with reversed-phase liquid chromatography. J. Chromatogr. A. 2021. V. 1653. https://doi.org/10.1016/j.chroma.2021.462382

  4. Li H., Zhang F., Jin Q., Zhu T. Preparative separation and purification of Cyclosporin D from fungus Hypoxylon Spp. by improved closed-loop recycling counter-current chromatography. J. Chromatogr. A. 2021. V. 1649. https://doi.org/10.1016/j.chroma.2021.462221

  5. He J.M., Huang J., Wu W.L., Mu Q. Unlimited recycling counter-current chromatography for the preparative separation of natural products: naph- thaquinones as examples. J. Chromatogr. A. 2020. V. 1626. https://doi.org/10.1016/j.chroma.2020.461368

  6. Yuan Y., He X., Wang T., Zhang X.X., Li Z., Xu X., Zhang W., Yan X., Li S., He S. Efficient preparation of Bafilomycin A1 from marine streptomyces lohii fermentation using three-phase extraction and high-speed counter-current chromatog raphy. Mar. Drugs. 2020. V. 18. 332. https://doi.org/10.3390/md18060332

  7. Kostanyan A., Martynova M. Modeling of two semi-continuous methods in liquid–liquid chromatography: Comparing conventional and closed-loop recycling modes. J. Chromatogr. A. 2020. V. 1614. https://doi.org/10.1016/j.chroma.2019.460735

  8. Kostanyan A.E., Belova V.V. Theoretical study of industrial scale closed-loop recycling counter-current chromatography separations. J. Chromatogr. A. 2020. V. 1633. https://doi.org/10.1016/j.chroma.2020.461630

  9. Kostanyan A.E., Galieva Z.N., Semenov A.A., Aldushkin A.V. Chromatographic behavior of six lanthanides on a centrifugal mixer-settler extractor cascade. J. Chromatogr. A. 2020. V. 1634. https://doi.org/10.1021/np501065h

  10. Kostanyan A.A., Voshkin A.A., Belova V.V. Analytical, Preparative, and Industrial-Scale Separation of Substances by Methods of Countercurrent Liquid-Liquid Chromatography, Molecules. 2020. V. 25. P. 6020. https://doi.org/10.3390/molecules25246020

  11. Jerz G., Winterhalter P. The 10th International Conference on Countercurrent Chromatography held at Technische Universität Braunschweig, Braunschweig, Germany, August 1–3, 2018, J. Chromatogr. A. 2020. V. 1617. https://doi.org/10.1016/j.chroma.2019.460698

  12. Morley R., Minceva M. Operating mode and parameter selection in liquid–liquid chromatography. J. Chromatogr. A. 2020. V. 1617. https://doi.org/10.1016/j.chroma.2019.460479

  13. Roehrer S., Minceva M. Evaluation of interapparatus separation method transferability in countercurrent chromatography and centrifugal partition chromatography. Separations. 2019. V. 6. P. 36.https://doi.org/10.3390/separations6030036

  14. Wang C., Sun W., X. Wang X., Jin Y., Zhao S., Luo M., Tong S. Large-scale separation of baicalin and wogonoside from Scutellaria baicalensis Georgi by the combination of pH-zone-refining and conventional counter-current chromatography. J. Chromatogr. A. 2019. V. 1601. P. 266. https://doi.org/10.1016/j.chroma.2019.05.028

  15. Peng A., Hewitson P., Sutherland I., Chen L., Ignatova S. How changes in column geometry and packing ratio can increase sample load and throughput by a factor of fifty in counter-current chromatography. J. Chromatogr. A. 2018. V. 1580. P. 120. https://doi.org/10.1016/j.chroma.2018.10.012

  16. Friesen J.B., McAlpine J.B., Chen S.-N., Pauli G.F. The 9th International Countercurrent Chromatography Conference held at Dominican University, Chicago, USA, August 1–3, 2016, J. Chromatogr. A. 2017. V. 1520. P. 1. https://doi.org/10.1016/j.chroma.2017.08.077

  17. Ito Y. Golden rules and pitfalls in selecting optimum conditions for high-speed counter-current chromatography, J. Chromatogr. A. 2005. V. 1065. P. 145. https://doi.org/10.1016/j.chroma.2004.12.044

  18. Kostanyan A.E. Modeling of preparative closed-loop recycling liquid–liquid chromatography with specified duration of sample loading. J. Chromatogr. A. 2016. V. 1471. P. 94. https://doi.org/10.1016/j.chroma.2016.10.012

  19. Conway W.D. Counter-current chromatography: Simple process and confusing terminology. J. Chromatogr. A. 2011. V. 1218. P. 6015. https://doi.org/10.1016/j.chroma.2011.03.056

  20. Friesen J.B., Ahmed S., Pauli G.F. Qualitative and quantitative evaluation of solvent systems for countercurrent separation, J. Chromatogr. A. 2015. V. 1377. P. 55. https://doi.org/10.1016/j.chroma.2014.11.085

  21. Friesen J.B., McAlpine J.B., Chen S.-N., Pauli G.F. Countercurrent separation of natural products: An update. J. Nat. Prod. 2015. V. 78. P. 1765. https://doi.org/10.1021/np501065h

  22. Ignatova S., Sutherland I. The 8th International Conference on Counter-current Chromatography held at Brunel University. London, UK, July 23–25, 2014, J. Chromatography A. 2015. V. 1425. P. 1. https://doi.org/10.1016/j.chroma.2015.10.096

  23. Guan Y.H., Hewitson P., van den Heuvel R., Zhao Y., Siebers R.P.G., Zhuang Y.-P., Sutherland I. Scale-up protein separation on stainless steel wide bore toroidal columns in the type-J counter-current chromatography. J. Chromatography A. 2015. V. 1424. P. 102. https://doi.org/10.1016/j.chroma.2018.02.022

  24. Kostanyan A.E., Voshkin A.A., Kodin N.V. Controlled-cycle pulsed liquid–liquid chromatography. A modified version of Craig’s counter-current distribution. J. Chromatogr. A. 2011. V. 1218. № 36. P. 6135–6143. https://doi.org/10.1016/j.chroma.2010.12.103

  25. Berthod A., Maryutina T., Spivakov B., Shpigun O., Sutherland I.A. Countercurrent chromatography in analytical chemistry (IUPAC technical report). PureAppl. Chem. 2009. V. 81. P. 355.

  26. Ito Y. High-speed countercurrent chromatography. Nature. 1987. V. 326. P. 419–20.

  27. Ito Y. Origin and evolution of the coil planet centrifuge: a personal reflection of my 40 years of CCC research and development. Sep. Purif. Rev. 2005. V. 34. P. 131–54.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал